A Machine Learning-based Course Enrollment Recommender System
Xiwei Wang
1
, Longyin Cui
2
, Muhammad Bangash
1
, Mohammad Bilal
1
,
Luis Rosales
1
and Wali Chaudhry
1
1
Department of Computer Science, Northeastern Illinois University, Chicago IL, U.S.A.
2
Department of Computer Science, University of Kentucky, Lexington KY, U.S.A.
Keywords:
Course Enrollment, Recommender System, Matrix Factorization, Contextual Information.
Abstract:
As an integral component of human society, higher education has been undergoing a transformation in multiple
aspects, such as administrative reorganization, pedagogical reform, and technological innovation. To line up
with the latest trends, many institutions constantly update their curriculum, which poses challenges to students
and their advisors. This paper proposes a machine learning-based course enrollment recommender system
that aims to make personalized suggestions to students who expect to take classes in the upcoming semester.
Using matrix factorization as the core algorithm, the model exploits several available types of information,
including student course enrollment history and other contextual features, such as prerequisite restrictions,
course meeting times, instructional methods, and course instructors. The system not only helps students but
also facilitates their advisors’ work. Our experimental results show that the recommended courses were highly
relevant while providing plenty of options to students.
1 INTRODUCTION
Over the past decades, higher education has evolved
considerably to serve students better and enhance
their academic success. This includes structural re-
organization (de Boer et al., 2017), adopting new in-
structional technologies (Garrison and Akyol, 2009;
Aldowah et al., 2017), updating curriculum, etc. Us-
ing computer science as an example, due to the na-
ture of this discipline, the curriculum is constantly up-
dated at many universities to align with the state-of-
the-art technologies in the field. With more courses
proposed and prerequisite restrictions changed, stu-
dents can often feel overwhelmed by the abundance
of information. To help them decide which classes
to take, one or more program advisors are set up to
address their common questions. Based on students’
current knowledge and the courses they have com-
pleted, suggestions and recommendations are made
so that the sequence of the courses can match their
individual goals and interests while fulfilling the de-
gree requirements.
In this model, once the course registration win-
dow is open, there can be a large number of student
inquiries about their progress and the courses they
should take, which can easily overwhelm the advi-
sors. Meanwhile, when meeting with students, an
advisor needs to profile them by understanding their
preferences, e.g., favorite instructors, meeting times,
course delivery methods (online, hybrid, and face-
to-face), and reviewing their already passed courses.
There are a few potential challenges in this process:
(1) talking to each student and trying to profile the
individual from scratch is time-consuming; and (2)
many students are not prepared before they meet the
advisors, meaning that they do not have any courses
in mind and usually need multiple meetings with the
advisors before they can make their final selection.
A recommender system that can automatically profile
students based on their registration history and pro-
vide personalized course enrollment suggestions for
the upcoming semester will be beneficial for both stu-
dents and advisors. For advisors, because the sys-
tem allows them to view student preferences easily
and intuitively, their work will become more efficient
which enables them to serve students better. For stu-
dents, the system makes recommendations based on
their previously passed courses and their favorite in-
structors, campuses, meeting times, and more. It pro-
vides the students with helpful information and pre-
pares them before meeting with advisors. In some
cases, such meetings may become unnecessary.
As a constituent component of many online ser-
vices, e.g., e-commerce (Amazon, eBay), video
436
Wang, X., Cui, L., Bangash, M., Bilal, M., Rosales, L. and Chaudhry, W.
A Machine Learning-based Course Enrollment Recommender System.
DOI: 10.5220/0011109100003182
In Proceedings of the 14th International Conference on Computer Supported Education (CSEDU 2022) - Volume 1, pages 436-443
ISBN: 978-989-758-562-3; ISSN: 2184-5026
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

streaming (Netflix, YouTube), and social media
(Facebook, Tiktok), recommender systems (Ricci
et al., 2011) aim to learn the preferences of their users
based on their past behaviors (e.g., purchase records,
browsing history) and make personalized suggestions
on various types of items such as movies, products,
news, friends, and others. Recommender systems sig-
nificantly improve user experience and help them es-
cape from information overload. With such systems,
people can easily find content tailored to their inter-
ests and save considerable time.
As we digitize higher education, recommender
systems have gained increasing popularity in this field
since early 2000. One of the applications is to make
automated course suggestions to students looking to
register for courses in the upcoming semester. Al-
Badarenah et al. (Al-Badarenah and Alsakran, 2016)
proposed a course recommendation system that rec-
ommends elective courses with expected grades to
students based on other similar students. The authors
believed that students could get an acceptable grade
by taking the recommended courses. When identify-
ing similar students, their proposed method utilized
data mining techniques, such as association rule min-
ing, to find student clusters based on their commonly
taken courses and grades. (Byd
ˇ
zovsk
´
a, 2016) pro-
posed a more comprehensive recommender system
that took into account several factors, such as most
selected courses, courses enrolled by similar students,
courses taught by most popular teachers, and courses
enrolled by friends (identified by discussion forums
activities, explicit friendship, co-authoring publica-
tions, and other contextual information). The sys-
tem was designed to remind students of their duties,
warn them against challenging courses, and recom-
mend potentially beneficial courses. They tested a pi-
lot version of the recommender system at their univer-
sity, and they believed that it would become part of the
university information system in the future. On top
of these researches, there are other proposed frame-
works for course recommender systems using collab-
orative filtering (O’Mahony and Smyth, 2007), data
mining (Bendakir and A¨ımeur, 2006; Sac
´
ın et al.,
2011), and machine learning (Tomczak, 2010; Khalid
et al., 2021) techniques.
This paper proposes a machine learning-based
course enrollment recommender system that aims to
make personalized suggestions to students looking
to register for courses in the upcoming semester. It
utilizes several types of information to make per-
sonalized recommendations: student course enroll-
ment history, prerequisite restrictions, course meeting
times (morning, afternoon, and night), instructional
methods (face to face, online, and hybrid), course
instructors, and more. The framework uses matrix
factorization methods (Lee and Seung, 2001) to ex-
plore critical latent features of students and courses
from these data. Recommendations to each student
are made based on their course enrollment history and
personal preferences.
The remainder of this paper is organized as fol-
lows. Section 2 gives the related work, Section 3 de-
scribes the main idea of the proposed approach, and
Section 4 presents the experiments and discusses the
results. Some concluding remarks are given in 5.
2 RELATED WORK
Course recommendation has been an essential part of
student advising for a long time. Since before the
birth of computers and the internet, advisors have
been the “recommender systems” of students. An
electronic version of such a recommender system
can be traced back to year 2000 (Tang et al., 2000).
Several data mining techniques were combined to
help build a personalization algorithm. Other works
such as (Chu et al., 2003) and (Lee and Cho, 2011)
also tried different approaches to develop such rec-
ommender systems. Later, with the prosperity of
Massive Open Online Courses (MOOCs), more re-
searchers began to automate offering guidance for on-
line students to select the right course and knowledge.
For example, (Zhang et al., 2018) tried to combine
conventional course recommendation techniques with
a big data framework.
As a core building block of many online appli-
cations, recommender systems received significant
recognition and improvement, from the content-based
methods to collaborative filtering, and from utilizing
only a single type of information to various contex-
tual signals. Matrix factorization (Lee and Seung,
2001), as a foundational model in collaborative fil-
tering, is a dimensionality reduction technique that
was extensively explored in recommender system re-
search. (Koren, 2008) proposed a hybrid collaborative
filtering framework that incorporates latent features
into a neighborhood model. The approach captures
these features using matrix factorization to boost the
learning effectiveness. It was highly successful and
was later popularized by Simon Funk (Funk, 2006).
Studies on course recommender systems using this
model can be easily identified (Thanh-Nhan et al.,
2016; Nguyen et al., 2021).
Although the hybrid model proposed by Koren
gained popularity, it did not take advantage of addi-
tional information, such as contextual data associated
with the ratings or users/items. (Ma et al., 2011) pro-
A Machine Learning-based Course Enrollment Recommender System
437

Table 1: A sample dataset.
Student ID Course ID Semester Instructor ID Method Campus Meeting Time
S001 CS200 Fall 2020 I225 Online Main 11:00-12:15 MW
S001 CS205 Fall 2020 I312 Remote North 13:30-14:45 TR
S002 CS421 Spring 2021 I225 F2F South 15:45-17:00 TR
S003 CS327 Fall 2021 I182 F2F Main 10:45-12:00 MW
posed a recommender system with social regulariza-
tion. It takes into account users’ social relationships
when learning latent features to perform more com-
prehensive training. Our proposed model uses a simi-
lar idea but for course recommendations and with dif-
ferent contextual information.
3 METHODOLOGY
In a typical course enrollment system, the database
maintains the registration records for each student.
Our proposed model involves two major types of enti-
ties, students and courses. A utility matrix, R ∈ R
m×n
,
is used to represent the registration history, where
there are m students and n courses. An element r
ui
in
R indicates whether student u took course i in the past.
r
ui
= 1 means the student has already taken the course,
otherwise, r
ui
= 0. The goal is to predict whether a
student is likely to register for a course in the upcom-
ing semester.
The model proposed in this paper utilizes matrix
factorization (Koren, 2008) as the underlying method
to learn latent features for students and courses. These
features capture the most critical characteristics of the
two types of entities, which are essential for accu-
rate course recommendations. A classical and pre-
vailing matrix factorization-based collaborative filter-
ing model is shown in Eq. (1).
ˆr
ui
= µ + b
u
+ b
i
+~p
T
u
~q
i
(1)
where µ is the mean value of all observed ratings, the
scalars b
u
and b
i
are the observed deviations of user
u and item i, respectively
1
, from µ, whereas the s-
dimensional vectors ~p
u
and ~q
i
are the embeddings in
the latent space for user u and item i, respectively (s
is the rank of the embeddings). The corresponding
objective function is presented in Eq. (2).
f
MF
= min
b
u
,b
i
,~p
u
,~q
i
∑
u,i∈κ
(r
ui
− ˆr
ui
)
2
+ α(b
2
u
+ b
2
i
+ k~p
u
k
2
+ k~q
i
k
2
)
(2)
1
In this paper, user and student are used interchangeably
and the same rule applies to item and course as well.
where r
ui
is an observed rating, κ is the training set,
and α is a hyperparameter that controls the regular-
ization term to avoid overfitting. The goal is to find
b
u
and ~p
u
for each user u, as well as b
i
and ~q
i
for each
item i, so that f
MF
is minimized.
In real-world scenarios, besides the direct interac-
tion between users and items, there are usually other
types of contextual information available. For exam-
ple, social recommender systems (Ma et al., 2011;
Qian et al., 2016) exploit social networking data and
trustworthy user relationships to boost prediction ac-
curacy. Similarly, in course recommendations, on top
of student registration history, additional contextual
data are readily available, such as the course meet-
ing times and instructional methods. We consider this
information the student preferences because it shows
when a student prefers to take classes and whether
they like online, face-to-face, or hybrid courses.
In this research, we propose a course recommen-
dation model that fuses contextual information into
student course registration history to improve predic-
tion accuracy. More specifically, a user similarity ma-
trix is constructed using student preference data, and
the model uses the matrix as a constraint to guide the
learning procedure. The model uses the same predic-
tion formula as Eq. (1) but with a modified objective
function:
f
MF
U
= min
b
u
,b
i
,~p
u
,~q
i
∑
u,i∈κ
(r
ui
− ˆr
ui
)
2
+ α(b
2
u
+ b
2
i
+ k~p
u
k
2
+ k~q
i
k
2
)
+ β
∑
j∈N(u)
s
u j
(~p
u
−~p
j
)
2
(3)
where s
u j
is the similarity between user u and user j,
and N(u) is the set of similar users, a.k.a. neighbors
of u. β controls the weight of the constraint term.
The only modification that Eq. (3) made over Eq.
(2) is that the similarity between two users imposes
influence on the update of their embeddings. In other
words, if two students u and j share common pref-
erences, e.g., taking courses with the same instruc-
tors and only registering for online classes, then the
embeddings ~p
u
and ~p
j
should be close as well. In
a nutshell, contextual information brings in external
knowledge not available in the original student-course
interaction data, rendering more informed training.
CSEDU 2022 - 14th International Conference on Computer Supported Education
438

Student-Course
Registration Data
Contextual
Data
Stochastic Gradient Descent
Registration Rules
Predicted CoursesFinal List of
Recommended Courses
Student Deviations Course Deviations Course EmbeddingsStudent Embeddings
Predictor
Model Training
Prediction and
Filtering
Recommendation
Figure 1: The proposed model.
For each student u, we identify their similar peers
by computing the cosine similarity between u and
the rest of the students, concerning four attributes:
instructor, instructional method, meeting time, and
campus (some universities have multiple locations),
and then keep those with highest similarities. Table
1 illustrates a few sample records that include these
attributes.
When identifying similarities, we use one-hot en-
coding (Harris and Harris, 2007) to convert each at-
tribute into a binary representation, and then compute
the cosine similarities: instructor – s
i
(u, j), instruc-
tional method – s
m
(u, j), campus – s
c
(u, j), and meet-
ing time – s
t
(u, j), where u and j are any two students.
Weighted average is calculated over the four values as
the similarity between u and j:
s
u j
= w
1
s
i
(u, j) + w
2
s
m
(u, j) + w
3
s
c
(u, j)
+ (1 − w
1
− w
2
− w
3
)s
t
(u, j)
(4)
where w
1
, w
2
, and w
3
control the weight of each at-
tribute respectively.
The objective function in Eq. (3) can be optimized
by the stochastic gradient descent (SGD) method.
The corresponding update formulas are listed below:
b
u
← b
u
+ θ (e
ui
− α · b
u
)
b
i
← b
i
+ θ (e
ui
− α · b
i
)
~q
i
←~q
i
+ θ (e
ui
·~p
u
− α ·~q
i
)
~p
u
←~p
u
+ θ (e
ui
·~q
i
− (α + β
∑
j∈N(u)
s
u j
)~p
u
+ β
∑
j∈N(u)
s
u j
~p
j
)
(5)
where e
ui
= r
ui
− ˆr
ui
and θ is the learning rate. SGD
first initializes b
u
and ~p
u
for each student, and b
i
and
~q
i
for each course. Then it updates these variables
by iteratively performing the update formulas for a
specific number of epochs.
Once training is completed, the system predicts
course scores ˆr
ui
for each student based on the learned
model. A candidate course list is generated by sorting
the courses according to their predicted scores, with
the highest showing up at the top and the lowest at the
bottom. Due to the nature of the curriculum, there are
usually restrictions on course registration specific to
the program. We consider the following rules when
filtering these courses in our proposed approach:
• If a candidate course has already been taken by
the student, it should not be recommended again
unless the student failed it.
• If a candidate course has been taken by the student
but he/she failed it, then if this course is a prereq-
uisite of other courses, it should be recommended
again.
• A candidate course cannot be recommended if the
student has not taken all its prerequisites. The sys-
tem should recommend one or more prerequisites
to the student.
• In case a prerequisite course requires other
courses that have not been taken by the student
yet, the system recursively searches on the pre-
requisite path to find the course that the student is
eligible to take. For example, a candidate course
CS257 requires CS203 which requires CS117, but
the student has not taken CS117 yet - in this case,
A Machine Learning-based Course Enrollment Recommender System
439

only CS117 can be recommended, assuming that
it does not require any other courses or the student
has fulfilled the prerequisite for it.
On the final recommendation list, we prioritize
the courses that were failed by the student and need
to be retaken. To put it another way, these courses
should override the prediction scores and show up at
the top of the list. The rest of the candidate courses
will remain sorted based on their scores. Only top k
courses are recommended to each student. The com-
plete framework of the approach is illustrated in Fig-
ure 1.
4 EXPERIMENTAL STUDY
In this section, we will discuss the dataset on which
the model was tested, the evaluation strategy, and re-
sults analysis.
4.1 Dataset Preprocessing
The proposed approach was examined on a registra-
tion dataset consisting of student enrollment records
on Computer Science courses at Northeastern Illinois
University (NEIU), collected between Fall 2009 and
Spring 2021. The dataset includes 5,949 users, 67 in-
structors, 75 courses, and 37,423 registration records.
Although there are 22 attributes included, we only
used pertinent ones, such as student pseudo ID, course
ID, the course title, instructor pseudo ID, instructor
name, semester, meeting time, instructional method,
and campus.
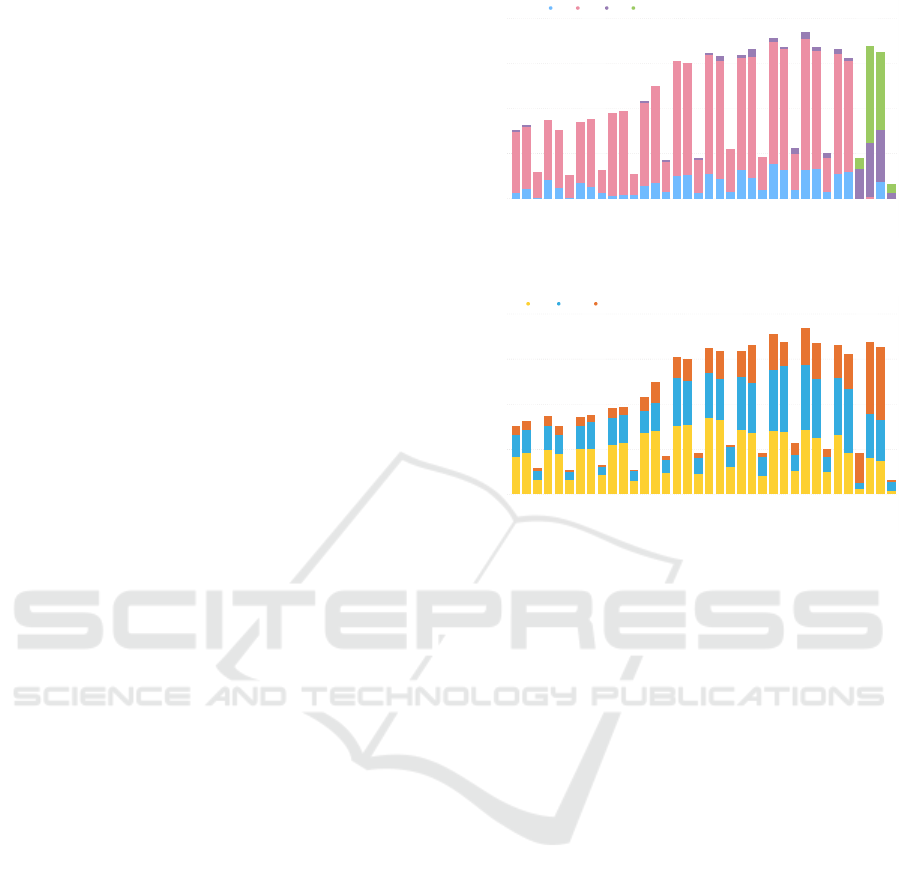
Figure 2 shows the enrollment distribution in
terms of four instructional methods: hybrid, lecture
(face-to-face), online, and remote. Due to COVID-
19, the university started offering remote learning in
Spring 2020, but it was not reflected in the record
until Summer 2020. The university also increased
online offerings significantly since Summer 2020 to
accommodate students who preferred asynchronous
learning. With regard to meeting times, because a
large portion of students who attend NEIU are non-
traditional students, many of the courses are offered
in the afternoon or evening, as depicted in Figure 3.
A careful inspection on the dataset reveals a few
observations that the data preprocessing step needs to
deal with:
1. Transfer student records were not complete - the
dataset did not include what courses they took be-
fore their transfer.
2. Some of the courses became obsolete and were no
longer offered.
0
500
1,000
1,500
2,000
Academic Semester
Enrollment
Fall 2009
Spring 2010
Summer 2010
Fall 2010
Spring 2011
Summer 2011
Fall 2011
Spring 2012
Summer 2012
Fall 2012
Spring 2013
Summer 2013
Fall 2013
Spring 2014
Summer 2014
Fall 2014
Spring 2015
Summer 2015
Fall 2015
Spring 2016
Summer 2016
Fall 2016
Spring 2017
Summer 2017
Fall 2017
Spring 2018
Summer 2018
Fall 2018
Spring 2019
Summer 2019
Fall 2019
Spring 2020
Summer 2020
Fall 2020
Spring 2021
Summer 2021
63
102
209
114
168
123
137
177
72
255
261
60
275
222
68
316
229
92
386
313
100
312
324
70
272
299
182
673
688
282
664
648
254
685
759
264
926
931
232
918
1070
330
1265
1243
370
1316
1305
477
1240
1342
365
1349
1343
394
1453
1309
384
1335
1226
84
71
76
331
600
580
61
123
1070
866
97
Instructional Method Hybrid Lecture Online Remote Learning
Figure 2: Enrollment by instructional methods.
0
500
1,000
1,500
2,000
Academic Semester
Enrollment
Fall 2009
Spring 2010
Summer 2010
Fall 2010
Spring 2011
Summer 2011
Fall 2011
Spring 2012
Summer 2012
Fall 2012
Spring 2013
Summer 2013
Fall 2013
Spring 2014
Summer 2014
Fall 2014
Spring 2015
Summer 2015
Fall 2015
Spring 2016
Summer 2016
Fall 2016
Spring 2017
Summer 2017
Fall 2017
Spring 2018
Summer 2018
Fall 2018
Spring 2019
Summer 2019
Fall 2019
Spring 2020
Summer 2020
Fall 2020
Spring 2021
Summer 2021
408
457
154
488
444
161
504
506
211
541
569
153
674
699
241
757
769
220
850
823
298
710
684
207
702
688
258
718
621
247
657
460
60
403
365
244
254
102
272
216
84
249
292
97
309
308
103
253
317
140
533
487
178
489
455
224
595
553
210
672
730
182
714
661
165
628
709
63
492
461
98
110
106
113
102
100
84
103
90
156
231
230
248
279
306
281
418
407
266
125
409
399
95
369
384
331
795
802
Meeting Time Evening Afternoon Morning
Figure 3: Enrollment by meeting times.
3. There is no indication whether a student is gradu-
ate or undergraduate.
To resolve these issues, we first removed all the
students who had no records of Programming I and
Programming II, which are the required core courses
by the Computer Science Bachelor’s degree; Then
we discarded the records before Fall 2014 to elimi-
nate obsolete courses; Last but not least, we deleted
all students who took CS400-level courses as these
are usually for graduate students. After preprocess-
ing, we split the records into two sets: a training
set with 9,618 records and a test set with 2,243
records. The test set only includes each test stu-
dent’s last semester’s records to simulate the “upcom-
ing” semester. The split procedure ensured that stu-
dents who showed up in the test set had at least two
semesters’ records because the goal of the recom-
mender system is to suggest courses that a student can
take in the upcoming semester. It uses the knowledge
learned from the training set to make predictions on
the records that are present in the test set.
4.2 Evaluation Strategy
In course recommendation research, some papers
measure prediction errors, such as RMSE (root
mean squared error) and MAE (mean absolute er-
ror) (Khalid et al., 2021; Thanh-Nhan et al., 2016),
CSEDU 2022 - 14th International Conference on Computer Supported Education
440

whereas some focus on precision and recall (Al-
Badarenah and Alsakran, 2016; O’Mahony and
Smyth, 2007; Bendakir and A¨ımeur, 2006; Salehudin
et al., 2019). The error measurements can accurately
reflect how close the predicted value is to the observed
value, so they are more suitable for precisely profiling
users, such as movie and product recommendations.
On the opposite, precision and recall are often used
to evaluate the performance of top-k recommenda-
tions where no ratings are available, e.g., in point-of-
interest recommendations, a customer might or might
not visit the recommended place.
The experiments on the proposed approach ex-
ploited both metrics to study its performance at differ-
ent stages. We recorded the RMSE during the training
process and computed the precision and recall for the
predictions. The RMSE is defined as follows:
RMSE =
s
1
|τ|
Σ
r
ui
∈τ
(ˆr
ui
− r
ui
)
2
(6)
where τ is the test set.
Although RMSE can be easily computed over the
entire test set, precision and recall in recommender
systems are computed based on each user and then
aggregated. Their definitions are presented in Eq. (7):
Precision
u
@k =
|R
u
| ∩ |T
u
|
k
Recall
u
@k =
|R
u
| ∩ |T
u
|
|T
u
|
(7)
where R
u
is the list of courses recommended to stu-
dent u and T
u
represents the courses that are actually
taken by u. | ∗ | denotes the size of a set ∗. The final
precision and recall are the sums of Precision@k and
Recall@k for all test students, respectively.
4.3 Results and Discussion
There were several hyperparameters that needed to be
set beforehand, including the weights for each con-
textual attribute when computing student similarities
(Eq. (4)), α and β that control the impacts of the regu-
larization and constraint terms, respectively (Eq. (3)),
as well as s, the targeted rank of user and course em-
beddings. Additionally, the learning rate θ (Eq. (5))
had to be determined.
For simplicity purposes, we initially set w
1
, w
2
,
and w
3
all to 0.25, which gives the same weight to all
four attributes, i.e., instructor, instructional method,
campus, and meeting time. The prediction outcome
did not present noticeable variation with different val-
ues, so we kept them as is in the rest of the experi-
ments. Table 2 lists the setup.
Table 2: Parameter setup.
w
1
w
2
w
3
α β θ
0.25 0.25 0.25 0.01 0.01 0.0002
Table 3: RMSE on test set with varying s.
s 5 10 20 30
RMSE 0.3827 0.3840 0.3853 0.3855
We began the experiment by probing s and in-
specting the training loss over epochs. Figure 4 shows
that the loss kept decreasing with more iterations of
the SGD update. It is also apparent that the variation
between different values of s is minimal, and more
latent features did not positively contribute to the re-
sult. A further test regarding RMSE on the test set
confirms this observation, as shown in Table 3. In the
subsequent evaluation procedure, we set s to 5 as it
produced relatively the lowest prediction error. Note
that we ran the update for 20 epochs in this test.
0.0
0.2
0.4
0.6
0.8
Epoch
Training Loss
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
s 5 10 20 30
Figure 4: Training loss over epochs.
Depending on the student preference, the number
of courses recommended (k) can vary. It will not af-
fect the RMSE but will significantly impact the pre-
cision and recall of the prediction. In our experiment,
we measured the outcomes produced by different ks.
Figure 5 plots the precision, recall, and F1-score for
six different ks. The highest F1-score (∼0.62) was
achieved when k = 3.
With more courses recommended to students, the
recall increases while precision moves in the oppo-
site direction. The result is reasonable as it renders a
broader range of courses for students to select from.
However, recommending too many courses does not
help them make decisions due to the lack of person-
alization. In real-world scenarios, students can deter-
mine the value of k according to their needs – some
may prefer to take only one course per semester, while
A Machine Learning-based Course Enrollment Recommender System
441

0.3
0.4
0.5
0.6
0.7
0.8
0.9
k
1 2 3 4 5 6 7 8 9 10
Precision@k Recall@k F1-score
Figure 5: Precision@k and Recall@k over k.
some may push this number to six. Figure 6 plots the
distribution of courses registered by each student per
semester over three and a half years. As mentioned
before, many students at NEIU are non-traditional
and usually keep a relatively lower and more manage-
able course load than those from more conventional
institutions. That said, without losing generality, we
set k to 6 in our next experiment, where we evaluated
how many epochs would generate the best results.
Spring 2018 Summer 2018 Fall 2018 Spring 2019 Summer 2019 Fall 2019 Spring 2020 Summer 2020 Fall 2020 Spring 2021 Summer 2021
Academic Semester
2
4
6
8
10
12
Number of Courses per Student
Figure 6: Distribution of enrollment by student.
Granted, with more epochs, the SGD method was
able to lower the training loss over time. Neverthe-
less, spending longer time does not necessarily pro-
duce better outcomes. It can be seen in Figure 7,
that all three metrics ramped up quickly in the first
few epochs and then stayed stable afterward. The
highest combination occurred when we ran the up-
date for 10 epochs, where Precision@6 = 0.5 and
Recall@6 = 0.78.
The results show that about half of the courses rec-
ommended to students were actually taken by them
and on average four courses were correctly predicted
for students who took five per semester. Although
recommending fewer courses will improve precision,
we believe that it is more beneficial to the students
when more options are offered. Figure 8 is a screen-
shot that shows the five courses recommended to a
random student in our prototype system for a partic-
0.3
0.4
0.5
0.6
0.7
0.8
Epochs
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
Precision@k Recall@k F1 Score
Figure 7: Precision@k and Recall@k over epochs.
ular semester. The lower table in this figure lists the
courses that were actually taken by the student in the
same semester. It can be seen that all three courses
that the student actually took showed up in the rec-
ommendation list, which demonstrates the high rele-
vance of the suggestions.
Figure 8: A screenshot of the recommended courses.
5 CONCLUSION
In this paper, we proposed a machine learning-based
course enrollment recommender system that aims to
make personalized suggestions to students who ex-
pect to take classes in the upcoming semester. Us-
ing matrix factorization as the core algorithm, the
model exploits several available types of informa-
tion, including student course enrollment history and
other contextual features, such as prerequisite restric-
tions, course meeting times, instructional methods,
and course instructors. A prototype system was de-
signed and implemented according to the proposed
framework. The experimental results show that when
recommending six courses to each student, the sys-
tem attained a precision of 50% and a recall of 78%,
which demonstrate a high relevance of the recommen-
dations.
CSEDU 2022 - 14th International Conference on Computer Supported Education
442

Future work would include the integration of
more contextual data, e.g., student demographics and
grades, into the model and refining it with a deep
neural network-based framework. By doing this, on
top of linear relations between the entities in the data,
more comprehensive correlations can be captured as
well, and therefore the recommendation relevance can
be further improved.
ACKNOWLEDGEMENTS
This research was supported by a Committee on Orga-
nized Research (COR) grant and a Student Center for
Science Engagement (SCSE) summer research grant
from Northeastern Illinois University.
REFERENCES
Al-Badarenah, A. and Alsakran, J. (2016). An automated
recommender system for course selection. Interna-
tional Journal of Advanced Computer Science and Ap-
plications, 7(3):166–175.
Aldowah, H., Rehman, S. U., Ghazal, S., and Umar, I. N.
(2017). Internet of things in higher education: A study
on future learning. Journal of Physics: Conference
Series, 892:1–10.
Bendakir, N. and A¨ımeur, E. (2006). Using association
rules for course recommendation. In Proceedings
of the AAAI Workshop on Educational Data Mining,
pages 31–40.
Byd
ˇ
zovsk
´
a, H. (2016). Course enrollment recommender
system. In Proceedings of the 9th International Con-
ference on Educational Data Mining, pages 312–317.
Chu, K.-K., Chang, M., and Hsia, Y.-T. (2003). Design-
ing a course recommendation system on web based on
the students’ course selection records. In EdMedia+
Innovate Learning, pages 14–21. Association for the
Advancement of Computing in Education (AACE).
de Boer, H., File, J., Huisman, J., Seeber, M., Vukasovic,
M., and Westerheijden, D. F. (2017). Structural reform
in european higher education: An introduction. Policy
Analysis of Structural Reforms in Higher Education:
Processes and Outcomes, pages 1–28.
Funk, S. (2006). Netflix update: Try this at home. https:
//sifter.org/
∼
simon/journal/20061211.html.
Garrison, D. R. and Akyol, Z. (2009). Role of instructional
technology in the transformation of higher education.
Journal of Computing in Higher Education, 21:19–30.
Harris, D. M. and Harris, S. L. (2007). Digital Design and
Computer Architecture. Amsterdam: Morgan Kauf-
mann Publishers.
Khalid, A., Lundqvist, K., Yates, A., and Ghzanfar, M. A.
(2021). Novel online recommendation algorithm for
massive open online courses (NoR-MOOCs). PLOS
ONE, 16(1):1–21.
Koren, Y. (2008). Factorization meets the neighbor-
hood: a multifaceted collaborative filtering model.
In Proceedings of the 14th International conference
on Knowledge Discovery and Data Mining (ACM
SIGKDD), pages 426–434.
Lee, D. D. and Seung, H. S. (2001). Algorithms for non-
negative matrix factorization. Advances in Neural In-
formation Processing Systems, 13:556–562.
Lee, Y. and Cho, J. (2011). An intelligent course recom-
mendation system. SmartCR, 1(1):69–84.
Ma, H., Zhou, D., Liu, C., Lyu, M. R., and King, I. (2011).
Recommender systems with social regularization. In
Proceedings of the Fourth ACM International Confer-
ence on Web Search and Data Mining, pages 287–296.
Nguyen, V. A., Nguyen, H., Nguyen, D., and Le, M. (2021).
A course recommendation model for students based
on learning outcome. Education and Information
Technologies, 26:5389–5415.
O’Mahony, M. P. and Smyth, B. (2007). A recommender
system for on-line course enrolment: An initial study.
In Proceedings of the ACM conference on Recom-
mender systems (RecSys ’07), pages 133–136.
Qian, F., Zhao, S., Tang, J., and Zhang, Y. (2016). SoRS:
Social recommendation using global rating reputation
and local rating similarity. Physica A: Statistical Me-
chanics and its Applications, 461:61–72.
Ricci, F., Rokach, L., and Shapira, B. (2011). Introduction
to recommender systems handbook. Recommender
Systems Handbook, pages 1–35.
Sac
´
ın, C. V., Chue, J., Peche, J., Alvarado, G., Vinatea,
B., Estrella, J., and Ortigosa, A. (2011). A data min-
ing approach to guide students through the enrollment
process based on academic performance. User Mod-
eling and User-Adapted Interaction, 21(1):217–248.
Salehudin, N. B., Author, H. K., Abdulgabber, M. A.,
and Al-bashiri, H. (2019). A proposed course rec-
ommender model based on collaborative filtering for
course registration. International Journal of Advanced
Computer Science and Applications, 10:162–168.
Tang, C., Lau, R. W., Li, Q., Yin, H., Li, T., and Kilis, D.
(2000). Personalized courseware construction based
on web data mining. volume 2, pages 204–211. IEEE.
Thanh-Nhan, H.-L., Nguyen, H.-H., and Thai-Nghe, N.
(2016). Methods for building course recommenda-
tion systems. In Proceedings of the 8th International
Conference on Knowledge and Systems Engineering
(KSE), pages 426–434.
Tomczak, J. S. M. (2010). Student courses recommendation
using ant colony optimization. In Proceedings of the
Second International Conference on Intelligent Infor-
mation and Database Systems, pages 124–133.
Zhang, H., Huang, T., Lv, Z., Liu, S., and Zhou, Z.
(2018). MCRS: A course recommendation system
for MOOCs. Multimedia Tools and Applications,
77(6):7051–7069.
A Machine Learning-based Course Enrollment Recommender System
443