Sea Level Rise Future Predictions: A Case Study in Crete

Antigoni Panagiotopoulou

1,*

, Lemonia Ragia

and Froso Sarri

1,2

Information Management Systems Institute, Athena Research Center, Artemidos 6, Marousi 151 25, Greece

School of Electronic and Computer Engineering, Technical University of Crete, Kounoupidiana, Chania, Greece

Keywords: Sea Level Rise, Mediterranean Coastal Database, Coastal Data Estimator, Crete Island.

Abstract: This work presents an estimation approach for coastal data with regard to climate change. Specifically,

future sea level rise (SLR) values are predicted on the basis of initial corresponding values, which are

identical to the values for the year 2025 that are provided by the Mediterranean Coastal Database (MCD).

The proposed estimator is named Coastal Data Estimator (CDE) and is used for predictions in the Crete

island, Greece. During the years from 2030 to 2100, the CDE estimation performance is evaluated against

the MCD regarding the representative concentration pathways 2.6 (RCP26), 4.5 (RCP45) and 8.5 (RCP85)

as well as the medium and high ice-sheet melting scenarios. Concerning the high ice-sheet melting scenario

in RCP26, the CDE deviates less than 10% for the years 2030-2065 and 2080-2100. In the case of RCP45,

the CDE estimator achieves predictions with deviations less than 10% from the year 2030 to the year 2080

and 2075 for medium and high scenario, correspondingly. Future work includes the CDE testing in other

Mediterranean sites. Additionally, the CDE equation could become multibranch as well as estimations

should be automized, excluding the per year constants.

Corresponding author

1 INTRODUCTION

Coastal erosion to be managed during climate

change needs valid projections of shoreline change

across large time scales i.e. decades and hundreds of

years. Nevertheless, coastal erosion modelling

presents important challenges like that the long-term

evolution of the shoreline entails interacting and

coupled short-to-long term coastal processes, also

influenced by the climate change. Besides, future

estimates of shoreline change are affected by multi-

source uncertainties (Toimil et al., 2020).

Several works on coastal erosion estimations

have appeared in the literature. A collection of

numerical models is used to assess coastal erosion

and the performance of various recommended

solutions, along a section of coast in southern Rhode

Island, US, in (Hayward et al., 2018). The study in

(Cham et al., 2020) proposes a novel method, of

utilizing multitemporal remote sensing images

during 1965-2018 and digital evaluation model with

tidal correction, to analyse the changes in shoreline

and estimate the rate of erosion and accretion in the

Cua Dai estuary, Vietnam. In the work of (Scardino

et al., 2020) a new predictive model of submersion is

developed to support coastal management in sea

level rise (SLR) conditions over the next decades up

to 2100 for the Gulf of Taranto in southern Italy.The

paper in (Toimil et al., 2020) reviews the

contemporary techniques which are used to model

climate change-induced coastal erosion.

Robust estimations penalizing outliers

(Panagiotopoulou, 2012; Panagiotopoulou, 2013;

Tukey, 1983) could prove useful for the prediction

of coastal data values. Actually, individual coastal

adaptation practitioners may have different

preferences and acceptable degrees of risk. The

particular uncertainty should be passed onto end

users and get incorporated into decision analysis

(Hinkel et al., 2019).

In the present work a novel estimation approach

for SLR is presented. Specifically, SLR values get

predicted for the future based on corresponding

present time values. The starting point of estimation,

thus present values, is equivalent to the

Mediterranean Coastal Database (MCD) provided

values for the year 2025. The proposed estimator is

called Coastal Data Estimator (CDE) and serves for

predictions in the Crete island, Greece. SLR values

that are provided by the MCD are utilized for the

166

Panagiotopoulou, A., Ragia, L. and Sarri, F.

Sea Level Rise Future Predictions: A Case Study in Crete.

DOI: 10.5220/0011112900003185

In Proceedings of the 8th International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2022), pages 166-172

ISBN: 978-989-758-571-5; ISSN: 2184-500X

evaluation of the CDE estimation performance

throughout the years from 2030 to 2100.

2 THE SEA LEVEL RISE EFFECT

GLOBALLY

Enhanced greenhouse effects on earth environment

have brought the global climate change. Thermal

expansion of sea water, resulting from temperature

increment of the ocean upper layer, is defined as the

main source of SLR (Woodworth, 2017; Shannon et

al., 2019). SLR is anticipated to have a tremendous

impact on human activity near coastal regions. In fact,

inundation of low-lying coastal areas is a direct

outcome of SLR and constitutes a long-term problem

having been under consideration in a variety of fields

(Pickering et al., 2017; IPCC, 2021).

The ocean thermal expansion and the melting of

glaciers, ice-sheets cause SLR that demonstrates a

timescale of 100–200 years, which is related to the

continuance of CO2 in the atmosphere and therefore

the radiative forcing time span. In accordance with

the model of (Jevrejeva et al., 2012), SLR of 0.57–

1.10 m by 2100 has been predicted. In effect,

simulation indicates that sea level will keep at rising

for many centuries after stabilization of radiative

forcing, finally outstretching between 1.84 and 5.48

m above sea level by 2500 concerning all scenarios,

apart from the RCP3PD low emission scenario. The

work (Hinkel et al., 2014) evaluates on a global

scale the coastal flood damage and adaptation costs

under 21

century SLR. Devoid of adaptation, it is

expected that 0.2–4.6% of the world’s population

will be flooded annually by 2100 within 25–123 cm

of a global mean SLR. Moreover, concerning coastal

sea level changes and the associated risks of

flooding and erosion, wind waves are a key factor.

The work (Melet et al., 2020) is based on empirical

formulations, different estimates of beach slopes and

an ensemble of global wave models, to propose a

first‐order estimate of the correlation significance of

the input of atmospheric climate directed wave setup

changes to 20‐year mean projected coastal sea level

changes at global scale.

Thereafter, the challenge for coastal regions

globally is the projection of SLR and its effects into

the future. The Intergovernmental Panel on Climate

Change (IPCC) is seriously concerned with the latter,

but also governments individually are simultaneously

trying to estimate future SLR projections for their

own regions. Future climate projections are attainable

through global climate models. In these models,

uncertainties and assumptions regarding future

greenhouse gas emissions (i.e., Representative

Concentration Pathways-RCPs) are contained whilst

the factors that will influence global climate,

including ice melt and consequently SLR, are

modeled (Griggs and Reguero, 2021). Nowadays, all

predictions for the next few decades, generally agree,

but projections in concern with the end-of-century

vary between models. In fact, RCPs play a substantial

role, with growingly broader uncertainties and ranges

in estimations by 2100. By the newest estimates, the

values for the end-of-century (2100) range from a low

of ~50 cm to as high as ~310 cm, independence of

greenhouse gas emission scenarios and various proba-

bilities, mainly regarding the extent of Greenland and

Antarctica ice melt (De Conto et al, 2016).

Virtually definitely, global mean sea level

(GMSL) will keep up rising over the 21st century

coming after the continued warming of the climate

system (IPCC, 2021). The SLR will carry on with

over the centuries and millennia following emissions

stopping, which is related to continuing ocean heat

growth and the slow adjustment of the ice sheets. By

2100, GMSL is projected to increase per 0.28–0.55

m under SSP1-1.9 and per 0.63–1.02 m under SSP5-

8.5 relative to the 1995–2014 average (IPCC, 2021),

where SSP represents a shared socio-economic

pathway. Concerning the scenarios of higher CO2

emissions, sea level projections for 2100 and beyond

are strongly debatable, which is linked with the ice-

sheet responses to warming. In the case of a low

probability, hard plot and a high CO2 emissions

scenario, ice-sheet processes, that are characterized

by deep unpredictability, could bring GMSL rise up

to about 5 m by 2150.

Considering the long-term commitment,

uncertainty in relation to the timetable of

outstretching different GMSL rise levels is an

important contemplation for adaptation planning.

Regional sea level changes differ from global

estimates. This happens due to alterations in ocean

density and circulation, in atmospheric pressure as

well as in Earth Gravity, in Earth Rotation and in

viscoelastic solid-Earth deformation with regards to

mass redistributions such as ice melting and

groundwater extractions (Gregory et al., 2019;

Toilim et al., 2020). In fact, SLR tends to increase at

lower latitudes and decrease at higher latitudes.

Due to the great uncertainty issues and the

complex factors that have to be considered in

simulation models, future climate projections and in

specific SLR projections, would need an alternative

way of estimating. Here lies the usability of the CDE

estimator which is proposed in the current work. The

Sea Level Rise Future Predictions: A Case Study in Crete

167

CDE estimator constitutes a novel mathematical

model for future SLR predictions. The proposed

estimator could prove useful for predicting how much

the sea level will rise, without the need for gathering

the various data of global patterns in the ocean and

atmosphere, that climate models get as input.

3 SEA LEVEL RISE PROVIDED

BY THE MEDITERRANEAN

COASTAL DATABASE

The area of interest in the present study is Crete

island in Greece. Six geographical locations in

Crete, whose the latitude and longitude coordinates

are given in Table 1, are considered. For this region,

coastal data are available through the MCD (Argus

et al., 2014; Peltier et al., 2015; Wolf et al., 2018).

Table 1: Geographical Point Coordinates in Crete island.

Location Numbe

Latitude Longitude

1 35.5296 23.9249

2 35.5145 23.9790

3 35.5162 24.0269

4 35.5296 24.0488

5 35.5193 23.8993

6 35.5357 24.0480

In particular, there are regionalized SLR

scenarios, which take into account the effects of

regional gravity and rotation due to changes in ice

mass distribution and steric changes i..e. changes

caused by ocean temperature and salinity variations.

Particularly, mean SLR relative to 1985-2005 in

meters for RCP values equal to 2.6, 4.5 and 8.5 for a

high ice-sheet melting scenario as well as for a

medium ice-sheet melting scenario are given (Hinkel

et al., 2014). The latter study provides results of

equal range as those of national studies (Molinari et

al., 2019) but a couple of uncertainties inherent to

the nature of the global socioeconomic coastal

analysis endure. Also, the study in (Hinkel et al.,

2014) mistreats the issue of groundwater depletion

for human use, which was projected to contribute up

to about 8 cm to global SLR by the end of the

century (Wada et al., 2012). Along with SLR,

potential storminess changes and possible rise in

cyclone intensity could modify flood damage

(Jevrejeva et al., 2012) but are not regarded here. An

additional primary element of uncertainty is human-

induced subsidence resulting from the withdrawal of

ground fluids, particularly within densely populated

deltas, which may lead to rates of local relative SLR

that are one order of magnitude higher than current

rates of climate-induced global-mean SLR (Syvitski

et al., 2009).

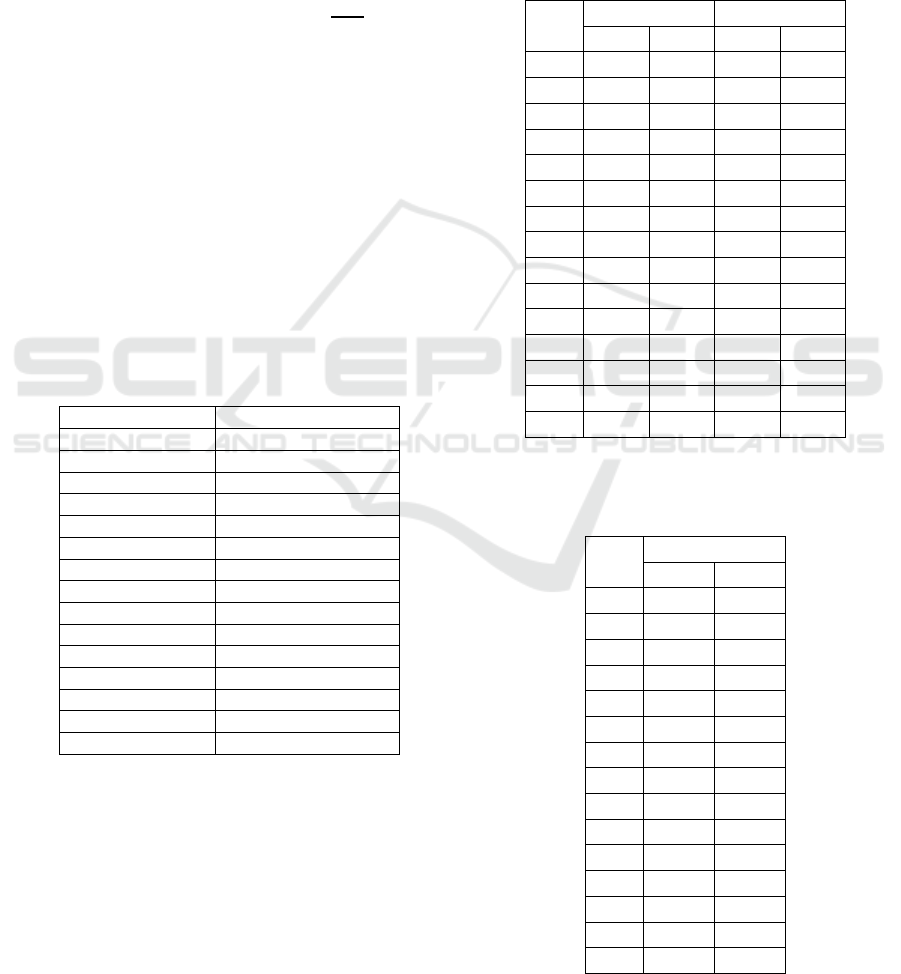
In Tables 2-3 the MCD values for the mean SLR

in meters are presented. The six geographical points

in Crete island which are described in Table 1 are

attributed approximately the same mean SLR (Wolf

et al., 2018). The SLR shows an increasing trend

throughout the years from 2025 to 2100. Also, the

high ice-sheet melting scenario values supersede

those of the medium scenario (Hinkel et al., 2014).

The aforementioned facts hold true for all three RCP

values.

Table 2: Mean Sea Level Rise in meters for representative

concentration pathways 2.6 and 4.5 (Hinkel et al., 2014).

Year RCP26 RCP45

M H

2025 0.079 0.110 0.080 0.111

2030 0.101 0.145 0.100 0.140

2035 0.121 0.174 0.119 0.168

2040 0.138 0.200 0.141 0.202

2045 0.156 0.228 0.164 0.236

2050 0.178 0.260 0.190 0.275

2055 0.197 0.288 0.218 0.317

2060 0.215 0.318 0.246 0.361

2065 0.232 0.345 0.276 0.410

2070 0.250 0.374 0.306 0.461

2075 0.267 0.402 0.337 0.510

2080 0.284 0.429 0.368 0.557

2085 0.302 0.458 0.397 0.604

2090 0.320 0.486 0.428 0.651

2095 0.338 0.513 0.457 0.698

2100 0.356 0.542 0.487 0.746

Medium scenario,

High scenario

Table 3: Mean Sea Level Rise in meters for representative

concentration pathway 8.5 (Hinkel et al., 2014).

Year RCP85

2025 0.086 0.124

2030 0.108 0.154

2035 0.134 0.190

2040 0.156 0.227

2045 0.188 0.268

2050 0.221 0.317

2055 0.255 0.371

2060 0.295 0.434

2065 0.336 0.450

2070 0.381 0.568

2075 0.426 0.639

2080 0.475 0.718

2085 0.528 0.803

2090 0.583 0.893

2095 0.638 0.988

2100 0.696 1.090

Medium scenario,

High scenario

GISTAM 2022 - 8th International Conference on Geographical Information Systems Theory, Applications and Management

168

4 THE COASTAL DATA

ESTIMATOR

In this section the proposed estimator, called CDE,

is presented. The values of mean SLR for the years

2030 to 2100 are estimated, where as starting point

or present value is taken the mean SLR value for the

year 2025 that is provided by the MCD.

The CDE mathematical formula is given in

equation (1):

𝑆𝐿𝑅



𝑆𝐿𝑅



 100  𝜎 





.





(1)

where 𝑆𝐿𝑅



stands for the mean SLR in year 𝑦 and

𝜎 denotes the standard deviation of the set of mean

SLR values in the year 𝑦.

As far as 𝑐 in equation (1) is concerned, it is a

constant relating to the year as described in Table 4.

Mean SLR values for medium and high scenario as

well as for all three RCP values are included in the

aforementioned set. For the year 2030 predictions,

the CDE utilizes the SLR values of 2025 as given by

the MCD. Regarding all other years, the CDE

estimates SLR values by taking into consideration its

own predictions five years behind.

Table 4: Constant 𝑐 values in relation to the year of

prediction.

Yea

𝑐

2030 1

2035 2.4

2040 3.8

2045 4.4

2050 5.6

2055 7.1

2060 8.6

2065 9.8

2070 11.2

2075 13.2

2080 15.1

2085 15.1

2090 15.1

2095 16.4

2100 17.6

The CDE estimations as resulting from equation

(1) are given in Tables 5-6. The % deviation

between the MCD and CDE estimations is presented

in Tables 7 and 8, where the MCD values are

considered as the groundtruth ones. With regard to

RCP26 and medium scenario, the CDE deviations

are smaller than 10% for the years 2030-2060 and

2085. Concerning the high scenario in RCP26, the

CDE deviates less than 10% for the years 2030-2065

and 2080-2100. In the case of RCP45, the CDE

estimator achieves predictions with deviations less

than 10% from the year 2030 to the year 2080 and

2075 for medium and high scenario, respectively. As

far as RCP85 is concerned, for both medium and

high scenarios, during the years 2030-2050 the CDE

deviations are smaller than 10%. This holds true

additionally for the year 2065 in the high scenario.

Table 5: Mean Sea Level Rise in meters for representative

concentration pathways 2.6 and 4.5 by the Coastal Data

Estimator.

Year RCP26 RCP45

2030 0.101 0.141 0.103 0.142

2035 0.121 0.169 0.124 0.170

2040 0.135 0.189 0.138 0.190

2045 0.157 0.220 0.161 0.222

2050 0.183 0.257 0.188 0.259

2055 0.209 0.293 0.215 0.296

2060 0.233 0.327 0.240 0.331

2065 0.260 0.365 0.268 0.370

2070 0.295 0.414 0.304 0.419

2075 0.324 0.455 0.334 0.461

2080 0.327 0.459 0.337 0.465

2085 0.330 0.463 0.340 0.469

2090 0.377 0.513 0.377 0.520

2095 0.402 0.547 0.402 0.555

2100 0.429 0.583 0.429 0.592

Medium scenario,

High scenario

Table 6: Mean Sea Level Rise in meters for representative

concentration pathway 8.5 by the Coastal Data Estimator.

Year RCP85

2030 0.110 0.159

2035 0.132 0.191

2040 0.147 0.213

2045 0.171 0.248

2050 0.199 0.289

2055 0.227 0.330

2060 0.253 0.368

2065 0.283 0.411

2070 0.321 0.466

2075 0.353 0.513

2080 0.356 0.517

2085 0.359 0.521

2090 0.398 0.577

2095 0.425 0.615

2100 0.453 0.656

Medium scenario,

High scenario

Sea Level Rise Future Predictions: A Case Study in Crete

169

With regard to all considered RCPs and the two

ice-sheet melting scenarios, the time spans of CDE

estimation deviations smaller than 10% are clearly

presented in Table 9. Also, Figure 1 plots the mean

SLR predictions of MCD and CDE that are

presented in Tables 2-3 and 5-6. The prediction

accuracy of CDE is smallest in the case of RCP85.

Table 7: Percentage deviation (%) regarding the

comparison of mean sea level rise estimations, for

representative concentration pathways 2.6 and 4.5, by the

Coastal Data Estimator to the Mediterranean Coastal

Database values. The minus symbol denotes

underestimation.

Year RCP26 RCP45

M H

2030 0 -2.8 3.0 1.4

2035 0 -2.9 4.2 1.2

2040 -2.2 -5.5 -2.1 -5.9

2045 0.6 -3.5 -1.8 -5.9

2050 2.8 -1.2 -1.1 -5.8

2055 6.1 1.7 -1.4 -6.6

2060 8.4 2.8 -2.4 -8.3

2065 12.1 5.8 -2.9 -9.8

2070 18.0 10.7 -0.7 -9.1

2075 21.3 13.2 -0.9 -9.6

2080 15.1 7.0 -8.4 -16.5

2085 9.3 1.1 -14.4 -22.3

2090 17.8 5.5 -11.9 -20.1

2095 18.9 6.6 -12.0 -20.5

2100 27.2 7.6 -11.9 -20.6

Medium scenario,

High scenario

Table 8: Percentage deviation (%) regarding the

comparison of mean sea level rise estimations, for

representative concentration pathway 8.5, by the Coastal

Data Estimator to the Mediterranean Coastal Database

values. The minus symbol denotes underestimation.

Year RCP85

2030 1.9 3.2

2035 -1.5 0.5

2040 -5.8 -6.2

2045 -9.0 -7.5

2050 -9.9 -8.8

2055 -11.0 -11.0

2060 -14.2 -15.2

2065 -15.8 -8.7

2070 -15.7 -18.0

2075 -17.1 -19.7

2080 -25.0 -28.0

2085 -32.0 -35.1

2090 -31.7 -35.4

2095 -33.4 -37.7

2100 -34.9 -39.8

Medium scenario,

High scenario

Table 9: Time spans where the percentage deviation (%),

regarding the comparison of mean sea level rise

estimations by the Coastal Data Estimator to the

Mediterranean Coastal Database values, is smaller than

10%. The three representative concentration pathways and

both ice-sheet melting scenarios are shown.

Scenario RCP26 RCP45 RCP85

Medium

2030-2060,

2085

2030-2080 2030-2050

High 2030-2065,

2080-2100

2030-2075 2030-2050,

2065

5 CONCLUSIONS

Managing coastal erosion in the process of climate

change needs valid projections of shoreline change

across very large time scales. However, coastal

erosion modelling presents significant challenges

while future estimates of shoreline change get

affected by uncertainties arising from multiple

sources. Robust estimations could prove useful for

the prediction of coastal data values, where the

prediction uncertainty may be evaluated by

individual coastal adaptation practitioners and be

passed on to end users as well as to decision

analysis.

In the present work a new estimation approach

for sea level rise is proposed. The starting point of

estimation is equivalent to the Mediterranean

Coastal Database provided values for the year 2025.

The proposed estimator is named Coastal Data

Estimator and is used for predictions in the Crete

island, Greece throughout the years from 2030 to

2100. There is calculated the % deviation between

the MCD and CDE estimations, where the MCD

values are considered as the groundtruth ones.

Concerning the high ice-sheet melting scenario in

RCP26, the CDE deviates less than 10% for the

years 2030-2065 and 2080-2100. In the case of

RCP45, the CDE estimator achieves predictions with

deviations less than 10% from the year 2030 to the

year 2080 and 2075 for medium and high scenario,

correspondingly.

The current study presents certain limitations

which need to be addressed in future work. In

specific, future work includes the CDE application

and testing in other Mediterranean sites. Also, the

CDE mathematical formula could become multi-

branch to better adapt to medium and high ice-sheet

melting scenarios and/or RCP values. Additionally,

the CDE formula automation, excluding the per year

constants, should be worked out.

GISTAM 2022 - 8th International Conference on Geographical Information Systems Theory, Applications and Management

170

ACKNOWLEDGEMENTS

This study has been financially supported by the

National R&D Project “ECITO: Effects of climate

change in the old city of Chania”,

https://ecito.athenarc.gr/, that is funded by John S.

Latsis, Public Benefit Foundation.

(a)

(b)

Figure 1: The Mediterranean Coastal Database and the

Coastal Data Estimator predictions for mean sea level rise

throughout the years up to 2100, per representative

concentration pathway (a) Medium ice-sheet melting

scenario (b) High ice-sheet melting scenario.

REFERENCES

Argus, D. F., Peltier, W. R., Drummond, R., Moore, A. W.

(2014). The Antarctica component of postglacial

rebound model ICE-6G_C (VM5a) based on GPS

positioning, exposure age dating of ice thicknesses,

and relative sea level histories. InGeophysical Journal

International, vol. 198, pp. 537–563,

https://doi.org/10.1093/gji/ggu140.

Cham, D. D., Son, N. T., Minh, N. Q., Thanh, N. T.,

Dung, T. T. (2020). An analysis of shoreline changes

using combined multitemporal remote sensing and

digital evaluation model, In Civil Engineering

Journal, vol. 6, no. 1. http://dx.doi.org/10.28991/cej-

2020-03091448

DeConto, R. M. and Pollard, D. (2020). Contribution of

Antarctica to past and future sea-level rise, In Nature,

vol. 531, pp. 591–597, https://doi.org/10.1038/

nature17145

Gregory J. M. et al. (2019). Concepts and terminology for

sea level: mean, variability and change, both local and

global, In Surveys in Geophysics, pp. 1-39,

https://doi.org/10.1007/s10712-019-09525-z

Griggs G. and Reguero B.G. (2021). Coastal adaptation to

climate change and sea-level rise, Water, vol. 13, no.

2151, https://doi.org/10.3390/w13162151

Hayward, S. et al. (2018). Numerical simulation of coastal

erosion and its mitigation by living shoreline methods:

A case study in Southern Rhode Island, In Shore &

Beach, vol. 86, no. 4, pp. 13-25.

Hinkel, J. et al. (2014). Coastal flood damage and

adaptation costs under 21st century sea-level rise.

In Proceedings of the National Academy of Sciences,

U.S.A, vol. 111, pp. 3292–3297, https://doi.org/10.10

73/pnas.1222469111.

Hinkel, J. et al. (2019). Meeting user needs for sealevel

rise information: a decision analysis perspective. In

Earth’s Future 7, https://doi.org/10.1029/2018EF00

1071

Masson-Delmotte, V. P.et al., (In Cambridge University

Press). IPCC, 2021: Summary for Policymakers, In

Climate Change 2021: The Physical Science Basis.

Contribution of Working Group I to the Sixth

Assessment Report of the Intergovernmental Panel on

Climate Change.

Jevrejeva S, Moore J, Grinsted A. (2012). Sea level

projections to ad2500 with a new generation of climate

change scenarios.In Global Planet Change,vol.80–81,

pp. 14–20.

Melet A. et al., (2020). Contribution of wave setup to

projected coastal sea level changes, In Journal of

Geophysical Research: Oceans, https://doi.org/10.10

29/2020JC016078

Molinari, D. et al., (2019). Validation of flood risk

models: current practice and possible improvements,

In International Journal of Disaster Risk Reduction,

vol. 33, pp. 441-448. https://doi.org/10.1016/j.ijdrr.20

18.10.022

Panagiotopoulou, A. (2012). Multi-frame super-resolution

image reconstruction employing the novel estimator

L1inv-norm. In Proceedings of International

Conference on Systems, Signals and Image

Processing, (IWSSIP), pp. 562-565.

Panagiotopoulou, A. (2013). Iterative multi-frame super-

resolution image reconstruction via variance-based

fidelity to the data. In International Journal of Remote

Sensing Applications, vol. 3, pp. 203-214.

Sea Level Rise Future Predictions: A Case Study in Crete

171

Peltier, W. R., Argus, D. F., Drummond, R. (2015). Space

geodesy constrains ice age terminal deglaciation: The

global ICE-6G_C(VM5a) model. In Journal of

Geophysical Research: Solid Earth, vol. 120, pp. 450–

487, https://doi.org/10.1002/2014jb011176.

Pickering M. D. et al., (2017). The impact of future sea-

level rise on the global tides, In Continental Shelf

Research, vol. 142, pp. 50-68, http://dx.doi.org/10.10

16/j.csr.2017.02.004

Scardino, G. et al., (2020). Sea-level rise and shoreline

schanges along an open sandy coast: case study of gulf

of Taranto, Italy, In Water, vol. 12, no. 1414,

doi:10.3390/w12051414

Shannon S. et al., (2019). Global glacier volume

projections under high-end climate change scenarios,

In The Cryosphere, vol. 13, pp. 325-350,

https://doi.org/10.5194/tc-13-325-2019

Syvitski, J.P.M. et al. (2009). Sinking deltas due to human

activities. In Nature Geoscience, vol. 2, pp. 681-686.

Toimil, A. et al. (2020). Climate change-driven coastal

erosion modelling in temperature sandy beaches:

Methods and uncertainty treatment. In Earth-Science

Reviews, vol. 202. https://doi.org/10.1016/j.earscirev.

2020.103110

Tukey, J.(1983).Understanding Robust and Exploratory

DataAnalysis. John Wiley and Sons. New York, USA.

Wada, Y. et al. (2012). Past and future contribution of

global groundwater depletion to sea-level rise.In

Geophyical Research Letters,vol. 39, no . 16.

Wolf, C. et al. (2018). Data Descriptor: A Mediterranean

costal database for assessing the impacts of sea-level

rise and associated hazards. In Scientific Data. DOI:

10.1038/sdata.2018.44.

Woodworth, P.L. (2017). Differences between mean tide

level and mean sea level, In Journal of Geodesy, vol.

91, pp. 69-90, https://doi.org/10.1007/s00190-016-

0938-1

GISTAM 2022 - 8th International Conference on Geographical Information Systems Theory, Applications and Management

172