Mechanism of Overﬁtting Avoidance Techniques for Training Deep

Neural Networks

Bihi Sabiri

, Bouchra El Asri

1 b

and Maryem Rhanoui

2 c

IMS Team, ADMIR Laboratory, Rabat IT Center, ENSIAS, Mohammed V University in Rabat, Morocco

Meridian Team, LYRICA Laboratory, School of Information Sciences, Rabat, Morocco

Keywords:

Data Overﬁtting, Machine Learning, Dropout, Deep Learning, Convolutional Neural Network, Max Pooling,

Early Stopping.

Abstract:

The objective of a deep learning neural network is to have a ﬁnal model that performs well both on the data

used to train it and the new data on which the model will be used to make predictions. Overﬁtting refers to

the fact that the predictive model produced by the machine learning algorithm adapts well to the training set.

In this case, the predictive model will capture the generalizable correlations and the noise produced by the

data and will be able to give very good predictions on the data of the training set, but it will predict badly on

the data that it has not yet seen during his learning phase. This paper proposes two techniques among many

others to reduce or prevent overﬁtting. Furthermore, by analyzing dynamics during training, we propose a

consensus classiﬁcation algorithm that avoids overﬁtting, we investigate the performance of these two types of

techniques in convolutional neural network. Early stopping allowing to save the hyper-parameters of a model

at the right time. And the dropout making the learning of the model harder allowing to gain up to more than

50% by decreasing the loss rate of the model.

1 INTRODUCTION

Overﬁtting is a concept in data science and a serious

problem in Deep neural networks with a large number

of parameters that are very powerfulmachine learning

systems (Hinton et al., 2012).

Deep neural networks contain multiple non-linear

hidden layers and this makes them very expressive

models that can learn very complicated relationships

between their inputs and outputs. With limited train-

ing data, however, many of these complicated rela-

tionships will be the result of sampling noise, so they

will exist in the training set but not in real test data

even if it is drawn from the same distribution. This

leads to overﬁtting and many methods have been de-

veloped for reducing it (Wu et al., 2022).

Early stopping is a method that seeks to pause

training before the model starts to overﬁt or before

learning the noise within the model(Yingbin et al.,

2021). This approach risks halting the training pro-

cess too soon, leading to the opposite problem of un-

https://orcid.org/0000-0003-4317-568X

https://orcid.org/0000-0001-8502-4623

https://orcid.org/0000-0002-0147-8466

derﬁtting. Finding the “sweet spot” between underﬁt-

ting and overﬁtting is the ultimate goal.

Dropout is another technique for addressing

this overﬁtting problem (Senen-Cerda and Sanders,

2020). Dropout is a powerful and widely used tech-

nique to regularize the training of deep neural net-

works (Xiaobo et al., 2021). The key idea is to ran-

domly drop units (along with their connections) from

the neural network during training. This prevents

units from co-adapting too much. During training,

dropout samples from an exponential number of dif-

ferent thinned networks. At test time, it is easy to

approximate the effect of averaging the predictions

of all these thinned networks by simply using a sin-

gle unthinned network that has smaller weights. This

signiﬁcantly reduces overﬁtting and gives major im-

provements over other regularization methods.

But how is it possible to add malfunctions in the

learning of our machines to allow them to be more

efﬁcient ?

In general, making errors in a program prevents

the program from functioning well but strangely if we

program a neural network then it is indeed desirable

to artiﬁcially create random bugs including the func-

tioning of the neurons of the network.

418

Sabiri, B., El Asri, B. and Rhanoui, M.

Mechanism of Overﬁtting Avoidance Techniques for Training Deep Neural Networks.

DOI: 10.5220/0011114900003179

In Proceedings of the 24th International Conference on Enterprise Information Systems (ICEIS 2022) - Volume 1, pages 418-427

ISBN: 978-989-758-569-2; ISSN: 2184-4992

Well, to combat overﬁtting, we could simply seek to

have more training data, but suppose that we only

have access to the data that has been collected for us

and there, instead of seeking to collect more data, we

could try to create data from those that we typically

have if we want to learn to recognize cats from a car

image we can slightly rotate the zoom out of the zoom

small changes in the white balance or make a mirror

image of the photo in order to obtain new data which

we can still reasonably think of as images of cars, we

then speak of an increase in data or data augmenta-

tion.

In this article, we will take a closer look at

two techniques for addressing the overﬁtting problem

ealy-stopping and dropout. The rest of this paper is

organized as follows. In Section 2 we brieﬂy compare

and position our solution with other proposals ﬁnd in

the literature. Section 3 describes the problem han-

dled. In Section 4, we describe our proposed method

that can be potentially applied to convolutional neu-

ral network. Section 5 describes the Dropout Neu-

ral Network Model. Finally, we carry out extensive

experiments with standard datasets and different net-

work architectures to validate the effectiveness

2 STATE-OF-THE-ART

Without any attempt at being exhaustive, here we

point out a few connections between dropout and pre-

vious literature (Shaeke and Xiuwen, 2019) (Senen-

Cerda and Sanders, 2020) :

Sochastic Gradient Descent Method: The ﬁrst de-

scription of a dropout algorithm was in (Hinton et al.,

2012) as an effective heuristic for algorithmic regu-

larization. The authors used the standard stochastic

gradi- ent descent procedure to train neuronal stall

networks on mini-batches of training cases, but they

modiﬁed the penalty term which was normally used to

keep weights from getting too big. At the time of the

test, they used the ”average network” which contains

all units hidden but with their the outgoing weights

have been halved to compensate for the fact that twice

as many of them are active. In practice, this gives very

similar performance to the average over a large num-

ber of dropout networks.

Regularized Dropout for Neural Networks: R-drop

is a simple yet very effective regularization method

built upon dropout, by minimizing the bidirectional

KL-divergence of the output distributions of any pair

of sub models sampled from dropout in model train-

ing (Liang et al., 2021). Concretely, in each mini-

batch training, each data sample goes through the for-

ward pass twice, and each pass is processed by a dif-

ferent sub model by randomly dropping out some hid-

den units. R-Drop forces the two distributions for the

same data sample outputted by the two sub models to

be consistent with each other, through minimizing the

bidirectional Kullback-Leibler (KL) divergence be-

tween the two distributions (Liang et al., 2021).

Implicit and Explicit Regularization. In a recent

work, (Wei et al., 2020) disentangle the explicit and

implicit regularization effects of dropout; i.e. the reg-

ularization due to the expected bias that is induced

by dropout, versus the regularization induced by the

noise due to the randomnessin dropout. They propose

an approximation of the explicit regularizer for deep

neural networks and show it to be effective in prac-

tice. Their generalization bounds, however, are lim-

ited to linear models and require weights to be norm

bounded (Arora et al., 2020).

3 PROBLEM DESCRIPTION

Overﬁtting is a concept in data science, which oc-

curs when a statistical model ﬁts exactly against its

training data, but badly in the test set. When this

happens, the algorithm unfortunately cannot perform

accurately against unseen data, defeating its purpose

(IBM

Cloud Education, 2021). When machine learn-

ing algorithms are con- structed, they leverage a sam-

ple dataset to train the model. However, when the

model trains for too long on sample data or when the

model is too complex, it can start to learn the “noise,”

or irrelevant informa- tion, within the dataset. When

the model memorizes the noise and ﬁts too closely

to the training set, the model becomes “overﬁtted,”

and it is unable to gen- eralize well to new data. If

a model cannot generalize well to new data, then it

will not be able to perform the classiﬁcation or pre-

diction tasks that it was intended for. Low error rates

and a high variance are good in- dicators of overﬁt-

ting. In order to prevent this type of behavior, part of

the training dataset is typically set aside as the “test

set” to check for overﬁtting. If the training data has a

low error rate and the test data has a high error rate, it

signals overﬁtting. There are too many feature dimen-

sions, model assumptions, and parameters, too much

noise, but very few training data. As a result, the ﬁt-

ting function perfectly predicts the training set, while

the prediction result of the test set of new data is poor.

4 HOW TO AVOID OVERFITTING

Much has been written about overﬁtting and the

bias/variance tradeoff in neural nets and other ma-

Mechanism of Overﬁtting Avoidance Techniques for Training Deep Neural Networks

419

chine learning models (Brownlee, 2018).

4.1 Early Stopping

Early termination is the default option for overﬁtting

prevention in ML programs. When premature termi-

nation is enabled, the loss of excluded data is mon-

itored during training, and it is terminated when the

loss improvement in the last iteration falls below a

given threshold. Since the excluded data is not used

during training, it represents a good estimate of model

loss on the new data. The behavior of the early stop-

ping is controled by the activation of early

stop option

(Maren et al., 2017).

There are three elements to using early stopping,

they are :

4.2 Training Model over a Predeﬁned

Number of Epochs

This method is a simple method but risks stopping

the training early before reaching a satisfactory train-

ing point. With a higher learning rate, the model

could eventually converge with fewer epochs, but this

method requires a lot of trial and error. Due to ad-

vances in machine learning, this method is quite ob-

solete.

4.3 Stop When the Loss Function

Update Becomes Small

This approach is more sophisticated than the ﬁrst be-

cause it relies on the fact that the gradient descent

weight updates become signiﬁcantly smaller as the

model gets closer to the minima. Usually, the drive is

stopped when the update becomes as small as 0.001,

because stopping at this point minimizes loss and

saves computing power by preventing unnecessary

epochs. However, overﬁtting can still occur.

4.4 Overall Validation Strategy

This smart technique is the most popular early stop-

ping approach (see Figure 2) (Caruana et al., 2001).

To understand how this works, it is important to look

at how the training and validation errors change with

the number of epochs (as in Figure 2). The learn-

ing error decreases exponentially until the increasing

epochs no longer have such a large effect on the error.

The validation error, however, initially decreases with

increasing epochs, but after a certain point it begins

to increase. This is the point where a model should

be stopped early because beyond that the model will

start to overﬁt.

While the validation set strategy is the best in

terms of preventing overﬁtting, it usually takes a large

number of epochs before a model starts to overﬁt,

which can cost a lot of computing power. A smart way

to get the best of both worlds is to design a hybrid ap-

proach between the commit set strategy and then stop

when the loss function update gets small. For exam-

ple, training may stop when either is achieved.

4.5 Dropout

Dropout is a regularization technique for neural net-

works that drops a unit (along with connections) at

training time with a speciﬁed probability. Dropout

changed the concept of learning all the weights to-

gether to learning a fraction of the weights in the net-

work in each training iteration (Moolayil, 2019). It

signiﬁcantly improve the performance of deep neu-

ral networks on various tasks (Hinton et al., 2012),

including vision problems (Krizhevsky et al., 2017)

and randomly sets hidden Unit activities to zero with

a probability of 0.5 during training. In Figure 1:

Left(a):All neurons are used during training of a

model. Right(b) : Dropout a simple way to prevent

neural networks from overﬁtting, When p = 0.5, each

neuron has a 50 in 100 chances of being turned off in

training.

(a) Full network (b) Network with Dropout.

Figure 1.

This issue resolved the overﬁtting issue in large

networks. And suddenly bigger and more accurate

Deep Learning architectures became possible (LeCun

et al., 2015).

Before Dropout, a major research area was regu-

larization. Introduction of regularization methods in

neural networks, such as L1 and L2 weight penal-

ties, started from the early 2000s (Bengio et al.,

2007). However, these regularizations did not com-

pletely solve the overﬁtting issue. The reason was

Co-adaptation.

ICEIS 2022 - 24th International Conference on Enterprise Information Systems

420

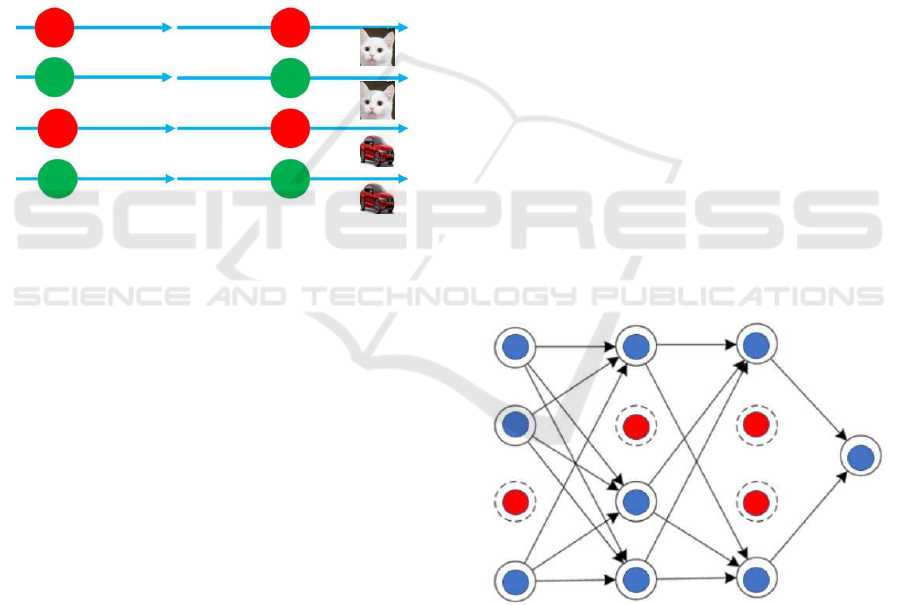
4.6 Co-adaptation in Neural Network

One major issue causing overﬁtting in learning large

networks is co-adaptation. So, in neural network, co-

adaptation means that some neurons are highly depen-

dent on others. If those independent neurons receive

“bad” inputs, then the dependent neurons can be af-

fected as well, and ultimately it can signiﬁcantly al-

ter the model performance, which is what might hap-

pen with overﬁtting. In such a network, if all the

weights are learned together it is common that some

of the connections will have more predictive capabil-

ity than the others. In such a scenario, as the net-

work is trained iteratively these powerful connections

are learned more while the weaker ones are ignored.

Over many iterations, only a fraction of the node con-

nections is trained. And the rest stop participating.

Figure 2: Co-adaptation of node connections.

In ﬁgure 2, the red circles are neurons that are

independent on others, the green one are the neu-

rons that are highly dependant on others. This phe-

nomenon is called co-adaptation. This could not be

prevented with the traditional regularization, like the

L1 and L2 (Ng, 2004). The reason is they also reg-

ularize based on the predictive capability of the con-

nections. Due to this, they become close to determin-

istic in choosing and rejecting weights. And, thus

again, the strong gets stronger and the weak gets

weaker. A major fallout of this was: expanding the

neural network size would not help. Consequently,

neural networks’ size and, thus, accuracybecame lim-

ited. Then came Dropout. A new regularization ap-

proach. It resolved the co-adaptation. Now, we could

build deeper and wider networks. And use the pre-

diction power of all of it. With this background, let’s

dive into the Mathematics of Dropout.

Model combination always improves the perfor-

mance of machine learning methods. With large neu-

ral networks, however, the obvious idea of averaging

the outputs of many separately trained nets is pro-

hibitively expensive. Combining several models is

most helpful when the individual models are different

from each other and in order to make neural net mod-

els different, they should either have different archi-

tectures or be trained on different data. Training many

different architectures is hard because ﬁnding optimal

hyperparameters for each architecture is a daunting

task and training each large network requires a lot of

computation. Moreover, large networks normally re-

quire large amounts of training data and there may not

be enough data availableto train differentnetworks on

different subsets of the data. Even if one was able to

train many different large networks, using them all at

test time is infeasible in applications where it is im-

portant to respond quickly.

Dropout is a technique that addresses both these

issues. It prevents overﬁtting and provides a way of

approximately combining exponentially many differ-

ent neural network architectures efﬁciently. The term

“dropout” refers to dropping out units (hidden and

visible) in a neural network. By dropping a unit out,

we mean temporarily removing it from the network,

along with all its incoming and outgoing connections,

as shown in Figure 1. The choice of which units to

drop is random.

In the simplest case, each unit is retained with a

ﬁxed probability p independent of other units, where

p can be chosen using a validation set or can simply

be set at 0:5, which seems to be close to optimal for

a wide range of networks and tasks. For the input

units, however, the optimal probability of retention is

usually closer to 1 than to 0:5. ( The mathematical

aspect of the choice of these values will be treated

below in section 5)

Figure 3: Partial learning with random choice of inactive

neurons : color red are the neurons that are not used during

training.

This very simple technique which is dropout

which consists quite simply in programming the tem-

porary vulnerability of artiﬁcial neurons is in fact a

formidably effective technique to ﬁght against over-

interpretation. Since it makes it possible both to

ﬁght against the lack of learning data against errors

in learning data and against learning a single model

Mechanism of Overﬁtting Avoidance Techniques for Training Deep Neural Networks

421

rather than learning a whole forest in short, neural

balls are in fact very intelligent errors.

The Initialization Process, through the idea of

multi start, amounts to starting with several initial

neural networks whose initialization is random and

we can keep the best of our neural networks during

learning or perhaps even better.

5 DROPOUT NEURAL

NETWORK MODEL

This section describes the dropweak neural network

model (Srivastava N et al., 2014). Consider a neural

network with L hidden layers.

Let l ∈ {1, 2, . . . . . . L}

indexes the hidden layers of the network (Srivastava

N et al., 2014). Let z

denote the vector of inputs into

layer l, y

denote the vector of outputs from layer l (y

is the input vector of the neural network). W

and b

are the weights and biases at layer l. The feed-forward

operation of a standard neural network (Figure 4a) can

be described as

( for l ∈ {0, 1, 2, . . . . . . L− 1}

and any hidden unit i)

The training phase of the standard network with-

out dropout can be represented mathematically as:

l+1

= W

l+1

∗Y

+ b

l+1

= f(z

l+1

)

where f is any activation function, for example

sigmoid function , f(x) =

1+e

−x

The dot product of the weights w

l+1

and the

input(y

) are added to a bias term(b

l+1

) and passed

through an activation function(f), to introduce non-

linearity to give the output y

l+1

, which is the predic-

tion, meaning all the neurons are involved in the mak-

ing of a decision.

During dropout, the training is updated to be-

come: (Figure 4b)

= Bernoulli(p)

ˆy

= r

× y

l+1

= w

l+1

haty

+ b

l+1

= f(z

l+1

)

The training is very similar to the standard net-

work, but a new term r which is a new neuron, is in-

troduced, which keeps the neuron active or turns it off,

by assigning a 1 ( neuron participates in the training)

or 0 (neuron does not participate or is turned off), then

the training process continues. This way, overﬁtting

(a) Full network (b) Dropout network.

Figure 4: Comparison of the basic operations of a standard

and dropout network.

is reduced and our model can now make excellent and

accurate predictions on real-world data (data not seen

by the model). At test time, the weights are scaled

as W(l)test = pW(l). The resulting neural network is

used without dropout.

6 EXPERIMENTAL SETUP AND

RESULTS

In this section, ﬁrst, we conﬁrm empirically that

hyper-parameters provide characterizations after a

certain number of iterations. In early stopping regu-

larization, we stop training the model when the per-

formance of the model on the validation set starts

to deteriorate, which decreases accuracy or increases

loss.

6.1 Experimental Results with

Stop-early

By plotting the error on the training dataset and the

validation dataset together, the errors decrease with a

number of iterations until the point where the model

begins to overﬁt. After this point, the validation er-

ror increases, but the training error still decreases.

So even though training continues after this point,

stopping early essentially returns the set of parame-

ters that have been used at this point and is therefore

equivalent to stopping training at this point. Thus, the

ﬁnal parameters returned will allow the model to have

better generalization and low variance.

The model at the time when the training is stopped

will have a better generalization performance than the

model with the least training error. Early cessation

can be considered implicit regularization, unlike reg-

ularization through weight loss. This method is also

efﬁcient because it requires less training data, which

is not always available. Because of this, early quitting

requires less training time compared to other regular-

ization methods. Repeating the early stopping process

ICEIS 2022 - 24th International Conference on Enterprise Information Systems

422

multiple times can lead to overﬁtting of the model to

the validation dataset, just as overﬁtting occurs in the

case of training data. The number of iterations taken

to train the model can be thought of as a hyperparam-

eter. Then the model must ﬁnd an optimal value for

this hyperparameter for the best performance of the

training model.

Early stopping is a regularization technique for

deep neural networks that stops training when pa-

rameter updates bring no improvement over a valida-

tion set. Therefore, we store and update the current

best parameters during training, and when parameter

updates no longer produce improvement (after a set

number of iterations), we stop training and use the

latest best settings. It works as a regularizer by limit-

ing the optimization procedure to a smaller volume of

parameter space.

From the plot bellow (Figure 5) we can see that

without Early Stopping (Caruana et al., 2001) the

model continues to diverge after the optimal point

where the two errors are equal and if the process does

not stop the performance of the model will be further

degraded

Figure 5: Loss & Early Stopping checkpoint.

At this point the performance of the model is opti-

mal. EarlyStopping needs the validation loss to check

if it has decreased, and in this case it will make a

checkpoint of the current model

6.2 Experimental Results with Dropout

Experiments are conducted on three datasets :

MNIST (Etzold, 2022) , SONAR (Brownlee et al.,

2017) and Diabetes (Larxel, 2021).

In order to test the robustness of dropout, classiﬁ-

cation experiments were done with networks of many

different architectures keeping all hyperparameters,

including p ﬁxed. Figure 9a and 9b shows the test er-

ror rates obtained for these different architectures as

training progresses. The same architectures trained

with and without dropout have drastically different

test errors as seen as by the two separate clusters of

trajectories.

Dropout gives a huge improvement across all ar-

chitectures, without using hyperparameters that were

tuned speciﬁcally for each architecture. The algo-

rithm tested with some classiﬁcation datasets gives

the results as indicated in Figure 6a and 9b : It illus-

trates accuracy and loss without Dropout on the left

and with Dropout on the right): The model is formed

of is formed of 7 hidden layers alternated by 6 dropout

layers with a percentage of 50%, i.e. p = 0.5, each

neuron has a chance in 2 to be deactivated. At each

epoch, this random deactivation is applied. That is,

with each pass (forward propagation) the model will

learn with a conﬁguration of different neurons, the

neurons activating and deactivating randomly. This

procedure effectively generates slightly different pat-

terns with different neural conﬁgurations at each iter-

ation. The idea is to disrupt the characteristics learned

by the model.

Usually, model learning is based on the syn-

chronicity of neurons... with dropout, the model must

exploit each neuron individually, its neighbors can be

randomly disabled at any time. The Dropout is ac-

tive only during model training. In tests, each neuron

remains active and its weight is multiplied by proba-

bility p. With Keras & Tensorﬂow it is enough to add

a dropout layer is to indicate the desired probability

of deactivation.

It is true that dropout hinders performance, in

some way, since it suppresses neuron activations dur-

ing training. However, dropout is highly useful as a

regularization technique - since any one neuron has

a decent change of being ignored during one for-

ward pass, the neural network cannot rely strongly

on any one neuron. This has the effect of prevent-

ing overﬁtting and helping the neural network gener-

alize to examples it has never seen before, since it be-

comes harder to simply memorize training data with

this added suppression. This means that performance

is improved during inference/validation even if per-

formance during training is reduced. After training

is completed, however, dropout is generally removed

when the neural net is used for prediction.

According to the curve of the accuracy and that of

the loss of the Figure 6a, we can see that the predictive

model produced by the automatic learning algorithm

adapts well to the Training Set in the event of non-use

of dropout, which justiﬁes an overﬁtting, because the

training data has a low error rate and a high accuracy.

while this adaptation is less remarkable when using

Mechanism of Overﬁtting Avoidance Techniques for Training Deep Neural Networks

423

(a) Without Dropout. (b) With Dropout.

Figure 6: Dropout slows down everﬁtting.

dropout.

Another example with different dataset (dia-

betes.csv, 2021) gives the results bellow [Figure 7a

and b]:

(a) Without Dropout. (b) With Dropout.

Figure 7: By using dropout layer test accuracy increased

from 0.75 to 0.81 while loss decreased from 81% to 45%.

In this example, unlike the previous case, we

represent the evolution of the precision for the test

sample with or without dropout and we see that if

the dropout is not used, the loss of test dataset in-

creases constantly ( 81% at iteration 100) whereas

with dropout it stabilizes around 45% at the same it-

eration. As for the accuracy of the test sample, it is

75% without dropout and 81% with dropout

In this third example, experiments are conducted

on MNIST which consists of 28x28pixel images with

1 channel. We use rectiﬁed linear function (Cerisara

et al., 2021) for dense layer and Maxpooling for con-

volutional and fully-connected layers, and softmax

activation function for the output layer.

The CNN (Iraji et al., 2021) architecture for

MNIST is 1x28x28, which represents a CNN with 1

input image of size 28x28, a convolutional layer with

6 feature maps and 5x5 ﬁlters, a pooling layer with

pooling region 2x2, a convolutional layer with 16 fea-

ture maps and 5x5 ﬁlters, a pooling layer with pool-

ing region 2x2, a fully-connected layer with 1000 hid-

den units, and an output layer with 10 units (one per

class).

We represent the evolution of the precision and the

loss for the training and test sample with or without

dropoutand we note that in the case where the dropout

is not used the accuracies of the dataset of training and

test diverge (Figure8), the same is true for the losses

of the 2 datasets which shows an overﬁtting, while

with dropout the accuracies and the losses converge

after ten iterations.

In this example, each hidden unit is randomly

omitted from the network with a probability of p ∈

[0.2, 0.5], so a hidden unit cannot rely on other hidden

units being present.

In the other example, the dropout technique con-

sists of to zero the output of each hidden neuron

with probabilities 0.25 on the ﬁrst two layers, 0.5 on

the third and 0.25 on the last. The neurons that are

”dropped” in this way does not contribute to forward

passage and does not participate in backpropagation.

This way, each time an input is presented, the neu-

ral network samples a different architecture. Because

a neuron cannot count on the presence of other spe-

ciﬁc neurons. It is therefore forced to learn more ro-

bust features that are useful in conjunction with many

different random subsets of other neurons, which re-

duces co-adaptations of neurons. During the test, we

use all the neurons by multiplying their outputs by

the coefﬁcients indicated above which is a reasonable

approximation for taking the geometric mean of the

predictivedistributions producedby the many dropout

networks.

From the ﬁgure 8 above (upper part), we can see

that the accuracy of the validation has almost become

stagnant after a few epochs. The accuracy grows lin-

early at the beginning and stagnates rapidly thereafter.

As for the loss of validation, the ﬁgure 8 (lower

part) shows that it decreases linearly at the beginning

to increase after a few epochs, which shows that it is

a sign of overﬁtting.

In this case, it is advisable to introduce some

dropoutin our model and see if that helps reduce over-

ﬁtting.

Using the dropout, we can see that validation loss

and validation accuracy are both synchronized with

training loss and training accuracy , see Figure9. The

gap between the training and the validation accuracy

is very small, even if the validation loss and the accu-

racy line are not linear, it shows that the model is not

overﬁtting and the validation loss decreases when the

ICEIS 2022 - 24th International Conference on Enterprise Information Systems

424

Figure 8: Full Network: Accuracy & Loss.

Figure 9: Dropout Network : Accuracy & Loss.

activation of the dropout.

As a result, we can conclude that the model’s gen-

eralization capability became much better since the

loss on the validation set was only slightly higher

compared to the training loss.

Another example for classiﬁcation based on of

dataset (Dogs vs. Cats) (M.Sarvazyan, 2022), we will

investigate the performance of Full network on simu-

lated data, and compare it to standard dropout.

Figure 10: Full Network: Accuracy & Loss.

The gap between training accuracy and validation

accuracy is very high showing that the model is over-

ﬁtting (see ﬁgure 10). Training accuracy approaches

1 and training loss approaches 0. Thus, the model

perfectly ﬁts the training set, which is a sign of over-

ﬁtting.

Using the dropout technique (ﬁgure 11), although

the model is not totally stable, we can see that the the

gap between trainning accuracy and validation con-

verge slowly and the gap between training and valida-

tion loss is smaller. Actually, the difference between

these two curves is small enough to consider that the

model is not overﬁtting anymore. Training and val-

idation loss conﬁrm that the model doesn’t overﬁt.

Both loss values are similar.

Also, the model does not predict the training set

perfectly anymore.

This is also a sign that the model is not overﬁtting and

it generalizes better.

These tables show the variation of the accuracy

[Table 1] and loss [Table 2] of validation dataset with

and without Dropout. We observe a pretty good per-

formance, this further reinforces the motivation about

the potential of Dropout methods for improving the

predictive performance (Belciug, 2020).

Mechanism of Overﬁtting Avoidance Techniques for Training Deep Neural Networks

425

Figure 11: Full Network: Accuracy & Loss.

Table 1: Accuracy of a validation dataset.

Dataset Normal-Accuracy Accuracy-Dropout

SONAR 99% 95%

Diabetes 75% 81%

MNIST 98% 99%

Dogs/Cats 100% 100%

Table 2: Loss of a validation dataset.

Dataset Normal-Loss Loss-Dropout

Diabetes 0.99% 0.45%

MNIST 5.00% 3.00%

Dogs/Cats 55% 22.80%

7 CONCLUSION

This paper mainly addresses the problem of under-

standing and using Early stopping as well as Dropout

on the entry into the maximum pooling layers of

convolutional neural networks. Early stopping is a

method to stop the training of a neural network when

the validation loss stops improving.

Dropout is a technique for improving neural net-

works by reducing overﬁtting. It forces a neural net-

work to learn more robust features that are useful

by deactivating certain units (neurons) in a layer

with a certain probability p. We presents precise iter-

ation complexity results for dropout training in two-

layer ReLU networks using the logistic loss.

In the future, we would like to explore applica-

tions of deep network compression (Li et al., 2020)

and investigate the sparsity property of learned reten-

tion rates to encourage a sparse representation of the

data and the neural network structure (Wang et al.,

2019). Another line of research is to dynamically

adjust the architecture of deep neural networks and

therefore reduce the complexity of the model using

dropout rates.

REFERENCES

Arora, R., Bartlett, P., Mianjy, P., and Srebro, N. (2020).

Dropout: Explicit Forms and Capacity Control.

OCLC: 1228394951.

Belciug, S. (2020). Artiﬁcial intelligence in cancer: diag-

nostic to tailored treatment. OCLC: 1145585080.

Bengio, Y., Lamblin, P., Popovici, D., and Larochelle,

H. (2007). Greedy Layer-Wise Training of Deep

Networks. Advances in neural information process-

ing systems., (19):153–160. Place: San Mateo,

CA Publisher: Morgan Kaufmann Publishers OCLC:

181070563.

Brownlee, J. (2018). How to Avoid Overﬁtting in Deep

Learning Neural Networks.

Brownlee, J., Machine Learning, and Mastery (2017). de-

velop deep learning models on Theano and Tensor-

Flow using Keras, volume 1. Machine Learning Mas-

tery, Melbourne, Australia.

Caruana, R., Lawrence, S., Giles, L., and 14th Annual Neu-

ral Information Processing Systems Conference, N. .

(2001). Overﬁtting in neural nets:. Adv. neural inf.

proces. syst. Advances in Neural Information Process-

ing Systems. OCLC: 5574566588.

Cerisara, C., Caillon, P., and Le Berre, G. (2021). Unsuper-

vised post-tuning of deep neural networks. In IJCNN,

Proceedings of the 2021 International Joint Confer-

ence on Neural Networks (IJCNN), Virtual Event,

United States.

diabetes.csv.en. URL: https://kaggle.com/saurabh00007/di

abetescsv (visited on 12/29/2021)

Etzold, D. (2022). MNIST — Dataset of Handwritten Dig-

its.

Hinton, G. E., Srivastava, N., Krizhevsky, A., Sutskever, I.,

and Salakhutdinov, R. R. (2012). Improving neural

networks by preventing co-adaptation of feature de-

tectors, volume 1.

IBM

Cloud Education (2021). What is Overﬁtting?

ICEIS 2022 - 24th International Conference on Enterprise Information Systems

426

Iraji, M. S., Feizi-Derakhshi, M.-R., and Tanha, J. (2021).

COVID-19 Detection Using Deep Convolutional Neu-

ral Networks. Complexity, 2021:1–10.

Krizhevsky, A., Hinton, G. E., and Sutskever, I. (2017).

ImageNet classiﬁcation with deep convolutional neu-

ral networks. Commun ACM Communications of the

ACM, 60(6):84–90.

Larxel (2021). Early Diabetes Classiﬁcation.

LeCun, Y., Hinton, G., and Bengio, Y. (2015). Deep learn-

ing. Nature, 521(7553):436–44. OCLC: 5831400088.

Li, C., Mao, Y., Zhang, R., Huai, J., and SpringerLink

(Online service) (2020). A revisit to MacKay algo-

rithm and its application to deep network compres-

sion. OCLC: 1196515065.

Liang, X., Wu, L., Li, J., Wang, Y., and Meng, Q. (2021).

R-Drop: Regularized Dropout for Neural Networks.

OCLC: 1269560920.

Maren, M., Lukas, B., Christoph, L., and Philipp, H. (2017).

Early Stopping without a Validation Set. OCLC:

1106261430.

Moolayil, J. (2019). Learn Keras for deep neural networks:

a fast-track approach to modern deep learning with

Python. OCLC: 1079007529.

M.Sarvazyan, A. (2022). Kaggle: Your Home for Data Sci-

ence.

Ng, A. Y. (2004). Feature selection, L1 vs. L2 regulariza-

tion, and rotational invariance. OCLC: 8876667046.

Senen-Cerda, A. and Sanders, J. (2020). Almost sure con-

vergence of dropout algorithms for neural networks.

OCLC: 1144830913.

Shaeke, S. and Xiuwen, L. (2019). Overﬁtting Mechanism

and Avoidance in Deep Neural Networks. OCLC:

1106327112.

Srivastava N, Hinton G, Krizhevsky A, Sutskever I, and

Salakhutdinov R (2014). Dropout: A simple way to

prevent neural networks from overﬁtting. J. Mach.

Learn. Res. Journal of Machine Learning Research,

15:1929–1958. OCLC: 5606582392.

Wang, Z., Fu, Y., and Huang, T. S. (2019). Deep learn-

ing through sparse and low-rank modeling. OCLC:

1097183504.

Wei, C., Kakade, S., and Ma, T. (2020). The Implicit and

Explicit Regularization Effects of Dropout. OCLC:

1228392785.

Wu, J.-W., Chang, K.-Y., and Fu, L.-C. (2022). Adap-

tive Under-Sampling Deep Neural Network for Rapid

and Reliable Image Recovery in Confocal Laser Scan-

ning Microscope Measurements. IEEE Trans. In-

strum. Meas. IEEE Transactions on Instrumentation

and Measurement, 71:1–9. OCLC: 9359636331.

Xiaobo, L., Lijun, W., and Juntao, L. (2021). R-Drop:

Regularized Dropout for Neural Networks. OCLC:

1269560920.

Yingbin, B., Erkun, Y., and Bo, H. (2021). Understand-

ing and Improving Early Stopping for Learning with

Noisy Labels. OCLC: 1269561528.

Mechanism of Overﬁtting Avoidance Techniques for Training Deep Neural Networks

427