Scoring-based DOM Content Selection with Discrete Periodicity Analysis

Thomas Osterland

1,2

and Thomas Rose

1,2

Fraunhofer FIT, Schloss Birlinghoven 1, Sankt Augustin, Germany

RWTH Aachen University, Ahornstr. 55, Aachen, Germany

Keywords:

Web Scraping, Periodicity Analysis, Content Extraction.

Abstract:

The comprehensive analysis of large data volumes forms the shape of the future. It enables decision-making

based on empiric evidence instead of expert experience and its utilization for the training of machine learning

models enables new use cases in image recognition, speech analysis or regression and classiﬁcation. One

problem with data is, that it is often not readily available in aggregated form. Instead, it is necessary to search

the web for information and elaborately mine websites for speciﬁc data. This is known as web scraping. In

this paper we present an interactive, scoring based approach for the scraping of speciﬁc information from

websites. We propose a scoring function, that enables the adaption of threshold values to select speciﬁc sets of

data. We combine the scoring of paths in a web pages DOM with periodicity analysis to enable the selection

of complex patterns in structured data. This allows non-expert users to train content selection models and to

label classiﬁcation data for supervised learning.

1 INTRODUCTION

The substantial advances in data analytics, machine

learning and stochastic modeling are only a few ex-

amples, that demonstrate the importance of data for

use cases and applications of the future. The world

wide web makes data provision efﬁcient and easily

available almost everywhere and also enables the col-

lection of new data on a large scale.

Often data is not readily available in a format, that

is easily accessible by computer systems. Web pages

are often optimized to improve the visual appeal to

humans. The document object model (DOM) struc-

tures the content of websites. Thereby, a substantial

part of the DOM is not concerned with the direct pre-

sentation of information, but with the layout and look

to present the information pleasantly, i.e., to improve

the presentation such that a human reader can quickly

and efﬁciently identify and extract the most important

parts.

Although, this approach is beneﬁcial for human

readers, it obfuscates the presentation for computer

systems, since those mostly do not understand the

data on a semantic level and thus, are not capable to

distinguish presentation related data from actual data.

Web scraping or more general screen scraping de-

scribes the automated extraction of information from

the computer screen or in our case websites. For

many applications it is an important pre-processing

step before applying machine learning and data an-

alytics (Glez-Pe

na et al., 2014; Mahto and Singh,

2016).

The usual process of web scraping involves users,

that decide what data to extract from websites. The

extraction is determined by models given as regex or

selector languages like XPath. Then in consecutive

execution steps scrapers use these models to extract

data from websites. This can be done in certain in-

tervals and also throughout a large set of structurally

equal websites, that contain different data. If a web-

site changes, for instance if an owner of a website ap-

plies A/B testing to compare different websites de-

signs, new models must be ﬁtted. Although, the ac-

tual scraping step is executed automatically without

user interaction, the model generation is done by a

user, who must be an expert or speciﬁcally trained if

the model ﬁt requires programming.

Besides, scraping large amounts of data from

equally structured websites another use case, that mo-

tivates our approach comes in the form of browser

plugins, web automation (Leshed et al., 2008) or gen-

eral software, that directly interacts with speciﬁc data

from websites. If the websites changes a ﬁxed model

(as, for instance an XPath expression), that was spec-

iﬁed by a programmer might not longer be able to ex-

tract the important information. Then a new software

280

Osterland, T. and Rose, T.

Scoring-based DOM Content Selection with Discrete Periodicity Analysis.

DOI: 10.5220/0011116300003179

In Proceedings of the 24th International Conference on Enterprise Information Systems (ICEIS 2022) - Volume 2, pages 280-289

ISBN: 978-989-758-569-2; ISSN: 2184-4992

version is necessary. However, if the model gener-

ation is as simple as clicking on an element on the

website, we can let the user update the model. In par-

ticular, if the model is transferable, such an updated

model can be shared among all users of a software

and some users might not even notice, that the web-

site changed.

A third use case, that beneﬁts from the proposed

selector is supervised machine learning. To train

models large data sets needs to be prepared and la-

beled or categorized. Since the data sets are often

large, the combined work of many people is required.

In this case, it is an advantage if these people do not

need to be experts in programming, that are capa-

ble of creating regular expressions or XPath deﬁni-

tions. This enables the utilization of crowd worker

platforms, as Amazon’s Mechanical Turk. Our ap-

proach allows the identiﬁcation of complex selection

patterns based on mouse clicks of a user. This makes

our approach particularly accessible to untrained per-

sonnel.

The general idea of our approach is to weight dif-

ferent paths in the websites DOM tree depending on

the user inputs. Thereby, the user inputs are evaluated

to obtain a model, that can be used to assess whether

a given path is likely to be a selected one. The nov-

elty of our approach is the idea to combine the path

scoring with discrete periodicity analysis to identify

speciﬁc patterns selected by a user. For instance, se-

lecting every second or third row of a table or two

consecutive rows followed by one row that is not se-

lected. These are often properties, that can be easily

expressed in scripting-based selectors as XPath, but

are difﬁcult or elaborate to obtain with click events.

The paper is structured as follows. In Section 2,

we review related work, that discusses web scraping

and technical approaches to extract speciﬁc informa-

tion. We then start in Section 3 with the introduction

of the path scoring approach, that is based on anal-

yses of CSS classes and HTML tag names mapped

to states of the DOM tree. We introduce periodicity

analysis in Section 3.1 and a bisimulation relation to

asses the similarity of subtrees in Section 3.2, which

further improves the selection results of our approach.

We evaluate the model sizes and the time complexity

of our approach in Section 4 and also discuss experi-

mental results. The results of this paper and potential

future work are discussed in Section 5.

2 RELATED WORK

Glez-Pe

na et al. differentiate three different classes

of web scraping approaches “(i) libraries for general

purpose programming languages, (ii) frameworks and

(iii) desktop-based environments“ (Glez-Pe

na et al.,

2014). Thereby, the ﬁrst category supports in the uti-

lization of programming languages as Perl or Python

to extract information from websites. Glez-Pe

na et al.

also count commandline tools, as curl or wget to this

category, what softens the clear separation of the three

categories. The second category entails frameworks,

as Scrapy or jARVEST and demarcates itself from the

other categories by containing approaches, that are a

“more integrative solution“ (Glez-Pe

na et al., 2014).

The ﬁnal category, enables layman programmers to

fathom web scraping.

Thereby, the proposed categorization demon-

strates the fundamental paradigms: On the one hand

approaches, that can be in practice only used by

trained personnel, since they require programming

and those, that support users with elaborate interfaces.

However, the categorization appears partially incon-

sistent in the sense, that there exists overlaps between

categories (some frameworks can be also used as a li-

brary (for instance Scrapy)) and we further argue, that

tools as curl or wget are independent programs. It is

possible to call these programs within program code,

but it stretches the concept of program code libraries.

A different family of approaches to extract infor-

mation from web pages is based on semantic infor-

mation. Thereby, DOM elements are enriched with

ontological information. The World Wide Web Con-

sortium (W3C)

proposes a language, called Web On-

tology Language (OWL), that provides different ex-

pressions to deﬁne relationsships and afﬁliations be-

tween content. Lamy (Lamy, 2017) presents how

this additional information can be used to automat-

ically classify data. Fern

andez et al. present a se-

mantic web scraping approach based on resource de-

scription framework (RDF) models, that are used to

map DOM elements to “semantic web resources“

(Fern

andez Villamor et al., 2011). One problem of

these approaches is that often semantic annotations

are not available for websites.

Mahto et al. discuss in their paper the ethics of

web scraping and provide web scraping examples

written in Python with BeautifulSoup (Mahto and

Singh, 2016), which is categorized by Glez-Pe

na et

al. as a library (Glez-Pe

na et al., 2014).

Krosnick and Oney (Krosnick and Oney, 2021)

discuss the potential use of scripting based scraping

techniques for web automation and end-to-end user

interface testing. They conduct two studies to assess

usual challenges, that users face when they implement

web automation scripts. In the ﬁrst study all users

needed to develop selection scripts in a simple editor,

https://www.w3.org/

Scoring-based DOM Content Selection with Discrete Periodicity Analysis

281

while in the second there was a simple IDE that pro-

vided visual feedback during development. All test

participants were programmers with varying degrees

of experience.

Munoz et al. present in their paper µRaptor, which

is a tool designed to extract hCard information from

webpages (Munoz et al., 2014). They use a training

set of DOMs to extract a set of rules in the form of

CSS selectors. The rules are then used to identify

DOM subtrees, that represent hCards.

The layman category of web scraping tools intro-

duced by Glez-Pe

na et al. is not primarily targeted

by Krosnick and Oney. However, they discuss in

their related work tools that use Programming-by-

Demonstration (PbD) approaches for the model cre-

ation. One major motivation of PbD is to empower

non-experts to handle complex tasks. Frank (Frank,

1995) demonstrates this for interactive systems by

comparing snapshots before and after a user interac-

tion. Barman et al. (Barman et al., 2016) use this ap-

proach for the selection of DOM elements and similar

to our approach they use similarity measures. How-

ever, they do not apply periodicity analysis to identify

complex selection patterns.

Rousillon developed by Chasins et al. (Chasins

et al., 2018) is a tool that uses PbD for web scrap-

ing. It allows a user to record actions, that can be

replayed for automation. Similar functionality is pro-

vided by the academic tools CoScripter of Leshed et

al. (Leshed et al., 2008) and SUGILITE from Li et al.

(Li et al., 2017). Additionally, there exists a variety

of commercial tools, as Selenium

, iMacros

and Cy-

press Studio

Kadam and Pakle present DEUDS (Kadam and

Pakle, 2014) an approach to learn extraction rules

from training data. They describe a three step pro-

cedure: In the ﬁrst step a user can interactively select

the important information, then the approach will ex-

tract semantic tokens in the second and hierarchical

information in the third step to build a selector model,

that allows the page wise extraction of information.

However, most existing approaches, either rely

on existing technologies, as CSS selectors or XPath

statements or provide their own domain-speciﬁc lan-

guage. In particular for the use case of web automa-

tion PbD is used to record user interactions. Our ap-

proach employs discrete periodicity analysis to en-

able the selection of complex patterns. Hence, we

target the third category of Glez-Pe

na et al. that en-

ables layman programmers or web users in general to

train models and thus, allow the methodical extraction

https://www.selenium.dev

https://www.imacros.net

https://www.cypress.io/

html

head

body

class1

class2

class3

class2

class3

div

Figure 1: Example of DOM (abstract representation). The

CSS classes assigned to the HTML elements are displayed

in gray. The index of an element in the child array of the

parent, which is important for the periodicity analysis is dis-

played in dark gray.

of dedicated information from websites. We develop

the approach focusing on two applications: For once

machine learning requires a lot of carefully reviewed

information, that often can only be provided by hu-

mans. Clickworkers or crowdworkers on platforms as

for instance Amazon’s Mechanical Turk are a com-

mon solution. However, these workers are rarely pro-

gramming experts and the quality of their work of-

ten depends on the usability of the data processing.

The second use case are for instance browser plugins

that work with the data of speciﬁc websites. Com-

panies and organizations frequently update their web-

sites, for instance when applying A/B testing to ﬁnd

more efﬁcient presentations or in case of regular up-

dates. Often this will break existing selectors spec-

iﬁed as regular expressions or XPath code. In such

cases an update of the browser plugin is necessary,

but in particular in case of A/B testing it is not en-

sured that the developer will obtain the same website

version as the plugin user. An adaption of the content

selector is difﬁcult. Instead, our approach empowers

the user of a browser plugin to retrain the model if she

notices, that the existing selection logic is not longer

able to extract the important data from a website.

3 PATH SCORING

Figure 1 shows an abstract representation of a doc-

ument object model (DOM). A DOM structures the

HTML (or XHTML) elements of a web page in a tree

structure. The root node of a DOM is the document

that is usually followed by an HTML tag. In the exam-

ple in Figure 1, we start with the HTML tag.

In the following we present a DOM as a directed

acyclic graph (or labeled transition system (LTS))

ICEIS 2022 - 24th International Conference on Enterprise Information Systems

282

G = (S,→,root,TAG,CSS,L), with S a set of states,

→⊆ S × S a relation, that represents the child-parent

relationship between elements of different levels in

the DOM tree, root ∈ S the root node, which has

no incoming transitions, i.e., {(v,root) | ∀v ∈ S} *→,

TAG is a set of HTML tag names and CSS a set of

CSS classes. L : S → 2

CSS

∪ HTML is a labeling func-

tion, that assigns CSS classes and HTML tag names

to states of the graph. Note, that the mapping L can

assign an arbitrary number of CSS classes to a state,

but only one HTML tag name. G is the set of all DOM

DAGs.

We further deﬁne the set of siblings siblings(s) =

| ∃ q ∈ S : (q, s) ∈→⇒ (q, s

) ∈→}. Note, that q

is unambiguous due to the tree structure of the DOM.

Since, the order of elements in the DOM is impor-

tant for the presentation, we deﬁne the natural total

order < on a set of siblings, according to their appear-

ance in the DOM. For example in Figure 1 the order

on the set of siblings siblings(BODY) = {HEAD,BODY}

with HEAD < BODY.

We use this graph structure together with the →

relation to deﬁne a path semantic on the DOM. In

early experiments, we tested Markov chains for the

classiﬁcation of selected elements. Thereby, we mod-

eled different elements of the DOM as states in the

Markov chain, that was weighted in accordance to

the training data provided by the user, as for instance

by selecting some elements. However, a usual DOM

contains a substantial number of equal HTML ele-

ments and CSS classes. The redundancies within the

graph together with the Markov property (memory-

less) of the model lead to poor classiﬁcation results.

Better results can be obtained, when we increase the

order of the Markov chain. If we increase the order to

the path length of the largest training path, we obtain

the best classiﬁcation results, but hardly beneﬁt from

the locality of the Markov property anymore.

A path is an ordered sequence of states ω =

·· ·s

with n ∈ N and ∀ i ∈ {1,·· · , n − 1} it holds,

that (s

i+1

) ∈→. The length of a path ω is |ω| = n.

We use | · | also to denote the cardinality of sets. The

set of all paths over an LTS G ∈ G is denoted as P

For two states s,s

in a path we write s < s

, if s ap-

pears earlier in the path than s

. We call a path ω a root

path if s

= root and a leaf path, if @ x ∈ S : (s

,x) ∈→.

A path, that is a root path and a leaf path is called

complete. In Figure 1 paths, that contain the div tags

are leaf paths and a non-rigorously written example

for a complete path is ω = html body div.

The training set T is a set of root paths. In prac-

tice, we can obtain this set by adding a click event lis-

tener to a website and then construct the path by iter-

ating through the parents of the selected element until

we reach the document root. Our model (see Equation

2) evaluates the sizes of training paths and thus, we

are not limited to leaf paths in the training set. How-

ever, it is often desired, since the goal is the extraction

of information, which is often the text attribute of a

leaf HTML element. Note, that when we use the click

event listener approach to obtain the training samples

it is easy for a user to hit the wrong element. So for in-

stance instead of hitting a span element, that directly

contains the desired information the surrounding div

element is chosen. This is a challenge that must be

considered, when collecting the training samples with

this approach.

In the following, we deﬁne the set of training tags

TAG

= {L(s) ∩ TAG | ∀ s ∈ ω ∀ ω ∈ T } and the set

of training CSS classes T

CSS

= {L(s) ∩ CSS | ∀ s ∈

ω ∀ ω ∈ T }. This allows us to deﬁne the scoring

functions, that measures the overlap of TAGs and CSS

classes in the training set and a given path ω:

(ω) =

|{s | ({L(s)} ∩ Q 6=

0 ∧ s ∈ ω}|

|ω|

(1)

In the equation Q ∈ {T

CSS

TAG

}, i.e., we use the

same scoring function to measure the overlap in CSS

classes and HTML tags. Note, that in case of perfect

overlap, that means in case a path ω ∈ P is part of

the training set p

(ω) = 1. Generally it holds, that

(ω) ∈ [0,1],∀ ω ∈ P.

We gradually penalize deviations from path

lengths, that are present in the training set.

(ω) = 1 −

|k − |ω||

max(k, |ω|)

(2)

We determine k by evaluating the expression

min

k=|ω

|,ω

∈T

||ω| − k|. That means, k is the length of

a path in the training set, that is closest in length to the

path ω. Again p

(ω) ∈ [0,1],∀ ω ∈ P and p

(ω) = 1

if the scored path ω ∈ P is present in the training set.

3.1 Discrete Periodicity Analysis

The most distinctive feature of our approach com-

pared to other approaches is based on the utilization

of discrete periodicity analysis to make assumptions

about the intended selection pattern of a user. For ex-

ample often data on websites is provided as tables. If

only every second row or even a more complex pat-

tern, as two consecutive rows followed by three ir-

relevant rows need to be selected most mouse-based

approaches cannot provide this functionality.

Scripting based approaches, as XPath or CSS se-

lectors have an advantage in these situations, but are

not equally accessible by uneducated workers. Of

Scoring-based DOM Content Selection with Discrete Periodicity Analysis

283

course, the approach is not limited to table rows, but

can be also used to extract patterns from arbitrary

HTML elements, as for instance ﬂoat or CSS grid

screen layouts.

The discrete periodicity analysis, that we employ

originates in approaches to mine association rules

(Agrawal and Srikant, 1994), which are probably best

known for the association example of diapers and

beer, which is best placed next to each other in stores.

Agrawal and Srikant present in their paper

(Agrawal and Srikant, 1994) the A priori property,

which uses subsets of potential patterns to analyze the

frequency of occurrence of larger patterns. This can

then be used to derive a conﬁdence score, that a cer-

tain pattern appears periodically. The challenge dur-

ing the mining process is that, we assume noisy data,

which means that the pattern will not match exactly at

certain periods.

Hang et al. (Han et al., 1999) deﬁne the problem

of periodicity mining as follows: For a time series of

features S = D

,· ·· ,D

, where D

,i ∈ {1,··· ,n}

are sets generated from a sequence of chronologi-

cally ordered database entries, we try to mine pat-

terns s = s

·· · ,s

with s

∈ L, i ∈ {1,··· , p} with

L = ((D

∪ ··· ∪ D

) −

0) ∪ {∗}. Hang et al. use ∗

as a don’t care character. If this appears in a pattern

it indicates, that we are not interested in the charac-

ter at this position, but only on the periodicity of the

surrounding elements.

To evaluate the quality of an extracted pattern,

they deﬁne a conﬁdence score, that is based on the

occurrence frequency of a pattern s:

frequency count(s) = |{i | 0 ≤ i ≤ m,s holds in

i|s|+1

·· ·D

i|s|+|s|

}| (3)

The conﬁdence is then the frequency divided by

m, which is the number of times the pattern ﬁts into

the analyzed sequence.

conf(s) =

frequency count(s)

(4)

Note that we can control the minimal required

number of pattern repetitions with the conﬁdence

value. If for instance a pattern needs to be at least

two times present in the sequence, we can derive a

minimal bound and only work with patterns that have

at least this conﬁdence. With regard to our content

selection use case, we use this minimal bound (of two

present repetitions), since one occurrence cannot be

identiﬁed as periodic and more than two are too much

work for a user to train. Although, the conﬁdence

will increase if the user further selects elements, that

ﬁt the pattern. For instance our model must respond,

if a user selects two alternating rows in a table.

However, not every selection of a user constitutes

a pattern repetition. Depending on the pattern mul-

tiple selections represent one pattern and therefore,

more selections from the users are necessary to reach

the conﬁdence level of at least two. For instance in

Figure 1, if the user wants to select the ﬁrst and the

second div, but not the third div, she needs to click

on the ﬁrst, the second, the fourth and the ﬁfth div to

reach the required conﬁdence.

Hang et al. present in their paper (Han et al.,

1999) a more efﬁcient adaption of the association rule

mining algorithm presented by Agrawal and Srikant,

which they call max-subpattern hit-set. They in-

troduce a sophisticated tree datastructure, the max-

subpattern tree, which efﬁciently organizes scanned

patterns and their variations. In a consecutive step we

can evaluate the datastructure, to derive the patterns

with the highest conﬁdence. For an explanation of the

algorithm, we refer the reader to the paper of Hang et

al. (Han et al., 1999).

In the following, we refer to the max-subpattern

hit-set algorithm as a function max hit set : L

× R×

N → 2

×N

, that maps from a sequence (L

) a mini-

mal conﬁdence threshold (R) and a pattern length (N)

to a set of patterns (L

) and the number of their oc-

currences (N). We further use the restricted feature set

L = {1,∗}. Equation 5 shows, how we encode the el-

ements of a training sample as a sequence L

, that we

can feed into the max-subpattern hit-set algorithm.

pattern : s 7→ (x

,· ·· ,x

),with

(

= 1 ∃ ω

∈ T : s

∈ ω

= ∗ otherwise

(5)

with s

∈ siblings(s), s

< · ·· < s

and 1 ≤ i ≤

|siblings(s)| = m ∈ N. We use superscript indices to

indicate, that we iterate over the siblings of a state and

not over the states of a path.

The idea of Equation 5 is to encode DOM ele-

ments of one level, that are part of the training set

as 1 and all the remaining elements as ∗ (don’t care).

For an element we look at all its siblings, whether it is

also part of the training set. For example if in Figure

1 a user wants to select every other DIV element and

selects the ﬁrst and the third DIV element. Then we

construct an input sequence 1 ∗ 1 ∗ ∗ and the pattern

1∗ occurs two times in the sequence.

The pseudocode in Algorithm 1 describes how we

interface the periodicity algorithm. For a given state

s of a training path s ∈ ω, we derive the input pattern

with the function of Equation 5. For sequences of

length |p| = 1, we directly return the considered state

s if it is part of the training set, since there is no sense

ICEIS 2022 - 24th International Conference on Enterprise Information Systems

284

Input: s ∈ ω

Output: period(s) = R

p ← pattern(s);

if |p| = 1 then

if ∃ ω

∈ T : s ∈ ω

then

return {s};

else

return

end

U ←

while i ∈ {2,·· · , |p|} do

U ← U ∪ {max hit set(p,2i/|p|,i)};

end

M ← {(p,q) | (p,q) ∈ U : max|p| ∧ max q};

if |M| > 1 then

// request additional training data

else

r ← M[0];

end

R ←= {s

| s

∈ siblings(s) : p

[< (s

)

mod |p

|] = 1 ∨ p[< (s

)

mod |p|] = 1, (p

,q) = r};

Algorithm 1: Identify the periods.

analyzing the periodicity in sequences of length one

and if it is part of the training set it is translated into a

1 in the input pattern. For sequences of length |p| > 1

we apply the max hit set function for every period

length 2 ≤ i ≤ |p|. From the uniﬁed result set, we

choose the detected pattern, that is largest and has

the highest frequency of occurrences. If the set M

of selected patterns contains more than one element

we require additional training data, otherwise we will

choose the pattern. We use this selected pattern to

derive those siblings, that match the extrapolated pat-

tern. Note, that we use < (s) = i as a loose syntactic

expression to denote the index of s in the order of its

siblings s

< ·· · < s

i−1

< s < s

i+1

< ·· · < s

and p[i]

to access the i’th element of the pattern. We also se-

lect an element if it is one in the input sequence, i.e.,

we force the inclusion of states, that are part of the

training set, since those are provided by the user and

even if they do not belong to a pattern the user wants

those elements to be selected.

We use Algorithm 1 to score paths as follows:

(ω) =

|{s | s ∈ ω ∧ s ∈ period(s)}|

|ω|

(6)

Every state of a path s ∈ ω is checked, whether it

is part of a detected periodic pattern. We count the

number of states at which this is the case and divide

it by the number of total states in the path. For train-

ing samples the score will be p

(ω) = 1, ω ∈ T and

(ω) ∈ [0,1],∀ ω ∈ P.

We combine the introduced individual scoring

functions into a combined score in Equation 7 and

further introduce parameters a

TAG

CSS

with

TAG

CSS

= 1 to weight certain scores dif-

ferently if required.

path

(ω) =

TAG

(ω)+

CSS

(ω) + a

(ω)) (7)

An example of a situation in which different

weights become useful is if a websites colors alternat-

ing rows of a table differently by assigning different

CSS classes. In this case we can reduce the weight

of the CSS scoring function to make sure, that it does

not weight the rows of the table too differently.

3.2 (Bi)Simulation to Identify Similar

Subtrees

For the example presented in Figure 1, the periodicity

analysis will work in the sense, that it selects those

div elements, that are part of the identiﬁed pattern.

However, this will not directly work if the div ele-

ment is again the root element of a subtree. This is

demonstrated in the example in Figure 2.

If a user selects sub-elements of the ﬁrst and the

third div the ﬁfth div will be identiﬁed by the peri-

odicity analysis, but this will not inﬂuence the scores

of the leaf elements in the subtree. That means, we

cannot decide whether to select the ﬁrst or the second

span.

We use a bisimulation relation to compare the

branching structure of different subtrees in the DOM.

Baier and Katoen present a deﬁnition of bisimulation

equivalence on labeled transition systems (Baier and

Katoen, 2008), which we use in a slightly adapted

form.

For two labeled transition systems G

= (S

,→

,root

,TAG

,CSS

),i ∈ {1,2} a bisimulation for

) is a binary relation R ⊆ S

× S

with:

1. For s ∈ S

∧ s = root

: ∃ s

∈ S

∧ s

= root

(s,s

) ∈ R and for s ∈ S

∧ s = root

: ∃ s

∈

∧ s

= root

: (s, s

) ∈ R

2. ∀ (s

) ∈ R :

(a) L

) = L

)

(b) ∀s ∈ S

with (s

,s) ∈→

: ∃ s

∈ S

with

) ∈→

and (s,s

) ∈ R

with (s

,s) ∈→

: ∃ s

∈ S

with

) ∈→

and (s,s

) ∈ R

Scoring-based DOM Content Selection with Discrete Periodicity Analysis

285

We write G

∼ G

for two labeled transition sys-

tems G

, that are bisimilar.

Note, that we deviate from the deﬁnition of Baier

and Katoen in particular on the ﬁrst item, since transi-

tion systems are usually not limited to directed acyclic

graphs (DAGs). Hence, there exists a set of initial

states. Since our transition systems represents a DOM

tree or a subset of it, we always have the case, that the

initial set is a single state, that we designate as root.

The ﬁrst item of the second property 2 − 1 :

) = L

) allows us to decide the equality of

states. We deﬁned the labeling function L based on

the TAG and assigned CSS classes. States that share

these properties are considered as equal by our algo-

rithm. The second and the third property enforce the

same branching structure on the tree.

We write G

sub

(s) ⊆ G = (S, →

,root,TAG, CSS,L) : s ∈ S for a subtree induced

by choosing a state s ∈ S as its root and only

keep states and transitions, that are connected in

a successor relationship. G

sub

: G × S → G with

(G,s) 7→ (S

,→

,s, TAG

,CSS

• S

:= S ∩ {s

| ∃ ω ∈ P

: s ∈ ω ∧ s

∈ ω ∧ s < s

}

• →

:= {(s, s

) | (s,s

) ∈→ ∧ s,s

∈ S

}

• TAG

:= TAG ∩ {q | ∃ s

∈ S

: L(s

) = (A,q),A ∈

CSS

}

• CSS

:= CSS ∩ {x | ∃ s

∈ S

,∃ A ∈ 2

CSS

: L(s

) =

(A,q) ∧ x ∈ A,q ∈ TAG}

• L

:= L

denotes the restriction of the labeling function

to the preimage set, that only contains states of the

subtree. Consequently, we obtain a subtree, that only

comprises the restricted labeling function with corre-

sponding CSS classes and tags that are still present in

the remaining states.

For a path ω and a state s ∈ ω =

,· ·· ,s

j−1

,s, s

j+1

,· ·· ,s

) and @ ω

∈ T : s ∈ ω

i.e., the state s is not part of a training path and

s ∈ period(s) is part of an identiﬁed pattern we search

for bisimilar subtrees induced by the siblings of s,

that are part of a training path and construct a path

that is used in the scoring function p

(ω

) with

the following method:

∀s

∈ siblings(s) : (s

6= s∧

∃ ω

= (s

,· ·· ,s

i−1

i+1

,· ·· ,s

) ∈ T : s

∈ ω

∧

∈ pattern(s) ∧ G

sub

(s) ∼ G

sub

)) ⇒

,· ·· ,s

j−1

,s, s

i+1

,· ·· ,s

) = ω

(8)

Equation 8 describes our method to apply the pe-

riodicity scoring on paths selected by the periodicity

analysis. For selected paths we search in the train-

ing set for a path that is most similar to the selected

one and then combine the periodicity data from these

two paths by joining the state sequences. This allows

us to transfer the periodicity analysis model from the

training set to paths, that are not directly part of the

training set, but are identiﬁed by the periodicity anal-

ysis.

Of course, if the training set is large there are mul-

tiple states s

in different training paths, that might ﬁt

the target state. However, since all these eligible state

induce bisimilar subtrees, we can select an arbitrary

training state and obtain the same result.

Note, that the bisimulation relation is strict, since

it requests that transition steps can be replayed in both

systems, i.e., a speciﬁc move in one system must be

repeatable in the other and vicit versa. For our ap-

proach it is often sufﬁcient if we can ﬁnd a training

path, that is capable of repeating every transition step

of the target system. That means in contrast to de-

manding an equivalence relationship, we just demand

it in one direction. This can be achieved with the help

of a simulation relation, which is basically a one-sided

bisimulation relation.

4 EVALUATION

For the evaluation of our approach we analyze the

computational complexity of the scoring and also the

space, that is required to store the models derived

from the training data. This is important, since those

will be stored for the extraction of speciﬁc content

and it might be necessary to update this model if a

webpage changes. In case of an application, as for

instance a browser plugin, the model must be shared

among all the users of the application.

We are also interested in the performance of our

scoring approach with respect to accuracy and preci-

sion. That means, we measure the elements that the

approach extracts correctly and those, that it extracts,

but are not intended, i.e., true positives and false pos-

itives.

For this we conduct an experiment. Our method-

ology is to randomly select leaf DOM elements,

that contain text content, i.e., ASCII characters,

from the seven most popular websites google.com,

youtube.com, facebook.com, wikipedia.org, ya-

hoo.co.jp, amazon.com, instagram.com as listed by

statista.com

. These randomly selected elements

simulate the user input and thus our training data.

We derive models from these elements and then in

a second step evaluate the scores of the paths on the

https://www.statista.com/statistics/1201880/most-

visited-websites-worldwide/

ICEIS 2022 - 24th International Conference on Enterprise Information Systems

286

·· ·

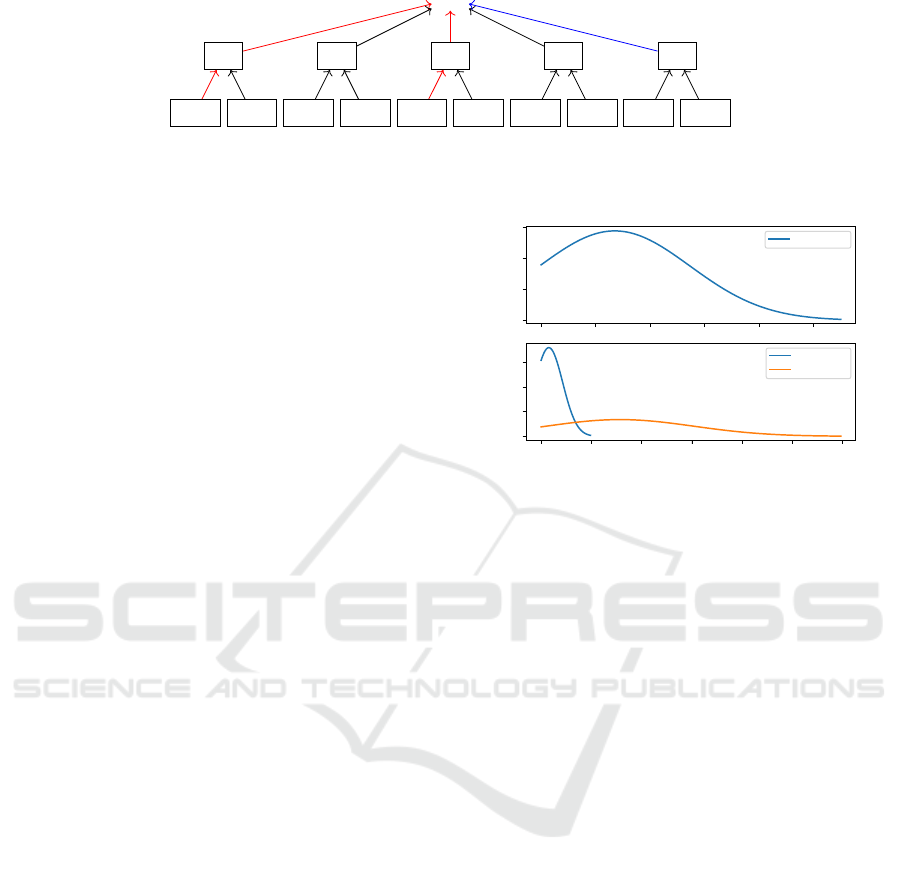
div div div div div

span span span span span span span span span span

Figure 2: Example to showcase the necessity of evaluating the bisimilarity of subtrees in case of identiﬁed periodicity. The

red lines represent the training paths and the blue path is selected by the periodicity analysis. The question mark indicates the

problem, that a selection path for the subtree cannot be directly deduced from the periodicity analysis of the parent elements.

DOM for the model. We measure execution time and

the correctness of selected elements.

4.1 Model Size and Runtime

Complexity

The model size depends directly on the training set.

For a path ω ∈ T we need to store for every state s ∈ ω

the corresponding tag TAG

, the assigned CSS classes

CSS

and a pair of (p,q) ∈ {0,1}

× N, that contains

the evaluated pattern and its period.

In worst case every path of a DOM is a path in the

training set, and we use the number of states in the

DOM |S| as an upper bound for the pattern. Thus,

we have a complexity of O(|S||CSS| + |S| + |S|

where the ﬁrst term assumes, that every available CSS

class is assigned to every state in the DOM. The sec-

ond term presents, that every state is unambiguously

mapped to a tag and the third term assumes, that we

need to store for every state a pattern consisting of

all the other states in the DOM. Of course, in prac-

tice the worst case model size is not realistically ob-

tained. CSS classes are usually assigned to only a

very small number of states and the number of sib-

lings of most states are by a large margin smaller than

the total number of states in the DOM. In Figure 3,

we analyzed the number of elements in the DOM, the

average CSS classes assigned to a state and the aver-

age number of siblings of a state collected from the

popular websites mentioned above.

Note in particular, that the average number of

classes and siblings are much smaller than the total

number of DOM elements. Also, the number of CSS

classes assigned to a single DOM element is below

20. Hence, in practice we can expect much smaller

models, than suggested by the worst case analysis.

To determine the time complexity of the proposed

approach we need to distinguish the evaluation phase

and the training phase. For the evaluation we only

need to traverse the DOM tree, what can be done with

a tree traversal algorithm in O(|S|) with S the states

in the tree. During traversal, we iteratively extend the

paths and apply the scoring. The counts of the earlier

scoring can be cached, such that we are not forced to

0 1000 2000 3000 4000 5000

0.0000

0.0001

0.0002

0.0003

Total nodes

0 20 40 60 80 100 120

0.00

0.02

0.04

0.06

CSS classes

Siblings

Figure 3: Total number of DOM elements, average number

of classes assigned to DOM states and the average number

of siblings collected from the most popular websites.

traverse the entire path for every additional state with

which the path is extended. We can use the index of

a state to determine, whether it is part of a pattern to

evaluate the periodicity score.

The time complexity will deteriorate if we use

bisimulation to compare subtrees of identiﬁed pat-

terns. Baier and Katoen give the complexity of check-

ing the equivalence of two labeled transition sys-

tems LTS

,LTS

as O((|S

| + |S

|) ∗ |AP| + (M

)log(|S

| + |S

|) (Baier and Katoen, 2008). S

represent the set of states, AP the sets of labels, which

are in our case composed by CSS and TAG and M

is the number of edges in the corresponding transition

systems.

The training phase requires in worst case O(|S|

)

operations. This is since in worst case every path and

thus, every state in the DOM is part of the training

set. Jiawei et al. (Han et al., 1999) specify the run-

time complexity of the max-subpattern hit-set algo-

rithm with O(M), where M is the length of the se-

quence, that need to be scanned for detecting patterns.

We call the max-subpattern hit-set algorithm for ev-

ery periodicity p ∈ {1, ··· ,M}, which means that the

complexity will be O(M

). Since, the input sequence

is generated by the siblings of a state, and S is the set

of all states, we can use |S| = M as an upper bound.

With the necessary traversal through the DOM tree,

i.e., the training set (remember in worst case every

path in the DOM is a training path) we obtain the

complexity of O(|S|

Scoring-based DOM Content Selection with Discrete Periodicity Analysis

287

0 200 400 600 800

0.0000

0.0005

0.0010

0.0015

Selection time

0.0 0.5 1.0 1.5 2.0

0.0

0.2

0.4

Training time

Figure 4: Total number of DOM elements, average number

of classes assigned to DOM states and the average number

of siblings collected from the most popular websites.

Since, we randomly select a single leaf path for

training in our experiment, we do not need to identify

selection patterns, which is difﬁcult to test automat-

ically. The approach identiﬁed in 100% of the test

cases the correct DOM element, which is explained

by the periodicity analysis, that favors element in-

dices, that are part of the training set. That means,

even if there is only a single training path and thus,

it is not possible to derive a sequence for periodic-

ity analysis, that contains more than one 1, this single

one is stronger weighted than all the siblings of the

element.

Figure 4 particularly emphasizes the expensive

costs of the periodicity analysis of O(|S|

). In our

implementation, we applied the periodicity analysis

during the selection phase. Of course, in a production

implementation this should be done during training

and then the results of the analysis must be stored in

the model, as described above. The numbers of the

abscissa represent time in milliseconds. For websites

with large DOMs trees the selection training required

almost a full second, although the majority requires

around 200 milliseconds. Please note, that we focused

in our implementation on experimenting and correct-

ness and less on computational complexity. Hence,

there is much room for improvement. Both, with re-

gard to efﬁcient execution and to compact storing of

trained models.

5 CONCLUSIONS

In this paper we demonstrated how periodicity analy-

sis can be used as an approach to empower non-expert

users to extract speciﬁc information from websites.

Our approach represents an extension of existing ap-

proaches, since it allows the simple deﬁnition of com-

plex selection patterns derived from user clicks. We

further employed bisimulation relations to measure

the similarity of subtrees to further improve our ap-

proach.

Although, our complexity analysis shows, that the

computational complexity and model sizes of our ap-

proach can be substantial in worst case, experimen-

tal results and empirical evaluation of the DOM trees

of the most popular websites revealed, that in prac-

tice the worst case considerations are rarely observed

and thus, the performance is much better in practice.

Additionally, we need to distinguish the runtime com-

plexity of the training phase and the selection phase.

The majority of required computations is part of the

training phase, which is for most uses cases less fre-

quently necessary, than the less expensive selection

phase. The selection phase can be efﬁciently com-

puted in O(|S|), but worsens when we employ bisim-

ulation to check different subtress.

The experiment also indicates possible future

work, as the performance tuning of our algorithm. A

termination condition in the selection phase will pre-

vent the traversal of the entire DOM tree and we can

utilize for periodicity analysis the fact, that in con-

trast to our worst case assumption, that every DOM

path is a training path, the training set is usually much

smaller.

ACKNOWLEDGEMENTS

This research was partially founded by the b-it foun-

dation (Bonn-Aachen International Center for Infor-

mation Technology)

REFERENCES

Agrawal, R. and Srikant, R. (1994). Fast algorithms for

mining association rules in large databases. In Pro-

ceedings of the 20th International Conference on Very

Large Data Bases, VLDB ’94, page 487–499, San

Francisco, CA, USA. Morgan Kaufmann Publishers

Inc.

Baier, C. and Katoen, J. (2008). Principles of Model Check-

ing. MIT Press.

Barman, S., Chasins, S., Bodik, R., and Gulwani, S. (2016).

Ringer: web automation by demonstration. In Pro-

ceedings of the 2016 ACM SIGPLAN international

conference on object-oriented programming, systems,

languages, and applications, pages 748–764.

Chasins, S. E., Mueller, M., and Bodik, R. (2018). Rousil-

lon: Scraping distributed hierarchical web data. In

Proceedings of the 31st Annual ACM Symposium on

User Interface Software and Technology, pages 963–

975.

https://www.b-it-center.de/

ICEIS 2022 - 24th International Conference on Enterprise Information Systems

288

Fern

andez Villamor, J. I., Blasco Garcia, J., Iglesias Fer-

nandez, C. A., and Garijo Ayestaran, M. (2011). A

semantic scraping model for web resources-applying

linked data to web page screen scraping.

Frank, M. (1995). Inference bear: Designing interactive

interfaces through before and after snapshots.

Glez-Pe

na, D., Lourenc¸o, A., L

opez-Fern

andez, H.,

Reboiro-Jato, M., and Riverola, F. F. (2014). Web

scraping technologies in an api world. Brieﬁngs in

bioinformatics, 15 5:788–97.

Han, J., Dong, G., and Yin, Y. (1999). Efﬁcient mining of

partial periodic patterns in time series database. pages

106–115.

Kadam, V. B. and Pakle, G. K. (2014). Deuds: Data ex-

traction using dom tree and selectors. International

Journal of Computer Science and Information Tech-

nologies, 5(2):1403–1410.

Krosnick, R. and Oney, S. (2021). Understanding the

challenges and needs of programmers writing web

automation scripts. In 2021 IEEE Symposium on

Visual Languages and Human-Centric Computing

(VL/HCC), pages 1–9.

Lamy, J.-B. (2017). Owlready: Ontology-oriented pro-

gramming in python with automatic classiﬁcation and

high level constructs for biomedical ontologies. Arti-

ﬁcial intelligence in medicine, 80:11–28.

Leshed, G., Haber, E., and Matthews, T. (2008). Coscripter:

Automating & sharing how-to knowledge in the enter-

prise. pages 1719–1728.

Li, T., Azaria, A., and Myers, B. (2017). Sugilite: Cre-

ating multimodal smartphone automation by demon-

stration.

Mahto, D. K. and Singh, L. (2016). A dive into web scraper

world. In 2016 3rd International Conference on Com-

puting for Sustainable Global Development (INDIA-

Com), pages 689–693.

Munoz, E., Costabello, L., and Vandenbussche, P.-Y.

(2014). µraptor: A dom-based system with appetite

for hcard elements. In LD4IE@ ISWC, pages 67–71.

Citeseer.

Scoring-based DOM Content Selection with Discrete Periodicity Analysis

289