Safe Robotized Polishing of Plastic Optical Fibers for Plasmonic Sensors

Francesco Arcadio, Marco Costanzo, Giulio Luongo, Luigi Pellegrino, Nunzio Cennamo

and Ciro Natale

Dipartimento di Ingegneria, Universit

a degli Studi della Campania ”Luigi Vanvitelli”, Via Roma 29, Aversa, Italy

Keywords:

Human-robot Collaboration, Workspace Monitoring, Compliance Control, Plasmonic Optical Fiber

Biosensors.

Abstract:

Plastic optical ﬁbers (POFs) biosensors are getting widespread in a number of application ﬁelds owing to

their low cost, high performance, and for their extreme ﬂexibility in terms of detection ability of a large

number of speciﬁc substances in different matrices. A speciﬁc category of such sensors are those based on

the surface plasmon resonance (SPR) phenomenon, which can be made very speciﬁc by suitable integration

with a biological or chemical molecular recognition element (MRE), speciﬁcally designed for binding with the

desired substance (the analyte). Despite the ﬂexibility of the SPR-POF sensors, their production is still difﬁcult

to automate on a large scale because of the special polishing process of the plastic optical ﬁber. Such a process

is currently performed by a human trained operator who rubs the surface of a short ﬁber segment against a

sandpaper sheet by following an 8-shaped path while exerting a speciﬁc force in the direction normal to the

contact surface. The present paper proposes the adoption of a collaborative robot programmed to perform the

same task based on the data acquired from the human operator. To ensure the safe use of the robotic cell by

operators who share the same workspace of the robot, the system is endowed with a workspace monitoring

system that ensures the polishing task execution while minimizing the possible occurrence of collisions with

human operators by suitable exploiting the kinematic redundancy of the robot.

1 INTRODUCTION

Highly sensitive plasmonic POF probes, com-

bined with speciﬁc molecular recognition elements

(MREs), can be obtained by exploiting modiﬁed

POFs to obtain the interaction with the analyzed

medium directly. For instance, a D-Shaped region

must be realized to deposit a metal nanoﬁlm, use-

ful to excite the SPR phenomenon in this sensing

area. The SPR phenomenon is a label-free technique

where MREs, coupled to a metal surface (usually gold

nanoﬁlms), selectively recognize and capture the sub-

stance of interest, producing a local change in the re-

fractive index at the metal surface interface by chang-

ing the resonance condition. This sensing approach,

based on SPR-POF probes combined with MREs, can

be used in several applications, such as medical di-

agnostics, environmental monitoring, industry, food

safety, and security (Cennamo et al., 2021). The au-

thors have combined the same SPR-POF platforms

with different kinds of MREs, such as antibodies, ap-

tamers, and molecularly imprinted polymers (MIPs),

by obtaining interesting detection ranges in many ap-

plications. The limit of this sensing approach is the

production process of the POF platforms because it

is based on a polishing step, currently handmade.

This limit yields inefﬁcient process control to realize

very similar sensors or to change their performances;

hence, this kind of sensor cannot be produced on an

industrial scale.

Automation of such a production process might

be performed through the design of speciﬁc polishing

machines or through a ﬂexible automation approach

like the use of robots. In the former case, the rigid-

ity of the automation solution might be characterized

by a low return on investment, since the scale of the

automation system highly depends on the actual mar-

ket demand of the sensor, which is very difﬁcult to

forecast for a new product. Therefore, such a rigid

solution might be risky, especially for a startup. This

motivated the approach proposed in the paper, which

explores the possibility to adopt a modern collabora-

tive robot (cobot) that can safely work in a highly dy-

namic environment shared with human operators (Na-

tale, 2019). Programming of cobots is usually done

by hand guidance but in the application at hand the

motion trajectory the robot has to follow is very spe-

ciﬁc and it can be easily programmed by resorting to

a motion primitive (Siciliano et al., 2009). Further-

more, following the given trajectory is not enough

to carry out the polishing task properly, but a suit-

able normal force should be exerted during the mo-

Arcadio, F., Costanzo, M., Luongo, G., Pellegrino, L., Cennamo, N. and Natale, C.

Safe Robotized Polishing of Plastic Optical Fibers for Plasmonic Sensors.

DOI: 10.5220/0011123100003271

In Proceedings of the 19th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2022), pages 361-368

ISBN: 978-989-758-585-2; ISSN: 2184-2809

361

tion to ensure a proper abrasion of the plastic ﬁber

cladding. This requires a force/motion control algo-

rithm (Villani, 2020) and the approach proposed in

this paper is inspired to (Haddadin et al., 2009), which

is speciﬁcally suitable for elastic joint manipulators.

A relevant aspect of any force control robotic appli-

cation is the speciﬁcation of the desired force proﬁle.

This work followed the well-known programming by

demonstration strategy (Calinon, 2018); a human op-

erator performs the task which has to be repeated by

the robot and the necessary data are acquired. In this

case, the contact force proﬁle is recorded and a Gaus-

sian Mixture Model is learned and then used to gen-

erate the force proﬁle to track with the force control

loop. The robot control system is eventually com-

pleted with a safe reaction strategy to the presence

of human operators close to the robot arm. The robot

workspace is constantly monitored by a RGB-D cam-

era which track the skeletons of all human operators

inside the workspace. The skeleton data are then used

to compute the minimum distance from the robot that

is the basis for a virtual repulsive action on the robot

elbow which pushes this far away from the human op-

erator. As soon as the operator goes out the robot

worksapce, the elbow is brought to its nominal con-

ﬁguration by an elastic torque.

The collaborative robotic cell has been tested for

the production of 10 sensor platforms, which have

then been tested by using several water-glycerin solu-

tions with different refractive indices. The results in

terms of sensitivity and full width at half maximum

of the resonance curve of all sensors demonstrate that

the robotized polishing process ensures the expected

quality and relieves the human operator from a rele-

vant physical burden.

2 PRODUCTION PROCEDURE

OF THE SPR-POF SENSOR

Intrinsic POF plasmonic sensors, where the mod-

iﬁed POF interacts with the analyzed medium di-

rectly, have been presented to exploit different ap-

proaches, such as making a D-shaped POF sensing

region. More speciﬁcally, about ten years ago, Cen-

namo et al. have presented a very simple to realize,

low-cost, and high sensitive SPR sensor in Plastic Op-

tical Fibers (Cennamo et al., 2011). To realize this

SPR-POF sensor are necessary only three steps. In

the ﬁrst step, the optical ﬁber is ﬁxed in a resin block

to remove the cladding and part of the core in order to

realize a D-shaped POF sensing area. These polishing

steps are handmade exploiting two different polishing

papers: a 5µm polishing paper and a 1 µm polishing

Figure 1: The collaborative robot for sensor polishing with

the reference desk frame (RGB convention).

paper. The realized D-shaped sensing region is about

10mm in length. In the second step, a thin buffer layer

(e.g. a layer of Microposit S1813 photoresist), a layer

with a refractive index major than the core of the POF,

is deposited by a spin coater, to improve the interac-

tion between the light and the plasmonic (SPR) phe-

nomenon. Finally, in the third step, a gold nano-ﬁlm

(about 60 nanometers) is deposited by a sputter coater.

The used POF has a PMMA core of 980µm and a ﬂu-

orinated polymer cladding of 10 µm (1,000 µm in total

diameter). The experimental results reported in (Cen-

namo et al., 2011) have indicated that the conﬁgura-

tion with the buffer layer exhibits better performance

in terms of detectable refractive index range and of

full width at half maximum of the SPR curve. In this

work, sensor conﬁgurations without the buffer layer

will be realized and tested. The buffer layer has been

not used to test the automatic polishing process.

3 THE COLLABORATIVE CELL

This section describes the approach used to automate

the polishing task of the SPR-POF sensor through the

collaborative work cell shown in ﬁgure 1, in which

a seven-joint robot and humans can work together.

A Cartesian force/compliance control algorithm has

been used to carry out the polishing task. A depth

camera has been used to detect and avoid collisions

with human operators in the robot workspace.

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

362

3.1 Perception System

The depth camera is a Microsoft Kinect v1 (see Fig-

ure 1). To correctly use the data provided by the cam-

era in the robot control algorithm, it is necessary to

perform the extrinsic calibration procedure aimed at

determining the homogeneous transformation matrix

representing the pose of the camera frame with

respect to the robot base frame. The following cali-

bration procedure has been used:

1. A reference frame on the desk has been chosen as

shown in Fig. 1.

2. Using an algorithm for the reconstruction of Point

Cloud, the following three points have been iden-

tiﬁed: the origin of the desk frame, a point of the

x axis and a point of the y axis of the desk frame.

The three points were then used to compute the

homogeneous transformation matrix T

desk

3. By positioning the robot through hand guidance

and calculating the end-effector position through

the direct kinematics, the following three points

have been identiﬁed: the origin of the desk frame,

a point of the x axis and a point of the y axis of the

desk frame. The three points were then used to

compute the homogeneous transformation matrix

desk

4. The homogeneous transformation matrix T

eventually computed as

= T

desk

)

−1

(1)

3.2 Skeleton Tracking

Realizing a safe Human Robot Collaboration (HRC)

application requires a fast tracking algorithm which

detects human operators in real time. For this pur-

pose, the NiTE’s skeleton tracking algorithm has been

used. OpenNI/NiTE is a well known open-source

framework that provides a set of APIs for body mo-

tion tracking that work with several perception sys-

tems, including the Microsoft Kinect v1 (PrimeSense,

2011). The algorithm tracks 15 joints for each oper-

ator in the scene in the form of a skeleton (see ﬁgure

2b) and returns the 3D position for each one of them:

i,k

, k = 1, 2,.. .,15, i = 0, ... ,N, being N the num-

ber of operators, that is 0 if no operator is detected

in the scene. These positions are then used to com-

pute the minimum distance d between a point on the

robot elbow with position p

and all human opera-

tors joints. Spheres were used to incorporate the un-

tracked body portions and improve safety: a sphere

with radius r

= 0.14 m was chosen for the head joint,

(a) Human operator close to the robot.

(b) Kinect depth view with the skeleton overlay.

Figure 2: The perception system for workspace monitoring.

a sphere with radius r

= 0.11m for the robot el-

bow and spheres with radius r

= 0.07 m for the other

joints of the skeletons. Once every captured joint po-

sition is expressed in the robot base frame through the

homogeneous transformation matrix T

, the compu-

tation of d proceeds as follows

1. For each operator i in the scene, compute the min-

imum distance from the robot elbow and the hu-

man joints

= min

d(p

i,k

) i = 1,. .., N (2)

where d(p

i,k

) is computed as

d(p

i,k

) =

(

−s

i,k

k−(r

+ r

) if r

+ r

≤ kp

−s

i,k

0 otherwise

2. Determine the minimum distance d as the smallest

distance among the previously calculated ones

d = min

(3)

To correctly use the computed distance d in the con-

trol law of Section 3.3, the position s

n,m

of the closest

joint (m) of the closest operator (n) is stored.

Safe Robotized Polishing of Plastic Optical Fibers for Plasmonic Sensors

363

3.3 Robot Control System

The torque control law proposed in this paper consists

of three terms, i.e.,

τ (t) = τ

(t) + τ

(t). (4)

The ﬁrst term τ

(t) corresponds to the

force/compliance control law, a hybrid force control

scheme, which provides the robot with the capability

to track a motion trajectory along the directions

lying on the plane of the sandpaper while following

a force proﬁle in the orthogonal direction. In detail,

the ﬁrst control torque has been selected inspired by

the passivity approach proposed in (Schindlbeck and

Haddadin, 2015)

(t) = J

(q(t))

˜x(t) + K

(t) −h

(t))

(σ) −h

(σ))dσ + K

˜x(t)



(5)

where ˜x(t) = x

(t)−x

(t) is the pose tracking error,

∈R

6x6

and K

∈R

6x6

are the position and damp-

ing gain positive deﬁnite diagonal matrices, K

∈

6x6

and K

∈ R

6x6

are diagonal positive deﬁnite

matrices for the proportional and the integral control

action on the force error, respectively, J(q) is the ma-

nipulator Jacobian, consistent with the chosen orien-

tation representation, and h

(t) = (f

(t) 0

)

and

(t) = (f

(t) µ

(t))

are the desired and the mea-

sured wrench vectors at the end effector, respectively.

Note that, friction and gravity compensation terms are

not reported since they are applied at low-level by the

control interface of the robot.

The second term τ

(t) is designed to endow the

collaborative robot with a collision avoidance behav-

ior. Time dependence will be omitted for brevity. The

term τ

consists of two contributions:

1. τ

rep

. This term corresponds to a repulsive wrench

, computed starting from the minimum distance

d, so as to generate an internal motion that moves

the elbow away from the operator. The repulsive

wrench is deﬁned as

= (f

)

where f

has been selected inspired by (Flacco

et al., 2012) as follows

max

1 + e



d−1



u (6)

where F

max

is the maximum admissible magni-

tude, α is a shape factor, ρ represents the distance

at which the magnitude of the repulsive force will

approach zero and u is the unit vector along the

direction deﬁned by

u =

−s

n,m

−s

n,m

The torque τ

rep

is obtained by premultiplying the

repulsive wrench by the transpose of the Jacobian

) of the manipulator consisting of

the ﬁrst 4 links only, i.e.,

rep



)

3×6



(7)

2. τ

. This term generates an elastic action so as to

bring back the manipulator in the high-elbow con-

ﬁguration when no operator is in the workspace.

= K

−q), (8)

where K

∈ R

7x7

is the stiffness matrix, q

a high-elbow conﬁguration and q is the current

conﬁguration of the manipulator.

To ensure that the primary task is performed accu-

rately even in the presence of an operator in the

collaborative workspace, the repulsive and elastic

torques have been projected into the null space of

the transpose of the dynamically consistent pseudo-

inverse of the Jacobian

(q) (Khatib, 1987), i.e.,



I −J

(q)



rep

+ τ



(9)

The third term τ

(t) is a compensation term,

which ensures that the projected torque τ

(t) does not

contribute to the end-effector acceleration, namely

= −B(q)

J(q)

J(q, ˙q) ˙q (10)

4 LEARNING FROM THE

HUMAN OPERATOR

The polishing task requires a long training phase of

the human operator, not only in terms of the speciﬁc

motion trajectory required to rub the optical ﬁber on

the sandpaper, but also in terms of the normal force

proﬁle applied during the polishing. Therefore, we

decided to transfer this skill from a trained human op-

erator to the robot through a learning by demonstra-

tion approach (Calinon, 2018).

The ﬁrst step of the learning from demonstration

process is that of data acquisition. If it is well known

that the motion trajectory to follow during the pol-

ishing process is a 8-shaped ﬁgure (Cennamo et al.,

2011), no information on the most suitable normal

force proﬁle can be found in the literature. Thus, the

actual force applied by a well-trained human operator

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

364

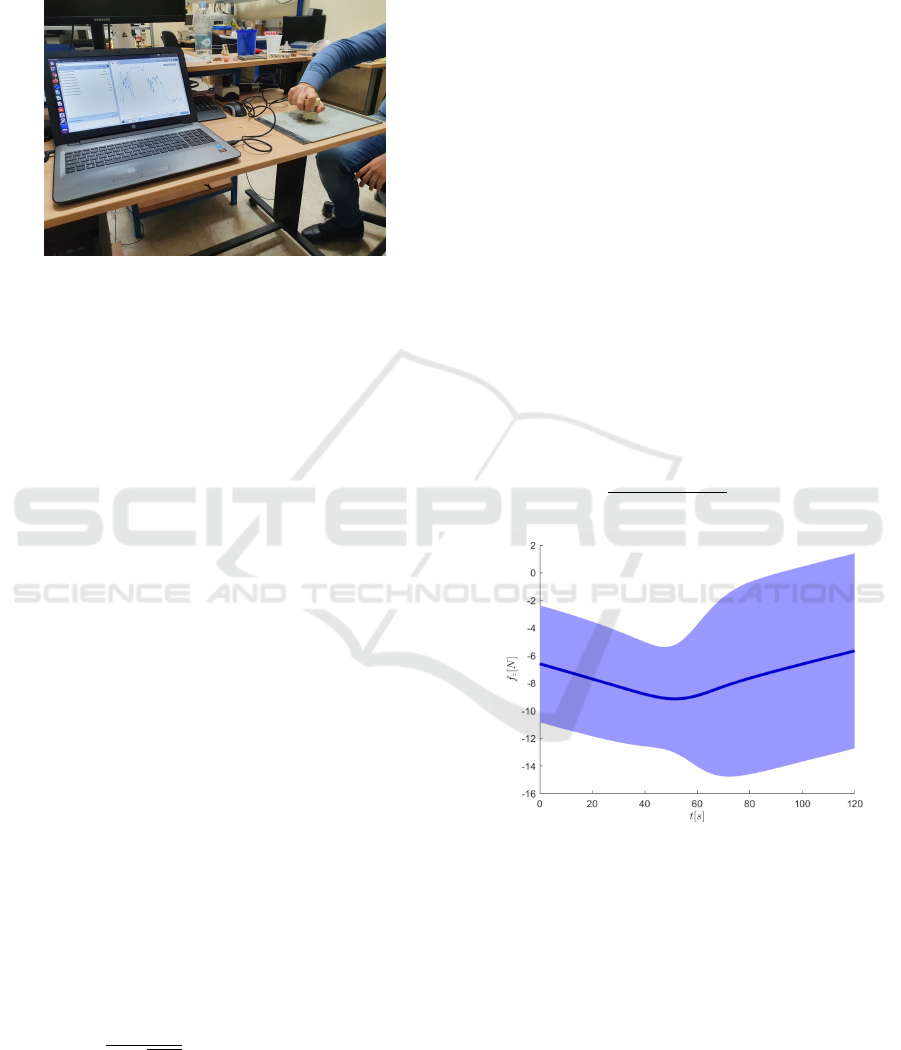
was acquired during a set of polishing trials through

a 6D force sensor mounted on an handle suitably de-

signed to keep the sensor platform hosting the POF in

contact with the sandpaper.

Figure 3: The human observation system.

The setup for the human observation depicted in

Fig. 3 includes a Robotous RFT-40 force/torque sen-

sor connected to a Ubuntu laptop via USB, so as to

acquire the contact force along the normal to the sur-

face at a rate of 200Hz.

4.1 Contact Force Planning

The desired force proﬁle f

(t) used in the robot

controller presented in Section 3.3 is generated by

a Gaussian Mixture Regression (GMR), which was

trained on the basis of the force data set acquired dur-

ing four polishing trials, each 2minutes long. In par-

ticular, the chosen Gaussian Mixture Model (GMM)

of K Gaussian components (Calinon, 2018) is deﬁned

by the probability density function

p(ξ) =

∑

k=1

p(k)p(ξ|k), (11)

where ξ is the generic data point of the data set, p(k)

is the prior and p(ξ|k) is the conditional probability

density function. A temporal regression problem for

the normal force trajectory has to be solved, hence

each data point is a couple ξ = (t f

)

∈ R

and the

parameters of the model are {p(k), µ

,Σ

}

k=1

, being





, Σ



t f



(12)

the mean and the covariance matrix of the normal dis-

tribution of the kth component, respectively, i.e.,

p(ξ|k) =

2π

|Σ

−1/2(ξ−µ

)

−1

(ξ−µ

)

. (13)

These parameters can be estimated through the

standard expectation maximization (EM) algorithm

(Dempster et al., 1977). The method ﬁrst requires an

estimation of the number of components K and this

can be carried out by training multiple models with

different values of K and then selecting the value of

K that optimize a given criterion. In this paper ten

models have been estimated with K = 1, ... ,10 and

the Bayesian information criterion (BIC) has been

adopted (Schwarz, 1978) to select the the optimal

number of components K = 2.

Once the model has been trained, a GMR is used

to generate the desired contact force proﬁle f

(t) =

(0 0 f

(t))

(Cohn et al., 1996), i.e.,

(t) = β

(t) + β

(t) (14)

= β

+ β

(15)

where

(t) = µ

+ σ

f t,k

/σ

(t −µ

) (16)

= σ

−σ

t f

/σ

(17)

are the conditional expectation and covariance of the

desired force given the time t of each component. The

two components are then weighted by the probability

that the Gaussian component k has, being responsible

for t, namely

p(t|k)

p(t|1) + p(t|2)

, k = 1, 2. (18)

Figure 4: Result of the GMR retrival process.

Figure 4 reports the desired force proﬁle generated

by the GMR (14),(15), which has an average around

−7N but with a signiﬁcant variance due to the large

variability of the force exerted by the human operator

in the different polishing trials despite his/her skill.

4.2 Motion Trajectory Planning

In order to execute the 8-shaped ﬁgure described in

Section 2, the end-effector path has been deﬁned ac-

cording to a Lissajous ﬁgure, which is a curve lying

Safe Robotized Polishing of Plastic Optical Fibers for Plasmonic Sensors

365

on a plane with parametric equation

x(t) = A

sin(ω

t + φ)

y(t) = A

sin(ω

t + φ)

t ∈ [0,2π] (19)

The shape of the curve is highly sensitive to the ra-

tio ω

/ω

. In particular, the Lissajous ﬁgure that best

suits the polishing task considered in this work is the

one obtained with ω

/ω

= 1/2 that corresponds to a

8-shaped path. To allow the robot end effector follow

the path described by the previous parametric equa-

tions, the desired end-effector position with respect to

a frame f centered in the center of the Lissajous ﬁgure

has to follow the path primitive

(s) =





sin(ω

2πk

s + π/2)

sin(ω

2πk





s ∈ [0,L] , (20)

where L is the total path length (k times the length

of a single Lissajous ﬁgure, being k the lap num-

ber). Denoting with c

the position of the origin of

the Lissajous ﬁgure and with R

the rotation matrix

representing the orientation of the Lissajous frame f

with respect to the robot base frame, the end-effector

planned position with respect to robot base frame is

(s) = c

+ R

(s).

To obtain a desired end-effector position trajectory, a

time law linked to the path described by the Lissajous

ﬁgure is necessary. This can be accomplished by us-

ing a ﬁfth-order polynomial with zero initial and ﬁnal

velocity and acceleration.

Finally, the desired orientation trajectory has to

be speciﬁed, representing the end-effector orientation

with the XYZ set of Euler angles. By making sure

that at the beginning of the task the approach axis of

the end-effector frame is orthogonal to the table, the

desired orientation is set constant, i.e.,

(t) = φ

(0) = φ

Moreover, in order to avoid the representation singu-

larity (the pitch angle equal to π/2), the end-effector

frame has been rotated of 180deg about the y axis

of the nominal end-effector frame so as to align the

end-effector frame with the robot base frame, namely

φ = 0. Eventually, the desired end-effector pose used

in the control law (5) is

(t) =



(s(t))



, ˙x

(t) =



˙p

(s(t))



. (21)

5 EXPERIMENTAL VALIDATION

This section discusses the results obtained with the

control law described in Section 3.3 in terms of per-

formance of the robot and quality of the SPR-POF

sensor obtained at the end of the polishing.

5.1 Testing of the Robot Controller

The following parameters have been selected for the

control law described in Section 3.3

= diag{2000, 2000, 650, 140, 140, 140}

= diag{0, 0, 0.5, 0, 0, 0}

= diag{100, 100, 650,

√

50,

√

50,

√

50}

= diag{0, 0, 1, 0, 0}, K

= 5.5I

The proportional gain K

along x and y directions has

been chosen high enough to obtain a tracking error in

the order of 1 cm, while along the z direction it has

been chosen lower because along that direction the

force control action should predominate. The damp-

ing gain K

has been chosen so as to obtain a well-

damped behaviour along all directions. The propor-

tional K

and integral K

gains of the force con-

troller have been tuned based on a linearized model

of the system obtained considering an estimated con-

tact stiffness of about 2600N/m. Finally, the elastic

gain K

has been set as a trade off between the sensi-

tivity to the virtual repulsive wrench f

in (6) and the

elastic torque that drives the elbow point towards the

equilibrium conﬁguration q

in (8).

Figure 5: Minimum distance d during the experiment.

During the experiment a human operator has been

trained to enter the robot workspace while the polish-

ing task was being executed. The minimal distance d

between the human operator and the robot elbow is re-

ported in Fig. 5. Some spikes can be observed in the

ﬁgure due to an occasionally wrong tracking of the

skeleton by the Primesense algorithm. Nevertheless,

their duration is negligible and they are ﬁltered out by

the torque controller, hence no corrections have been

made.

Joint torque commands computed by the control

algorithm in (4) allow the manipulator end-effector

follow the Lissajous ﬁgure as reported in Fig. 6. Po-

sition and orientation errors are shown in Fig. 7.

During the polishing, the force f

generated by the

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

366

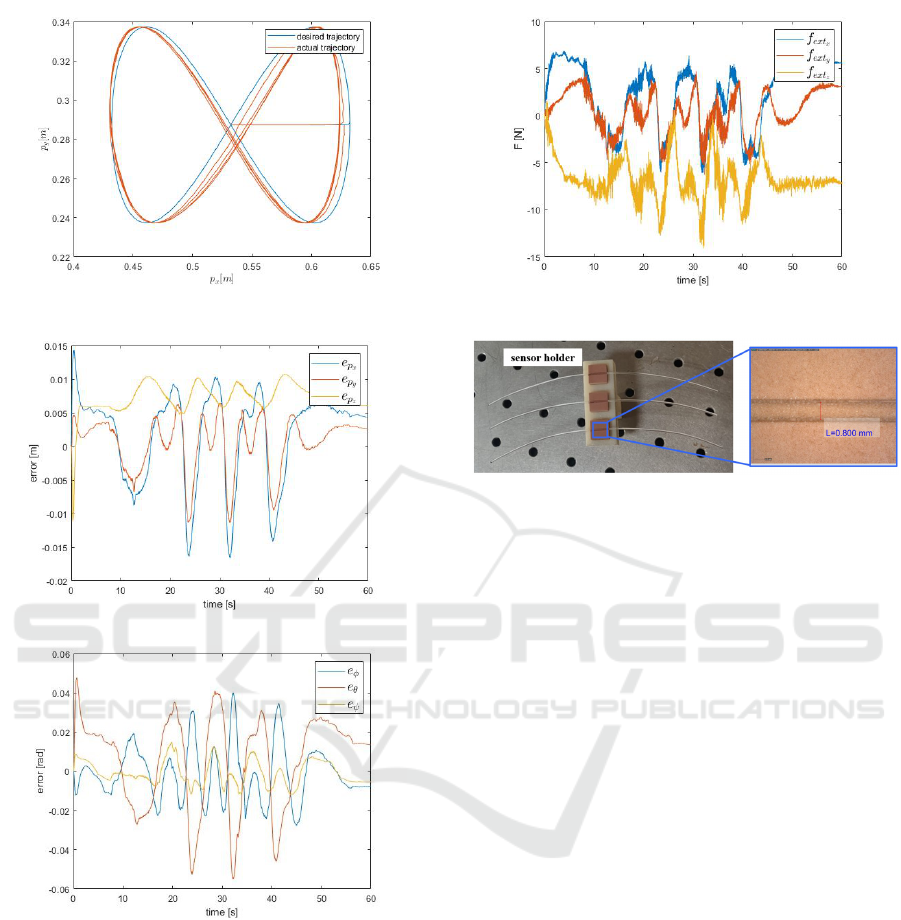
Figure 6: Desired and actual trajectories.

(a) Position tracking error.

(b) Orientation tracking error.

Figure 7: Position and orientation tracking errors.

contact between the ﬁber and the sandpaper on the ta-

ble is shown in Fig. 8. The x and y components are

due to the friction necessary to carry out the polish-

ing task successfully, hence they should not be coun-

teracted, that is why proportional and integral gains

along these directions are zero. The contact force

has been estimated from joint torques and a dynamic

model of the robot, according to the algorithm in (Ma-

grini et al., 2014).

Figure 8: Force proﬁle during motion.

Figure 9: Top view of three POF sensor platforms at the

end of the polishing task. The digital microscope view on

the right shows the obtained length of the D-shaped ﬁber.

5.2 Sensor Production

Figure 9 shows the designed sensor holder, together

with a view of the polished region, for one of the

three sensors through a digital microscope. The D-

shaped POF width of about 0.8mm has been ob-

tained through the automatic polishing process after

one minute. It is worth emphasizing that the imple-

mented automated procedure leads to noticeable time-

saving. A reduction of about 70% can be achieved

with respect to the handmade one. Note that the use

of a robot for performing the polishing process allows

to accurately control the depth of the D-shaped POF

area and its roughness, by acting on the desired con-

tact force and the speed of the motion trajectory. The

depth parameter is particularly relevant for the sen-

sor performance as it affects the quality factor of the

plasmonic resonance (Gasior et al., 2014). After the

automatic polishing process, a gold sputtering process

has been used to realize the SPR-POF sensor.

5.3 Sensor Testing

Figure 10 reports the SPR transmission spectra ob-

tained experimentally, normalized to the spectrum

achieved with air as the surrounding medium, for sev-

eral water-glycerin solutions with a refractive index

ranging from 1.332 to 1.371. In particular, these re-

sults have been obtained exploiting a sensor conﬁgu-

ration without a buffer layer. So, after the automatic

Safe Robotized Polishing of Plastic Optical Fibers for Plasmonic Sensors

367

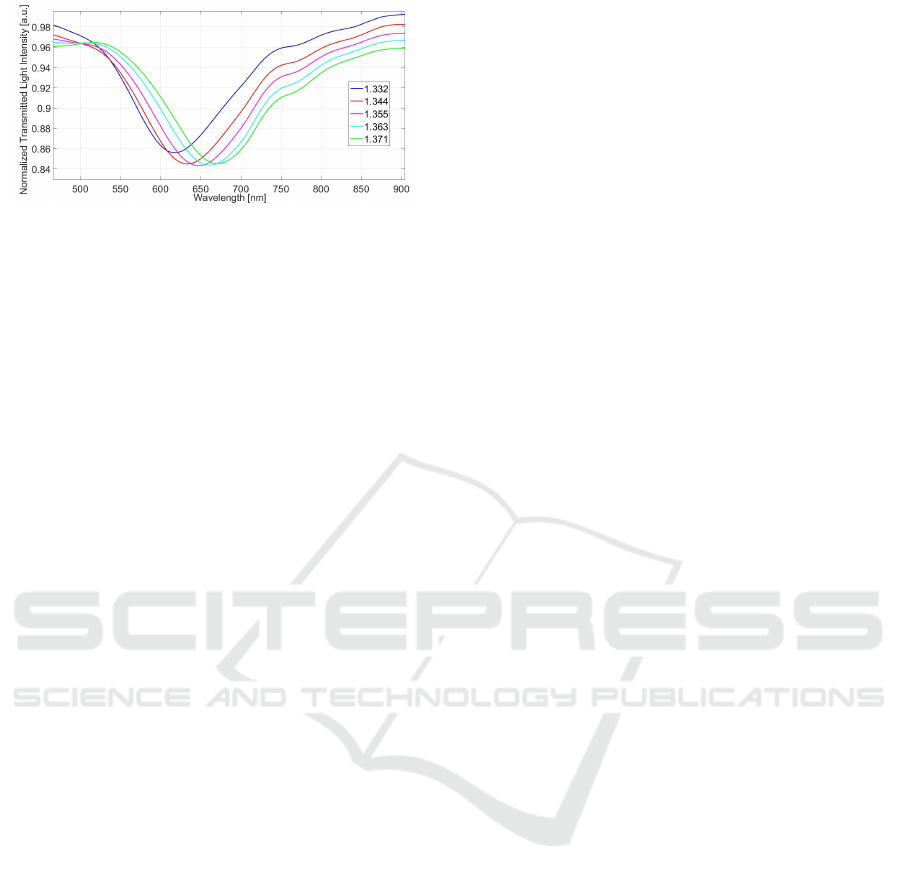
Figure 10: SPR spectra obtained by a D-shaped POF sen-

sor without the buffer layer (with a gold nanoﬁlm on the

core of POF, directly) at different water-glycerin solutions

in contact with the gold nanoﬁlm.

polishing process here proposed, only a gold sputter-

ing has been used to carry out the SPR-D-shaped POF

sensor. We have characterized the SPR-POF sensor

conﬁguration without the buffer layer to better test the

automatic polishing process here proposed. With re-

spect to the SPR curves reported in (Cennamo et al.,

2011) in the same conﬁguration, the SPR curves here

obtained present better performances in terms of full

width at half maximum of the SPR curve, due to the

automatic polishing process here proposed.

6 CONCLUSIONS

The experimental results presented in this paper

demonstrate the feasibility of the proposed approach

for automatic production of a SPR-POF sensor based

on the human-robot collaboration paradigm. The

robotized polishing phase results into a duration 70%

shorter than the current handmade process. The qual-

ity of the polishing process is at least comparable to

the handmade one as demonstrated by the SPR-POF

sensor tests. A characterization of the actual rough-

ness will be carried out by resorting to Atomic force

microscope measurements. This will allow to opti-

mize the process parameters. Moreover, the possi-

bility to establish the contact force so as to obtain a

given D-shaped depth with the aim to optimize the

plasmonic resonant quality factor will be investigated.

ACKNOWLEDGEMENTS

This work was supported by the VALERE program of

the University of Campania, CAMPANIA project.

REFERENCES

Calinon, S. (2018). Learning from Demonstration (Pro-

gramming by Demonstration), pages 1–8. Springer

Berlin Heidelberg, Berlin, Heidelberg.

Cennamo, N., Massarotti, D., Conte, L., and Zeni, L.

(2011). Low cost sensors based on spr in a plastic

optical ﬁber for biosensor implementation. Sensors

(Basel), 11(12):11752–11760.

Cennamo, N., Pesavento, M., and Zeni, L. (2021). A re-

view on simple and highly sensitive plastic optical

ﬁber probes for bio-chemical sensing. Sens. and Act.

B: Chemical, 331:129393.

Cohn, D., Ghahramani, Z., and Jordan, M. (1996). Active

learning with statistical models. J. Art. Intell. Res.,

4:129–145.

Dempster, A., Laird, N., and Rubin, D. (1977). Maxi-

mum likelihood from incomplete data via the em al-

gorithm. J. Royal Statist. Soc.: Series B (Methodolog-

ical), 29(1):1–38.

Flacco, F., Kroger, T., Luca, A. D., and Khatib, O. (2012). A

depth space approach to human-robot collision avoid-

ance. In 2012 IEEE Int. Conf. on Rob. and Aut. IEEE.

Gasior, K., Martynkien, T., and Urbanczyk, W. (2014).

Effect of constructional parameters on the perfor-

mance of a surface plasmon resonance sensor based

on a multimode polymer optical ﬁber. Appl. Opt.,

53(35):8167–8174.

Haddadin, S., Albu-Schaffer, A., Frommberger, M., Ross-

mann, J., and Hirzinger, G. (2009). The dlr crash

report: towards a standard crash-testing protocol for

robot safety - part II: Discussions. In 2009 IEEE Int.

Conf. on Rob. and Aut., pages 280–287. IEEE.

Khatib, O. (1987). A uniﬁed approach for motion and force

control of robot manipulators: The operational space

formulation. IEEE J. Rob. and Aut., 3(1):43–53.

Magrini, E., Flacco, F., and De Luca, A. (2014). Estimation

of contact forces using a virtual force sensor. In 2014

IEEE/RSJ Int. Conf. on Intell. Rob. and Syst., pages

2126–2133.

Natale, C. (2019). Physical Human-Robot Interaction,

pages 1–9. Springer London, London.

PrimeSense (2011). PrimeSense NITE Algorithms

1.5. https://www.yumpu.com/en/document/view/

11580035/primesense-nite-algorithms-15-openni.

Accessed on December 2021.

Schindlbeck, C. and Haddadin, S. (2015). Uniﬁed passivity-

based cartesian force/impedance control for rigid and

ﬂexible joint robots via task-energy tanks. In 2015

IEEE Int. Conf. on Rob. and Aut. (ICRA), pages 440–

447.

Schwarz, G. (1978). Estimating the dimension of a model.

Annals of Statistics, 6(2):461–464.

Siciliano, B., Sciavicco, L., Villani, L., and Oriolo, G.

(2009). Robotics – Modelling, Planning and Control.

Springer.

Villani, L. (2020). Hybrid Force and Position Control,

pages 1–6. Springer Berlin Heidelberg, Berlin, Hei-

delberg.

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

368