SEVIL: Secure and Efficient VerifIcation over Massive Proofs of
KnowLedge
Souha Masmoudi
1,2 a
, Maryline Laurent
1,2 b
and Nesrine Kaaniche
1,2 c
1
SAMOVAR, Telecom SudParis, Institut Polytechnique de Paris, Evry, France
2
Member of the Chair Values and Policies of Personal Information, Institut Mines-Telecom, Paris, France
Keywords:
Group Signatures, NIWI Proofs, Aggregated Verification, Batch Verification.
Abstract:
This paper presents SEVIL, a group signature construction that offers an efficient, aggregated and batch ver-
ification over multiple signatures. The proposed group signature scheme is built upon Groth-Sahai Non-
Interactive Witness-Indistinguishable proofs, in an effort to reduce the computation complexity, closely as-
sociated with the number the number of signatures. SEVIL fulfills the main security and privacy properties,
proven through a detailed analysis. The implementation of SEVIL algorithms demonstrates the high efficiency
of the aggregated and batch verification with up to 50% of gain in comparison with naive verification of NIWI
proofs.
1 INTRODUCTION
The emergence of data-centric applications and ser-
vices have asserted various concerns related to the
massive data collection and analysis by different ac-
tors belonging to different levels of trust. Thus, the
need to continuously authenticate data origin and ver-
ify its integrity has significantly increased. To achieve
the aforesaid security requirements, digital signatures
are commonly considered as promoting cryptographic
primitives and main building blocks of authentication
protocols. However, in a multi-owner context, ad-
ditional requirements are needed, namely (i) ensur-
ing that various signers are trustful and (ii) protecting
their privacy.
For this purpose, group signatures are the best
primitive to fulfill the desired properties. In fact,
group signatures allow a group member to sign a mes-
sage on behalf of the group while remaining anony-
mous. Group signatures support privacy properties,
namely unlinkability. Indeed, they prevent both the
linkability between multiple signatures issued by the
same member and the identification of the signer of
a given signature. However, in order to ensure that a
signer is trustworthy, the signing key should be ver-
ified, which harms the signer’s privacy. Thus, to en-
sure the trade-off between trust and privacy, the group
signature scheme might rely on a proof of knowl-
a
https://orcid.org/0000-0002-7194-8240
b
https://orcid.org/0000-0002-7256-3721
c
https://orcid.org/0000-0002-1045-6445
edge (PoK) scheme. A proof of knowledge enables a
prover (i.e., signer) to convince a verifier that he owns
a secret (i.e., a valid pair of keys) without disclosing
it, in an interactive session.
Giving consideration to the huge number of proofs
collected, in many applications, and to the process-
ing time needed to verify a single proof, there is a
crucial need to optimize the verification algorithm by
verifying multiple proofs at once. To this question,
batch verification has been introduced by Naccache
et al. (Naccache et al., 1994) enabling the verification
of multiple signatures generated by different signers.
Batch verification has been applied to some group sig-
nature schemes to efficiently verify the huge number
of transactions on Blockchain (Zhang et al., 2021) and
data transmitted in the Internet of Things (Alamer,
2020). However, to the best of our knowledge, no
batch verifier has been constructed over PoK-based
group signature schemes, i.e., signatures that endorse
the verification of the signer key.
In this paper, we present SEVIL, a novel group
signature that offers an efficient, aggregated and
batch verification over multiple Groth-Sahai Non-
Interactive Witness-Indistinguishable proofs (Groth
and Sahai, 2008). SEVIL supports a decentralized
data certification and a centralized multi-signer data
aggregated and batch verification. Indeed, SEVIL al-
lows a signer, belonging to a trusted group, to gen-
erate anonymous group signature (i.e., NIWI proof).
Relying on this proof, the signer is able to prove to
a verifier the integrity of the data without revealing
the signing keys. For efficiency reasons, the verifier
Masmoudi, S., Laurent, M. and Kaaniche, N.
SEVIL: Secure and Efficient VerifIcation over Massive Proofs of KnowLedge.
DOI: 10.5220/0011125800003283
In Proceedings of the 19th International Conference on Security and Cryptography (SECRYPT 2022), pages 13-24
ISBN: 978-989-758-590-6; ISSN: 2184-7711
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
13

is given the capacity to proceed to the verification of
multiple proofs at once. If the batch verification fails,
the verifier proceeds to a divide and conquer verifi-
cation. It splits the list of proofs into sub-lists and
performs verification to each sub-list recursively until
all invalid signatures are identified.
In a nutshell, SEVIL satisfies several properties of
interest. First, it ensures data integrity without reveal-
ing the data contents, thanks to the use of proofs of
knowledge. Second, SEVIL ensures a high level of
security as it allows the verifier to check the valid-
ity of signers’ keys. Third, the proposed system pre-
serves signers’ privacy. It ensures that a verifier is
not able to link two or several pieces of information
signed by the same signer. Fourth, SEVIL proposes
a concrete construction of its algorithms, while giv-
ing a detailed aggregated and batch verification over
Groth-Sahai NIWI proofs. Finally, a complete imple-
mented prototype of SEVIL, introducing two steps of
computation improvements (multithreading and pre-
processing), proves its efficiency as the aggregated
verification reaches a gain of up to 50% compared to
the individual verification.
The remainder of this paper is organized as fol-
lows. Section 2 presents the design system and goals
of this work including the involved entities and the
desired security, privacy and performance properties.
Section 3 gives an overview of the solution and a high
level presentation of its phases and algorithms. After
presenting the underlying cryptographic background
in Section 4, the proposed scheme is introduced in
Section 5. Security and performance discussions are
given in Section 6 and Section 7, respectively. Section
8 compares most closely-related works to SEVIL. Fi-
nally, Section 9 concludes the paper.
2 DESIGN SYSTEM AND GOALS
This section defines the involved entities and illustrate
the design goals that need to be supported by SEVIL.
2.1 Design System
As depicted in Figure 1, SEVIL involves four different
entities, defined as follows:
• The trusted authority (T A), is the central entity
which is responsible for initializing the whole sys-
tem.
• The signer (S) signs data on behalf of a group of
signers. The group of Ss is dynamically generated
and managed by a group manager (G).
• The group manager (G) sets-up the group of sign-
ers and certifies their keys.
• The verifier (V ) checks the correctness of the re-
ceived data and their associated signatures of mul-
tiple signers in a single transaction.
2.2 Design Goals
The design of SEVIL is motivated by the fulfillment
of the following security and performance properties.
2.2.1 Security and Privacy Requirements
The proposed SEVIL system aims at ensuring the fol-
lowing security and privacy requirements:
• unforgeability: ensures that malicious entities
are not able to forge signatures over data.
• unlinkability: ensures that an attacker is not able
to link several signatures to the same signer.
2.2.2 Performance Requirements
SEVIL system should consider the following require-
ments for efficiency purposes:
• Computation Overhead: SEVIL should provide
low computation overhead, i.e. should have effi-
cient verification time even with high number of
messages.
• Communication Overhead: SEVIL should pro-
vide low communication overhead, i.e. should
maintain an acceptable communication cost be-
tween entities.
3 SEVIL Overview
SEVIL involves three main phases: SETUP, SIGNING
and VERIFYING presented hereafter.
The SETUP phase consists of initializing the
whole system. It relies on three algorithms, referred
to as Set params, Setup SGr
G
and Join SGr
S/G
.
During the SETUP phase, a trusted authority generates
the system public parameters published to all involved
entities, relying on Set params algorithm. The group
manager defines the group of signers. It generates the
group signature parameters using the Setup SGr
G
al-
gorithm and it interacts with each group member (i.e.,
signer) to derive the associated keys relying on the
Join SGr
S/G
algorithm.
The SIGNING phase occurs to sign a message m.
Indeed, a signer generates a group signature over the
message m, while executing the G Sign
S
algorithm.
The resulting signature is locally stored.
SECRYPT 2022 - 19th International Conference on Security and Cryptography
14

Figure 1: SEVIL Architecture.
The VERIFYING phase is run by the verifier to
check the correctness of the signed data provided by
multiple signers in a single transaction. Indeed, V
executes the Batch Verify
V
algorithm to verify mul-
tiple group signatures issued by members of the same
group, in a single verification. Note that if the batch
verification fails, V should proceed progressively by
dividing the data list in sub-lists and then by verifying
the invalid sub-list message by message. To verify a
single message, V performs the Agg Verify
V
Hereafter, we detail the three phases of SEVIL
including the five algorithms that are represented in
a chronological sequence in Figure 2. Note that
Agg Verify
V
algorithm is not represented in the se-
quence as it occurs only when the batch verification
fails.
For ease of presentation, we consider only two
signers in the sequence diagram. Recall that verifica-
tion can be performed on a large number of messages
generated by the same signer or by different signers.
3.1 SETUP Phase
The SETUP phase initializes the whole system, re-
lying on three main algorithms, referred to as:
Set params, Setup SGr
G
and Join SGr
S/G
defined as
follows.
• Set params(λ) → pp – performed by the trusted
authority. Given the security parameter λ, this al-
gorithm generates pp i.e., the system public pa-
rameters that will be given as a default input for
all the following algorithms.
• Setup SGr
G
() → (sk
G
,vk
G
) – run by the group
manager in order to set up the group signature pa-
rameters. It returns the signers’ group verifica-
tion key vk
G
encompassing pk
G
the public key of
the group manager and Σ
NIWI
of a Non-Interactive
Witness-Indistinguishable (NIWI) proof (Groth
and Sahai, 2008) associated with the public key.
The Setup SGr
G
algorithm also outputs the secret
key sk
G
of G.
• Join SGr
S/G
(sk
G
) → (sk
S
,pk
S
,σ
k
) – executed
through an interactive session between the signer
and the group manager. It takes as input the secret
key sk
G
of the group manager, and outputs the
pair of keys (sk
S
,pk
S
) of the group member (i.e.,
signer) S, and a signature σ
k
over S’s public key
pk
S
. Indeed, S is responsible for generating his
pair of keys, while G is in charge of the signature
σ
k
generation aiming to certify S’s keys.
3.2 SIGNING Phase
The SIGNING phase is performed by a signer. In this
phase, S relies on the G Sign
S
algorithm to sign a
message m ∈ G
2
:
• G Sign
S
(vk
G
,sk
S
,pk
S
,σ
k
,m) → (σ
m
,Π) – per-
formed by the signer as a group member. This
algorithm takes as input the group public param-
eters vk
G
, the pair of keys (sk
S
,pk
S
) of S, the
signature σ
k
over S’s public key and the message
m. The G Sign
S
returns a signature σ
m
over the
message m and a NIWI proof Π over the two sig-
natures σ
k
and σ
m
. The proof Π is locally stored
with the message m.
Note that the NIWI proof represents the group signa-
ture generated by S as a group member.
SEVIL: Secure and Efficient VerifIcation over Massive Proofs of KnowLedge
15

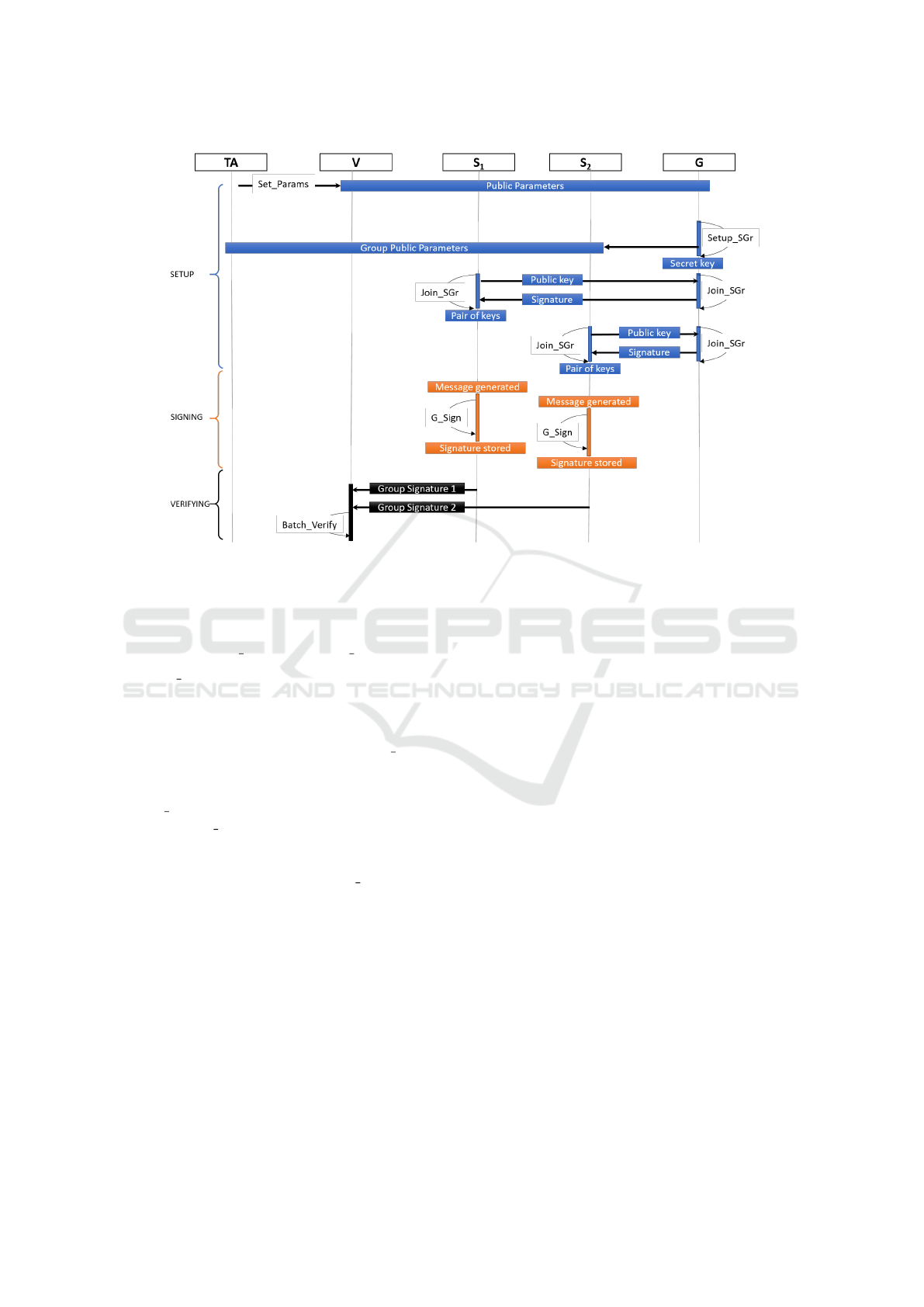
Figure 2: Workflow of the SEVIL system.
3.3 VERIFYING Phase
The VERIFYING phase involves two main algorithms
referred to as Batch Verify
V
and Agg Verify
V
:
• Batch Verify
V
(vk
G
,{m
i
,Π
i
}
N
i=1
) → b – per-
formed by V . Given the public parameters vk
G
, a
list of N messages m
i
and N corresponding proofs
Π
i
sent by multiple signers (i.e., a signer can send
to V more than one message), the Batch Verify
V
algorithm returns a bit b ∈ {0,1} stating whether
the list of proofs is valid or not.
• Agg Verify
V
(vk
G
,m, Π) → b – performed by V
when Batch Verify
V
returns 0 over a list or a sub-
list of messages. Given the public parameters
vk
G
, a message m and the corresponding proof
Π, from an invalid sub-list, the Agg Verify
V
algo-
rithm returns a bit b ∈ {0,1} stating whether proof
is valid or not.
4 CRYPTOGRAPHIC
BACKGROUND
In this section, we first present the Non-Interactive
Witness-Indistinguishable (NIWI) proofs introduced
by Groth and Sahai (Groth and Sahai, 2008). Then,
we propose a group signature scheme built upon
NIWI proofs.
4.1 Non-Interactive
Witness-Indistinguishable Proofs
Here, we present the Groth-Sahai NIWI proof scheme
applied to pairing product equations when consider-
ing an asymmetric bilinear map.
The NIWI scheme, involves four PPT algorithms
(NIWI.Setup, NIWI.CRS, NIWI.Proof, NIWI.Verify):
• NIWI.Setup: This algorithm outputs a setup
(gk,sk) such that gk = (n,G
1
,G
2
,G
3
,g
1
,g
2
,e)
and sk = (p,q) where n = pq.
• NIWI.CRS: This algorithm generates a
common reference string CRS. It takes
(gk,sk) as inputs and produces CRS =
(G
1
,G
2
,G
3
,e,ι
1
, p
1
,ι
2
, p
2
,ι
3
,U, V), where
U = rg
1
, V = sg
2
; r,s ∈ Z
∗
n
and
ι
1
: G
1
→ G
1
ι
2
: G
2
→ G
2
ι
3
: G
3
→ G
3
x 7→ x y 7→ y z 7→ z
p
1
: G
1
→ G
1
p
2
: G
2
→ G
2
p
3
: G
3
→ G
3
x 7→ λx y 7→ λy z 7→ z
λ
• NIWI.Proof: This algorithm generates a NIWI
proof for satisfiability of a set of pairing product
equations of the form of
k
∏
i=1
e(A
i
,Y
i
)
l
∏
i=1
e(X
i
,B
i
)
l
∏
i=1
k
∏
j=1
e(X
i
,Y
i
)
γ
i j
= t
SECRYPT 2022 - 19th International Conference on Security and Cryptography
16

also written as
(
⃗
A ·
⃗
Y )(
⃗
X ·
⃗
B)(
⃗
X · Γ
⃗
Y ) = t
It takes as input gk, CRS and a list of pairing
product equations {(
⃗
A
i
,
⃗
B
i
,Γ
i
,t
i
)}
N
i=1
and a sat-
isfying witness
⃗
X ∈ G
k
1
,
⃗
Y ∈ G
l
2
. To generate
a proof over a pairing product equation, the al-
gorithm, first, picks at random R ← Vec
k
(Z
n
)
and S ← Vec
l
(Z
n
), commits to all variables as
⃗
C :=
⃗
X + R U and
⃗
D :=
⃗
Y + SV, and computes
π = R
⊤
ι
2
(
⃗
B) + R
⊤
Γι
2
(
⃗
Y ) + R
⊤
ΓSV
θ = S
⊤
ι
1
(
⃗
A) + S
⊤
Γ
⊤
ι
1
(
⃗
X )
The algorithm outputs the proof (π,θ).
• NIWI.Verify: This algorithm checks if the proof
is valid. It takes gk, CRS, {(
⃗
A
i
,
⃗
B
i
,Γ
i
,t
i
)}
N
i=1
and
{(
⃗
C
i
,
⃗
D
i
,π
i
,θ
i
)}
N
i=1
as inputs and for each equa-
tion, checks the following equation:
e(ι
1
(
⃗
A
i
),
⃗
D
i
)e(
⃗
C
i
,ι
2
(
⃗
B
i
))e(
⃗
C
i
,Γ
i
⃗
D
i
) = ι
3
(t
i
)e(U,π
i
)e(θ
i
,V)
(1)
The algorithm outputs 1 if the equation holds, else it
outputs 0.
4.2 Group Signatures
We present an instantiation of a group signature
scheme that relies on a witness-indistinguishable
proof of knowledge system NIWI and structure-
preserving signatures.
A group signature scheme GSIG relies on the
four following algorithms (GSIG.Setup, GSIG.Join,
GSIG.Sign, GSIG.Verify):
• GSIG.Setup : represents the setup algorithm. It
generates the key pair (sk
g
,pk
g
) of the group
manager and sets up a CRS Σ
NIWI
for the NIWI
proof. The group verification key is set as vk
g
=
(pk
g
,Σ
NIWI
), while the certification secret key sk
g
is privately stored by the group manager.
• GSIG.Join: represents the join algorithm. It is
composed of two steps. In the first one, the group
member generates his own key-pair (sk
p
,pk
p
).
The public key pk
p
is sent to the group manager.
This latter generates a signature σ
p
over the key
pk
p
that he sends to the group member.
• GSIG.Sign: represents the signing algorithm run
by a group member on a message m ∈ Z
q
. The
group member generates, over the message m, a
signature σ
m
and a NIWI proof Π.
• GSIG.Verify: represents the group signature ver-
ification algorithm run by a verifier. It takes
(vk
g
,m, Π) as input and verifies the correctness
of the NIWI proof Π w.r.t. pub = (pk
g
,m) and the
CRS Σ
NIWI
.
5 SEVIL ALGORITHMS
This section gives the concrete construction of SEVIL.
Based on the Groth-Sahai NIWI proof scheme pro-
posed in Section 4, it details the three phases of the
SEVIL, including the six algorithms presented in Sec-
tion 3 .
5.1 SETUP Phase
• Set params – given λ, T A selects an asymmetric
bilinear group (n, G
1
, G
2
, G
3
, g
1
, g
2
, e) where G
1
and G
2
are two cyclic groups of prime order n, g
1
and g
2
are generators of respectively G
1
and G
2
and e is a bilinear map such that e : G
1
× G
2
→
G
3
. The Set params algorithm outputs the tuple
(n,G
1
,G
2
,G
3
,g
1
,g
2
,e) denoted by pp. pp repre-
sents the system global parameters that are given
as a default input to all the algorithms run by the
system’s entities.
• Setup SGr
G
– G sets up the public parameters of
the group of signers. It generates a group public
key vk
G
and a certification secret key sk
G
as de-
tailed in Algorithm 1.
• Join SGr
S/G
– First, S generates his pair of keys
(sk
S
,pk
S
) as depicted in Algorithm 2 (line 4 –
line 9). Afterwards, G generates a signature σ
k
over the public key pk
S
as detailed in Algorithm
2 (lines 11 – 17).
5.2 SIGNING Phase
• G Sign
S
– S sets a message m ∈ G
2
S that he signs
on behalf of the group. Indeed, S generates a sig-
nature σ
m
over the message m, and computes a
proof Π over the signatures σ
k
and σ
m
as shown
in Algorithm 3.
5.3 VERIFYING Phase
• Batch Verify
V
– We consider a list of N messages
m
i
and the corresponding proofs Π
i
. Each proof
Π
i
is composed of six sub-proofs (i.e., two sub-
proofs generated over the signature σ
m
w.r.t. the
message m, and four sub-proofs generated over
the signature σ
k
w.r.t. the signer key pk
S
). The
list of proofs can be presented as follows:









{(
⃗
A
i jm
,
⃗
B
i jm
,Γ
i jm
,t
i jm
)}
i=N, j=2
i, j=1
,
{(
⃗
C
i jm
,
⃗
D
i jm
,π
i jm
,θ
i jm
)}
i=N, j=2
i, j=1
,
{(
⃗
A
ilk
,
⃗
B
ilk
,Γ
ilk
,t
ilk
)}
i=N,l=4
i,l=1
,
{(
⃗
C
ilk
,
⃗
D
ilk
,π
ilk
,θ
ilk
)}
i=N,l=4
i,l=1
.
SEVIL: Secure and Efficient VerifIcation over Massive Proofs of KnowLedge
17

1: Input: the system public parameters pp
2: Output: the group public parameters vk
G
and the se-
cret key sk
G
3: // The next iterations are executed to generate the
pair of keys of G
4: pick at random g
r1
,h
u1
← G
∗
1
, g
r2
,h
u2
← G
∗
2
for i = 1
to 2 do
pick at random γ
1i
,δ
1i
← Z
∗
n
compute g
1i
←
g
r1
γ
1i
, h
1i
← h
u1
δ
1i
end
for j = 1 to 7 do
pick at random γ
2 j
,δ
2 j
← Z
∗
n
compute g
2i
←
g
r2
γ
2 j
and h
2 j
← h
u2
δ
2 j
end
5: pick at random γ
1z
,δ
1z
,γ
2z
,δ
2z
← Z
∗
n
;
6: compute g
1z
← g
r1
γ
1z
, h
1z
← h
u1
δ
1z
, g
2z
← g
r2
γ
2z
and
h
2z
← h
u2
δ
2z
;
7: pick at random α
1
,α
2
,β
1
,β
2
← Z
∗
n
;
8: pk
1
← (g
2z
,h
2z
,g
2r
,h
2u
,g
α
2
1
,g
β
2
1
,{g
2 j
,h
2 j
}
7
j=1
) and
sk
1
← (pk
1
,α
2
,β
2
,γ
2z
,δ
2z
,{γ
2 j
,δ
2 j
}
7
j=1
) ;
9: pk
2
← (g
1z
,h
1z
,g
1r
,h
1u
,g
α
1
2
,g
β
1
2
,{g
1i
,h
1i
}
2
i=1
) and
sk
2
← (pk
2
,α
1
,β
1
,γ
1z
,δ
1z
,{γ
1i
,δ
1i
}
2
i=1
) ;
10: set pk
g
← (pk
1
,pk
2
) and sk
g
← (sk
1
,sk
2
) ;
11: // The next iterations are executed to generate
Σ
NIWI
12: pick at random r, s ← Z
∗
n
and set U = rg
1
and V = sg
2
;
13: set Σ
NIWI
= (G
1
,G
2
,G
3
,e,ι
1
, p
1
,ι
2
, p
2
,ι
3
,U,V) ;
14: vk
G
← (pk
g
,Σ
NIWI
) ;
15: return (sk
G
,vk
G
)
Algorithm 1: Setup SGr
G
algorithm.
Referring to the generation of the group sig-
nature, the tuples {(
⃗
A
jm
,
⃗
B
jm
,Γ
jm
,t
jm
)}
2
j=1
and
{(
⃗
A
lk
,
⃗
B
lk
,Γ
lk
,t
lk
)}
4
l=1
are unchanged for all N
proofs and all signers. Thus, for a given list of
messages, V verifies the validity of the proofs by
checking if equations (2) and (3), depicted in Fig-
ure 3, hold:
• Agg Verify
V
– We consider a mes-
sage m belonging to an invalid proof-
list and its corresponding proof Π. Us-
ing the tuples {(
⃗
A
jm
,
⃗
B
jm
,Γ
jm
,t
jm
)}
2
j=1
and {(
⃗
A
lk
,
⃗
B
lk
,Γ
lk
,t
lk
)}
4
l=1
along with
the tuples {(
⃗
C
jm
,
⃗
D
jm
,π
jm
,θ
jm
)}
j=2
j=1
and
{(
⃗
C
lk
,
⃗
D
lk
,π
lk
,θ
lk
)}
l=4
l=1
derived from Π, V
checks if equations (4) and (5), depicted in Figure
4, hold.
1: Input: the security parameter λ and the secret
key of the group manager sk
G
2: Output: the pair of keys of a signer (sk
S
,pk
S
)
and the signature σ
k
over the public key pk
S
3: // The next is set by S
4: pick at random g
r
,h
u
← G
∗
1
, γ,δ ← Z
∗
n
;
5: compute g
γ
← g
r
γ
and h
δ
← h
u
δ
;
6: pick at random γ
z
,δ
z
← Z
∗
n
;
7: compute g
z
← g
r
γ
z
and h
z
← h
u
δ
z
;
8: pick at random α,β ← Z
∗
n
;
9: set pk
S
= (g
z
,h
z
,g
r
,h
u
,g
α
2
,g
β
2
,g
γ
,h
δ
) and sk
S
=
(pk
S
,α,β,γ
z
,δ
z
,γ,δ) ;
10: // The next is set by G
11: pick at random ζ
2
,ρ
2
,τ
2
,ϕ
2
,ω
2
← Z
∗
n
;
12: compute z
2
= g
ζ
2
2
, s
2
= g
1r
ρ
2
, t
2
= g
2
τ
2
,
r
2
= g
2
α
1
−ρ
2
τ
2
−γ
1z
ζ
2
∏
2
i=1
m
2i
−γ
1i
, u
2
=
g
2
β
1
−ϕ
2
ω
2
−δ
1z
ζ
2
∏
2
i=1
m
2i
−δ
1i
, v
2
= h
1u
ϕ
2
, w
2
= g
2
ω
2
; where ⃗m
2
= (g
α
2
,g
β
2
) ;
13: set σ
2
= (z
2
,r
2
,s
2
,t
2
,u
2
,v
2
,w
2
) ;
14: pick at random ζ
1
,ρ
1
,τ
1
,ϕ
1
,ω
1
← Z
∗
n
;
15: compute z
1
= g
ζ
1
1
, s
1
= g
2r
ρ
1
, t
1
= g
1
τ
1
,
r
1
= g
1
α
2
−ρ
1
τ
1
−γ
2z
ζ
1
∏
7
j=1
m
1 j
−γ
2 j
, u
1
=
g
1
β
2
−ϕ
1
ω
1
−δ
2z
ζ
1
∏
7
j=1
m
1 j
−δ
2 j
, v
1
= h
2u
ϕ
1
, w
1
= g
1
ω
1
;
where ⃗m
1
= (g
z
,h
z
,g
r
,h
u
,g
γ
,h
δ
,s
2
);
16: set σ
1
= (z
1
,r
1
,s
1
,t
1
,u
1
,v
1
,w
1
) ;
17: set σ
k
= (σ
1
,σ
2
) ;
18: return (sk
S
,pk
S
,σ
k
)
Algorithm 2: Join SGr
S/G
algorithm.
6 SECURITY DISCUSSION
In this section, we prove that SEVIL’s construction
is secure and privacy-preserving w.r.t. the properties
defined in Section 2.2. In order to appropriately ad-
dress security and privacy requirements mentioned is
Section 2.2.1, we consider two main adversaries, as
follows:
• A Malicious Adversary: attempts, by himself or
when colluding with other malicious adversaries,
to generate a valid group signature over a mes-
sage without being authorized by the group man-
ager. A malicious adversary plays the role of an
outsider and is mainly considered against unforge-
ability property.
• A Honest but Curious Adversary: given a valid
group signature, a honest but curious adversary
tries to identify the signer of a particular message.
He may also attempt to link two signatures issued
by the same group member. A curious adversary
plays the role of a verifier (V ), and considered
against unlinkability
1
requirement.
1
We assume that unlinkability property includes the
anonymity of signers as group members.
SECRYPT 2022 - 19th International Conference on Security and Cryptography
18

∏
i
∏
j

e(
⃗
C
i jm
,Γ
m
⃗
D
i jm
)

= e(U,
∑
i
∑
j
π
i jm
)e(
∑
i
∑
j
θ
i jm
,V) (2)
∏
l
e(ι
1
(
⃗
A
lk
),
∑
i
⃗
D
ilk
)e(
∑
i
⃗
C
ilk
,ι
2
(
⃗
B
lk
))
∏
i
∏
l

e(
⃗
C
ilk
,Γ
lk
⃗
D
ilk
)

=

∏
l
ι
3
(t
l
k)
N

e(U,
∑
i
∑
l
π
ilk
)e(
∑
i
∑
l
θ
ilk
,V) (3)
Figure 3: Verification equations of Batch Verify
V
algorithm.
∏
j

e(
⃗
C
jm
,Γ
m
⃗
D
jm
)

= e(U,
∑
j
π
jm
)e(
∑
j
θ
jm
,V) (4)
∏
l
e(ι
1
(
⃗
A
lk
),
⃗
D
lk
)e(
⃗
C
lk
,ι
2
(
⃗
B
lk
))
∏
l

e(
⃗
C
lk
,Γ
lk
⃗
D
lk
)

=

∏
l
ι
3
(t
l
k)

e(U,
∑
l
π
lk
)e(
∑
l
θ
lk
,V) (5)
Figure 4: Verification equations of Agg Verify
V
algorithm.
1: Input: the public parameters of the signers’ group vk
G
, the pair of keys (sk
S
,pk
S
), the signature σ
k
over the
signer public key and the message m
2: Output: a signature σ
m
over the message m and a proof Π over the signatures σ
k
and σ
m
3: // The next is executed by S to sign m
4: pick at random ζ, ρ,τ,ϕ,ω ← Z
∗
n
;
5: run z = g
ζ
2
, r = g
2
α−ρτ−γ
z
ζ
m
−γ
, s = g
r
ρ
, t = g
2
τ
, u = g
2
β−ϕω−δ
z
ζ
m
−δ
, v = h
u
ϕ
, w = g
2
ω
;
6: set σ
m
= (z,r,s,t, u, v,w) ;
7: // The next is set to generate a proof on equations {(
⃗
A
im
,
⃗
B
im
,Γ
im
,t
im
)}
2
i=1
where
⃗
A
im
=
⃗
B
im
=
⃗
0,
Γ
im
= M AT
3×3
(1) for i = 1,2, t
1m
= t
2m
= 1
G
3
8:
⃗
X
1m
= (g
z
,g
r
,s),
⃗
X
2m
= (h
z
,h
u
,v) ,
⃗
Y
1m
= (z,g
2
α−ρτ−γ
z
ζ
,t) and
⃗
Y
2m
= (z,g
2
β−ρτ−δzζ
,w) ;
9: π
m
= {(
⃗
C
im
,
⃗
D
im
,π
im
,θ
im
)}
2
i=1
← NIWI.Proof(vk
g
, {(
⃗
A
im
,
⃗
B
im
,Γ
im
,t
im
)}
2
i=1
, {(
⃗
X
im
,
⃗
Y
im
)}
2
i=1
) ;
10: // The next is set to generate a proof on equations {(
⃗
A
ik
,
⃗
B
ik
,Γ
ik
,t
ik
)}
4
i=1
where
⃗
A
1k
= (g
α
2
1
),
⃗
A
2k
= (g
β
2
1
),
⃗
A
3k
=
(g
1z
,g
1r
),
⃗
A
4k
= (h
1z
,h
1u
),
⃗
B
1k
= (g
2z
,g
2r
),
⃗
B
2k
= (h
2z
,h
2u
),
⃗
B
3k
= (g
α
1
2
),
⃗
B
4k
= (g
β
1
2
), Γ
1k
= (γ
2z
,−1), Γ
2k
= (δ
2z
,−1),
Γ
3k
= (γ
1z
,−1), Γ
4k
= (δ
1z
,−1), t
1k
= e(g
α
2
1
,g
2r
), t
2k
= e(g
β
2
1
,h
2u
), t
3k
= e(g
1r
,g
α
1
2
) and t
4k
= e(h
1u
,g
β
1
2
)
11:
⃗
X
1k
= (z
1
,g
1
α
2
−ρ
1
τ
1
−γ
2z
ζ
1
),
⃗
X
2k
= (z
1
,g
1
β
2
−ρ
1
τ
1
−δ
2z
ζ
1
),
⃗
X
3k
= (g
1r
),
⃗
X
4k
= (h
1u
) ,
⃗
Y
1k
= (g
2r
),
⃗
Y
2k
= (h
2u
),
⃗
Y
3k
=
(z
2
,g
2
α
1
−ρ
2
τ
2
−γ
1z
ζ
2
), and
⃗
Y
4k
= (z
2
,g
2
β
1
−ρ
2
τ
2
−δ
1z
ζ
2
) ;
12: π
p
= {(
⃗
C
ik
,
⃗
D
ik
,π
ik
,θ
ik
)}
4
i=1
← NIWI.Proof(vk
g
,{(
⃗
A
ik
,
⃗
B
ik
,Γ
ik
,t
ik
)}
4
i=1
, {(
⃗
X
ik
,
⃗
Y
ik
)}
4
i=1
) ;
13: set π
k
= ((π
ik
,θ
ik
)
4
i=1
) ;
14: set Π = (π
k
,π
m
) ;
15: return (σ
m
,Π)
Algorithm 3: G
Sign
S
algorithm.
6.1 Unforgeability
The unforgeability property states that a malicious
outsider is not able to forge the SEVIL group signa-
ture.
Let us consider an adversary A that is allowed to
query, as many times as he wants, the G Sign algo-
rithm on a message m
i
. Then, during the challenge
phase, A is asked to produce a valid message signa-
ture pair (m
∗
,Π
∗
) such that the message m
∗
was not
queried before.
For this purpose, we consider two adversaries B
1
and B
2
respectively against the unforgeability of the
group signature
2
scheme GSIG and the soundness
3
of
the proof system NIWI. The advantage of A to break
2
Unforgeability of group signatures states that it is not
possible to generate a valid message signature pair unless
secret keys are known.
3
The soundness property ensures that is it not possible
to prove a false statement.
SEVIL unforgeability is expressed as follows:
Adv
un f or
A
(1
λ
) ≤ Adv
un f or
GSIG,B
1
(1
λ
) + Adv
sound
NIWI,B
2
(1
λ
)
According to (Bellare et al., 2003), the unforgeability
property can be directly inherited from the traceabil-
ity property stating that it is not possible to generate
signatures without tracing its originator. As the group
signature scheme GSIG, relying on the construction
of Bellare et al. (Bellare et al., 2003), is proven to
be traceable, then the unforgeability property of GSIG
is also satisfied. Thus, the Adv
un f or
GSIG,B
1
(1
λ
) function
is negligible. The advantage function Adv
sound
NIWI,B
2
(1
λ
)
can be expressed as follows:
Adv
sound
NIWI,B
2
(1
λ
) = Pr[B
2
out puts (m,Π) :
NIWI.Verify(m,Π) = 1]
Referring to (Bellare et al., 2003),
Pr[B
3
out puts (m,Π) : NIWI.Verify(m,Π) =
1] ≤ 2
−λ
as the NIWI proof system is sound. As
SEVIL: Secure and Efficient VerifIcation over Massive Proofs of KnowLedge
19

such, the advantage function Adv
sound
NIWI,B
3
(1
λ
) is neg-
ligible. Thus, the advantage function Adv
un f or
A
(1
λ
)
is also negligible proving that SEVIL satisfies the
unforgeability property.
6.2 Unlinkability
The unlinkability property states that a curious ver-
ifier is not able neither to link two or several group
signatures issued by the same signer nor to identify
the originator of a group signature.
Let us consider an adversary A that is al-
lowed to query, as many times as he wants, the
G Sign algorithm on the same message m
∗
, for
two signers S
0
and S
1
. For each session, A re-
ceives a group signature represented by the tuple
((
⃗
C
i
jm
,
⃗
D
i
jm
,π
i
jm
,θ
i
jm
)
2
j=1
, (
⃗
C
i
jk
,
⃗
D
i
jk
,π
i
jk
,θ
i
jk
)
4
j=1
). Af-
terwards, A is given a pair of group signatures over
the same message m
∗
. The first signature is gener-
ated for the signer S
0
and is represented by the tuple
((
⃗
C
∗
jm
,
⃗
D
∗
jm
,π
∗
jm
,θ
∗
jm
)
2
j=1
, (
⃗
C
∗
jk
,
⃗
D
∗
jk
,π
∗
jk
,θ
∗
jk
)
4
j=1
). The
second signature is generated either for signer S
0
or
signer S
1
, according to a randomly selected bit b ∈
{0,1}. This second signature is represented by the tu-
ple ((
⃗
C
b
jm
,
⃗
D
b
jm
,π
b
jm
,θ
b
jm
)
2
j=1
, (
⃗
C
b
jk
,
⃗
D
b
jk
,π
b
jk
,θ
b
jk
)
4
j=1
).
A is asked to guess if the two group signatures are
generated by the same signer or two different signers
with a probability greater than
1
2
.
Let us suppose that A has an advantage ε
against the unlinkability property of SEVIL. A
simulator B against the computational witness-
indistinguishability property can be constructed with
the help of the adversary A. Indeed, B is given
two commitments (C,D) and (C
b
,D
b
). The commit-
ment (C,D) is generated over a witness (X
0
,Y
0
), while
(C
b
,D
b
) is computed over a witness (X
b
,Y
b
), where
b ∈ {0,1}. B is asked, by its own challenger C , to
guess guess the bit b i.e., guess whether the com-
mitments were generated over the same witness or
two different witnesses. Thus, B selects two tuples
(A
0
,B
0
,Γ
0
,t
0
) and (A
b
,B
b
,Γ
b
,t
b
) and computes the
corresponding proofs (π
0
,θ
0
) and (π
b
,θ
b
) over (C,D)
and (C
b
,D
b
). The two proofs are given back to A
that outputs a bit b
′
and sends it to B. This latter an-
swers its own challenger C with the same bit b
′
. As
such, A succeeds in breaking the unlinkability prop-
erty of SEVIL with the same probability of breaking
the computational witness-indistinguishability prop-
erty, which is negligible. Thus, SEVIL ensures the un-
linkability property w.r.t. the computational witness-
indistinguishability property of Groth-Sahai NIWI
proofs.
7 PERFORMANCE ANALYSIS
This section first introduces the test environment.
Then, it presents the performances’ analysis of SEVIL
according to the computation time, the complexity
and the communication cost of the different algo-
rithms. This evaluation is complemented with (1) a
comparative analysis of the computation time of the
SEVIL aggregated verification against the naive veri-
fication of group signatures, and (2) the evaluation of
the impact of the messages’ number on the computa-
tion time.
7.1 Test Environment
The implementation includes the three phases
SETUP, SIGNING and VERIFYING of SEVIL includ-
ing the six algorithms referred to as Set params,
Setup SGr
G
, Join SGr
S/G
, G Sign
S
, Batch Verify
V
and Agg Verify
V
. For comparison purposes, the four
primitives of the group signature scheme presented in
Section 4.2 are also implemented relying on the pub-
lic parameters obtained through the Set params algo-
rithm.
Our tests are conducted on an Ubuntu 18.04.3 ma-
chine - with an Intel Core i7@1.30GHz processor and
8GB memory. Based on JAVA version 11, the associ-
ated cryptographic library JPBC
4
and the implemen-
tation of Groth-Sahai proofs
5
, the SEVIL test-bed is
built upon four main java classes, w.r.t. to the differ-
ent entities of SEVIL, referred to as TrustedAuthor-
ity.java, GroupManager.java, Signer.java and Veri-
fier.java. For each class, we defined different meth-
ods w.r.t. the algorithms performed by each entity as
described in Section 3.
For efficiency purpose, two types of improve-
ments are introduced in SEVIL algorithms. The
improvements are applied, in particular, on G Sign
and Batch Verify algorithms of SEVIL and the
GSIG.Verify algorithm of GSIG signature scheme, as
follows:
• Multithreading: applied on the four algo-
rithms G Sign, Batch Verify, Agg Verify and
GSIG.Verify. It enables to simultaneous execute
multiple threads on different processor cores. The
multithreading helps G Sign to compute different
parts of the NIWI proof simultaneously, while for
Batch Verify, Agg Verify and GSIG.Verify algo-
rithms, it enables higher computation throughput
on both sides of the verification equations of the
NIWI proof.
4
http://gas.dia.unisa.it/projects/jpbc/
5
https://github.com/gijsvl/groth-sahai
SECRYPT 2022 - 19th International Conference on Security and Cryptography
20

• Preprocessing: applied only on the Batch Verify,
Agg Verify and GSIG.Verify algorithms. It helps
reduce the computation time when some variables
need to be computed several times during the ex-
ecution of the algorithm. This is the case for the
variables (e.g., U and V of the CRS Σ
NIWI
) which
can be prepared in advance (i.e., before the exe-
cution of algorithms) for next be provided as in-
put to the pairing functions of the Batch Verify,
Agg Verify and GSIG.Verify algorithms.
Those two improvements are efficient as the compu-
tation time can be decreased by up to 50%.
Based on the JPBC library, we choose to evalu-
ate the computation time of each algorithm relying
on two different types of bilinear pairings, referred to
as pairings type A and type F. Pairing type A repre-
sents the fastest symmetric pairing type while relying
on the elliptic curve y
2
= x
3
+ x with an embedding
degree equal to 2. Pairing type F supports asymmet-
ric pairing features and was introduced by Barreto and
Naehrig (pai, ) with an embedding degree equal to 12.
Two different levels of security are considered for the
pairings type A and type F referred to as 112-bits and
128-bits security levels
6
.
The tests rely on 100 samples of randomly gener-
ated messages. Each algorithm is run 100 times, and
the given computation times are the average of the
100 runs. The standard deviation of an order 10
−2
is
considered.
7.2 Computation Overhead of SEVIL
This section presents the theoretical and experimental
computing costs of SEVIL’s six algorithms.
Table 1 shows that the G Sign and Batch Verify
are the most consuming algorithms in terms of expo-
nentiation and pairing operations. To sign a single
message, G
Sign requires 302 exponentiations and 18
multiplications in both groups G
1
and G
2
. The the-
oretical computation cost of Batch Verify mainly de-
pends on the number of messages, especially in terms
of multiplication and pairing operations. The signif-
icant computation costs of G Sign and Batch Verify
algorithms are reduced thanks to the two steps of im-
provements presented in Section 7.1.
Table 1 shows that the selected pairing types along
with the security level strongly impact the computa-
tion times. Note that both Set params and Setup SGr
algorithms, as part of the SETUP phase, are consum-
ing but they are limited to only one execution, respec-
tively from a powerful trusted authority and a group
6
The 112-bits and 128-bits security levels are recom-
mended by the US National Institute of Standards and Tech-
nology (NIST) (http://keylength.com).
manager. The performances of the Join SGr algo-
rithm depend on the selected pairing type and secu-
rity level, with respectively 2 and 6 seconds for sym-
metric pairing settings (i.e., pairing type A ) for re-
spectively 112 and 128 bit security, and 1,2 and 1,4
seconds for asymmetric pairing settings (i.e., pairing
type F ), for respectively 112 and 128 bit security. For
the SIGNING phase, the G Sign algorithm is also con-
suming, with respectively 19 and 40 seconds in sym-
metric pairing settings, and 3 and 4 seconds in asym-
metric pairing settings. Finally, for the VERIFYING
phase, the Batch Verify algorithm executed to verify
100 messages simultaneously, requires approximately
4 and 8 minutes for pairing type A and 17 and 22 min-
utes for pairing type F. However, when it is needed to
verify a single message, the Agg Verify algorithm re-
quires 3 and 7 seconds for pairing type A and 16 and
19 seconds for pairing type F. It is worth noticing that,
for a number of messages N = 100, the execution of
the Batch Verify algorithm gives improved computa-
tional costs compared to the Agg Verify algorithm ex-
ecuted 100 times, separately.
Experimental results depicted in Table 1, confirm
the theoretical results that G Sign, Batch Verify and
Agg Verify are the most consuming algorithms. This
is logical as they include a large number of exponenti-
ations and pairing functions. However this result must
be put into perspective as both the signer and the ver-
ifier are assumed to be powerful and have advanced
hardware features.
From Table 1, it is also clear that the G Sign
algorithm performed with asymmetric pairing set-
tings is faster than with symmetric settings. Indeed,
the elementary functions of multiplication and expo-
nentiation are more consuming for pairing type A
than for pairing type F
7
. However the Batch Verify
and Agg Verify algorithms have an opposite behavior
with a faster execution with pairing type A than with
pairing type F. This can be explained by the excessive
memory allocation and deallocation needed by pair-
ing type F.
7.3 Communication Overhead of SEVIL
This section discusses the communication costs of
SEVIL. As shown in Table 1, the communication
cost is evaluated according to the size of group el-
ements G
1
, G
2
, G
3
and Z
n
. Each pairing type and
each security level are characterized with different
group sizes. From Table 1, it is worth noticing that
the SETUP phase is the most consuming in terms
7
The experimental results are thus compliant to
the JPBC library http://gas.dia.unisa.it/projects/jpbc/
benchmark.html
SEVIL: Secure and Efficient VerifIcation over Massive Proofs of KnowLedge
21

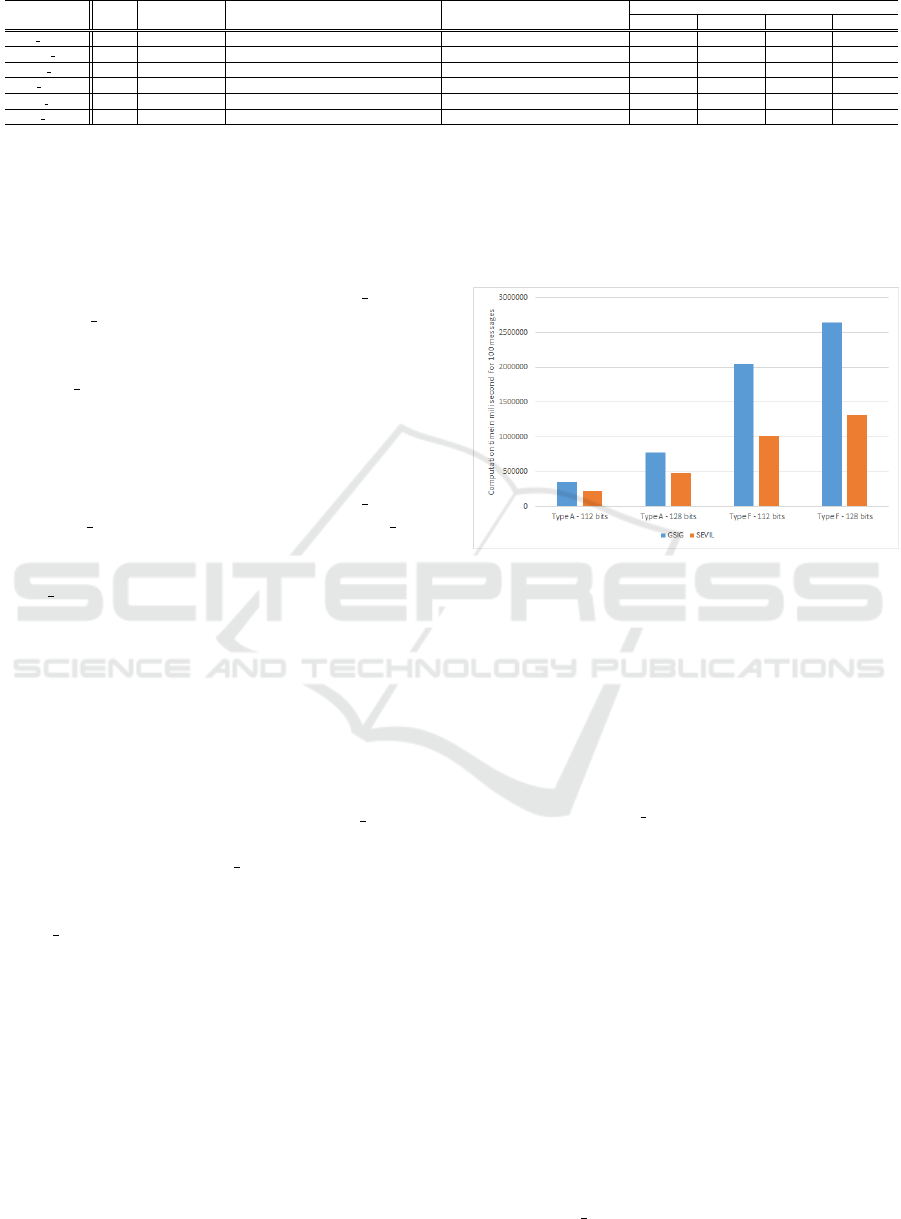
Table 1: Computation and communication cost of SEVIL.
Algorithm Entity Synch/Asynch Communication cost Complexity
Computation time (ms)
A/112-bits A/128-bits F/112-bits F/128-bits
Set params T A Asynch. |Z
n
| + |G
1
| + |G
2
| + |G
3
| γ
G
874 2521 1230 1364
Setup SGr G Asynch. 21|(G
1
| + |G
2
|) 24γ
E
1,2
1955 4075 346 451
Join SGr S/G Synch. (S): 8|G
1
| + 2|G
2
| / (G): 7(|G
1
| + |G
2
|) (S ): 6γ
E
1,2
/ (G): 32γ
E
1,2
+ 22γ
M
1,2
2861 6014 1159 1409
G Sign
a
S Synch. 6(|G
1
| + |G
2
|) 302γ
E
1,2
+ 18γ
M
1,2
19353 40371 3164 4170
Batch Verify
b
V Asynch. N.A. 4γ
E
3
+ (6N + 10)γ
M
3
+ (6N +9)γ
P
222989 485233 1018375 1312879
Agg Verify V Asynch. N.A. 4γ
E
3
+ 16γ
M
3
+ 15γ
P
3096 6916 16065 18834
NOTE: Synch./Asynch. indicates whether the algorithm must be run online (i.e. in real time) or offline (i.e. later);
a
indicates
that the algorithm is performed on a single message;
b
indicates that the algorithm is performed on N messages where N = 100
for computation times; |G
1
| (resp. |G
2
|, |G
3
| and |Z
n
|) indicates the size of an element in G
1
(resp. G
2
, G
3
and Z
n
); γ
G
is the cost of the cyclic group generation; γ
M
1,2
and γ
M
3
are the costs of multiplication in resp. G
1
/G
2
and G
3
; γ
E
1,2
and γ
E
3
are the costs of exponentiation in resp. G
1
/G
2
and G
3
; γ
P
is the cost of a pairing function; N.A. is the abbreviation for Not
Applicable.
of bandwidth. In fact, it includes the Set params
and Setup SGr algorithms that output the system
and group public parameters shared with other en-
tities. The SETUP phase also includes the interac-
tive Join SGr algorithm that introduces communica-
tion overheads of 8|G
1
|+2|G
2
| and 7(|G
1
|+|G
2
|) to
respectively send the signer’s keys to the G and give
back G’s signature over the keys of S . The communi-
cation cost introduced by the SETUP phase must be
put into perspective as both algorithms Set params
and Setup SGr are executed once, and the Join SGr
algorithm is performed only when a new signer wants
to join the group. The SIGNING phase, including only
the G Sign algorithm repeatedly performed by sign-
ers, has an acceptable communication overhead due
to the size of the NIWI proof.
7.4 Benefit of SEVIL Aggregated
Verification over GSIG Naive
Verification
In this section, we focus on the VERIFYING phase.
We consider 100 messages signed with the G Sign al-
gorithm. The resulting proofs are given as input to
both GSIG.Verify and Batch Verify algorithms. The
GSIG.Verify algorithm is executed 100 times as it al-
lows to verify only one proof at a time, while the
Batch Verify algorithm performs the verification of
all proofs at a time. Thus, we compare the computa-
tion time required by the two algorithms when being
executed over 100 messages.
Figure 5 shows that the aggregated verification is
more efficient than the naive one. Indeed, the ag-
gregation reduces the computation time, for verify-
ing 100 messages, by approximately 37%, for pairing
type A for the two security levels. The computation
time moves from 356 seconds (resp. 777 seconds)
with the naive signature verification to 223 seconds
(resp. 485 seconds) with SEVIL aggregated verifica-
tion. For pairing type F, the gain reaches 50% for
Figure 5: Computation time of aggregated verification vs
naive verification over 100 messages.
the two security levels. The computation time moves
from 2048 seconds (resp. 2642 seconds) to 1018 sec-
onds (resp. 1313 seconds).
The gain obtained through the aggregating veri-
fication is substantiated by the decrease in the num-
ber of pairings. To verify N messages (i.e., 6 NIWI
proofs are verified per messages), the GSIG.Verify al-
gorithm requires 30N pairings (according to Equation
1), while the Batch Verify algorithm only requires
6N + 9 pairings. Thus, we expect to obtain a gain
of approximately 80%, but experimental results show
smaller gains than expected. These results are jus-
tified by the number of additions introduced while
aggregating the verification equations (i.e., 14N ad-
ditions). As mentioned before, the elementary addi-
tion operations are more consuming for pairing type
A than for pairing type F. Hence, the gain is more
significant with asymmetric pairing settings.
7.5 Impact of Messages’ Volume on the
Verification
Referring to equations (2) and (3), depicted in Fig-
ure 3, it is clear that the number N of messages (resp.
proofs) to be verified, influences the time computation
of the Batch Verify algorithm. Indeed, the greater
SECRYPT 2022 - 19th International Conference on Security and Cryptography
22

the number of messages, the greater the number of
pairing functions. For this objective, we evaluate the
computation time of the Batch Verify algorithm when
varying the number of messages from 5 to 1000. Note
that all messages are signed with the G Sign algo-
rithm.
Figure 6: Influence of messages’ volume on Batch Verify
computation time.
The curves depicted in Figure 6 show that the
computation time of the Batch Verify algorithm is
a rising affine function of the messages number, for
the two types of pairings and the two security lev-
els. When varying the number of messages from 5
to 1000, the computation time varies from 15 to 2602
seconds (resp. from 59 to 10677) for the pairing type
A (resp. pairing type F ), for 112-bits level. For the
128-bits security, the computation time varies from
26 to 4817 (resp. 72 to 12978) for the pairing type A
(resp. pairing type F ).
8 COMPARISON WITH
RELATED WORK
Data-centric applications, e.g., cloud-based technolo-
gies (di Vimercati et al., 2019), recommendation sys-
tems (Kaaniche et al., 2020b; Rahali et al., 2021) and
IoT applications (Alamer, 2020; Zhang et al., 2021;
Belguith et al., 2018), have raised several concerns
regarding the massive collection, processing and ac-
cess to data from different users with different priv-
ileges (Kaaniche et al., 2020a). Several works have
been proposed, in the literature, to efficiently verify
a large number of signatures, referred to as signature
schemes with batch verification. This method helps
to solve the resource constraints’ problems in many
applications. Batch verification for signatures was
first proposed by Naccache et. al (Naccache et al.,
1994) for DSA-type signatures. Since then, several
batch verification methods have been proposed for
other digital signature schemes, namely for group sig-
natures. Indeed, batch verification over group signa-
tures was introduced by Ferrara et. al (Ferrara et al.,
2009). Wasef and Shen proposed to use batch verifi-
cation. Vehicular ad hoc networks (Wasef and Shen,
2010). In (Kim et al., 2011), authors exploited Fer-
rara et. al scheme to build a new batch vertification
scheme that supports invalid signatures identification.
They rely on the divide-and-conquer approach (Pas-
tuszak et al., 2004). In (Feng et al., 2017), authors
presented a group signature scheme with batch verifi-
cation that allows to deal with the excessive need for
signatures verification in pervasive social networking.
The proposed scheme do not support bad signatures
identification, i.e., if the batch verification fails, all
the signatures are rejected. Recently, Alamer pro-
posed a secure and privacy-preserving group signa-
ture scheme supporting batch verification. It aims at
mitigating the increasing computation delay in IoT
systems (Alamer, 2020). In (Zhang et al., 2021), au-
thors designed a novel group signature scheme with
batch verification for IoT consortium blockchain. It
suggests two types of verification, i.e., a naive veri-
fication for urgent transactions and batch verification
for ordinary ones.
Table 2 illustrates differences between SEVIL and
closely related schemes in terms of security and pri-
vacy properties and supported functionalities.
From Table 2, it is worth stating that SEVIL satis-
fies several properties of interest, compared to closely
related proposals. It leverages the trade-off between
security, privacy and utility. Indeed, as all others
schemes, SEVIL fulfills the unforgeability require-
ment. Unlike (Wasef and Shen, 2010), (Kim et al.,
2011), (Alamer, 2020) and (Zhang et al., 2021), the
proposed scheme adds security features, referred to
as trust on signers. SEVIL also addresses a criti-
cal privacy concern which is unlinkability. In terms
of utility, we note that, unlike (Wasef and Shen,
2010), (Feng et al., 2017), (Alamer, 2020) and (Zhang
et al., 2021) which only support batch verification, the
SEVIL system is designed to support identification of
invalid signatures, which is very relevant for informa-
tion accuracy.
9 CONCLUSION
In this paper, we introduce a concrete construction
of a novel secure and privacy-preserving Groth-Sahai
NIWI proof-based signature. The proposed scheme
enables the efficient verification of multiple signa-
tures, i.e. allowing verifiers to check the correctness
of multiple proof-based group signatures, at once.
Our contribution is proven to support security and
SEVIL: Secure and Efficient VerifIcation over Massive Proofs of KnowLedge
23

Table 2: Comparison of SEVIL and related works.
SEVIL (Wasef and Shen, 2010) (Kim et al., 2011) (Feng et al., 2017) (Alamer, 2020) (Zhang et al., 2021)
Security and
privacy properties
Unforgeability ✓ ✓ ✓ ✓ ✓ ✓
Trust on signers ✓ ✗ ✗ ✓ ✗ ✗
Unlinkability ✓ ✓ ✗ ✗ ✓ ✓
Functional properties
Batch verification ✓ ✓ ✓ ✓ ✓ ✓
Invalid signatures identification ✓ ✗ ✓ ✗ ✗ ✗
privacy properties, through a comprehensive security
analysis. Thanks to SEVIL’s proof of concept that
fully implement the different algorithms, we show
that the aggregated verification achieves a gain of up
to 50% with regard to the naive verification of group
signatures. This gain proves the efficiency of SEVIL
and must be put into perspective as in real world
applications, verifiers are assumed to have advanced
hardware features.
ACKNOWLEDGEMENTS
Authors are thankful to Mr. Fadel Radji for im-
plementing SEVIL’s algorithms and for providing
valuable suggestions to improve the system’s perfor-
mances.
REFERENCES
Jpbc library: Bilinear pairing parameters generators. http:
//gas.dia.unisa.it/projects/jpbc/docs/ecpg.html.
Alamer, A. (2020). An efficient group signcryption scheme
supporting batch verification for securing transmitted
data in the internet of things. Journal of Ambient In-
telligence and Humanized Computing.
Belguith, S., Kaaniche, N., Mohamed, M., and Russello,
G. (2018). Coop-daab: Cooperative attribute based
data aggregation for internet of things applications.
In OTM Confederated International Conferences” On
the Move to Meaningful Internet Systems”, pages
498–515. Springer.
Bellare, M., Micciancio, D., and Warinschi, B. (2003).
Foundations of group signatures: Formal definitions,
simplified requirements, and a construction based on
general assumptions. In Biham, E., editor, Advances
in Cryptology — EUROCRYPT 2003, pages 614–629,
Berlin, Heidelberg. Springer Berlin Heidelberg.
di Vimercati, S. D. C., Foresti, S., Livraga, G., and Sama-
rati, P. (2019). Data security and privacy in the cloud.
In Agaian, S. S., Asari, V. K., and DelMarco, S. P., ed-
itors, Mobile Multimedia/Image Processing, Security,
and Applications 2019, pages 84 – 96. SPIE.
Feng, W., Yan, Z., and Xie, H. (2017). Anonymous authen-
tication on trust in pervasive social networking based
on group signature. IEEE Access, 5:6236–6246.
Ferrara, A., Green, M., Hohenberger, S., and Pedersen, M.
(2009). Practical short signature batch verification.
pages 309–324.
Groth, J. and Sahai, A. (2008). Efficient non-interactive
proof systems for bilinear groups. In Smart, N., editor,
Advances in Cryptology – EUROCRYPT 2008, pages
415–432, Berlin, Heidelberg. Springer Berlin Heidel-
berg.
Kaaniche, N., Laurent, M., and Belguith, S. (2020a). Pri-
vacy enhancing technologies for solving the privacy-
personalization paradox: Taxonomy and survey. Jour-
nal of Network and Computer Applications, page
102807.
Kaaniche, N., Masmoudi, S., Znina, S., Laurent, M., and
Demir, L. (2020b). Privacy preserving cooperative
computation for personalized web search applications.
In Proceedings of the 35th Annual ACM Symposium
on Applied Computing, page 250–258.
Kim, K., Yie, I., Lim, S., and Nyang, D. (2011). Batch
verification and finding invalid signatures in a group
signature scheme. International Journal of Network
Security, 12:229–238.
Naccache, D., M’Ra
¨
ıhi, D., Vaudenay, S., and Raphaeli, D.
(1994). Can d.s.a. be improved? complexity trade-
offs with the digital signature standard. In Advances in
Cryptology - EUROCRYPT ’94, Workshop on the The-
ory and Application of Cryptographic Techniques, Pe-
rugia, Italy, May 9-12, 1994, Lecture Notes in Com-
puter Science, pages 77–85. Springer.
Pastuszak, J., Michałek, D., Pieprzyk, J., and Seberry, J.
(2004). Identification of bad signatures in batches.
pages 28–45.
Rahali, S., Laurent, M., Masmoudi, S., Roux, C., and
Mazeau, B. (2021). A validated privacy-utility pre-
serving recommendation system with local differen-
tial privacy.
Wasef, A. and Shen, X. (2010). Efficient group signature
scheme supporting batch verification for securing ve-
hicular networks. In 2010 IEEE International Confer-
ence on Communications, pages 1–5.
Zhang, A., Zhang, P., Wang, H., and Lin, X. (2021).
Application-oriented block generation for consortium
blockchain-based iot systems with dynamic device
management. IEEE Internet of Things Journal,
8(10):7874–7888.
SECRYPT 2022 - 19th International Conference on Security and Cryptography
24