Swept-source Phase-Stabilized Optical Coherence Tomography Setup

for Elastography

Ana Batista

, Carlos Correia

, Sílvia Barbeiro

, João Cardoso

, José P. Domingues

1,3 e

Rafael Henriques

, Custódio Loureiro

, Mário J. Santos

, Pedro Serranho

1,5 i

Rui Bernardes

1,6 j

and Miguel Morgado

1,3,* k

University of Coimbra, Coimbra Institute for Biomedical Imaging and Translational Research (CIBIT),

Institute for Nuclear Sciences Applied to Health (ICNAS), Coimbra, Portugal

University of Coimbra, CMUC, Department of Mathematics, Coimbra, Portugal

University of Coimbra, Department of Physics, Faculty of Science and Technology, Coimbra, Portugal

University of Coimbra, Department of Electrical and Computer Engineering, Faculty of Science and Technology,

Coimbra, Portugal

Universidade Aberta, Mathematics Section, Department of Science and Technology, Lisbon, Portugal

University of Coimbra, Clinical Academic Center of Coimbra (CACC), Faculty of Medicine (FMUC), Coimbra, Portugal

Keywords: Optical Coherence Elastography, Swept-source OCT, Phase Stabilization.

Abstract: We present an Optical Coherence Elastography (OCE) system, based on a swept-source Optical Coherence

Tomography (OCT) setup, and evaluate its performance in terms of phase stability and minimum detectable

displacement. The ability to record sub-pixel movements in samples under dynamic conditions was also

assessed. The OCE system has a time stability of 396.9 ± 46.7 ps. The phase stability, given by the standard

deviation of the measured phase difference, was 72.44 mrad, which corresponds to a minimum detectable

displacement of 6.11 nm. Tests showed that the OCE system can detect and measure sub-pixel movements in

samples under dynamic mechanical excitation.

1 INTRODUCTION

Optical Coherence Elastography (OCE) is a recent

imaging modality that maps mechanical properties,

by using Optical Coherence Tomography (OCT) to

measure tissue displacement after mechanical

excitation (Kirby et al., 2017; Larin & Sampson,

2017). Elastography is an inherently highly sensitive

technique, since tissue stiffness provides a dynamic

https://orcid.org/0000-0002-5672-8266

https://orcid.org/0000-0002-2947-1880

https://orcid.org/0000-0002-2651-5083

https://orcid.org/0000-0002-8832-8208

https://orcid.org/0000-0002-0562-8994

https://orcid.org/0000-0003-4173-8469

https://orcid.org/0000-0001-7856-2124

https://orcid.org/0000-0002-0188-7761

https://orcid.org/0000-0003-2176-3923

https://orcid.org/0000-0002-6677-2754

https://orcid.org/0000-0001-9455-1206

* Corresponding author

range that can reach six orders of magnitude and OCT

has the potential of measuring sub-nanometric

displacements. Compared to current clinical

elastography techniques, based on ultrasound or

magnetic resonance imaging, OCE has the advantage

of providing better spatial resolution (1 to 10 μm), and

imaging rate (higher than 1 kHz). The main limitation

of OCE is its low penetration depth of just a few

millimetres (Kennedy et al., 2014). However, this

Batista, A., Correia, C., Barbeiro, S., Cardoso, J., Domingues, J., Henriques, R., Loureiro, C., Santos, M., Serranho, P., Bernardes, R. and Morgado, M.

Swept-source Phase-Stabilized Optical Coherence Tomography Setup for Elastography.

DOI: 10.5220/0011126500003209

In Proceedings of the 2nd International Conference on Image Processing and Vision Engineering (IMPROVE 2022), pages 269-274

ISBN: 978-989-758-563-0; ISSN: 2795-4943

269

disadvantage is not a limiting factor when imaging

ocular tissues.

The high sensitivity of OCE is obtained using

phase-sensitive detection techniques. Therefore, OCT

instruments for elastography must have a high phase

stability, being necessary to minimize the timing

jitters and mechanical instabilities and to maximize

the signal-to-noise ratio (SNR). Timing jitters are

more relevant in swept-source systems than

spectrometer-based Fourier-domain setups, because

of the frequency jitter introduced by wavelength

sweeping based on mechanical moving mirrors

(Moon & Chen, 2018).

Several approaches have been implemented to

improve phase-stabilisation. Common solutions

include using optical timing references, implemented

with Mach-Zehnder Interferometers (MZI) optical

clocks and Fiber Bragg Gratings (FBG) wavelength-

dependent triggers (Moon & Chen, 2018). The MZI

provides a clock signal that is periodic in the

wavenumber space, usually called k-clock, which is

responsible for relative timing. The FBG triggers

provide an accurate timing of a given spectral

wavelength. Additional reference signals, by setting

up a second reference arm, also were proposed

(Vakoc et al., 2005). The best results are obtained

with a common-path OCT configuration, allowing to

measure displacements as low as 0.3 𝑛𝑚 (Li et al.,

2020). However, with a common-path configuration,

space compatibility between the setups for

mechanical excitation and optical sensing is difficult

(Lan et al., 2017). This is particularly true for eye

fundus imaging.

Here, we report on our swept-source OCE (SS-

OCE) setup and its phase stability. The OCE system

was implemented with the purpose of imaging

mechanical properties of the retina of mice. Phase

stability performance was achieved by using a MZI

optical clock and a FBG optical trigger, combined

with a novel algorithm for measuring phase-

differences (Batista et al., 2022, submitted), and post-

processing timing correction using the digitised

trigger signal as reference. Tests performed in

dynamic conditions, using agarose phantoms that

mimic the optical and mechanical properties of

biological tissues, showed that the OCE system can

detect and measure movements smaller than the axial

pixel size, which is around 320 nm in our system,

Measurements of phase stability resulted in a

minimum measurable displacement of 6.11 nm.

2 SS-OCE SETUP AND DATA

ACQUISITION

2.1 Instrumentation

Figure 1 presents the schematic of our home-built SS-

OCE system. It consists of a swept-source OCT (SS-

OCT) and uses, for the dynamic mechanical

excitation of the sample, a piezoelectric actuator (P-

287, Physik Instrumente GmbH & Co., Karlsruhe,

Germany), or a 10 MHz ultrasound A-scan probe

(Imasonic, Voray sur L'Ognon, France). The SS-OCT

is based on a swept-source laser (Axsun, Excelitas

Technologies Corp., Mississauga, Canada) emitting

at a central wavelength of 1060 𝑛𝑚, with a bandwidth

of 110 𝑛𝑚 and a repetition rate of 100 𝑘𝐻𝑧. The

wavelength sweep is implemented by a tunable

MEMS (micro-electromechanical system) filter. The

laser source includes a fiber-based MZI to provide a

k-clock output, evenly spaced in wavenumber space,

for direct analogue-to-digital (A/D) sampling. This

makes possible to sample the OCT interferogram

linearly in wavenumber, allowing its subsequent

direct Fourier processing.

The laser output is split by a 90 to 10 optical fiber

coupler, with 90% of the light being used to produce

the SS-OCT interferograms and the remaining 10%

directed into an FBG (OE Land, Quebec, Canada,

= 990 𝑛𝑚, reflectivity of 99.99%, Δλ = 0.352 𝑛𝑚).

The FBG is used to produce trigger pulses

synchronised with the spectral event corresponding to

the Bragg wavelength of 990 𝑛𝑚 (measured

value = 990.128 𝑛𝑚). The optical reflection signal of

the FBG, occurring at 990 nm, is converted into an

electrical signal by a photodiode amplifier and

formatted by a digital delay and pulse generator

(DG535, Stanford Research Systems, CA, USA).

The light used by the OCT is further split 90:10,

respectively, into the sample and reference arms. In

the sample arm, the light is delivered and collected

from the sample using a 50:50 optical fiber coupler

and a long working distance, infinity-corrected,

microscope objective (LSM03-BB, Thorlabs Inc.,

Newton, NJ, USA). The optical setup of the sample

arm can be changed when imaging samples

containing optical elements, like mice’s eyes. In the

reference arm, light is reflected from a stationary

reference mirror. An in-line fiber optic polarization

controller is used to remove differences in

polarisation between the sample and reference

signals.

Imaging4OND 2022 - Special Session on New Developments in Imaging for Ocular and Neurodegenerative Disorders

270

Figure 1: Schematic representation of the SS-OCE system. C – Collimator, L –Lens (microscope objective), M – Mirror, GM

– Galvanometric mirrors, ADC – analogue-to-digital converter channel, FC – Fiber Coupler, FBG – Fiber Bragg Grating.

Interference between light coming from the

sample and reference arms occurs in a 50:50 optical

fiber coupler. The interference fringes are detected by

a balanced photodetector (PDB471C, Thorlabs Inc.),

which removes common-mode noise. The output of

the photodetector is digitised by a data acquisition

(DAQ) board (X5-400M, Innovative Integration,

Inc., Indianapolis, IN, USA), using the trigger derived

from the FBG-generated signal and the laser k-clock

output as the sampling clock. Samples are acquired at

400 MHz, with a resolution of 14-bit.

The optical transmission signal from the FBG is

also digitised, using the second A/D channel of the

DAQ board. This signal is used as timing reference

during a post-processing step for additional timing

jitter correction. In this step, any shift occurring in the

timing reference signal is compensated by shifting the

interferogram by an equivalent value. This correction

is seldom used, as shifts in the timing reference signal

are rare events.

The two-dimensional scanning of the sample is

achieved by a pair of galvanometric mirrors

(GVS002, Thorlabs, Inc.). Their servo drivers are

driven by two 16-bit DACs (LTC2642 from Linear

Technology) with a settling time of 1 μs, programmed

through a 50 MHz SPI interface.

System synchronisation and timing control is the

task of a custom-programmed Xilinx XC6SLX45

field-programmable gate array (FPGA). This device

receives the trigger from the digital delay generator

and produces, with adequate timing, the DAQ board

trigger, the transient pulse that triggers mechanical

excitation and the signal that enables galvanometers

to move. The FPGA is programmed by the SS-OCE

control software running on a PC, through an SPI link

provided by an Adafruit FT232H Breakout module.

2.2 Control and Acquisition Software

The OCE control software was developed using

object-oriented programming (Microsoft Visual

C++/IDE) for the 64-bit Microsoft Windows

operating system. Libraries from Innovative

Technologies were used to deal with data acquisition

and DAQ board control.

The software implements the standard OCT

acquisition modes: axial A-scan in the sagittal plane,

cross-sectional B-scan, in the transversal plane and

volumetric acquisition, which can be used to present

C-like scans in the coronal plane. Elastography

measurements require collecting data using the M-B

scanning protocol (Kirby et al., 2017). In this

protocol, axial scans are repeated 512 times at a given

location. This corresponds to a scanning time of

5.12 ms per location. B-scans are then generated by

matching in time several distinct lateral locations.

Typically, imaging is performed in 512 distinct lateral

positions covering approximately 6.25 mm, in steps

of 12.20 μm. Sample mechanical excitation occurs

once per each lateral location, with a delay of 200 μs

(corresponding to 20 A-scans) to the beginning of

data acquisition for that location.

Swept-source Phase-Stabilized Optical Coherence Tomography Setup for Elastography

271

3 DISPLACEMENT

CALCULATION

In phase-resolved OCE, the displacement Δ𝑑 is

calculated from the measured phase difference, 𝛥𝜙,

according to (Kennedy et al., 2014):

Δ𝑑  𝛥𝜙

𝜆



𝜋𝑛

(1)

where, 𝜆

is the central wavelength of the laser, and 𝑛

is the sample’s refractive index.

The phase difference, 𝛥𝜙, at each depth 𝑧, is

computed as the difference between the phase of two

consecutive A-scans (𝜙

(𝑧) and 𝜙

(𝑧)), acquired at

the same lateral location:

𝛥𝜙



𝑧



 𝜙





𝑧



 𝜙





𝑧



. (2)

A-scan phases are obtained from the inverse

Fourier transform of the interferograms.

We developed a new method to measure phase

differences in OCE (Batista et al., 2022, submitted).

Briefly, if we consider 𝐺(𝑘) a function in the

wavenumber (frequency) k-space, obtained by

concatenating two consecutive interferograms from

the same location, 𝐹

(𝑘) and 𝐹

(𝑘), where 𝐹

(𝑘) is

flipped prior to concatenation, its phase (ϕ

𝐺

), given by

the angle of its inverse discrete Fourier transform

(IDFT), 𝑔(𝑧), is equivalent to:

𝜙



 𝜙





 𝜙





 𝑟𝑎𝑚𝑝  Δ𝜙  𝑟𝑎𝑚𝑝

(3)

where ramp corresponds to an amount linearly

dependent on depth that ranges from 0 to 2π for the

entire signal. So, phase differences can be computed

directly from the IDFT of the concatenated spectra.

4 SYSTEM EVALUATION

Here we present results concerning the timing and

phase stability performance of the SS-OCE system

and show that the system can detect and measure axial

movements smaller than its axial pixel size.

4.1 Time and Phase Stability

For assessing the time and phase stability of our OCE

system, we made measurements in static conditions,

i.e., without any mechanical excitation, using a gold-

coated mirror as sample. Data was recorded with the

sample located at the position where the optical path

difference between the sample and the reference arm

of the OCT interferometer is close to zero, with this

position corresponding to the highest signal to noise

ratio (SNR).

The system’s time stability was assessed by the

standard deviation of the interference fringes arrival

time at zero-crossing (Li et al., 2020). For finer

analysis, we used a cubic interpolation of the data, at

zero-crossing, to achieve a time resolution of 3.5 ps.

Measurements showed that our SS-OCE has a time

stability of 396.9 ± 46.7 ps.

The phase stability was assessed by the standard

deviation of the measured phase difference (σ

𝜙

) in

static conditions. Following equation (1), this value

can measure the minimum detectable displacement.

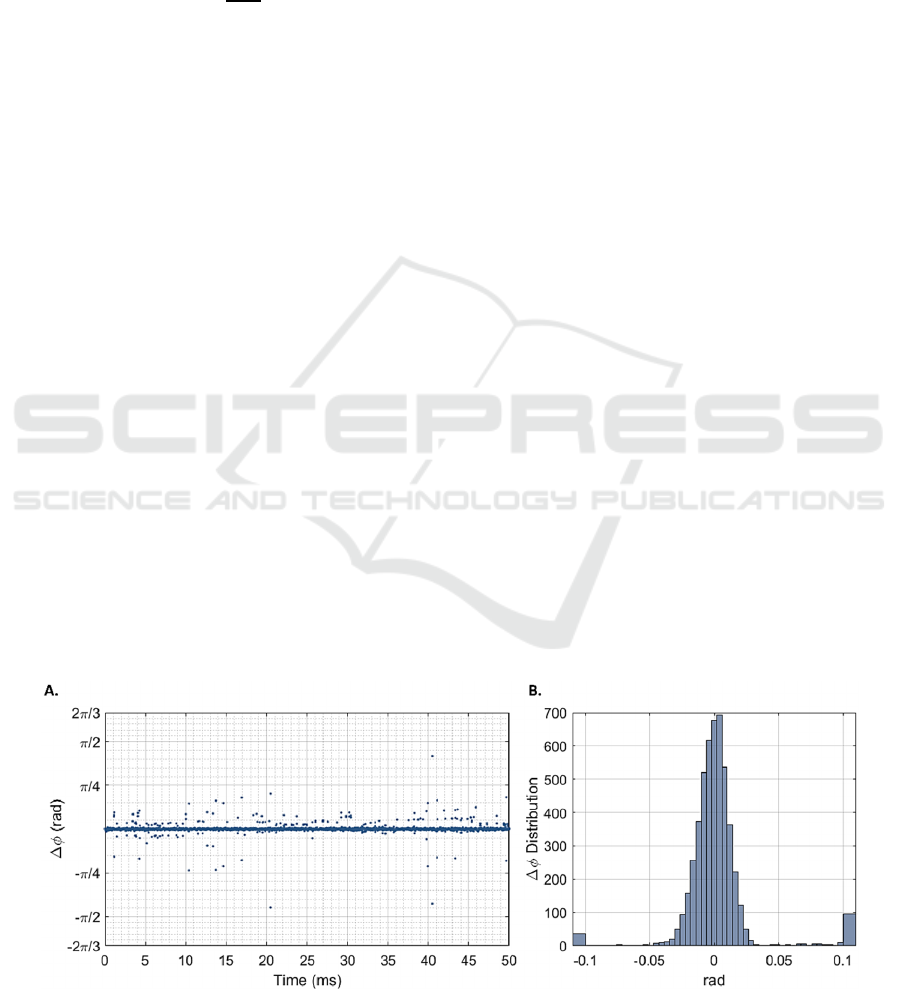
Figure 2 shows the phase differences over 5000

consecutive interferograms and their distribution.

When considering full volumes of 512 M-scans, the

distribution of phase differences presents a standard

deviation σ

𝜙

of 72.44 mrad, which, according to

equation 1, corresponds to a minimum detectable

displacement of 6.11 nm.

Figure 2: Phase differences (𝛥𝜙) for a static gold-mirror at highest signal-to-noise ratio, over 5000 consecutive interferograms

(A) and their overall distribution (B). This distribution presents a standard deviation σ

Δ𝜙

equal to 72.44 mrad.

Imaging4OND 2022 - Special Session on New Developments in Imaging for Ocular and Neurodegenerative Disorders

272

4.2 Performance in Dynamic

Conditions

To assess the performance of the SS-OCE in dynamic

conditions, we used transient pulses to induce surface

motion in homogeneous agarose phantoms with

tissue-mimicking characteristics. These phantoms

were prepared by mixing, while stirring, agar with

distilled water at high temperature (85

C). Glass

microspheres were added to the mixture to increase

optical scattering. The mixture was placed into

cylindrical containers for moulding and cured for

24 h. The produced phantoms had diameters and

heights of approximately 5.2 cm and 3.5 cm,

respectively.

The mechanical excitation of the phantoms was

provided by the piezoelectric actuator, driven by

different pulse widths of 200 μs, 300 μs, 400 μs and

500 μs, at a fixed amplitude of 200 mV. These pulses

induced, on the surface of the phantoms,

displacements lower than the size of the A-scan pixel

of the SS-OCT system (around 320 nm). This implies

that these displacements were not measurable from

the OCT A-scans, which correspond to the plot of the

amplitude of the IDFT of the interferograms.

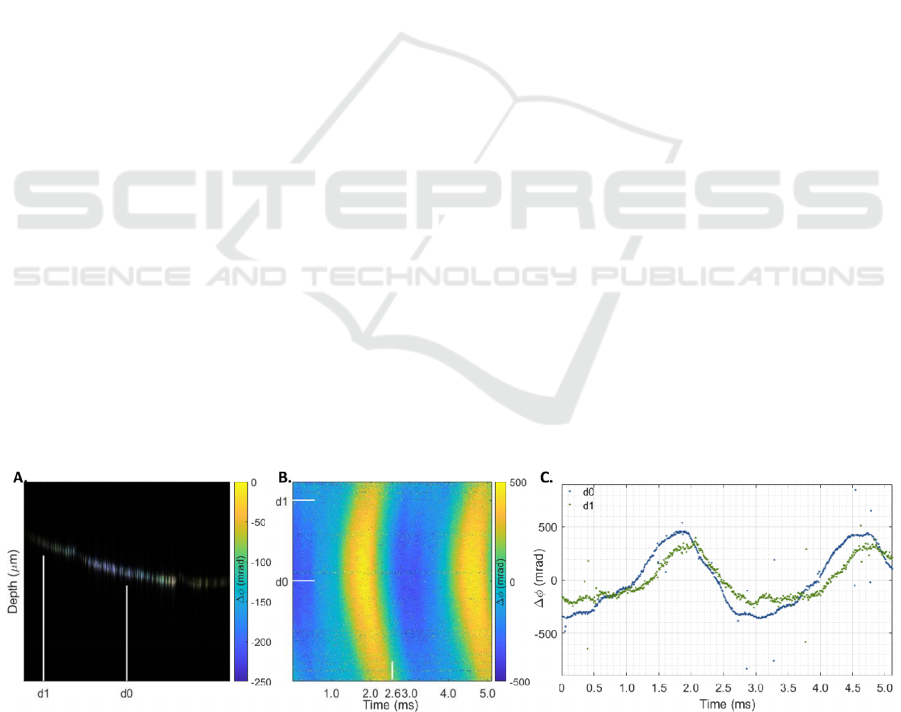
Figure 3 shows the phase difference ( 𝛥𝜙 )

reconstruction for a homogeneous phantom with an

agarose concentration of 10 g/l, after mechanical

excitation by a transient pulse of 200 μs. The figure

includes the structural B-scan and 𝛥𝜙 overlay at

2.56 ms (A), the projection over time for all 512

locations (B) and the 𝛥𝜙 curves for two locations

closer to (d0) and further away (d1) from the

excitation point (C). The mechanical excitation was

applied approximately 1 mm away from the OCT

beam scanning direction (C). From these figures, the

SS-OCE system’s ability to record sub-pixel

displacements is evident.

5 CONCLUSION

We presented a custom-built, swept-source OCE

system, and evaluated its performance under static

and dynamic conditions.

The developed SS-OCE presented a time stability

of 396.9 ± 46.7 ps. The measured phase stability,

given by the standard deviation of the distribution of

phase-differences measured in stationary conditions,

was 72.44 mrad. This corresponds to a minimum

detectable displacement of 6.11 nm.

Tests under dynamic conditions showed that the

OCE system can detect and measure sub-pixel

movements in samples under dynamic mechanical

excitation. The observed phase-differences and,

therefore, sample displacements confirm that the

system meets the requirements posed by biomedical

applications of optical coherence elastography.

The phase stability performance of the OCE

system can still be improved. In the shot noise limit,

the minimum measurable phase difference

corresponds to the reciprocal of the square root of the

signal-to-noise ratio (Hyle Park et al., 2005). The

phase stability of our system is still one order of

magnitude higher than this theoretical limit. One

approach to improve the phase performance of the

OCE system is to optimize the delays between the

timing signals (trigger and clock) and the

interferogram. It was shown that signal relative

delays have a large impact on phase stabilization due

to incoherent timing corrections and collisions

between the timing signals (Moon & Chen, 2018).

Delay optimization can improve phase stabilization

by an order of magnitude, allowing to achieve noise

limited performance.

Figure 3: Phase difference (𝛥𝜙) reconstruction for a 10 g/l homogenous agarose phantom after a transient pulse of 200 μs.

Structural B-scan and 𝛥𝜙 overlay at 2.56 ms (A), 𝛥𝜙 projection over time (B), and 𝛥𝜙 curves at two lateral positions located

closer (d0) and further (d1) from the piezoelectric actuator contact rod (mechanical excitation), positioned approximately

1 mm away from the OCT beam scanning direction (C). Lateral positions are indicated in the overlay images and projections.

Swept-source Phase-Stabilized Optical Coherence Tomography Setup for Elastography

273

ACKNOWLEDGEMENTS

This work was financed by FEDER Funds through

the Operational Program for Competitiveness Factors

- COMPETE and by Portuguese National Funds

through FCT-Foundation for Science and

Technology under the PTDC/EMD-

EMD/32162/2017 project.

REFERENCES

Batista, A., Serranho, P., Santos, M. J., Correia, C.,

Domingues, J. P., Loureiro, C., Cardoso, J., Barbeiro,

S., Morgado, M., & Bernardes, R. (2022). Improving

Displacement Measurements in Phase-resolved Optical

Coherence Elastography. Submitted.

Hyle Park, B., Pierce, M. C., Cense, B., Yun, S.-H., Mujat,

M., Tearney, G. J., Bouma, B. E., de Boer, J. F., Huang,

D., Swanson, E., Lin, C., Schuman, J., Stinson, W.,

Chang, W., Hee, M., Flotte, T., Gregory, K., Puliafito,

C., Fujimoto, J., … Bouma, B. (2005). Real-time fiber-

based multi-functional spectral-domain optical

coherence tomography at 1.3 µm. Optics Express, Vol.

13, Issue 11, Pp. 3931-3944, 13(11), 3931–3944.

https://doi.org/10.1364/OPEX. 13.003931

Kennedy, B. F., Kennedy, K. M., & Sampson, D. D. (2014).

A Review of Optical Coherence Elastography:

Fundamentals, Techniques and Prospects. Ieee Journal

of Selected Topics in Quantum Electronics, 20(2).

isi:000329997200032

Kirby, M. A., Pelivanov, I., Song, S., Ambrozinski, Ł.,

Yoon, S. J., Gao, L., Li, D., Shen, T. T., Wang, R. K.,

& O’Donnell, M. (2017). Optical coherence

elastography in ophthalmology. Journal of Biomedical

Optics, 22(12), 1. https://doi.org/10.1117/1.JBO.22.12.

121720

Lan, G., Singh, M., Larin, K. V., & Twa, M. D. (2017).

Common-path phase-sensitive optical coherence

tomography provides enhanced phase stability and

detection sensitivity for dynamic elastography.

Biomedical Optics Express, 8(11), 5253.

https://doi.org/10.1364/BOE.8.005253

Larin, K. V., & Sampson, D. D. (2017). Optical coherence

elastography – OCT at work in tissue biomechanics

[Invited]. Biomedical Optics Express, 8(2), 1172.

https://doi.org/10.1364/BOE.8.001172

Li, Y., Moon, S., Chen, J. J., Zhu, Z., & Chen, Z. (2020).

Ultrahigh-sensitive optical coherence elastography.

Light: Science & Applications 2020 9:1, 9(1), 1–10.

https://doi.org/10.1038/s41377-020-0297-9

Moon, S., & Chen, Z. (2018). Phase-stability optimization

of swept-source optical coherence tomography.

Biomedical Optics Express, 9(11), 5280.

https://doi.org/10.1364/BOE.9.005280

Vakoc, B. J., Yun, S. H., de Boer, J. F., Tearney, G. J.,

Bouma, B. E., Huang, D., Swanson, E. A., Lin, C. P.,

Schuman, J. S., Stinson, W. G., Chang, W., Hee, M. R.,

Flotte, T., Gregory, K., Puliafito, C. A., Fujimoto, J. G.,

Izatt, J. A., Kulkami, M. D., Yazdanfar, S., … Nelson,

J. S. (2005). Phase-resolved optical frequency domain

imaging. Optics Express, Vol. 13, Issue 14, Pp. 5483-

5493, 13(14), 5483–5493. https://doi.org/10.1364/

OPEX.13.005483

Imaging4OND 2022 - Special Session on New Developments in Imaging for Ocular and Neurodegenerative Disorders

274