Blind Side Channel on the Elephant LFSR

Awaleh Houssein Meraneh

, Christophe Clavier

, H

ene Le Bouder

, Julien Maillard

2,3

and Ga

el Thomas

IMT-Atlantique, OCIF, IRISA, Rennes, France

Universit

e de Limoges, XLIM-CNRS, Limoges, France

Universit

e de Grenoble Alpes, CEA, LETI MINATEC Campus, F-38054 Grenoble, France

DGA Ma

ıtrise de l’Information, Bruz, France

Keywords:

Blind Side Channel Analysis, Hamming Weight, Elephant, LFSR, NIST.

Abstract:

Elephant is a ﬁnalist to the NIST lightweight cryptography competition. In this paper, the ﬁrst theoretical blind

side channel attack against the authenticated encryption algorithm Elephant is presented. More precisely,

we are targetting the LFSR-based counter used internally. LFSRs are classic functions used in symmetric

cryptography. In the case of Elephant, retrieving the initial state of the LFSR is equivalent to retrieving the

encryption key. The paper ends by the study of different ways to tweak the design of Elephant to mitigate our

attack.

1 INTRODUCTION

Internet of things (IoT) devices become more and

more widespread within our day-to-day life. From

military grade to general purpose hardware, the need

for strong security raises. The cryptosystems imple-

mented on those devices must ensure both security

and low power consumption overhead. In this con-

text, the National Institute of Standards and Technol-

ogy (NIST) started the competition for lightweight

cryptography candidates for authenticated encryp-

tion (NIST, 2018). An authenticated encryption al-

gorithm should ensure conﬁdentiality and integrity of

the communications.

The security of authenticated encryption schemes

can be supported by several strategies. Various ap-

proaches have been considered by the lightweight

cryptography competition candidates:

• cryptographic permutation with sponge or du-

plex construction (Dobraunig et al., 2014; Beierle

et al., 2019; Daemen et al., 2020),

• block cipher combined with a mode (e.g. AES

combined with Galois/Counter Mode) (Iwata

et al., 2020; Beyne et al., 2021),

• stream cipher paradigms (Hell et al., 2021).

When discussing about the security of a crypto-

graphic algorithm, numerous tools allow the cryp-

tographers to prove the security of a cipher. Un-

fortunately those tools do not consider the interac-

tion of the computing unit with its physical environ-

ment. Physical attacks are a real threat, even for cryp-

tographic algorithms proved secure mathematically.

Physical attacks are divided in two families: Side-

Channel Analysis (SCA) and the fault injection at-

tacks.

Motivations

Many attacks exist on the different traditional cryp-

tographic algorithms, for example on AES (Brier

et al., 2004; Giraud, 2004). Lightweight cryptogra-

phy, much younger and used in embedded devices,

has been far less studied. For example, attacks on

stream ciphers (Rechberger and Oswald, 2004) or

sponge functions (Samwel and Daemen, 2017) are

less common. That is why we chose to study SCA

against new authenticated encryptions. The chosen

algorithm is the cryptosystem Elephant (Beyne et al.,

2021). More precisely, in this paper, the focus is

about using Linear Feedback Shift Registers (LFSR),

in a block cipher combined with a mode construction.

Some attacks exist yet as in (Rechberger and Oswald,

2004; Joux and Delaunay, 2006; Burman et al., 2007;

Chakraborty et al., 2014; Kazmi et al., 2017; Jurecek

et al., 2019), but the main difference is in model of

the attacker. To the best our knowledge, there is no

blind side channel attack on LFSR in the context of

authenticated encryption. So in this paper, a blind side

channel attack targeting the LFSR of the Elephant al-

gorithm, is presented.

Houssein Meraneh, A., Clavier, C., Le Bouder, H., Maillard, J. and Thomas, G.

Blind Side Channel on the Elephant LFSR.

DOI: 10.5220/0011135300003283

In Proceedings of the 19th International Conference on Security and Cryptography (SECRYPT 2022), pages 25-34

ISBN: 978-989-758-590-6; ISSN: 2184-7711

Contribution

In this paper, we present the ﬁrst theoretical blind

side channel attack targeting the LFSR of the Ele-

phant algorithm. We exploit the usage of intermediate

variables that are statistically dependent to the secret

(here the secret LFSR initial state) and show that this

structure could eventually threaten the security of a

cryptosystem’s regarding side-channel analysis.

Also the study of the inﬂuence of the choice of the

LFSR is presented.

Organisation

The paper is organized as follows. In section 2 the

context about blind side channel attack and the Ele-

phant are introduced. The theoretical attack is ex-

plained in section 3. Details of implementation attack

are described in section 4. The section 5 presents ex-

perimental results and discussion about LFSR design.

Finally, a conclusion is drawn in 6.

2 CONTEXT

In this section, ﬁrst Elephant description is presented,

then the context of blind SCA is introduced.

2.1 Elephant

An authenticated encryption algorithm should ensure

conﬁdentiality and integrity. It takes as input dif-

ferent parameters: a plaintext, data associated to the

plaintext, a secret key, and an initialisation vector also

called a nonce. The nonce is public but must be dif-

ferent for each new plaintext. The algorithm ensures

conﬁdentiality of the plaintext and integrity of both

the plaintext and the associated data.

Elephant (Beyne et al., 2020; Beyne et al., 2021)

is a nonce-based authenticated encryption with asso-

ciated data (AEAD) ﬁnalists to the NIST lightweight

cryptography competition. It is an Encrypt-then-

MAC construction that combines CTR-mode encryp-

tion with a variant of the protected counter sum (Bern-

stein, 1999; Luykx et al., 2016).

It uses a cryptographic permutation masked with

LFSRs in an Even-Mansour-like fashion (Granger

et al., 2016) in place of a blockcipher.

Let P be an n-bit cryptographic permutation, and

ϕ an n-bit LFSR. Let the function mask : {0, 1}

128

N × {0, 1,2} → {0, 1}

be deﬁned as follows:

mask

i,b

= (ϕ ⊕ id)

◦ ϕ

◦ P(K||0

n−128

) (4)

K || 0

∗

mask

0,0

N || A

mask

1,0

•

· · ·

mask

`−1,0

· · ·

|| 10

∗

•

ϕ ⊕ id

mask

0,1

N || 0

∗

•

ϕ ⊕ id

mask

1,1

N || 0

∗

•

ϕ ⊕ id

mask

`−1,1

N || 0

∗

•

Trunc

· · ·

|| 10

∗

mask

`−1,2

ϕ ⊕ id

•

mask

1,2

ϕ ⊕ id

•

mask

0,2

ϕ ⊕ id

•

· · ·

Trunc

•

Figure 1: Elephant associated data authentication (top),

plaintext encryption (middle), and ciphertext authentication

(bottom).

Let Split(X) be the function that splits the input X

into n-bit blocks, where the last block is zero-padded.

Let Trunc

(X) be the t left-most bits of X .

Encryption enc under Elephant gets as input a

128-bit key K, a 96-bit nonce N, associated data

A ∈ {0, 1}

∗

, and a plaintext M ∈ {0, 1}

∗

. It outputs

a ciphertext C as large as M, and a t-bit tag T . The

description of enc is given in Algorithm 1 and is de-

picted on Figure 1.

Decryption dec gets as input a 128-bit key K, a

96-bit nonce N, associated data A ∈ {0, 1}

∗

, a cipher-

text C ∈ {0, 1}

∗

, and t-bit tag T . It outputs a plaintext

M as large as C if the tag T is correct, or the symbol

⊥ otherwise. The description of dec easily follows

from that of enc.

Elephant comes in three ﬂavours which differ on

the n-bit cryptographic permutation P and the LFSR

ϕ used, as well as the tag size t.

SECRYPT 2022 - 19th International Conference on Security and Cryptography

. . .

≪ 3

 7  7

Figure 2: 160-bit LFSR ϕ

Dumbo

. . .

≪ 1

 7  7

Figure 3: 176-bit LFSR ϕ

Jumbo

. . .

≪ 1 ≪ 1

 7

Figure 4: 200-bit LFSR ϕ

Delirium

Dumbo

: (x

,··· , x

) 7→ (x

,··· , x

≪ 3 ⊕ x

 7 ⊕ x

 7) (1)

Jumbo

: (x

,··· , x

) 7→ (x

,··· , x

≪ 1 ⊕ x

 7 ⊕ x

 7) (2)

Delirium

: (x

,··· , x

) 7→ (x

,··· , x

≪ 1 ⊕ x

 7) (3)

Algorithm 1: Elephant encryption algorithm enc.

Input: (K,N,A, M) ∈ {0,1}

128

× {0,1}

{0,1}

∗

× {0, 1}

∗

Output: (C, T ) ∈ {0, 1}

|M|

× {0, 1}

1: M

,··· , M

← Split(M)

2: for i ← 1 to `

3: C

← M

⊕ P(N||0

n−96

⊕ mask

i−1,1

) ⊕

mask

i−1,1

4: end for

5: C ← Trunc

|M|

||··· ||C

)

6: T ← 0

7: A

,··· , A

← Split(N||A||1)

8: C

,··· ,C

← Split(C||1)

9: T ← A

10: for i ← 2 to `

11: T ← T ⊕ P(A

⊕ mask

i−1,0

) ⊕ mask

i−1,0

12: end for

13: for i ← 1 to `

14: T ← T ⊕ P(C

⊕ mask

i−1,2

) ⊕ mask

i−1,2

15: end for

16: T ← P(T ⊕ mask

0,0

) ⊕ mask

0,0

17: return (C, Trunc

(T ))

Dumbo uses the 160-bit permutation Spongent-

π[160] (Bogdanov et al., 2011), the LFSR ϕ

Dumbo

given by equation 1 and illustrated on Figure 2, and

has tag size t = 64 bits.

Jumbo uses the 176-bit permutation Spongent-

π[176] (Bogdanov et al., 2011), the LFSR ϕ

Jumbo

given by equation 2 and illustrated on Figure 3, and

has tag size t = 64 bits.

Delirium uses the 200-bit permutation Keccak-

f [200] (Bertoni et al., 2011; NIST, 2015), the LFSR

Delirium

given by equation 3 and illustrated on Fig-

ure 4, and has tag size t = 128 bits.

The three n-bit LFSRs used for the variants of Ele-

phant are the GF(2)-linear maps given at the byte-

level by the equations (1), (2) and (3).

2.2 Blind Side Channel Analysis

Even if an algorithm has been proven to be math-

ematically secure, its implementation can open the

gate to the so-called physical attacks. (SCA) are

a subcategory of physical attacks. They exploit

the fact that some physical values of a device

depend on intermediate values of the computation.

Blind Side Channel on the Elephant LFSR

This is the so-called leakage of information of the cir-

cuit. It could be used to retrieve secrets, as a secret

key.

Different kind of leakage can be exploited as

times (Handschuh and Heys, 1998), power consump-

tion or electromagnetic radiations (Standaert, 2010).

In this paper, the leakage is power consumption. At

each instant, the measurement of the intensity of the

electric current reﬂects the activity of the circuit. The

power consumption of a device is the sum of the

power consumptions of each of its logic gates. An

attacker therefore has the possibility of distinguishing

a transition from 0 to 1 from a transition from 1 to 0.

A SCA is often leaded with a divide-and-conquer

approach. Namely, the secret is divided into small

pieces that are analysed independently. Different kind

of analysis exist.

The Simple Power Analysis (SPA) (Mangard,

2002) are called simple because they determine di-

rectly, from an observation of the power consumption,

during a normal execution of an algorithm, informa-

tion on the calculation performed or the data manipu-

lated.

The family of Correlation Power Analysis

(CPA) (Kocher et al., 1999; Brier et al., 2004; Gier-

lichs et al., 2008) uses a mathematical model for the

leakage. A confrontation between measurement and

model is performed. More precisely, a statistic tool

called distinguisher gives score to the different tar-

gets.

Template attacks are statistical categoriza-

tions (Chari et al., 2002). No mathematical model is

required.

The blind side channel analysis family is new im-

provement in SCA (Joux and Delaunay, 2006; Bur-

man et al., 2007; Chakraborty et al., 2014; Linge

et al., 2014; Le Bouder et al., 2016; Clavier and Rey-

naud, 2017). The main idea is to not use the data as

plaintext or ciphertext. Only the leakage is used. The

power consumption leakage is very correlated to the

Hamming Weight (HW) of the data. So in blind SCA,

a strong assumption is make. The attacker can retrieve

HW with the leakage. More precisely, the power con-

sumption can be seen as a noisy HW. In this paper,

the considered adversary model is that: the HW of

bytes can be obtained by an attacker. This model is

made feasible by the fact that the attacker can average

power traces.

The ﬁrst theoretical result on SCA on LFSRs

are (Joux and Delaunay, 2006) where the authors

leverage the dependence between the leakage and the

unique feedback bit of a Galois LFSR. The case of

Fibonacci LFSRs where a single new value is com-

puted at each iteration is studied in (Burman et al.,

2007). Finally, both kind of LFSRs are theoreti-

cally and practically compared in (Chakraborty et al.,

2014).

3 THEORETICAL ATTACK

3.1 Goal

LFSRs are used in different lightweight cryptography

candidates, and its initial state often depends on both

the key and the nonce. As the nonce needs to be

changed for each encryption, attacks on such schemes

are limited to the decryption algorithm. In the case of

Elephant, the LFSR only depends on the secret key,

Consequently, our attack can be applied in an encryp-

tion scenario.

The goal of the presented attack is to retrieve the

LFSR secret initial state. One has to remark three im-

portant points.

• Retrieving the initial state of the LFSR which is

equal to mask

0,0

is equivalent to retrieving the se-

cret key. Indeed, the initial state is just the result

of the known permutation P applied to the key.

• As the retroaction polynomial is publicly known,

it is possible to shift the LFSR backwards: an at-

tacker who knows 20 consecutive bytes of the se-

cret stream is able to recover the initial state.

• The smaller the LFSR is, the more the attack is

able to succeed. As a consequence, the Dumbo 2

instance is the most vulnerable instance: the focus

is on Dumbo in the following of this paper.

3.2 Leakage in the LFSR

In this attack, it is assumed that the Hamming Weight

of all bytes of the LFSR can be obtained by an at-

tacker.

Let x be a byte, so x can take 256 values in

[[0, 255]]. With the HW of x, the attacker reduces the

list of possible values, as shown in Table 1.

Table 1: Number of possible values for an Hamming

weight.

HW (x) 0 1 2 3 4 5 6 7 8

#x 1 8 28 56 70 56 28 8 1

Since the LFSR generates a single new byte at

each iteration, let x

,··· , x

be the content of the

Dumbo LFSR initialised with mask

0,0

, and extend the

notation for j ≥ 20, by letting x

be the new byte gen-

erated at iteration j − 20. In other words, the attacker

has the following relation (L1).

SECRYPT 2022 - 19th International Conference on Security and Cryptography

L1 x

j+20

= (x

≪ 3) ⊕ (x

j+3

 7) ⊕ (x

j+13

 7).

The ﬁrst idea is to use the knowledge of the

following Hamming weights: HW (x

j+20

HW (x

) = HW (x

≪ 3), HW (x

j+3

) and

HW (x

j+13

Moreover, one has to remark that:

HW (x

) = HW (x

≪ 3). (5)

So with the two equations (L1) and (5) the attacker has:

HW (x

j+20

) =











HW (x

)

HW (x

) + 1

HW (x

) − 1

HW (x

) + 2

HW (x

) − 2

(6)

Looking more precisely at equation (L1), it can be

seen that the difference HW (x

j+20

) − HW (x

) de-

pends on only four bits. Letting x

[i] denote the

i-th least signiﬁcant bit of byte x

, these four bits

are {x

j+3

[0];x

j+13

[7];x

[4];x

[5]}. Table 2 gives the

value of observed difference HW(x

j+20

) − HW (x

)

depending on the values of these four bits. In the

worst case, there are only 6 possibilities left, out of

16.

Table 2: Values of HW



j+20



− HW





according to

j+3

[0];x

j+13

[7];x

[4];x

[5]}.

j+3

[0],x

j+13

[7]) =



j+20



− HW (x

) (0,0) (0,1) (1,0) (1,1)

[4],x

[5]) =

(0,0) 0 +1 +1 +2

(1,0) 0 +1 −1 0

(0,1) 0 −1 +1 0

(1,1) 0 −1 −1 −2

3.3 Link between the Different Masks

The value mask

i,1

can be expressed in terms of

mask

∗,0

as in (7).

mask

i,1

= (ϕ ⊕ id)



mask

i,0



= ϕ



mask

i,0



⊕ mask

i,0

= mask

i+1,0

⊕ mask

i,0

(7)

Likewise, for mask

i,2

, equation (8) holds.

mask

i,2

= (ϕ ⊕ id)



mask

i,0



= (ϕ

⊕ id)



mask

i,0



= ϕ



mask

i,0



⊕ mask

i,0

= mask

i+2,0

⊕ mask

i,0

(8)

As in the case of mask

i,0

, let y

denote either the

byte j of mask

0,1

when 0 ≤ j ≤ 19, or the new byte

obtained after j −20 iterations of the LFSR initialised

with mask

0,1

. Likewise, let z

denote either the byte

j of mask

0,2

when 0 ≤ j ≤ 19, or the new byte ob-

tained after j − 20 iterations of the LFSR initialised

with mask

0,2

Equation (7) then translates to equation (9).

= x

⊕ x

j+1

(9)

Likewise, the equation 8 translates to (10).

= x

⊕ x

j+2

. (10)

The evolutions of the LFSR are analogous to (L1):

j+20

= (y

≪ 3) ⊕ (y

j+3

 7) ⊕ (y

j+13

 7).

(11)

j+20

= (z

≪ 3) ⊕ (z

j+3

 7) ⊕ (z

j+13

 7).

(12)

The attacker can thus exploit two attack vectors:

on the one hand, equations (L1), (11), and (12) coming

from iterating the LFSR, and on the other hand, equa-

tions (9) and (10) coming from the different masks

used for domain separation.

4 ATTACK STRATEGY

The whole search space corresponding to the initial

state of the LFSR is represented as a rooted tree. The

nodes at depth j correspond to the all possible values

for the bytes x

to x

of the LFSR. The tested candi-

dates are denoted by (x

,··· , x

). The nodes in the

graph of the search space are labelled as follows:

• the nodes at depth j correspond to the all possible

values of (x

,··· , x

);

• the children of node (x

,··· , x

), are the nodes la-

belled: (x

,··· , x

j+1

) for all values of x

j+1

In practice, to reduce the number of nodes, only the

nodes having the correct Hamming weights are con-

sidered. In other words, it sufﬁces to consider nodes

with HW (x

) = HW (x

). An example of such tree is

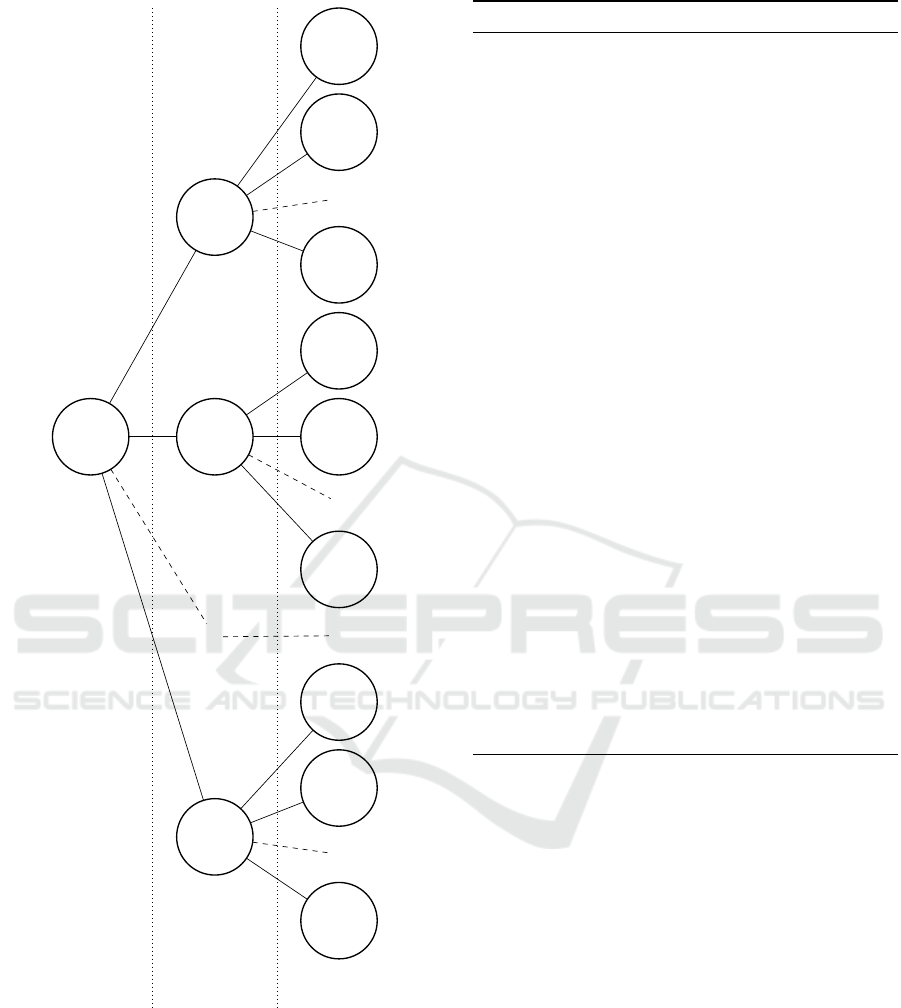
given on Figure 5.

A backtracking algorithm is used. The tree is tra-

versed in a depth-ﬁrst manner. For each step, the at-

tacker tests whether the current candidate (x

,··· , x

)

satisﬁes the different conditions given by the observed

Hamming weights. This test is given by algorithm 2.

If the test succeeds, the algorithm goes down to

the next layer to test the values of the byte x

j+1

. If it

reaches the bottom of the tree, then a good candidate

Blind Side Channel on the Elephant LFSR

= 03

= 2F

= 03

= 1F

= 03

= F8

= 03

= 2F

= 17

= 03

= 2F

= 0F

= 03

= 2F

= F0

= 03

= 1F

= F0

= 03

= 1F

= 17

= 03

= 1F

= 0F

= 03

= F8

= 0F

= 03

= F8

= 17

= 03

= F8

= F0

HW (x

) = 4HW (x

) = 5HW (x

) = 2

Figure 5: Example of the tree representation of the LFSR

initial state for the Hamming weights given at the bottom.

Only the ﬁrst three layers of the subtree rooted at x

= 03

are shown.

has been found, and can be saved. The algorithm then

iterates upon the next untested node.

If, at some point, the Hamming weights condi-

tions do not hold for the current (partial) candidate,

then no node in the sub-tree rooted at that node can

lead to a good candidate. Thus, it can be pruned

Algorithm 2: isvalid(X

,··· ,x

Input: Byte-wise partial candidate (x

,··· , x

) of

length 1 ≤ j + 1 ≤ 20

Assumes isvalid(x

,··· , x

j−1

) is true.

Output: true if candidate (x

,··· , x

) is compatible

with the observations, false otherwise

# Hamming weights of the xors

1: if HW(x

) 6= HW (x

) then

2: return false

3: end if

4: if HW(x

⊕ x

j−1

) 6= HW (y

j−1

) then

5: return false

6: end if

7: if HW(x

⊕ x

j−2

) 6= HW (z

j−2

) then

8: return false

9: end if

# Hamming weights of the feedbacks

10: if |HW(x

≪ 3) − HW (x

j+20

)| > 2 then

11: return false

12: end if

13: if |HW (x

j−3

≪ 3 ⊕ x

 7) − HW (x

j+17

)| > 1

then

14: return false

15: end if

16: if HW (x

j−13

≪ 3 ⊕ x

j−10

 7 ⊕ x

 7) 6=

HW (x

j+7

) then

17: return false

18: end if

19: return true

from the whole tree, saving the cost of searching it.

Finally, the algorithm ends when the whole tree has

been searched. A pseudocode of the attack is given

by algorithm 3.

To improve the efﬁciency of algorithm 3, the at-

tacker can overlook some of the ﬁrst iterations of the

LFSR, and start the attack at a time they deem more

satisfying. Indeed, the complexity of the attack de-

pend on the number of nodes visited in the tree. Look-

ing only at the ﬁrst four layers, that number, denoted

by N

, can be expressed using binomial coefﬁcients as

a function of (HW (x

),HW (x

)):



HW (x

)



HW (x

)



HW (x

)



HW (x

)



The idea is then to look at the quadru-

plet at the next iteration, namely

(HW (x

),HW (x

)), and so

on, until the number of nodes in the ﬁrst four layers

of the tree is sufﬁciently small. One has to remark

that the number 4 is arbitrary here, and the attacker

SECRYPT 2022 - 19th International Conference on Security and Cryptography

Algorithm 3: Attack.

Input: Observed Hamming weights

HW (x

),··· , HW (x

), HW (y

),··· , HW (y

and HW (z

),··· , HW (z

). For the sake of

clarity, they are seen as global variables.

Output: S set of keys compatible with the observed

Hamming weights

1: (x

,··· , x

) ← (0,·· · , 0)

2: ` ← 0

3: S ← {}

4: while true do

5: if j < 19 and isvalid(x

,··· , x

) then

6: j ← j + 1

7: x

← 0

8: else

9: if j = 19 and isvalid(x

,··· , x

) then

10: S ← S ∪ {(x

,··· , x

)}

11: end if

12: while j ≥ 0 and x

= FF do

13: j ← j − 1

14: end while

15: if j ≥ 0 then

16: x

← x

+ 1

17: else

18: break

19: end if

20: end if

21: end while

22: return S

can choose whatever value they might prefer.

The question is now, what bound on N

does the

attacker choose? We have chosen to ﬁx a threshold

at N

≤ 1, 756,160. With this, about 25% of the all

quadruplets are kept. Luckily, the probability to ﬁnd

such a quadruplet in the LFSR rapidly increases to

one when iterating, because of the good statistical

properties of LFSRs.

5 RESULTS AND DISCUSSION

5.1 Elephant Attack

We have simulated the attack on N

runs

= 560 ran-

domly generated Dumbo keys. For each, the num-

ber N

nodes

of nodes effectively traversed in the tree

has been counted. This number roughly corresponds

to the time complexity of the attack. Among those

nodes, we have speciﬁcally counted the number N

keys

of nodes on the last layer; i.e. nodes that correspond

to plausible guesses that remain to be brute forced to

ﬁnish the attack.

Unfortunately, only just above half (53.57%) of

the runs have ended after two days, and about a quar-

ter has been still running after a week. On average,

for the runs that ﬁnished after two days, the number

of nodes traversed is N

nodes

= 2

41.82

, and the number

of remaining keys is N

keys

= 2

36.59

5.2 Impact of the Generation of Masks

The natural question is about what could be done to

mitigate this attack. Outside of using generic coun-

termeasures, like e.g. boolean masking, there seem

to be two possibilities for improvement. Indeed, the

attacker gains information from two sources:

• from equations (7) and (8) used to derive the

masks for domain separation;

• from the LFSR state update equation (L1).

Thus either the mask derivation, or the LFSR can be

changed, or both. This section studies the former

case.

We ran two experiments, similar to that in sec-

tion 5.1 except that the attacker does not gain infor-

mation on every Hamming weights. In the ﬁrst exper-

iment, they only know the values of the HW (x

), and

the HW(y

) for sufﬁciently j. In other words, com-

pared to the experiment in section 5.1, they lost the

knowledge of the HW (z

). Likewise, in the second

experiment, they only know the values of the HW(x

)

for sufﬁciently j. Unfortunately, in both cases, none

of the N

runs

= 120 runs done has terminated after a

week.

From these experiments, it seems that the knowl-

edge of the HW(x

), HW (y

), and HW (z

) con-

tributed heavily on the success of the attack. It would

then seem a good idea to tweak the cryptographic

mode of operation by ﬁnding another way of gener-

ating masks for domain separation.

5.3 Studies on Different LFSRs

This section is dedicated to the study of the inﬂuence

of the choice of the LFSR. To keep the spirit of the

original Elephant, only Fibonacci-like LFSRs, at the

byte level, are considered. More speciﬁcally, LFSRs

considered are: LFSRs where a single new byte is

computed from a combination of three bytes using

byte-wise shifts and rotations. As usual, the associ-

ated feedback polynomial must be primitive to ensure

only maximum-length sequences can be generated.

Among all possible candidates, different be-

haviours can be triggered.

In this paper, the type of an LFSR is deﬁned as the

sequence of number of bits unknown to the attaquer at

each depth in the tree where a new feedback occurs.

Blind Side Channel on the Elephant LFSR

Looking at equation (L1), it can be seen that:



HW (x

j+20

) − HW (x

≪ 3)



≤ 2

since there are only 2 bits that are modiﬁed by:

j+3

 7 ⊕ x

j+13

 7.

Thus, if other feedback function are used, with more

bits involved, it can be expected to have an impact on

the attack.

Later in the attack, when at depth 3 in the tree, the

same idea can be applied to check whether:



HW (x

j+17

) − HW (x

j−3

≪ 3 ⊕ x

 7)



≤ 1

since now only the single bit x

j+10

 7 is unknown.

In conclusion, the type of the Dumbo LFSR is [2,1].

LFSR with different types can be a ﬁrst criterion

when testing our attack.

A second criterion can be: how far apart the feed-

back bytes are. Indeed, the tighter they are, the faster

the attacker can use equation (L1) at its full potential.

In the case of Dumbo, the feedback bytes are at in-

dices 0, 3, and 13. We call 13 the depth, this is simply

the highest index of the feedbacks.

We chose LFSR based on these two criteria. Types

is deﬁned from [2, 1] to [8,8]. For types [2, 1], and

[5,∗], we looked at all the possible LFSRs in order to

study the inﬂuence of their depth.

The state update function of the different LFSR

tested are given by equations (L2) to (L21). Their type

and depth are given at the second, respectively third,

column of Table 3.

L2 x

j+20

← x

≪ 3 ⊕ x

j+1

 7 ⊕ x

j+11

 7

L3 x

j+20

← x

≪ 3 ⊕ x

j+14

 3 ⊕ x

j+17

 7

L4 x

j+20

← x

≪ 1 ⊕ x

j+3

 3 ⊕ x

j+13

 7

L5 x

j+20

← x

≪ 1 ⊕ x

j+9

 3 ⊕ x

j+15

 7

L6 x

j+20

← x

≪ 3 ⊕ x

j+9

 4 ⊕ x

j+19

 7

L7 x

j+20

← x

≪ 3 ⊕ x

j+1

 5 ⊕ x

j+3

 6

L8 x

j+20

← x

≪ 1 ⊕ x

j+4

 3 ⊕ x

j+19

 5

L9 x

j+20

← x

≪ 1 ⊕ x

j+7

 3 ⊕ x

j+18

 5

L10 x

j+20

← x

≪ 1 ⊕ x

j+3

 3 ⊕ x

j+9

 5

L11 x

j+20

← x

≪ 3 ⊕ x

j+1

 7 ⊕ x

j+17

 4

L12 x

j+20

← x

≪ 3 ⊕ x

j+5

 7 ⊕ x

j+19

 3

L13 x

j+20

← x

≪ 1 ⊕ x

j+5

 7 ⊕ x

j+16

 3

L14 x

j+20

← x

≪ 1 ⊕ x

j+1

 7 ⊕ x

j+9

 3

L15 x

j+20

← x

≪ 1 ⊕ x

j+13

 5 ⊕ x

j+19

 3

L16 x

j+20

← x

≪ 3 ⊕ x

j+14

 7 ⊕ x

j+17

 3

L17 x

j+20

← x

≪ 3 ⊕ x

j+4

 1 ⊕ x

j+5

 6

L18 x

j+20

← x

≪ 1 ⊕ x

j+3

 1 ⊕ x

j+9

 1

L19 x

j+20

← x

≪ 1 ⊕ x

j+4

 1 ⊕ x

j+5

 1

L20 x

j+20

← x

≪ 3 ⊕ x

j+1

 1 ⊕ x

j+8

≪ 7

L21 x

j+20

← x

≪ 3 ⊕ x

j+3

 5 ⊕ x

j+4

≪ 5

We ran the same experiment as in section 5.1 for

every considered LFSR with N

tests

= 120. For each

LFSR, we noted the proportion of runs ﬁnished af-

ter two days of computations, the average number of

nodes effectively traversed in the tree, and average

number of remaining keys. Results are summarized

in Table 3.

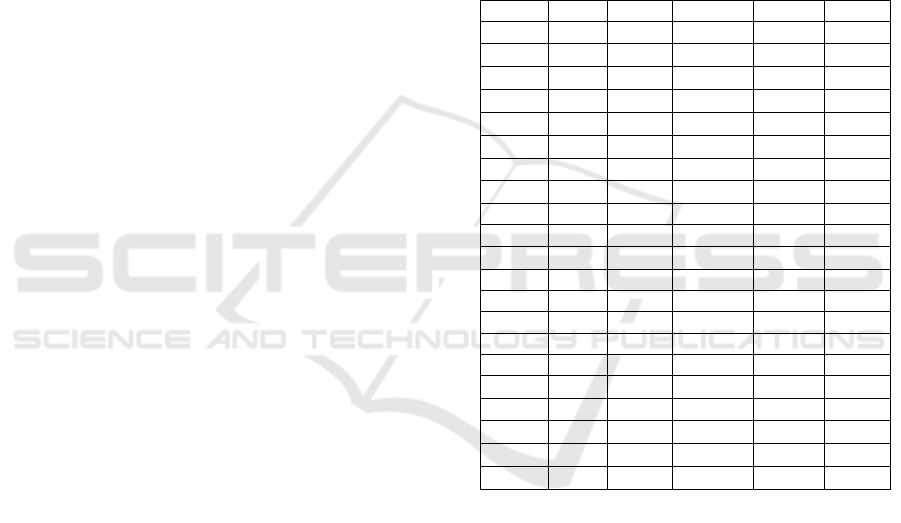
Table 3: Type, depth, proportion of runs ﬁnished after two

days of computations, average number of nodes traversed,

and number of remaining keys for Dumbo (L1), and LF-

SRs (L2) to (L21).

LFSR type depth ﬁnished N

nodes

keys

(L1) [2,1] 13 53.57% 2

41.82

36.59

(L2) [2,1] 11 82.5% 2

41.23

36.39

(L3) [5,1] 17 0.83% 2

42.89

34.68

(L4) [5,1] 13 94.17% 2

39.68

33.68

(L5) [5,1] 15 28.33% 2

42.13

35.25

(L6) [5,1] 19 11.67% 2

42.38

36.77

(L7) [5,2] 3 100.0% 2

30.93

24.93

(L8) [5,3] 19 0.83% 2

43.99

37.59

(L9) [5,3] 18 0.0% − −

(L10) [5, 3] 9 95.83% 2

40.32

34.0

(L11) [5, 4] 17 0.83% 2

43.58

35.6

(L12) [5, 5] 19 0.0% − −

(L13) [5, 5] 16 0.0% − −

(L14) [5, 5] 9 82.5% 2

41.43

34.95

(L15) [5, 5] 19 0.0% − −

(L16) [5, 5] 17 0.0% − −

(L17) [8, 2] 5 100.0% 2

35.53

29.17

(L18) [8, 7] 9 78.75% 2

41.56

34.79

(L19) [8, 7] 5 100.0% 2

35.41

29.42

(L20) [8, 8] 8 79.17% 2

41.59

35.78

(L21) [8, 8] 4 100.0% 2

34.76

29.29

From these experiments, it seems that the depth

has a much more relevant impact than the type. Yet,

this seems to be quite tailored to our particular attack.

Changing the generation of the different masks is gen-

erally more impactful, since it can cut down in three

the amount of information given to the attacker.

6 CONCLUSION

In this paper, a theoretical blind side channel at-

tack targeting the LFSR of the Elephant algorithm

has been presented. Elephant is a good target.

First, Elephant is a ﬁnalist to the (NIST) competition

for lightweight cryptography candidates for authenti-

cated encryption. Moreover, Elephant is an interest-

ing target because the internal LFSR only depends on

SECRYPT 2022 - 19th International Conference on Security and Cryptography

the secret key. In other words, in the use-case of Ele-

phant, retrieving the encryption key is equivalent to

retrieving the initial state of the LFSR.

Our attack is based on the fact that an attacker can

retrieve the Hamming weights of the different bytes

in the LFSR. The Elephant design, where there exist

relations between the different internal states of the

LFSR, is an added vulnerability to our attack. In half

the cases, the key is retrieved in less than two days.

Different tweaking options have been considered.

Going from the most impactful to the least, they are:

changing the mask derivation for domain separation;

modifying the LFSR, looking at the importance of

depth and type.

Future works may include the inclusion of noise in

the simulations, or even better performing the attack

on an actual implementation.

ACKNOWLEDGMENTS

This research is part of the chair CyberCNI.fr with

support of the FEDER development fund of the Brit-

tany region.

REFERENCES

Beierle, C., Biryukov, A., dos Santos, L. C., Großsch

adl,

J., Perrin, L., Udovenko, A., Velichkov, V., Wang,

Q., and Biryukov, A. (2019). Schwaemm and esch:

lightweight authenticated encryption and hashing us-

ing the sparkle permutation family. NIST round, 2.

Bernstein, D. J. (1999). How to Stretch Random Functions:

The Security of Protected Counter Sums. J. Cryptol.

Bertoni, G., Daemen, J., Peeters, M., and van Assche, G.

(2011). The Keccak Reference.

Beyne, T., Chen, Y. L., Dobraunig, C., and Mennink, B.

(2020). Dumbo, Jumbo, and Delirium: Parallel Au-

thenticated Encryption for the Lightweight Circus.

IACR Transactions on Symmetric Cryptology.

Beyne, T., Chen, Y. L., Dobraunig, C., and Mennink, B.

(2021). Elephant v2. NIST lightweight competition.

Bogdanov, A., Knezevic, M., Leander, G., Toz, D.,

Varici, K., and Verbauwhede, I. (2011). Spongent:

a Lightweight Hash Function. In CCryptographic

Hardware and Embedded Systems-CHES. Springer.

Brier, E., Clavier, C., and Olivier, F. (2004). Correla-

tion power analysis with a leakage model. In Cryp-

tographic Hardware and Embedded Systems-CHES.

Springer.

Burman, S., Mukhopadhyay, D., and Veezhinathan, K.

(2007). LFSR based stream ciphers are vulnerable

to power attacks. In INDOCRYPT, volume 4859 of

Lecture Notes in Computer Science, pages 384–392.

Springer.

Chakraborty, A., Mazumdar, B., and Mukhopadhyay, D.

(2014). Fibonacci LFSR vs. galois LFSR: which is

more vulnerable to power attacks? In SPACE, volume

8804 of Lecture Notes in Computer Science, pages

14–27. Springer.

Chari, S., Rao, J. R., and Rohatgi, P. (2002). Template

attacks. In Cryptographic Hardware and Embedded

Systems-CHES. Springer.

Clavier, C. and Reynaud, L. (2017). Improved blind side-

channel analysis by exploitation of joint distributions

of leakages. In International Conference on Crypto-

graphic Hardware and Embedded Systems, pages 24–

44. Springer.

Daemen, J., Hoffert, S., Peeters, M., Assche, G. V., and

Keer, R. V. (2020). Xoodyak, a lightweight crypto-

graphic scheme.

Dobraunig, C., Eichlseder, M., Mendel, F., and Schl

affer,

M. (2014). Ascon. Submission to the CAESAR com-

petition.

Gierlichs, B., Batina, L., Tuyls, P., and Preneel, B. (2008).

Mutual information analysis. In Cryptographic Hard-

ware and Embedded Systems-CHES. Springer.

Giraud, C. (2004). DFA on AES. In Advanced Encryption

Standard -AES. Springer.

Granger, R., Jovanovic, P., Mennink, B., and Neves, S.

(2016). Improved Masking for Tweakable Blockci-

phers with Applications to Authenticated Encryption.

In EUROCRYPT. Springer.

Handschuh, H. and Heys, H. M. (1998). A timing attack on

rc5. In International Workshop on Selected Areas in

Cryptography. Springer.

Hell, M., Johansson, T., Maximov, A., Meier, W., and

Yoshida, H. (2021). Grain-128aead, round 3 tweak

and motivation.

Iwata, T., Khairallah, M., Minematsu, K., and Peyrin, T.

(2020). Duel of the titans: the romulus and remus

families of lightweight aead algorithms. IACR Trans-

actions on Symmetric Cryptology.

Joux, A. and Delaunay, P. (2006). Galois LFSR, Embed-

ded Devices and Side Channel Weaknesses. In IN-

DOCRYPT, volume 4329 of Lecture Notes in Com-

puter Science, pages 436–451. Springer.

Jurecek, M., Bucek, J., and L

orencz, R. (2019). Side-

channel attack on the a5/1 stream cipher. In Euromicro

Conference on Digital System Design (DSD). IEEE.

Kazmi, A. R., Afzal, M., Amjad, M. F., Abbas, H., and

Yang, X. (2017). Algebraic side channel attack on

trivium and grain ciphers. IEEE Access.

Kocher, P. C., Jaffe, J., and Jun, B. (1999). Differen-

tial power analysis. In Advances in Cryptology -

CRYPTO. Springer.

Le Bouder, H., Lashermes, R., Linge, Y., Thomas, G., and

Zie, J. (2016). A Multi-round Side Channel Attack on

AES Using Belief Propagation. In Foundations and

Practice of Security. Springer.

Linge, Y., Dumas, C., and Lambert-Lacroix, S. (2014). Us-

ing the joint distributions of a cryptographic function

in side channel analysis. In International Workshop on

Constructive Side-Channel Analysis and Secure De-

sign. Springer.

Blind Side Channel on the Elephant LFSR

Luykx, A., Preneel, B., Tischhauser, E., and Yasuda, K.

(2016). A MAC Mode for Lightweight Block Ciphers.

In Peyrin, T., editor, Fast Software Encryption FSE.

Springer.

Mangard, S. (2002). A simple power-analysis (spa) at-

tack on implementations of the aes key expansion. In

ICISC. Springer.

NIST (2015). SHA-3 Standard: Permutation-Based Hash

and Extendable-Output Functions. FIPS 202.

NIST (2018). Lightweight Cryptography Standardization

Process.

Rechberger, C. and Oswald, E. (2004). Stream ciphers

and side-channel analysis. In In ECRYPT Workshop,

SASC-The State of the Art of Stream Ciphers. Citeseer.

Samwel, N. and Daemen, J. (2017). DPA on hardware im-

plementations of ascon and keyak. In Proceedings of

the Computing Frontiers Conference. ACM.

Standaert, F.-X. (2010). Introduction to side-channel at-

tacks. In Secure integrated circuits and systems.

Springer.

SECRYPT 2022 - 19th International Conference on Security and Cryptography