A Region-based Training Data Segmentation Strategy to Credit Scoring

Roberto Saia, Salvatore Carta, Gianni Fenu and Livio Pompianu

Department of Mathematics and Computer Science,

University of Cagliari, Via Ospedale 72 - 09124 Cagliari, Italy

Keywords:

Business Intelligence, Decision Support System, Risk Assessment, Credit Scoring, Machine Learning.

Abstract:

The rating of users requesting ﬁnancial services is a growing task, especially in this historical period of the

COVID-19 pandemic characterized by a dramatic increase in online activities, mainly related to e-commerce.

This kind of assessment is a task manually performed in the past that today needs to be carried out by automatic

credit scoring systems, due to the enormous number of requests to process. It follows that such systems play

a crucial role for ﬁnancial operators, as their effectiveness is directly related to gains and losses of money.

Despite the huge investments in terms of ﬁnancial and human resources devoted to the development of such

systems, the state-of-the-art solutions are transversally affected by some well-known problems that make the

development of credit scoring systems a challenging task, mainly related to the unbalance and heterogeneity of

the involved data, problems to which it adds the scarcity of public datasets. The Region-based Training Data

Segmentation (RTDS) strategy proposed in this work revolves around a divide-and-conquer approach, where

the user classiﬁcation depends on the results of several sub-classiﬁcations. In more detail, the training data

is divided into regions that bound different users and features, which are used to train several classiﬁcation

models that will lead toward the ﬁnal classiﬁcation through a majority voting rule. Such a strategy relies

on the consideration that the independent analysis of different users and features can lead to a more accurate

classiﬁcation than that offered by a single evaluation model trained on the entire dataset. The validation process

carried out using three public real-world datasets with a different number of features, samples, and degree

of data imbalance demonstrates the effectiveness of the proposed strategy, which outperforms the canonical

training one in the context of all the datasets.

1 INTRODUCTION

The exponential increase in e-commerce activities

that characterizes today’s modern societies has un-

dergone further growth as a result of the restrictions

on movement imposed by the COVID-19 pandemic,

which has prompted people to increase their online

purchases and, more generally, to increase the use of

the services offered by the Internet. This scenario

has at the same time increased requests for consumer

credit and therefore, generalizing, the need for ﬁnan-

cial operators to assess the solvency of their potential

customers. Unlike in the past, where the low number

of requests allowed human management, today this

activity is carried out through automatic systems that,

based on the outcome of past customers, evaluate the

new users, performing an operation that in the liter-

ature is named as Credit Scoring. The credit scor-

ing task is usually performed by classifying the new

users according to a binary (classiﬁcation as reliable

or unreliable) or continuous (assignment of credit rat-

ings) criterion. Such a classiﬁcation relies on a large

number of approaches, where the evaluation model is

trained by using the users’ information (which from

now on we deﬁne instances), e.g., age, current job,

total income, other loans in progress, etc.

It should be noted that the type of data involved

in the credit scoring processes has drastically reduced

the number of public datasets available to researchers,

compared to other domains. This is due to a whole se-

ries of reasons mainly related to the privacy of ﬁnan-

cial operators and their customers, as also when such

data are anonymized it is possible to extract privacy-

sensitive information. In addition to this problem of

data scarcity, the data available for the training of the

evaluation models are commonly affected by a high

degree of unbalance of the data classes, which are

typically two: reliable and unreliable users. This con-

ﬁguration, to deﬁne evaluation models not inﬂuenced

by the samples that belong to the majority class, must

be appropriately managed through re-sampling tech-

niques (Leevy et al., 2018), which add synthetic in-

Saia, R., Carta, S., Fenu, G. and Pompianu, L.

A Region-based Training Data Segmentation Strategy to Credit Scoring.

DOI: 10.5220/0011137400003283

In Proceedings of the 19th International Conference on Security and Cryptography (SECRYPT 2022), pages 275-282

ISBN: 978-989-758-590-6; ISSN: 2184-7711

275

stances to the minority class or remove them from the

majority one. However, such a process generates data

with similar series of features that characterize reli-

able and unreliable users.

Initially formalized by us for a different domain,

the proposed strategy revolves around the idea that we

can reduce the heterogeneity problem by adopting a

divide-and-conquer criterion, which relies on the con-

sideration that the instances that compose the datasets

used to train the evaluation models refer to different

users and features. On the basis of this consideration,

we can split the classiﬁcation task into several sub-

classiﬁcations, each of them performed by an evalua-

tion model trained by using a different region of the

dataset, in terms of instances and features. In this re-

gard, then we propose a Region-based Training Data

Segmentation (RTDS) strategy, according to which

the training dataset is divided into several regions by

following an experimentally-deﬁned number of rows

and columns that, respectively, bound a region com-

posed by certain instances (dataset rows) and features

(dataset columns). The deﬁned regions are then used

to train independent evaluation models and the ﬁnal

classiﬁcation of the new instances is reached accord-

ing to an ensemble criterion regulated by a majority

voting rule.

Unlike most credit scoring literature approaches,

all the experiments related to this work were carried

out by ensuring a real separation between the data

used to select the best credit scoring algorithm in the

context of a canonical training model process (to use

as competitor algorithm and strategy) and to deﬁne

the optimal number of regions for the proposed RTDS

strategy, and the data used to validate it (performance

comparison). In more detail, each dataset is divided

into two parts (50 percent each one) named in-sample

and out-sample, which are respectively used for the

aforementioned activities.

The scientiﬁc contributions of our work are sum-

marized as follows:

- formalization of the Region-based Training Data

Segmentation (RTDS) strategy, where the training

dataset is divided into several regions that bound

a certain number of instances (rows) and features

(columns), and the instance classiﬁcation depends

on a series of independent evaluation models, each

of them trained on a different region, according to

an ensemble approach regulated by a majority vot-

ing rule;

- formalization of criteria that allow the adoption of

the RTDS strategy even when the data conﬁguration

does not permit the division of the training dataset

into equal-size regions (padding criterion) or/and it

does not permit the application of the majority vot-

ing rule during the ensemble classiﬁcation (classi-

ﬁcation criterion) because the regions are even in

number;

- deﬁnition of a classiﬁcation algorithm that imple-

ments the RTDS strategy, classifying each new in-

stance as reliable or unreliable on the based of a

given training dataset;

- validation of the proposed RTDS strategy per-

formed by comparing its performance (using the

out-of-sample part of the dataset) to that of a canon-

ical training approach based on the same best clas-

siﬁcation algorithm (previously detected using the

in-sample part of the dataset).

2 BACKGROUND AND RELATED

WORK

Premising that an instance classiﬁcation as unreliable

indicates a default status, i.e., the failure for the user

to grant the legal obligations related to the requested

ﬁnancial service (e.g., a loan), the literature reports

three different risk models associated to the default

concept: Probability of Default (PD), when we need

to evaluate the likelihood of a default over a certain

period; Exposure At Default (EAD), when we need

to evaluate the total value of exposition of a ﬁnan-

cial operator in case of default; Loss Given Default

(LGD), when we need to evaluate the amount of mon-

etary losses of a ﬁnancial operator in case of default.

In the above context, the work we proposed is aimed

to perform binary classiﬁcation of the instances into

the reliable or unreliable classes, then it takes into ac-

count the PD model.

The literature shows how the credit scoring task

is faced by a large number of approaches, from those

focused on statistical algorithms to those that exploit

transformed data domains, machine and deep learning

algorithms, and a large number of hybrid approaches

that combine different algorithms and strategies. Re-

garding statistical approaches, literature offers many

works, such as the one that improve the Logistic Re-

gression algorithm with non-linear decision-tree ef-

fects (Dumitrescu et al., 2022), or that where the Lin-

ear Discriminant Analysis has been used for the credit

scoring task (Khemais et al., 2016). Regarding trans-

formed data domains approaches, in a work (Saia and

Carta, 2017b) the authors face the credit scoring task

by exploiting the Fourier Transform, similarly in an-

other work (Saia et al., 2018), which instead exploits

the Wavelet Transform, or in (Carta et al., 2021; Carta

et al., 2019), where the authors use a transformed fea-

ture space. Regarding machine learning approaches,

the Decision Tree and Support Vector Machine al-

SECRYPT 2022 - 19th International Conference on Security and Cryptography

276

gorithms were combined in a work (Roy and Urola-

gin, 2019) in order to deﬁne a credit scoring system,

whereas in the work (Liu et al., 2022) the authors de-

signed a credit scoring system based on tree-enhanced

gradient boosting decision trees. Regarding deep

learning approaches, an Artiﬁcial Neural Network is

exploited in a work (Liu et al., 2019) in order to per-

form the credit scoring task, whereas for the same

goal an Imbalanced Generative Adversarial Fusion

Network based both on a feed-forward neural net-

work and on a Bidirectional Long Short-Term Mem-

ory network is proposed in another work (Lei et al.,

2019). Regarding other approaches, an entropy crite-

rion is exploited by the authors in several works (Saia

and Carta, 2016a; Carta et al., 2020), whereas a

linear-dependence criterion is used in (Saia and Carta,

2016c; Saia and Carta, 2016b), and the combination

of different algorithms and strategies to perform the

credit scoring task is faced in another work (Zhang

et al., 2019). Another interesting work (Saia. et al.,

2021) investigates the feasibility to deﬁne a credit

scoring model based on the bank transactions instead

of the canonical users’ information.

Open Problems: Although over time state-of-the-art

credit scoring solutions have gradually improved their

performance, there are well-known problems that re-

duce the effectiveness of all the approaches, as they

depend on the nature of the involved data. The main

problems are the scarcity of public datasets to be

used for the deﬁnition of new credit scoring approach-

es/strategies, and the complication that those avail-

able typically present a high degree of data imbal-

ance because the examples of unreliable instances are

fewer in number than those relating to reliable ones.

In more detail, the scarcity of real-world datasets

is mainly related to the privacy policies adopted by

many public and private entities (Sloan and Warner,

2018) such as, for instance, the banks and other credit

institutions. Concerning the data imbalance, it leads

toward the underestimation of the unreliable cases

during the training of the credit scoring evaluation

models, since that process results biased by the ma-

jority class (i.e., reliable cases). In this case, the only

solution is the adoption of balancing techniques that

work by removing some majority class samples (un-

dersampling), or by adding some synthetic instances

to the minority class samples based on the existing

ones (oversampling), and, in some cases, these two

approaches can be combined. It should be observed

how the adoption of undersampling techniques that

remove samples from the majority class reduces the

available information about this class, making the

trained valuation model less accurate (Park and Park,

2021), whereas the adoption of oversampling tech-

niques (the most used in the literature) could lead

to an overﬁtting problem because the introduction of

synthetic samples in a class might overestimate it in

terms of probability (Weiss, 2004). In the light of the

current literature (Shen et al., 2021), which demon-

strates that the adoption of a data balancing technique

based on the oversampling of the minority class can

improve the performance of a credit scoring system,

we will adopt it for preprocessing the used datasets

during the experiments. A side effect related to the

scarcity of real-world datasets and the reduced num-

ber of unreliable cases available for the training of the

evaluation model is the cold start. It means that until

we have an adequate number of unreliable samples,

we can not train an evaluation model, not even by re-

curring to an oversampling technique.

Performance Evaluation: In order to evaluate

the performance of a credit scoring system, aimed

at the binary classiﬁcation of users as reliable or

unreliable, different metrics are used in the lit-

erature, many of which based on the confusion-

matrix, a matrix of size 2x2 that contains the

numbers of True Negatives (TN), False Nega-

tives (FN), True Positives (TP), and False Positives

(FP). Some of these metrics largely used are the

Accuracy =

T P+T N

T P+T N+FP+FN

, the Sensitivity =

T P

T P+FN

(also deﬁned True Positive Rate), the Speci f icity =

T N

T N+FP

(also deﬁned True Negative Rate), the

Fallout =

FP+T N

(also deﬁned False Positive

Rate), and the Matthews Correlation Coe f f icient =

T P·T N

√

(T P+FP)·(T P+FN)·(T N+FP)·(T N+FN)

(MCC).

The literature also shows how, in order to provide

a more reliable assessment of the credit scoring per-

formance with any data conﬁguration, then regardless

of the level of balance of the classes, these afore-

mentioned metrics are usually combined with other

metrics such as, for instance, those based on the Re-

ceiver Operating Characteristic (ROC) curve (Green

and Swets, 1966) the most used of which is the Area

Under the ROC Curve (AUC). The ROC plots the

Sensitivity on the y-axis, against the Fallout on the

x-axis, evaluating the separability, i.e., the ability to

discriminate the two data classes (i.e., reliable and un-

reliable) correctly.

3 RTDS STRATEGY

Before describing the proposed strategy, we report the

adopted formal notation. Denoting as |S| the cardi-

nality of a generic set S, we further denote a series

of instances I = {i

, i

, . .. , i

} composed by: a sub-

set I

= {i

, i

, . .. , i

} of reliable instances, then

A Region-based Training Data Segmentation Strategy to Credit Scoring

277

⊆ I; a subset I

−

= {i

−

, i

−

, . .. , i

−

} of unreliable

instances, then I

−

⊆ I; a subset

I = {

, . .. ,

} of

unclassiﬁed instances, then

I ⊆ I.

So we have that I = (I

∪ I

−

∪

I), and each in-

stance i ∈ I is characterized by the features in the set

F = {f

, f

, . .. , f

}, and it can belong to one of the

classes in the set C = {reliable, unreliable}, then we

also formalize: the training set T = {i

, i

, . . . , i

}

given by I

∪ I

−

; the possibility to divide T into

R = {r

, r

, . . . , r

} regions, according to the T in-

stances (set rows) and features (set columns); the re-

gions deﬁnition operation as R

(IR,FC)

, where IR is the

number of Instance Rows, and FC is the number of

Feature Columns, then |R| = Z = (IR ×FC).

As a result of the above: concerning the set I, each

region is composed by

instances and

features,

since |I| = N and |F| = W ; the bounds of IR and FC

are, respectively, 1 ≤ IR ≤ |T | and 1 ≤ FC ≤ |F|; it

should be observed that IR = FC = 1 indicates the

canonical data conﬁguration and that the IR value

must deﬁne a region with samples of both classes in

the set C, differently, the training process of an evalu-

ation model is not possible.

Problem Deﬁnition: Considering that we face the

credit scoring problem in terms of a binary classiﬁ-

cation related to the two classes deﬁned in the previ-

ously formalized set C, it is possible to deﬁne such a

problem as shown in the Equation 1, where α denotes

a generic classiﬁcation algorithm, and the evaluation

function of an instance

i (that returns 1 when performs

a correct classiﬁcation and 0 otherwise) is denoted as

Evaluate(

i, α). This means that the problem is for-

mulated as the maximization of the Θ value, since it

reports the sum of the instances correctly classiﬁed

(its upper bound is then |

I|).

max

0≤Θ≤|

Θ =

∑

m=1

Evaluate(

, α) (1)

Strategy Overview: The proposed strategy relies on

a fusion fashion independent evaluation model, this

means that several evaluation models are trained by

using a different region of the IR×FC regions, where

each of these regions bounds speciﬁc user’s instances

(rows) and user’s features (columns). Based on this

division into regions, the classiﬁcation process is per-

formed by several sub-processes, each of them based

on the training data bounded by the respective region,

according to our idea that such a strategy can reduce

the problem related to the data heterogeneity because

each new instance classiﬁcation depends on a differ-

ent group of instances and features.

Strategy Formalization: Based on the proposed

RTDS strategy, the problem deﬁned in Equation 1

needs to be revised by dividing the evaluation pro-

cess into Z sub-processes, i.e., |R|= Z. Therefore, the

generic credit scoring algorithm α runs Z times, and

the ﬁnal classiﬁcation depends on all the results, as

shown in Equation 2, which assumed K = 4, W = 4,

IR = 2, and FC = 2, giving rise to a subdivision

of the training set T into |R| = Z = (2 ×2) = 4 re-

gions, where each region is composed by

= 2

instances and

= 2 features, generating four

, m

evaluation models. In other words, the

training process of an evaluation model m related to a

classiﬁcation algorithm α uses the instances and fea-

tures bounded by the r

, r

regions, individually,

obtaining four m

, m

evaluation models.

(2,2)







1,1

2,1

3,1

4,1

1,2

2,2

3,2

4,2

1,3

2,3

3,3

4,3

1,4

2,4

3,4

4,4







⇒

(2)

Whereby, the process of classiﬁcation of a new in-

stance

i ∈

I will involve its f

, f

features,

which are compared to all the evaluation mod-

els m

, m

, producing the four classiﬁcation

, c

, as shown in Equation 3, where the com-

parison operation is denoted with ⇔.

⇔

(3)

Padding Criterion: The padding criterion is used

when the number of regions given by the IC and FC

values does not generate equal-size regions, as shown

inEquation 4.

(|T | mod IR) 6= 0

(|F| mod FC) 6= 0

(4)

According both to the notations µ

= (|T | mod IR)

and µ

= (|F| mod FC) and F = {f

, f

, . . . , f

}

and T = {i

, i

, . . . , i

}, Equation 5 formalizes the

padding criterion.

pad(T ) = {i

, i

, . . . , i

, i

K+1

, i

K+2

, . . . , i

K+µ

}

with i

K+1

= i

, i

K+2

= i

K−1

, . . . = i

K+µ

= i

K−µ

pad(F) = {f

, f

, . . . , f

, f

W +1

, f

W +2

, . . . , f

W +µ

}

with f

W +1

= f

W +2

= . . . = f

W +µ

= f

(5)

The adopted criterion is aimed at not altering the in-

formation signiﬁcantly since it follows two different

strategies: concerning T , it duplicates the last rows

(instances) µ

times, facing the risk that the added in-

stances belong to the same class in C; concerning F, it

duplicates the last column of data (features) µ

times.

This approach does not bias the machine learning pro-

cess because it involves both the training and the test

data. It should be noted that, in order to simplify the

exposition of the proposed strategy, we assume that

SECRYPT 2022 - 19th International Conference on Security and Cryptography

278

this criterion is used as preprocessing step, automati-

cally, during the deﬁnition of the regions.

Classiﬁcation Criterion: The classiﬁcation criterion

is aimed to face the case when is not possible to ap-

ply a majority criterion during the ensemble classi-

ﬁcation. In this regard, taking into account that the

application of the RTDS strategy (except in the case

IR = FC = 1) generates c

, c

, . . . , c

classiﬁcations,

this can lead to the two cases reported in Equation 6,

where, differently from the Case 2 that allows us the

use of the majority criterion to perform a classiﬁca-

tion of the instance, in the Case 1 it is not possible.

For this reason, we need to introduce a discriminat-

ing element, which is an additional classiﬁcation c

Z+1

performed through a canonical training approach for

the algorithm, then by using for this purpose the

whole set E, obtaining as result the c

, c

, . . . , c

, c

Z+1

classiﬁcations, which lead us to the Case 2.

Case 1 : Z = 2n, n ∈ N

Case 2 : Z = 2n −1, n ∈ N

(6)

In other words, by taking into consideration the sce-

nario related to the Case 1, assuming IR = FC = 2, it

leads toward m

, m

classiﬁcation models and

, c

classiﬁcations of an instance

i, then we

add the the classiﬁcation c

by training an additional

evaluation model on the whole set T . This makes it

possible to apply the X criterion The majority crite-

rion can be apply by following the classiﬁcation cri-

terion ρ that is formalized in Equation 7, where c

and

are, respectively, the elements reliable and unreli-

able of the set C.

ρ( ˆe) =











, i f

∑

i=1

φ(c

, c

) >

∑

i=1

φ(c

, c

)

, i f

∑

i=1

φ(c

, c

) <

∑

i=1

φ(c

, c

)

, i f

∑

i=1

φ(c

, c

) =

∑

i=1

φ(c

, c

) ∧c

Z+1

= c

, i f

∑

i=1

φ(c

, c

) =

∑

i=1

φ(c

, c

) ∧c

Z+1

= c

with

φ(a, b) =



0, i f a 6= b

1, i f a = b

(7)

Classiﬁcation Algorithm: The Algorithm 1 exploits

the proposed RTDS Strategy in order to classify the

new instances in the set

I: it takes as input the clas-

siﬁcation algorithm α, the training set T, the set of

unclassiﬁed instances

I, and the values (IR) and (FC)

for the division of the training set into regions, return-

ing as output the classiﬁcation of all the instances in

the set

Algorithm 1: RTDS strategy classiﬁer algorithm.

Input: α=Classiﬁcation algorithm, T =Training set,

I=Unevaluated in-

stances, IR=Instances rows, FC=Feature columns

Output: κ=Classiﬁcation of the

I instances

1: procedure CLASSIFIER(α, T ,

I, IR, FC)

2: if Z is even then  Veriﬁes if the number of regions is even

3: m

← getTraining(α, T )  Trains model using the whole set T

4: end if

5: R ←getRegions(T, IR, FC)  Divides training set into regions

6: for each r ∈R do  Trains an evaluation model for each region

7: m ←getTraining(α, r)  Trains evaluation model

8: M.add(m)  Stores evaluation model

9: end for

10: for each

i ∈

I do  Processes instances in

11: R

← getRegions( ˆe, IR, FC)  Divides instance into regions

12: for each m ∈ M do  Gets all instances classiﬁcations

13: c ←getInstanceClass(m, R

)  Classiﬁes instance

according to regions

14: C.add(c)  Stores classiﬁcation

15: end for

16: if Z is even then  Veriﬁes if the number of regions is even

17: c

← getInstanceClass(m

, ˆe)  Classiﬁes instance

according to the whole set T

18: C.add(c

)  Adds classiﬁcation to the set C

19: end if

20: κ.add(getFinalClassi f ication(

i,C))  Gets and store ﬁnal

instance classiﬁcation

21: end for

22: return κ  Returns classiﬁcation of

I instances

23: end procedure

4 EXPERIMENTS

All the code related to this work was developed

in the Python language with the scikit-learn (http:

//scikit-learn.org) library. We set the seed of the

pseudo-random number generator to 1 to grant the

experiments reproducibility. We also performed

the independent-samples two-tailed Student’s t-test,

which showed no statistical difference between the re-

sults (p > 0.05).

The validation process was performed by us-

ing three real-world datasets widely used in the

literature and publicly available(https://archive.ics.

uci.edu/ml/machine-learning-databases/statlog/): the

Australian Credit Approval (ACD), the Default of

Credit Card Clients (DCD), and the German Credit

(GCD) datasets, whose characteristics are summa-

rized in Table 1.

Table 1: Datasets Characteristics.

Dataset Total Reliable Unreliable Feature Unreliable

name instances instances instances number (%)

ACD 690 307 383 15 55.50

DCD 30,000 23,364 6,636 24 22.12

GCD 1,000 700 300 24 30.00

A Region-based Training Data Segmentation Strategy to Credit Scoring

279

The ﬁrst two metrics used to evaluate the perfor-

mance of the proposed RTDS strategy are the Sen-

sitivity and the Speciﬁcity. These two metrics (for-

malized in Equation 8) assess, respectively, the true

positive rate and the true negative rate, evaluating the

capability of a credit scoring approach to classify the

reliable and unreliable instances correctly.

Sensitivity(

I) =

T P

(T P+F N)

, Speci f icity(

I) =

T N

(T N+FP)

(8)

In addition, we used the AUC since it allows us

to evaluate the performance regardless of the level of

data balancing. Considering the reliable (I

) and un-

reliable (I

−

) subsets of instances in I, it is formalized

in the Equation 9, where α denotes all possible com-

parisons between the scores of each instance i, and

the result in the range [0, 1] (where 1 indicates the best

performance) is the average of them.

α(i

, i

−

) =











1, i f i

> i

−

0.5, i f i

= i

−

0, i f i

< i

−

AUC =

·I

−

∑

−

∑

α(i

, i

−

)

(9)

The experiments were performed by dividing each

dataset into two parts: in-sample and out-of-sample

parts, respectively 50% and 50%. The in-sample part

is used to detect the best credit scoring algorithm to

use as a competitor and in the ensemble approach re-

lated to the proposed RTDS strategy, in addition to the

optimal values of IR and FC, and the out-of-sample

part is instead used in order to perform the validation

process. It should be added that a canonical k-fold

cross-validation criterion with k = 10 is still used in

all the experiments. In addition to the k-fold cross-

validation criterion, this dataset division, largely used

in the literature with regard to some crucial data do-

mains (e.g., ﬁnancial market forecasting), allows us to

avoid any over-ﬁtting (Hawkins, 2004) problem, con-

sidering that it operates a real separation between the

data used to deﬁne and tune the evaluation model and

the ones used for the performance evaluation. In or-

der to avoid that after the oversampling process (per-

formed by us as preprocessing step on all the datasets)

the two classes of instances are contiguous, creating

issues during the k-fold cross-validation and the divi-

sion into the region operations (i.e. due to the absence

of one of the two data classes in a data fold/region),

the oversampled datasets were also shufﬂed. The al-

gorithms used in the experiments are those reported

in Table 2 together with their conﬁguration.

Results and Discussion: As a ﬁrst step we evalu-

ate the state-of-the-art algorithms in the context of a

canonical approach, i.e., in order to train the related

Table 2: Algorithms Conﬁguration.

Algorithm Parameter Value

AdaBoost n estimators 50

(ABA) learning rate 0.1

algorithm SAMME.R

Decision Tree min samples split 2

(DTA) max depth none

min samples lea f 1

Gradient Boosting n estimators 100

(GBA) learning rate 0.1

max depth 3

Multilayer Perceptron al pha 0.0001

(MPA) max iter 200

solver adam

Random Forests n estimators 10

(RFA) max depth none

min samples split 2

evaluation models we use the whole in-sample subset

of data, applying the k-fold cross-validation criterion.

The results are shown in Table 3, where the Average

column reports the mean value of the three used met-

rics and where the best performance for each metric is

highlighted in bold, indicating as the most performing

algorithm to use RFA (i.e., Random Forests).

Table 3: Algorithms Canonical Performance.

Algorithm Dataset Sensitivity Speciﬁcity AUC Average

ABA ACD 0.8278 0.8372 0.8322 0.8324

DTA ACD 0.7994 0.7763 0.7850 0.7869

GBA ACD 0.8577 0.8454 0.8487 0.8506

MPA ACD 0.7986 0.7937 0.7824 0.7916

RFA ACD 0.8811 0.8675 0.8716 0.8734

ABA DCD 0.7597 0.7398 0.7492 0.7496

DTA DCD 0.7243 0.7398 0.7319 0.7320

GBA DCD 0.7999 0.7654 0.7813 0.7822

MPA DCD 0.5972 0.6649 0.5771 0.6131

RFA DCD 0.8377 0.8088 0.8224 0.8230

ABA GCD 0.7476 0.7547 0.7512 0.7512

DTA GCD 0.6580 0.6865 0.6731 0.6725

GBA GCD 0.7846 0.7745 0.7796 0.7796

MPA GCD 0.7918 0.7566 0.7718 0.7734

RFA GCD 0.7987 0.7841 0.7940 0.7923

As a second step we identify the optimal number

of regions (i.e., IR and FC values) to partition the

training set. Also in this case we use the whole in-

sample subset of data and the k-fold cross-validation

criterion. In this context we tested all the IR and FC

values in the range {2, 3, . . . , 6} (i.e., the most signiﬁ-

cant range of values, and the pair of values IR=1 and

FC=1 is not considered, as it refers to a canonical

conﬁguration without regions). We perform the eval-

uation using the average value of all the used metrics

on the y-axis, since this offers a global vision of the

strategy performance, considering that it takes into ac-

count both the capability to detect the reliable (Sensi-

tivity) and unreliable (Speciﬁcity) cases, and the ca-

pability to discriminate them effectively (AUC). The

results indicate (IR=1, FC=2) as optimal values in the

context of all the datasets with the previously selected

RFA algorithm.

As a last step we compare the canonical approach

(denoted as BASE) based on the whole training set to

SECRYPT 2022 - 19th International Conference on Security and Cryptography

280

the proposed RTDS strategy conﬁgured according to

the optimal number of regions deﬁned in the previous

step. The comparison process was performed in the

context of the out-of-sample subset of data, applying

the k-fold cross-validation criterion, and the results

for each metric and in terms of the average of all met-

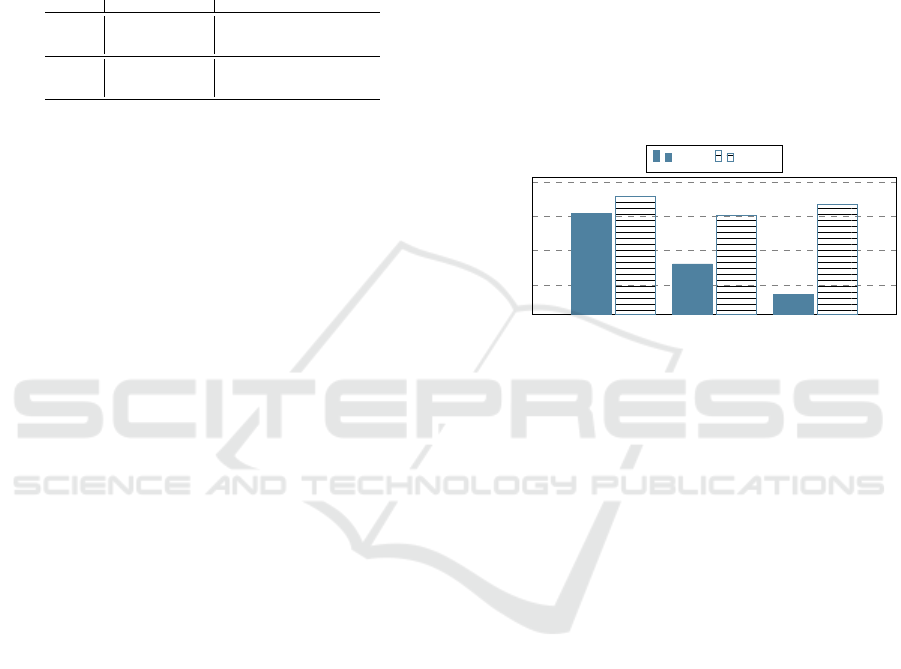
rics are reported, respectively, in Table 4 and Figure 1.

Table 4: Performance Comparison.

Approach Algorithm Dataset Sensitivity Speciﬁcity AUC

BASE RFA ACD 1.0000 0.8000 0.9130

BASE RFA DCD 0.8507 0.8117 0.8302

BASE RFA GCD 0.7429 0.8286 0.7878

RTDS RFA ACD 0.9376 0.9224 0.9266

RTDS RFA DCD 0.9111 0.8911 0.9008

RTDS RFA GCD 0.9259 0.9085 0.9166

Based on the experimental results, we can make

the following considerations:

- the experiments aimed to detect the optimal IR and

FC values for each dataset show regions bounded

only along with the features since these optimal pa-

rameters (i.e., IR=1 and FC=2 for all the datasets)

do not split in terms of instances, and it depends

on the nature of the training data, since in these

datasets each row refers to a different user, differ-

ently from other domains where there is a relation

between the dataset rows (time-series);

- additional experiments we conducted showed two

aspects: the average value we used for the tuning of

the IR and FC parameters leads to the same results

of the AUC metric, proving the effectiveness of this

combined metric as a criterion of optimization; it

is possible an optimization based on a single met-

ric, which leads toward different IR values (i.e., by

Sensitivity in the ACD, DCD, and GCD datasets we

get, respectively, 1, 2, and 6, and by Speciﬁcity in

the ACD, DCD, and GCD datasets we get, respec-

tively, 5, 3, and 3), but only in one case the IR value

is different from 1 (i.e., 2 by Sensitivity in the ACD

dataset), supporting the initial hypothesis we made;

- the comparison of the canonical approach of train-

ing to the proposed RTDS strategy, performed in

the out-of-sample part of the datasets, shows that

it outperforms the canonical approach, except for

the Sensitivity in the context of the ACD dataset,

but it is directly related to the increase of unreliable

instances erroneously classiﬁed as reliable, as evi-

denced by the Speciﬁcity and AUC values;

- in more detail, in spite of a lower performance re-

garding Sensitivity in the ACD dataset (−6.24%)

we get better performance in terms of Speciﬁcity

(+15.30%) and AUC (+1.49%), analogously to

the DCD dataset, where in terms of Sensitivity,

Speciﬁcity and AUC we get, respectively, +7.10%,

+9.78%, and +8.50%, and to the GCD dataset,

where we get in terms of Sensitivity, Speciﬁcity

and AUC, respectively, +24.63%, +9.64%, and

+16.35%;

- the best performance of the proposed RTDS strat-

egy is further highlighted by the average perfor-

mance reported in Figure 1, where it outperforms

the canonical approach in all the datasets;

- in the light of the above considerations, strength-

ened by the fact that the adoption of the in-

sample/out-of-sample and k-fold cross-validation

criteria ensure experimental results not biased by

over-ﬁtting (since they grant that the algorithm se-

lection and the RTDS parameter tuning operations

do not affect the results), the experiment demon-

strated how the proposed RTDS strategy can im-

prove the performance of a credit scoring system.

ACD DCD GCD

0.80

0.85

0.90

0.95

0.9043

0.8309

0.7864

0.9289

0.9010

0.9170

Average of metrics

BASE RTDS

Figure 1: Average Performance.

5 CONCLUSIONS AND FUTURE

DIRECTIONS

The Region-based Training Data Segmentation strat-

egy proposed in this work relies on the idea that it is

possible to improve the performance of a credit scor-

ing system dividing the training set of a classiﬁcation

model into several regions, along with instances and

features, using each of them to deﬁne an independent

model, and obtaining the instance classiﬁcation based

on all classiﬁcation models, according to an ensemble

criterion regulated by a majority voting rule. The ex-

perimental results were performed on three real-world

datasets by following an in-sample/out-of-sample cri-

terion aimed at creating an effective separation be-

tween the data used for the operations of choosing the

classiﬁcation algorithm and those related to the tuning

of the parameters of the proposed strategy, together

with the k-fold cross-validation criterion, demonstrate

the advantages of the proposed strategy. This is be-

cause its adoption leads toward an improvement of the

credit scoring system in the context of all the datasets.

As future work, we would like to experiment with

this strategy in different data domains, such as, for in-

stance, those related to the Intrusion Detection (Saia

et al., 2019) and Fraud Detection (Saia and Carta,

2017a) areas, in order to evaluate its effectiveness on

A Region-based Training Data Segmentation Strategy to Credit Scoring

281

different nature of data, such as the time-series.

ACKNOWLEDGEMENTS

This research is partially funded and supported by:

project “Studio per l’adeguamento di aree portale

per tematismo - BRIC INAIL 2019 - FENU” CUP

F24G20000100001”; “PON R&I 2014-2020 Action

IV.6 - CUP F25F21002270003”.

REFERENCES

Carta, S., Fenu, G., Ferreira, A., Recupero, D. R., and

Saia, R. (2019). A two-step feature space transform-

ing method to improve credit scoring performance. In

International Joint Conference on Knowledge Discov-

ery, Knowledge Engineering, and Knowledge Man-

agement, pages 134–157. Springer.

Carta, S., Ferreira, A., Recupero, D. R., Saia, M., and Saia,

R. (2020). A combined entropy-based approach for a

proactive credit scoring. Engineering Applications of

Artiﬁcial Intelligence, 87:103292.

Carta, S., Ferreira, A., Recupero, D. R., and Saia, R. (2021).

Credit scoring by leveraging an ensemble stochastic

criterion in a transformed feature space. Progress in

Artiﬁcial Intelligence, pages 1–16.

Dumitrescu, E., Hue, S., Hurlin, C., and Tokpavi, S.

(2022). Machine learning for credit scoring: Improv-

ing logistic regression with non-linear decision-tree

effects. European Journal of Operational Research,

297(3):1178–1192.

Green, D. M. and Swets, J. A. (1966). Signal Detection

Theory and Psychophysics. Wiley, New York.

Hawkins, D. M. (2004). The problem of overﬁtting. Jour-

nal of chemical information and computer sciences,

44(1):1–12.

Khemais, Z., Nesrine, D., Mohamed, M., et al. (2016).

Credit scoring and default risk prediction: A compar-

ative study between discriminant analysis & logistic

regression. International Journal of Economics and

Finance, 8(4):39.

Leevy, J. L., Khoshgoftaar, T. M., Bauder, R. A., and Seliya,

N. (2018). A survey on addressing high-class imbal-

ance in big data. Journal of Big Data, 5(1):42.

Lei, K., Xie, Y., Zhong, S., Dai, J., Yang, M., and Shen,

Y. (2019). Generative adversarial fusion network for

class imbalance credit scoring. Neural Computing and

Applications, pages 1–12.

Liu, C., Huang, H., and Lu, S. (2019). Research on personal

credit scoring model based on artiﬁcial intelligence. In

International Conference on Application of Intelligent

Systems in Multi-modal Information Analytics, pages

466–473. Springer.

Liu, W., Fan, H., and Xia, M. (2022). Credit scoring based

on tree-enhanced gradient boosting decision trees. Ex-

pert Systems with Applications, 189:116034.

Park, S. and Park, H. (2021). Combined oversampling

and undersampling method based on slow-start al-

gorithm for imbalanced network trafﬁc. Computing,

103(3):401–424.

Roy, A. G. and Urolagin, S. (2019). Credit risk assess-

ment using decision tree and support vector machine

based data analytics. In Creative Business and So-

cial Innovations for a Sustainable Future, pages 79–

84. Springer.

Saia, R. and Carta, S. (2016a). An entropy based algorithm

for credit scoring. In International Conference on Re-

search and Practical Issues of Enterprise Information

Systems, pages 263–276. Springer.

Saia, R. and Carta, S. (2016b). Introducing a vector space

model to perform a proactive credit scoring. In In-

ternational Joint Conference on Knowledge Discov-

ery, Knowledge Engineering, and Knowledge Man-

agement, pages 125–148. Springer.

Saia, R. and Carta, S. (2016c). A linear-dependence-based

approach to design proactive credit scoring models. In

KDIR, pages 111–120.

Saia, R. and Carta, S. (2017a). Evaluating credit card trans-

actions in the frequency domain for a proactive fraud

detection approach. In SECRYPT, pages 335–342.

Saia, R. and Carta, S. (2017b). A fourier spectral pattern

analysis to design credit scoring models. In Proceed-

ings of the 1st International Conference on Internet of

Things and Machine Learning, page 18. ACM.

Saia, R., Carta, S., and Fenu, G. (2018). A wavelet-based

data analysis to credit scoring. In Proceedings of the

2nd International Conference on Digital Signal Pro-

cessing, pages 176–180. ACM.

Saia, R., Carta, S., Recupero, D. R., Fenu, G., and Stan-

ciu, M. (2019). A discretized extended feature space

(defs) model to improve the anomaly detection per-

formance in network intrusion detection systems. In

KDIR, pages 322–329.

Saia., R., Giuliani., A., Pompianu., L., and Carta., S. (2021).

From payment services directive 2 (psd2) to credit

scoring: A case study on an italian banking institution.

In Proceedings of the 13th International Joint Confer-

ence on Knowledge Discovery, Knowledge Engineer-

ing and Knowledge Management - KDIR,, pages 164–

171. INSTICC, SciTePress.

Shen, F., Zhao, X., Kou, G., and Alsaadi, F. E. (2021).

A new deep learning ensemble credit risk evaluation

model with an improved synthetic minority oversam-

pling technique. Applied Soft Computing, 98:106852.

Sloan, R. H. and Warner, R. (2018). When is an algorithm

transparent? predictive analytics, privacy, and public

policy. IEEE Security & Privacy, 16(3):18–25.

Weiss, G. M. (2004). Mining with rarity: A unifying frame-

work. SIGKDD Explor. Newsl., 6(1):7–19.

Zhang, W., He, H., and Zhang, S. (2019). A novel multi-

stage hybrid model with enhanced multi-population

niche genetic algorithm: An application in credit scor-

ing. Expert Systems with Applications, 121:221–232.

SECRYPT 2022 - 19th International Conference on Security and Cryptography

282