Stacked Ensemble Model for Enhancing the DL based SCA

Anh Tuan Hoang, Neil Hanley, Ayesha Khalid, Dur-e-Shahwar Kundi and Maire O’Neill

Centre for Secure Information Technologies (CSIT), ECIT, Queen’s University Belfast, U.K.

Keywords:

SCA, AES, Deep Learning, CNN, CNNP, Stacked Ensemble, Key Reveal, Multi Masking.

Abstract:

Deep learning (DL) has proven to be very effective for image recognition tasks, with a large body of research

on various models for object classiﬁcation. The application of DL to side-channel analysis (SCA) has already

shown promising results, with experimentation on open-source variable key datasets showing that secret keys

for block ciphers like Advanced Encryption Standard (AES)-128 can be revealed with 40 traces even in the

presence of countermeasures. This paper aims to further improve the application of DL in SCA, by enhanc-

ing the power of DL when targeting the secret key of cryptographic algorithms when protected with SCA

countermeasures. We propose a stacked ensemble model, which trains the output probabilities and Maximum

likelihood score of multiple traces and/or sub-models to improve the performance of Convolutional Neu-

ral Network (CNN)-based models. Our model generates state-of-the art results when attacking the ASCAD

variable-key database, which has a restricted number of training traces per key, recovering the key within 20

attack traces in comparison to 40 traces as required by the state-of-the-art CNN-based model with Plaintext

feature extension (CNNP)-based model. During the proﬁling stage an attacker needs no additional knowledge

of the implementation, such as the masking scheme or random mask values, only the ability to record the

power consumption or electromagnetic ﬁeld traces, plaintext/ciphertext and the key is needed. However, a two

step training procedure is required. Additionally, no heuristic pre-processing is required in order to break the

multiple masking countermeasures of the target implementation.

1 INTRODUCTION

Since SCA was introduced in 1996 (Kocher, 1996)

based on the difference in the power consumption of

bit transitions, much research has been conducted on

efﬁcient methods to both break and protect crypto-

graphic implementations. Common attack methods

such as differential power analysis (DPA) (Kocher

et al., 1999), correlation power analysis (CPA) (Brier

et al., 2004), or differential frequency-based analy-

sis (DFA) (Gebotys et al., 2005), allow divide and

conquer strategies to signiﬁcantly reduce the compu-

tational complexity of key recovery when additional

power (or electromagnetic) information is available.

For example, in the case of the AES-128, it is re-

duced from O



128



to O



16 × 2



. In order to pro-

tect against such attacks a number of countermeasures

have been proposed, many of which are now standard

in commercial security products such as credit cards

etc. At the hardware layer techniques such as dual-

rail logic (Tiri et al., 2002; Popp and Mangard, 2005;

Chen and Zhou, 2006; Hoang and Fujino, 2014) at-

tempt to equalise the power consumption of the un-

derlying algorithm regardless of the data being pro-

cessed, while at the algorithmic layer techniques such

as masking (D and Tymen, 2002; Goubin L., 2011;

Nassar et al., 2012) introduce fresh randomness to re-

duce the useful leakage available to an attacker. All

countermeasures techniques come with various trade-

offs for the level of protection provided in terms of ex-

ecution time, randomness required, silicon (or mem-

ory) size etc.

While statistical and machine learning (ML) have

a long history, recent progress in DL in particular, has

led to such techniques being applied in the SCA con-

text for key recovery in the presence of countermea-

sures. These attacks fall under the proﬁling adversar-

ial model, where it is assumed that the attacker has a

similar (or identical) training device(s) to measure a

large quantity of traces in order to build an accurate

power model, which then allows key recovery from

the target device in relatively few traces. Among the

DL approaches, convolutional neural network (CNN)

based models seem most promising (Maghrebi et al.,

2016; Picek et al., 2018; Timon, 2019; Hoang et al.,

2020) due to their effectiveness when training with

raw data, with the convolutional layer acting as a ﬁl-

ter to pick out the relevant features for classiﬁcation.

Hoang, A., Hanley, N., Khalid, A., Kundi, D. and O’Neill, M.

Stacked Ensemble Model for Enhancing the DL based SCA.

DOI: 10.5220/0011139700003283

In Proceedings of the 19th International Conference on Security and Cryptography (SECRYPT 2022), pages 59-68

ISBN: 978-989-758-590-6; ISSN: 2184-7711

1.1 Related Work

There are a large number of available ML and DL al-

gorithms and models, as well as more general statis-

tical learning techniques that can be applied to SCA.

Some initial DL based SCA attacks have been pro-

posed by (Markowitch et al., 2013; Gilmore et al.,

2015; Martinasek et al., 2016). However, these at-

tacks are based on an assumption that the number of

masks are either very limited, or an adversary is able

to fully access the internal values of the target devices

when proﬁling, including the values of the random

masks, which is generally not feasible in practice.

The effectiveness of using CNN models is shown

in (Weissbart et al., 2019), with no dimensionality re-

duction required when attacking implementations of

public-key cryptography when compared to other pro-

ﬁling attack algorithms such as support vector ma-

chine (SVM), template attack (TA) or random forest

(RF). In efforts to increase the effectiveness of DL

performance in the context of SCA, an in-depth anal-

ysis in (Prouff et al., 2018; Maghrebi, 2019) noted

that the size of ﬁlter in a CNN model is an important

factor as its length should cover the most interesting

points of interest (PoI) to enable the combination of

the corresponding leakage while (Kim et al., 2019)

shown that adding artiﬁcial noise to the source traces

was found to greatly reduce over-ﬁtting the model to

the training set, improving classiﬁcation accuracy.

State of the art efforts in proﬁling attack seen to in-

clude SCA domain knowledge into DL architectures

as proposed by (Hettwer et al., 2018; Hoang et al.,

2020), in which the plaintext was given as an addi-

tional input to increase the accuracy when directly

training on the key value. Additional efforts to im-

prove CNN models for SCA were presented by (Perin

et al., 2020), in which the Maximum likelihood score

is applied to a number of simple CNN or multilayer

perceptrons (MLPs) models and traces with classiﬁ-

cation based on Hamming weight. Raw traces are also

used by (Lu et al., 2021) to ﬁnd the leakage informa-

tion not only from AES computation but also from

other execution like the preparation of the masked

SBox to attack AES implementation.

While this paper shares a similar approach to in-

putting domain knowledge as in (Hoang et al., 2020)

and the use of multiple models as in (Perin et al.,

2020), there is a signiﬁcant difference with regards

to architectural aspects such as the structures and the

way multiple models and/or traces are combined for

re-training from error , enabling our model to further

reduce the number of traces in an attack. Different

from those research, our proposed model combines

the outputs of multiple traces from multiple CNN-

based model with Plaintext feature extension (CNNP)

models and their maximum likelihood score (MLS) in

stacked ensemble model for re-training from error to

increase the accuracy with smaller number of traces.

The main ﬁnding of the proposed research are as

follows:

• The use of multiple models and trace combination

increases the accuracy of a ML model.

• MLS is an efﬁcient method for models and trace

combination and should be included in the ensem-

ble model.

• Classiﬁcation based on byte values should be used

instead of hamming weight to avoid many hy-

pothesis keys statistically located in the same high

rank (probability).

• The probability outputs of multiple traces and

models should be trained (in a stacked ensemble

model) to increase the accuracy rather than simply

summing up using the MLS method.

Given these ﬁndings, we built a complex model

with multiple sub-models working together on the

same group of traces to generate inputs for the pro-

posed stacked ensemble model. Additionally, the

MLS of those outputs are also considered as input fea-

tures. We label the traces using the output values of

the SBox in round 1 so that no projection issues be-

tween byte values and hamming weights occurs.

1.2 Our Contributions

This paper shows the limitations of applying MLS

when combining sub-models for an ensemble model

in the ﬁeld of SCA (based on traces from a protected

AES implementation). We propose stacked ensemble

models developed from CNN model with Plaintext

extension (CNNP at (Hoang et al., 2020)) that looks

to enhance DL from a side-channel aspect, taking the

strength of number of models (Perin et al., 2020),

MLS and re-training from error into consideration.

Our proposed models allow key recovery when target-

ing an AES implementation protected with multiple

masking scheme, outperforming previous research on

TAs, MLs or current CNN and CNNP models in terms

of required traces for key recovery (24 on the ASCAD

(Prouff et al., 2018) variable key database).

Our main contributions include:

1. Demonstrating the advantage of using the stacked

ensemble model as a method for combining multi-

ple models and traces over the ordinary MLS and

MLS-based ensemble method.

2. Propose a novel stacked ensemble convolutional

neural network with Plaintext feature extension

SECRYPT 2022 - 19th International Conference on Security and Cryptography

(SECNNP) model architecture for side channel

analysis. SECNNP model exploits the advantage

combining multiple models and traces over the or-

dinary MLS and MLS-based ensemble methods.

3. Provide an evaluation and veriﬁcation of our pro-

posed SECNNP model on the ASCAD database.

While the ASCAD masked AES design is an ex-

ample target of the architecture, it can be applied

to any AES implementation. We demonstrate

a reduction in the requirements of applying DL

in SCA, particularly when attacking implementa-

tions with countermeasures, in which thousands

of traces can be required to break protected AES

implementations using DL. SECNNP enables a

key recovery with only 24 traces, which is a half

the reduction of 42 traces required by the state of

the art models.

4. Discussion on the optimal number of sub-models

and traces required in the SECNNP model as well

as the trade-off between accuracy and training

time for single and multiple convolutional ﬁlter

kernel size models.

2 BACKGROUND

2.1 SCA, Countermeasures and

ASCAD Database

Side channel attacks work on the principal that the

power consumed by a device is dependent on the op-

eration being performed and the data being processed.

This allows an adversary to estimate what the power

consumption should be for some intermediate value

that is a function of some known data (e.g. a plaintext

or ciphertext byte), and some unknown data (e.g. a

secret key byte). In a proﬁled attack, as in this paper,

it is assumed that an attacker has a similar or identi-

cal device on which they can record a large number

of acquisitions, allowing an accurate proﬁling of the

actual power leakage of the device. Leakage mod-

els can be Hamming weight (HW) or Identity (ID). In

the HW leakage model, the sensitive variable’s Ham-

ming weight of the 8-bit Sboxes is considered as the

leakage information. In the ID leakage model, as in

this paper, an intermediate value of the cipher is con-

sidered as the leakage. It allows the model to learn

a broad range of features at different points in time

but results in a high volume of classes (256 classes

for 8-bit data) in the training and attacking process

but the data is more balanced in training and there is

a low probability that many hypothesis keys achieve

a high-rank even with single trace attacks, and so it

is applicable with a small number of traces, e.g. less

than 100.

While a number of SCA countermeasures in both

hardware and software have been proposed in the lit-

erature (such as dual-rail logic, dummy operations,

threshold implementations etc.), here we focus on

masking as this is the countermeasure that is applied

to the traces under consideration. Masking (includ-

ing higher-order variants) applies one or several ran-

dom masks to the sensitive data such as to the input

of the S-Box or the S-Box itself, respectively forming

-order or higher-order masking schemes (Reparaz

et al., 2015).

Multi additive masking for AES implementations

can be seen as masking of the plaintext by:

= p

⊕ m

(1)

and masking the S-Box for value i ∈ [0 . . . 255], which

can be prepared in advance:

S-Box(x) = S-Box (x ⊕ m

i,in

) ⊕ m

i,out

(2)

in which, p and m are the plaintext and mask, respec-

tively in equation 1 and x is the masked input for the

S-Box, ⊕m

i,in

and ⊕m

i,out

are the masks used to un-

mask the input and mask the output of S-Box in equa-

tion 2. Equation 1 ensures that the linear AddRound-

Key operation which follows the S-Box works as ex-

pected on the masked data, but no unmasked data is

processed. Equation 2 ensures that the non-linear S-

Box operation will be masked by unknown pair val-

ues m

i,in

and m

i,out

so that on every execution different

data will be processed regardless of the input value.

In our experiment on ASCAD database (Prouff

et al., 2018), the target implementation on 8-bit AVR

ATMega8515 embedded device has a multi masking

scheme, in which the plaintext and SBox are masked

by two independent masks as shown in equations 1

and 2. Even though a new ASCAD-v2 implementa-

tion is provided with afﬁne masking, this paper aims

to ASCAD-v1 due to the availability of dataset and

reference models like CNNP (Hoang et al., 2020),

TA, MLP and ASCAD-CNN (VGG16 like) models

(Prouff et al., 2018). There are two sub-datasets of

ﬁxed and variable key in ASCAD-v1 but due to the

availability of bijection of S[(.) ⊕ K] into ﬁxed K, we

will not take the ASCAD ﬁxed key dataset into our

consideration. The ASCAD variable-key dataset has

a set of 200, 000 traces for training and 100, 000 traces

for testing. The training traces have random variable

keys, as well as random plaintext and mask values.

The 100, 000 testing traces have the same key with

random plaintext and mask values. Each trace has

1, 400 features and is again labelled by the output of

the 3

S-Box in the ﬁrst round, giving ≈ 781 traces

Stacked Ensemble Model for Enhancing the DL based SCA

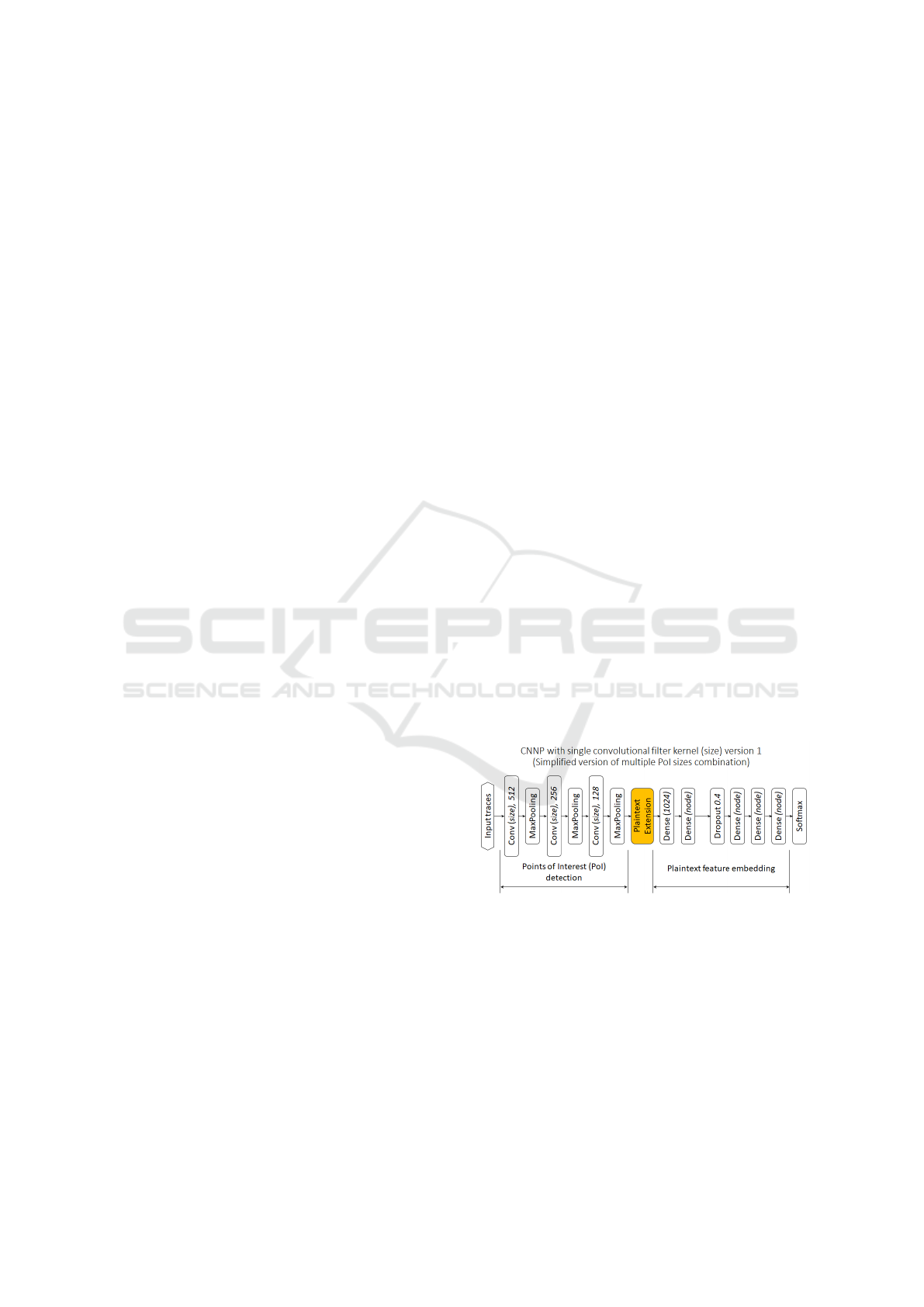
per label. Even though a number for reference models

of TA, MLP, and CNN are provided as part of the AS-

CAD database (Prouff et al., 2018), CNNP (Hoang

et al., 2020) shows its advanced performance in at-

tacking the database. We utilize CNNP as sub-models

in building our proposed SECNNP model.

2.2 Convolutional Neural Networks

with Plaintext Feature Extension

2.2.1 Convolutional Neural Networks

CNNs are a DL architecture that incorporates several

different types of layers for detecting features for clas-

siﬁcation as follows.

1. Convolutional layers are based on a convolution

process, where a small array of small size, known

as ﬁlter is passed over the input sequence signal

(i.e. in our case the trace). The ﬁlter runs or strides

over the traces so that if the same feature (i.e. leak-

age) appears in a different position, it can still be

detected.Convolutional layers can be stacked to

ﬁnd higher abstractions of feature.

2. A pooling layer is often used in conjunction with

the convolutional layer to reduce the size of the

parameters to be learned and the subsequent com-

putational requirements. MaxPooling layer con-

siders the maximum value in a region as the most

important feature of that region.

3. A fully-connected layer ﬂattens the output of the

previous layer, combining all previous nodes (or

input features) together by multiplying those input

nodes with corresponding weights and summing

with the bias to calculate each output node.

4. Dropout is known as a simple way to prevent neu-

ral networks from over-ﬁtting.Dropout is imple-

mented by randomly disconnecting a percentage

of neurons in the network, preventing any particu-

lar feature having a disproportionate effect on the

model as a whole.

5. Rectiﬁed Linear units (ReLu) are used as the acti-

vation function in intermediate layers, i.e. the con-

volutional and fully-connected layers by replacing

a value by itself if positive or else zero is negative.

This helps mitigate the vanishing gradients prob-

lem which can happen in large networks.

6. Softmax is used for the activation function in

the last fully-connected layer. This function is

also known as a normalised exponential function,

which converts the raw logistic scores into corre-

sponding probabilities.

2.2.2 Convolutional Neural Network with

Plaintext Feature Extension

It is clearly shown in (Hoang et al., 2020) that the

plaintext (or ciphertext) is an important factor in

building leakage models as it is XORed with the key

prior to the S-Box in the ﬁrst round. The output of

this operation is used for labelling traces when train-

ing DL models.

y = S-Box(p

⊕ k

) (3)

in which, p and k are the plaintext and key, respec-

tively.

Regardless of the countermeasure utilised, the de-

signer needs to modify the plaintext in some way in

order to hide the sensitive value input to the S-Box.

Whatever the designers do to protect the sensitive data

from side-channel leakage, they will need to modify

some signal or variable related to plaintext, and this

processing will leave either ﬁrst or higher-order leak-

age. The model for Convolutional Neural Network

with Plaintext input (CNNP) with a single convolu-

tional ﬁlter kernel size can be given by the following

formula:

s ◦ [λ

] ◦ β ◦ [λ

] ◦ [P

ext

◦ [δ ◦ [α ◦ γ

]]

] (4)

in which, s, λ, β, P

ext

, δ, α, and γ are the softmax,

fully-connected, dropout, plaintext feature extension,

MaxPooling, activation, and convolutional layers, re-

spectively. γ

is a convolutional layer with ﬁlter kernel

size of 3. CNNP with one-hot encoding (Hoang et al.,

2020) is used as sub-models in our Stacked Ensemble

CNNP (SECNNP) and is shown in ﬁgure 1.

Figure 1: CNNP sub-models.

2.2.3 Maximum Likelihood Scores

Maximum likelihood scores (MLS) can be used for

combining results of attacks from multiple different

traces (Standaert et al., 2009) and/or different models

(Perin et al., 2020) with the same key. It estimates the

likelihood of each hypothesis key by multiplying the

classiﬁcation probability given by independent traces

and/or models to create a scores vector. Values in this

scores vector are then sorted according to probability

for ranking. Accuracy is considered as the location

SECRYPT 2022 - 19th International Conference on Security and Cryptography

of the correct key in the ranked scores vector. The

closer the rank of the correct key is to 1, the higher

the accuracy of the evaluated model.

3 STACKED ENSEMBLE

METHOD FOR DL BASED SCA

3.1 Ensemble Methods

Deep learning relies on minimizing some loss func-

tion in a given environment, and so, the algorithm will

decide the type of patterns it can learn. Hence, for

given traces, different algorithms (or different mod-

els) will be able to capture different SCA leakage

and in many cases, their predictive power complement

each other, making a model fails to ﬁnd the good fea-

tures in a trace but another succeeds. Ensemble mod-

els learn the optimal combination of the base model

predictions to increase accuracy.

3.2 CNNP based Stacked Ensemble

Model (SECNNP)

3.2.1 Model Development Assumptions

When building a model of the power consumption for

the target device, the following assumptions hold:

• The attacker cannot access the design or values

used for random number generation but can pro-

ﬁle keys on the device as well as access the plain-

text and/or ciphertext for a proﬁling attack.

• The attacker does not know any implementation

details except the algorithm being targeted.

• The CNNP model is capable of attacking the AES

implementations due to the reduction in the num-

ber of unknown factors in training and attacking.

• Multiple models and/or trace combination in a

trained model would increase the performance

better than that of MLS.

3.2.2 Attack Model

The proposed SECNNP model attacks AES imple-

mentations based on recovering the unmasked value

of the S-Box output (even where that value is masked)

which allows key recovery given knowledge of the

plaintext. In particular, we trained the proposed

CNNP model by labelling the traces by the 3

S-

Box byte, which is computed from values known to

the attacker during the proﬁling process as given in

equation 3. The trained CNNP models then are used

as sub-models in the SECNNP model, in which the

same labelling is used but the inputs are the hypoth-

esis key probabilities predicted by those sub-models.

This labelling method follows that used by the refer-

ence models in the ASCAD databases (v1) and by the

CNNP models in (Hoang et al., 2020). In order to at-

tack the remaining key bytes, the traces would have to

be relabelled for each S-Box output and the model re-

trained. However the same power traces can be used

to attack the other key bytes.

3.2.3 Two Step Stacked Ensemble Model

Training

Different from (Perin et al., 2020), who applied MLS,

in which the probability of hypothesis keys corre-

sponding to the hamming weight class are multiplied,

we apply a two step training method to build our pro-

posed stacked ensemble model.

• The ﬁrst training step is the training of a number

of general machine learning models, in which a

number of CNNP (Hoang et al., 2020) instances

are trained. The accuracy of those instances must

be diverse (Wang, 2008), and so different num-

bers of epochs, hyperparameters and dropout lay-

ers are used in the CNNP sub-models training.

• The use of a second training step is proposed

in this paper, in which a number of traces with

the same class (from the same plaintext in other

words) are provided to the model(s) trained in the

ﬁrst step for their probability of hypothesis key

outputs. The MLS of the same trace on multiple

models, the MLS of multiple traces on each model

and the MLS of all traces on all models are calcu-

lated. The output probabilities of each hypothesis

key by each sub-model, together with the MLSs

calculated above are grouped together as inputs to

a MLP. The MLP is trained by the corresponding

class given by the trace(s) at the ﬁrst step. Even

though, there is no limitation on the number of

traces and models involved in the MLP, we limit

the number of models and traces to 3 and 6 due to

the computational complexity.

Since the MLSs of traces and models received

from the ﬁrst step are used as an additional input for

the MLP, they will be called inner-MLS. The pro-

posed stacked ensemble model will need either mul-

tiple traces or multiple sub-models or both for the

availability of the inner-MLS. Due to the limitation

in the number of traces and sub-models given above,

an outer-MLS is used to combine the attacking results

from more traces than a input together. Differing from

the ﬁrst and second training step, where the traces are

Stacked Ensemble Model for Enhancing the DL based SCA

from the same classes, traces in this MLS combina-

tion can come from different classes. Hence, we have

two kinds of attack: a single plaintext attack, where

all traces come from the same plaintext in the SEC-

NNP model and the ﬁnal MLS and a multiple plain-

text attack, where all traces in the SECNNP model

come from the same plaintext, but different plaintexts

are used in the ﬁnal MLS.

3.2.4 Multi-trace Multiple CNNP Sub-models

Stacked Ensemble Model

The multi-trace multiple CNNP sub-models stacked

ensemble model utilizes key probabilities result from

multiple CNNP sub-models with multiple trace for

hypothesis key probability calculation independently.

Since two independent hypothesis key probability

outputs are given from different CNNP instances and

different traces, two inner MLSs are used as addi-

tional inputs for the SECNNP model. One is the MLS

from multiple traces predicted by each CNNP sub-

model and the other is the MLS of all traces and all

sub-models.

Figure 2 shows the proposed SECNNP model with

n input traces and m CNNP sub-models. The number

of CNNP sub-models and traces can change within

the limitation of computational power.

Figure 2: SECNNP model with multiple traces and multiple

CNNP sub-models.

The ﬁrst MLS (MLS

) is used to combine the

probabilities of the hypothesis keys predicted by each

CNNP sub-model while the second MLS (MLS

)

layer is used to combine the prediction of all n traces

predicted by all CNNP sub-models. The computa-

tion of the MLS

and MLS

for a hypothesis key i

are given by equations 5 and 6, respectively:

MLS

[i] =

∏

l=1

(prob[l][i]); i ∈ [0..255] (5)

MLS

[i] =

∏

p=1

∏

l=1

(prob[p][l][i]); i ∈ [0..255]

(6)

in which, l is the input trace number, p is the

CNNP model number, i is the hypothesis key, and so,

prob[p][l][i] is the probability of hypothesis key i of

the input trace l predicted by the CNNP sub-model p.

The fully-connected layer with m CNNP sub-

models and n traces receives m× n probability inputs.

The formula for that layer with M nodes is now:

Dense

1024[ j] =

∑

p=1

∑

l=1

256

∑

i=1

(b[ j] + prob[p][l][i]

× w[ j][p][l][i]); j ∈ [1..M]

(7)

in which Dense

1024[ j] is the j

output of the

fully-connected layer, prob[p][l][i] and w[ j][p][l][i] are

the probability and corresponding weight of the hy-

pothesis key i of the input trace l predicted by the

CNNP sub-model p.

The fully-connected layer Dense

(1024) receives

m inputs, which are the MLS of the CNNP sub-

models (MLS

). The formula of that layer with M

nodes is now:

Dense

1024[ j] =

∑

p=1

256

∑

i=1

(b[ j] + MLS[p][i]

×w[ j][p][i]); j ∈ [1..M]

(8)

in which Dense

1024[ j] is the j

output of the fully-

connected layer, MLS[p][i] and w[ j][p][i] are the prob-

ability and corresponding weight of the hypothesis

key i of all n input traces predicted by the CNNP sub-

model p and combined by MLS

The fully-connected layer Dense

(1024) receives

3 inputs, which are the three 256 hypothesis keys

probabilities given by Softmax

, Softmax

and the

combined MLS

of all n traces predicted by all m

CNNP sub-models (MLS

). The formula of that layer

with M nodes is now:

Dense

1024[ j] =

256

∑

i=1

(b[ j] + MLS

[i] × w

MLS

[ j][i])+

256

∑

i=1

(b[ j] + prob

So f tmax

[i] × w

So f tmax

[ j][i])+

256

∑

i=1

(b[ j] + prob

So f tmax

[i] × w

So f tmax

[ j][i]);

j ∈ [1..M]

(9)

SECRYPT 2022 - 19th International Conference on Security and Cryptography

in which Dense

1024[ j] is the j

output of the fully-

connected layer Dense

(1024), MLS

[i] is the output

probability of hypothesis key i from module MLS

and w

MLS

[j][i] is the weight of the corresponding in-

put MLS

[i] for the node j. Similarly, prob

So f tmax

[i],

So f tmax

[j][i], prob

So f tmax

[i] and w

So f tmax

[j][i] are

the output probability of hypothesis key i and its

weight from the Softmax

and Softmax

modules.

The structure given in the ﬁgure 2 can be sim-

pliﬁed by limiting the number of input or the num-

ber of CNNP sub-model to one, making single trace

multiple CNNP sub-moldes and multi-trace single

CNNP sub-model stacked ensemble models. How-

ever, only the multiple CNNP sub-models stacked en-

semble model will be discussed due to the signiﬁcant

performance compared with the reference.

4 EXPERIMENTAL RESULTS

Even though (Prouff et al., 2018) provides a number

of reference models such as TA, MLPs and a pre-

trained CNN, the CNNP models are used for bench-

marking and as sub-models for the proposed SEC-

NNP model due to their better performance.

While a number of variants of the SECNNP ar-

chitecture with different hyperparameter (number of

traces, number of sub-models, number of layers and

number of nodes) were tested, in the following we

present results from SECNNP models with the archi-

tectures shown in ﬁgure 2. The number of traces is

in the range of [1..6] and the number of CNNP sub-

models is in the range of [1..3].

SECNNP models develop from CNNP with single

convolutional ﬁlter kernel size of 3 and CNNP with

two convolutional ﬁlter kernel sizes of 3 and 5. The

models are trained and evaluated using the ASCAD

v1 database traces on a variable-key dataset. Training

is performed on a VMware virtual machine, with ac-

cess to virtual NVIDIA GRID M60-8Q and M40-4Q

GPUs with 8GB and 4GB memory, respectively.

In the experiments using the ASCAD database,

the number of training epochs and time for each

model, together with the rank of the correct key are

reported. Our comparison method is straightforward,

in that we train the CNNP models with the training

dataset group. The hyperparameters are taken from

(Hoang et al., 2020), in which, we focus on the CNNP

models with convolutional ﬁlter kernel size of 3 and

the transfer learning CNNP model with convolutional

ﬁlter kernel sizes of 3 and 5. Three models with

different epochs are selected as sub-models for the

SECNNP structure in ﬁgure 2. The SECNNP struc-

tures are then retrained on the same training dataset

group for the ﬁnal SECNNP models. We evaluate the

trained models on the separate test dataset group pro-

vided in the ASCAD database.

Traces in the test dataset group are sorted by the

plaintext. Those belonging to the same plaintext are

then grouped by [1..6] depending on the number of

traces required by the SECNNP model. Multiple

groups of traces with different plaintexts are used if

more traces (e.g. 42) are required.

At each run, a number of trace groups are ran-

domly selected from the test dataset for the attack

phase, with the maximum likelihood score (MLS) of

each hypothesis key calculated as a function of the

number of traces. These maximum likelihood scores

are then sorted after each run and the rank of the cor-

rect key is recorded. N runs are evaluated and the

mean of the correct key rank is computed. We eval-

uate our models using 100,000 traces from the test

dataset. Depending on how fast the key rank con-

verges, the number of traces for each run is differ-

ent. In the evaluation, we set the number of traces to

42 and the number of runs N is set to 50 for average

rank calculation to identify with (Hoang et al., 2020).

The better performing models are the ones that have a

lower key rank with similar or less traces required.

In our experiments, we consider the number of

traces required for a model be able to attack the

key as the number where the correct sub-byte key

achieves rank 3 or below because a brute force key

search for the entire key should then take at least

= 43, 046, 721 loops, an acceptable computational

for modern computers.

4.1 SECNNP Evaluation with Single

Convolutional Filter Kernel Size

In this section, we will compare the accuracy in at-

tacking traces using the SECNNP models with single

convolutional ﬁlter size, with the CNNP sub-models

(reference models) and the MLS of those sub-models.

The evaluation has been done for the SECNNP

models with convolutional ﬁlter kernel size 3 on

traces belonging to multiple plaintexts groups, in

which trace groups are randomly selected. As can be

seen in ﬁgure 3, the proposed SECNNP model with

1 input trace and 3 CNNP sub-models reduces the

required number of traces for attacking the sub-byte

key 3 to a half compared with the reference models,

in which the MLS of the reference models required

42 traces to achieve key rank 3 while the proposed

SECNNP needs just 24 to achieve the same key rank

(more than a half).

Stacked Ensemble Model for Enhancing the DL based SCA

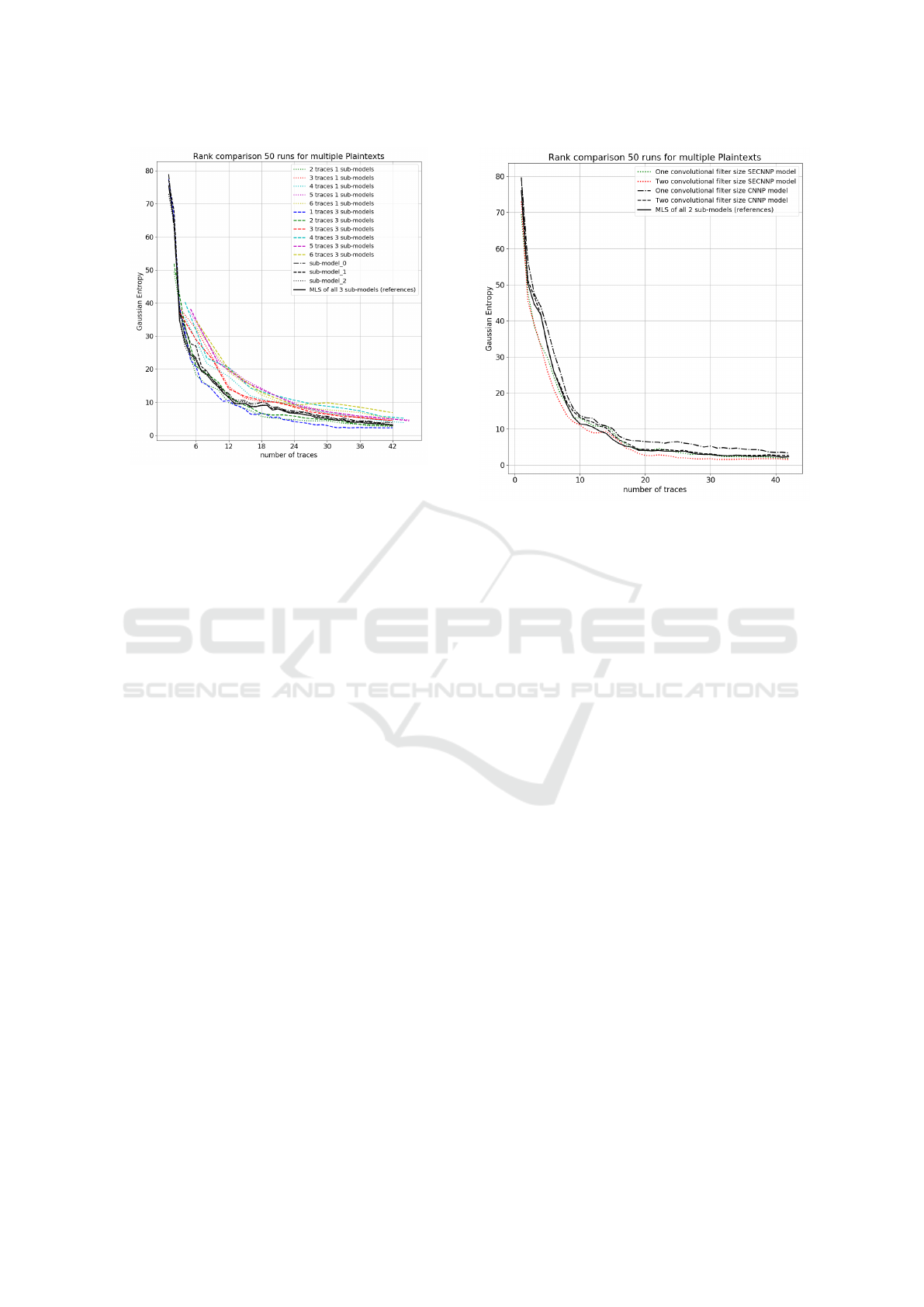
Figure 3: Key rank comparison between proposed SECNNP

models with single convolutional ﬁlter kernel size and ref-

erence models and their MLS.

4.2 SECNNP Evaluation with Multiple

Convolutional Filter Kernel Size

Due to the better accuracy achieved with the SEC-

NNP model with three CNNP sub-models and a sin-

gle trace input as shown in 3, in this section, we

evaluate a different SECNNP model with the same

structure but three 2-convolutional-ﬁlter-kernel-size

CNNP sub-models are used. The proposed model uti-

lizes the CNNP model with convolutional ﬁlter kernel

sizes of 3 and 5 as detailed in (Hoang et al., 2020) as

the sub-models.

An evaluation of the SECNNP model using multi-

ple plaintexts is given in ﬁgure 4. The SECNNP has a

single input trace, and so 42 traces are randomly used

for each run and 50 runs are tested for average key

rank. Even though three CNNP sub-models of each

type (single and two convolutional ﬁlter size) are uses,

we use only one CNNP model with the best accuracy

among the three of each type as the reference. As can

be seen in ﬁgure 4, the combined MLS (in black) of

the reference models (CNNP with single and two con-

volutional ﬁlter kernel sizes) is equivalent with that

of the CNNP with two convolutional ﬁlter sizes and

SECNNP with single convolutional ﬁlter size (in dot

green) and achieve key rank 2 after 40 traces. The

proposed model (in dot red) reduces the number of

required traces from 40 to a half (20 traces) in com-

parison to the MLS of the two best reference CNNP

models.

Figure 4: Key rank comparison between proposed SECNNP

models with one and two convolutional ﬁlter kernel sizes

and reference models and their MLS.

5 DISCUSSION

The evaluation of the proposed SECNNP models re-

vealed the following:

• Re-training from the mistakes of the classiﬁers

(sub-models) improves the accuracy. The pro-

posed SECNNP is re-trained from the same

dataset with the probability of each hypothesis

key. This training gives the model a chance to

learn from its mistakes by looking at the relation-

ship between the probabilities of the correct and

incorrect hypothesis keys. Diversity among the

sub-models (Wang, 2008) is considered as a fac-

tor for the improvement in key rank.

• It is not necessary to have combination of many

different CNN structures to achieve higher accu-

racy. Instead, the same structure trained with a

different number of epochs so that they show di-

versity in attacking traces are good to combine in

an stacked ensembles model.

• A deeper structure which combines models with

different input data improves the accuracy. Even

though a deeper CNNP on its own does not im-

prove the accuracy, making the model deeper to-

gether with changing the input data from traces to

hypothesis key probabilities and combining mod-

els can increase the accuracy of the SECNNP

model. It reduces the number of required traces

SECRYPT 2022 - 19th International Conference on Security and Cryptography

to a half, from 40 to 20 making a brute force at-

tack possible.

• A trade-off in time and accuracy. In our experi-

ment, the SECNNP model with a single convolu-

tional kernel size requires double the training time

compared with the equivalent CNNP model. Con-

sequently, training the SECNNP model with two

convolutional ﬁlter kernel size requires double the

efforts compared with that of the single convolu-

tional ﬁlter kernel size SECNNP model.

6 CONCLUSION

This paper has proposed a modiﬁed approach for

building CNN-based models for proﬁling SCAs. A

MLS layer which combines the Maximum likelihood

scores of multiple models and multiple traces into

the training of the model is proposed. A new net-

work structure, which includes the input of the MLS

and the probability of the hypothesis keys predicted

from different traces by different CNNP models into

the re-training process is introduced for improved re-

sults over the state-of-the-art. The proposed SEC-

NNP models require half of the traces in compari-

son with the state-of-the-art CNNP models in attack-

ing a masked AES implementation from the open-

source ASCAD database and key recovery from just

20 traces is possible when targeting the variable key

database.

While considerable work has been done in the area

of ML for SCA, there is still signiﬁcant scope for

improvement in current approaches. The experimen-

tation in this work is conducted on traces acquired

from an embedded device with software based coun-

termeasures. Future work could involve an analysis

of how the plaintext embedding approach transfers to

attack against hardware based countermeasures such

as threshold or dual-rail logic approaches.

ACKNOWLEDGEMENTS

We would like to thank the people and organizations

who support the research and helped improve the

paper: The UK Research Institute in Secure Hard-

ware and Embedded Systems (RISE) and The EPSRC

Quantum Communications Hub (EP/T001011/1).

REFERENCES

Brier, E., Clavier, C., and Olivier, F. (2004). Correlation

Power Analysis with a Leakage Model. volume 3156,

pages 16–29.

Chen, Z. and Zhou, Y. (2006). Dual-Rail Random Switch-

ing Logic: A Countermeasure to Reduce Side Channel

Leakage. In Goubin, L. and Matsui, M., editors, Cryp-

tographic Hardware and Embedded Systems - CHES

2006, pages 242–254, Berlin, Heidelberg. Springer

Berlin Heidelberg.

D, J. and Tymen, C. (2002). Multiplicative Masking and

Power Analysis of AES. IACR Cryptology ePrint

Archive, 2002:91.

Gebotys, C. H., Ho, S., and Tiu, C. C. (2005). EM Anal-

ysis of Rijndael and ECC on a Wireless Java-Based

PDA. In Rao, J. R. and Sunar, B., editors, Crypto-

graphic Hardware and Embedded Systems – CHES

2005, pages 250–264, Berlin, Heidelberg. Springer

Berlin Heidelberg.

Gilmore, R., Hanley, N., and O’Neill, M. (2015). Neu-

ral network based attack on a masked implementation

of AES. In 2015 IEEE International Symposium on

Hardware Oriented Security and Trust (HOST), pages

106–111.

Goubin L., M. A. . (2011). Protecting AES with Shamir’s

Secret Sharing Scheme., volume 6917 of Lecture

Notes in Computer Science. Springer, Berlin, Heidel-

berg.

Hettwer, B., Gehrer, S., and G

uneysu, T. (2018). Proﬁled

Power Analysis Attacks Using Convolutional Neural

Networks with Domain Knowledge. In Cid, C. and

Jr., M. J. J., editors, Selected Areas in Cryptography -

SAC 2018 - 25th International Conference, Calgary,

AB, Canada, August 15-17, 2018, Revised Selected

Papers, volume 11349 of Lecture Notes in Computer

Science, pages 479–498. Springer.

Hoang, A.-T. and Fujino, T. (2014). Intra-Masking Dual-

Rail Memory on LUT Implementation for SCA-

Resistant AES on FPGA. ACM Trans. Reconﬁgurable

Technol. Syst., 7(2):10:1–10:19.

Hoang, A.-T., Hanley, N., and O’Neill, M. (2020). Plain-

text: A Missing Feature for Enhancing the Power of

Deep Learning in Side-Channel Analysis? Break-

ing multiple layers of side-channel countermeasures.

IACR Transactions on Cryptographic Hardware and

Embedded Systems, 2020(4):49–85.

Kim, J., Picek, S., Heuser, A., Bhasin, S., and Han-

jalic, A. (2019). Make Some Noise. Unleashing

the Power of Convolutional Neural Networks for

Proﬁled Side-channel Analysis. IACR Transactions

on Cryptographic Hardware and Embedded Systems,

2019(3):148–179.

Kocher, P. C. (1996). Timing Attacks on Implementa-

tions of Difﬁe-Hellman, RSA, DSS, and Other Sys-

tems. In Proceedings of the 16th Annual Interna-

tional Cryptology Conference on Advances in Cryp-

tology, CRYPTO ’96, pages 104–113, London, UK,

UK. Springer-Verlag.

Kocher, P. C., Jaffe, J., and Jun, B. (1999). Differential

Power Analysis. In Proceedings of the 19th Annual

International Cryptology Conference on Advances in

Cryptology, CRYPTO ’99, pages 388–397, Berlin,

Heidelberg. Springer-Verlag.

Stacked Ensemble Model for Enhancing the DL based SCA

Lu, X., Zhang, C., Cao, P., Gu, D., and Lu, H. (2021). Pay

Attention to Raw Traces: A Deep Learning Architec-

ture for End-to-End Proﬁling Attacks. IACR Trans-

actions on Cryptographic Hardware and Embedded

Systems, 2021(3):235–274.

Maghrebi, H. (2019). Deep Learning based Side Channel

Attacks in Practice. IACR Cryptology ePrint Archive,

2019:578.

Maghrebi, H., Portigliatti, T., and Prouff, E. (2016).

Breaking Cryptographic Implementations Using Deep

Learning Techniques. IACR Cryptology ePrint

Archive, 2016:921.

Markowitch, O., Medeiros, S., Bontempi, G., and Lerman,

L. (2013). A Machine Learning Approach Against a

Masked AES. volume 5.

Martinasek, Z., Dzurenda, P., and Malina, L. (2016). Pro-

ﬁling power analysis attack based on MLP in DPA

contest V4.2. In 2016 39th International Conference

on Telecommunications and Signal Processing (TSP),

pages 223–226.

Nassar, M., Souissi, Y., Guilley, S., and Danger, J.-L.

(2012). RSM: A Small and Fast Countermeasure for

AES, Secure Against 1st and 2Nd-order Zero-offset

SCAs. In Proceedings of the Conference on Design,

Automation and Test in Europe, DATE ’12, pages

1173–1178, San Jose, CA, USA. EDA Consortium.

Perin, G., Chmielewski,

A., and Picek, S. (2020). Strength

in Numbers: Improving Generalization with Ensem-

bles in Machine Learning-based Proﬁled Side-channel

Analysis. IACR Transactions on Cryptographic Hard-

ware and Embedded Systems, 2020(4):337–364.

Picek, S., Samiotis, I. P., Kim, J., Heuser, A., Bhasin, S.,

and Legay, A. (2018). On the Performance of Convo-

lutional Neural Networks for Side-Channel Analysis.

In SPACE.

Popp, T. and Mangard, S. (2005). Masked Dual-Rail Pre-

charge Logic: DPA-Resistance Without Routing Con-

straints. In Rao, J. R. and Sunar, B., editors, Cryp-

tographic Hardware and Embedded Systems – CHES

2005, pages 172–186, Berlin, Heidelberg. Springer

Berlin Heidelberg.

Prouff, E., Strullu, R., Benadjila, R., Cagli, E., and Du-

mas, C. (2018). Study of Deep Learning Techniques

for Side-Channel Analysis and Introduction to AS-

CAD Database. Cryptology ePrint Archive, Report

2018/053. https://eprint.iacr.org/2018/053.

Reparaz, O., Bilgin, B., Nikova, S., Gierlichs, B., and

Verbauwhede, I. (2015). Consolidating Masking

Schemes. In CRYPTO.

Standaert, F.-X., Malkin, T. G., and Yung, M. (2009). A

Uniﬁed Framework for the Analysis of Side-Channel

Key Recovery Attacks. In Joux, A., editor, Advances

in Cryptology - EUROCRYPT 2009, pages 443–461,

Berlin, Heidelberg. Springer Berlin Heidelberg.

Timon, B. (2019). Non-Proﬁled Deep Learning-based

Side-Channel attacks with Sensitivity Analysis. IACR

Transactions on Cryptographic Hardware and Em-

bedded Systems, 2019(2):107–131.

Tiri, K., Akmal, M., and Verbauwhede, I. (2002). A dy-

namic and differential CMOS logic with signal inde-

pendent power consumption to withstand differential

power analysis on SmartCards. pages 403 – 406.

Wang, W. (2008). Some fundamental issues in ensemble

methods. In 2008 IEEE International Joint Confer-

ence on Neural Networks (IEEE World Congress on

Computational Intelligence), pages 2243–2250.

Weissbart, L., Picek, S., and Batina, L. (2019). One trace

is all it takes: Machine Learning-based Side-channel

Attack on EdDSA. Cryptology ePrint Archive, Report

2019/358. https://eprint.iacr.org/2019/358.

SECRYPT 2022 - 19th International Conference on Security and Cryptography