Segmenting Maps by Analyzing Free and Occupied Regions with Voronoi

Diagrams

Alicia Mora, Adri

an Prados and Ram

on Barber

Robotics Lab, Universidad Carlos III de Madrid, Legan

es, Spain

Keywords:

Room Segmentation, Voronoi Diagram, Occupancy Grid Map, Indoor Environments, Mobile Robots.

Abstract:

Traditional mapping techniques rely on metric properties, which represent indoor information with speciﬁc

geometric characteristics. This fact highly differs from the way in which people interpret their surroundings.

By geometrically segmenting occupancy grid maps into rooms, robots are brought closer to the way in which

we understand indoor environments. In this work, Voronoi diagrams are proposed as the main tool to locate

map partitions. As a novelty, they are extracted from free and occupied spaces to analyze their shape. This

allows to locate narrow passages on free zones which coincide with protruding parts on occupied zones,

indicating a nearby door. An additional advantage is the use of a varying threshold that depends on the map

structure. This dynamic value can adjust to multiple scenarios, avoiding the use of a ﬁxed threshold that

cannot be generalized. Experiments have been conducted in multiple maps, showing the potential of the

propose method.

1 INTRODUCTION

Indoor environments have been traditionally repre-

sented by occupancy grid maps because of their fa-

cility of being built with techniques such as Simulta-

neous Localization and Mapping (SLAM). A grid is

used to partition the environment and each of its cells

is then classiﬁed as either occupied, unoccupied or

unknown. However, this way of representing indoor

locations differs from the way in which we humans

interpret our surroundings. Typical indoor scenarios

are divided into rooms and corridors, to which people

assign a different utility. That is why geometrically

segmenting occupancy grid maps is nowadays a ma-

jor subject of study. Knowing where these regions are

gets robots a step closer to understanding indoor lo-

cations meaningfully. Additionally, partitions can be

used for multiple applications such as extracting topo-

logical maps (Joo et al., 2010), applying coverage al-

gorithms for cleaning robots (Kleiner et al., 2017) or

performing multi-robot tasks (Wurm et al., 2008).

In this work, we propose an ofﬂine method based

on the use of Voronoi diagrams as the main tool for

segmenting occupancy grid maps into meaningful re-

gions. The main purpose is segmenting static envi-

ronments for further uses such as topological plan-

ning on robotic applications. Other works have al-

ready proposed these diagrams as a tool for geometri-

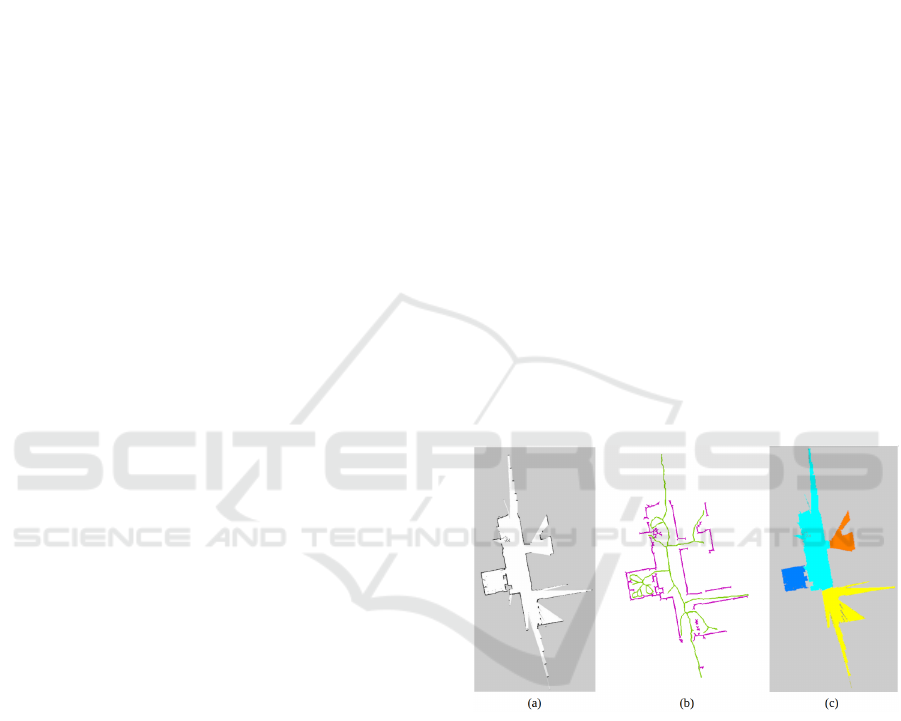
Figure 1: Representative example of the proposed method:

(a) occupancy grid map, (b) Voronoi diagrams extracted

from free regions (green) and occupied regions (ma-

genta), (c) ﬁnal map segmentation resulting from analyzing

Voronoi diagrams properties.

cally segmenting indoor scenarios. However, they are

only extracted from free space, similarly to the way in

which they are used for path planning. A major draw-

back of these methods is that they typically require

additional procedures such as combining Voronoi di-

agrams with image processing techniques or merging

small regions after segmenting. The main novelty of

the proposed method is using Voronoi diagrams to an-

alyze the structure of both free and occupied zones.

The diagram corresponding to free space allows us

to locate narrow passages, where the occupied space

Mora, A., Prados, A. and Barber, R.

Segmenting Maps by Analyzing Free and Occupied Regions with Voronoi Diagrams.

DOI: 10.5220/0011141600003271

In Proceedings of the 19th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2022), pages 395-402

ISBN: 978-989-758-585-2; ISSN: 2184-2809

395

happens to have protruding areas. By locating these

zones, we deﬁne a method that does not depend on

other procedures and does not require any merging

steps. Fig. 1 shows a representative example of the

extracted Voronoi graphs from an occupancy grid map

and the resulting map partitions. The use of the terms

Voronoi diagram and Voronoi graph are used inter-

changeably in the rest of the paper.

The rest of the paper is divided as follows. Sec-

tion 2 reviews related work on room segmentation. In

Section 3, the proposed method based on Voronoi di-

agrams is described. Results obtained from applying

this method to multiple occupancy grid maps is shown

in Section 4. Finally, conclusions and future work are

derived in Section 5.

2 RELATED WORK

Many of the works on room segmentation rely on ex-

tracting features from occupancy grid maps. Authors

in (Joo et al., 2010) propose the extraction of corner

features to partition an occupancy grid map. These

features are selected by analyzing curvature and angle

at each individual cell on the grid. Then, doorways

are deﬁned by segments that relate two features with

a length smaller than 1.2 m. Additionally, genetic al-

gorithms are used as a second check to remove un-

necessary segments. Another method is presented in

(Fermin-Leon et al., 2017), where the proposed tool

for segmenting an occupancy grid map is its bound-

aries. Regions between the map’s boundaries and the

convex hull, named pockets, are iteratively partitioned

to calculate their concavity. Those with a value big-

ger than a threshold are selected as division points.

Room partitions are then created by joining them. In

(Liu et al., 2018), free cells on the grid map are clus-

tered into groups marked by randomly selected ini-

tial points according to the distance among them and

proving that no occupied cells are in between. Result-

ing regions are merged by analyzing their connectiv-

ity using Breath-First Search algorithm. It can be no-

ticed that most of these methods rely on heuristically

determined thresholds, which could not be suitable

for every scenario, or they require a second step in

which exceeding divisions are removed or segmented

regions are merged, adding extra computational costs.

Another typically used method is Watershed algo-

rithm. It is based on the way in which rivers drain

basins in nature, where deeper zones are ﬁrst ﬁlled

up until water from different basins touch each other.

Authors in (Fabrizi and Safﬁotti, 2000) propose the

application of the Watershed algorithm on fuzzy grid

maps, where each cell value ranges from 0 to 1 indi-

cating the probability of being occupied. This method

is adapted to work online in (Buschka and Safﬁotti,

2002). In (Kleiner et al., 2017), the distance trans-

form of a binary occupancy grid map is calculated

before applying the Watershed segmentation proce-

dure. Then, heuristics are applied for room and corri-

dor merging. As it happened with previous methods,

heuristics need to be included in order to merge re-

gions after applying the segmentation procedure. The

main disadvantage of the Watershed algorithm is that

it tends to oversegment regions since it is highly sen-

sitive to local minima. In order to mitigate this fact,

authors in (Ryu, 2020) propose the use of morpho-

logical operations before segmenting. By combining

erosion and dilation, an initial estimation of the num-

ber and location of the different rooms is computed.

Due to these operations, the initial map size is lost, so

regions need to be grown afterwards until they reach

the original map size. This procedure results in a mis-

localization of some doorways, since some regions

grow faster than others.

Voronoi graphs are one of the most applied tech-

niques for room segmentation. In (Thrun, 1998), the

Voronoi graph of free zones is analyzed. Points of

local minima on the graph are selected as critical

points. Then, critical lines which represent doorways

are formed by joining these points to their closest

occupied cells. A similar procedure is presented in

(Beeson et al., 2005), which computes gateway loca-

tions in real time. Voronoi graphs and morphological

operations are combined in (Myung et al., 2009) to

locate door positions. First, the door C-space is cal-

culated by eroding free space by half of doors width.

Then, it is overlapped with the Voronoi graph to locate

doorways. Authors in (Hou et al., 2019) propose the

combination of Voronoi diagrams and alpha-shapes.

Every free cell on the map is assigned to one Voronoi

edge, creating multiple small regions. Alpha shapes

are ﬁnally computed on the map to calculate which

areas should be merged. A review of some room

segmentation approaches is presented in (Bormann

et al., 2016), where the Voronoi graph-based method

turned out to be the most stable one, being closer to

the ground-truth segmentation. Voronoi graphs are

proven to be a handy tool for region characterization.

However, they still have the same problem of being

conditioned to determining a ﬁxed threshold, which

does not always work properly on all possible scenar-

ios, deriving into erroneous door location and over-

segmentation.

Other segmentation methods rely on learning

techniques. Authors in (Mozos et al., 2007) propose

the use of the AdaBoost classiﬁer to identify locations

corresponding to corridors, rooms or doorways. Simi-

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

396

larly, in (Goeddel and Olson, 2016) a CNN is applied.

In the work presented in (Friedman et al., 2007), con-

ditional random ﬁelds are applied to Voronoi graphs

to label places. Authors in (Hiller et al., 2019) pro-

pose to concatenate two CNNs. Even though these

methods are effective, their design is complex and

computationally expensive since they require training

procedures. This is why we mainly focus this work

review on geometric procedures.

In contrast to the methods described above, our

proposal does not depend on a ﬁxed heuristically de-

termined threshold and does not need any merging

steps. By analyzing properties of Voronoi diagrams

from both free and occupied zones, doorway locations

are estimated.

3 MAP SEGMENTATION

The proposed method is based on extracting features

from occupancy grid maps by using Voronoi diagrams

as the main tool. Fig. 2 shows a summary of the pro-

posed steps for segmenting these maps into meaning-

ful regions.

Figure 2: Methodology steps: the left branch corresponds

to free space and the right branch corresponds to occu-

pied space. By analyzing them with Voronoi diagrams, key

points are extracted from both and are used to deﬁne door

locations.

It can be seen that there are two main branches

on the procedure, one for analyzing free space and

the other one for occupied space. Finally, both are

merged to deﬁne door locations. With respect to free

space, steps are focused on locating narrow passages.

For that reason, points of minimum value with re-

spect to distance are selected on the Voronoi branches.

Then, intersection points are deﬁned by their two

closest occupied cells on the map. With respect to

occupied space, we look for protruding parts, which

can be found by locating endpoints on Voronoi dia-

grams, given that they indicate a change in the struc-

ture of occupied zones. By analyzing the location of

intersection points and endpoints, door locations are

found. In the following subsections, a more detailed

explanation of these steps is provided.

3.1 Analyzing Free Space

One of the main processes of the proposed method

is analyzing free space. More speciﬁcally, it is in-

tended to ﬁnd narrow passages by using Voronoi dia-

grams. For that reason, an auxiliary binary image is

created in which free space of the occupancy grid map

is marked with value 1 and occupied and unknown

spaces are marked with value 0. This image is prepro-

cessed to remove noise, the Voronoi graph is extracted

and points of minimum value with respect to distance

are located on its branches to indicate possible door

locations. Details on how these processes are carried

out are provided below.

3.1.1 Preprocessing Free Space

Before extracting Voronoi diagrams, it is important to

preprocess the corresponding binary image. This is

because this type of diagrams are highly sensitive to

noise, producing additional branches that do no pro-

vide any relevant information. For that reason, typical

image processing techniques are applied to the map.

First, an erosion process is conducted with a structur-

ing element of rounded shape. Then, a median ﬁlter

is applied to round corners (Zuo et al., 2020). A rep-

resentative example of results can be seen in Fig. 3.

(a) (b)

Figure 3: Preprocessing of free space: (a) original occu-

pancy grid map, from which free space is selected, (b) re-

sulting binary image after preprocessing free space.

Segmenting Maps by Analyzing Free and Occupied Regions with Voronoi Diagrams

397

3.1.2 Extracting the Voronoi Diagram from Free

Space

Once the binary image has been correctly prepro-

cessed, the Voronoi diagram is calculated. As an ap-

proximation, the image skeleton is proposed. It can

be represented by the set of points corresponding to

the centers of the maximal disks enclosed in free ar-

eas, touching its boundaries at two or more points

(Saha et al., 2016). Since each disk is tangent to map

boundaries at multiple points, and being the position

of the center equidistant to them, the skeleton repre-

sents paths equidistant to objects. This deﬁnition is

similar to the Voronoi diagram, which ensures a graph

as far as possible from obstacles. Morphological op-

erations are used to obtain the skeleton of the im-

age. More speciﬁcally, MATLAB’s function bwskel

(MathWorks, 2022) is applied. Fig. 4 shows results of

applying this method to the preprocessed map shown

in Fig. 3. Finally, nodes are removed from the graph,

leaving only its branches separately. Those with less

that 10 pixels are additionally removed. Fig. 4 shows

the resulting labeled branches.

(a) (b)

Figure 4: Extracted Voronoi diagram by using the image

skeleton: (a) resulting image skeleton, (b) labeled branches.

3.1.3 Selecting Minima from Voronoi Branches

Branches extracted on the previous step are used to lo-

cate points corresponding to possible doorways. For

that reason, the distance transform of free space is

used to assign the distance to the closest occupied

cell for each branch point. Then, every branch is

separately analyzed. For each of them, the smallest

value of its points is found and pixels with such value

±2 pixels of margin are selected. This is done to help

the creation of pixel sets, avoiding loose pixels. The

result is a set of line segments corresponding to nar-

row passages on the scenario, which can be seen as

promising door locations. For every segment, cen-

troid and orientation are saved.

3.1.4 Locating Intersection Points

The next step for locating doors is ﬁnding intersec-

tion points. They are deﬁned as the closest occupied

points on the binary map to the centroids of the pre-

viously computed line segments in perpendicular di-

rection with respect to their orientation, one on each

sense. By joining the two points corresponding to the

same centroid, a line segment is deﬁned, which cor-

responds to promising door locations. Fig. 5 shows a

representative example, where minimum value points

are marked with green dots and line segments are

drawn by joining each pair of intersection points.

(a) (b)

Figure 5: Promising door locations: (a) Points of minimum

value on the Voronoi graph, (b) derived line segments cor-

responding to promising door locations.

3.2 Analyzing Occupied Space

Another main process of the proposed method is ana-

lyzing occupied regions. It is intended to ﬁnd protrud-

ing zones by using Voronoi diagrams. The ﬁrst step

is creating a binary image where occupied zones are

marked with value 1 and free and unknown regions

are marked with value 0. Then, it is preprocessed,

Voronoi diagrams are extracted and endpoints are lo-

cated. A more detailed explanation of these steps is

given below.

3.2.1 Preprocessing Occupied Space

As it happened for free space, it is essential to pre-

process the binary image corresponding to occupied

space before extracting Voronoi diagrams. Image pro-

cessing techniques are again applied. In this case, we

are interested in highlighting protruding areas. For

that reason, rounding corners needs to be avoided. In

contrast to the previous case, the selected structuring

element for applying image processing techniques is a

square with which a dilation process is performed. A

representative example of results can be seen in Fig. 6.

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

398

(a) (b)

Figure 6: Preprocessing of occupied space: (a) original

occupancy grid map, where occupied space is marked in

black, (b) resulting binary image after preprocessing occu-

pied space.

3.2.2 Extracting Voronoi Diagrams from

Occupied Space

Voronoi graphs are extracted from the binary image

corresponding to occupied space in the same way as

explained in Sec. 3.1.2, where skeletons are used

as an approximation. In this case, multiple Voronoi

graphs are obtained, each one corresponding to a dif-

ferent occupied zone, in contrast to free space, where

a single Voronoi diagram was obtained since all free

space is connected. Additionally, those branches with

less than 20 pixels are removed. In this way, small

mapped zones normally corresponding to mapping er-

rors due to sensor noise are removed. Fig. 7 shows

the resulting diagrams obtained from the binary map

shown in Fig. 6 and a labeled image with a different

color assigned for each of the diagrams.

(a) (b)

Figure 7: Extracting Voronoi graphs from occupied space:

(a) resulting Voronoi graphs, each one corresponding to a

different occupied zone, (b) labeled graphs.

3.2.3 Locating Endpoints

Voronoi graphs extracted from occupied zones are a

helpful tool for locating protruding parts, which are

placed near door locations. Every change in the shape

of occupied zones results into a new branch on the

Voronoi graphs. By locating these branches, protrud-

ing parts can be easily deﬁned. In order to do so, end-

points are selected as representative points on Voronoi

graphs. They are deﬁned as pixels with exactly one

pixel neighbor using connectivity 8.

3.3 Deﬁning Door Locations

Door locations are deﬁned as narrow passages in

free space, where protruding parts occur in occupied

zones. Intersection points deﬁned in Sec. 3.1.4 indi-

cate narrow passages found on free space, whereas

endpoints deﬁned in Sec. 3.2.3 deﬁne protruding

parts in occupied zones. By relating these two sources

of information, a ﬁnal estimation of where doors are

can be made. For that reason, the ﬁrst step is locat-

ing the closest endpoint to each intersection point on

free space. By joining the two resulting endpoints,

another line segment is deﬁned. Fig. 8 shown an ex-

ample of the resulting line segments, where the green

line is deﬁned by joining intersection points IP

and

(free space information) and the pink line is de-

ﬁned by joining the two closest endpoints EP

and

, respectively (occupied space information).

Figure 8: Information linkage for deﬁning door locations.

The green segment joins intersection points IP

and IP

obtained from free space, and the pink segment joints end-

points EP

and EP

, obtained from occupied space. IP

and EP

are the central points of the segments, respec-

tively. Yellow bidirectional arrows indicate distance be-

tween paired points.

Once information from free and occupied spaces

is related, distances between each intersection point -

endpoint couple as well as distances between the two

central points of each line segment are analyzed (yel-

low arrows from Fig. 8). In order to do so, a threshold

is proposed to compare distances. The main advan-

tage of the proposed threshold is that it varies accord-

Segmenting Maps by Analyzing Free and Occupied Regions with Voronoi Diagrams

399

ing to the map in which the segmentation procedure

is being applied, contrary to the majority of segmen-

tation works in which thresholds are generalized for

all kinds of scenarios. By varying its value according

to the structure of the occupancy grid map, it is bet-

ter adjusted to data that is being processed, so door

locations are better estimated. The proposed thresh-

old value is an estimation of walls thickness. In this

case, the distance transform is applied on occupied

spaces to assign the distance to the closest free cell for

each point on Voronoi graphs obtained from occupied

space. Then, the mean value of these points multi-

plied by two (since skeletons are found in the middle

of occupied zones) is selected, which indicates how

wide occupied zones are. For each grouped data, the

following conditions need to be accomplished in or-

der to be accounted as a door location:

• d

(IP

, EP

) ≤ thres

• d

(IP

, EP

) ≤ thres

• d

(IP

, EP

) ≤

thres

where d

is the euclidean distance. Additionally, none

of the line segments should intersect with any Voronoi

graph from occupied space. If these conditions are

met, a door location is ﬁnally deﬁned by the line seg-

ment joining the two intersection points.

4 EXPERIMENTAL RESULTS

In this section, the proposed method is compared

against other map segmentation procedures. More

speciﬁcally, three methods are compared against our

proposal. The ﬁrst two are morphological operations

and the traditional use of Voronoi diagrams as pre-

sented in (Bormann et al., 2016). The third method is

based on Watershed (Fabrizi and Safﬁotti, 2000) ap-

plied on the distance transform of an occupancy grid.

The selected dataset for the experiments is obtained

from (Bormann et al., 2016), where both furnished

and unfurnished scenarios with varying sizes can be

found, as well as ground-truth segmentations. A to-

tal of 18 furnished and 18 unfurnished scenarios are

selected from the complete number of available maps.

Evaluation metrics are also computed according to the

methods proposed in (Bormann et al., 2016): execu-

tion times, precision and recall. As explained in the

original work, precision is high if estimated rooms ﬁt

inside ground-truth rooms, which means that it is an

indicator of undersegmentation. The opposite applies

for recall, which is high when ground-truth rooms ﬁt

inside estimated rooms, being an indicator of overseg-

mentation. Both values need to be high for a good per-

formance of the methods. Moreover, they need to be

balanced in order to ensure a robust operation in dif-

ferent situations. Computations have been performed

on an AMD Ryzen 7 4700u CPU.

Results for execution times, precision and recall

on unfurnished scenarios are provided in Table 1 and

some representative segmented maps are shown in

Fig. 9. Morphological operations turn out to be

the worst method, providing the lowest precision and

recall values. With respect to execution times, tra-

ditional Voronoi graphs need a signiﬁcantly higher

amount of time to be executed, which produces the

method to be unsuitable for online applications. The

proposed method however signiﬁcantly reduces com-

putation times by analyzing Voronoi graphs from both

free and occupied spaces. Only Watershed is faster

than the proposed method. Additionally, it has a

higher precision value and only a slightly lower re-

call. For a better comparison of both methods, they

are tested on furnished scenarios.

Metrics for furnished scenarios using Watershed

and the proposed method are collected in Table 2.

Visual results are also provided in Fig. 10, where

it can be clearly seen how our method outperforms

Watershed. Due to to presence of furniture, Water-

shed highly oversegments scenarios, creating multi-

ple rooms where there is a single one. This does not

happen in our method, which is signiﬁcantly less af-

fected by the presence of clutter. Numerical results

support these observations. Precision and recall on

our method maintain similar results for both furnished

and unfurnished scenarios. However, in the case of

Watershed, recall descends to a 44.1%, which means

that scenarios are highly oversegmented. Precision

and recall turn out to be highly unbalanced, producing

an erratic segmentation performance.

Table 2: Metrics for furnished scenarios.

Watershed Ours

Runtime [s] 0.21 4.72

Precision 91.6 ± 11.4 83.9 ± 16.8

Recall 44.1 ± 9.5 70.2 ± 6.8

Table 1: Metrics for unfurnished scenarios.

Morphological Voronoi Watershed Ours

Runtime [s] 5.55 109.43 0.33 2.06

Precision 75.1% ± 17.7% 83.9% ± 14.1% 94.0% ± 9.4% 89.3% ± 11.9%

Recall 80.3% ± 9.4% 90.5% ± 8.9% 81.1% ± 9.0% 82.1% ± 8.8%

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

400

Figure 9: Examples of segmentation results for ﬁve unfurnished scenarios from (Bormann et al., 2016).

Figure 10: Examples of segmentation results for three furnished scenarios from (Bormann et al., 2016).

Segmenting Maps by Analyzing Free and Occupied Regions with Voronoi Diagrams

401

5 CONCLUSIONS AND FUTURE

WORK

In this work, Voronoi diagrams have been used as

the main tool for segmenting indoor scenarios into

rooms. By extracting them from both free and occu-

pied spaces, segmentation results have outperformed

state of the art techniques, with high invariability in

furnished environments. With respect to other meth-

ods, no additional steps have been required to unify

areas after segmenting. Additionally, a method has

been proposed to extract a threshold dependent on the

scenario in which it is being applied, adjusting to the

speciﬁc needs of each map.

In future work, it is intended to use the proposed

method for locating doors. By knowing where doors

are, the main challenge is modifying robots behaviour

to facilitate door trespassing.

ACKNOWLEDGEMENTS

This work was supported by the funding from HERO-

ITEA: Heterogeneous Intelligent Multi-Robot Team

for Assistance of Elderly People (RTI2018-095599-

B-C21), funded by Spanish Ministerio de Economia

y Competitividad, and the RoboCity2030 DIH-CM

project (S2018/NMT-4331, RoboCity2030 Madrid

Robotics Digital Innovation Hub).

REFERENCES

Beeson, P., Jong, N. K., and Kuipers, B. (2005). Towards

autonomous topological place detection using the ex-

tended voronoi graph. In Proceedings of the 2005

IEEE ICRA, pages 4373–4379. IEEE.

Bormann, R., Jordan, F., Li, W., Hampp, J., and H

agele,

M. (2016). Room segmentation: Survey, implementa-

tion, and analysis. In 2016 IEEE international confer-

ence on robotics and automation (ICRA), pages 1019–

1026. IEEE.

Buschka, P. and Safﬁotti, A. (2002). A virtual sensor for

room detection. In IEEE/RSJ international conference

on intelligent robots and systems, volume 1, pages

637–642. IEEE.

Fabrizi, E. and Safﬁotti, A. (2000). Extracting topology-

based maps from gridmaps. In Proceedings 2000

ICRA. Millennium Conference. IEEE International

Conference on Robotics and Automation. Symposia

Proceedings (Cat. No. 00CH37065), volume 3, pages

2972–2978. IEEE.

Fermin-Leon, L., Neira, J., and Castellanos, J. A. (2017).

Incremental contour-based topological segmentation

for robot exploration. In 2017 IEEE ICRA, pages

2554–2561. IEEE.

Friedman, S., Pasula, H., and Fox, D. (2007). Voronoi ran-

dom ﬁelds: Extracting topological structure of indoor

environments via place labeling. In IJCAI, volume 7,

pages 2109–2114.

Goeddel, R. and Olson, E. (2016). Learning semantic place

labels from occupancy grids using cnns. In 2016

IEEE/RSJ IROS, pages 3999–4004. IEEE.

Hiller, M., Qiu, C., Particke, F., Hofmann, C., and Thi-

elecke, J. (2019). Learning topometric semantic maps

from occupancy grids. In 2019 IEEE/RSJ Interna-

tional Conference on Intelligent Robots and Systems

(IROS), pages 4190–4197. IEEE.

Hou, J., Yuan, Y., and Schwertfeger, S. (2019). Area graph:

Generation of topological maps using the voronoi di-

agram. In 2019 19th International Conference on Ad-

vanced Robotics (ICAR), pages 509–515. IEEE.

Joo, K., Lee, T.-K., Baek, S., and Oh, S.-Y. (2010). Gener-

ating topological map from occupancy grid-map using

virtual door detection. In IEEE Congress on Evolu-

tionary Computation, pages 1–6. IEEE.

Kleiner, A., Baravalle, R., Kolling, A., Pilotti, P., and

Munich, M. (2017). A solution to room-by-room

coverage for autonomous cleaning robots. In 2017

IEEE/RSJ International Conference on Intelligent

Robots and Systems (IROS), pages 5346–5352. IEEE.

Liu, B., Zuo, L., Zhang, C.-H., and Liu, Y. (2018). An

approach to graph-based grid map segmentation for

robot global localization. In 2018 IEEE International

Conference on Mechatronics and Automation (ICMA),

pages 1812–1817. IEEE.

MathWorks (2022). Morphological operations on binary

images - matlab bwmorph.

Mozos, O. M., Triebel, R., Jensfelt, P., Rottmann, A., and

Burgard, W. (2007). Supervised semantic labeling of

places using information extracted from sensor data.

Robotics and Autonomous Systems, 55(5):391–402.

Myung, H., Jeon, H.-m., Jeong, W.-Y., and Bang, S.-W.

(2009). Virtual door-based coverage path planning for

mobile robot. In FIRA RoboWorld Congress, pages

197–207. Springer.

Ryu, H. (2020). Hierarchical path-planning for mobile

robots using a skeletonization-informed rapidly ex-

ploring random tree. Applied Sciences, 10(21):7846.

Saha, P. K., Borgefors, G., and di Baja, G. S. (2016). A

survey on skeletonization algorithms and their appli-

cations. Pattern recognition letters, 76:3–12.

Thrun, S. (1998). Learning metric-topological maps for in-

door mobile robot navigation. Artiﬁcial Intelligence,

99(1):21–71.

Wurm, K. M., Stachniss, C., and Burgard, W. (2008). Coor-

dinated multi-robot exploration using a segmentation

of the environment. In 2008 IEEE/RSJ International

Conference on Intelligent Robots and Systems, pages

1160–1165. IEEE.

Zuo, X., Yang, F., Liang, Y., Gang, Z., Su, F., Zhu, H., and

Li, L. (2020). An improved autonomous exploration

framework for indoor mobile robotics using reduced

approximated generalized voronoi graphs. ISPRS An-

nals of the Photogrammetry, Remote Sensing and Spa-

tial Information Sciences, 1:351–359.

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

402