Persistent Homology based Classification of Chaotic Multi-variate Time
Series with Application to EEG Data
Martina Flammer and Knut H
¨
uper
Institute of Mathematics, Julius-Maximilians-Universit
¨
at W
¨
urzburg, Emil-Fischer-Straße 31, W
¨
urzburg, Germany
Keywords:
Bottleneck Distance, Dimension Reduction, Dynamical Component Analysis, Persistent Homology,
Simplicial Complex, Topological Data Analysis.
Abstract:
An application of persistent homology for detection of epileptic events in EEG data is presented. Given
point cloud data, persistent homology is a tool from topological data analysis to describe the structure of the
underlying space on which the data was sampled by utilizing topological invariants and tracking their behavior
on several spatial scales. As a preprocessing step, a novel method called Dynamical Component Analysis is
used that reduces the dimension of a multi-variate time series by incorporating information about the dynamics
of the system. The results show that our proposed method is appropriate to detect the occurence of petit-mal
epileptic seizures in EEG signals.
1 INTRODUCTION
According to the WHO, almost 50 million people suf-
fer under epilepsy, which makes it one of the most
frequent neurological diseases. Being unable to cure
epilepsy, patients are usually dependent on medica-
tion, making the detection and forecast of epilep-
tic events a particularly important task that is com-
monly accomplished by measuring brain activity us-
ing an electroencephalogram (EEG). These data are
measured by placing electrodes on the scalp of pa-
tients that measure the summed electrical brain activ-
ity. However, even for experts it can be difficult and
time-consuming to classify EEG data of every single
patient, which makes the automated classification and
interpretation of EEG data a tremendous challenge for
data scientists from various fields, in particular, from
a mathematical and an engineering point of view.
Since it is assumed that during epileptic events the
activity of neurons is more synchronized, we believe
that the EEG data set is revealing some mathemati-
cal structure that is the key ingredient to classify EEG
data with respect to seizure and non-seizure activ-
ity. Such an assumption follows the paper (van Veen
and Liley, 2006) where Shilnikov chaos was proposed
during epileptic events.
Being on the intersection of topology, the tradi-
tional mathematical field that investigates structures,
and data science, topological data analysis seems to
be an appropriate approach to the above mentioned
task. Especially its main method, persistent homol-
ogy, is considered here as a procedure to describe the
structure of spaces on which data was sampled. Basi-
cally, it uses tools from computational topology com-
bined with geometric insight to provide connectivity
information of the underlying space on several spa-
tial scales. Having its theoretical fundaments in alge-
braic topology leads to a well-understood foundation
of persistent homology. Further advantages are that
the method is robust with respect to small perturba-
tions of the input data and is able to cope with com-
plex data sets, making it particularly useful for analy-
sis of big data. Since the original formulation of per-
sistent homology in the early 2000s, a lot of research
is going on in order to extend the field in various di-
rections and to complete the framework.
Although persistent homology is able to process
high-dimensional data sets it still requires a lot of
computational time. To circumvent this drawback
we preprocess the data using Dynamical Component
Analysis (DyCA) (Uhl et al., 2020), a novel method
to reduce the dimension of a time series by regarding
the dynamics of the underlying system. It can be ap-
plied whenever the dynamics is modeled by a system
of ordinary differential equations (ODEs) with linear
as well as non-linear equations, which is the case for
EEG data (Friedrich and Uhl, 1996).
The outline of this paper is the following. In Sec-
tion 2, the preprocessing of the data with DyCA is
described. Section 3 will focus on the mathematical
Flammer, M. and Hüper, K.
Persistent Homology based Classification of Chaotic Multi-variate Time Series with Application to EEG Data.
DOI: 10.5220/0011144800003271
In Proceedings of the 19th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2022), pages 595-604
ISBN: 978-989-758-585-2; ISSN: 2184-2809
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
595

description of persistent homology, from its algebraic
basics to its application to point cloud data and its vi-
sualization. In Section 4, the EEG data sets are speci-
fied that are used to test out proposed approach. Sec-
tion 5 is devoted to the description of the exact proce-
dure in our numerical experiments and the presenta-
tion of the results, which is followed by an outlook to
future work in Section 6.
2 PREPROCESSING
In (Uhl et al., 2020), the authors introduced a novel
method for dimensionality reduction and separating
the deterministic part of the data from the stochastic
part that corresponds to the noise components. This
method, called DyCA, can be applied to multivariate
time-series if the underlying model for the dynam-
ics follows a system of ODEs which consists of lin-
ear as well as non-linear equations. Using the lin-
ear part, amplitudes and multivariate modes are de-
termined that fit the system of ODEs optimally. This
task is accomplished by solving a generalized eigen-
value problem that is derived from a least squares
minimization problem. The eigenvalue problem leads
to a collection of eigenvalues and associated eigen-
vectors together with some corresponding vectors v
i
,
which both together form the set of projection vec-
tors. Eigenvalues close to 1 correspond to modes for
which the linear approximation fits well. Introduc-
ing a threshold for the eigenvalues allows to estimate
the number of linearly coupled components. Further-
more, also the total number of equations n, governed
by the ODE system, is estimated as being the dimen-
sion of the span of the projection vectors. The set of
eigenvectors u
i
is completed by suitable v
i
, where the
v
i
are the projection vectors corresponding to the non-
linear equations, to a basis of R
n
, the relevant sub-
space. Using the projection vectors, one can project
the initial multivariate time series onto the relevant
subspace, which results in the estimated amplitudes.
The last step is again solving a least squares prob-
lem in order to obtain the pseudoinverse of the pro-
jection matrix and therefore get an estimate for the
DyCA components. In the end, the time-varying sig-
nal is reconstructed as a linear combination of the
estimated time-varying amplitudes and the estimated
DyCA components. The derivation can be found in
detail in the paper (Uhl et al., 2020).
The authors of (Uhl et al., 2020) thought of sev-
eral ways to utilize DyCA, for example for using the
eigenvalue spectrum to classify the dynamics of the
time series, for eliminating noise components of the
signal or for modeling the signal by an data-driven
approach. In our paper, we use it as a preprocess-
ing step for the projection of the given data onto a
lower-dimensional subspace and for incidentally re-
ducing the noise.
3 PERSISTENT HOMOLOGY
Persistent homology is a central topic in the field of
topological data analysis. In topological data analy-
sis, one frequently faces the problem that a set of data
is given that was sampled on a space but the struc-
ture of the space is unknown. Persistent homology
provides a tool which allows to study the topolog-
ical invariants of this space by building a sequence
of simplicial complexes from the data, also known as
the persistence complex. By regarding several scales,
which is accomplished by tracking the topology of the
data set when the point cloud is thickened, one gets
information about connectivity of the space, such as
connected components, holes, voids, etc., which can
be used for example for the analysis of networks, dy-
namical systems and protein structures. A detailed
overview can be found in (Otter et al., 2017).
3.1 From Data to Simplicial Complexes
The first step in the pipeline of the computation of per-
sistent homology consists of constructing a simplicial
complex from the given point cloud data. A simplicial
complex is a way to approximate a topological space
by a set of vertices, edges, triangles, tetrahedrons and
higher-dimensional equivalents. Such an approxima-
tion is called a triangulation of the space, however,
not every space is triangulable, but in our application
the assumption of triangulable spaces is appropriate.
Definition 3.1 (Simplicial complex). A simplicial
complex K is a set consisting of non-empty subsets of
a set K
0
such that the following two properties hold:
1. {v} ∈ K for all v ∈ K
0
and
2. τ ∈ K for all τ ⊂ σ,σ ∈ K.
The elements of K are called simplices and ele-
ments of K
0
are referred to as vertices of K. A simplex
is called p-simplex or equivalently, is said to have di-
mension p, if its cardinality is p+1. The dimension of
the simplicial complex K is defined as the maximum
of dimensions of all its simplices.
A simplex τ is called a face of a simplex σ if τ ⊂ σ.
τ is called a face of σ of codimension k if the di-
mensions of τ and σ differ by k. For two simplicial
complexes K and L, a map of simplicial complexes
f : K → L is a map on the corresponding vertex sets
ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics
596

f : K
0
→ L
0
with the property that simplices in K are
mapped to simplices in L, i.e. f (σ) ∈ L for all σ ∈ K.
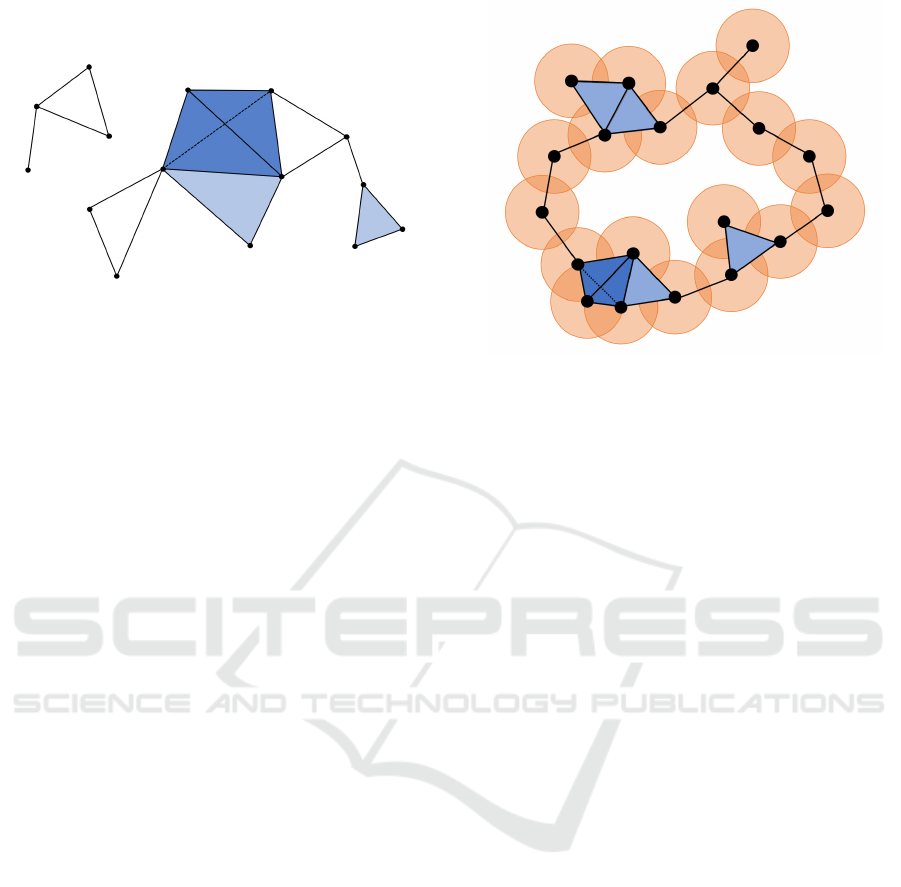
Figure 1: Example of a simplicial complex.
In Figure 1, an example of a three dimensional
simplicial complex is shown. It consists of 0-
simplices (points), of 1-simplices (edges between
points), of 2-simplices (triangles) and of one 3-
simplex (the tetrahedron).
Given data in form of a finite point cloud, there
are several ways to construct a simplicial complex of
that data set. One of the most important complexes is
the so-called
ˇ
Cech complex.
Definition 3.2. For a finite point set M in a metric
space X and some ε > 0, consider the non-empty
union M
ε
=
S
x∈M
B(x,ε), where B(x, ε) denotes the
closed ball centered at x and with radius ε. Let
ˇ
C(M,ε) be the simplicial complex with vertex set M
and where a k-simplex {x
1
,...,x
k
} ⊂ M is added to the
simplicial complex
ˇ
C(M,ε) if and only if B(x
1
,ε) ∩
... ∩ B(x
k
,ε) 6=
/
0.
ˇ
C(M,ε) is called the
ˇ
Cech complex
on M at scale ε.
An example of a
ˇ
Cech complex at a certain scale ε
is shown in Figure 2. The black dots denote the point
cloud data set and the orange balls are the closed balls
around each data point. As one can see in the Figure,
an edge between two points is added to the simplicial
complex if the intersection of the two associated balls
is non-empty. In a analogue manner, triangles, tetra-
hedrons and higher-dimensional simplices are added.
Theoretically, the dimension of the
ˇ
Cech complex
might become very large, namely up to |M| − 1. Ad-
ditionally, in order to check whether a subset of M is
actually a simplex, one has to check the above condi-
tion for a large number of intersections. This makes
the calculation of the
ˇ
Cech complex computationally
expensive. A way to overcome these difficulties is by
regarding the lazy version of this simplicial complex.
That means that one only checks for pairwise inter-
sections, i.e. a simplex {x
1
,...,x
k
} is added to the sim-
plicial complex if and only if the pairwise intersec-
tions B(x
i
,ε) ∩ B(x
j
,ε) are non-empty for all indices
1 ≤ i < j ≤ k. We call this simplicial complex the
Figure 2: Example of a
ˇ
Cech complex.
Vietoris-Rips complex of M at scale ε. The Vietoris-
Rips complex still can have a very large dimension,
but it is computationally cheaper, making it one of the
most popular choices for building a simplicial com-
plex on point cloud data.
3.2 Simplicial Homology
Homology is a way of classifying topological spaces.
The idea behind homology is to distinguish spaces
by their n-dimensional holes, for every n ∈ N
0
. 0-
dimensional holes correspond to connected compo-
nents, 1-dimensional holes to holes in the usual sense,
2-dimensional holes to voids, and so on. The homol-
ogy of a simplicial complex is constructed as follows:
Let C
p
(K) be the vector space over F
2
with basis
consisting of the p-simplices of K. Now, we define
linear maps d
p
on the basis elements for every p ∈
{1,2,...} as follows:
d
p
: C
p
(K) → C
p−1
(K),
σ 7→
∑
τ⊂σ,τ∈K
p−1
τ
(1)
and for p = 0, let d
0
be the zero map. Here and in
the following, let K
p
denote the set of all p-simplices.
If the dimension of the simplicial complex K is n,
then the set of p-simplices K
p
is empty for all p > n.
Hence, the corresponding vector space C
p
(K) is the
zero vector space. As a consequence, the following
sequence of vector spaces and F
2
-linear mappings is
obtained:
0
d
n+1
−→C
n
(K)
d
n
−→···
d
2
−→C
1
(K)
d
1
−→C
0
(K)
d
0
−→0, (2)
which is also called a chain complex. The maps d
p
are referred to as boundary maps and by simple cal-
culations it follows that they have the property
d
p
◦ d
p+1
= 0 for all p ∈ {0,1,2,...}. (3)
Persistent Homology based Classification of Chaotic Multi-variate Time Series with Application to EEG Data
597

As a consequence, im d
p+1
⊂ kerd
p
. This condition
allows us to consider the quotient of the two vector
spaces kerd
p
and imd
p+1
.
Definition 3.3. For any p ∈ {0, 1,2,...}, define Z
p
:=
kerd
p
and B
p
:= im d
p+1
. The elements of B
p
are re-
ferred to as p-boundaries and the elements of Z
p
are
called p-cycles. Then, the quotient vector space
H
p
(K) := Z
p
/B
p
(4)
is called the p-th homology of a simplicial complex
K. The p-th Betti number of the simplicial complex
K is defined as the dimension of the p-th homology
vector space,
β
p
(K) := dim H
p
(K) = dim Z
p
− dim B
p
. (5)
One property of homology is that maps between
simplicial complexes f : K → L induce linear maps
between the corresponding homology vector spaces
f
p
: H
p
(K) → H
p
(L) for all p. Another important
property is functoriality: given maps of simplicial
complexes f : K → L and g : L → M, for the map-
ping (g◦ f )
p
: H
p
(K) → H
p
(M) it holds that (g◦ f )
p
=
g
p
◦ f
p
.
3.3 Filtrations
A sequence of nested subcomplexes of a simplicial
complex K
/
0 = K
0
⊂ K
1
⊂ ··· ⊂ K
l
= K (6)
is called a filtration of K. Considering the homology
of each of the subcomplexes, for every i ≤ j the in-
clusion maps from K
i
to K
j
induce linear maps
f
i, j
p
: H
p
(K
i
) → H
p
(K
j
) (7)
for all p. Consequently, we also obtain for each di-
mension p a sequence of homology spaces
0=H
p
(K
0
)→H
p
(K
1
)→··· → H
p
(K
l
)=H
p
(K) (8)
where the arrows between subsequent vector spaces
H
p
(K
i
) and H
p
(K
i+1
) are the above defined maps
f
i,i+1
p
. Due to the already mentioned functoriality
condition it holds:
f
j,k
p
◦ f
i, j
p
= f
i,k
p
, for all i ≤ j ≤ k. (9)
Definition 3.4 (p-th persistent homology). Consider
a filtration of a simplicial complex K
0
⊂ K
1
⊂ ·· · ⊂
K
l
= K. Then, the p-th persistent homology of K is
defined as
H
i, j
p
:= im f
i, j
p
= Z
p
(K
i
)/(B
p
(K
j
) ∩ Z
p
(K
i
)), (10)
where f
i, j
p
: H
p
(K
i
) → H
p
(K
j
) are the linear maps in-
duced by the inclusions maps K
i
→ K
j
for all i, j with
0 ≤ i ≤ j ≤ l.
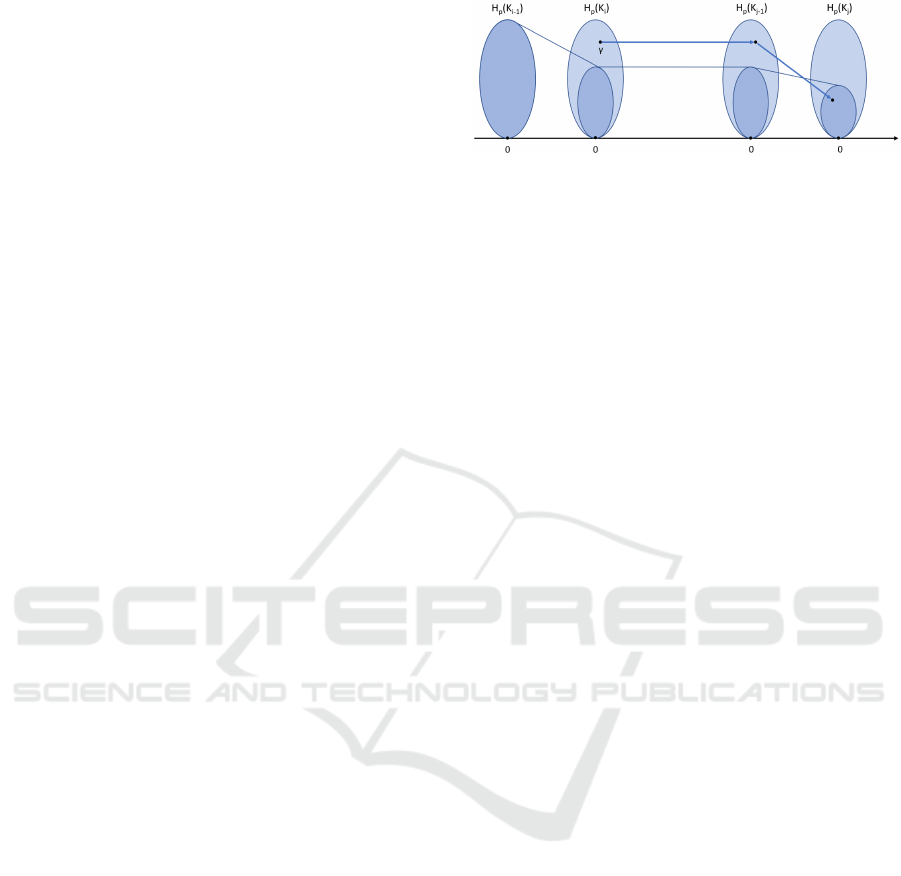
Figure 3: Class γ is born at filtration step i and dies entering
filtration step j, inspired by (Edelsbrunner and Harer, 2010).
Definition 3.5. A homology class γ ∈ H
p
(K
i
) is said
to be born at filtration step i if ( f
i−1,i
p
)
−1
(γ) =
/
0, i.e. it
does not lie in the image of f
i−1,i
. Intuitively, it means
that i is the smallest index on which the class appears.
Further, we say that a class γ ∈ H
p
(K
i
) dies entering
K
j
if it merges with an older class as we go from K
j−1
to K
j
, that is, f
i, j−1
p
(γ) 6∈ H
i−1, j−1
p
but f
i, j
p
(γ) ∈ H
i−1, j
p
.
In the literature, this is referred to as elder rule.
The main idea of persistent homology is to track
the lifetime of homology classes, i.e. when classes
are born and when they die. Classes that persist on
a large scale are regarded as actual features whereas
classes with only a short lifetime are said to be caused
by noise. A way to visualize this is through a set of
intervals of the form [b
i
,d
i
), where each interval cor-
responds to a class γ
i
with birth time b
i
and death time
d
i
. If a class with birth time b
j
does not die through-
out the entire filtration we say that it lives forever and
associate it to the interval [b
j
,∞). This collection of
intervals is called the barcode.
Definition 3.6. A barcode is a finite set of half-open
intervals [i, j), where 0 ≤ i < j ∈ R ∪ {∞}.
An equivalent way to visualize the lifetime of
the persistent homology classes is the so-called per-
sistence diagram, which is defined as a multiset of
points in R
2
where each class γ
i
corresponds to a point
(b
i
,d
i
). In Figure 5, Subfigures 5c and 5e, one can see
an example for a barcode and a persistence diagram in
dimensions 0 and 1, respectively. In a persistence dia-
gram, points that are close to the diagonal correspond
to short intervals and points far from the diagonal to
long, persistent features. Since for every class it holds
that it dies after it is born, i.e. b
i
< d
i
, all the points
lie above the diagonal.
3.4 Comparison of Persistence
Diagrams
For technical reasons, in the formal definition of a per-
sistence diagram we also include each point on the
diagonal ∆ = {(x,y) ∈ R
2
|x = y} with infinite mul-
tiplicity. This guarantees that there exists a bijection
ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics
598

for any two persistence diagrams by assuring that they
have the same cardinality.
Definition 3.7 (Persistence diagram). A persistence
diagram is the union of a countable multiset of points
(x,y) in (R ∪ {∞})
2
with x < y and the diagonal ∆ =
{(x,y) ∈ R
2
|x = y}, where each point on the diagonal
has infinite multiplicity. (Mileyko et al., 2011)
The most frequently used way to compare persis-
tence diagrams or equivalently, barcodes, with each
other is the bottleneck distance.
Definition 3.8 (Bottleneck distance). The bottleneck
distance between two persistence diagrams D
1
and D
2
is defined as
W
∞
(D
1
,D
2
) = inf
ϕ:D
1
→D
2
sup
x∈D
1
kx − ϕ(x)k
∞
, (11)
where ϕ : D
1
→ D
2
ranges over all bijections from D
1
to D
2
. (Mileyko et al., 2011)
In words, the bottleneck distance is the longest
distance of two matched points, where the matching
between the two diagrams is chosen in an optimal
way such that it minimizes the longest distance of two
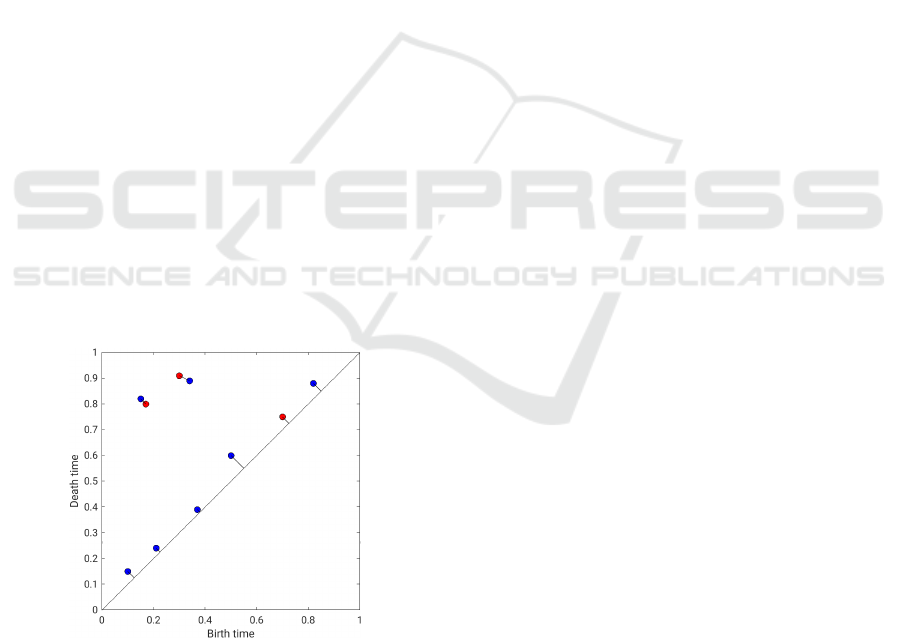
matched points. In Figure 4, one can see two persis-
tence diagrams in red and blue, respectively, and the
matching between the closest points. Points close to
the diagonal are matched to the diagonal.
In the particular case where one computes the bot-
tleneck distance of an arbitrary diagram D
1
and the
empty diagram D
/
0
that contains only the diagonal, all
the points in the first diagram are matched to the di-
agonal and the bottleneck distance is proportional to
the length of the longest bar in the barcode.
Figure 4: Example for the bottleneck distance for two per-
sistence diagrams (red and blue).
4 EEG DATA
In order to apply DyCA to a multi-variate time se-
ries, a system of ordinary differential equations with
both linear and non-linear equations has to be given
to model the underlying dynamics. In (van Veen and
Liley, 2006), the authors showed via bifurcation anal-
ysis the existence of Shilnikov chaos during epileptic
seizures. The authors of (Friedrich and Uhl, 1996)
verified that the dynamics in EEG data during epilep-
tic seizures can be accurately modeled by the follow-
ing system of differential equations
˙x
1
= x
2
,
˙x
2
= x
3
,
˙x
3
= f (x
1
,x
2
,x
3
),
(12)
with f being a non-linear polynomial function.
Hence, the assumptions for applying DyCA are ful-
filled. However, if the patient is out of seizure, the
system exhibits no structure.
For the experiments, we used EEG data from a
German hospital that was measured with 25 chan-
nels using a sampling rate of 256 Hz. The data set
consists of 6 time series with lengths of 10 to 40
seconds. The EEG was recorded from patients that
suffer under a special kind of epilepsy with seizures
that are called absence seizures or petit-mal seizures.
These absences are characterized by impairment of
consciousness and an abrupt beginning and end. Usu-
ally, absence seizures last from a few seconds to half
a minute (Commission on Classification and Termi-
nology of the International League Against Epilepsy,
1981).. We chose a moving window setup with win-
dows of 0.5 second length in order to assure that the
window size is long enough to contain at least one cy-
cle of the recurrent trajectories and short enough to
detect the absence. The beginning time of the moving
window is shifted by 0.1s, resulting in an overlap of
80% for neighboring windows.
5 NUMERICAL EXPERIMENTS
5.1 Methodology
For the preprocessing with DyCA the algorithm as de-
scribed in (Uhl et al., 2020) was used. All the compu-
tations of simplicial complexes, persistent homology
and the bottleneck distance were performed by means
of the software library JAVAPLEX (Tausz et al., 2014).
Written in Java, it can be accessed from MATLAB
and contents many relevant functions from persistent
homology. It was applied to the point-cloud data
that was obtained by applying DyCA on the entire
multi-variate time series and windowing the result-
ing four dimensional data into windows of length 0.5
seconds. This resulted in approximately 128 points
Persistent Homology based Classification of Chaotic Multi-variate Time Series with Application to EEG Data
599

in R
4
per window. From this point-cloud data, a fil-
tered Vietoris-Rips complex was calculated using the
JAVAPLEX library. After applying persistent homol-
ogy, the barcode for every window is calculated.
As mentioned in Section 4, during the epilep-
tic seizures one assumes that there is structure in
the data after projecting it with DyCA onto a lower-
dimensional subspace. Contrarily, in time periods
without epileptic seizures one assumes that the data
has no structure. In order to distinguish these two
states, our approach regards the 1-dimensional persis-
tent homology of the windowed, projected time-series
and compares the barcodes/persistent diagrams of ev-
ery window with the empty diagram, i.e. the diagram
which consists only of the diagonal. This is based on
the assumption that in windows without an epileptic
seizure there is no structure, hence in an ideal case
there should be no persistent features. Thus, for every
window the bottleneck distance is calculated between
the persistence diagram of the current window and the
empty diagram. For windows without an absence we
expect the bottleneck distance to the empty diagram
to be small whereas for windows where an epileptic
event is happening we expect it to be higher.
In Figure 5, one can exemplary see the results for
two windows, where Subfigures 5a, 5c and 5e were
generated using a window during an epileptic event
and Subfigures 5b, 5d and 5f correspond to a window
without an absence. The length of the windows was
chosen to be 0.7s in order to assure that the trajec-
tory shows more than two cycles. In the actual ex-
periments, a shorter window length is chosen to pre-
vent the blurring of the transition time between the
two states.
In the first row, the trajectory projected with
DyCA is shown. To be precise, the point cloud was
projected with DyCA onto a four dimensional sub-
space, but for sake of visibility only plots in a three
dimensional subspace are shown.
In the second row, one can see the barcodes corre-
sponding to the persistent homology of both windows
in dimensions 0 and 1, respectively. The barcode dur-
ing the absence shows a completely different behavior
than the barcode in the window without an absence.
In dimension 1, one can see that there are a lot of con-
nected components during the absence until the filtra-
tion value, where all connected components merge to
one component. A bit before all the connected com-
ponents except for one die, the most persistent hole
(feature in dimension 1) is born and it survives until
filtration value 0.47. However, in 5c one can also see
a lot of other non-persistent holes in dimension 1, but
their lifetime is rather short. One could suspect that
the second longest bar in the barcode of dimension 1
corresponds to the little hole in the trajectory, but it is
hard to verify.
In Subfigures 5e and 5f, the corresponding per-
sistence diagrams for both windows are shown. Red
dots denote features in dimension 1 whereas blue dots
correspond to features in dimension 0. The triangles
denote features that do not die throughout the filtra-
tion and therefore they correspond to the arrows in the
barcode of the 0-th persistent homology. As it was
already mentioned, dots that are far from the diago-
nal correspond to long bars in the barcode. Hence, in
Subfigure 5e the red dot that is far from the diagonal is
the persistent hole and the dots near the diagonal are
considered as topological noise. In case of the chaotic
behavior, i.e. the trajectory in the window where no
epileptic event is happening, there are no persistent
holes visible. The only holes are three holes that are
born right in the beginning of the filtration and die
shortly after they are born. Hence, the multiplicity of
the red dot in the persistence diagram in 5f is three.
The barcode in dimension 0 in Subfigure 5d shows
that there is only one connected component through-
out the entire filtration. In order to differentiate win-
dows with and without an epileptic event we consider
the most persistent hole in dimension 1 as the distinc-
tion feature.
5.2 Results
In Figure 6, the results for the bottleneck distance ob-
tained by applying the above described methodology
to the 6 different EEG time series are shown. First
of all, the given multi-variate time series is projected
onto a 4 dimensional subspace using DyCA. After-
wards, at each time step the bottleneck distance of the
persistence diagram of the point cloud in the corre-
sponding window and the empty persistence diagram
is calculated. Thus, the x-axis of every plot in Figure
6 shows the time in seconds and on the y-axis, one
can see the bottleneck distance of the window start-
ing at time x and ending at time x + 0.5s. The red
dotted lines denote the beginning and the end of an
absence, as it was detected by a medical doctor (ex-
pert). The beginning of an absence is marked with
two dotted lines at a distance of 0.5s in order to indi-
cate that the moment of the transition of the two state
can only be determined with a precision subject to the
window length. The second of the two lines that de-
note the beginning of an epileptic event is the starting
time determined by the expert.
In Subfigures 6a, 6b, 6c and 6f, the beginning of
the absence is detected sharply, whereas in Subfigures
6d and 6e the epileptic event seems to start shortly be-
fore the starting time that was detected by the expert.
ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics
600

(a) Trajectory during absence.
(b) Trajectory without absence.
(c) Barcode during absence. (d) Barcode without absence.
(e) Persistence diagram during absence.
(f) Persistence diagram without absence.
Figure 5: Overview of the results for two exemplary windows with (left column) and without (right column) an epileptic
seizure.
However, for each data set the end of an absence is
sharp and is situated exactly where it was identified
by the expert.
To get some numerical results, for every time se-
ries f
i
we chose a threshold α
i
, such that the classifi-
cation task is performed in an optimal way. Windows
where the bottleneck distance is above that threshold
are classified as absence windows and windows with a
lower bottleneck distance are categorized as windows
without an epileptic event. In Table 1, one can see for
Persistent Homology based Classification of Chaotic Multi-variate Time Series with Application to EEG Data
601

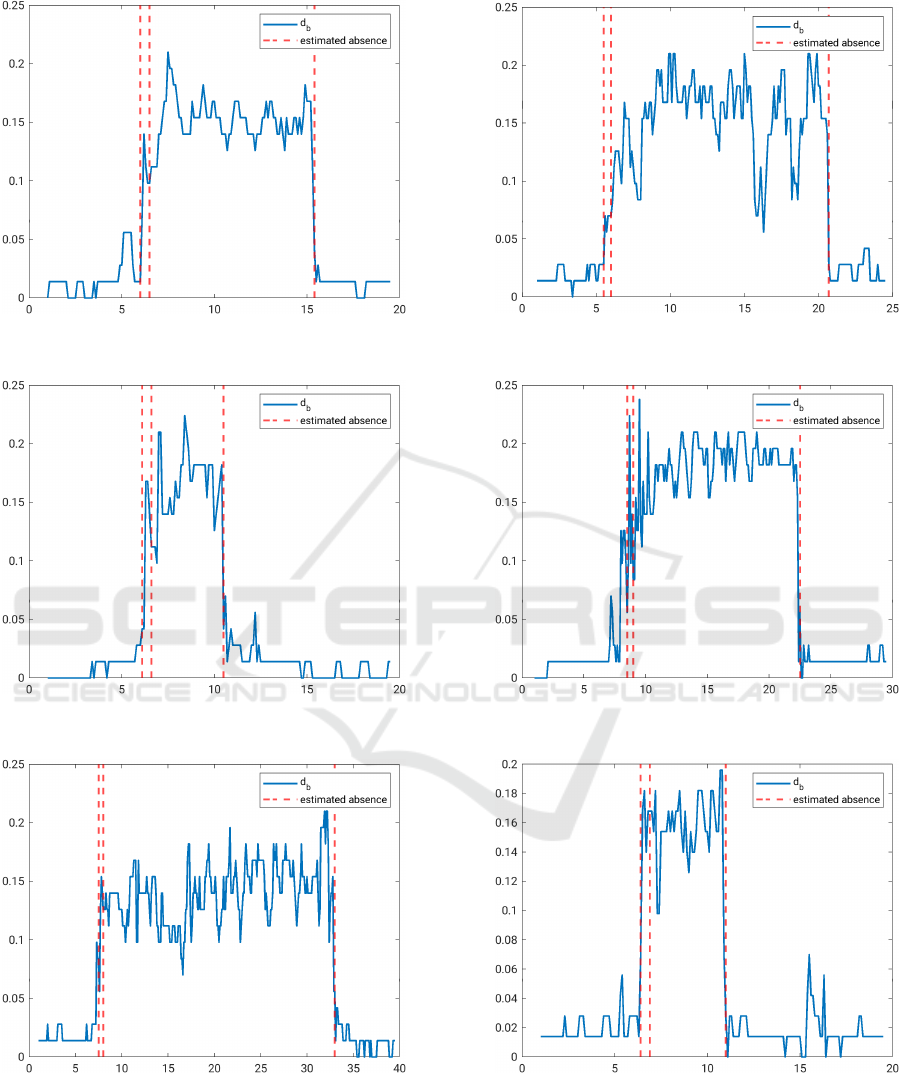
(a) Time Series 1.
(b) Time Series 2.
(c) Time Series 3. (d) Time Series 4.
(e) Time Series 5. (f) Time Series 6.
Figure 6: Bottleneck distance d
B
for 6 data sets to detect epileptic seizures.
every time series (TS) the chosen threshold value α
and the resulting wrongly classified frames by using
the threshold. In the last column, the corresponding
percentage is shown. Since in Subfigures 6d and 6e
the beginning of the absence is approximately half a
second after the increase of the bottleneck distance,
it is impossible to find a threshold α that divides the
windows into windows with or without absence.
ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics
602

Table 1: Results for the classification task of the 6 evaluated
data sets.
α Wrong frames Percentage
TS 1 0.06 0/186 0%
TS 2 0.05 0/236 0%
TS 3 0.08 1/186 0.5%
TS 4 0.08 6/286 2.1%
TS 5 0.05 4/386 1.0%
TS 6 0.08 1/186 0.5%
Even though there are some outliers, such as in
Subfigure 6f around second 15.6 and in Subfigure 6b
around second 16.3, the results show a clear differ-
ence between windows in which an epileptic event
occurs and windows without an epileptic event. Fur-
thermore, the results in Table 1 show that we achieve
a very good classification performance with our pro-
posed approach, with the percentage of falsely cat-
egorized frames ranging from 0% to 2.1%. Addi-
tionally, it shows that without an epileptic event the
conditions of the DyCA are not fulfilled and hence it
fails. We conclude that the combination of DyCA and
persistent homology is well-suited to detect absence
seizures in EEG data.
6 OUTLOOK
Despite the promising results presented in the previ-
ous Section, there are still some improvements that
can be done. To be precise, EEG data can vary a lot
between different patients as well as between different
hospitals and measurement setups. Hence, the struc-
ture of the projected trajectory with DyCA can differ a
lot, making the relevant holes more or less persistent.
Also, adding a data point that lies exactly in the cen-
ter of the most persistent cycle considerably alters the
persistence diagram. Hence, even though persistent
homology is robust with respect to small perturbation
of the input data, it is not very robust with respect to
single outliers, that lie significantly outside the struc-
ture. Future work could address this issue, either by
making the DyCA more robust or by using some so-
phisticated extensions of persistent homology.
Additionally, the structure of the attractor resem-
bles more than one loop, i.e. an outer big loop and a
smaller loop inside. However, in our investigation we
only assumed that there is one relevant hole whose
persistence was used as a classification feature. As
an improvement, one could use more advanced tech-
niques that include the information of the entire per-
sistence diagram.
As last point, we would like to mention that the au-
thors of this paper are aware of two other papers, (Pi-
angerelli et al., 2018) and (Merelli et al., 2016), that
also investigate the use of persistent homology to de-
tect the differences between the states where epileptic
events occur (ictal states) and the states without event
or right before the event (preictal state), respectively.
To discriminate the respective states they used an en-
tropy measure that can be defined on barcodes, called
the persistent entropy. By calculating a Pearson corre-
lation coefficient matrix between windows of the time
series and using it as weighted edges, that give rise to
a filtration of a simplicial complex, and computing
the persistent entropy of every barcode, the authors of
(Merelli et al., 2016) showed that when it comes to
the phase transition between the preictal and the ic-
tal state the number of connected components drops
to one and increases again after the phase transition.
Additionally, in (Piangerelli et al., 2018) the authors
discriminated epileptic states from non-epileptic ones
by regarding each channel as a piecewise linear func-
tion, from which a so-called lower-star filtration of a
simplicial complex can be computed. From each fil-
tered simplicial complex they calculated the persistent
entropy and averaged this value over all channels, us-
ing the result to train a supervised classifier. They got
a strong separation of the values for the averaged per-
sistence entropy between the two states. However, the
comparison of our approach to the approaches men-
tioned above is out of the scope of this paper and will
be addressed in subsequent papers, this is ongoing re-
search.
ACKNOWLEDGEMENTS
This work has been supported by the German Federal
Ministry of Education and Research (BMBF-Projekt
05M20WWA: Verbundprojekt 05M2020 - DyCA).
REFERENCES
Commission on Classification and Terminology of the In-
ternational League Against Epilepsy (1981). Proposal
for revised clinical and electroencephalographic clas-
sification of epileptic seizures. Epilepsia, 22(4):489–
501.
Edelsbrunner, H. and Harer, J. (2010). Computational
Topology: An Introduction. Applied Mathematics.
American Mathematical Society, Providence, RI.
Friedrich, R. and Uhl, C. (1996). Spatio-temporal analysis
of human electroencephalograms: Petit-mal epilepsy.
Physica D: Nonlinear Phenomena, 98(1):171–182.
Merelli, E., Piangerelli, M., Rucco, M., and Toller, D.
(2016). A topological approach for multivariate
time series characterization: The epileptic brain. In
Persistent Homology based Classification of Chaotic Multi-variate Time Series with Application to EEG Data
603

Proceedings of the 9th EAI International Confer-
ence on Bio-Inspired Information and Communica-
tions Technologies (Formerly BIONETICS), BICT’15,
page 201–204, Brussels, BEL. ICST (Institute for
Computer Sciences, Social-Informatics and Telecom-
munications Engineering).
Mileyko, Y., Mukherjee, S., and Harer, J. (2011). Proba-
bility measures on the space of persistence diagrams.
Inverse Problems, 27(12):124007.
Otter, N., Porter, M. A., Tillmann, U., Grindrod, P., and
Harrington, H. A. (2017). A roadmap for the com-
putation of persistent homology. EPJ Data Science,
6(17).
Piangerelli, M., Rucco, M., Tesei, L., and Merelli, E.
(2018). Topological classifier for detecting the emer-
gence of epileptic seizures. BMC Research Notes,
11(1).
Tausz, A., Vejdemo-Johansson, M., and Adams, H. (2014).
JavaPlex: A research software package for persistent
(co)homology, pages 129–136. Lecture Notes in Com-
puter Science 8592. Springer, Berlin.
Uhl, C., Kern, M., Warmuth, M., and Seifert, B. (2020).
Subspace detection and blind source separation of
multivariate signals by dynamical component analy-
sis (dyca). IEEE Open Journal of Signal Processing,
1:230–241.
van Veen, L. and Liley, D. T. J. (2006). Chaos via
Shilnikov’s saddle-node bifurcation in a theory of the
electroencephalogram. Phys. Rev. Lett., 97:208101.
ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics
604