BBBD: Bounding Box Based Detector for Occlusion Detection and Order
Recovery
Kaziwa Saleh
1 a
and Zolt
´
an V
´
amossy
2 b
1
Doctoral School of Applied Informatics and Applied Mathematics,
´
Obuda University, Budapest, Hungary
2
John von Neumann Faculty of Informatics,
´
Obuda University, Budapest, Hungary
Keywords:
Occlusion Handling, Object Detection, Amodal Segmentation, Depth Ordering, Occlusion Ordering, Partial
Occlusion.
Abstract:
Occlusion handling is one of the challenges of object detection and segmentation, and scene understanding.
Because objects appear differently when they are occluded in varying degree, angle, and locations. Therefore,
determining the existence of occlusion between objects and their order in a scene is a fundamental requirement
for semantic understanding. Existing works mostly use deep learning based models to retrieve the order of
the instances in an image or for occlusion detection. This requires labelled occluded data and it is time-
consuming. In this paper, we propose a simpler and faster method that can perform both operations without
any training and only requires the modal segmentation masks. For occlusion detection, instead of scanning the
two objects entirely, we only focus on the intersected area between their bounding boxes. Similarly, we use the
segmentation mask inside the same area to recover the depth-ordering. When tested on COCOA dataset, our
method achieves +8% and +5% more accuracy than the baselines in order recovery and occlusion detection
respectively.
1 INTRODUCTION
Real-world scenes are complex and cluttered, as hu-
mans we observe and fathom them effortlessly even
when objects are not fully visible. We can easily de-
duce that an object is partially hidden by other ob-
jects. For machines, this is a challenging task partic-
ularly if the object(s) are occluded by more than one
object. Nevertheless, for a machine to comprehend its
surrounding, it has to be capable of inferring the order
of objects in the scene, i.e. to determine if the object
is occluded and by which object(s).
Working with occlusion is difficult because an ob-
ject can be hidden by other object(s) in varying ra-
tio, location, and angle. Yet, handling it plays a key
role in the machine perception. Many works in the
recent literature address occlusion in various appli-
cations (Saleh et al., 2021; T
´
oth and Sz
´
en
´
asi, 2020).
The focus is either on detecting and segmenting the
occluded object (Ke et al., 2021) (Zheng et al., 2021),
completing the invisible region (Wang et al., 2021)
(Ling et al., 2020), or depth-ordering (Zhan et al.,
a
https://orcid.org/0000-0003-3902-1063
b
https://orcid.org/0000-0002-6040-9954
2020)(Ehsani et al., 2018).
However, almost all the works in the literature
rely on deep learning based network to retrieve the
amodal mask (the mask for occluded region) of the
object and utilize it for occlusion presence detection
and depth ordering. Although this produces good re-
sults, it is time-consuming and it requires a labelled
occluded dataset which may not be available (Finta
and Sz
´
en
´
asi, 2019).
In this work, we propose a simpler approach.
The method only requires the modal masks and their
bounding boxes which can easily be obtained. In con-
trast to scanning the entire mask of objects to deter-
mine if they occlude each other or not, we only focus
on the intersected area (IA) of the bounding boxes.
We utilize the portion of the mask that falls into this
area. Since we concentrate on a smaller region, our
method is faster and can produce instant results.
Our method called Bounding Box Based Detector
(BBBD) takes the bounding boxes and modal masks
of the instances detected in the image as input, and
outputs a matrix that contains the order of the ob-
jects. By calculating the IA of the bounding boxes
and checking the mask in that area, we infer the exis-
tence of occlusion. The method is tested on COCOA
78
Saleh, K. and Vámossy, Z.
BBBD: Bounding Box Based Detector for Occlusion Detection and Order Recovery.
DOI: 10.5220/0011146600003209
In Proceedings of the 2nd International Conference on Image Processing and Vision Engineering (IMPROVE 2022), pages 78-84
ISBN: 978-989-758-563-0; ISSN: 2795-4943
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

(a) (b) (c)
(d) (e) (f)
Figure 1: Cases considered in BBBD: (a): IA is zero, (b): IA of bounding boxes 1 and 2 is non-zero, however it does not
contain mask from 2, (c) masks from bounding boxes 1 and 2 do not collide inside the IA, (d) bounding boxes 0 and 1 are
inside 2, (e) object in bounding box 0 is the occluder since it has bigger area inside the IA with 2, (f) IA is zero.
(Zhu et al., 2017) dataset, and the achieved results are
higher than the baselines. This makes BBBD suitable
for integration with other deep learning based models,
particularly for occlusion detection.
In summary, this work contributes as follows: 1)
We propose BBBD, a simple and fast method that re-
quires only the bounding boxes and the modal masks
of the objects in an image, to recover the depth or-
der of the objects. 2) By calculating the IA between
bounding boxes and only checking the modal mask
in that area, we can also determine the presence of
occlusion. 3) BBBD can achieve higher accuracy in
order recovery and occlusion detection when com-
pared against the baselines. 4) The method does not
require any training or amodal segmentation mask,
which makes it easier to use.
2 RELATED WORK
Occlusion Detection: Li and Malik in (Li and Ma-
lik, 2016) propose an Iterative Bounding Box Expan-
sion method which predicts the amodal mask by it-
eratively expanding the amodal segmentation in the
pixels whose intensities in the heatmap is above a
threshold. Then by using the predicted modal and
amodal segmentation masks, they compute the area
ratio which shows how much an object is occluded.
Qi et al. in (Qi et al., 2019) propose Multi-Level
Coding (MLC) network that combines the global and
local features to produce the full segmentation mask,
and predicts the occlusion existence through an occlu-
sion classification branch.
Order Recovery: Ehsani et al. (Ehsani et al., 2018)
recover the full mask of an object and use it to infer
the depth order from the depth relation between the
occluder and occludee. In (Yang et al., 2011), authors
propose a layered object detection and segmentation
method in order to predict the order of the detected
objects. (Tighe et al., 2014) predict the semantic label
for each pixel and order the objects based on inferred
occlusion relationship. (Zhan et al., 2020) use a self-
supervised model to partially complete the mask of
objects in an image. For any two neighbouring in-
stances, the object which requires more completion
is considered to be an occludee. (Zhu et al., 2017)
manually annotate a dataset with occlusion ordering
and segmentation mask for the invisible regions. Then
they rely on the amodal mask to predict the depth or-
dering.
In contrast to the above-mentioned methods,
BBBD does not require any training or amodal mask.
It merely relies on the modal mask and the bounding
boxes to retrieve the order of the instances and predict
the existence of occlusion.
3 METHODOLOGY
In this section, we describe how BBBD works. Once
the bounding boxes and the modal segmentation
masks are detected using any off-shelf detector (e.g.
Detectron2 (Wu et al., 2019)), for any two bounding
boxes we find the IA. We can determine that there is
no occlusion if any of these cases were true:
• IA is zero (see cases ’a’ and ’f’ in figure 1).
• IA is non-zero, however, one or both objects’
mask is zero in that area. It means that although
the bounding boxes intersect, the IA does not ac-
tually contain any parts of the object(s) (case ’b’
BBBD: Bounding Box Based Detector for Occlusion Detection and Order Recovery
79

in figure 1).
• IA is non-zero, but the objects’ mask do not col-
lide (case ’c’ in figure 1.
If none of the above cases is true, and IA is non-
zero then we conclude that there is occlusion. In the
case of occlusion presence, we perform the following
checks to obtain the order matrix:
• If one of the bounding boxes is fully contained in
another one, and both masks in that area are non-
zero, then the object with a bigger bounding box
is considered the occludee and the smaller one as
the occluder (case ’d’ in figure 1).
• We count the number of non-zero pixels in each
mask inside the IA, the object with a larger mask
is the occludee (case ’e’ in figure 1).
Algorithm 1 describes BBBD in detail.
4 RESULTS
We compared our method to two baselines, Area (the
bigger object is the occluder, and the smaller is the oc-
cludee), and Y-axis (The instance with larger Y value
is considered to be the occluder) (Zhu et al., 2017).
In the following sections we present the results for
occlusion presence detection and order recovery sep-
arately.
4.1 Occlusion Detection
To test our method in occlusion existence detection,
we relied on the order matrix that we obtained after
the order recovery. The size of the matrix is based
on the number of detected objects in the image. The
value of a cell is ’-1’ if the instance in the correspond-
ing row is occluded by the instance in the column. If
the instance is the occluder, the value in the cell is ’1’.
Otherwise, it is ’0’.
For each instance, if the corresponding row con-
tains no ’-1’ values then we determine that that is no
occlusion for that instance. The values ’0’ or ’1’ show
that the object is either isolated or it is the occluder,
respectively.
The same approach is used to evaluate the results
from the order matrix obtained from the two base-
lines.
The method is tested on COCOA validation set,
which contains the occlusion ratio for 1323 images.
The dataset in total includes 9508 objects, with 4300
negative samples and 5208 positive samples. Table 1
illustrate that BBBD achieves better accuracy in de-
tecting the occlusion presence.
Algorithm 1: Pseudocode for BBBD for occlusion exis-
tence detection and order recovery.
Require: Bounding box and masks of instances in
the image: B
0:N
, and M
0:N
for i ← 0 : N do
for j ← i : N do
OrderMatrix ←a zero matrix with size i × j
IA = B
i
∩ B
j
if IA 6= 0 then
MB
1
and MB
2
← values inside IA region in
M
i
and M
j
MC
1
, MC
2
← number of pixels in MB
1
and
MB
2
if MC
1
or MC
2
= 0 then
skip to the next iteration
end if
if MB
1
and MB
2
do not collide then
skip to the next iteration
end if
if B
i
is inside B
j
then
OrderMatrix[i][ j] ← 1
OrderMatrix[ j][i] ← −1
else if B
j
is inside B
i
then
OrderMatrix[i][ j] ← −1
OrderMatrix[ j][i] ← 1
end if
if MC
1
> MC
2
then
OrderMatrix[i][ j] ← 1
OrderMatrix[ j][i] ← −1
else if MC
1
< MC
2
then
OrderMatrix[i][ j] ← −1
OrderMatrix[ j][i] ← 1
end if
end if
end for
end for
return OrderMatrix
Table 1: Accuracy and precision results for the occlusion
detection.
BBBD Y-axis Area
Accuracy 73.05% 68.56% 65.16%
Precision 78.49% 70.09% 66.50%
Recall 69.99% 74.33% 73.31%
As the results of occlusion detection depend on
the order matrix, any false prediction in the occlu-
sion order leads to false outcomes of occlusion de-
tection. This explains the results from table 2. The ta-
ble shows that BBBD has less true positive and more
false negative predictions by only 2.4% and 1.8%
compared to Y-axis and Area algorithms, respectively.
However, it has less false positive and more true nega-
tive predictions by 6.9% and 9.7% compared to Y-axis
IMPROVE 2022 - 2nd International Conference on Image Processing and Vision Engineering
80

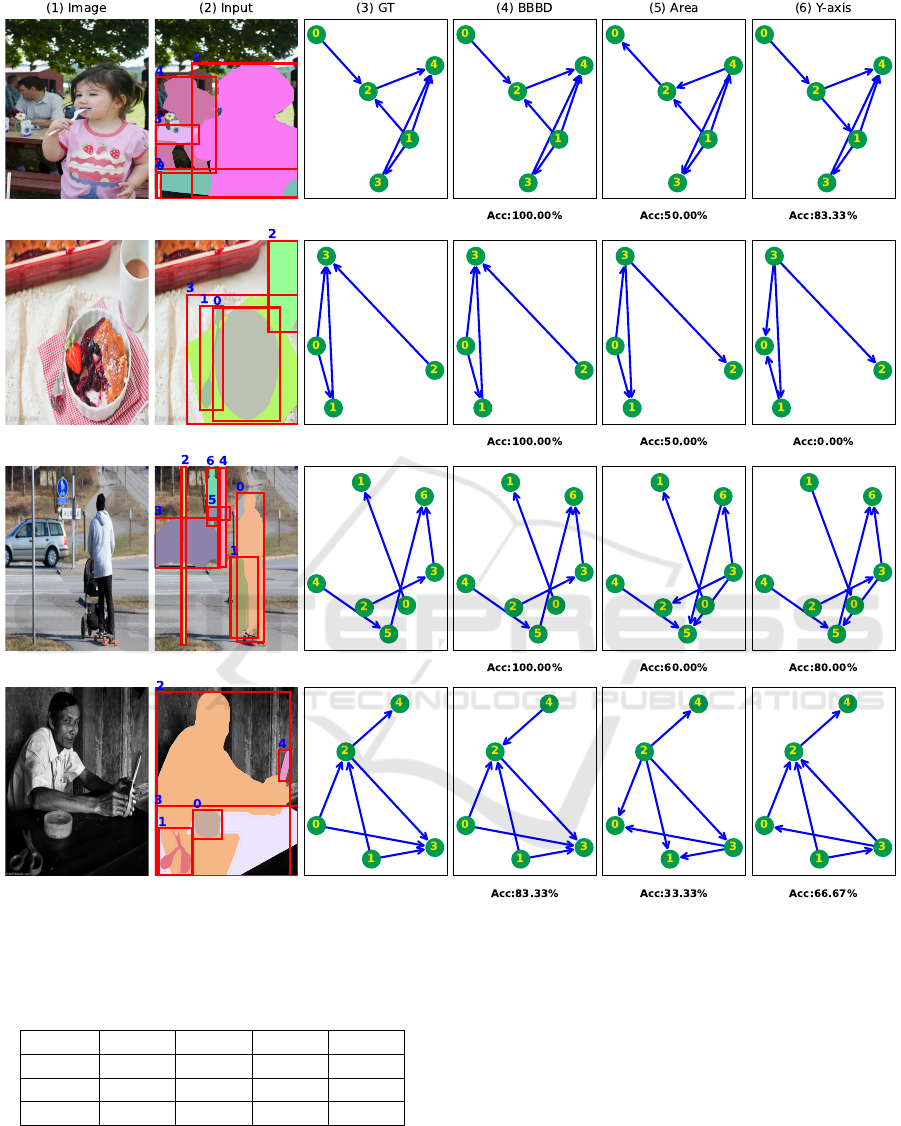
Figure 2: Results for the order recovery. The nodes depict the detected objects. The directed edges show the occlusion
relationship between the objects. The occludee and the occluder are described by the source and the target nodes, respectively.
Table 2: Confusion matrix for the occlusion detection. The
percentage is calculated from the total of 9508 objects.
TP FP TN FN
BBBD 38.3% 10.5% 34.7% 16.4%
Y-axis 40.7% 17.4% 27.9% 14.1%
Area 40.2% 20.2% 25.0% 14.6%
and Area algorithms, respectively.
4.2 Order Recovery
The results in the obtained order matrix are evaluated
against the ground truth order matrix from COCOA
validation dataset. Table 3 illustrates that our method
surpasses the baselines. Figure 2 visualizes the or-
der matrix from BBBD and the baselines (the plots
are created by heavily building on the GitHub repos-
itory of (Zhan et al., 2020)’s paper). Similarly, figure
3 shows that our method achieves acceptable results
even in cluttered scenes.
BBBD: Bounding Box Based Detector for Occlusion Detection and Order Recovery
81

Figure 3: Results for crowded scenes.
Table 3: Accuracy results for the order recovery.
BBBD Y-axis Area
69.53% 65.43% 61.36%
4.3 Limitations
Although the previous results shows that BBBD can
give higher accuracy compared to the baselines, in
some cases the method does not perform as well as
expected. Occlusion ordering by comparing the area
inside the IA does not always produce correct out-
put. Since the two tasks of depth ordering and occlu-
sion detection are related, the result of one affects the
other. And because there is no other method to eval-
uate the result of occlusion detection, we had to rely
on order matrix to assess the accuracy. Otherwise, we
believe the results would have been higher for occlu-
sion detection. Figure 4 shows some examples where
our method fails to give correct predictions.
5 CONCLUSIONS
Due to the significance of occlusion handling in ma-
chine vision, determining the occlusion ordering and
predicting its presence is essential. These two tasks
are related and depend on each other. In this paper, we
presented a simple and fast method that can deduce
the existence of occlusion between objects in a scene
and retrieve their ordering. The method depends only
on the bounding box and the modal masks of the ob-
jects. From the quantitative results we conclude that
BBBD has higher accuracy than its baselines. The
method is simple to implement as it does not require
any training. However, it can easily be integrated and
used with other deep learning methods. Therefore, in
the future we plan to use this approach with a trained
model to retrieve the occlusion order to obtain opti-
mal results.
IMPROVE 2022 - 2nd International Conference on Image Processing and Vision Engineering
82

Figure 4: Results where our algorithm fails.
ACKNOWLEDGEMENTS
We acknowledge the support of the Doctoral School
of Applied Informatics and Applied Mathematics at
the
´
Obuda University, both research groups: the
GPGPU Programming and the Applied Machine
Learning at the
´
Obuda University, and the ’2020-
1.1.2-PIACI-KFI-2020-00003’ project.
We would also like to thank NVIDIA Corporation
for providing graphics hardware through the CUDA
Teaching Center program. On the behalf of ”Occlu-
sion Handling in Object Detection”, we thank the us-
age of ELKH Cloud (https://science-cloud.hu/) that
significantly helped us achieving the results published
in this paper.
REFERENCES
Ehsani, K., Mottaghi, R., and Farhadi, A. (2018). Segan:
Segmenting and generating the invisible. In Proceed-
ings of the IEEE conference on computer vision and
pattern recognition, pages 6144–6153.
Finta, I. and Sz
´
en
´
asi, S. (2019). State-space analysis of
the interval merging binary tree. Acta Polytech. Hung,
16:71–85.
Ke, L., Tai, Y.-W., and Tang, C.-K. (2021). Deep occlusion-
aware instance segmentation with overlapping bilay-
ers. In Proceedings of the IEEE/CVF Conference
on Computer Vision and Pattern Recognition, pages
4019–4028.
Li, K. and Malik, J. (2016). Amodal instance segmentation.
In Leibe, B., Matas, J., Sebe, N., and Welling, M.,
editors, Computer Vision – ECCV 2016, pages 677–
693, Cham. Springer International Publishing.
Ling, H., Acuna, D., Kreis, K., Kim, S. W., and Fidler,
S. (2020). Variational amodal object completion.
Advances in Neural Information Processing Systems,
33:16246–16257.
Qi, L., Jiang, L., Liu, S., Shen, X., and Jia, J. (2019).
Amodal instance segmentation with kins dataset. In
Proceedings of the IEEE/CVF Conference on Com-
puter Vision and Pattern Recognition, pages 3014–
3023.
Saleh, K., Sz
´
en
´
asi, S., and V
´
amossy, Z. (2021). Oc-
clusion handling in generic object detection: A re-
view. In 2021 IEEE 19th World Symposium on Ap-
plied Machine Intelligence and Informatics (SAMI),
pages 477–484.
BBBD: Bounding Box Based Detector for Occlusion Detection and Order Recovery
83

Tighe, J., Niethammer, M., and Lazebnik, S. (2014). Scene
parsing with object instances and occlusion ordering.
In Proceedings of the IEEE Conference on Computer
Vision and Pattern Recognition, pages 3748–3755.
T
´
oth, B. T. and Sz
´
en
´
asi, S. (2020). Tree growth simulation
based on ray-traced lights modelling. Acta Polytech-
nica Hungarica, 17(4).
Wang, H., Liu, Q., Yue, X., Lasenby, J., and Kusner, M. J.
(2021). Unsupervised point cloud pre-training via oc-
clusion completion. In Proceedings of the IEEE/CVF
International Conference on Computer Vision (ICCV),
pages 9782–9792.
Wu, Y., Kirillov, A., Massa, F., Lo, W.-Y., and Girshick, R.
(2019). Detectron2.
Yang, Y., Hallman, S., Ramanan, D., and Fowlkes, C. C.
(2011). Layered object models for image segmenta-
tion. IEEE Transactions on Pattern Analysis and Ma-
chine Intelligence, 34(9):1731–1743.
Zhan, X., Pan, X., Dai, B., Liu, Z., Lin, D., and Loy, C. C.
(2020). Self-supervised scene de-occlusion. In Pro-
ceedings of the IEEE/CVF Conference on Computer
Vision and Pattern Recognition, pages 3784–3792.
Zheng, C., Dao, D.-S., Song, G., Cham, T.-J., and Cai, J.
(2021). Visiting the invisible: Layer-by-layer com-
pleted scene decomposition. International Journal of
Computer Vision, 129(12):3195–3215.
Zhu, Y., Tian, Y., Metaxas, D., and Doll
´
ar, P. (2017).
Semantic amodal segmentation. In Proceedings of
the IEEE conference on computer vision and pattern
recognition, pages 1464–1472.
IMPROVE 2022 - 2nd International Conference on Image Processing and Vision Engineering
84