Candle Flame Simulation Considering Temperature Change in the

Environment

Nobuhiko Mukai

1,2 a

, Reina Arai

and Youngha Chang

Knowledge Engineering, Tokyo City University, 1-28-1 Tamazutsumi, Setagaya, Tokyo 158-8557, Japan

Institute of Industrial Science, The University of Tokyo, 4-6-1 Komaba, Meguro, Tokyo, 153-8505, Japan

Keywords:

Fluid Dynamic Simulation, Particle Method, SPH, Candle Flame.

Abstract:

Fire simulations are utilized in many scenes such as explosion and conﬂagration in movies or games, and a lot

of techniques have been developed. Some are used to control the ﬂame shape for animations, and others are for

real and real-time visualizations. In fact, the ﬂame color changes according to the combustion states: complete

combustion, incomplete combustion, and non-combustion. Almost all previous studies, however, performed

ﬂame simulations considering only one state of incomplete combustion. Then, we have been researching

the candle ﬂame visualization considering three combustion states, and the color changed depending on the

combustion state. However, the candle ﬂame length was too short in the previous method. Therefore, we

propose a method to consider the temperature change that affects the air density in the environment. The

change of the environmental air density induces the external force, which makes the shape of the candle ﬂame.

As the result of the simulation, the candle ﬂame shape has become thinner than before and has been similar to

that of a real candle ﬂame.

1 INTRODUCTION AND

RELATED WORKS

It is said that human is the only animal who can treat

ﬁre, and this speciﬁc character differentiates human

beings from other animals. Fire is very familiar to

us and important in our daily life. In TV dramas,

movies, and games, there are many scenes where the

ﬁre appears such as explosions and conﬂagrations;

however, ﬁre is also dangerous so careful attention

should be paid when it is treated. Then, some scenes

are generated by using computer graphics instead of

real videos; however, it is difﬁcult to create realistic

movies by controlling the ﬂame because the shape

changes dynamically according to the environment

such as wind, obstacles, and ﬂammable materials.

With these backgrounds, there are many kinds

of previous research related to ﬁre. For example,

(Louchez et al., 2006) proposed a model to simulate

and represent a candle ﬂame by solving the Navier-

Stokes equations with a particle method, and de-

cided the shape as the NURBS (Non-Uniform Ratio-

nal B-Spline) surface that is deﬁned with particle po-

sitions. The ﬂame shape was physically correct; how-

https://orcid.org/0000-0001-8909-9454

ever, artists could not control the shape of the ﬁre.

Then, (Bangalore and House, 2012) enabled artists to

draw ﬁre paintings freely. Their approach was based

on the physical simulation; however, the individual

ﬂames were drawn along the curve that artists speci-

ﬁed by controlling the direction of the gravity and the

buoyancy. (Sato et al., 2017) also proposed a feed-

back control method for users to design a ﬁre shape

with control points. Their method employed a PID

(Proportional Integral Derivative) controller to adjust

the force and the temperature. In addition, (Hladk

2018) proposed a system, with which users could con-

trol the ﬁre. Their method extended the Navier-Stokes

equations by considering the wind ﬁeld, the diffusion,

the source motion, and the buoyancy terms, and the

in-between images were generated based on the hand-

drawn keyframes.

On the other hand, there are some particle-based

researches related to the simulations and the rendering

techniques of ﬁre since it requires a lot of particles and

computational resources to simulate and visualize the

ﬂame of ﬁre. (Wei et al., 2002) employed the LBM

(Lattice Boltzmann Model) for physically-based sim-

ulation, and used textured splats for the rendering.

(Horvath and Geiger, 2009) also proposed a GPU-

based volume rendering method. Their method used

Mukai, N., Arai, R. and Chang, Y.

Candle Flame Simulation Considering Temperature Change in the Environment.

DOI: 10.5220/0011166100003274

In Proceedings of the 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2022), pages 36-43

ISBN: 978-989-758-578-4; ISSN: 2184-2841

the combination of the coarse particle grid simulation,

and the ﬁne and view-oriented reﬁnement simulation.

In the method, the multiple independent GPUs reﬁned

the ﬁnal simulation for the rendering. In addition,

(Cha et al., 2009) used pre-calculated CFD (Com-

putational Fluid Dynamics) data to generate the ﬁre

scene and developed a ﬁreﬁghter training simulator.

On the other hand, (Guay et al., 2011) proposed an

animation method to generate direct 2D images with-

out 3D simulations by considering the 2.5D velocity

ﬁeld. (Sato et al., 2012) also proposed a method that

generated high-resolution 3D animations from low-

resolution ﬂuid simulations. Their database was con-

structed with only 2D ﬂuid simulation results, and the

low-resolution 3D simulation was performed based

on the database, and the simulation results were con-

verted to high-resolution animations.

As mentioned above, there is a lot of research on

the simulation and the visualization of ﬁre, which

aim is to control the shape or to generate the im-

ages rapidly, and these methods are based on physi-

cal simulations. (Nguyen et al., 2002) also proposed a

method for the physically-based modeling and the an-

imation of ﬁre. They used the incompressible Navier-

Stokes equations and considered vaporized fuels and

hot gaseous products. They also rendered the simula-

tion results with a blackbody radiation model and rep-

resented the blue core in the chemical reaction zone.

(Hamins and Bundy, 2005) simulated a candle ﬂame

with CFD (Computational Fluid Dynamics) model

considering mass burning rate, candle regression rate,

ﬂame height, and heat ﬂux obtained by their experi-

ments. (Ogunedo and Okoro, 2017) also performed

CFD ﬂow simulation on a candle ﬂame considering

burning velocity, ﬂame thickness, fuel ﬂow rate, mass

consumption rate, view factor, and heat ﬂux.

However, they did not consider the combustion

states. In fact, the ﬂame color depends on the combus-

tion states, which are divided into three kinds: com-

plete combustion, incomplete combustion, and non-

combustion. In addition, the combustion states de-

pend on the physical property of the ﬂammable mate-

rials. Then, (Mukai et al., 2019) proposed a method

to simulate a candle ﬂame by estimating the physical

property of the material and to visualize the results

by discriminating the combustion states. However,

the result of the previous method showed a candle

ﬂame whose length was too short compared to that

of a real candle. Therefore, this paper proposes a new

method to simulate and visualize a candle ﬂame by

considering the temperature change in the environ-

ment because the temperature change affects the ex-

ternal force that elongates the candle ﬂame.

2 CANDLE FLAME

2.1 Combustion States

Flame is divided into two types: premixed ﬂame and

diffusion ﬂame. Premixed ﬂame appears when the

fuel gas and the air is uniformly premixed where the

composition of the materials, the density, and the tem-

perature are almost constant, while diffusion ﬂame is

generated as the fuel gas diffuses being mixed with

the air when the combustion states are different and

depend on the mixture ratio of the fuel gas and the air.

The combustion states of the diffusion ﬂame are di-

vided into three types: complete combustion, incom-

plete combustion, and non-combustion. The color of

the premixed ﬂame is almost constant blue although

the intensity is partly different, while the color of the

diffusion ﬂame is different according to the combus-

tion states. The combustion states of a candle are

shown in Fig. 1. Non-combustion and the wick of the

candle are not ﬁred so that the color is black, and the

color of the incomplete combustion is almost orange

or yellow, while the color of the complete combustion

looks blue; however, it depends on the material and is

decided by ion excitation.

Figure 1: Combustion states of a candle ﬂame.

2.2 Candle Property

The primary component of a candle is parafﬁn wax,

which is the generic name of linear alkane and the

chemical formula is C

2n+2

(20 ≤ n ≤ 40); how-

ever, the composition is not clear. Then, this paper

supposes that a candle is composed of only Icosane,

which is the simplest material of linear alkanes, and

the formula is C

. Even if we assume that a can-

dle is composed of only Icosane, there are a lot of

unknown things that we have to estimate for the simu-

lation. The chemical formula of complete combustion

for Icosane is as follows.

+ 61O

→ 40CO

+ 42H

O (1)

On the other hand, the air is composed of 78% Ni-

trogen (N

), 21% Oxygen (O

), and 1% others. Then,

Candle Flame Simulation Considering Temperature Change in the Environment

in Eq. (1), 61O

is replaced with 290Air as follows

since 290 Air includes 61(= 290 × 0.21) Oxygen.

+ 290Air → 40CO

+ 42H

O (2)

Then, the volume ratio of complete combustion

for Icosane is 0.68 (=2/(2+290)) [vol%] since the vol-

ume ratio equals the mole ratio. This means that if the

volume ratio of the fuel gas is more than 0.68 [vol%],

the combustion state is incomplete because oxygen is

not enough for the fuel gas.

On the other hand, if the volume ratio of the fuel

gas is less than the threshold, the combustion state

becomes non-combustion since the fuel gas is not

enough. Then, the lower and the upper explosive lim-

its of the combustion state is necessary for the sim-

ulation. However, the lower and the upper explosive

limits of combustion states for Icosane are unknown.

Then, they should be estimated from the simpler ma-

terials of linear alkane, which lower and upper explo-

sive limits are shown in Table 1 (Nassimi et al., 2017).

Table 1: Lower and upper explosive limits of linear alkane.

[vol%]

Material Formula # of Lower Upper

Carbon limit limit

Methane C

1 5.00 15.00

Ethane C

2 3.00 12.40

Propane C

3 2.10 9.50

Butane C

4 1.80 8.40

Pentane C

5 1.40 7.80

Hexane C

6 1.20 7.40

Heptane C

7 1.05 6.70

Octane C

8 0.92 6.50

Nonane C

9 0.80 6.00

Decane C

10 0.70 5.00

In addition, Fig. 2 shows the approximate curves

of the lower and the upper explosive limits for lin-

ear alkanes and Icosane that carbon number is 20, and

the lower and the upper explosive limits for Icosane

are estimated as 0.02 [vol%] and 1.35 [vol%], respec-

tively, from the extrapolation of the graph.

Then, the combustion states are summarized as

shown in Table 2.

Table 2: Volume ratios and combustion states of Icosane.

Volume ratio r [vol%] Combustion state Burnable

r < 0.02 non-combustion no

0.02 ≤ r < 0.68 complete yes

0.68 ≤ r < 1.35 incomplete yes

1.35 ≤ r non-combustion no

Figure 2: Approximate curves for the lower and the upper

explosive limits.

2.3 Viscosity

The viscosity of a fuel gas changes depending on the

material and the temperature. The viscosity of a mate-

rial can be calculated with Sutherland’s formula (CF-

DOnline, 2022), which is written in Eq. (3).

µ =

T +C

, (3)

where, µ is the viscosity, T is the absolute tempera-

ture, C

and C

are the constants that depend on the

material.

Then, if C

and C

are decided, the viscosity at

the speciﬁc temperature can be calculated. However,

the relationship between the viscosity and the temper-

ature of Icosane is unknown. Then, it should be esti-

mated with the simpler linear alkane, which viscosity

for the temperature is shown in Table 3.

Table 3: Viscosity of the simpler linear alkane.

[×10

−2

mPa · s]

Material # of Temperature [

◦

C 0 20 50 100 200

Methane 1 1.02 1.08 1.18 1.33 1.47

Ethane 2 0.86 0.92 1.01 1.15 1.43

Propane 3 0.75 0.80 0.88 1.01 1.25

Hexane 6 0.60 0.65 0.71 0.82 1.04

Fig. 3 shows the approximate curves estimated

from Table 3, and the viscosity of Icosane, which car-

bon number is 20, can be estimated with Fig. 3.

Fig. 4 shows the relationship between the absolute

temperature and the viscosity of Icosane, which is es-

timated by plotting all points at 20 on x axis in Fig. 3.

With Fig. 4, we can estimate the viscosity from the

absolute temperature, and calculate the constants of

Sutherland’s formula, C

and C

, which are decided

SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

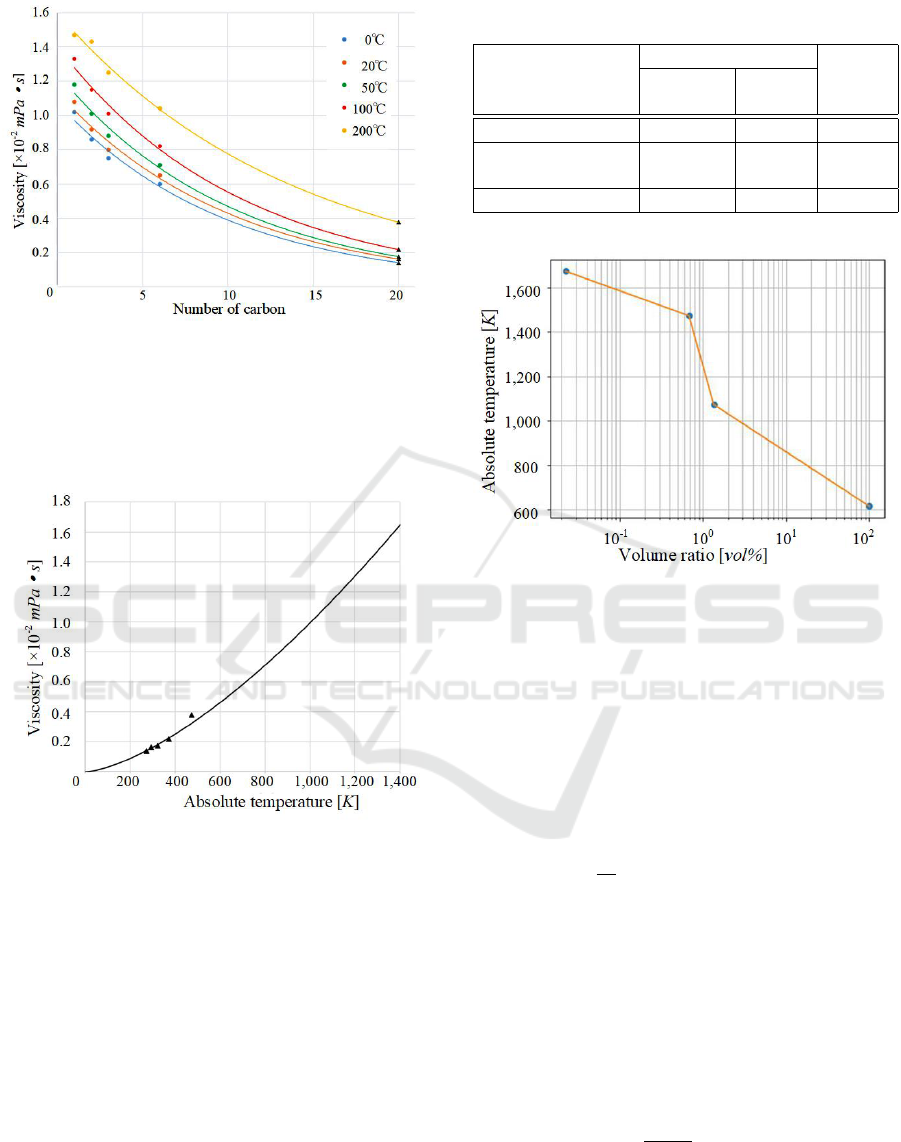
Figure 3: Approximate curves of the viscosity for simpler

linear alkanes.

as 6.95 × 10

and 2.21 × 10

, respectively. In Fig. 4,

the horizontal axis is absolute temperature [K], which

is calculated by adding 273.15 to Celsius degree [

◦

C].

Figure 4: Relationship between the absolute temperature

and the viscosity of Icosane.

The viscosity of Icosane is calculated from its

temperature with Fig. 4. On the other hand, com-

bustion states are decided by the volume ratio. Then,

the relationship between the volume ratio and the tem-

perature is necessary. Table 4 shows the relationship

between combustion states and the limit temperature

of a candle ﬂame (ExplainThatStuff, 2022), where the

volume ratios are added according to Table 2. In addi-

tion, the boiling point of Icosane is 615.85 [K], which

volume ratio is 100 [vol%]. Then, Fig. 5 is obtained

by plotting all data, and shows the relationship be-

tween the volume ratio and the absolute temperature

based on Table 4 and the boiling point of Icosane.

Table 4: Relationship between combustion states and limit

temperatures.

Temperature Volume

Combustion State Absolute Celsius ratio

[K] [

◦

C] [vol%]

Complete (max) 1,673.15 1,400 0.02

Complete (min) 1,473.15 1,200 0.68

Incomplete (max)

Incomplete (min) 1,073.15 800 1.35

Figure 5: Relationship between volume ratio and absolute

temperature of Icosane.

3 METHOD

3.1 Governing Equations

We employ SPH (Smoothed Particle Hydrodynamics)

method for the simulation, and the governing equation

is the Navier-Stokes equations written in Eq. (4).

∂⃗u

∂t

= −∇p + η∇

⃗u +

⃗

f , (4)

where, ρ is the density, ⃗u is the velocity, t is the time,

p is the pressure, η is the viscosity coefﬁcient,

⃗

f is the

external force.

Here, the density ρ(⃗x

) at the position of ⃗x

is cal-

culated as follows (Ertekin, 2015).

ρ(⃗x

∑

j̸=i

(⃗x

−⃗x

)

∑

j̸=i

315

64πr

− |⃗x

−⃗x

)

, (5)

where, m

is the mass of a particle j, W

is the kernel

function of the density, r

is the radius of inﬂuence,

and only ⃗x

within r

for ⃗x

is counted.

Candle Flame Simulation Considering Temperature Change in the Environment

Next, the pressure and the viscous terms at the po-

sition of ⃗x

are calculated as follows (Ertekin, 2015).

−∇p =−

∑

j̸=i

+ p

2ρ

∇W

(⃗x

−⃗x

)

=−

∑

j̸=i

+ p

2ρ

πr

− |⃗x

−⃗x

(⃗x

−⃗x

)

|⃗x

−⃗x

(6)

η∇

⃗u = η

∑

j̸=i

⃗u

−⃗u

∇

(⃗x

−⃗x

)

= η

∑

j̸=i

⃗u

−⃗u

πr

− |⃗x

−⃗x

|), (7)

where, W

and W

are the kernel functions of the pres-

sure and the viscosity, respectively.

The density ρ(⃗x

) at the position of ⃗x

is calcu-

lated with Eq. (5), and suppose that the density of

the ﬂammable material that has only the fuel gas and

no air is ρ

max

. Then, the volume ratio of a particle i,

which position is ⃗x

, is calculated as follows.

ρ(⃗x

)

max

(8)

Then, the absolute temperature of a particle is es-

timated from the volume ratio with Fig. 5, and the

viscosity (η) of the particle at the temperature is de-

rived from Fig. 4.

At last, gravity, buoyancy, and environmental air

pressure are considered as an external force. The

buoyancy works for the fuel gas and the air in the

combustion state. Then, the force that drives the

buoyancy is calculated as follows.

⃗

= (ρ

− ρ

⃗g + (ρ

− ρ

⃗g, (9)

where, ρ

, ρ

, V

, and V

are the densities and the

volumes of the fuel gas and the air in the combustion

state, respectively. ρ

is the density of the air that is

placed in the environment, which has the room tem-

perature (298.15 [K] = 25 [

◦

C]), and ⃗g is the gravity.

The environmental air pressure is calculated with

the following equation (Ueda and Fujishiro, 2014).

⃗

=−α∇p

=−α

∑

j̸=i

− p

)

∇W

(⃗x

−⃗x

)

=−α

∑

j̸=i

− p

)

πr

− |⃗x

−⃗x

(⃗x

−⃗x

)

|⃗x

−⃗x

(10)

= ρ

, (11)

where, R and T

are the coefﬁcient of the ideal gas

and the temperature of the environmental air, which is

298.15 [K] (=25 [

◦

C]), respectively, and α is the ad-

justment factor for the simulation, and 0.01 is used in

the simulation according to the experimental results.

Finally, the external force

⃗

f in Eq. (4) becomes as

follows.

⃗

f = (ρ

+ ρ

)⃗g +

⃗

(12)

Here, the ﬁrst term of the right-hand side is the

gravity for the fuel gas and the air.

3.2 Temperature Change

In Eq. (11), p

can be assumed as 1.0 [atm] (= 0.1

[MPa]), and R is the coefﬁcient of the ideal gas that

has the value (8.3145 [J/(mol · K)]). This means that

the air density in the environment (ρ

) can be calcu-

lated with the temperature in the environment (T

which depends on the distance from the wick of the

candle. The candle ﬂame is vertically long, while it

is short in the horizontal direction. Then, the temper-

ature change in the vertical direction from the wick

of the candle is needed for the density calculation of

the air. However, the particles of the air in the en-

vironment are not arranged, although the particles of

the fuel gas are arranged considering the memory re-

sources and the calculation time because a lot of par-

ticles are necessary for the simulation in the particle

method. Then, the temperature of the air in the envi-

ronment must be estimated.

The temperature in the position at 10 [cm] (= 100

[mm]) in the vertical direction from the bottom of the

candle ﬂame was measured experimentally as 298.15

[K] (= 25 [

◦

C]) that is the environmental tempera-

ture, while the temperature at the position in the hor-

izontal direction was 298.15 [K] (= 25 [

◦

C]) even if

the position was near the candle ﬂame. Then, we

can estimate the air temperature in the vertical di-

rection with interpolation between the wick of the

candle and the position at 10 [cm] from the wick.

Here, the temperature of the wick of the candle was

1,262.44 [K] in the simulation, although the average

temperature of the incomplete state is 1.273.15 [K] (=

(1,073.15 + 1,473.15)/2[K]).

In addition, a lot of particles are needed for the

precise simulation, and in this paper, the size of the

candle is 1/4 of that in the previous research (Mukai

et al., 2019) for more precise simulation. Then,

the interpolation equation of the temperature in the

vertical direction becomes as follows.

SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

[K] =







1,262.44[K] −

1,262.44[K]−298.15[K]

100[mm]/4

(0 ≤ d ≤ 25)

298.15[K] (Otherwise),

(13)

where, d is the distance in the vertical direction from

the wick of the candle, which unit is [mm].

4 SIMULATION AND

RENDERING

The simulation algorithm is as follows.

< Simulation Algorithm >

1. Initialization: Set parameters and place particles

around the wick of the candle.

2. Density calculation: Calculate the particle density

with Eq. (5).

3. Pressure term calculation: Calculate the pressure

term with Eq. (6).

4. Volume ratio calculation: Calculate the volume

ratio with Eq. (8).

5. Temperature decision: Decide the particle temper-

ature from the volume ratio with Fig. 5.

6. Viscosity decision: Decide the particle viscosity

at the temperature with Fig. 4.

7. Viscosity term calculation: Calculate the viscosity

term with Eq. (7).

8. Environmental temperature calculation: Estimate

the environmental air temperature with Eq. (13).

9. External force term calculation: Calculate the ex-

ternal force with Eq. (12).

10. Particle position calculation: Calculate the accel-

eration, the velocity, and the position of a particle

by solving Eq. (4).

11. Particle addition and removal: Add particles at the

wick of the candle and remove particles that have

burned out in the environment of the candle.

12. Rendering: Render the particles with the volume

rendering method, which is described in the fol-

lowing.

13. Repeat the simulation from 2.

The simulation is performed with a particle

method; however, the number of particles is not

enough for the rendering. Then, the volume render-

ing method is employed to represent a candle ﬂame

by interpolating the density of each voxel in the grid.

The rendering algorithm is as follows.

< Rendering Algorithm >

1. Grid space decision: Set the gird space that in-

cludes all particles, and expands it from the outer-

most positions by the radius of inﬂuence.

2. Voxel size: Set the voxel size as 1.1 times the par-

ticle diameter.

3. Density set: Set each voxel density. If there are

some particles in a voxel, set the average as the

density of the voxel. If there is no particle in a

grid, set the density with IDW (Inverse Distance

Weighting) interpolation (GISGeography, 2022),

which is calculated with Eqs. (14) and (15).

The density is interpolated with the following equa-

tions.

ρ(⃗x)=

∑

i=1

(⃗x)ρ(⃗x

)

∑

j=1

(⃗x)

, (14)

(⃗x)=

d(⃗x,⃗x

)

, (15)

ρ(⃗x) is the density of the voxel at the position of ⃗x ,

d(⃗x,⃗x

) is the distance between the voxel at the posi-

tion of ⃗x and the particle at the position of ⃗x

, and p is

the order of the distance, which is 1 in this simulation.

N is the number of particles that are within the radius

of inﬂuence for the center of the voxel at the position

of ⃗x.

5 RESULTS

The simulation was performed with the PC, which

speciﬁcation is shown in Table 5. The grid size for

the volume rendering changes dynamically according

to the number of particles and the space the particles

occupy. The maximum grid size was 65 × 65 × 65 =

274,625.

Table 5: Speciﬁcation of the PC used for the simulation.

OS Windows 10 Education 64 bits

CPU Intel Core i5-6400

Memory 8GB

GPU NVIDIA GeForce GTX 1060

with 6 GB memory

Table 6 shows the comparison of the parameters

between the previous simulation (Mukai et al., 2019)

and the proposed one. The environmental air temper-

ature was 298.15 [K] (= 25 [

◦

C]).

The ﬂame color in the incomplete combustion

state is decided with the linear interpolation accord-

ing to Table 7, which shows the color of the blackbody

Candle Flame Simulation Considering Temperature Change in the Environment

Table 6: Comparison of the simulation parameters.

Parameters Previous Proposed

Particle radius 125 [µm] 31.25 [µm]

Grid size 125 [µm] 37.50 [µm]

Time steps 800 1,000

Real time per step 1.25 [µs] 0.3125 [µs]

radiation (MitchellCharity, 2022). The temperature in

the incomplete combustion state is between 1,073.15

[K] and 1,473.15 [K] according to Table 4.

Table 7: Candle ﬂame color.

Temperature [K] R G B

1,000 255 56 0

1,200 255 83 0

1,400 255 101 0

1,600 255 115 0

1,673 255 120 0

On the other hand, the ﬂame color in the com-

plete combustion state is decided by ion excitation,

and there is no reference on it. Then, the color is

picked from the photograph of a real candle and de-

cided as (94, 232, 255) in (R, G, B) color space.

Fig. 6 shows the simulation results of a candle

ﬂame. The left side images are the results in the pre-

vious simulation (Mukai et al., 2019), while the right

side images are the results in the proposed method. In

the simulation, spontaneous combustion at the wick

of the candle is supposed. In Fig. 6, the size of this

simulation is 1/4 of the previous one so the images on

the right side are smaller than those on the left side.

The shape of the ﬂame on the right side is, however,

thinner than that on the left side and the ﬂame is ver-

tically elongated because the proposed method calcu-

lates the external force

⃗

in Eq. (10) by considering

the temperature change in the environment with the

Eq. (13).

In addition, Fig. 7 shows the comparison of the

simulation result with a real candle ﬂame. Fig. 7 (a)

shows the simulation results of the proposed method

at the time step of 1,000, while Fig. 7 (b) shows a

real candle ﬂame. The shape of the ﬂame in (a) is

similar to that in (b), and the color at the bottom of

the ﬂame is orange in both (a) and (b); however, the

color at the tip of the ﬂame in (a) is orange, while that

in (b) is yellow, which means the temperature in the

simulation is lower than that in the real candle. In ad-

dition, the color at the center of the ﬂame in (a) is yel-

low, which means that the temperature of the center

is higher than that of the surroundings in the simula-

tion result (a), while the temperature of the center is

lower than that of the surroundings in the real candle.

Figure 6: Comparison of the results between the previous

and the proposed methods.

In real combustion, oxygen in the center of the candle

is less than that in the surroundings, and the state is

incomplete combustion so that the temperature in the

center is lower than that in the surroundings. On the

other hand, the surroundings of the ﬂame have plenty

of oxygen so that the state is the complete combus-

tion, and the temperature is high although the blue

color that indicates the complete combustion is not

seen in the real candle because the color of the back-

ground is black, while the tip and the bottom of the

ﬂame in (a) have slight blue color that indicates the

complete combustion.

Figure 7: Comparison with a real candle ﬂame.

SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

6 CONCLUSIONS

Fire is very familiar to human beings and there are

many scenes using ﬁre in movies, games, and so on.

Then, a lot of studies have been performed to simulate

and visualize ﬁre. Some of them are on controlling

the shape by users, and others are methods to repre-

sent realistic ﬁre in real time. However, most previous

works treated the ﬁre only in the incomplete combus-

tion state without the complete combustion. In addi-

tion, the most familiar ﬁre is a candle ﬂame; however,

the component of a candle is unknown although the

material is parafﬁn.

Then, we proposed a method to simulate and vi-

sualize the candle ﬂame with a particle method by

considering the three states of combustion: com-

plete combustion, incomplete combustion, and non-

combustion in the previous method. We also assumed

that the candle is composed of only one material of

“Icosane”, and estimated the viscosity that depends

on the absolute temperature, which also depends on

the volume ratio of the fuel gas. However, the ﬂame

shape of the simulation result in the previous method

was not similar to that of a real candle. Then, in this

paper, we have proposed a new method to simulate

the candle ﬂame by interpolating the environmental

air temperature, which affects the density of the envi-

ronmental air that changes the external force.

As the comparison of the simulation results be-

tween the previous and the proposed methods, the

shape of the ﬂame in the proposed method was thin-

ner than that of the previous method and was elon-

gated vertically. It was similar to the ﬂame of the real

candle, and the overall color was also similar.

However, the color of the surroundings in the sim-

ulation result was orange, while the color of the area

in the real candle ﬂame was yellow. In addition, the

temperature at the center of the simulated ﬂame was

higher than that in the surroundings, while the tem-

perature at the surroundings was higher than that at

the center in the real candle ﬂame. Then, we plan to

investigate the reasons for these differences and con-

sider the more precise simulation method in the fu-

ture.

REFERENCES

Bangalore, A. and House, D. H. (2012). A technique for art

direction of physically based ﬁre simulation. In The

8th Annual Symposium on Computational Aesthetics

in Graphics, Visualization, and Imaging,pages 45–54.

CFDOnline (Referenced in March 2022). Sutherland’s law.

https://www.cfd-online.com/Wiki/Sutherland’s law.

Cha, M., Lee, J., Choi, B., Lee, H., and Han, S. (2009). A

data-driven visual simulation of ﬁre phenomena. In

ACM SIGGRAPH Posters, page Article No.74.

Ertekin, B. (2015). Fluid Simulation using Smoothed Parti-

cle Hydrodynamics. Bournemouth University.

ExplainThatStuff (Referenced in March 2022). The science

of candles. https://www.explainthatstuff.com/candles.

html.

GISGeography (Referenced in March 2022).

Inverse distance weighting (IDW) in-

terpolation. https://gisgeography.com/

inverse-distance-weighting-idw-interpolation.

Guay, M., Colin, F., , and Egli, R. (2011). Screen space

animation of ﬁre. In ACM SIGGRAPH Asia Sketches,

page Article No.10.

Hamins, A. and Bundy, M. (2005). Characterization of can-

dle ﬂames. Journal of Fire Protection Engineering,

15:265–285.

Hladk

y, J. (2018). Fire simulation in 3d computer anima-

tion with turbulence dynamics including ﬁre separa-

tion and proﬁle modeling. International Journal of

Networking and Computing, 8(2):186–204.

Horvath, C. and Geiger, W. (2009). Directable, hight-

resolution simulation of ﬁre on the gpu. ACM Trans-

actions on Graphics, 28(3):Article No.41.

Louchez, F. B., Leblond, M., and Rousselle, F. (2006).

Enhanced illumination of reconstructed dynamic en-

vironments using a real-time ﬂame model. In

AFRIGRAPHAFRIGRAPH, pages 31–40.

MitchellCharity (Referenced in March 2022). What color

is a blackbody? - some pixel rgb values. http://www.

vendian.org/mncharity/dir3/blackbody.

Mukai, N., Akasaka, S., and Chang, Y. (2019). Candle

ﬂame simulation considering combustion states. In

IIEEJ International Conferences on Image Electron-

ics and Visual Computing, page 4.

Nassimi, A. M., Jafari, M., Farrokhpour, H., and Keshavarz,

M. H. (2017). Constants of explosive limits. Chemical

Engineering Science, 173:384–389.

Nguyen, D. Q., Fedkiw, R., and Jensen, H. W. (2002). Phys-

ically based modeling and animation of ﬁre. ACM

Transactions on Graphics

, 21(3):721–728.

Ogunedo, M. B. and Okoro, V. I. (2017). Cfd simulation

of a candle ﬂame propagation. Elixir Journal of Me-

chanical Engineering, 108:47813–47817.

Sato, S., Mizutani, K., Dobashi, Y., Nishita, T., and Ya-

mamoto, T. (2017). Feedback control of ﬁre simu-

lation based on computational ﬂuid dynamics. Com-

puter Animation and Virtual Worlds, 28(3-4 e1766).

Sato, S., Morita, T., Dobashi, Y., and Yamamoto, T.

(2012). A data-driven approach for synthesizing high-

resolution animation of ﬁre. In The Digital Production

Symposium, pages 37–42.

Ueda, K. and Fujishiro, I. (2014). Splashing liquids with

ambient gas pressure. In ACM SIGGRAPH Asia Tech-

nical Briefs, page Article No.6.

Wei, X., Li, W., Mueller, K., and Kaufman, A. (2002). Sim-

ulating ﬁre with texture splats. In The conference on

Visualization, pages 227–235.

Candle Flame Simulation Considering Temperature Change in the Environment