Design and Validation of an Adaptive Force Control Algorithm with

Parameter Estimation Unit for Electromechanical Feed Axis

André Sewohl

, Manuel Norberger

, Stefan Sigg

, Holger Schlegel

and Martin Dix

Institute for Machine Tools and Production Processes, Chemnitz University of Technology, Reichenhainer Str. 70,

09126 Chemnitz, Germany

Fraunhofer Institute for Production Systems and Design Technology, Pascalstraße 8, 10587 Berlin, Germany

Keywords: Electromechanical Feed Axis, Force Control, Adaptive Control, Parameter Estimation.

Abstract: Production technology is characterized by the use of electromechanical feed axes, for which the concept of

cascade control has become established. The concept is based on linear control engineering. It is not suitable

for the control of process forces, which is associated with nonlinearities. Here, adaptive control algorithms

from the field of higher control engineering represent a promising approach for improvements of

manufacturing strategies and processes in terms of stability, quality, and efficiency. This can also ensure in

reducing the number of parts rejected due to bad quality and thus aiding as a significant economic benefit. In

this paper, the development of an adaptive control concept that automatically reacts to different and changing

environmental conditions during the process is presented. The digital, parameter-adaptive controller consists

of a recursive online parameter estimation unit, the controller design procedure, which is based on the setting

rule for the symmetric optimum, and the control algorithm. The functionality of the adaptive control concept

is demonstrated in simulation and validated by means of experiments on a test setup. It is real-time capable

and implemented directly on the machine control together with all calculation algorithms.

1 INTRODUCTION

Currently, production technology is subjected to the

influence of global markets more than ever and is

forced towards high productivity and economy. A

trend towards smaller batch sizes and more individual

products is currently being established without

compromising on the quality requirements, process

reliability, and life cycle costs (Tolio and Urgo,

2013). This leads to new challenges for the industry

and hence resulting in promoting the development of

flexible and adaptable machines and processes. In

modern production machines, mainly electro-

mechanical feed axes are used to generate a motion.

There are many strategies for controlling machine-

specific quantities, such as the position or speed of

electromechanical axes. The concept of cascade

structure, also known as servo control, has already

been established in this field (Leonhard, 2012).

https://orcid.org/0000-0003-2031-6603

https://orcid.org/0000-0002-0276-697X

https://orcid.org/0000-0002-4717-1953

https://orcid.org/0000-0002-2344-1656

However, the performance of this conventional

control concept at the machine level has been

exhausted. It cannot meet the ongoing efforts to

further improve the manufacturing strategies and

processes in terms of stability, quality, and efficiency.

One possibility for ensuring stable process conditions

and reducing rejected parts is closed loop control of

quality determining parameters (Allwood et al.,

2016). The development of suitable control concepts

at the process level, in which significant process

variables are taken into account as controlled values,

offers considerable scope for improvement at this

point. There are many process variables which have

an influence to the quality of a part. However, usually

it is very difficult to control these values. The

metrological acquisition of corresponding parameters

constitutes a further challenge.

The process force is a suitable parameter that can

be detected well by measurement and provides

Sewohl, A., Norberger, M., Sigg, S., Schlegel, H. and Dix, M.

Design and Validation of an Adaptive Force Control Algorithm with Parameter Estimation Unit for Electromechanical Feed Axis.

DOI: 10.5220/0011191500003271

In Proceedings of the 19th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2022), pages 629-639

ISBN: 978-989-758-585-2; ISSN: 2184-2809

629

significant economic benefits for many use cases. It

is of particular relevance for the majority of processes

in the field of production technology and often the

limiting factor for the design of the processes and the

choice of parameters. Excessive loads can cause

damage and defects to the workpiece, tool or

machine. In addition, process forces provide

important information about the process state and

allow conclusions about deviations in the production

process (Yao et al., 2013), (Allwood et al., 2016). As

a controlled variable, it is predestined to ensure

stability and safety of many processes. Direct

influence also enables increasing productivity and

improving part quality. However, there are many

challenges and requirements associated with force

control.

The process itself is part of the controlled system,

so that deviations of the controlled system and

nonlinearities occur more frequently. With classic

proportional - integral - derivative (PID) - controllers,

this results in poor performance or even instability.

PID-control forms the basis of the established cascade

control for electromechanical feed axes. The use of

higher control concepts is recommended for

controlling non-linear systems. But complex control

structures and algorithms are difficult to integrate in

machine tools with conventional industrial control.

Additional hardware usually has to be used for the

sensors and control algorithms. The resulting

communication times in turn reduce performance and

reaction speed is limited. Direct access to the control

level is necessary to ensure real-time capability. In

this context, measuring the process forces with

additional sensors is also problematic. The cycle time

is increased even further through signal processing

and integration into the control system. Due to the

delay times in signal processing, real-time capability

is not guaranteed for dynamic movements of feed

axes. High-resolution and fast measurement inputs

are particularly relevant here. Thus, the design of a

suitable control concept with real-time capability

represents a significant challenge.

In particular, adaptive algorithms that can react to

deviations of the controlled system represent a

promising approach to meet the challenges. Adaptive

control concepts have been investigated and

developed for many tasks in production engineering.

A dynamic threshold-based fuzzy adaptive control

algorithm for hard-sphere grinding processes was

introduced by (Li et al., 2012). (Vrabel et al., 2016)

examined an adaptive control system with constraints

for a drilling process. (Maher et al., 2015) developed

an adaptive neuro-fuzzy inference system, which uses

a cutting force signal for the surface roughness

prediction in computerized numerical control (CNC)

end milling. An online parameter self-adaptive force

controller for robot milling was designed in

consideration of the robot feed-direction dynamics

and the time-varying first-order model of the cutting

process by (Xiong et al., 2020). (Deng et al., 2021)

presented a learning adaptive force control concept

based on real-time object stiffness detection for

medical robots. (Calanca and Fiorini, 2018) analyzed

the behaviour of an adaptive force controller for

series elastic actuators in very different environments.

However, control of process forces in production

machines with electromechanical feed axes is still a

developing field and offers space for potential

improvement. The focus of this work is on the

development of an adaptive control concept that

automatically reacts to different and changing

environmental conditions during the process. This

ensures the stability of the control loop. In addition,

the adaptation concept with all calculation algorithms

is implemented directly on the machine control and is

real-time capable.

In the next section, the adaptation concept, its

components and functionality are explained.

Section 3 deals with the experimental set-up. The

simulation results are described in detail in section 4.

Subsequently, the execution of the experiments and

the validation of the control concept are presented in

section 5. The publication concludes with a summary

and outlook.

2 ADAPTIVE CONTROL

The application of an adaptive control concept is

suitable for preventing poor performance or

instability caused by deviations of the controlled

system or non-linearities. Non-linear adaptive

controllers have the ability to adapt the controller

parameters of the basic control loop automatically

during the process to a changing or unknown process

behaviour by means of a parameter setting unit

(Landau et al., 2011). With the independent

adjustment, an improved performance and

functionality of the controller can be achieved. A

comprehensive description on the classification and

categorisation of the different adaptive control

concepts with regard to their mode of operation and

execution principle can be found, for example, in

(Åström and Wittenmark, 2013). The structure,

components and functionality of the selected

adaptation concept are explained in the following.

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

630

2.1 Adaptation Principle

In general, it is desirable to keep the complexity of a

controller as low as possible. In particular, real-time

capability must also be ensured for complex control

concepts. For force control, the effective stiffness in

the contact situation is the determining system

parameter. Direct measurement is not possible.

Therefore, a parameter-adaptive, indirect adaptation

is suitable for the implementation of the control

concept. Model identification adaptive control

(MIAC) is used for this purpose. Here, changes in the

controlled system are detected by an identification

stage and the control parameters are adapted on the

basis of a quality criterion. The digital, parameter-

adaptive controller typically consists of the three

methods of recursive online parameter estimation, the

controller design procedure and the control algorithm

(Isermann, 1991). The basic structure is shown as a

signal flow diagram in Figure 1.

The concept is based on estimating controlled

system parameters and using this information to

calculate the basic control loop parameters. The

calculation rule for the controller parameters is called

adaptive law and results according to (Schulze and

Rehberg, 1988) to:

𝛽



𝑡





𝑓

𝐼



; 𝛼







𝑡



; 𝜉







𝑡



; 𝑘





.

)

The inputs of the adaptive controller are

summarised in the form of the design criterion 𝐼



, the

constant vector 𝑘





and the signal vector 𝜉







𝑡



. The

process parameter vector 𝛼







𝑡



is calculated by

means of the estimation unit. With this, the adaptation

parameter of the basic control loop 𝛽



𝑡



determined in the controller design unit. Here, the

foot index 1 represents the parameters for the

parameter estimation unit and the foot index 2

represents the parameters for the controller design

unit. After selecting all free design parameters, a

parameter-adaptive controller can be put into

operation. In the start-up phase, however, an

unpredictable transient behaviour of the controller is

possible until a correct parameter estimation is

available. In this case, the adaptive controller could

be instable from the start. Therefore, a stable basic

loop controller is kept in the control algorithm as a

start model. The three essential components and

structures of the adaptive controller, including the

functionality, are explained in more detail in the

following sections.

2.2 Control Algorithm

For the control of electromechanical feed axes, the

cascade structure has established as a proven concept.

It consists of several control loops that are

superimposed on each other. In this application, the

velocity and current controller are subordinated to the

adaptive force controller. Accordingly, the control

plant of the force controller consists of the

subordinated velocity and current control loop, as

well as the mechanics of the axis and the process. This

is illustrated in the simplified signal flow diagram in

Figure 2.

The influence of the process is taken into account

by the effective stiffness K

. In addition, the current

control loop is shown here as a proportional-time

(PT1)-element for simplification. On the test setup,

both current and velocity controllers are implemented

as proportional-integral (PI)-controllers. Thus, the

controlled system including the process already

contains an integrating part. Therefore, the force

controller can be designed as a proportional (P)-

Figure 1: Block diagram and signal flow diagram of the parameter-adaptive controller.

Controller

Design Unit

Basic Control

Loop

Controlled

System

Parameter

Estimation Unit

Design and Validation of an Adaptive Force Control Algorithm with Parameter Estimation Unit for Electromechanical Feed Axis

631

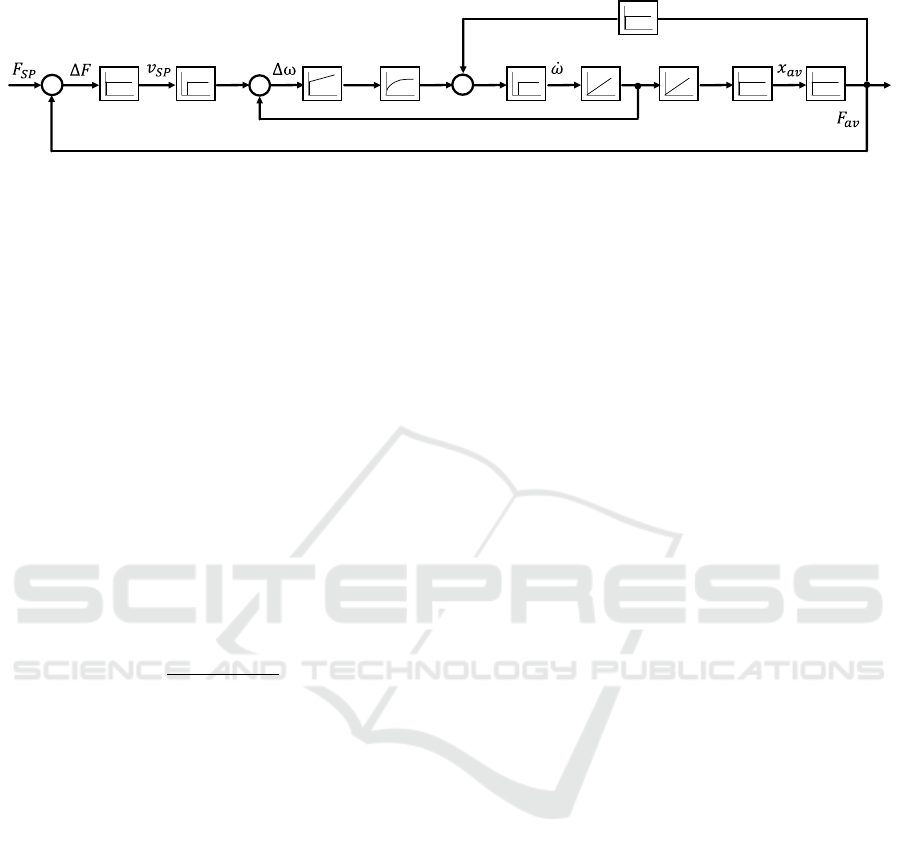
Figure 2: Simplified signal flow diagram of the basic control loop and the controlled system.

controller. This offers the additional advantage that it

can be designed quickly and easily with just one

parameter. Moreover, only one parameter then has to

be calculated and adapted during operation. This

results in less complexity, error-proneness and

calculation time, which favours real-time capability.

2.3 Controller Design Unit

The controller design is based on the setting rule for

the symmetric optimum (SO). This method is a

common design procedure for the controllers of

integrative-time (IT1)-systems. It has also proven to

be suitable in previous investigations to achieve good

performance. A more detailed description of this can

also be found in (Sewohl et al., 2020). Thus, the gain

factor K

for the force controller is calculated

according to the following equation:

𝐾





𝑎∗ 𝐾



∗ 𝑇



(2)

Here 𝑎 corresponds to the damping factor, which

is usually set to the value 2. The parameter 𝑇



represents the substitute time constant of the

subordinated system. The integral gain of the force

control loop is determined by the effective stiffness

𝐾



. While the other parameters are constant, this

value varies in the process, which can lead to

instability in conventional control concepts. The

adaptive controller is aimed at making the stability

and performance of the closed-loop force control

largely independent of the stiffness 𝐾



. In order to

achieve this, the gain 𝐾



of the force controller is

adjusted in the programmable logic control (PLC)-

cycle of the control system every 2 ms. This requires

the determination of the stiffness during operation.

Direct measurement is not possible, so a parameter

estimation unit is implemented for this purpose, with

which online estimation is carried out continuously.

The estimated stiffness 𝐾





is transferred to the

controller design unit and replaces 𝐾



. In this way the

gain factor is calculated accordingly the SO.

In addition, further monitoring functions are

implemented in the controller design unit. For the

detection of a setpoint violation, a comparison of the

actual force value and the force setpoint with the

permissible difference is made. If the force control

loop starts to oscillate with a low force or

displacement amplitude, no stiffness estimation is

performed and a permanent instability may occur.

Therefore, oscillation detection is performed using a

sign comparison of the velocity setpoint from the

current and previous PLC-cycle. If one of these

criteria is violated, the parameter set for a stable basic

control loop is used. This is based on the maximum

stiffness of the controlled system. Thus, a backup

controller is kept available for critical operating

situations. After the force control loop has been

stabilised by the backup-controller, a continuous

stiffness estimation and parameter adaptation takes

place again.

2.4 Parameter Estimation Unit

Good adaptation performance requires estimation of

the effective stiffness as quickly and with as little

noise as possible. The estimation time is particularly

relevant for rapid increases in stiffness. In this case,

the force controller amplification is too high, which

results from the previous, lower stiffness. Thus, in the

event of a sudden increase in stiffness, there is a risk

of overshooting of the actual force value and even

instability of the force control loop. The low-noise

estimation is necessary because the estimated

stiffness directly influences the velocity setpoint. For

a strongly noisy parameter estimation, permanent and

distinct acceleration and braking phases would

follow. These could both reduce the lifetime of the

servo drive and negatively affect the quality of the

stiffness estimation due to dynamic inertia effects.

Thus, the task of the parameter estimation unit is to

estimate the effective stiffness online as quickly as

possible and at the same time with as little noise as

possible. This is essential for the functionality of the

adaptive controller. The basic structure is shown in

Figure 3. The parameter estimation unit consists of

1/J

1/i

gear

1/i

gear

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

632

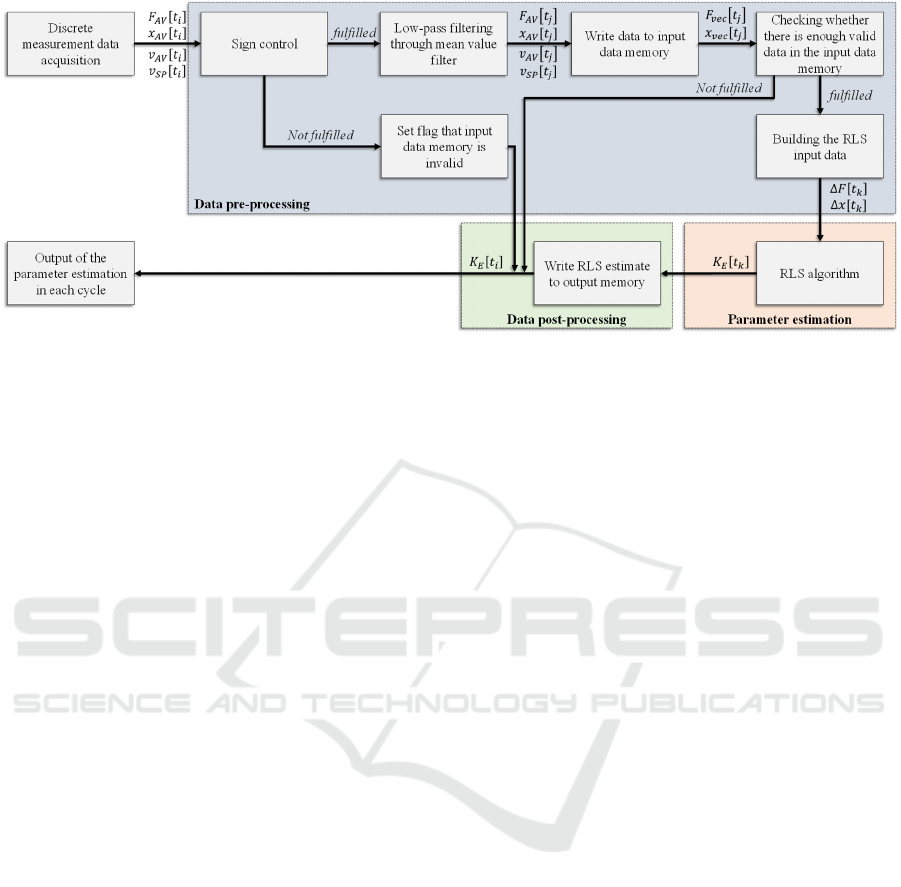
Figure 3: Basic structure and functionality of the parameter estimation unit.

the three steps of data pre-processing, parameter

estimation using the RLS-algorithm and data post-

processing. The detailed explanation of the design,

functionality and validation of the parameter

estimation unit is given in (Norberger et al., 2022).

2.5 Mode of Operation

The sequence of the PLC-program with the adaptive

force control consists of two basic sections. In the

first initialisation phase, the tool is moved at a defined

feed rate until a threshold force is reached. The

initialisation phase is necessary to obtain a reliable

estimate 𝐾





of the effective stiffness 𝐾



. An

exemplary value for the threshold force is, for

example, 50 N. When the threshold force is exceeded,

the initialisation phase ends and the adaptive force

control is activated. The adaptation cycle of the

controller runs with the following steps:

1. Initialisation: The process image as well as the

design and control parameters are imported. The

associated cycle time corresponds to the PLC

working cycle.

2. Calling the parameter estimation unit: The

stiffness is estimated from the current measured

values. The stiffness value 𝐾





is then output. If no

new stiffness estimation has taken place, the last

estimated value is used. Thus, a stiffness value is

available in each PLC-cycle. When the adaptation

unit is switched on, the initialisation estimate is

output first, which is gradually adjusted by current

estimations.

3. Calling the controller design unit: Here, the

calculation of the force controller gain 𝐾



takes

place on the basis of the SO. The information about

the force and velocity signals is also transferred to the

monitoring functions.

4. Adaptation: The controller parameter 𝐾



overwritten in the control loop. This parameter is used

to control the electromechanical feed axis in the

current cycle.

The controller gain is continuously adapted after

the initialisation phase according to the previously

described steps.

3 TEST SETUP

A test-setup of an electromechanical feed axis with a

control from Beckhoff was selected for the

implementation and validation of the control concept.

The basic structure of the test-setup with the

individual components is illustrated in Figure 4. The

sequence programs and operating modes, the force

control, the controller design unit with the adaptation

algorithm, the parameter estimation unit and the

setpoint generation are implemented in the IPC. This

means that all algorithms are implemented directly in

the control system. In addition, the IPC is coupled via

the backplane bus with the safety modules, I/O

modules and the measuring amplifier for the force

sensor. In this way, the communication times are

reduced from the millisecond range to the

microsecond range and the performance can be

increased. The servo inverter is connected via the

EtherCAT connection. The subordinate velocity and

current control are located here. The servo motor is

controlled here, too. In the mechanical part, the

rotational movement of the servo motor is

synchronously transmitted to the two ball screw

spindles via several belts and gears. Here exists a

mechanical forced coupling. The rotational

movement is converted into translation via the nuts

and the crosshead attached to them. In the workspace,

Design and Validation of an Adaptive Force Control Algorithm with Parameter Estimation Unit for Electromechanical Feed Axis

633

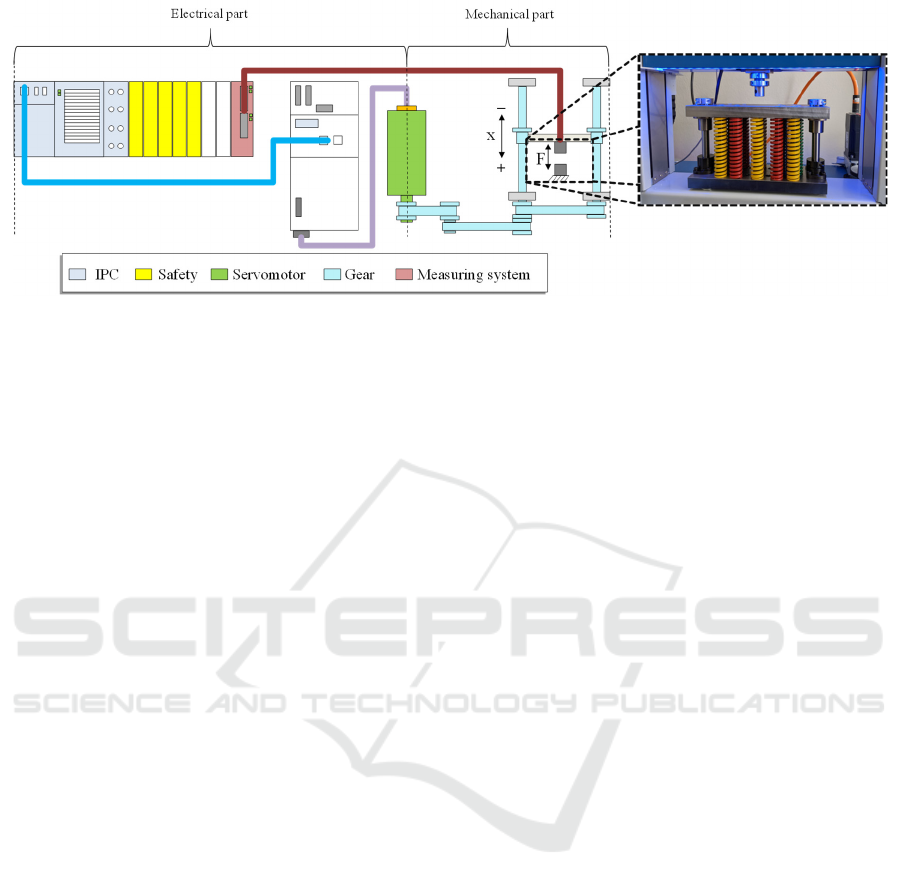
Figure 4: Experimental setup and schematic structure of the electromechanical feed axis.

the load is applied to the workpieces via the

crosshead, in which the sensor for detecting the

process forces is also integrated. The experimental

setup is designed for loads up to 10 kN. A modular

and exchangeable spring package was designed in

order to cause reproducible deviations and non-

linearities in stiffness. This load module is used to

simulate a process or a resulting process force. In this

way, variable load characteristics can be initiated

with high reproducibility by a movement of the axis

against the load module. This allows systematic

replication and investigation of changes and

deviations in the system stiffness for adaptive force

control. More detailed information on the individual

components, the commissioning and

parameterisation of the test setup can also be found in

(Sewohl et al. 2020).

4 SIMULATION

The development of the adaptive control concept was

accompanied by model-in-the-loop simulations.

MATLAB/Simulink serves as the simulation

environment. The generation of a simulation model

for the test setup has the goal of cyclically providing

the adaptive control system with a realistic process

image for iterative function tests. For this purpose, the

essential components of the adaptive control, such as

the control algorithm, the parameter estimation and

the controller design unit are created in separate

function blocks. The mechanical model of the test

setup was also inserted in a single subsystem. Due to

the modular structure, the adaptive control can be

iteratively tested and improved independently of the

test setup. Using the TwinCat C++ target for

Matlab/Simulink and the Simulink coder, it is

possible to export the control algorithm directly to the

Beckhoff machine controller.

To simulate the real system behaviour, the

mechanics of the test setup were implemented in the

simulation model as a 2-mass oscillator. The relevant

parameters, such as stiffnesses, damping, mass

moments of inertia and transmission ratios, were

determined from the technical data sheets and the

CAD-model. In addition, the signals are also

approximated as closely as possible to reality. For this

purpose, the corresponding sampling frequencies,

quantisation and noise behaviour were determined on

the experimental setup and transferred to the control

structure of the model. Computing and

communication times in the control system were also

taken into account. The implementation of a friction

model was dispensed with. The parameterisation of

the control was carried out according to the procedure

and parameters from (Sewohl et al., 2020).

Based on the comparison of real measurement

data and the response of the simulation model, a

verification of the model behaviour for relevant

operating situations was carried out. The behaviour of

the force control was examined for different

stiffnesses, force amplifications and setpoint profiles.

It was checked whether the Simulink-model can

represent the behaviour of the test setup with

sufficient accuracy for the controller design. The

contouring error as well as the starting and braking

behaviour are particularly relevant for this. The

results for a trapezoidal force setpoint profile are

shown in Figure 5. Up to the threshold value of

100 N, the feed axis is moved under velocity control.

Afterwards, the system switches to force-controlled

operation. A comparison of the contouring error as

well as the starting and braking behaviour shows that

the simulation model reproduces reality very closely.

Therefore, it is suitable for the development and

testing of the adaptive force controller. In addition to

the control structure, the controller design unit and the

parameter estimation unit were integrated into the

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

634

Figure 5: Comparison of actual force values from

simulation and experiment. (a) Overview of the force

profile. (b) Switching process. (c) Transition area.

model. The parameter estimation unit acts

independently of the mechanical behaviour of the test

setup and has already been validated in (Norberger et

al., 2022).

The testing of the adaptation concept in

interaction with the parameter estimation unit and the

controller design unit is first carried out in the

simulation environment using various stiffness

jumps. The reaction of the adaptive controller to a

stiffness jump from 100 N/mm to 500 N/mm is

shown in Figure 6. The diagram shows that the

adaptive controller is able to ensure a stable control

loop in the case of abrupt changes in the system

behaviour. This applies both to abrupt increases and

decreases in the effective stiffness 𝐾



. In this case,

the contouring error is also temporarily reduced or

increased. After about 50 ms, the parameter

estimation unit fully adjusts to the jump in stiffness

and the adaptive controller compensates the

contouring error again. In contrast, the conventional

controller becomes instable shortly after the change

in stiffness. For better illustration of this case, the data

are only displayed up to the time point of 5.5 s.

For the controller design, there is a freely

definable influence parameter with the design

parameter 𝐼



𝑎. This parameter is first varied in the

simulation and the results are shown in Figure 7.

Through the investigation, the effects and further

modification possibilities can be assessed. The force

curve shows that the parameter 𝑎 has an effect on the

performance. Smaller values cause smaller and higher

values correspondingly larger contouring errors.

However, small values also increase the risk of

overshooting in the event of abrupt changes and the

control loop becoming instable. But this can be

avoided by the implemented safety functions. In the

event of a setpoint violation, the parameter estimation

is stopped and the backup-controller is used. This is

illustrated in diagram (b). Diagram (c) shows the

characteristic of the controller gain 𝐾



, which is

adjusted on the basis of the stiffness estimate 𝐾





. In

the case of a setpoint violation, the calculation is re-

initiated. As soon as the parameter estimation unit

delivers reliable values again, the controller

parameter is automatically adapted.

The considered example with a sudden increase of

the stiffness from Figure 6 is to be considered as a

critical application. With a large change in the

controlled system parameters, there is a risk of an

instable control loop. It was shown that the developed

control concept nevertheless remains stable for this

critical case and the desired adaptation takes place. In

reality, such jumps are not to be expected at the test

setup. Therefore, the behaviour for a further stiffness

Figure 6: (a) Overview of the simulated behaviour of the adaptive and conventional controller during a stiffness jump. (b)

Detail of the stiffness change.

8910

Time [s]

-400

-200

Force [N]

(b)

12 13 14

Time [s]

-1100

-1000

-900

Force [N]

(c)

10 15 20 25 30 35 40

Time [s]

-3000

-2000

-1000

Force [N]

(

)

Exp

Sim

Design and Validation of an Adaptive Force Control Algorithm with Parameter Estimation Unit for Electromechanical Feed Axis

635

Figure 7: Influence of the design parameter a on the behaviour of the control system. (a) Comparison of the actual force

values. (b) Comparison of the stiffness estimation. (c) Comparison of the controller gain.

Figure 8: Complete profile of forces and stiffnesses for the simulative investigation of the adjusted stiffness profile.

profile is examined in the simulation. This is

approximated to the characteristic curve of the test

setup. Here, a staircase-shaped increase in stiffness

from 130 N/mm to 1000 N/mm is distributed in

several steps over the stroke process. The variation

range of the stiffness corresponds to the variation that

can actually be generated with the spring assembly.

The result is shown in Figure 8. Here it can be also

seen that the adaptive controller remains stable and

can follow the setpoint profile very well over the

entire range of variation of the stiffness change. This

is true for both compression and decompression.

Thus, the basic functionality of the concept could first

be proven in the simulation.

5 EXPERIMENTS AND

VA L I D AT I O N

In order to transfer the adaptive force control

developed in Matlab/Simulink to the test setup, it is

necessary to integrate the function modules into the

control system. Beckhoff allows direct integration of

the Simulink-model in the machine controller. For

this purpose, the model is translated into C++ code

using the Simulink code generator. The TE1400

TwinCAT Target can be used to generate a TwinCAT

Component Object model (TcCOM) from the code

(Beckhoff, 2020). The TcCOM has the inputs and

outputs defined in the Simulink model and can be

linked to a corresponding task in the Beckhoff

development environment. The inputs and outputs are

linked with the associated variables from the process

image. In this way, the two function blocks for

adaptive control with the parameter estimation unit

are transferred directly from the existing Simulink-

model to the real machine control. The algorithms are

integrated in the runtime of the machine control and

are processed cyclically in real-time.

The practical testing of the concept is carried out

with the help of the modular spring package shown in

Figure 9. By combining the springs and using spacer

elements, variable path-dependent non-linear

stiffness characteristics can be specified. The

adaptive control concept is validated using the two

illustrated spring configurations with different

stiffness profiles. At the beginning of the

compression of the spring assembly, only 4 springs

are engaged. Only when the spring assembly has been

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

636

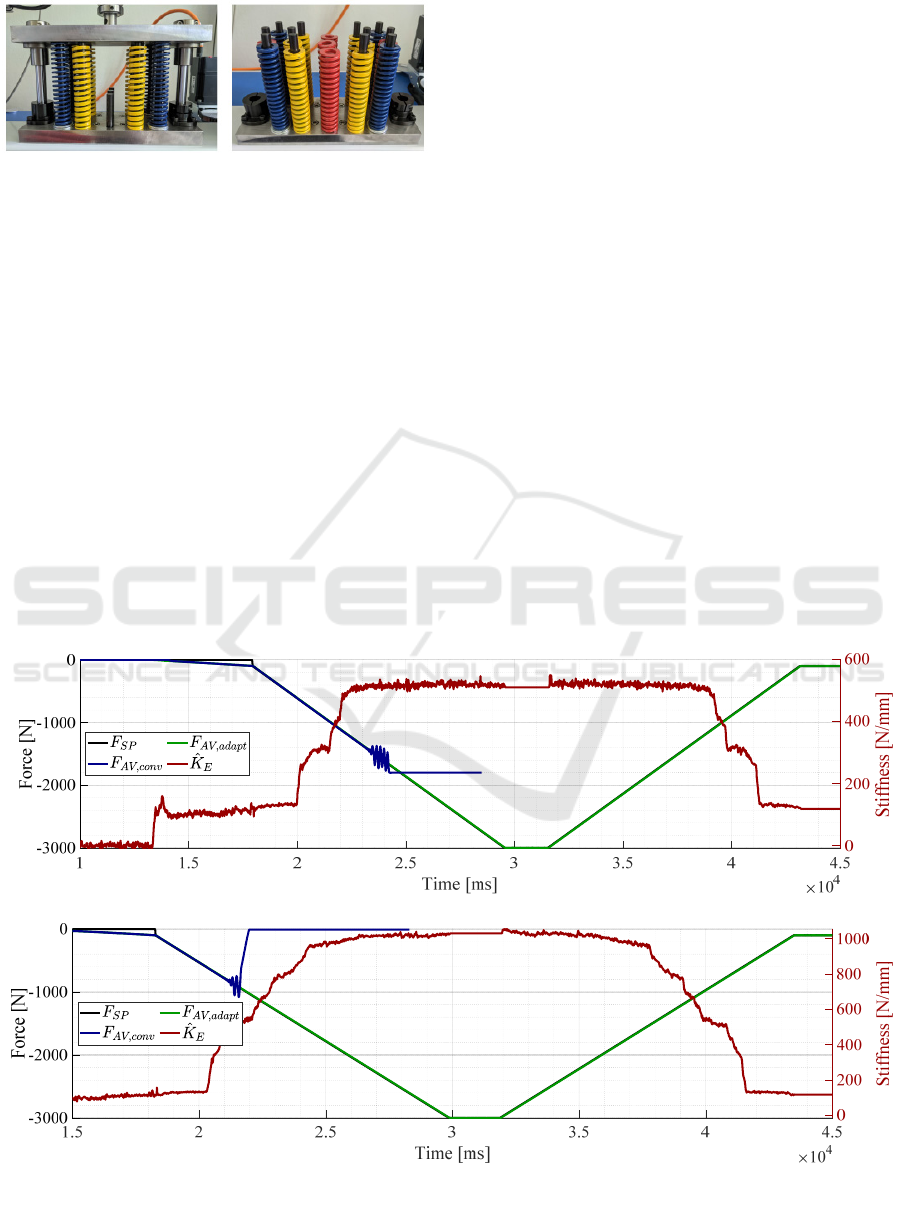
(a) (b)

Figure 9: Combination of spring elements for stiffness

jumps. (a) Change S1 from 130 N/mm to 500 N/mm. (b)

Change S2 from 130 N/mm to 1000 N/mm.

compressed by a certain deflection do the other

springs engage. This results in a rapid increase in

stiffness. Due to the manufacturing tolerances of the

springs, there is no abrupt jump in stiffness. Rather,

the increase in stiffness from the initial to the final

stiffness takes place within a transition range of

around 2 mm. The complete curves of the

measurements for the two spring configurations are

illustrated in Figure 10. The behaviour of the

conventionally tuned force controller is also

compared here. Corresponding to the composition of

the spring assembly, the initial stiffness results in

𝐾



= 132 N/mm. The conventional controller was set

to this system behaviour without adaptation

according to the SO and the design parameter 𝑎 = 2.

During validation, the behaviour was examined at

several rates of force change (1000 N/s, 500 N/s and

250 N/s). Figure 10 (a) shows the behaviour for

250 N/s and a stiffness jump to 500 N/mm. In

Figure 10 (b) the stiffness changes to 1000 N/mm.

The stiffness changes are well reproduced by the

parameter estimation unit. It can also be clearly seen

that the conventional force controller becomes

instable and oscillates without adaptation in both

cases. Therefore, the tests were stopped at this point

by the implemented safety function and the data

recording was interrupted. The conventional force

control also became instable during all other tests. In

contrast, it is also clear that the adaptive controller

reacts very well to the change in system in practice

and follows the setpoint profile without any

instability occurring. This applies to all the tests

carried out with the three different increases in the

force setpoint ramp.

In addition, the effects resulting from a variation

of the free design parameter 𝑎 were also considered.

The results for a force increase of 1000 N/s are shown

for the stiffness jumps in Figure 11. It can be seen that

the performance of the adaptive controller can be

influenced with the free design parameter. With

smaller factors, the following error decreases, as in

the simulation. However, this also increases the

proneness to errors and the tendency to oscillate.

Figure 10: Experimental validation of the adaptive control concept. (a) Results for the stiffness jump S1. (b) Results for the

stiffness jump S2.

(a)

(b)

Design and Validation of an Adaptive Force Control Algorithm with Parameter Estimation Unit for Electromechanical Feed Axis

637

Figure 11: Measurement data of the adaptive and conventional force control for the force increase of 1000 N/s and different

design parameter 𝑎. (a) Stiffness change S1. (b) Stiffness change S2.

Conversely, larger factors result in an increased

contouring error. However, this also increases the

robustness of the control. Furthermore, the back-up

controller was implemented for the adaptive

controller as an additional safety criterion on the test

setup. This is designed for the frame rigidity of the

machine and intervenes as soon as a setpoint violation

occurs. The adaptation process is then restarted. This

functionality of the safety mechanism is illustrated in

Figure 11 (b). Here the stiffness jump S2 is shown for

a force increase of 1000 N/s. For the design factor 𝑎

= 2, a setpoint violation occurs with the change in

stiffness. In this case, the input data memory of the

parameter estimation unit is reset, the estimation is

stopped and reinitialised. This is expressed in by the

horizontal line of the parameter estimation value 𝐾





As soon as sufficient input data are available, new

estimated values are transferred and the adaptation

process is continued. This is the case here after about

60 ms. It can also be seen that the control then

stabilises and adjusts to the changed system. With the

use of the backup controller, the functionality of the

adaptive controller can also be ensured for critical

operating situations in practice.

6 SUMMARY

In this paper, the concept of an adaptive force

controller for an electromechanical feed axis was

presented. The individual components, the structure

and the mode of operation were explained. The

algorithm was first tested and optimised on a model

in the simulation environment. The concept was then

transferred to the test setup and experimentally

validated. In the context of this, the adaptive

controller was exported by means of the Simulink-

coder. The TcCOM was instantiated in the machine

controller and linked to the corresponding tasks,

which are processed in real-time on the PLC. The

adaptive controller behaves identically on the

machine controller to the Simulink-model in Matlab.

This principle allows optimisations and further

developments to be carried out modularly in

Matlab/Simulink and implemented with little effort.

Furthermore, it was proven in the scope of the

work that the developed controller with the parameter

estimation unit is capable of detecting changes in

stiffness and reacting to them accordingly. This

applies to both compression and decompression

processes. The adaptive controller is able to adapt the

gain factor to the controlled system during operation

based on the estimated stiffness. Even with highly

variable system behaviour, the controller remains

stable due to the adaptation of the gain factor and

improved performance is achieved. In addition, the

use of the backup-controller ensures functionality

even for critical operating situations. The behaviour

of the adaptive control can basically be influenced by

the choice of design parameters for the parameter

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

638

estimation unit and the controller design unit.

Compared to conventional control with unchanging

parameters, an improved compromise between

stability and performance is achieved. This is

especially true if essential parameters of the

controlled system are not known a priori or are time-

variant. For small stiffness values, the adaptation

enables a higher proportional gain. At the same time,

improved stability was achieved in the range of larger

values. The investigations also demonstrated the real-

time capability of the developed control system.

Depending on the process, changes in the controlled

system are already compensated after 40-50 ms.

7 CONCLUSION AND OUTLOOK

The adaptation concept presented can be transferred

to many areas in production technology and offers a

wide range of applications. A major limitation of the

method is currently that the process force must be

dependent on the stiffness. Potential use cases are, in

particular, forming processes, material testing,

grinding, joining and assembly operations. The

concept can be used on machine tools, forming

machines and robots. Here, an analysis of the system

behaviour should first be carried out. This allows the

design parameters for the parameter estimation unit

and the controller design unit to be adjusted and

optimised to the corresponding application. In

addition, the fast responsiveness and real-time

capability are an essential characteristic of the

concept. For processes where the stiffness changes

very slowly, the design parameters and limits of the

parameter estimation algorithm have to be adapted. In

principle, it is also possible to transfer the concept to

more complex processes with different conditions. In

the case of machining operations (such as milling), it

could be used for individual force components.

Furthermore, the algorithm could also be extended or

supplemented with process models that take into

account additional influencing variables.

Future work will focus in particular on

investigating possibilities for improving the learning

phase and the switchover process for adaptive

control. In addition, an optimisation of the

empirically set design parameters is intended in

further investigations. The extension of the algorithm

with a compensation of weight and acceleration

forces is also aimed at. Furthermore, the suitability

and effects of other control structures in the control

loop shall be investigated. The safety functionalities

also still offer potential for improvement.

REFERENCES

Leonhard, W. (2012). Control of Electrical Drives - Power

Systems, Springer-Verlag. Berlin, 3

edition.

Tolio, T. and Urgo, M. (2013). Design of flexible transfer

lines: a case-based reconfiguration cost assessment, In

Journal of Manufacturing Systems, 32(2), pp. 325-334.

Allwood, J. M. et al. (2016). Closed-loop control of product

properties in metal forming. In CIRP Annals –

Manufacturing Technology, 65, pp. 573-596.

Yao, X. et al. (2013). Machining force control with intelligent

compensation. In International Journal of Advanced

Manufacturing Technology, 69(5-8), pp. 1701-1715.

Li, D. et al. (2012). A dynamic threshold-based fuzzy

adaptive control algorithm for hard sphere grinding. In

International Journal of Advanced Manufacturing

Technology, 60, pp. 923-932.

Vrabel, M. et al. (2016). Monitoring and control of

manufacturing process to assist the surface workpiece

quality when drilling. In Procedia CIRP, 41, pp. 735-

739.

Maher, I. et al. (2015). Cutting force-based adaptive neuro-

fuzzy approach for accurate surface roughness prediction

in end milling operation for intelligent machining. In

International Journal of Advanced Manufacturing

Technology, 76, pp. 1459-1467.

Xiong, G. et al. (2020). Integration of optimized feedrate into

an online adaptive force controller for robot milling. In

International Journal of Advanced Manufacturing

Technology, 106, pp. 1533–1542.

Deng, Z. et al. (2021). Learning Based Adaptive Force

Control of Robotic Manipulation Based on Real-Time

Object Stiffness Detection. In arXiv preprint,

arXiv:2109.06702.

Calanca, A. and Fiorini, P. (2018). Understanding

Environment-Adaptive Force Control of Series Elastic

Actuators. In IEEE/ASME Transactions on

Mechatronics, 23(1), pp. 413-423.

Landau, I. D. et al. (2011). Adaptive control: algorithms,

analysis and applications. Springer Science & Business

Media. London, 2

edition.

Åström, K. J. and Wittenmark, B. (2013). Adaptive control.

Dover Publications. Mineola, 2

edition.

Schulze, K.P. and Rehberg, K.-J. (1988). Design of Adaptive

Systems - A Presentation for Engineers. Verlag Technik,

Berlin. (in German)

Isermann, R. (1991). Digital Control Systems - Volume 2:

Stochastic Control, Multivariable Control, Adaptive

Control, Applications. Springer, Berlin.

Sewohl, A. et al. (2020). Performance Analysis of the Force

Control for an electromechanical Feed Axis with

Industrial Motion Control. In ICINCO2020, pp. 667-674.

Norberger, M. et al. (2022). Development and Validation of

a Model for Online Estimation of Process Parameters for

Adaptive Force Control Algorithms. In Proceedings of

the 2

Winter IFSA Conference ARCI2022, (ed. Yurish,

S.Y.), 006, pp. 19-24.

Beckhoff Automation GmbH, (2020). Manual - TC3 Target

for Matlab/Simulink, TwinCAT 3, TE1400. Beckhoff

Automation GmbH.

Design and Validation of an Adaptive Force Control Algorithm with Parameter Estimation Unit for Electromechanical Feed Axis

639