Minimum Size Build Environment Sets and Graph Coloring

Stephen R. Tate

and Bo Yuan

Department of Computer Science, UNC Greensboro, Greensboro, NC, U.S.A.

Keywords:

Build Environments, Large Scale Analysis.

Abstract:

In this paper, we formalize the problem of designing build environments for large-scale software build and

analysis, addressing issues with dependencies and conﬂicts between components required for each source

package. We show that this problem can be fully captured by constructing a graph, which we call the “con-

ﬂict graph,” from dependency and conﬂict information, and then ﬁnding a minimum set of build environments

corresponds exactly to ﬁnding minimum colorings of the conﬂict graph. As graph coloring is an NP-hard prob-

lem, we deﬁne several graph simpliﬁcations that can reduce the size of the graph, to improve the performance

of heuristic coloring algorithms. In experimental results, we explore basic conﬂict graph metrics over time

for various releases of the Ubuntu Linux distribution, and examine coloring results for the latest LTS release

(Ubuntu 20.04). We ﬁnd that small numbers of build environments are sufﬁcient for building large numbers

of packages, with 4 different environments sufﬁcient for building the 1000 most popular source packages, and

11 build environments sufﬁcient for building all 30,646 source packages included in Ubuntu 20.04.

1 INTRODUCTION

In this paper, we explore algorithmic problems that

arise in designing environments for large-scale soft-

ware build and analysis. While this paper focuses

on high-level issues that are not speciﬁc to any par-

ticular system, the problems arose and are motivated

by experience setting up an environment to support

building and analyzing open source software that is

included in the Ubuntu 18.04 distribution, which con-

sists of over 29,000 source packages that create over

63,000 different binary packages that end users can

install. Building binaries from a source package in-

volves certain software requirements, or dependen-

cies, which must be installed to support the build. An

obvious example of such a requirement is that any

source package containing C code will need a C com-

piler to build the binaries, but beyond the obvious lan-

guage tools most packages also require certain sup-

port libraries be installed to perform the build. Fur-

thermore, dependencies can have their own dependen-

cies, and those dependencies can have dependencies,

and so on. Large scale static analysis has an almost

identical set of requirements — for example, running

the Clang static analyzer on a source package uses

the actual build process while analyzing the code, so

https://orcid.org/0000-0001-9315-2705

https://orcid.org/0000-0002-9862-967X

needs all of the build requirements to be installed to

perform the analysis.

Tools exist to simplify the build process, creat-

ing a minimal build environment using either a ch-

root jail (e.g., pbuilder

) or a Docker container

(e.g., whalebuilder

) and adding the necessary de-

pendencies to that environment before starting the

build. While these tools are excellent for perform-

ing an isolated build of a single package, when used

for building multiple packages the cost of creating

each package’s minimal build environment becomes

very high. Describing work to re-build an entire De-

bian distribution from sources, (Nussbaum, 2009) re-

ported that some packages required a large amount

of time to simply set up the build environment, in-

cluding a requirement for 485 additional package in-

stallations before the build process could even be-

gin for openoffice.org. This problem has got-

ten even worse since Nussbaum’s 2009 work, with

the version of LibreOfﬁce in Ubuntu 18.04 requir-

ing 830 additional packages, above and beyond the

“build essentials” that all build environments include,

which took almost 13 minutes to set up before the

build could even begin. While both pbuilder and

whalebuilder can save created build environments

for future use, this is mostly useful for working on

https://pbuilder-team.pages.debian.net/pbuilder/

https://gitlab.com/uhoreg/whalebuilder

Tate, S. and Yuan, B.

Minimum Size Build Environment Sets and Graph Coloring.

DOI: 10.5220/0011263200003266

In Proceedings of the 17th International Conference on Software Technologies (ICSOFT 2022), pages 57-67

ISBN: 978-989-758-588-3; ISSN: 2184-2833

a single package that will reuse the exact same build

environment on future runs. When creating pre-made

build environments, can we create generally-useful

environments that can be used for large sets of pack-

ages? Doing so would greatly improve the efﬁciency

of building or analyzing large sets of packages, and

this is the problem we examine in this paper.

When planning to build a large set of packages, it

is tempting to think that the right solution is to in-

stall all dependencies required by all packages be-

ing built. Unfortunately, dependencies can conﬂict

with one another, meaning that certain combinations

of packages cannot be installed at the same time. For

example, in Ubuntu 18.04, building firefox requires

a speciﬁc version of autoconf to be installed (ver-

sion 2.13) while building apache2 requires a newer

version. Since only one version of autoconf can

be installed at a time, there is no way to set up a

single build environment that can support building

both firefox and apache2. While this is a direct

and obvious conﬂict, some conﬂicts only appear with

deeper digging. For example, building firefox re-

quires libcurl4-openssl-dev and cfengine2 re-

quires the libssl1.0-dev, and the two dependen-

cies, libcurl4-openssl-dev and libssl1.0-dev,

conﬂict with each other. Therefore, to get a com-

plete picture of possible build environments, all de-

pendencies and conﬂicts, both direct and transitively

induced, must be considered.

In this paper, we show how to construct a graph

that captures the necessary information on dependen-

cies and conﬂicts for a set of source packages, and

show how variants of the graph coloring problem on

this graph reﬂect the design of build environments.

Due to the NP-completeness of minimum graph col-

oring, we cannot efﬁciently compute optimal solu-

tions, but we explore how well various heuristic ap-

proaches perform in practice. In this paper, we make

the following speciﬁc contributions:

• Deﬁne how to construct a graph that captures

software build dependencies and conﬂicts, and

explore the properties of this graph for various

Ubuntu “Long Term Support” (LTS) releases.

• Show how ﬁnding a minimum graph coloring on

this graph provides the smallest set of different

build environments that need to be created to sup-

port building all packages.

• Explore how graph coloring on nested subgraphs

supports the ability to analyze subsets of packages

(e.g., support analyzing both “the 500 most pop-

ular packages” and “the 1000 most popular pack-

ages” with a single set of build environments).

• Present experimental results from applying

heuristic graph coloring algorithms to these

problems.

The problems that we explore are interesting from

an abstract modeling and algorithms standpoint, and

the reduction and algorithms result in direct practical

gains for designing systems for large scale software

build and analysis. All code and data reported on in

this paper is freely available (see Section 4).

2 DEPENDENCY AND CONFLICT

COMPUTATIONS

In this section we deﬁne the basic terminology and

model required for representing packages, dependen-

cies, and conﬂicts. Our model does contain some sim-

pliﬁcations from real-world package speciﬁcations,

which we discuss in Section 2.3. Packages are sim-

ply sets of ﬁles coupled with attributes that give vari-

ous information about the package. In our model we

have a set of source packages S and set of binary

packages B, where source packages contain ﬁles and

information necessary to build binary packages. At-

tributes for either type of package can include lists of

binary package dependencies and conﬂicts, which we

denote for package p by D(p) and C(p), respectively.

If p ∈ S is a source package, then D(p) is the set of

binary package that must be installed in order to build

binary packages from this source package, and C(p)

is the set of all binary packages that must not be in-

stalled when building using this source package. If

p ∈ B is a binary package, then D(p) is the set of all

binary packages that must be installed any time p is

installed, and C(p) is the set of all binary packages

that cannot be installed at the same time as p. In all

cases, the D(p) and C(p) deﬁnitions are immediate

dependencies and conﬂicts — these can induce addi-

tional dependencies and conﬂicts as described in the

following subsection.

2.1 Dependency Sets

Package dependencies are deﬁned by package main-

tainers, and generally give just immediate dependen-

cies, or what we will call ﬁrst-level dependencies,

which we denote D

(p) = D(p). Packages in D

(p)

can have their own depenencies, which are called

“second-level dependencies,” which in turn deﬁne

“third-level depenpencies,” and so on. To simplify

later cases, we deﬁne “level-0 dependencies” of p to

be simply the set {p}, giving the recursive deﬁnition

(p) =



{p} if k = 0;

x∈D

k−1

(p)

D(x) if k ≥ 1.

ICSOFT 2022 - 17th International Conference on Software Technologies

The full set of dependencies for package p is then

∗

(p) =

[

k≥0

(p),

which is unambiguously deﬁned since the set of pack-

ages is ﬁnite. If p is a source package, then all pack-

ages in D

∗

(p) must be installed in order to build bi-

nary packages from p. Since dependencies are di-

rected relations between packages, we can view pack-

ages and dependencies as a directed graph (the “de-

pendency graph”). Then D

∗

(p) is the set of vertices

reachable from p in the dependency graph, or equiv-

alently D

∗

(p) consists of the neighbors of p in the

transitive closure of the dependency graph.

While we could add an extra level of abstraction

and perform analysis on the dependency graph,

we instead work directly with dependency sets.

The following algorithm computes a new level of

dependencies for package p, where packages in de-

pendencies at prior levels are passed in as parameter E

(the “exclusion set”). If the algorithm recurses on line

4, it must be the case that E

is at least one element

larger than E (since E

contains x but E does not), and

since there are only a ﬁnite number of items that can

be added to E the recursion must be ﬁnite and the al-

gorithm always completes in a ﬁnite number of steps.

ALLDEPS(p, E)

1 S = {p}

2 E

= E ∪ D(p)

3 for x ∈ D(p) − E

4 S = S ∪ ALLDEPS(x, E

)

5 return S

Since ALLDEPS recurses through all levels of depen-

dencies until no additional packages can be added,

the end result is D

∗

(p) = ALLDEPS(p,

0) for any

package p. Since at most one recursive call is made

per package in the ﬁnal dependency set, given an

efﬁcient set implementation this algorithm is very fast

for computing a single dependency set. To improve

performance when computing dependency sets of

many packages, we cache results for binary packages

as they are completed, so we can short-circuit the

recursion with pre-computed sets. We discuss this

and experimental performance results in Section 4.

2.2 Conﬂict Sets and Relation

In addition to dependencies, packages can conﬂict

with other packages, which means that they cannot

be installed simultaneously. While real package man-

agers have different types of conﬂicts (e.g., “Con-

ﬂicts” and “Breaks” attributes in Debian packages),

in our model we consider different types of conﬂicts

as the same and refer to them generically as “con-

ﬂicts.” For any package p, we deﬁne C(p) to be the

set of packages that the package deﬁnes as conﬂicting

with it. As with D(p), this only denotes immediate

conﬂicts, and indirect conﬂicts can also be induced

through dependencies.

Note that C(p), as deﬁned by a package attributes,

is not necessarily a symmetric relation between pack-

ages. For example, the package maintainer for pack-

age p

may recognize that there is a conﬂict with a

package p

, so p

∈ C(p

), but the package main-

tainer for p

may not know about package p

and

so p

6∈ C(p

). Regardless of whether or not both

packages recognize the conﬂict, if it exists in either

direction then the packages cannot be installed simul-

taneously. We take care of both the possible lack of

symmetry and indirect conﬂicts from dependencies in

the following deﬁnition.

∗

(p) = {r | r ∈ C(d) for some d ∈ D

∗

(p) or

d ∈ C(r) for some d ∈ D

∗

(p)}. (1)

Note that C

∗

(p) is symmetric, meaning that r ∈ C

∗

(p)

if and only if p ∈ C

∗

(r). The package p in this deﬁni-

tion can be either a source package or a binary pack-

age, and if p

and p

are source packages with p

∈

∗

) that means that their build environments are

incompatible (some package required to build p

con-

ﬂicts with some package required to build p

). Con-

versely, if p

6∈ C

∗

) then the build environments

are compatible: all packages in D

∗

) ∪ D

∗

) can

be installed together, and that environment will sup-

port building binary packages from both p

and p

2.3 Model vs Real World

Our model captures the basic ideas of dependencies

and conﬂicts, but simpliﬁes and avoids some compli-

cations found in real-life package management sys-

tems. Below, we summarize the key differences be-

tween our model and the Debian package manage-

ment system that inspires this work.

Disjunctions in dependencies: While our model

deﬁnes dependencies D(p) to be a simple set of

packages, the Debian package manager allows

each dependency to be a disjunction which can

be satisﬁed in multiple ways. For example, in

Ubuntu 18.04, the xserver-xorg-input-all

has a single dependency, which is satisﬁed

by either xserver-xorg-input-libinput or

xserver-xorg-input-libinput-hwe-18.04. We

propagate these disjunctions up to the level of the

source package when computing C

∗

(p), and then

select a set of non-conﬂicting packages to satisfy

each disjunction in left-to-right preference order.

Minimum Size Build Environment Sets and Graph Coloring

This is the same choice made by the ofﬁcial Debian

build systems, as described in the Debian Policy

Manual: “To avoid inconsistency between repeated

builds of a package, the autobuilders will default

to selecting the ﬁrst alternative, after reducing any

architecture-speciﬁc restrictions for the build archi-

tecture in question” (Jackson et al., 2021). Our code

ﬁrst removes all disjunctions that are met by some

other (possibly transitively-induced) dependency, and

then performs an exhaustive search over disjunctions

to satisfy dependencies, which can take exponential

time in the worst case. In fact, other authors have

shown that the basic co-installability question for

packages is NP-complete due to the these disjunc-

tions (see the “Related Work” section). However, we

found the prioritization of packages leads to quick

dependency resolution in practice, with backtracking

in our search being very rare.

“Provides” pseudo-packages: Similar to explic-

itly providing alternatives for a dependency, Debian

allows for certain package names to represent “vir-

tual packages” which can be satisﬁed by a number of

real packages. For example, in Ubuntu 18.04, lpr

is both a binary package and a virtual package, and

the virtual package is provided by not only the binary

package named lpr but also by packages lprng and

cups-bsd which are drop-in replacements for the lpr

package. Our tools treat virtual packages the same as

disjunctions, described above.

Versions requirements in dependencies: Depen-

dencies can include version numbers as well as pack-

age names. For example, in Ubuntu 18.04 the

libfwsi1 requires libc6 version 2.14 or newer.

While these can technically specify arbitrary version

requirements, at least in Ubuntu 18.04 all version re-

quirements are met with the current (“candidate”) ver-

sion in all cases, and this seems to be mostly used for

systems that include packages from a mixture of ma-

jor distribution releases. Because of this, we ignore

version requirements in our tools.

Recommended packages: Dependencies and con-

ﬂicts aren’t the only relations between packages, and

packages can also “Recommend” or “Suggest” other

packages. Since these are not necessary in a build en-

vironment, our tools ignore these packages.

3 THE CONFLICT GRAPH AND

COLORING

In this section we deﬁne the “conﬂict graph” and

show how a valid vertex coloring of this graph deﬁnes

a feasible set of build environments. This provides

a standard and well-understood graph theory context

for understanding sets of build environments.

The conﬂict graph is an undirected graph that has

one vertex for each source package, and each edge

represents a conﬂict in the minimum build environ-

ments for two source packages that the edge connects.

In particular, we deﬁne the graph G = (V, E) where

the vertex set V = S (the set of source packages), and

E = {(p

, p

)| p

, p

∈ S and p

∈ C

∗

)}.

Since vertices are source packages, we interchangably

use the terms “vertex” and “source package” in the

rest of this paper. If two vertices are connected in

this graph, it means that there are incompatibilities in

the build environments for the two source packages,

so there is no build environment that can be used for

both.

An example showing a conﬂict graph for four

source packages is shown in Figure 1. While only

the nodes and edges are part of the graph, additional

details are shown in the picture: For each package

p, part of the dependencies in D

∗

(p) are shown, and

conﬂicts between packages in the dependency list in-

dicate which packages are in conﬂict.

3.1 Colorings and Build Environments

Given a graph G = (V, E), a k-coloring of this graph

is a mapping from vertices to a set of k colors, c : V →

{1, . . . , k}, such that no edge in G has endpoints of the

same color. In other words, for every (u, v) ∈ E, we

have c(u) 6= c(v). The goal in graph coloring prob-

lems is generally to minimize the number of colors k

required, and the minimum k for a graph G is called

the chromatic number of the graph, which is denoted

χ(G) = k.

In this section we consider colorings of the con-

ﬂict graph, and establish a correspondence between

these colorings and deﬁning sets of build environ-

ments. Consider a k-coloring on our conﬂict graph:

two source packages (i.e., vertices) that have incom-

patible build environments due to a conﬂict are con-

nected by an edge, so those source packages must

be assigned different colors. We will associate each

color with a distinct build environment, so this prop-

erty ensures that two source packages with incompati-

ble build environments in fact use different build envi-

ronments. We now prove that colorings on the conﬂict

graph have a one-to-one correspondence with sets of

build environments for the source packages.

Lemma 3.1. Every set of k distinct build environ-

ments that can be used to build all source packages

can be used to deﬁne a k-coloring on the conﬂict

graph.

ICSOFT 2022 - 17th International Conference on Software Technologies

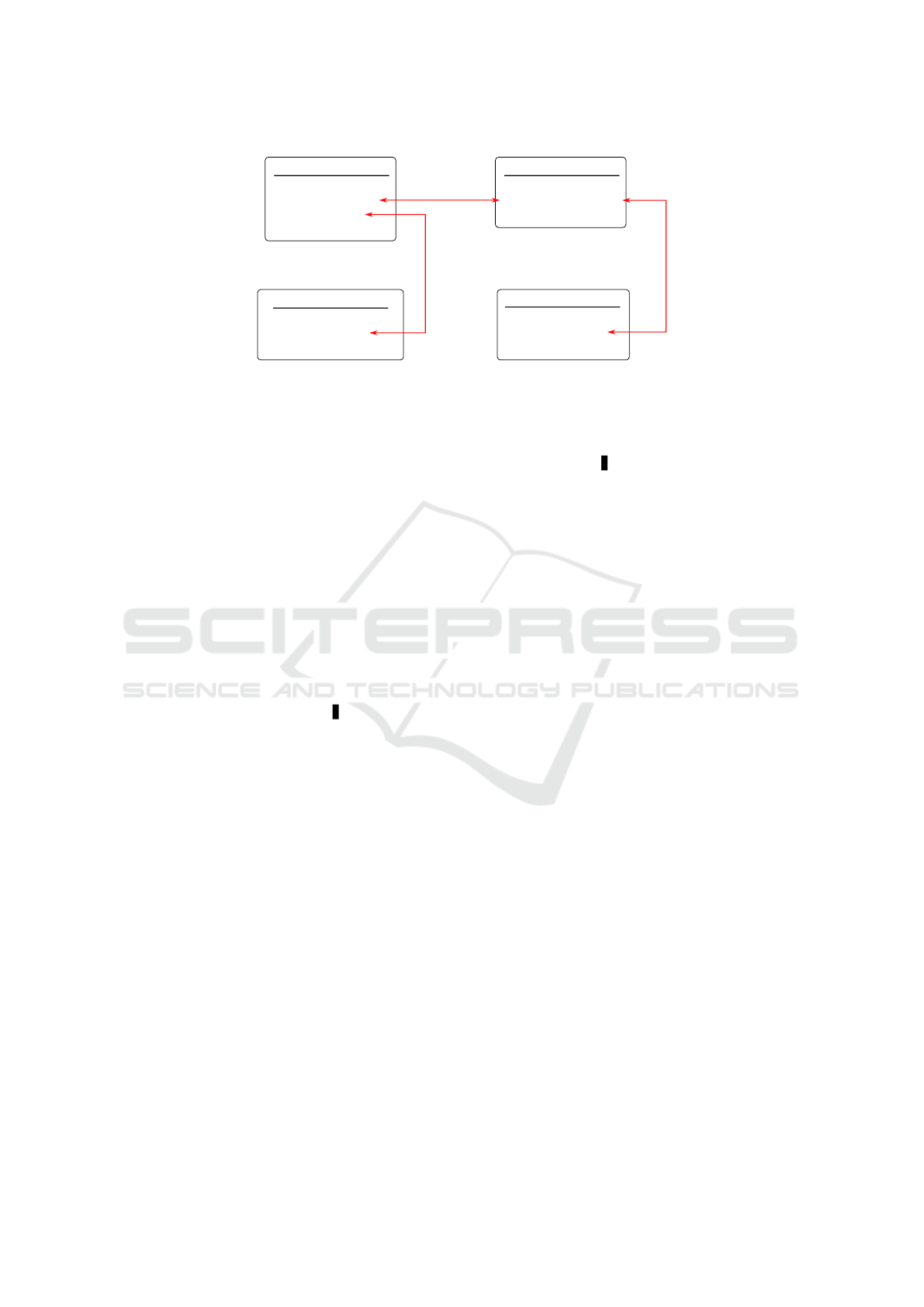
Package: wpa (#185)

Depends list:

libreadline-dev

libssl-dev

...

Package: lvm2 (#289)

Depends list:

libreadline-gplv2-dev

...

Package: openssl (#103)

Depends list:

libssl1.0-dev

...

Package: gnupg2 (#46)

Depends list:

libreadline-dev

...

Conflict

Figure 1: Example of source packages and dependencies producing a conﬂict graph.

Proof : For every i = 1, ·· · , k, let P

denote the set

of binary packages included in the ith build environ-

ment, and deﬁne a coloring c that assigns color i to

any vertex (source package) that uses this build en-

vironment. Since all source packages have a build

environment, every vertex is assigned a color. To see

that this is a valid coloring of the conﬂict graph, con-

sider two vertices v

and v

that are connected by

an edge (v

, v

) in the conﬂict graph, meaning that

∈ C

∗

). By (1) it follows that there is a d

∈

∗

) and d

∈ D

∗

) such that either d

∈ C(d

) or

∈ C(d

). Therefore, if v

uses build environment

and v

uses build environment P

, then d

∈ P

and

6∈ P

and so P

6= P

. Since v

and v

use different

build environments, they must have different colors

in c. As this holds for any edge (v

, v

) in the conﬂict

graph, and there are k build environments, c is a valid

k-coloring of the conﬂict graph.

Lemma 3.2. Every k-coloring of the conﬂict graph

can be used to create a set of k distinct build environ-

ments that is sufﬁcient to build all source packages.

Proof : Let c : V → {1, . . . , k} be a k-coloring of con-

ﬂict graph G = (V, E). The k-coloring partitions the

vertex set V , and we can deﬁne V

= {v|c(v) = i}.

Next, for each i = 1, . . . , k, deﬁne a set of binary pack-

ages P

= ∪

v∈V

∗

(v). We claim that for every source

package v ∈ V

, P

is a valid and feasible build envi-

ronment for that source package. The fact that P

sufﬁcient follows directly from the deﬁnition, since

that requires all dependencies of any v ∈ V

to be in-

cluded in P

For feasibility, we need to show that all packages

in P

can be installed simultaneously with no con-

ﬂicts. Consider to the contrary that there are conﬂict-

ing packages p

, p

∈ P

with p

∈ C(p

). The inclu-

sion of p

and p

must be the result of p

∈ D

∗

)

and p

∈ D

∗

) for some source packages v

, v

∈ V

This would mean that v

∈ C

∗

) by (1), and so there

is an edge (v

, v

) in the conﬂict graph. However,

since v

and v

are in the same V

partition compo-

nent, they must both have color i which violates the

basic coloring requirement. This contradiction com-

pletes the proof.

The following theorem follows directly from the

two preceding lemmas.

Theorem 3.1. The conﬂict graph has a k-coloring if

and only if there is a set of k distinct build environ-

ments that is sufﬁcient to build all source packages.

The above observations show that a minimum set

of build environments can be found by ﬁnding a min-

imum coloring of the conﬂict graph. However, the

question remains of whether ﬁnding build environ-

ments might in fact be easier than graph coloring –

is there some sort of structure to conﬂict graphs that

would lead to efﬁcient solutions, even though the min-

imum graph coloring problem is NP-complete?

Unfortunately, the answer to this question is “no.”

For an arbitrary graph G we can easily create a set

of source packages and conﬂicts for which the con-

ﬂict graph is G simply by making a distinct source-

to-source conﬂict for each edge in G. Note that we

don’t even need to consider binary packages and de-

pendencies for this construction. To be precise about

this, using the notation from Section 2 (where S is

a set of source packages, B is a set of binary pack-

ages, D is a dependency function, and C is a con-

ﬂict function), we deﬁne a decision problem (lan-

guage) MIN-BUILDENV= {hS , B, D, C, ki|there ex-

ist a set of k feasible build environments that is suf-

ﬁcient for building all source packages in S }. Then

what was described at the beginning of this paragraph

is a reduction from MIN-COLOR= {hG, ki| there is a

valid k-coloring of G}, a known NP-complete prob-

lem (problem [GT4] in (Garey and Johnson, 1979)),

to MIN-BUILDENV. This leads to the following the-

orem, which we state without further proof.

Theorem 3.2. MIN-BUILDENV is NP-complete.

While the reduction from MIN-COLOR to MIN-

Minimum Size Build Environment Sets and Graph Coloring

BUILDENV shows that MIN-BUILDENV has hard

worst-case instances, since the worst-case instances

created in that reduction are somewhat unnatural

it may be possible that real-world instances are

tractable. We explore properties of real-world soft-

ware conﬂict graphs in Section 4, but leave open the

question of whether typical real-world instances can

be solved efﬁciently. Before getting to the experimen-

tal results, however, we deﬁne and discuss an interest-

ing variant of our problem.

3.2 Nested Sets of Source Packages

As mentioned in the Introduction, our work in creat-

ing a formal framework in which to study this prob-

lem arose from our work in doing large-scale analy-

sis of open source software. To maximize the impact

of our software analysis work, we prioritize packages

based on how widely used they are, which we gauge

from the “Ubuntu Popularity Contest” project (The

Ubuntu Web Team, 2021). As we are working, we

might develop techniques on a small set of packages,

and then test on the most popular 100 Ubuntu pack-

ages. If that shows promising results, we might devote

more computational resources and analyze the most

popular 500, 1000, or even 5000 packages. In this

structure, we are working with nested sets of source

packages, and this motivates an extended version of

our build environment deﬁnition problem. For exam-

ple, if we set up a minimal set of build environments

for the most popular 500 packages, can we use those

environments (and possibly more) for the most popu-

lar 1000 packages? Unfortunately, this creates serious

difﬁculties, as we describe brieﬂy in this section.

To understand the problem, we will revisit the ex-

ample in Figure 1. The numbers beside each pack-

age name refer to the position of the package in the

Ubuntu Popularity Contest ranking, so openssl is

the 103rd most popular package, wpa is the 185th

most popular package, and so on. First consider what

would happen if we created build environments for

the most popular 150 packages, which would include

both openssl and gnupg2 in our computation. The

subgraph consisting of just those two packages can

be colored with a single color, meaning that a sin-

gle build environment can be constructed that can be

used to build both openssl and gnupg2. When we

expand this to the “top 300 packages,” we end up with

the full 4-vertex conﬂict graph shown in Figure 1.

To reuse the build environments we previously con-

structed, we would need to extend the existing color-

ing (where openssl and gnupg2 are given the same

color) into a coloring for the entire 4-vertex graph.

Unfortunately, when we retain those colors we require

3 colors (or 3 different build environments) for the 4-

vertex graph, while if we were to color the 4-vertex

graph from scratch we could do so with just 2 colors.

In other words, by trying to keep the same build en-

vironments from the “top 150 packages” solution, we

are forced to take a sub-optimal solution to the “top

300 packages” case.

Since extending from the smaller set of packages

to the larger doesn’t work, can we solve the larger

problem and restrict that solution to the smaller set?

Again, referring to Figure 1, we can see that any 2-

coloring of this graph results in the two more popular

packages, openssl and gnupg2, having different col-

ors. This means that when we restrict our larger so-

lution to just the two most popular packages, we are

forced to use two distinct build environments when

there is a single build environment that would work

in this situation.

It is important to recognize that using a larger set

of build environments not only increases storage re-

quirements, but also negatively impacts time required

for running a large set of builds. The reason for this

has to do with caching: If we build a package using

build environment A, and can reuse that same build

environment for a second package, many of the ﬁles

in build environment A will be cached in memory al-

ready, leading to a faster build for the second pack-

age. If the second package used a separate build en-

vironment B, as in the example in the previous para-

graph, then the ﬁles in environment B would need to

be loaded from disk in building the second package,

slowing down the process.

In our work, we have prioritized creating the

smallest set of build environments for each of the

nested sets of source packages, and do not try to reuse

environments from one collection of source packages

to the next. We feel that the gains while working

within that collection outweigh the costs associated

with maintaining an overall larger number of build

environments. We leave further optimization in this

setting to future work.

3.3 Conﬂict Graph Simpliﬁcation

When a conﬂict graph is created and examined, it

quickly becomes clear that there are some simpliﬁca-

tions that can be made to reduce the size of the graph

while still maintaining the correspondence between

coloring and build environments. The most obvious

is that approximately two-thirds of all source pack-

ages in modern Ubuntu releases have no conﬂicts at

all, so exist as isolated vertices in the conﬂict graph.

Since these vertices do not affect the coloring, they

can be removed from further processing and then as-

ICSOFT 2022 - 17th International Conference on Software Technologies

signed arbitrary colors at the end.

More generally, we can merge isomorphic vertices

into a single vertex. If source packages p

and p

have

the same set of conﬂicting source packages, meaning

that C

∗

)∩S = C

∗

)∩S, then vertices p

and p

can always be given the same color without affecting

anything else in a graph coloring. Because of this,

we merge isomorphic vertices, repeating this process

until a ﬁxed point is reached. As we’ll see in the next

section, this reduces the size of the graph we need

to color by over 90%, which is a great beneﬁt to the

heuristic graph coloring algorithms that we use.

4 EXPERIMENTAL RESULTS

In this section, we present experimental results that

we obtained in analyzing Ubuntu LTS releases. We

wrote software to extract dependency and conﬂict in-

formation from Debian package information using

Python and the Python APT Library

. This worked

well for Ubuntu releases 16.04 and later, but the ver-

sion of python-apt included with 14.04 lacked key

features that we relied on. Our code and results from

the base Ubuntu distributions is available in a pub-

lic GitHub repository under an open source license

where we describe the “hack” we had to perform to

extract 14.04 distribution graphs.

First, we examine basic properties of dependen-

cies and conﬂict graphs, as well as graph simpliﬁca-

tion as described above, to gain insight into the size

and structure of real-world data. Then in the follow-

ing section, we report on results from running heuris-

tic graph coloring algorithms on the generated graphs,

and discuss what that means for setting up build envi-

ronments.

4.1 Graphs from Ubuntu LTS Releases

We ﬁrst consider the overall graph metrics for four

major long-term-support (LTS) releases of the Ubuntu

Linux distribution, which were released at two year

intervals from 2014 to 2020. Understanding the ba-

sic graph metrics, and what has changed as well as

what has remained consistent over the years, allows

us to have a feel for what to expect in future releases.

Results for graph size for both the full conﬂict graph

and the simpliﬁed graph, as well as density measures,

are given in Table 1. All measures are made with the

original ofﬁcial release of each LTS version, installed

in virtual machines with updates disabled to ensure

https://apt-team.pages.debian.net/python-apt/library

https://github.com/srtate/BuildEnvAnalysis

that the original release is being used. In the table,

“Buildable SPKGS” refers to the number of buildable

source packages with each release. The “buildable”

part is signiﬁcant because both the 16.04 and 18.04

releases have six source packages included that could

not be built, since there were internal conﬂicts in their

dependency/conﬂict attributes. These were ﬁxed with

updates to the LTS release, but we wanted to be con-

sistent in using non-updated releases and so discarded

these unbuildable source packages.

As can be seen in the table, the number of source

packages has increased with every new release, giv-

ing an overall 39% increase from 2014 to 2020. Our

graph simpliﬁcation algorithm, as described in sec-

tion 3.3, consistently reduces the number of vertices

in the conﬂict graph by between 92% and 95%. Such

a signiﬁcant graph size reduction allows our heuristic

graph coloring algorithms to run signiﬁcantly faster,

allowing for more iterations of randomized strategies

to ﬁnd small colorings.

Also of interest is the structure and complex-

ity of the dependencies and conﬂicts. We origi-

nally predicted that dependency chains would be rel-

atively short, and while the vast majority of depen-

dency chains are under 10 links long, in our work

on the 18.04 release we found one dependency chain

of length 18. We found, unsurprisingly, a large

number of packages with mutual dependencies, al-

though some came from the same source package

and it’s unclear why separate binary packages are

built if they must always be installed together (e.g.,

language-pack-az and language-pack-az-base

depending on each other). While such mutual depen-

dencies give cycles of length two in the dependency

graph, there are simple cycles of varying lengths

larger than two as well (e.g., console-setup de-

pends on console-setup-linux, which depends on

kbd, which depends on console-setup.

With this understanding release sizes and metrics,

we next report our experimental results using heuris-

tic graph coloring algorithms on the constructed con-

ﬂict graphs.

4.2 Coloring Results for Ubuntu 20.04

Finding minimum graph colorings is NP-hard, and the

graphs we are considering, even the simpliﬁed graphs,

are far too large for any exact optimal graph color-

ing algorithm to succeed in a feasible amount of time.

Therefore, we need to rely on heuristic graph color-

ing algorithms, and in our work we use the suite of

graph coloring algorithms from Joseph Culberson

http://webdocs.cs.ualberta.ca/˜joe/Coloring/

Minimum Size Build Environment Sets and Graph Coloring

Table 1: Basic graph metrics for Ubuntu releases.

Ubuntu 14.04 Ubuntu 16.04 Ubuntu 18.04 Ubuntu 20.04

Buildable SPKGS 22,028 25,401 28,886 30,646

Full graph edges 207,894 214,982 376,028 387,175

Full graph density 0.0009 0.0007 0.0009 0.0008

Simpliﬁed graph vertices 1,646 1,943 1,476 1,770

Simpliﬁed graph edges 37,087 45,992 43,363 51,492

Simpliﬁed graph density 0.027 0.024 0.040 0.033

This software provides a variety of heuristics, rang-

ing from a simple greedy algorithm to versions that

use heuristics and randomization to ﬁnd better col-

orings. The programs take input in the “DIMACS

standard format,” as used in the DIMACS challenges

on graph coloring, so our conﬂict graph construction

software outputs the conﬂict graphs in this format,

along with a “translation table” that gives the mapping

from each source package name to its corresponding

vertex number.

We ﬁrst considered two versions of graphs that

represent all source packages, meaning the full con-

ﬂict graph and the simpliﬁed version as described in

Section 3.3. We automated the process of running

the coloring algorithms with different random seeds

and different heuristic options, and allowed the col-

oring programs to run for up to a full 24-hour day

on a Linux system with an Intel i7-7700 processor.

For both the full and simpliﬁed graphs generated from

the Ubuntu 20.04 distribution, the coloring software

found colorings using as few as 11 colors, meaning

that 11 distinct build environments are sufﬁcient to

build all 30,646 source packages. Since these are

approximation algorithms, we don’t know if 11 is

the minimum possible number of build environments

(or, equivalently, the chromatic number of the conﬂict

graph), but this is a small number of build environ-

ments for 30,646 packages.

Comparing the performance and success of color-

ing the full graph versus the simpliﬁed graph shows

the value of graph simpliﬁcation: the colorings found

on the simpliﬁed graph translate directly to the full

graph, but the reduced size allowed the coloring soft-

ware to run much faster and explore more options

with more random seeds. We completed over a mil-

lion (speciﬁcally, 1,050,000) runs on the simpliﬁed

graph in 24 hours, while we could only complete

23,835 runs on the full graph. Having a smaller graph

to work with also allowed the heuristic algorithms

to succeed more often, not getting stuck in parts of

the graph that lead to using larger numbers of colors.

Figure 2 shows histograms of the colors found over

all runs, for both the simpliﬁed and the full graphs.

Notice that the values are skewed more to the left,

meaning colorings with fewer colors, for the simpli-

Full Graph

12 14 16

Simpliﬁed Graph

0.08% of runs

give 11 colors

max # colors = 20

12 14 16 18 20 22

0.06% of runs

give 11 colors

max # colors = 22

Figure 2: Distribution on number of colors used by heuristic

run, as a percentage of all runs.

ﬁed graph. The range for the simpliﬁed graph is also

lower, with the coloring software producing colorings

ranging from 11 to 20 colors on the simpliﬁed graph,

and 11 to 22 colors on the full graph.

While the percentage of runs ﬁnding the smallest

(11 color) solution is only slightly higher for the sim-

pliﬁed graph (0.0806% of runs) than the full graph

(0.0587% of runs), that small advantage coupled with

the much higher rate of testing graphs, means that

the simpliﬁed graph found the smallest coloring much

faster than using the full graph. More speciﬁcally, the

ICSOFT 2022 - 17th International Conference on Software Technologies

ﬁrst coloring using 11 colors was found in just under

5 minutes on the simpliﬁed graph, but an 11-color re-

sult on the full graph was not obtained for an hour and

39 minutes.

4.3 Subgraph Colorings

We next consider ﬁnding colorings for nested sub-

graphs, as described in Section 3.2. To construct these

graphs for the Ubuntu 20.04 distribution, we ﬁrst used

the “Ubuntu Popularity Count” project data to ﬁnd the

top 500, 1000, 2000, and 4000 source packages. Note

that this is not as simple as just taking the ﬁrst names

from the popularity count ranking for two reasons:

First, not all packages listed are standard packages in

the Ubuntu release we are interested in (20.04 in this

case), and second, the ranking is for binary packages,

not source packages. To ﬁnd our lists, we ﬁrst ﬁl-

tered the popularity contest list to include only binary

packages that are a part of the Ubuntu 20.04 release,

then we mapped binary package names to the source

package used to build that package, and ﬁnally we re-

moved all but the ﬁrst occurrence of each source pack-

age (since a source package can build multiple binary

packages, it is common for multiple binary packages

for the same source package to be in the “Top X”

lists). As a result of this pre-processing, we obtained

a ranked list of source packages used in Ubuntu 20.04

from which we could extract the “Top X” lists.

Next, given the Top 500 source packages, we iden-

tiﬁed the vertices in the simpliﬁed conﬂict graph cor-

responding to those packages, removed duplicates,

and then computed the subgraph induced by those

vertices. We repeated this for the top 1000, 2000, and

4000 source packages. Given these graphs, we ran

105,000 iterations of the graph coloring algorithm on

each to determine the smallest coloring we could ﬁnd

in that amount of time. The results, showing graph

sizes and the best coloring we found, are in Table 2.

We were somewhat surprised at the graph sizes

and densities in the Top 500 and Top 1000 lists. We

initially expected that the main, most popular Ubuntu

packages would share a somewhat similar build envi-

ronment with few conﬂicts, leaving most conﬂicts to

arise from more esoteric packages that were less pop-

ular. This turned out not to be the case, with over a

hundred build environments deﬁned even in the small-

est Top 500 list, and a fairly consistent graph density

of 0.02-0.04 in each graph. The colorings we found

do reﬂect increasing levels of conﬂicts when more,

less popular packages are included, growing from just

4 colors (build environments) used for the Top 500

and Top 1000 lists, up to the 11 colors required for all

packages.

Due to the small sizes and number of colors found

for the Top 500 and Top 1000 graphs, we performed

another test. Since the size of the maximum clique in

a graph lower-bounds the chromatic number, and we

know the maximum clique of either of these smaller

graphs cannot be more than 4, we performed an ex-

haustive search to ﬁnd the maximum clique for both

graphs. For the Top 1000 graph, there is indeed a

maximum clique of size 4, so the 4-coloring of the

Top 1000 graph is optimal. However, the maximum

clique in the Top 500 graph has size 3, so it may be

possible to color the Top 500 graph with 3 colors.

Unfortunately, even guaranteeing a small chromatic

number doesn’t allow for efﬁcient, exact optimal col-

oring: The graph coloring problem is NP-complete

even for just distinguishing between 3-colorable and

4-colorable graphs.

As a ﬁnal note, this project was motivated by our

experience in an earlier project in which we were per-

forming large scale static analysis on the Top 1000

source packages in Ubuntu 18.04. When we ran into

build environment conﬂicts, we handled this problem

in an ad hoc way, resulting in around a dozen build

environments for the Top 1000 packages. Developing

a formal foundation for creating these build environ-

ments, as we report in this paper, reduces the number

of distinct build environments for that set of package

to just 4 distinct environments. This is a big improve-

ment for both efﬁciency of performing the analysis,

and for simplicity of managing the 1000 runs of the

static analyzer.

5 RELATED WORK

The public nature of the open-source software com-

munity provides a rich source of data for studying

large software systems. While we are not aware of

any prior work that looks speciﬁcally at the prob-

lem we study, deﬁning small sets of build environ-

ments, we brieﬂy survey some of the work related

to analyzing software distributions and dependencies

here. Early studies with Linux distributions, such

as (Gonz

alez-Barahona et al., 2003) focused on ba-

sic metrics such as distribution size, package size in

terms of ﬁles and lines of code, and programming lan-

guages used. Other studies, such as (Galindo et al.,

2010), used Linux distributions to study general con-

cepts such as variability models for software.

As distributions have grown, the complexity of

dependencies and conﬂicts have proven to be signif-

icant challenges for package and distribution main-

tainers, and modeling these relations has been studied

formally. (Mancinelli et al., 2006) developed an ex-

Minimum Size Build Environment Sets and Graph Coloring

Table 2: Basic graph metrics for Ubuntu 20.04 top-X subgraphs.

Top 500 Top 1000 Top 2000 Top 4000 All SPKGS

Vertices 117 198 355 594 1,770

Edges 151 375 2,388 6,385 51,492

Density 0.022 0.019 0.038 0.036 0.033

Best coloring 4 4 6 7 11

tended graph model that reﬂects both dependencies

and conﬂicts, and discussed dependency closures in

ways similar to our work, but with a focus on binary

packages and tasks a maintainer must do to accurately

deﬁne and visualize package relations. (de Sousa

et al., 2009) created a similar model, which they use

to study the properties of the dependency graph, look-

ing at degree connectivity distribution and modular-

ity, among other measures. While many of these

works use the Debian distribution due to its popularity

among academics, (Wang et al., 2015) perform simi-

lar graph modeling to visualize package dependencies

in Ubuntu 14.04, although they report only looking at

a graph with 2,240 vertices which would be a small

subset of the total Ubuntu 14.04 packages.

Researchers have also studied dependency and

conﬂict relations in regard to how changes in pack-

ages can violate relations. (Di Cosmo et al., 2013)

developed a formal model that was used for study-

ing update failures, with a focus on end-users up-

dating their systems as well as maintainers deﬁning

appropriate relations. They look speciﬁcally at “co-

installability” of packages, similar to our deﬁnition

of compatible build environments, although their fo-

cus is on binary packages and operational systems

rather than build environments. Installability from

an end-user standpoint was also studied by (Vouil-

lon and Cosmo, 2013), where they relate installability

tests to the satisﬁability (SAT) problem, bring up NP-

completeness issues as we have, and they also explore

graph simpliﬁcation/compression techniques similar

to our techniques in Section 3.3. (Claes et al., 2015)

study package conﬂicts and broken packages at a ﬁne-

grained level, using daily snapshots reﬂecting ongo-

ing developer work.

Recently, the appearance of language-speciﬁc

code repositories for developers, such as NPM (for

JavaScript), CRAN (for R), and PyPI (for Python),

have raised similar dependency challenges, but in a

different context (Decan et al., 2016; Kikas et al.,

2017; Decan et al., 2019). Of particular interest, (De-

can et al., 2016) show that topology of dependency

networks varies between different language ecosys-

tems, and while they did not compare with full operat-

ing system distributions it is a reasonable extension to

believe that the wide diversity of software included in

full operating system distirubions will be even more

different.

The above-mentioned work is focused primarily

on the challenges developers and end users face in

maintaining operational systems in light of dependen-

cies and conﬂicts, and do not address source packages

or build environments. The only work we’re aware

that looks speciﬁcally at large-scale software build-

ing in open source distributions is the work of (Nuss-

baum, 2009), which describes re-building an entire

Debian distribution from source packages. Nussbaum

was interested in whether the “build dependencies”

were deﬁned properly, so created a separate minimal

build environment for each package, and used a large

grid computing infrastructure to perform the builds.

Our work, focused on re-using build environments,

installs far more packages than the minimal set for

any package, so we would not be able to test this par-

ticular feature. We would be able to address another

question tested by Nussbaum, however, and that is the

question of whether updated tool-chains are still capa-

ble of successfully building from the provided source

packages.

6 CONCLUSIONS AND FUTURE

WORK

In this paper, we formalized the problem of design-

ing build environments for large-scale software build-

ing and analyzing, addressing issues with dependen-

cies and conﬂicts between components. We showed

that there is a one-to-one correspondence between the

problem of minimizing the number of build environ-

ments and the problem of minimizing the number of

colors required to color a constructed graph, which we

call the conﬂict graph. We also considered ways to

simplify the resulting conﬂict graph, and considered

the problem of coloring increasing-size nested sub-

graphs. Our results provide some interesting metrics

for the complexity of the build requirements (conﬂict

graph) for various Ubuntu LTS releases, and we use

heuristic graph coloring software to generate small

numbers of build environments for the Ubuntu 20.04

distribution. We were able to construct a set of 11

build environments that were sufﬁcient to build all

30,646 source packages in Ubuntu 20.04, and a set

ICSOFT 2022 - 17th International Conference on Software Technologies

of just 4 environments for building all of the top 1000

“most popular” source packages. The work reported

here provides a clear way to think about the build

environment problem, and the experimental results

show that small sets of build environments are sufﬁ-

cient, signiﬁcantly improving on the ad hoc approach

to setting up build environments.

There are several directions for future work, and

we describe two immediate open problems here.

First, since dependencies can include disjunctions

(“or-lists”) that can be satisﬁed in multiple ways,

is there a way to do this that can reduce the num-

ber of build environments? More speciﬁcally, our

or-list resolution uses the same process as the stan-

dard Debian build tools, taking the package main-

tainer’s order of the or-list as the priority order for

satisfying the dependency. While this is certainly

a sound approach when making a single build envi-

ronment, when considering build environments sup-

porting multiple packages we may be able to reduce

the number of conﬂicts by making different choices.

For example, most source packages require either the

pkg-config or pkgconf package, but while pkgconf

is a drop-in replacement for the older pkg-config

some packages keep dependency speciﬁcations that

prioritize the older package. Since these two packages

conﬂict with each other, could forcing all packages to

use pkgconf, despite the package maintainer prior-

ity speciﬁcation, reduce the number of conﬂicts and

hence the number of build environments required?

As a second open question, while we studied the

issue of coloring nested subgraphs, we were not able

to formulate a clear objective for this minimization.

Is there a metric for nested subgraph colorings that

makes sense in our setting? The metric may require

some additional information about the efﬁciency of

performing builds using these environments, or it

might depend on preferences of the users (i.e., priori-

tizing smaller overall number of environments or pri-

oritizing re-use of environments used for subgraphs),

so just determining the proper goal is a ﬁrst step in

considering algorithms to solve this problem.

REFERENCES

Claes, M., Mens, T., Di Cosmo, R., and Vouillon, J. (2015).

A Historical Analysis of Debian Package Incompati-

bilities. In 2015 IEEE/ACM 12th Working Conference

on Mining Software Repositories, pages 212–223.

de Sousa, O. F., de Menezes M.A., and Penna, T.

(2009). Analysis of the package dependency on De-

bian GNU/Linux. Journal of Computational Interdis-

ciplinary Sciences, 1(2):127–133.

Decan, A., Mens, T., and Claes, M. (2016). On the topol-

ogy of package dependency networks: a comparison

of three programming language ecosystems. In Proc-

cedings of the 10th European Conference on Software

Architecture Workshops (ECSAW), pages 1–4.

Decan, A., Mens, T., and Grosjean, P. (2019). An empirical

comparison of dependency network evolution in seven

software packaging ecosystems. Empirical Software

Engineering, 24(1):381–416.

Di Cosmo, R., Treinen, R., and Zacchiroli, S. (2013). For-

mal Aspects of Free and Open Source Software Com-

ponents. In 11th International Symposium on Formal

Methods for Components and Objects (FMCO), pages

216–239.

Galindo, J., Benavides, D., and Segura, S. (2010). Debian

Packages Repositories as Software Product Line Mod-

els. Towards Automated Analysis. In Proceeding of

the First International Workshop on Automated Con-

ﬁguration and Tailoring of Applications (ACOTA).

Garey, M. R. and Johnson, D. S. (1979). Computers and

intractability. W.H. Freeman, San Francisco.

Gonz

alez-Barahona, J. M., Robles, G., Ortu

no-P

erez, M.,

Rodero-Merino, L., Centeno-Gonz

alez, J., Matell

an-

Olivera, V., and Castro-Barbero, E. (2003). Analyzing

the Anatomy of GNU/Linux Distributions: Method-

ology and Case Studies (Red Hat and Debian). In

Free/Open Source Software Development, Idea Group

Inc, pages 27–58.

Jackson, I., Schwarz, C., and Morris, D. A.

(2021). Debian policy manual (version 4.6.0.1).

https://www.debian.org/doc/debian-policy/.

Kikas, R., Gousios, G., Dumas, M., and Pfahl, D. (2017).

Structure and Evolution of Package Dependency Net-

works. In 2017 IEEE/ACM 14th International Confer-

ence on Mining Software Repositories (MSR), pages

102–112.

Mancinelli, F., Boender, J., di Cosmo, R., Vouillon,

J., Durak, B., Leroy, X., and Treinen, R. (2006).

Managing the Complexity of Large Free and Open

Source Package-Based Software Distributions. In 21st

IEEE/ACM International Conference on Automated

Software Engineering (ASE’06), pages 199–208.

Nussbaum, L. (2009). Rebuilding Debian using distributed

computing. In Proceedings of the 7th International

Workshop on Challenges of Large Applications in Dis-

tributed Environments (CLADE), pages 11–16.

The Ubuntu Web Team (2021). Ubuntu popularity contest.

https://popcon.ubuntu.com/.

Vouillon, J. and Cosmo, R. D. (2013). On software compo-

nent co-installability. ACM Transactions on Software

Engineering and Methodology, 22(4):34:1–34:35.

Wang, J., Wu, Q., Tan, Y., Xu, J., and Sun, X. (2015).

A graph method of package dependency analysis on

Linux Operating system. In 2015 4th International

Conference on Computer Science and Network Tech-

nology (ICCSNT), pages 412–415.

Minimum Size Build Environment Sets and Graph Coloring