Multilinear Modeling and Simulation of a Multi-stack PEM Electrolyzer

with Degradation for Control Concept Comparison

Aline Luxa

1 a

, Niklas J

ores

1 b

,Carlos Cateriano Y

nez

1,2,3 c

, Marina Nascimento Souza

1 d

Georg Pangalos

1 e

, Leona Schnelle

2 f

and Gerwald Lichtenberg

2 g

Application Center for Integration of Local Energy Systems, Fraunhofer IWES, Hamburg, Germany

Faculty of Life Science, HAW Hamburg, Germany

Universitat Polit

ecnica de Val

encia, Instituto Universitario de Autom

atica e Inform

atica Industrial, Val

encia, Spain

Keywords:

Multilinear Simulation, Energy Systems, PEM Electrolyzer, Multi-stack Operation, Controller Design,

Degradation, Wind Energy.

Abstract:

Hybrid energy systems, e.g., with wind energy and hydrogen production, have a high model complexity due

to their multi-physics nature, which poses major control challenges for the optimization of plant operation.

This work aims at addressing this issues by introducing a highly efﬁcient modeling and simulation framework.

A proton exchange membrane (PEM) electrolyzer stack, including degradation and controller, has been mod-

eled using the multilinear class. This class enables the automatic append of individual models, which is used to

stack a 100 multi-stack PEM electrolyzer model. Moreover, the multilinear class models can be represented as

tensors, which allows for efﬁcient decomposition methods and formats. This is used to considerably enhance

the simulation performance of the system, making the simulation of a one year multi-stack electrolyzer opera-

tion possible, with a reasonable computational cost. In the simulation, two different high-level control modes

are compared regarding overall degradation gain and electrolyzer efﬁciency. The developed modeling and

simulation framework has proven its suitability for big-scale complex models, enabling efﬁcient simulations

for controller analysis.

1 INTRODUCTION

The transition of the energy system from centralized

to local holds a variety of challenges, which can be

tackled by model-based approaches. For this, simu-

lation problems are getting larger with an enormous

number of states. Therefore, innovative modeling

methods are needed to be able to solve control and

optimization tasks.

The future power grid will be constructed of

a multitude of local energy systems. These are

formed by combinations of renewable energy gen-

eration units, consumers, and energy storage sys-

tems. This results in a modeling problem for con-

https://orcid.org/0000-0002-3025-3274

https://orcid.org/0000-0003-2471-3892

https://orcid.org/0000-0001-5261-2568

https://orcid.org/0000-0003-2523-5669

https://orcid.org/0000-0001-5094-8033

https://orcid.org/0000-0002-2600-8110

https://orcid.org/0000-0001-6032-0733

trolling numerous local energy system (LES). One

possible composite of LES is a coupled wind park

with electrolyzers for hydrogen production. Accord-

ing to the coalition agreement 2021to2025, Germany

has a 10 GW goal of electrolysis capacity until 2030.

To achieve this goal, Germany would need to build

several plants in the larger MW range, many of which

are already being planned. Trianel and Stadtwerke

Hamm signed a joined venture with the goal to in-

stall 20 MW electrolyzer capacity in the natural gas

power plant Hamm-Uentrop by 2022. Shell, Mit-

subishi Heavy Industries, Vattenfall and W

arme Ham-

burg signed a declaration of intent to build 100 MW

installed capacity of electrolysis in the port of Ham-

burg, which is supposed to be in operation in 2025

(Geitmann, 2022).

In the near future, the mass production of proton

exchange membrane (PEM) electrolysis stacks in the

larger kW to MW range is expected. Systems of mul-

tiple GW capacity will be mostly composed of stacks

between 1 and 2 MW (P. Ayivor et al., 2018). There-

fore, electrolyzer systems with a nominal capacity in

Luxa, A., Jöres, N., Yáñez, C., Souza, M., Pangalos, G., Schnelle, L. and Lichtenberg, G.

Multilinear Modeling and Simulation of a Multi-stack PEM Electrolyzer with Degradation for Control Concept Comparison.

DOI: 10.5220/0011263300003274

In Proceedings of the 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2022), pages 52-62

ISBN: 978-989-758-578-4; ISSN: 2184-2841

the larger MW to GW area will be constructed of

several hundred stacks. In a modular approach for

a high power electrolysis system, stacks are usually

connected in parallel or sometimes in series, which

is then called string or cascade. Larger systems with

smaller stacks are constructed with strings connected

in parallel.

There are many stack manufactures that offer

modular scale-up solutions, e.g., Green Hydrogen

Systems (GHS) alkaline electrolyzer system is scal-

able up to 20 MW, while GHS current portfolio

is offering options in the range from 125to390 kW

(Green Hydrogen Systems, 2022). Similarly, H-

TEC SYSTEMS offers a PEM electrolyzer of 1 MW

containing 9 stacks (H-TEC SYSTEMS GmbH,

2022). Enapter approaches the market with a

highly modular anion exchange membrane (AEM)

system with nominal capacity of 1 MW composed

of 420 stacks (Enapter, 2022). Therefore, the mod-

eling problem of control and operation optimization

for the multi-stack electrolyzer (mELY) emerges.

When operating an mELY, there is the conﬂict be-

tween optimizing efﬁciency and stack lifetime. Gain-

ing a higher efﬁciency by running more stacks in par-

tial load conﬂicts with degradation of each stack, de-

pending on the load. A central main controller has

to decide between partial load operation and shutting

down stacks completely to prevent aging. Therefore,

electrolyzer degradation plays a special role in the

modeling problem and cannot be neglected. The in-

troduction of degradation models into control applica-

tions is known generally but is not yet done for mELY,

to the best of the authors’ knowledge (Zagorowska

et al., 2020). It can be assumed that this is because

suitable degradation models and powerful modeling

approaches are missing.

Overall, the main purpose of the paper is build-

ing the base for the optimization of large controlled

mELY systems considering stack degradation, by us-

ing the multilinear time-invariant (MTI) model class.

The MTI model class, which current developments

can be explored in (Lichtenberg et al., 2022), is

a powerful modeling tool, when it comes to com-

bining submodels of a system. The possible auto-

matic model generation can be coupled with model

reduction methods, for decreased complexity and in-

creased simulation performance. With the MTI model

approximation of nonlinear models, basic nonlinear

phenomena are representable. Furthermore, the MTI

models allow deterministic runtimes with a rank, that

is increasing linearly, and not exponentially with the

order of the system(Lichtenberg et al., 2022). There-

fore, the MTI framework is chosen for the autom-

atized combination of the submodels: electrolyzer,

electrolyzer controller, degradation, and main con-

troller for renewable power distribution, for an arbi-

trary number of stacks. The modeling framework al-

lows to later on substitute every submodel easily, if,

e.g., degradation models develop further. The evalua-

tion of the simulation results help to decide for differ-

ent control schemes for mELY operation.

First, in section 2 multilinear modeling and the

applied methods for model reduction are introduced.

Afterwards, the used individual models are described

in section 3, including the electrolyzer, electrolyzer

controller, and degradation, which will be composed

to the total single-stack electrolyzer (sELY) model.

In section 4 the main controller model and the stack-

ing for the mELY model composition is described.

The section 5 contains a code to code validation of

the stand alone MTI electrolyzer stack model approx-

imation by comparing nonlinear, linear, and multilin-

ear simulation results. Furthermore, the total mELY

system is simulated with renewable power input from

wind data. Afterwards, the analysis of the simulation

results is executed in section 6. Finally, in section 7

the key ﬁndings are derived, and further steps are de-

scribed for future work.

2 MULTILINEAR MODELING

In the following chapter, the explicit multilinear time-

invariant (eMTI) model description will be intro-

duced, which is an extension to the standard linear

time-invariant (LTI) class. In contrast, to LTI the

eMTI class allows for multiplication of states and/or

inputs (Pangalos et al., 2013).

Explicit multilinear models are no universal ap-

proximators per se like other model classes (Hornik

et al., 1989). However, they are able to model

general polynomial dependencies by either extension

of the state space (Kruppa, 2018) or using implicit

forms (Lichtenberg et al., 2022). This chapter also

includes the model reduction methods.

2.1 Multilinear Tensor Modeling

The state and output equations of an explicit multi-

linear model in tensor representation as introduced

in (Pangalos et al., 2013; Lichtenberg et al., 2022) is

given as

x =

M(x,u)

, (1a)

y =

M(x,u)

, (1b)

where

∼

denotes the contracted prod-

uct, F ∈ R

n+m

z }| {

2 ×. .. ×2 ×n

and G ∈ R

n+m

z }| {

2 ×. .. ×2 ×l

contain the

Multilinear Modeling and Simulation of a Multi-stack PEM Electrolyzer with Degradation for Control Concept Comparison

parameters of the model and M(x,u) ∈ R

n+m

z }| {

2 ×. .. ×2

the monomial tensor given in canonical polyadic

(CP) decomposed form as

M(x,u) =





,...,









,...,





(2)

with number of states n, number of inputs m, and

number of outputs l. An example for n = 2 and m = 1

is given as

In case of full tensors, the contracted product is

calculated as illustrated by the following example

for a tensor X ∈ R

2×2×3

and a tensor Y ∈ R

2×2

. To

calculate the contracted product Z =

∈ R

the matching dimensions, which are highlighted

in red, have to be multiplied element-wise

211

221

111

121

212

222

112

122

213

223

113

123

211

221

111

121

212

222

112

122

213

223

113

123

211

221

111

121

212

222

112

122

213

223

113

123

The element-wise multiplication is shown exemplar-

ily for z

= x

111

+ x

121

+ x

211

+ x

221

. (3)

To calculate the state update, when the model is

in CP tensor form with parameter tensors given as

F =



,...,F



, (4a)

G =



,...,G



, (4b)

the contracted product simpliﬁes to

x=F







~· · ·~







n+1





~· · ·~



m+n





, (5a)

y=G







~· · ·~







n+1





~· · ·~



m+n





, (5b)

where ~ denotes the element-wise or Hadamard prod-

uct.

2.2 Reduction of Simulation Complexity

To reduce simulation complexity, the transition ten-

sors F and G can be approximated using tensor de-

composition methods. The decomposition can be per-

formed by using the alternating least squares algo-

rithm (Kolda, 2006). In general, low values for the

ranks r

and r

are desired. However, a trade-off can

be seen between the rank and the approximation error.

Adequate values for r

and r

can be determined by

a parameter study, comparing the results of the mini-

mum possible rank for a solution of the optimization

and higher ranks until the error is acceptable (Bro and

Kiers, 2003). The approach on how to perform the CP

decomposition for MTI models is explained in (Pan-

galos et al., 2013; Lichtenberg et al., 2022).

The CP decomposed parameter tensor, as shown

in (4), can be normalized by applying different nor-

malization methods to the columns of the factor matri-

ces F

,i = x

,...,x

,...,u

,φ as shown in (Licht-

enberg et al., 2022) for 1-norm and in (Schnelle et al.,

2022) for the euclidean 2-norm. The normalized pa-

rameter tensor

,...,

∈R

n+m

}| {

2 ×. .. ×2 ×n

,(6)

is deﬁned by normalized factor matrices

∈ R

2×r

with i = 1...n + m, rank r, and

∈ R

n×r

with arbi-

trary values.

With the so called sparse-norm, the columns of

the factor matrices of the not normalized CP tensor F

were normalized to their ﬁrst elements such that all

ﬁrst elements get ﬁxed to one. This leads to a normal-

ized representation where only the second elements

need to be stored in a vector



2,1

1,1

2,2

1,2

,··· ,

2,r

1,r



∈ R

1×r

, (7)

where f

1, j

∈ R\{0}, with j = 1 · · · r. The vectors can

SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

be stored in a matrix

F =

















∈ R

(n+m)×r

, (8)

and the MTI model is fully deﬁned by this matrix and

= F

~ (λ

,λ

,...,λ

) ∈ R

n×r

, (9)

by element-wise multiplication with the weights of

normalization λ

∏

n+m

i=1

(1, j).

3 SINGLE-STACK

ELECTROLYZER MODELING

In this section all individual submodels for the sELY

combination will be described, followed by their

composition. Later on, the sELY units will be stacked

to build the total system for mELY simulation. The

shown example is a purely continuous-time problem

with all real variables. The current approach is re-

stricted to models with concentrated parameters de-

scribed by ordinary differential equations (ODE) and

not distributed parameters described by partial differ-

ential equations (PDE).

3.1 Electrolyzer Model

For this paper, a 46 kW PEM electrolyzer model

from literature is used to demonstrate the combi-

nation of the subsystems in eMTI format for large

mELY operations (Espinosa-L

opez et al., 2018). The

nonlinear model is built up in MATLAB/Simulink,

which is the base for the eMTI approximation, gener-

ated by the projection method (Kruppa et al., 2014).

The thermal dynamic electrolyzer model has two

states, i.e., temperature T and cooling power state x

two inputs, i.e., current i

ely

and membrane degrada-

tion r

, and two outputs, i.e., voltage v

ely

and stack

efﬁciency η

ely

. Thus, the state, input and output vec-

tors are

x =





,u =



ely



,y =



ely



. (10)

The ODE for describing the thermal dynamic

states are introduced in the following. The temper-

ature change is described by

∑

k=1

∑

k=1

∑

k=1

, (11)

with z

power

W , z

heat

Q and z

enthalpy

H streams,

and the lumped thermal capacity C

(Espinosa-L

opez

et al., 2018). As introduced in (Lichtenberg et al.,

2022), the cooling heat

cool

is directly controlled by

a PI controller, with state space model

cool

= x

+ K

∆T, (12a)

= K

∆T. (12b)

The electrolyzer efﬁciency is deﬁned as

ely

˙n

ely

, (13)

containing the higher heating value of hydrogen H

and the output hydrogen molar stream ˙n

, which is

deﬁned in (Espinosa-L

opez et al., 2018). For calcu-

lations of the electrolyzer voltage, cathode activation

overpotential and mass transfer losses are neglected.

Therefore, the equation reduces to

ely

= v

ocv

+ v

ohm

+ v

act−an

, (14)

including the open circuit voltage v

ocv

, ohmic overpo-

tential v

ohm

, and anode activation overpotential v

act−an

(Espinosa-L

opez et al., 2018).

For performing a multilinearization, an operating

range needs to be deﬁned for the application. PEM

electrolyzers can be operated in overload for some

time, which is mostly limited by the thermal man-

agement (Kopp et al., 2017). Also, there could be

a restriction regarding a minimum load, which is in-

ﬂuenced by the power consumption of ancillary com-

ponents. This would add a boolean state variable for

the electrolyzer operation for actually being turned on

or off. In mELY operation, running below minimum

load can mostly be prevented by completely turning

off stacks and shifting the power to different ones. Al-

lowing minimum or overload operation would there-

fore add another two boundary conditions to the main

controller introduced in subsection 4.1. Nevertheless,

for this demonstration there is no beneﬁt in this, since

the degradation model cannot yet include the effect

of start-stop events. Therefore, the operating range

is assumed to be 0to100 % of the nominal load p

nom

of 46 kW for each stack, at the state of begin of life

(BoL) (no degradation). Even though the electrolyzer

is only operated until 100 % load, the upper and lower

bounds for multilinearization of the model using the

projection method were determined with a load up to

150 % and 40 nodes. This was assumed to generate a

higher accuracy at the nominal operation point. Due

to limited space, the parameter tensors of the multi-

linear model of the electrolyzer are not shown here.

3.2 Electrolyzer Controller Model

Each electrolyzer stack has an individual integral

feedback controller, which is tracking the error of the

Multilinear Modeling and Simulation of a Multi-stack PEM Electrolyzer with Degradation for Control Concept Comparison

power reference given by the main multi-stack con-

troller and the current power of the stack, see Figure 2.

A key feature of this controller is the multilinear term

that calculates the current stack power. Thus the con-

troller can not be represented as a linear system but as

an MTI system. The stack controller can be expressed

in CP representation as follows,

ctrl



1 0

0 1





0 1

1 0





1 0

0 1





−K



(15a)

ctrl



















, (15b)

where K

= −1.28e−4 is the gain for the integrator.

3.3 Degradation Model

The current density, temperature, and pressure are

factors that affect the PEM membrane electrode as-

sembly (MEA) degradation mechanisms. Some of

these mechanisms are: thinning of the membrane, de-

composition of catalyst layer, and passivation of the

porous transport layer (PTL). The mechanisms are

caused by thermal and chemical stress, catalyst par-

ticle agglomeration at high temperature, dissolving

of catalyst particles at high current densities, poison-

ing by metallic species, and oxidation of metals (Bahr

et al., 2020). Separating the individual effects of each

mechanism is very challenging. The study (Rakousky

et al., 2017) reports degradation rates under different

current densities, discovering catalyst degradation on

the anode and increase of contact resistance at the ti-

tanium PTL as the two main degradation causes. In

(Frensch et al., 2019) degradation rates under constant

current and three different dynamic proﬁles are stud-

ied, concluding that anode catalyst degradation plays

a minor role compared to ohmic resistance change.

In (Bahr et al., 2020) a neural network application to

describe the degradation rate is developed, by apply-

ing experimental results of accelerated aging tests to

a data trained model. The study reports degradation

rates according to current density and can be further

developed with a broader database and under differ-

ent temperature and pressure conditions. However,

such a data-based model has no insight into changes

of electrochemical parameters and rely on the exper-

imental data. While predominant mechanisms have

been investigated, up to date there is still no model

for the description of aging due to ﬂuctuant operation

of PEM electrolysis.

In addition, stacks of an mELY system degradate

at different rates according to the operation condi-

tions. Therefore, the electrochemical model param-

eter of each stack can vary. As stated before, there

are no generic phenomenological degradation models

for PEM electrolyzers published, that can represent

the inﬂuence on partial or dynamic load, as well as

start-stop events. Nevertheless, for this work it is not

essential to apply a degradation model that describes

the electrochemical processes in detail. However, it

will be demonstrated, how the degradation model can

be integrated into the mELY system. The degrada-

tion model in this work is therefore to be considered

as an estimate. It cannot be validated, as data over

years of operation, even with accelerated aging tests,

would be needed, which are currently non-existing.

The combination of models establishes a basis to in-

clude more sophisticated degradation models to be

developed later on.

The ﬁrst assumption for the model is that

the degradation only affects the membrane resis-

tance (ohmic overpotential), and therefore just one

electrochemical parameter. This is based on the ﬁnd-

ings of (Rakousky et al., 2017) and (Frensch et al.,

2019) mentioned above, as well as on own experi-

mental work, which is not published yet. To describe

the variation of resistance, a total voltage drop rate,

according to nominal operation time, is assumed. In

(Buttler and Spliethoff, 2018) a rate of 4to8 µV h

−1

given, while 7 µV h

−1

total degradation rate is given

by (Kosonen et al., 2016). In this case 7 µV h

−1

degra-

dation rate at nominal load is used as base assump-

tion. The overall degradation is ﬁtted to the mem-

brane resistance as displayed in Figure 1.

0.5

1.5

1.2

1.4

1.6

1.8

2.2

Current density in A/cm

Cell voltage in V

begin of life degraded

time

Figure 1: IV-curve ﬁtted to total degradation at nominal

load.

The single cell starting IV-curve (BoL) in Fig-

ure 1, which is not yet affected by degrada-

tion, is calculated by the base PEM electrolyzer

model from (Espinosa-L

opez et al., 2018) at 60

◦

SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

and 35 bar cathode pressure. The aging process

of 7µV h

−1

is displayed at 1.48 A cm

−2

(46 kW at no

degradation) for 10 years with 4000 full load hours

(FLH) operation per year. The assumption of 10

years is a conservative lifetime estimation of different

sources (Buttler and Spliethoff, 2018; IRENA, 2020;

Cihlar et al., 2020) and at 4000 FLH green hydro-

gen gets cost competitive to fossil fuel based hydro-

gen (Agora Energiewende and Guidehouse, 2021).

As the voltage increases over time, the slope of

the IV-curve changes, which can be ﬁtted as displayed

in Figure 1. The ﬁt was done by an optimization,

adjusting the slope of the IV-curve by changing r

until the degradation point was crossed. By this, the

values for r

until end of life (EoL) were estimated.

The deviation of the description of v

ohm

in (Espinosa-

opez et al., 2018) is implemented into the elec-

trolyzer model as

ohm

= (R

mem

+ r

ely

. (16)

In the following, the degradation resistance could be

analyzed over time and ﬁtted by a linear function,

with a slope f

equal to the degradation rate. For the

overall degradation model, the aging is assumed to be

in linear proportion to the input current with 0 % at

no load and 100 % of f

at nominal load. This leads

to the general ODE description of

= i

ely

. (17)

The model for the degradation is linear and can

therefore be formulated as eMTI model in CP repre-

sentation as

deg









, f



, (18a)

deg



1 0

0 1





0 1

1 0





1 0

0 1



. (18b)

3.4 Series Composition of Models

The submodels will be connected in a series connec-

tion, which is described for eMTI models in (Licht-

enberg et al., 2022). The block diagram in Figure 2

shows the single input, multiple output (SIMO) degra-

dation and multiple input, single output (MISO) con-

troller system in composition with the electrolyzer

model. In further descriptions, the combination of the

three models will be referred to as sELY.

The upper bound on the rank of the sELY model

in CP form is r

= 12 and r

= 13. This can further

be reduced by using the alternating least squares algo-

rithm. A good approximation for the sELY was found

with r

= 6 and r

= 4, which reduces the memory

requirement by more than half.

ref

−

ELY

Controller

Degradation

sELY

Figure 2: Scheme of the series connection of the elec-

trolyzer controller, degradation and electrolyzer model.

4 MULTI-STACK

ELECTROLYZER

For the mELY simulation, the main controller is cre-

ating the power input vector p

ref

by distributing the

total wind power. The sELY models are composed

into one system and receive p

ref

as input. The power

distribution options and the composition method are

described in the following.

4.1 Main Controller Model

The main mELY controller is a high-level controller

with the principal objective of generating the power

set point for each individual stack

ref







ref







, (19)

where p

ref

≥ 0 for all i ∈ [1, · · · , N] and N is the num-

ber of stacks in mELY. Then p

ref

is supplied as an

input to mELY as seen in Figure 3.

There are two feedforward operation modes. In

the base mode (mode 1 - equal), the wind power input

data p

wind

will be distributed equally to each stack,

resulting in the same power reference

ref

(t) = min



nom

wind

(t)



, (20)

for each unit. This is equivalent to a set of P con-

trollers with the same gain for each stack, and a sat-

uration to prevent values above the single stack nom-

inal power p

nom

. Here, the difference in the initial

conditions of the degradation model of each stack, is

expected to be the main driver for the overall mELY

performance.

In the second mode (mode 2 - max), the power is

distributed in such a way that the number of fully shut

off stacks is maximized, while still providing the to-

tal requested power with the remaining online stacks.

Multilinear Modeling and Simulation of a Multi-stack PEM Electrolyzer with Degradation for Control Concept Comparison

This can be formulated as a minimization problem

min

ref

∑

σ(p

ref

, (21)

s.t.

∑

ref

= min (p

wind

,N p

nom

), (21a)

where σ is the Heaviside step function and r

is the

initial degradation of the i

stack.

This mode implies that almost all the remaining

online stacks will be operating at nominal power, ex-

cept when the total requested power is not a multiple

of the nominal stack power, in which case one stack

will need to take the remainder. In this strategy, the

stacks with the lowest initial degradation will be se-

lected ﬁrst for nominal operation, such that the ones

with the most initial degradation are shut off to im-

prove the overall mELY efﬁciency.

wind

Controller

ref

sELY

ref

sELY

ref

sELY

ref

mELY

Figure 3: Multi-stack operation scheme.

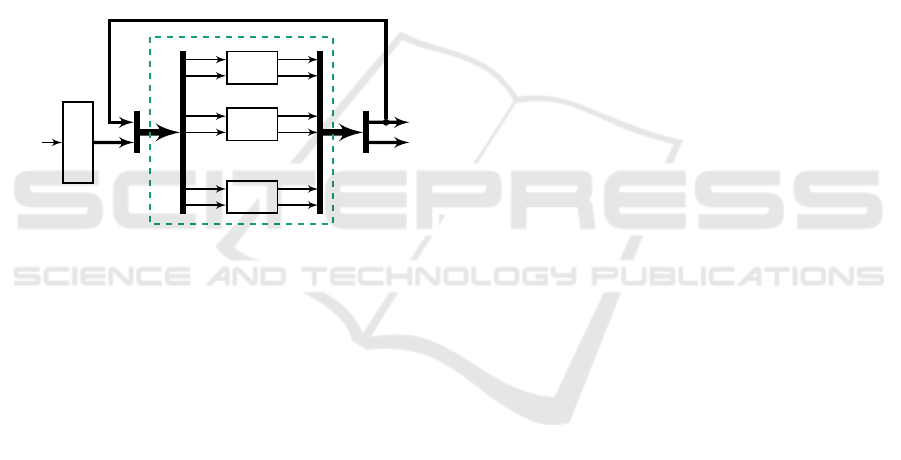
4.2 Composition

For the connection of systems, three different op-

tions, i.e., series, parallel, and feedback have been in-

troduced in (Lichtenberg et al., 2022).

In the case of an mELY, all subsystems can be fed

with different amounts of power between minimum

and maximum load. They work independently, with-

out inﬂuencing each other, see Figure 3. Therefore,

the sELY eMTI models are not connected in series,

parallel or feedback, when considering an indepen-

dent power supply for each unit. Hence, the append

connector must be implemented for eMTI systems,

which is grouping the submodels by appending their

inputs and outputs (The MathWorks, Inc., 2022).

An eMTI model is fully deﬁned with the nor-

malized factor matrices

F ∈ R

(n+m)×r

and the ma-

trix

∈ R

n×r

. The append connector can then be

applied easily by having the factor matrices of the in-

dividual stacks on the diagonal for the mELY

mELY







x,1

··· · · · ··· ··· ·· · 0

··· 0

x,N

··· ··· 0

u,1

··· 0

··· ··· ··· ··· ··· 0

u,N







(22a)

φ,mELY







φ,1

··· 0

φ,N







, (22b)

where

mELY

∈ R

N(n+m)×r

and

φ,mELY

∈ R

Nn×r

are

the factors of a system with N stacks and 0

∈ Z

n×r

and 0

∈ Z

m×r

and 0

∈ 0

n×r

are zero matrices. For

each stack i the corresponding factors

x,i

u,i

and

φ,i

are generated as given by (8) and (9).

Remark: While doing the appending of

mELY

the order for the states and inputs must be maintained,

such that all factor matrices for the states

x,N

and

then the factor matrices for the inputs

u,N

are ap-

pended ﬁrst. It can be seen, that these matrices con-

tain several zeros which are not needed to describe

the system behavior. Here, we can make use of the

sparsity to reduce memory requirements.

5 SIMULATION RESULTS

In this section, the simulation results of the eMTI

electrolyzer model individually and the mELY opera-

tion are presented.

5.1 Electrolyzer Individual Operation

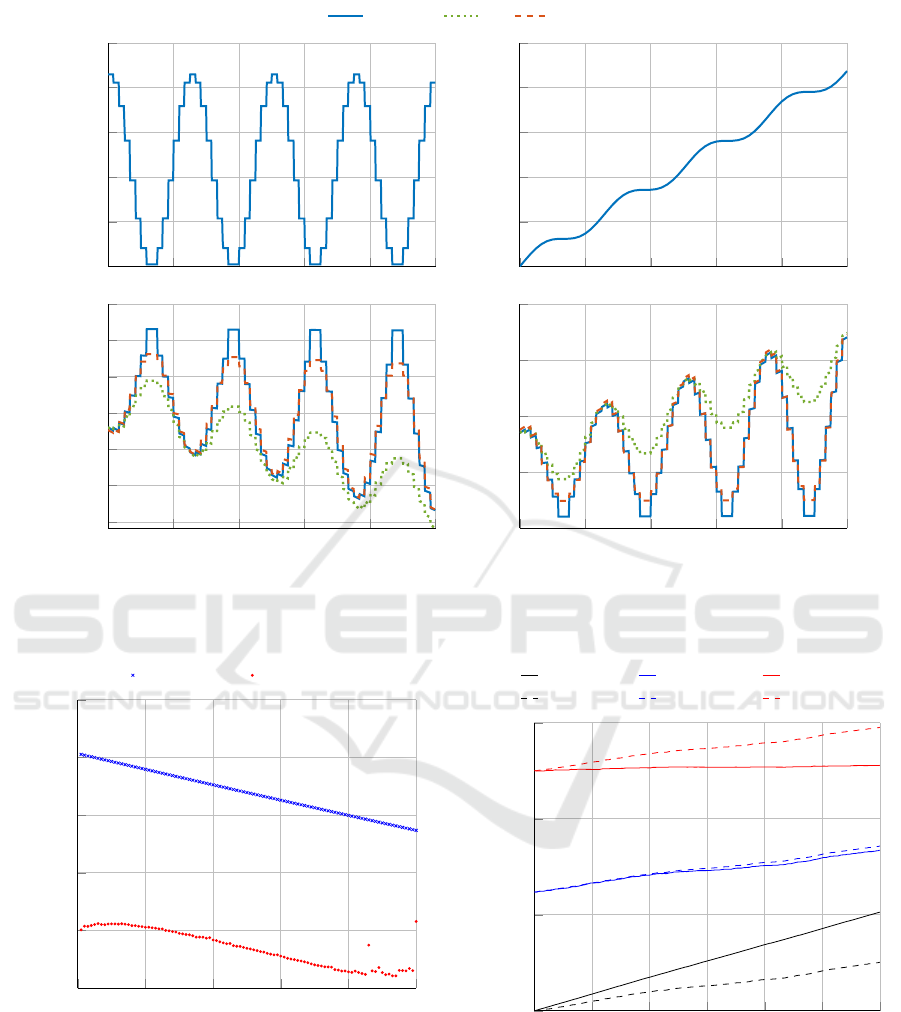
To display the advantage of eMTI class, one elec-

trolyzer stack model is compared to LTI and non-

linear simulation in Figure 4. The whole opera-

tion range over the planned 10 years electrolyzer

lifetime is reproduced by cycling the input current

from 0to100 % of the nominal loads current at no

degradation (i

nom

= 429.87 A, for 46 kW stack

power with 0 % degradation). In a real operation the

cycling would happen much faster and arbitrarily, ac-

cording to renewable energy production. Neverthe-

SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

less, for this demonstration the extended constant cur-

rent input operation periods allow seeing the effects

of degradation more clearly. The degradation is in

a range between 0 % at BoL and 100 % at the esti-

mated EoL, as described in subsection 3.3. As it can

be observed in Figure 4 (b), the model can also dis-

play operation after EoL. Overall, the output variables

of the eMTI model follow the nonlinear behavior over

time, with a stronger deviation at the lower bound-

aries of the operation range. This could be caused by

the increased range of the upper bounds to 150 % for

the multilinearization. The accuracy of the linear ap-

proximation is very good in the beginning at the lin-

earization point, but deviates at partial load, which is

getting worse over time.

The states were also analyzed, which are not dis-

played here for brevity. According to the degradation

caused rise of overpotentials, the change in tempera-

ture is increasing during fast load changes, which can

roughly be represented either by the LTI and eMTI

model. The requirement for standard Naﬁon

mem-

branes to stay below 90

◦

C (Christoph Edler, 2018) is

fulﬁlled at any time.

5.2 Multi-stack Electrolyzer Operation

For the mELY operation of 100 stacks, wind data has

been used to produce a power proﬁle. The wind data

of the year 2021 was taken from a measuring station

at 110 m height on the Fraunhofer IWES test ﬁeld in

Bremerhaven, with a sample rate of 10 min. By us-

ing an Enercon E-115 2.500 (2.5 MW) power curve,

the wind data was translated to the power proﬁle. Af-

terwards, it was scaled up to ﬁt the 4.6 MW power

demand of the mELY at nominal load (0 % degrada-

tion). For both operation modes, the same power data

was used as input to the main controller. Also, the ini-

tial degradation value was set from 0to50 % linearly

so that the 1

stack (sELY

) is not degraded at the

beginning and the 100

(sELY

100

) stack is degraded

by 50 %. In Table 1, the mean electrolyzer efﬁciency

over the whole year is compared. If p

ref

= 0, the ef-

ﬁciency value is not considered for the mean value

calculation. The degradation gain of the entire plant

in Table 1 is a mean value of all stacks.

Table 1: Comparison of two control modes for the power

distribution of a 100 stack mELY operation (one year).

Mode η

ely,mean

Degradation

in % gain in %

1 - equal 86.78 9.61

2 - max 82.33 9.35

The mean efﬁciency of mode 1 is higher, as can be

observed for the 100 stacks in Figure 5. Since mode 1

results into long periods of partial load operation this

behavior is reasonable. This can also be the reason

for the increased efﬁciency of sELY

and sELY

100

mode 2. The mean plant degradation gain is 0.26 %

less for mode 2. Theoretically, with the linear degra-

dation model and the same overall current input, the

degradation gain should be the same for both modes.

The deviation can result from the inaccuracy of the

controller and degradation models. In Figure 6, dif-

ferent aging rates can be observed for sELY

, sELY

and sELY

100

, showing a correlation of the degradation

slope and the individual stack load.

To perform the simulation an S-Function was im-

plemented using a MATLAB-ﬁle. For the simulation

settings, a ﬁxed time-step was used with automated

solver detection and T

= 36.9 s, which represents

the fastest dynamics of the electrolyzer. The overall

run time of the simulation was 2.81 h using MAT-

LAB R2021b. The simulations are performed on a

computer equipped with an Intel®Core™ i7-9850H

CPU @ 2.60GHz and 16 GB RAM.

6 DISCUSSION

In this section, the eMTI model accuracy and

the mELY simulation results are evaluated.

6.1 Multilinear Model Accuracy

Regarding the individual models for the electrolyzer

controller, degradation, and main controller, no mul-

tilinear approximation was needed, since the systems

are either linear or multilinear right away. However,

when combining the submodels to the overall sELY

model, an approximation was performed to improve

computational time.

To generate the eMTI electrolyzer model approx-

imation, the projection method was used. Overall, re-

garding the electrolyzer model accuracy, the follow-

ing basic statements can be made:

• the eMTI model is more accurate than the LTI

model over the total operating range,

• the LTI model is exact at operational current with

no degradation (linearization point),

• the LTI model cannot handle model changes due

to degradation,

• the eMTI model accuracy is rated as sufﬁcient for

this application.

For future improvements, a reasonable strategy would

be to re-linearize after a certain amount of time

Multilinear Modeling and Simulation of a Multi-stack PEM Electrolyzer with Degradation for Control Concept Comparison

100

200

300

400

500

(a)

current in A

100

125

(b)

degradation until EoL in %

0 2 4

8 10

100

t / years

(e)

efﬁciency in %

0 2 4

8 10

100

110

120

130

t / years

(d)

voltage in V

Nonlinear

LTI eMTI

Figure 4: Individual electrolyzer operation for comparison of LTI, eMTI and nonlinear simulation.

0 20 40

80 100

0.8

0.82

0.84

0.86

0.88

0.9

stack number

mean efﬁciency in %

Mode 1 - equal Mode 2 - max

Figure 5: Mean values for the individual stack efﬁciency

over one year of operation.

(degradation), wherefore the LTI model stays more

accurate over time. Nevertheless, this would not make

up for low performance of the LTI model in partial

load. Therefore, a combination of LTI and eMTI rep-

resentation is considered optimal, which can even be

combined in a single MTI system, by switching from

0 2 4

8 10 12

time in month

degradation until EoL in %

sELY

max sELY

100

max

sELY

equal sELY

100

equal

Figure 6: Comparison of degradation for 3 of 100 stacks

over one year of operation.

eMTI to LTI near the operational point. A different

option to enhance the accuracy of the eMTI represen-

tation would be to implement a weighting function to

the projection method, such that the approximation at

the nodes near nominal load is considered more im-

SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

portant (Kruppa et al., 2014). This would at the same

time mean a reduced accuracy at the other nodes of

the grids, representing the operation range. Overall,

the eMTI electrolyzer model accuracy can be consid-

ered sufﬁcient for this simulation task.

6.2 Multi-stack Electrolyzer Operation

The results in subsection 5.2 show a clear inﬂuence of

the main controller operation mode on the mELY per-

formance. With the same total power input and sim-

ply changing the power distribution to the stacks, the

efﬁciency can be enhanced. By including more com-

plex degradation phenomena also overall degradation

could be prevented. Therefore, this model provides

a base for a large optimization problem, with vari-

ous options for the cost function, e.g., the total eco-

nomic beneﬁt of the plant from BoL to EoL or sus-

tainable hydrogen production. Therefore, the degra-

dation model needs to be developed further, since

there is no inﬂuence of, e.g., temperature, dynamic

load changes or start-stop events included yet. By

also considering the effect of load changes on aging,

it could be beneﬁcial for speciﬁc stacks to buffer the

dynamic behavior.

The mELY model is built by appending the eMTI

models. This can be achieved by extending the ap-

pend function from MATLAB for the MTI class.

This process is considerably simpler than construct-

ing mELY with general nonlinear models in Simulink.

Modeling of the mELY in a single eMTI model

makes a further tensor decomposition possible, which

results in reduced memory and computational re-

sources for the simulation. However, the decompo-

sition method must be chosen carefully, as the struc-

tural zeros are removed due the factorization. This

can lead to inaccurate decompositions. An analysis of

appropriate decomposition methods will be part of fu-

ture work. In addition, implementing the S-Function

in C instead of using a MATLAB-ﬁle will increase the

simulation speed signiﬁcantly.

7 CONCLUSIONS

In this paper, a modeling and simulation framework

for an mELY operation has been developed. For this

purpose, a single electrolyzer stack eMTI model, with

degradation input was thoroughly tested. The intro-

duced eMTI electrolyzer model has shown sufﬁcient

accuracy for the application. The nonlinear behavior

and the dynamics of the mELY could be represented

by the eMTI model for the whole operation range.

However, modeling errors of the eMTI class could be

larger than for general nonlinear represention.

By including the append connector into the MTI

model class, the combination of 100 sELY units with

individual degradation and power controller model

could be done automatically. The performed model

reduction methods on the eMTI system were essen-

tial to reduce computational cost and generate output

data for one year. The output data of the mELY op-

eration showed that different control schemes have a

strong inﬂuence on the overall electrolyzer efﬁciency.

A similar effect can be observed in the single stack

level, where the degradation gain changes with the

load proﬁle of each control concept.

In general, eMTI models are suitable to represent

energy systems with large number of states. This

enables the implementation of modern model-based

control methods. By this work, the MTI model class

has been further established for engineering applica-

tions. This is important since the promising MTI tools

are not part of general educational programs, or as

well-tried as linear or nonlinear tools yet.

For future work, an electrolyzer model with im-

proved accuracy, by either using a weighting func-

tion or a combination with an LTI model, will be pur-

sued. Also, there are numerous options for further

simulation performance enhancement, like the use

of different tensor decomposition methods for ﬁnd-

ing low rank approximations or the implementation

of the S-Function in C. Prospectively, the submod-

els can be improved and easily exchanged. To up-

grade the degradation model, observers can be used

with accelerated stress test data, to ﬁnd further corre-

lations between aging, current, temperature, pressure,

and load changes. For the electrolyzer efﬁciency, the

ancillary components can be considered, as well as

a minimum load range. Also, an option for over-

load could be included, with consideration of heat and

hydrogen ﬂow management limitations. This can be

implemented in a main advanced feedback controller

model. By considering the degradation state and ef-

ﬁciency feedback, the main controller could perform

a multi-criteria optimization. Overall, this modeling

approach sets the base for various further develop-

ments, while also serving as a controller test bench.

Future studies are currently focused in mELY power

distribution operation schemes, which can be imple-

mented by electrolyzer operators for a larger return of

invest and plant lifetime.

ACKNOWLEDGEMENTS

This work was partly supported by the Free and

Hanseatic City of Hamburg and by the project

Multilinear Modeling and Simulation of a Multi-stack PEM Electrolyzer with Degradation for Control Concept Comparison

SONDE of the Federal Ministry of Education and Re-

search, Germany (Grant-No.: 13FH144PA8).

REFERENCES

Agora Energiewende and Guidehouse (2021). Making re-

newable hydrogen cost-competitive: Policy instru-

ments for supporting green H

Bahr, M., Gusak, A., Stypka, S., and Oberschachtsiek, B.

(2020). Artiﬁcial neural networks for aging simula-

tion of electrolysis stacks. Chemie Ingenieur Technik,

92(10):1610–1617.

Bro, R. and Kiers, H. A. (2003). A new efﬁcient method

for determining the number of components in parafac

models. Journal of Chemometrics: A Journal of the

Chemometrics Society, 17(5):274–286.

Buttler, A. and Spliethoff, H. (2018). Current status of water

electrolysis for energy storage, grid balancing and sec-

tor coupling via power-to-gas and power-to-liquids: A

review. Renewable and Sustainable Energy Reviews,

82:2440–2454.

Christoph Edler (2018). Untersuchung der Einsatz-

moeglichkeiten von Hochleistungselektrolyseuren

fuer Netzdienstleistungen. diploma thesis, TU Wien,

https://repositum.tuwien.at/handle/20.500.12708/

7708.

Cihlar, J., Villar Lejarreta, A., Wang, A., Melgar, F., Jens,

J., and Rio, P. (2020). Hydrogen generation in eu-

rope: Overview of costs and key beneﬁts. Luxem-

bourg. Publications Ofﬁce of the European Union.

Enapter (2022). The AEM Multicore: Lowest-Cost Flexible

Hydrogen at Megawatt-Scale. https://www.enapter.

com/aem-multicore, Accessed: 28.02.2022.

Espinosa-L

opez, M., Darras, C., Poggi, P., Glises, R., Bau-

cour, P., Rakotondrainibe, A., Besse, S., and Serre-

Combe, P. (2018). Modelling and experimental val-

idation of a 46 kW PEM high pressure water elec-

trolyzer. Renewable Energy, 119:160–173.

Frensch, S. H., Fouda-Onana, F., Serre, G., Thoby, D.,

Araya, S. S., and Kær, S. K. (2019). Inﬂuence of

the operation mode on PEM water electrolysis degra-

dation. International Journal of Hydrogen Energy,

44(57):29889–29898.

Geitmann, S. (2022). HZwei - Das Magazin f

ur Wasser-

stoff und Brennstoffzellen. Hydrogeit Verlag. Issue 1,

January 2022.

Green Hydrogen Systems (2022). HyProvide™: A-Series.

https://greenhydrogensystems.com/wp-content/

uploads/2021/02/A-Series-brochure-120421.pdf,

Accessed: 28.02.2022.

H-TEC SYSTEMS GmbH (2022). H-

TEC PEM-Elektrolyseur ME450/1400.

https://www.h-tec.com/produkte/detail/

h-tec-pem-elektrolyseur-me450-1400/me450-1400/,

Accessed: 17.03.2022.

Hornik, K., Stinchcombe, M., and White, H. (1989). Multi-

layer feedforward networks are universal approxima-

tors. Neural Networks, 2(5):359–366.

IRENA (2020). Green Hydrogen Cost Reduction: Scaling

up Electrolysers to Meet the 1.5

◦

C Climate Goal. In-

ternational Renewable Energy Agency. Abu Dhabi.

Kolda, T. G. (2006). Multilinear operators for higher-order

decompositions. Technical report, Citeseer.

Kopp, M., Coleman, D., Stiller, C., Scheffer, K., Aichinger,

J., and Scheppat, B. (2017). Energiepark Mainz:

Technical and economic analysis of the world-

wide largest Power-to-Gas plant with PEM electrol-

ysis. International Journal of Hydrogen Energy,

42(19):13311–13320.

Kosonen, A., Koponen, J., Huoman, K., Ahola, J., Ruuska-

nen, V., Ahonen, T., and Graf, T. (2016). Optimiza-

tion strategies of PEM electrolyser as part of solar

PV system. In 2016 18th European Conference on

Power Electronics and Applications (EPE’16 ECCE

Europe), pages 1–10. IEEE.

Kruppa, K. (2018). Multilinear Design of Decentralized

Controller Networks for Building Automation Sys-

tems. PhD thesis, HafenCity Universit

at Hamburg.

Kruppa, K., Pangalos, G., and Lichtenberg, G. (2014). Mul-

tilinear approximation of nonlinear state space mod-

els. IFAC Proceedings Volumes, 47(3):9474–9479.

Lichtenberg, G., Pangalos, G., Cateriano Y

nez, C., Luxa,

A., J

ores, N., Schnelle, L., and Kaufmann, C. (2022).

Implicit multilinear modeling. at - Automatisierung-

stechnik, 70(1):13–30.

P. Ayivor, J. Torres, M.A.M.M. van der Meijden, R. van der

Pluijm, and B. Stouwie (2018). Modelling of large

size electrolyzer for electrical grid stability studies in

real time digital simulation. IEEE.

Pangalos, G., Eichler, A., and Lichtenberg, G. (2013). Ten-

sor systems - multilinear modeling and applications.

3rd International Conference on Simulation and Mod-

eling Methodologies, Technologies and Applications

(SIMULTECH-2013), pages 275–285.

Rakousky, C., Reimer, U., Wippermann, K., Kuhri, S.,

Carmo, M., Lueke, W., and Stolten, D. (2017). Poly-

mer electrolyte membrane water electrolysis: Re-

straining degradation in the presence of ﬂuctuating

power. Journal of Power Sources, 342:38–47.

Schnelle, L., Lichtenberg, G., and Warnecke, C. (2022).

Using low-rank multilinear parameter identiﬁcation

for anomaly detection of building systems. 11th

IFAC Symposium on Fault Detection, Supervision and

Safety for Technical Processes. Status: accepted.

The MathWorks, Inc. (2022). append - Group models

by appending their inputs and outputs. https://de.

mathworks.com/help/control/ref/lti.append.html, Ac-

cessed: 16.03.2022.

Zagorowska, M., Wu, O., Ottewill, J. R., Reble, M., and

Thornhill, N. F. (2020). A survey of models of degra-

dation for control applications. Annual Reviews in

Control, 50:150–173.

SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications