Neural Networks for Indoor Localization based on Electric Field Sensing
Florian Kirchbuchner
1 a
, Moritz Andres
2 b
, Julian von Wilmsdorff
1
and Arjan Kuijper
1 c
1
Fraunhofer IGD Darmstadt, Fraunhoferstrasse 5, Darmstadt, Germany
2
Technische Universit
¨
at Darmstadt, Germany
Keywords:
Localization, Indoor Localization, Electronic Field Sensing, Neural Networks, Machine Learning, Data
Acquisition.
Abstract:
In this paper, we will demonstrate a novel approach using artificial neural networks to enhance signal process-
ing for indoor localization based on electric field measurement systems Up to this point, there exist a variety
of approaches to localize persons by using wearables, optical sensors, acoustic methods and by using Smart
Floors. All capacitive approaches use, to the best of our knowledge, analytic signal processing techniques to
calculate the position of a user. While analytic methods can be more transparent in their functionality, they
often come with a variety of drawbacks such as delay times, the inability to compensate defect sensor inputs or
missing accuracy. We will demonstrate machine learning approaches especially made for capacitive systems
resolving these challenges. To train these models, we propose a data labeling system for person localization
and the resulting dataset for the supervised machine learning approaches. Our findings show that the novel
approach based on artificial neural networks with a time convolutional neural network (TCNN) architecture
reduces the Euclidean error by 40% (34.8cm Euclidean error) in respect to the presented analytical approach
(57.3cm Euclidean error). This means a more precise determination of the user position of 22.5cm centimeter
on average.
1 INTRODUCTION
In the field of ambient assisted living, or AAL for
short, localization of an user is a key role of sensor
functionality. Many technologies capable of indoor
localization already found their way into our daily life
with the rise of smart homes. The applications are
numerous and range from navigation of indoor clean-
ing devices, such as automated vacuum cleaners, se-
curity applications like burglar detection and various
energy optimization tasks. The latter can be achieved
by controlling lights and heaters in a more granular
way, since these resource intensive actors are mostly
needed near the position of a person.
There are numerous solutions for indoor localiza-
tions. Fu et al. (Fu et al., 2020a) have classified the
sensor categories into acoustic, electric, optical, elec-
tromagnetic and hybrid systems. A deeper view is
given in Figure 1.
Currently, there are many publications on wire-
less localization solutions in the literature. Machine
a
https://orcid.org/0000-0003-3790-3732
b
https://orcid.org/0000-0001-6115-5098
c
https://orcid.org/0000-0002-6413-0061
Figure 1: Sensor categorization for indoor localization as
depicted by Fu et al.(Fu et al., 2020a).
learning methods are often used in this context. Obei-
dat et al. considered satellite-based, magnetic-based,
sound-based optical-based and RF-based technolo-
gies (Obeidat et al., 2021). The presented approaches
mainly operate in the 2.4GHz region and locate the
person using the angle of arrival, time of arrival as
well as by using the received signal strength. Also
Roy et al. summarized similar technologies for indoor
localization mainly based on wireless systems such as
WiFi, Infrared, RFID, Bluetooth and more(Roy and
Kirchbuchner, F., Andres, M., von Wilmsdorff, J. and Kuijper, A.
Neural Networks for Indoor Localization based on Electric Field Sensing.
DOI: 10.5220/0011266300003277
In Proceedings of the 3rd International Conference on Deep Learning Theory and Applications (DeLTA 2022), pages 25-33
ISBN: 978-989-758-584-5; ISSN: 2184-9277
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
25

Chowdhury, 2021). The authors focused on tech-
nologies using machine learning techniques, but in
contrast to our approach, none of them use capaci-
tive sensors in combination with machine learning ap-
proaches.
As shown, many systems rely on some sort of time
of flight or other optical solutions. While many of
these optical systems provide a superb resolution and
are robust for indoor localization, they lack a very im-
portant property - user acceptance.
As shown by Kirchbuchner et al. (Kirchbuchner
et al., 2015) most people have less concerns using a
smart floor system than using an equivalent localiza-
tion system based on cameras.
Frank et al. showed similar results in a conducted
survey(Frank and Kuijper, 2020). Although he pri-
marily considered capacitive sensors for the use in au-
tomotive systems, his results can be generalized.
A reason for the lack of machine learning ap-
proaches for indoor localization with capacitive sys-
tem could be the large amount of data that is required
to train such a system. Since there are no datasets
for these kind of problems because capacitive sys-
tems and their recorded data have not been standard-
ized in any shape of form, Fu et al. also published
approaches to augment time series of capacitive data
sets(Fu et al., 2020b). With this, datasets of capacitive
data can be artificially enlarged to improve training
results.
As described by Nam et al., some efforts have
been made to integrate machine learning techniques
in capacitive screen technologies(Nam et al., 2021).
These approaches were used to improve the sensing
performance of the devices, to discriminate individ-
ual touches and for user identification as well as au-
thentication. But as mentioned, these approaches use
systems with a much higher resolution.
Faulkner et al. closes the gap between capaci-
tive touch systems and indoor localization by present
a very fine granular localization approach(Faulkner
et al., 2020) - with the drawback of using a lot of
computing power to cover a small spacial area with
sensors. Faulkner et al. want to use machine learn-
ing as described in their future work section, but not
for the localization itself. But this case is particularly
interesting because it could lead to localization sys-
tems with a higher resolution and the need of less sen-
sors, which would lead to enormous savings in cost
for such an indoor localization system.
Figure 2: Test person walking on smart floor with visible
wire pattern.
2 OWN APPROACH
In this chapter we will describe the methods for the
person localization. First, we describe the analytical
approach which has been used up to now with an error
of 57.3cm. Afterwards, we will present the artificial
neural networks and show that these models are supe-
rior to the previous technique.
2.1 Analytic Approach
For our analytic method we used multi-staged pre-
processing pipeline for each sensor depicted in figure
3 and a heatmap pipeline as shown in figure 6.
Figure 3: Processing pipeline for each signal from the EFS
sensors.
The first stage of the pre-processing pipeline is
a high pass filter which removes the value drift of
the sensors and therefore helps to identify true sen-
sor activities. This is necessary since passive electric
field sensors (also called electric potential sensors) are
prone to distortions arising from the ambient electri-
cal 50Hz field, which occurs in every building from
the in-cooperated power-lines. The drift of these sen-
sors results from an aliasing effect when sampling this
nearly 50Hz ambient sine wave with a nearly 50Hz
clock. For this purpose we use a fast Fourier transfor-
mation (FFT) and its inverse (iFFT) to set the ampli-
tude of all frequencies above 2 Hz to zero and trans-
form it back to the time domain. Figure 4 depicts
a single electrode with walking activity. Note that
the walking activity results in a high frequency de-
flection of the sensor, while the overall low-frequency
sine wave behavior is the result of the previously men-
DeLTA 2022 - 3rd International Conference on Deep Learning Theory and Applications
26

tioned aliasing effects of the ambient 50Hz field.
Figure 4: Voltage of a single electrode. Areas marked in red
show walking activities on the electrode.
We use this new signal as a baseline and subtract it
from the original signal. The resulting high pass filter
is applied for each sensor independently.
Afterwards we pick the sample in the middle of
the filtered window as the new sensor value. We do
that because the FFT is most accurate for the center of
a window and hence the center has the most accurate
baseline.
This step results in a dead-time of the filter which
is half the size of the window and thus the window
size requires a balance between the frequency resolu-
tion of the FFT and the dead-time of the filter. Ad-
ditionally, due to the use of the FFT the number of
samples must be a power of two.
Therefore, our filter has a window size of 64 sam-
ples resulting in a dead-time of 0.64 seconds (32 sam-
ples at a sampling rate of 20 milliseconds). For sim-
plicity, a rectangular window function was used to
clip the window from the signal. The final filter is
characterized by the bode plot in figure 5.
Figure 5: Bode-plot of the fft-baseline. This plot does not
model the dead-time of the window-function used by the fft.
After removing the baseline, we calculate the ab-
solute value of the filtered sensor measurements and
normalize them. Even though, the maximum of the
sensor values is 4095 since the resolution of the used
ADC is 12bit, the algorithm caps all measured val-
ues to 255 to make better use of the normalized space
between 0 and 1. The cap was applied after baselin-
ing and smoothing through the use of the FFT be-
cause these pre-processing steps are the reason that
high sensor values over 255 were unlikely to occur.
Figure 6: Processing pipeline for the inference of all ampli-
tudes.
Further we established a method to infer a
heatmap from the pre-processed sensor values which
can be seen in figure 6. First, we emphasize the in-
fluence of close sensors to their positions by using a
discrete normal distribution for the weights of the sen-
sors. The mean represents the position for each sensor
whereas the variance indicates the level of influence
between neighboring sensors. We optimized the vari-
ance visually while walking over the smart floor. By
removing the values close to zero this resulted in the
following two gaussian kernels k
x
, k
y
for the x and the
y direction.
k
x
= (0.001, 0.140, 0.718, 0.140, 0.001)
T
k
y
= (0.016, 0.221, 0.527, 0.221, 0.016)
T
These values are well suited for visualization of the
heatmap since they are optimized towards a trade-off
between sharpness and blurriness in regions of active
sensors. We then apply the kernels with a zero-padded
convolution to the 12 sensors in x and the 18 sensors
in y direction which gives us the horizontal a
x
∈ R
12
and the vertical sensor activities a
y
∈R
18
for each po-
sition as a vector.
By calculating the dot product of those vectors
a
y
·a
T
x
= H ∈R
18×12
we receive a matrix of the corre-
lating sensor activities. This matrix gives us the infor-
mation how active a position or region on the smart
floor is and hence we call it the heatmap H. Because
of the use of the gaussian kernels which was described
beforehand, a visualization of this matrix with differ-
ent colors will already result in an image with smooth
color gradients.
To further emphasize the remaining peaks in the
heatmap and to make them more persistent in time
we use exponential moving average (Hyndman et al.,
2008) on each element a
t+1
of the heatmap with re-
spect to the previous activity a
t
of the last time frame.
ˆa
t+1
= αa
t
+ (1 −α) ˆa
t
If the new activity is higher than the old activity we
apply a high smoothing factor of α = 80% otherwise
a low smoothing factor of α = 1.5% is applied. This
results in the final heatmap
ˆ
H for each time frame.
The last step is to extract the position of the person
from the heatmap. First, we apply an average filter on
the heatmap
ˆ
H so that close local maxima can merge
Neural Networks for Indoor Localization based on Electric Field Sensing
27

together which happens due to the fact that a walk-
ing person creates two active regions because they
have two feet. Secondly, we search the maximum of
the heatmap matrix because in this evaluation, we are
only interested in a single user scenario and therefore
do not need to cluster regions of activity. The coor-
dinates of the maximum represent the position of the
person.
2.2 ANN Approach
In contrast to the analytic approach we shall now
present a data driven approach with artificial neural
networks (ANN). Therefore, the next sections will
first explain the process of the data acquisition since
the underlying data represent a crucial part of every
machine learning driven approach. Then, we will
present the different model architectures that were de-
signed for the localization of a person moving on the
smart floor.
2.2.1 Data Labeling
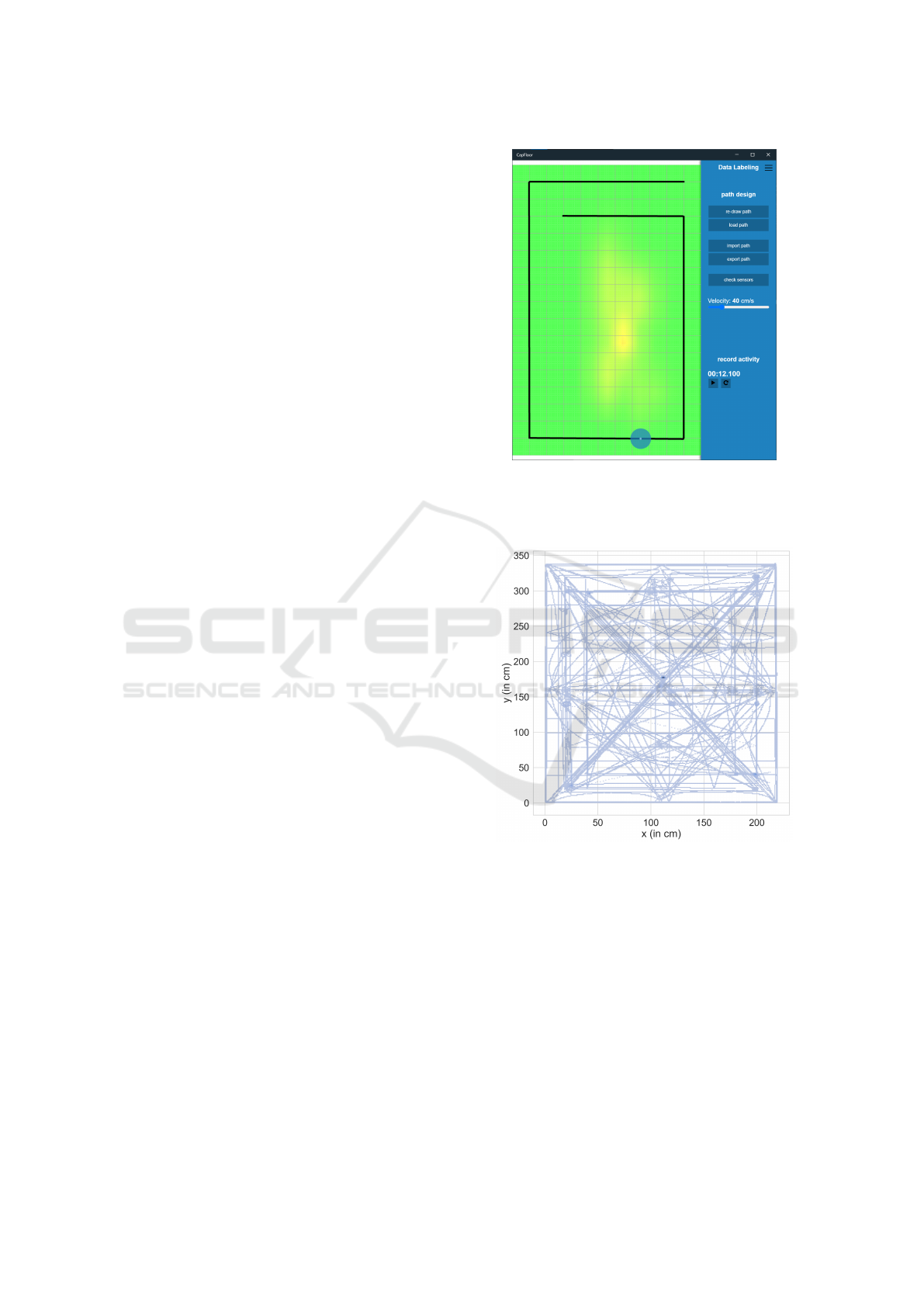
Our data labeling tool combines the sensor values
with a timestamp and the normalized position which
is the position on the smart floor with values between
zero and one for both axis. For this purpose, users can
draw a path (polyline) on the virtual depicted floor to
walk on and set their walking velocity in the GUI to
increase variability of the data (see figure 7). When
a user starts recording, a circle indicates the position
of the current label and thus the position where the
person should be standing. The circle will then move
along the previously drawn path, which the user has to
follow to generate the corresponding sensor data. All
labels are stored as a normalized position p ∈ [0, 1]
2
on the smart floor.
Figure 8 illustrates all paths that were recorded,
added in a single image, using absolute coordinates.
Note that this figure only contains pathways as cre-
ated by the ground truth data. The data shows that all
regions of the smart floor were covered.
2.2.2 Model Architecture
We will first discuss the input since it is the most rele-
vant factor for the architecture design. The input uses
the raw sensor values without any pre-processing to
avoid loosing information in the process and keeping
the choice of relevant patterns to the training process.
Moreover, changes in the pre-processing step would
require to retrain the models since the patterns in the
input change. However, one should note that this im-
plies an additional challenge to the ANN because it
Figure 7: Data labeling tool GUI to produce a dataset of
labeled sensor activities with the true position of a person.
The person needs to walk on a path while recording (floor
heatmap on the left).
Figure 8: Ground truth data of all recorded pathways.
has a more complex task at hand, which requires more
training.
The first type of input data is the concatenation of
the latest sensor values in the x and y direction. This
results in a vector s ∈ R
n
with the number of sensors
n = 30.
The second type of input data incorporates the his-
tory of the sensor values to include additional infor-
mation and improve the stability of the predictions
over time. To do that, the concatenated sensor val-
ues s can be stacked together to a matrix (s
1
, ..., s
t
) =
I ∈ R
n×t
for t time frames. I is labeled with the latest
label of s
t
to avoid learning a dead time in the model.
DeLTA 2022 - 3rd International Conference on Deep Learning Theory and Applications
28

In all architectures the output layer is a fully-
connected (FC) layer with two output units followed
by a sigmoid activation function. The two units be-
tween zero and one correspond to the normalized co-
ordinates of a person on the smart floor. The upper left
corner corresponds to the (0,0) coordinates and the
lower right corner corresponds to the position (1,1).
Next, a clarification of the tested architectures will
be listed to show their differences in structure and
complexity.
The Dense architecture (figure 9) has 13,854
trainable parameters and is mainly composed of three
FC layers plus the output layer. It uses the latest state
of the sensors s as input.
Due to the lack of pre-processing, the network
uses a batch normalization (BN) layer before each FC
layer and tanh as activation function after the first FC
layer. After the other FC layers the ReLU activation
functions (Rectified Linear Unit) is used, except for
the output layer.
Figure 9: Structure visualization of the Dense architecture.
The CNN1D architecture (figure 10) uses the s
vector as input and is similar to the Dense architecture
but applies additional pre-processing with use of local
feature extraction in the first layers. Specifically, it
uses 1D convolutional layers (Conv1D), BN and pool-
ing layers to enable the extraction of local features
from neighboring sensors. The first Conv1D layer is
followed by a tanh activation function to reduce the
influence of peaks in the data which can occur due to
wrong sensor measurements or errors emerging from
the data transmission on the used bus system. All
other activation functions continue with ReLU func-
tions. It has 12,800 trainable parameters.
The RNN architecture (figure 11) introduces the
use of time information and uses the time matrix input
I as described earlier. The architecture begins with a
BN layer followed by a tanh activation function on
the input to reduce the influence of peaks in the data.
It proceeds with a BN and a LSTM layer (long short
term memory) (Hochreiter and Schmidhuber, 1997)
Figure 10: Structure visualization of the CNN1D architec-
ture.
to process the time information. These are then fol-
lowed by two blocks of BN and FC layers plus the
output layer. It has 14,906 trainable parameters.
Figure 11: Structure visualization of the RNN architecture.
The CRNN architecture (figure 12) is similarly
motivated as the CNN1D and applies further pre-
processing to the RNN. To achieve this, it consists of
one Conv2D layer with tanh and one Conv2D layer
with ReLU activation function followed by BN and a
max-pooling layer. This is proceeded by a block of
BN and LSTM layers for time processing, a block of
BN and FC layers and the output layer. It has 10,507
trainable parameters.
Figure 12: Structure visualization of the CRNN architec-
ture.
The TCNN architecture (figure 13) is a CNN ar-
chitecture used on the time input matrix I. It consists
of multiple blocks of Conv2D, BN and pooling lay-
Neural Networks for Indoor Localization based on Electric Field Sensing
29

ers motivated by the VGGNet model (Simonyan and
Zisserman, 2014). This enables the extraction of lo-
cal features from neighboring sensors and close time
frames. The convolutional blocks are followed by two
FC layers plus the output layer. It has 14,948 trainable
parameters.
Figure 13: Structure visualization of the TCNN architec-
ture.
3 RESULTS
In this section, we will present out findings of the ac-
curacy for the different neural networks as well as the
results of the formerly discussed analytical approach.
3.1 Dataset
For training the different neural networks, we col-
lected 31 different path patterns from 4 test persons,
resulting in 258 data sheets. Combined to datasets
gives a total record duration of 4400 seconds of
persons walking over the smart floor equivalent to
220’023 samples of sensor-frames. A sensor-frame
consists of the aggregation of all sensors values within
a single time frame. A single sensor operates at a sam-
ple rate of 50 samples per second. These samples are
fairly distributed over the smart floor with a peak in
the center as you can see in figure 14. The dataset is
split into train (89%) and test (11%) datasets. The test
dataset is used to evaluate the models. This can also
be seen by comparing Figure 14 and Figure 15. While
the number of predictions in a single spot in Figure
14 sum up to over 3000 labeled positions per cluster,
there are much less predictions per cluster in Figure
15 just because of the different sizes of datasets.
As shown in Figure 16, using this test- and train-
ing dataset, all models will converge after approx-
imately 50 steps of training. The euclidean dis-
tance between the ground truth position of the user
and the calculated position from the respective net-
work is used to express the error. The training pro-
cess was terminated after 100 steps, since the conver-
gence nearly stopped afterwards for all models. The
Dense architecture showed signs of over-fitting after
80 training iterations. Figure 16 also hints that the
TCNN architecture converges faster than other mod-
els with a lower overall error.
Figure 14: Histogram of the labeled positions on the smart
floor showing how even the samples are distributed.
Figure 15: Histogram of all predictions of the validation set
from the TCNN model.
3.2 Model Performance
The evaulation of our methods is based on the eu-
clidean error. It is defined as the euclidean distance
between the model prediction and the true position of
the person.
q
(x
pred
−x
true
)
2
+ (y
pred
−y
true
)
2
This gives us a range from 0 to
√
2 since x and y are
normalized. One should note that the percent values
are simply scaled by 100 and therefore range from 0
to 141.42%.
The model performances differ in the x and y di-
rection due to the fact that our smart floor setup is
220cm wide and 340cm long with evenly spaced sen-
sors at a distance of 20cm in both directions resulting
DeLTA 2022 - 3rd International Conference on Deep Learning Theory and Applications
30

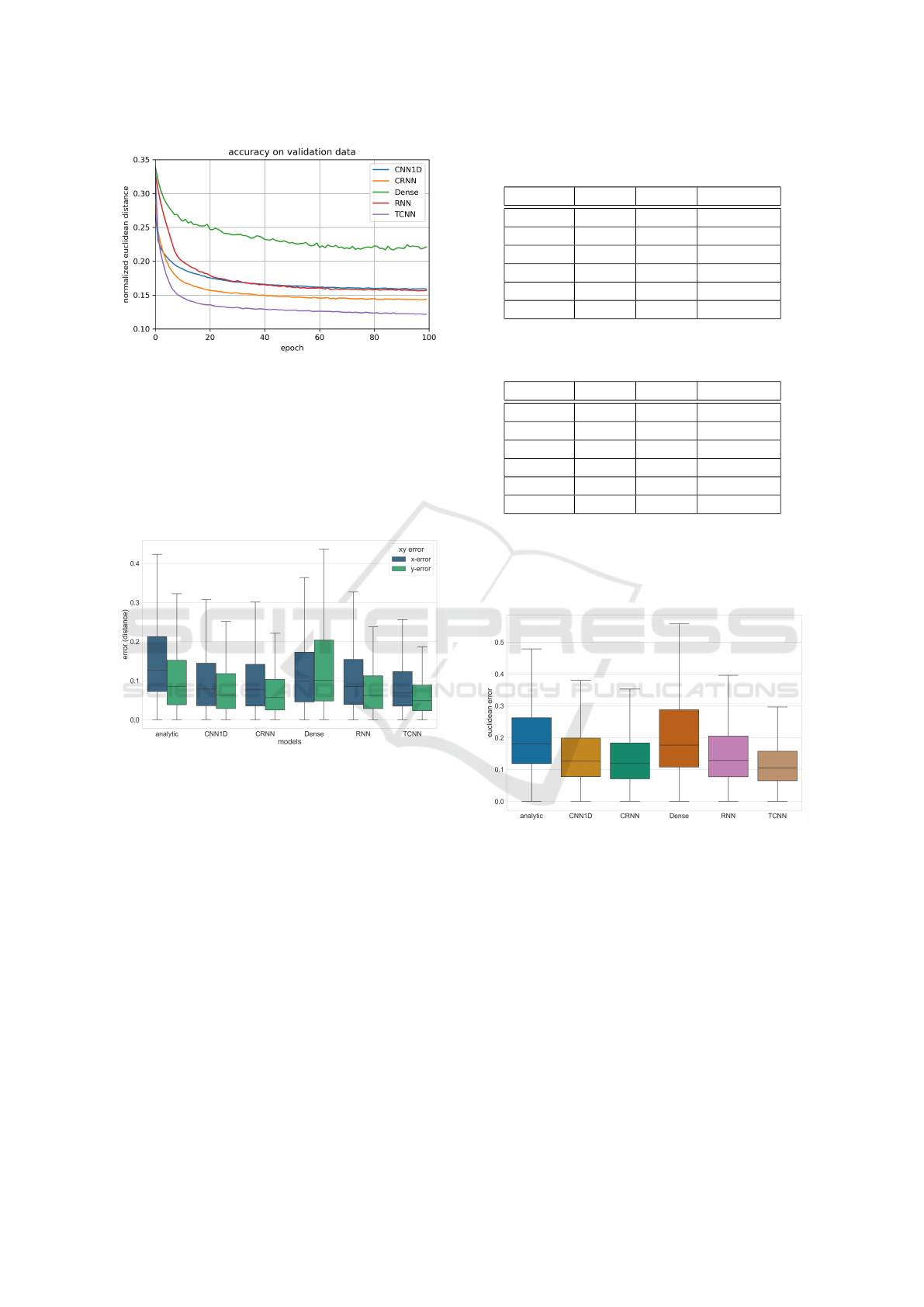
Figure 16: Comparison of the model performance on the
validation data during training.
in more data on the y axis. This difference of the nor-
malized distance can be seen in figure 17. However,
the scaled error to the true size of the smart floor re-
sults in a higher accuracy in the x direction due to the
higher scaling factor in the y-direction. The tables 1
for the normalized results and 2 for the results in cen-
timeters show these differences.
Figure 17: Visualization of the error in the x and y direction.
We can see that the convolutional pre-processsing
increases the performance for both CNN1D and
CRNN compared to the non-convolutional architec-
tures Dense and RNN. The performances are listed in
the following table 1 and visualized in figure 18.
After all, the TCNN was the best performing ar-
chitecture with the best model having a average accu-
racy of 12.8% and shows to have a good distribution
of predictions on the smart floor with no significant
bias as shown in figure 15. Another good indicator
of the model performances is that the overall shape of
Figure 14 can be recognized in 15.
Since the use of local feature extraction has shown
to be beneficial it is reasonable that the TCNN model
performed best, as it utilizes multiple layers for this
purpose. Moreover, the RNN did not perform as well
as the TCNN architecture which might be confusing
at first because it is a well established architecture
for time series data. This is because the LSTM uses
Table 1: The average errors of the models on the normalized
smart floor. All values in [%].
model x-error y-error eucl.-error
TCNN 9.17 7.03 12.83
CRNN 10.24 8.35 14.77
CNN1D 10.46 9.46 15.91
RNN 11.31 9.07 16.17
analytic 15.63 11.47 21.24
Dense 12.50 15.02 21.72
Table 2: The average errors of the models on the real scale
of the smart floor. All values in [cm].
model x-error y-error eucl.-error
TCNN 20.2 23.9 34.8
CRNN 22.5 28.4 40.5
CNN1D 23.0 32.2 44.3
RNN 24.9 30.8 44.2
analytic 34.4 39.0 57.3
Dense 27.5 51.1 63.2
global feature extraction for the time series. As previ-
ously inferred by the results of the other architectures,
this lacks the use of local feature extraction of neigh-
boring sensors and therefore tends to over-fit.
Figure 18: The euclidean-error of the normalized smart
floor. The box size represents the interquartile range.
4 DISCUSSION
The artificial neural networks provided a large im-
provement compared to the analytic approach. But
even if models perform seemingly the same com-
pared by error rate and convergent rate, such as the
RNN and the CNN1D architectures, their behavior
while displaying the position of a user in a live plot
can still differ significantly. While the RNN shows
much smoother transitions of the displayed position
of the user roaming over the smart floor, the posi-
tion displayed by the CNN1D has a strong jitter ef-
Neural Networks for Indoor Localization based on Electric Field Sensing
31

fect. The displayed position seemingly jumps around
the real user position in an uncontrolled manner. This
is because the RNN uses the information of multiple
time steps while the CNN1D only uses the latest time
frame of the sensor values. That is why, in the case of
these two architectures, the RNN network should be
preferred over the CNN1D.
Overall, using neural networks for this kind of
problem is a better approach than a purely analytical
one, since our problem can be modeled as a function
which maps values from the sensor measurements to
a person position. That is why this problem is well
suited for supervised learning techniques like neural
networks. Since we were able to label a good amount
of samples the NN approaches had much more op-
timization steps than the manually adjusted analytic
approach.
However, the dataset is still relatively small and
should by the focus of further studies to improve the
precision even further. As, for example, shown by
Chung et al. in their publication ”VoxCeleb2: Deep
Speaker Recognition”(Chung et al., 2018), a larger
dataset for training can decrease the error of a network
significantly. In their paper, the authors train a neural
network to recognize the voice of different celebrities.
They also use different datasets with different sizes
to train the same model. The result is a significantly
lower error rate by using the larger dataset.
Another important point of the data acquisition is
the labeling method. As already stated in section 2, in
order to record training data, a test person has to fol-
low an indicated position on a screen while walking
on a predefined pattern. The GUI provides a method
for fast and easy labeling and can be used by users
which are unfamiliar with the system. A down side
was the accuracy of the labels because users could
not determine the exact position of themselves on the
smart floor. Hence, the persons had to orientate them-
selves by estimating the position of the shown set-
point of the software. This is possible since the used
localization system has a relatively small size, but not
optimal in terms of repeatability.
The vision for the presented system is to install
a smart floor in a large amount of nursing homes
and hospitals. At the moment, this would require
a completely new dataset for each new smart floor
and the computationally intense training of a model.
Both of these tasks, especially the collection of a
dataset that also includes the necessary test data, are
very time consuming tasks and have to be realized
even for smart floors that are covering a small spa-
cial area. Therefore, further studies should investi-
gate size-invariant architectures similar to the TCNN
and one shot learning models to scale to those appli-
cations. However, the use of convolutional neural net-
works alone which can make the model size-invariant
will not accomplish this goal since the length of the
sensor electrodes changes in nearly every environ-
ment. This also changes the magnitude of the sen-
sor measurements, resulting again in the need of a
new data collection and training. Even a normaliza-
tion of the measured data is limited in its use because
the changes of the length of the wires used as elec-
trodes when scaling up a smart floor will in practice
never keep the ratio between the length of wires in
x-direction and y-direction. The analytical approach
struggles with the same problem. Fortunately as for
the analytical approach, this problem can be reduced
with a calibration routine which identifies the minimal
and maximal sensor values for each sensor by walking
over them once. As shown, this approach is signifi-
cantly less accurate than the use of neural networks.
This is why one of the most important topics for fu-
ture work will tackle the problem of size-invariant lo-
calization based on neural network architectures.
5 SUMMARY
This paper has presented an analytical approach for
the localization of a single person on the smart floor
as well as multiple neural networks to accomplish this
task. Moreover, we presented a tool for data acquisi-
tion and labeling and the resulting dataset of 220’023
samples.
Our Data showed that the TCNN architecture is
the method with the highest position accuracy com-
pared to the Dense, CNN1D, RNN and CRNN archi-
tecture. With an euclidean error of 34.8cm on average
which is an improvement of 22.5cm to the previously
used analytic method with an error of 57.3cm on av-
erage, the TCNN reduced the overall error by 40%.
We have also shown that the use of convolutions as
first layers for local feature extraction in the time do-
main and with neighboring sensors of the smart floor
resulted in significant better performance.
Overall, the data driven machine learning ap-
proach seems promising even though it suffers from
the missing scalability to multiple smart floors with
different sensor layouts.
REFERENCES
Chung, J. S., Nagrani, A., and Zisserman, A. (2018). Vox-
celeb2: Deep speaker recognition. Interspeech 2018.
Faulkner, N., Parr, B., Alam, F., Legg, M., and Demi-
denko, S. (2020). Caploc: Capacitive sensing floor
DeLTA 2022 - 3rd International Conference on Deep Learning Theory and Applications
32

for device-free localization and fall detection. IEEE
Access, 8:187353–187364.
Frank, S. and Kuijper, A. (2020). Privacy by design: Analy-
sis of capacitive proximity sensing as system of choice
for driver vehicle interfaces. In Stephanidis, C., Duffy,
V. G., Streitz, N., Konomi, S., and Kr
¨
omker, H., edi-
tors, HCI International 2020 – Late Breaking Papers:
Digital Human Modeling and Ergonomics, Mobility
and Intelligent Environments, pages 51–66, Cham.
Springer International Publishing.
Fu, B., Damer, N., Kirchbuchner, F., and Kuijper, A.
(2020a). Sensing technology for human activity
recognition: A comprehensive survey. IEEE Access,
8:83791–83820.
Fu, B., Kirchbuchner, F., and Kuijper, A. (2020b). Data
augmentation for time series: Traditional vs genera-
tive models on capacitive proximity time series. In
Proceedings of the 13th ACM International Confer-
ence on PErvasive Technologies Related to Assistive
Environments, PETRA ’20, New York, NY, USA. As-
sociation for Computing Machinery.
Hochreiter, S. and Schmidhuber, J. (1997). Long short-term
memory. Neural Computation, 9(8):1735–1780.
Hyndman, R., Koehler, A. B., Ord, J. K., and Snyder, R. D.
(2008). Forecasting with exponential smoothing: the
state space approach. Springer Science & Business
Media.
Kirchbuchner, F., Grosse-Puppendahl, T., Hastall, M. R.,
Distler, M., and Kuijper, A. (2015). Ambient intelli-
gence from senior citizens’ perspectives: Understand-
ing privacy concerns, technology acceptance, and ex-
pectations. In De Ruyter, B., Kameas, A., Chatzimi-
sios, P., and Mavrommati, I., editors, Ambient Intel-
ligence, pages 48–59, Cham. Springer International
Publishing.
Nam, H., Seol, K.-H., Lee, J., Cho, H., and Jung, S. W.
(2021). Review of capacitive touchscreen technolo-
gies: Overview, research trends, and machine learning
approaches. Sensors, 21(14).
Obeidat, H., Shuaieb, W., Obeidat, O., and Abd-Alhameed,
R. (2021). A review of indoor localization techniques
and wireless technologies. Wireless Personal Commu-
nications, 119(1):289–327.
Roy, P. and Chowdhury, C. (2021). A survey of machine
learning techniques for indoor localization and navi-
gation systems. Journal of Intelligent & Robotic Sys-
tems, 101(3):63.
Simonyan, K. and Zisserman, A. (2014). Very deep con-
volutional networks for large-scale image recognition.
arXiv preprint arXiv:1409.1556.
Neural Networks for Indoor Localization based on Electric Field Sensing
33