
Distributed Simulations of DNA Multi-strand Dynamics
Frankie Spencer
1 a
, Usman Sanwal
1,2 b
and Eugen Czeizler
3,4 c
1
Department of Information Technologies,
˚
Abo Akademi University, Turku, Finland
2
Malardalen University, Sweden
3
Faculty of Medicine, University of Helsinki, Finland
4
National Institute for Research and Development of Biological Sciences, Bucharest, Romania
Keywords:
DNA Self-assembly, Simulation Optimization, Computational Modelling, Multi-threaded Computing,
Rule-based Modelling.
Abstract:
In a recent study, Spencer et al. 2021, we have proposed a computational modeling framework for DNA multi-
strand dynamics implemented using the agent- and rule-based modeling methodology. While this modeling
methodology allows for compact representations for systems with large numbers of different species and
complexes, such as the case of self-assembly systems, one of its main drawbacks concerns its scalability.
Since each agent is individually represented and modeled in the system, the framework becomes slow when
dealing with tens- and hundreds of thousands of individual components. In this study we introduce a method
to parallelize the computational modeling process by distributing it over several CPU’s. We show that such
multi-thread models remain equivalent to their sequential counterpart, while the speedup of the computational
process can reach even a one-fold increase.
1 INTRODUCTION
Self-assembly of biological living organisms takes
place as a result of a natural phenomenon. There is
a well-defined assembly instrument built into DNA
itself which is directed by the Watson-Crick com-
plementarity mechanism. By exploiting these or-
ganic assembly instructions researchers were able to
build computational models that simulate the self-
assembly process of DNA single-stranded molecules.
Recently developed computational models show par-
ticular promising results (Mohammed et al., 2017;
Spencer. et al., 2021; Lakin and et al., 2011; Popple-
ton and et al., 2020). The dynamics of bio-chemical
systems is defined by the laws of physics and chem-
istry. However, computational models are running
by user-given criteria within a synthetic simulation
process. This is where Rule-Based Modeling (Har-
ris et al., 2015) comes into practice as a modeling
methodology. Here we can describe the systems dy-
namics by assigning local interaction rules.
When considering the computational modeling as-
a
https://orcid.org/0000-0002-1751-6770
b
https://orcid.org/0000-0002-2178-3329
c
https://orcid.org/0000-0002-1607-1554
pect, it is a profoundly difficult task to capture the
complexity of a structural self-assembly system. This
is due to the inherent nature of these systems which
have a theoretical un-bounded number of structural
and morphological different configurations, thus gen-
erating a combinatorial burst of the number of species
needed to mathematically capture these systems. In
our computational modeling approaches we faced this
challenge by applying a rule-based modeling method-
ology.
Rule-based modeling has a unique way of captur-
ing the different “species” of a DNA self-assembly
system (Spencer. et al., 2021). In our abstract model-
ing environment, DNA nucleotides within a (single-
stranded) molecule are implemented as individual
agents, each being assigned 3 specific docking sites.
Two of these, denoted as 5’ and 3’ sites, respectively,
are used to anchor the nucleotide within a single-
stranded DNA molecule (ssDNA), while the third
docking site, denoted as W, is used to bind the nu-
cleotide to a complementary pair, placed itself within
a different (or even from the same) ssDNA. While the
5’ and 3’ sites are to be initialized/bound only once,
as the ssDNA is created (or introduced) in the sys-
tem, and are never to be modified, the W sites usu-
ally undergo multiple agent-to-agent bindings and un-
234
Spencer, F., Sanwal, U. and Czeizler, E.
Distributed Simulations of DNA Multi-strand Dynamics.
DOI: 10.5220/0011266400003274
In Proceedings of the 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2022), pages 234-243
ISBN: 978-989-758-578-4; ISSN: 2184-2841
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

3’ 5’
A
W
T
W
3’ 5’
T
W
G
W
C
W
3’ 5’
T
W
A
W
3’ 5’
3’ 5’
3’ 5’
5’
3’
Figure 1: The schematic representation of the ssDNA complex ATTGCTA within our BNGL model.
bindings, thus leading to the development of double-
and multi-strand DNA molecular complexes. Reac-
tion rules are created based on provided local inter-
action patterns rather than the whole definition of the
reactants, thus providing a concise description of how
agents connect and interact. As a result, instead of
dealing with a huge number of model variables, we
only have a small number of local interaction rules to
deal with under this framework. Thus, the rule-based
regime is ideally suited to dealing with the issue of the
state space combinatorial burst (Harris et al., 2015).
The appropriateness of this approach for modeling
self-assembly systems has been formerly explored,
see e.g. (Am
˘
arioarei et al., 2021; Sorokin et al., 2018;
Thomas and Schwartz, 2017), along with its use for
the computational modeling of other types of DNA
assembly systems, see e.g. (Gautam. et al., 2020),
(Mohammed et al., 2017).
Computational rule-based models of biological
systems can be formulated by using the BioNetGen
(BNGL) language (Harris et al., 2015), which pro-
vides a text-based representation of such systems. We
can define reactions in terms of writing rules that
specify the necessary and inherit properties of the re-
actants, a transformation, and a rate law.
In (Spencer. et al., 2021) the authors have in-
troduced the VDNA-Lab platform (online available
on (Spencer et al., 2021)) as a generic computa-
tional modeling framework for DNA multi-strand dy-
namics using the BNGL Language formalism (Har-
ris et al., 2015) and the NFsim computational plat-
form (Sneddon et al., 2011). The DNA molecules
and the subsequent interactions are captured starting
from nucleotide level. Each nucleotide (as a bio-
entity) is represented as an individual instance of a
generic agent N (from nucleotide) which has 1 state-
characteristic site, b (from base), and 3 connecting
sites: 5’, 3’, and W. Relating to its biological coun-
terpart, the site b can be in exactly one of the four
possible states: A (Adenine), G (Guanine), C (Cyto-
sine), or T (Thymine); moreover, once initialized, site
b will never change its state. The remaining sites of
agent N are used for connecting the nucleotide within
the single-stranded molecule it is part of, i.e., us-
ing sites 5’ and 3’, and for connecting the nucleotide
with a complementary base-pair, using site W. For ex-
ample, within our rule-based model, the basic struc-
ture for the single-stranded DNA (ssDNA) molecule
ATTGCTA is shown in Figure 1.
Currently we observe parallelism in many other
fields such as machine learning, AI, scientific com-
puting, computer graphics, etc. allowing those fields
to grow in both complexity and usability. However
according to the current state of the art for rule-based
modeling, and particularly for the BioNetGen mod-
eling formalism, we find a lack of methodological
approaches involving parallel processing/simulation
which in turn creates a technical requirement bar-
rier to push this field forward. This technical bar-
rier appeared with the need of processing power, even
though computer processors become faster and more
powerful with their each newer generations. These
processors achieve higher performance mainly by
packing more processing cores. However, their sin-
gle thread clock frequency improvements are incre-
mental but not significant. This technological shift
did not provide the computational requirement for
the stochastic simulations employed in the case of
rule-based modeling, since in this case the employed
computation is channeled towards a single processing
thread per execution. Therefore, we had to look for al-
ternative methods in order to gain faster performance.
In this study we introduce a method to parallelize
the computational modeling process of DNA multi-
strand dynamics by distributing the computational ef-
fort over several CPU’s of a computing device. Our
approach automatically translates a sequentially de-
signed BNGL model implementation into a family
of corresponding models which can be run indepen-
dently on different slices of the state-space. These
models are run for a relatively small amount of time,
before aggregating their predictions into a new up-
dated state-space. The reaction rates of the new mod-
els are automatically adjusted such that even if now
the computational simulation is performed on just a
section of the entire state-space, the overall kinetics
of the reactions is comparable to their counterpart in
the sequential model implementation. The process of
state-space splitting, independent parallel simulation,
and state-space aggregation is repeated until the de-
sired time-span of the simulation is achieved.
Our results show that the predictions generated by
the multi-threaded distributed simulations are compa-
rable to those generated by the sequential simulation
(i.e., our reference model). Namely, we show that the
differences between these two models concerning the
Distributed Simulations of DNA Multi-strand Dynamics
235

Table 1: (Spencer. et al., 2021) The list of 12 rules governing the dynamics of the DNA self-assembly process, and the default
values of their associated kinetic rate constants. The kinetic rate constants are scaled according to the rate of the intra-complex
toehold binding of complementary segments, i.e., Rule 4, which is normalized to value 1.
Rule# Description of rule action kinetic
param.
(k.p.)
default
val. of
k.p.
Rule 1 toehold binding of compl. seq. (3-to-7 bases) of 2 un-connected ssDNA k
1
0.001
Rule 2 binding of s.c.b.
1
of two immediately-connected ssDNA segments
2
k
2
300
Rule 3 binding of s.c.b. of two closely-connected (1-off neighbor connection) ssDNA
segments
2
k
3
30
Rule 4 toehold binding of compl. seq. (3-to-7 bases) of two connected ssDNA k
4
1
Rule 5 un-binding of s.c.b. positioned at a split
3
k
5
30
Rule 6 un-binding of s.c.b. positioned in the middle of a compl. sequence k
6
0.1
Rule 7 un-binding of s.c.b. where at least one ssDNA ends on that position k
7
50
Rule 8 very rapid (instantaneous) un-binding between s.c.b. in abnormal conditions
4
k
8
K
max
5
Rule 9 random unbinding of a pair of bound nucleotides k
9
0.01
Rule
10
rapid un-binding of a size-2 comp. seq. in the middle of non-compl./non-bound
seq.
k
10
300
Rule
11
rapid un-binding of a size-3 comp. seq. in the middle of non-compl./non-bound
seq.
k
11
100
Rule
12
rapid un-binding of a size-4 comp. seq. in the middle of non-compl./non-bound
seq.
k
12
10
number of ssDNA complexes formed and their sizes
are in average statistically insignificant. However, we
gained a significant computer runtime efficiency: the
total runtime of the distributed model is from approx.
45% to up to a one-fold decrease of the sequential
model, depending on the number of threads the model
is split into. The python script of our automated
model translation from sequential to multi-threaded
implementation is freely available at (Spencer et al.,
2022).
1
Single complementary bases
2
The two interacting ssDNA segments can be part of
the same ssDNA molecule, i.e., a hairpin loop, or be two
distinct ssDNA molecules bound within the same complex.
3
That is, both ssDNA strands continue with pairwise
non-bounded sequences to one direction -at least one strand
should not be bound to anything else- and bound sequences
of length at least 1 to the other direction
4
There are several cases within the model where two
nucleotides become/remain bounded, although such a sit-
uation might not occur experimentally. These situations
are: i) single complementary bases in the middle of two
non-complementary (or non-bound) ssDNA sequences; ii)
single complementary base positioned at the end of a non-
complementary (or not-bound) sequence; iii) single com-
plementary base, where the complement is on the same ss-
DNA, at distance 0 or 1; iv) single complementary base
when the opposite neighbors of the pair are bound but not
complementary, i.e., are bound but not to each-other
5
The default value of the kinetic rate constant K
max
im-
plementing an instantaneous reaction is set to 10
5
2 MATERIAL AND METHODS
In (Spencer. et al., 2021) we have intro-
duced a computational modeling framework, VDNA-
Lab (Spencer et al., 2021), for DNA multi-strand dy-
namics, paired with an intuitive Graphical User In-
terface (GUI) for non-expert (i.e. non-computational
modeling expert) user interaction. The platform em-
ploys a course-grained modeling approach, where
each DNA nucleotide has its individual model coun-
terpart, while the overall employed modeling method-
ology is that of agent- and rule-based interac-
tions. Particularly, we use the BioNetGen Language
(BNGL) formalism (Harris et al., 2015) in order to
define our model, and the NFsim computational plat-
form (Sneddon et al., 2011) for numerical integration.
The platform accepts as input either simple se-
quences of ssDNA molecules (as A-T-C-G strings)
and their multiplicity, or more-complex, e.g. partially
bounded multi-ssDNA, structures such as those ob-
tained during previous simulations of the platform.
The system simulates the subsequent binding and dis-
sociation interactions of the input structures based
on 12 binding and un-binding local interaction rules.
Each of these rules has its own, user-adjustable, ki-
netic rate constant and each of them is implemented
through one or several rule-based reactions. The list
of these 12 local-interaction rules is presented in Ta-
ble 1 (Spencer. et al., 2021), together with the default
SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
236

(normalized) kinetic rate constants associated to each
of these rules.
In order to track and/or report the global mapping
of the components within a heterogeneous complex,
VDNA-Lab is equipped with a custom visualization
subroutine. The entire configuration of the dynami-
cal system is unloaded at user-defined time-intervals
within the simulation, and it is re-assembled for visu-
alization and further numerical analysis. A represen-
tative 2D graphical presentation of the various assem-
bled complexes is also displayed, in which one can
track the ssDNAs within the complex as well as all
the Watson-Crick (WK) binding interactions between
the various nucleotides.
Being designed on a rule-based modeling method-
ology, and moreover since its numerical integration
is implemented using a network-free approach where
model variables are created on a need-based manner,
VDNA-Lab can deal with the combinatorial explo-
sion of the different sub-assemblies, i.e., species, gen-
erated by an aggregating system such as the ssDNA
self-assembly process. However, as a classical exam-
ple of course-grain modeling methodology, its disad-
vantage lays in the difficulty to manage systems with
tens- and hundreds-of-thousands of individual com-
ponents. Since in the case of VDNA-Lab the unit-
elements to be modeled are the individual nucleotides,
such high number of individual units to be modeled
are quickly reached and exceeded.
To mitigate this situation, in the current study
we develop a distributed approach towards modeling
of DNA-assembly dynamics via rule-based modeling
approaches and respectively via BNGL/NFsim.
Distributed computing is one of the stan-
dard algorithmic approaches for reducing computa-
tional/simulation time, allowing in the same time to
increase the simulation scalability (Mazumder et al.,
2017). On a standard distributed processing model,
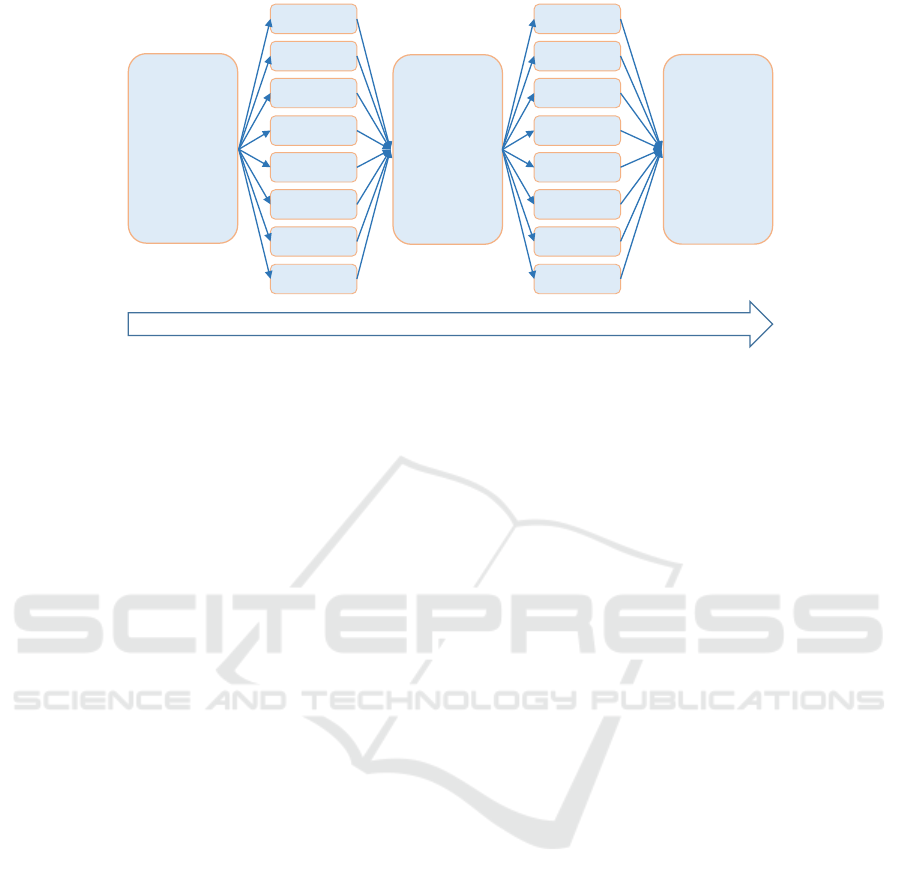
see Figure 2, one first splits the whole process into
several equally weighted modules, and then allocates
a single processing thread to each module to perform
computations independently. We can aggregate the
obtained results either at the final step, or during mid-
simulation/intermediary computational steps, see e.g.
Figure 3.
Within a standard parallel processing model, the
individual processing modules are required to be to-
tally independent of each other. However, the stochas-
tic synthetic simulations that we perform are based
on the Continuous-Time Markov Chain (CTMC)
paradigm, which does not always allow for a straight-
forward split of the processes into separate modules.
We remodeled our CTMC based simulation into a dis-
tributed model by using process clusters (aka threads)
1
2
3
4
5
6
7
8
1
1
1
1
1
1
1
1
+
1 + 1
2 + 1
3 + 1
4 + 1
5 + 1
6 + 1
7 + 1
8 + 1
2
3
4
5
6
7
8
9
T1
T2
T3
T4
T5
T6
T7
T8
Figure 2: Standard parallel processing model.
and process time-splits mechanism. We split the
total simulation time into separate processing time-
intervals and for each of these time-intervals we split
the populations of complexes and the computational
modeling process into N separate (and independent)
threads. Then, for each of the time-interval, at the end
of the parallel simulation processes of all the threads,
we shuffle the emerged distributed populations within
one common simulation pool, and continue to repeat
this routine for the next time-interval, until the time-
span of the entire simulation is covered, see Figure 3.
The above process clustering is not the only ad-
justment we have to perform to distribute our com-
putational modeling protocol. Some of the kinetic
rate constants of our reactions, where the modeling
paradigm is given by the Principle of Mass Action Ki-
netics (Voit et al., 2015), have to be modified too. De-
pending on the number of reactants within a modeled
reaction, we have reaction-rules with one and respec-
tively two reactants. Let us consider first the case of
one-reactant reaction rules:
A −→ C + D; (1)
the reasoning is similar if the number of products of
this reaction is different than two. We will denote
with k
1
and k
0
1
the kinetic rate constants of this reac-
tion in the initial vs. the distributed implementation of
this model. Also, let N be the number of distributed
threads in which the process is split; for ease of ap-
proximation, let us assume initially that all N threads
are split with an equal number of all of the species
populations, i.e., it is enough to analyze the popula-
tion changes within one thread, and multiply it with
N.
Considering the initial (non-distributed) model,
the rate ν
1
of reaction (1) is proportional to the ac-
tive mass of species A, denoted as [A], i.e., ν
1
=
k
1
[A]. In the distributed model case, for each of the
N threads we have that the rate ν
0
1
of this reaction
Distributed Simulations of DNA Multi-strand Dynamics
237
Simulation
pool
cluster 1
cluster 2
cluster 3
cluster 4
cluster 5
cluster 6
cluster 7
cluster 8
Simulation
pool
shuffle
cluster 1
cluster 2
cluster 3
cluster 4
cluster 5
cluster 6
cluster 7
cluster 8
Simulation
pool
result
---->| 5sec |--------------------------------------->| 5sec |---->
Figure 3: Distributed computational model; simulation time is 10 seconds.
is ν
0
1
= k
0
1
[A]/N, as the active mass of species A is
equally distributed in the N clusters. Since overall we
want the two models to behave in an equivalent man-
ner, we have that k
1
[A] = N × k
0
1
[A]/N, that is, k
1
= k
0
1
.
So, for reactions with only one reactant, the kinetic
rate constant of the reaction in the distributed model
is equal to the rate constant of the corresponding re-
action in the initial (non-distributed) model.
Let us consider now reactions involving two reac-
tants; as before, the number of products can be either
one or two, without any differences in reasoning:
A + B −→ C + D (2)
The rate ν
2
of reaction (2) in the initial model is ν
2
=
k
2
[A][B], while for the distributed case we have ν
0
2
=
k
0
2
· [A]/N · [B]/N. By equalizing the reaction rates in
the two models, i.e., ν
2
= N × ν
0
2
, we obtain that for
this type of reactions, k
0
2
= Nk
1
, i.e., the kinetic rate
constant of reaction (2) has to be updated accordingly
in the distributed model, depending on the number of
threads we decide to split the initial model.
In practice, we can not assume that all species
are equally split in between the N clusters. Let
A
1
,B
1
,A
2
,B
2
,...,A
N
,B
N
be the populations of reac-
tants within the N threads, where [A
1
] + [A
2
] + ... +
[A
N
] = [A], and [B
1
] + [B
2
] + ... + [B
N
] = [B]. For re-
action (1) we have k
1
[A] = k
0
1
[A
1
] + ... + k
0
1
[A
N
], so
also in this case we have k
1
= k
0
1
. For reaction (2)
we have k
2
[A][B] = k
0
2
[A
1
][B
1
] + ... + k
0
2
[A
N
][B
N
]. It
is impossible to correctly evaluate a unique value k
0
2
(as a function of k
2
and N) for the equation to be true
for all possible A and B population splits. We can
only say with certainty that k
0
2
≥ Nk
2
. We will ap-
proximate k
0
2
= ρNk
2
, where we have numerically es-
timated ρ as ρ = 1.225 after performing several test
samples with an increment of ρ by 0.025. In order
for this approximation of the distributed model not to
diverge too much from the initial model, even if same-
species populations are proportionally distributed be-
tween the N clusters, we have to simulate each of the
distributed processes for a reasonable short amount of
time before merging all the clusters within one popu-
lation pool, and then re-distributing the population for
the next time-unit simulation, see Figure 3.
In our numerical simulations we have considered
both the possibility of implementing constant time-
splits for the distributed model, e.g. time-splits of 0.1
seconds, as well as variable time-splits, depending on
the size of the populations in the model. In princi-
ple, we have observed that equal time-splits perform
marginally better, and we have generally considered
splitting the simulation time into 100 equally timed
intervals.
Regarding the process of splitting the various pop-
ulations of complexes i.e., ssDNA molecules or com-
plexes of partially bounded ssDNAs, into N balanced
clusters, we have implemented it by trying to balance
the total “weight” of these clusters, where each nu-
cleotide in a complex would add 1 to the weight of
the cluster in which that complex is placed. First, we
place the N largest complexes (taken each complex
individually) each into one of the N clusters. Then,
we pick one complex at random from the remaining
(merged) population of complexes, and we place it
into the cluster with the lowest weight. This process
is repeated as long as there are still complexes in the
(merged) population that have not been assigned into
a cluster.
In our numerical simulations we have run
distributed simulations where the number of
threads/clusters varied between N=2, 4, 6, 8, and 24.
SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
238
(a) Complex size = 1.
(b) Complex size = 2.
(c) Complex size = 3. (d) Complex size = 4.
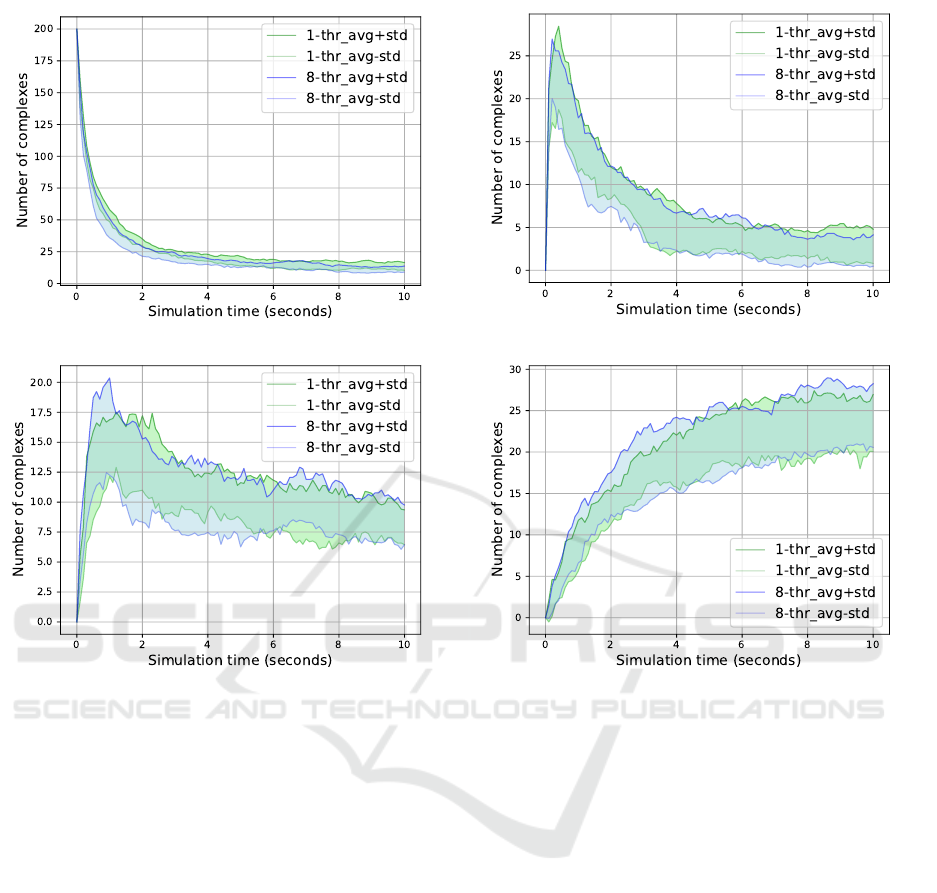
Figure 4: The Sequential vs 8-Thread Model; Complex sizes 1 to 4.
3 RESULTS
In order to compare our two simulation models, we
employed a two-step comparison method. First, we
ran a relatively smaller test trials to establish a base-
line on the accuracy of multi-threaded model to the
sequential model. Then we scaled up to larger test tri-
als by doubling the capacity of the tests we performed
while also increasing the number of CPU threads to be
utilized for processing. We observed how the single
strands of the simulation pool dissipate in both mod-
els throughout the process time, see Figure 4a. This
gave us an indication that the single strands bind to-
gether and form complexes or join an already formed
complex. Then we compared the number of formed
complexes, broken out by their size category; we
measured the size of a complex by the number of ss-
DNAs it consists of.
Since we are working on a highly stochastic com-
putational model, it is unrealistic to expect the same
type of complex formed in different occasions. How-
ever, in averages of 10 simulations we estimated that
all models should have approximately the same num-
ber of complexes by their sizes both during compar-
ative mid-simulation times, as well as at the end of
the simulation. To demonstrate that we employed the
following steps for all analyzed models:
• We identified the sizes of all available complexes
formed within the simulation and their count for
all test rounds, i.e. complexes of size 1 (i.e. single
ssDNA molecules), size 2, 3, 4, etc.
• We calculated the average number of complexes
(as well as the standard deviation σ+ and σ−) be-
longing to each category size in each time step.
• We performed a hypothesis test on the number of
complexes, distributed by their sizes, at the end
time of the simulation for the sequential vs the
multi-threaded simulations.
• We setup multi-line charts where X=Time and
Y= the number of complexes of a given size; the
Distributed Simulations of DNA Multi-strand Dynamics
239

Table 2: T-Test results. Columns represents the size of the complex. Tick, cross and hyphen shows whether the differences
are statistically insignificant, significant and not available respectively.
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
2-Threads vs Sequential X X X X X X X X X X X - X X X - - X X - - - X
4-Threads vs Sequential X X X X X X X X X X X - X X X - - X - - X - -
6-Threads vs Sequential X X X X X X X X X X X X X X X - - X - - - X X
8-Threads vs Sequential X X X X X X X X X X X - X X X - - - - - - - -
0
100
200
300
400
500
600
700
800
single-thread 2-threads 4-threads 6-threads 8-threads
RUNTIME
IN MINUTES
Figure 5: Runtime comparison of the simulation models from single threaded sequential model to 8-threads model by subse-
quent increases of two threads.
lines and their shaded area illustrate the margins
between σ+ and σ− of the simulation results.
• For each complex size, we made a compara-
tive analysis between the multi-line charts of the
single- and multi-threaded models.
Our null hypothesis is given by the assumption that at
the end of the simulated time, the sum of all com-
plexes of a given size N is equal in the sequential
model vs any of the multi-thread models. By com-
paring the complex sizes by the t-test using α = 0.01,
we were able to conclude that the differences between
any of the compared two models, i.e., sequential vs 2-
threaded model, vs 4-threaded model, vs 6-threaded
model, and vs 8-threaded model, respectively, are due
to a random chance. Our t-test results showed that
there were no statistically significant differences be-
tween the sequential vs any of the multi-(i.e., 2-, 4-,
6-, and 8-) threaded models on all cases and size cate-
gories, see Table 2. In Figure 4 we also illustrated the
similarities between the sequential and the 8-threaded
model during mid-simulation from 0 to 10 sec. This
further strengthens our assumption that the sequential
vs multi-thread models are evolving in a similar man-
ner, up to some reasonable level of stochasticity.
The main goal of this study was to build an effi-
cient distributed processing system to reduce the sim-
ulation runtime, while preserving the accuracy of the
initial (i.e., sequential) model. Our distributed models
showed a significant reduction in runtime in compar-
ison to the sequential model. In Figure 5 we identify
not only an improved time efficiency for the multi-
thread models, but also further scalability of the pro-
cess by utilizing more CPU threads for larger test
cases.
However, we also noticed a limitation associated
with this method. The more processing threads we
add, the more pre-processing the program has to per-
form in order to prepare the simulation loads for each
processing thread. Also, each thread has to initialize
its relevant simulation variables at the beginning of a
simulation round, thus consuming a lot of computa-
tional power. Thus, we estimate that from some level
on, adding more threads to a computational process
will stop generating a significant speedup, or even
would slow-down the overall simulation time.
After assessing the accuracy of the distributed
model by comparing it to its sequential counterpart,
we also investigated the level of scaling this approach
can lead to by exposing it to more complex simula-
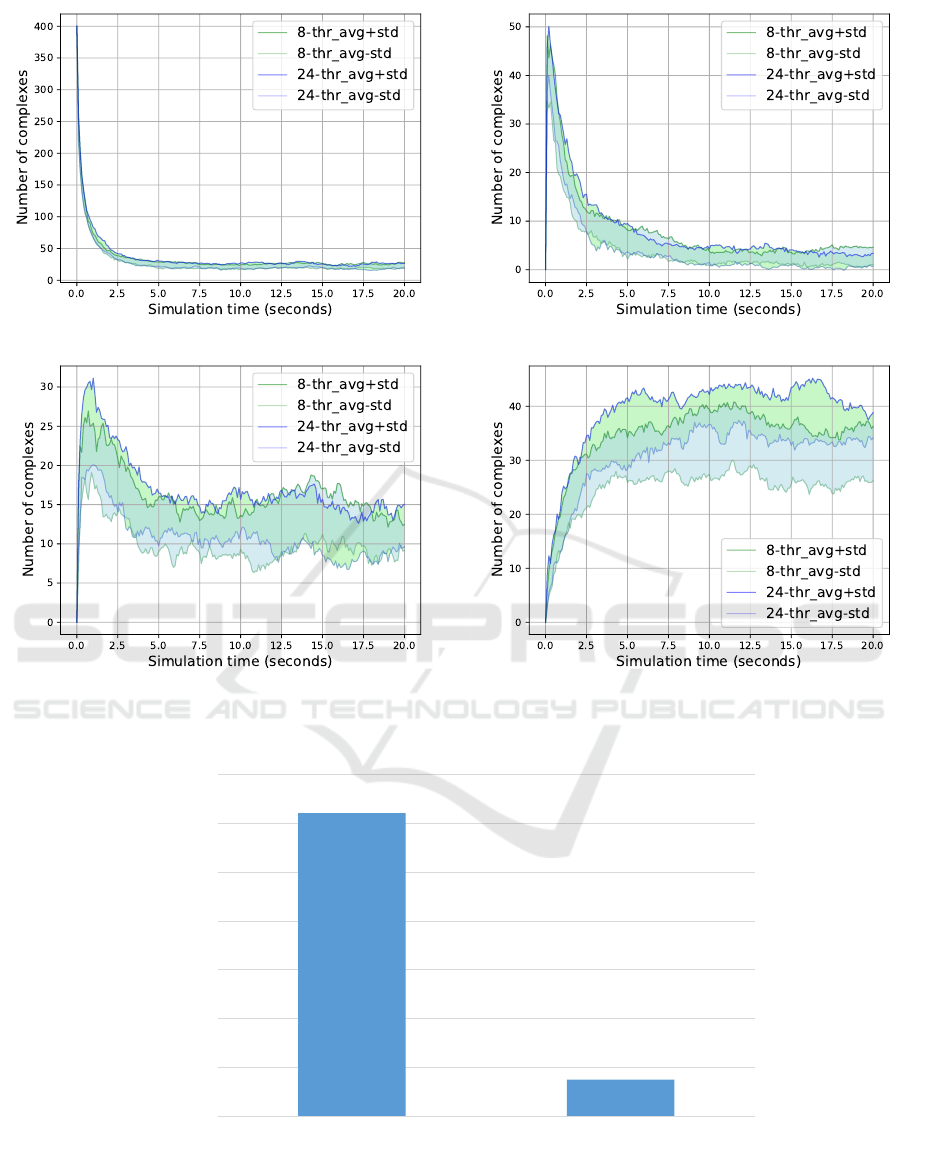
tions. In our scalability test we first doubled the in-
puts of the same simulation such that the amount of
ssDNAs copies was set to 100 and simulation time to
SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
240
(a) Complex size = 1. (b) Complex size = 2.
(c) Complex size = 3. (d) Complex size = 4.
Figure 6: 8-Threads vs 24-Threads; Complex sizes 1 to 4.
0
1000
2000
3000
4000
5000
6000
7000
8-threads 24-threads
RUNTIME IN MINUTES
Figure 7: Runtime comparison of the large scale simulation model run by 8-threads vs 24-threads.
20 seconds. Then, we run our simulation using an
8- and a 24-thread model, respectively. In Figure 6
and Figure 7 we reported on the performance of the
two models by examining the number of complexes of
Distributed Simulations of DNA Multi-strand Dynamics
241

each size category that was produced throughout the
process, as well as the total running time of the two
simulations. The comparison demonstrated that both
models produced very close results, while the runtime
of the 24-threaded model was significantly reduced.
The python script of our automated model trans-
lation from sequential to multi-threaded implementa-
tion is freely available at (Spencer et al., 2022).
4 CONCLUSIONS
In (Spencer. et al., 2021) we have intro-
duced a computational modeling framework, VDNA-
Lab (Spencer et al., 2021), for DNA multi-strand dy-
namics. The platform employs a course-grained mod-
eling approach and is implemented using the agent-
and rule-based modeling methodology. While one of
the main advantages of this methodology is the abil-
ity to deal with arbitrary large numbers of different
(macro-)complexes, one of its main drawbacks con-
cerns the scalability of the model. Since each agent,
i.e., in the case of our DNA model each nucleotide,
is individually represented and modeled in the sys-
tem, the framework becomes slow when dealing with
tens- and hundreds of thousands of individual com-
ponents. In order to address this issue in this research
we have introduced a distributed implementation of
the VDNA-Lab framework, which is able to speed up
the computational modeling process even by a one-
fold increase.
The distribution of the modeling environment did
not come as an off-the-shelf implementation. The ki-
netic rate constants of bi-reactant rules had to be ad-
justed, and the distribution process had to be split
up in shorter simulation rounds in order to com-
pensate for going from a one-pot (well-mixed) as-
sembly to a distributed compartmentalized simula-
tion process. Moreover, each simulation round had
to be preceded by a process of distributing the one-
pot species content into balanced-weighted compo-
nents, and succeeded by merging back the results of
the simulation round. Since neither BNGL nor NF-
sim had pre-developed procedures for generating a
sound split/merger of two (or more) simulation out-
puts, i.e., identifying similar macro-components in
two (or more) output files, such procedures had to be
implemented de novo.
The current implementation of the computational
distribution process of a rule-based model for DNA
multi-strand dynamics takes some advantages from
the particularities of the considered model. However,
it would be extremely useful for the rule-based re-
search community in large if this process could be
generalized for arbitrary rule-based model implemen-
tations. This remains as a relevant open problem for
further consideration.
ACKNOWLEDGEMENTS
This work was partially supported by Academy of
Finland under the grant 311371.
REFERENCES
Am
˘
arioarei, A., Spencer, F., Barad, G., Gheorghe, A.-M.,
It¸cus¸, C., Tus¸a, I., Prelipcean, A.-M., P
˘
aun, A., P
˘
aun,
M., Rodriguez-Paton, A., Trandafir, R., and Czeizler,
E. (2021). Dna-guided assembly for fibril proteins.
Mathematics, 9(4).
Gautam., V., Long., S., and Orponen., P. (2020). Ruledsd:
A rule-based modelling and simulation tool for dna
strand displacement systems. In Proceedings of the
13th International Joint Conference on Biomedical
Engineering Systems and Technologies - Volume 3:
BIOINFORMATICS,, pages 158–167.
Harris, L. A., Hogg, J. S., Tapia, J.-J., Sekar, J. A. P., Gupta,
S. A., Korsunsky, I., Arora, A., Barua, D., Sheehan,
R. P., and Faeder, J. R. (2015). BioNetGen 2.2: Ad-
vances in Rule-Based Modeling. arXiv e-prints, page
arXiv:1507.03572.
Lakin, M. R. and et al. (2011). Visual dsd: a design
and analysis tool for dna strand displacement systems.
Bioinformatics, 27:3211–3213.
Mazumder, S., Bhadoria, R., and Deka, G. (2017). Dis-
tributed Computing in Big Data Analytics: Concepts,
Technologies and Applications.
Mohammed, A., Czeizler, E., and Czeizler, E. (2017).
Computational modelling of the kinetic tile assembly
model using a rule-based approach. Theoretical Com-
puter Science, 701:203 – 215. At the intersection of
computer science with biology, chemistry and physics
- In Memory of Solomon Marcus.
Poppleton, E. and et al. (2020). Design, optimization and
analysis of large DNA and RNA nanostruc through in-
teractive visualization, editing and molecular simula-
tion. Nucleic Acids Research, 48(12):e72–e72.
Sneddon, M., Faeder, J., and Emonet, T. (2011). Efficient
modeling, simulation and coarse-graining of biologi-
cal complexity with nfsim. Nat Methods, 8(2):177–
183.
Sorokin, A., Heil, K., Armstrong, J., and Sorokina, O.
(2018). Rule-based modelling provides an extendable
framework for comparing candidate mechanisms un-
derpinning clathrin polymerisation. Scientific Reports,
8.
Spencer, F., Sanwal, U., and Czeizler, E. (2021). VDNA-
Lab. Available at https://github.com/Frankie-Spencer/
virtual dna lab, version 1.0.
SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
242

Spencer., F., Sanwal., U., and Czeizler., E. (2021). Vdna-
lab: A computational simulation platform for dna
multi-strand dynamics. In Proceedings of the 11th In-
ternational Conference on Simulation and Modeling
Methodologies, Technologies and Applications - SI-
MULTECH,, pages 288–294. INSTICC, SciTePress.
Spencer, F., Sanwal, U., and Czeizler, E. (2022).
An automated procedure for multi-threaded
transformation of rule-based models for DNA
multi-strand dynamics simulations. Avail-
able at https://github.com/Frankie-Spencer/
Distributed DNA Multi-strand Simulator, version
1.0.
Thomas, M. and Schwartz, R. (2017). Quantitative compu-
tational models of molecular self-assembly in systems
biology. Physical Biology, 14(3):035003.
Voit, E. O., Martens, H. A., and Omholt, S. W. (2015). 150
years of the mass action law. PLOS Computational
Biology, 11(1):1–7.
Distributed Simulations of DNA Multi-strand Dynamics
243
