Open-loop Control of a Soft Arm in Throwing Tasks

Diego Bianchi

1,2 a

, Michele Gabrio Antonelli

3 b

, Cecilia Laschi

4 c

and Egidio Falotico

1,2 d

The BioRobotics Institute, Scuola Superiore Sant’Anna, Pontedera, Italy

Department of Excellence in Robotics and AI, Scuola Superiore Sant’Anna, Pisa, Italy

Department of Industrial and Information Engineering and Economics, University of L’Aquila, L’Aquila, Italy

Department of Mechanical Engineering, National University of Singapore, Singapore, Singapore

Keywords:

Soft Robotics, Throwing, Open-loop Control, Neural Network.

Abstract:

This paper presents the implementation of an open-loop controller that allows a soft arm to throw objects

in target positions. This valuable ability enables the robotic arm to expand its working space by tossing the

objects outside it. Soft robots are characterized by high compliance and ﬂexibility, which is paid in terms of

dynamics that is highly non-linear and therefore hard to be modelled. An artiﬁcial neural network is employed

to approximate the relationship between the actuation set and the target landing position, i.e., the direct model

of the task. An optimization problem is deﬁned to ﬁnd the actuation set necessary to throw in a desired target.

The proposed methodology has been tested on a soft robotic simulator (Elastica). Results show that the open-

loop controller allows throwing objects in a target position with an average error of 0.90 mm and a maximum

error of 10.47 mm, which compared to the characteristic dimension of the work-space correspond respectively

to 0.07 % and 0.83 %.

1 INTRODUCTION

Characterised by compliant materials, soft robots can

implement embodied intelligence principles, and they

can conform surfaces, which is unthinkable for tradi-

tional robots that are often designed to maximise the

accuracy and the overall performance of an operation.

Soft robots can absorb much of the energy followed

by a collision that reduces the possibility of harm, en-

abling low-cost human-safe operations (Laschi et al.,

2016). For these reasons, soft robotics is thought to

bridge the gap in the interaction between machines

and people (Rus and Tolley, 2015). Indeed, intrin-

sic compliance makes soft robots suitable for delicate

handling, unstructured environment exploration, ap-

plication in medicine (Cianchetti et al., 2018), and

safe-human interaction (Zlatintsi et al., 2020).

Even though much work has been done about the

design of this kind of robots, their control is still an

open challenge. Indeed, there is not a common strat-

egy that allows exploiting all of their characteristics.

https://orcid.org/0000-0001-7148-1612

https://orcid.org/0000-0001-8437-9131

https://orcid.org/0000-0001-5248-1043

https://orcid.org/0000-0001-8060-8080

More speciﬁcally, there are several challenges far to

be addressed related to the mismatch between the

high-dimension morphology of the soft manipulator

compared to its actuation system; in addition, there

is the problem of the time-varying of the soft mate-

rial characteristics that present a non-linear behaviour.

Moreover, due to its compliance, the soft robotic plat-

form is highly inﬂuenced by the environment (Chin

et al., 2020). For these reasons, even if there are ex-

amples in the literature of model-based controllers for

soft robotic arm (Della Santina et al., 2018), (Mahl

et al., 2013), (Alqumsan et al., 2019), a promising

alternative is represented by machine learning tech-

niques thanks to their ability to discover the under-

lying structure in the data without prior knowledge.

Even if, compared to analytical/numerical models,

machine learning methods require (large) data col-

lection, they allow learning the unknown model of a

system with reliable performance (Kim et al., 2021).

Machine learning has been used to create static (kine-

matic) and dynamic controllers. One of the ﬁrst ex-

amples of inverse kinematics model learning in a

non-redundant soft robot based on neural networks is

shown in (Giorelli et al., 2013). This was further ex-

tended in (George Thuruthel et al., 2017) to account

for redundancies, based on the methods proposed in

138

Bianchi, D., Antonelli, M., Laschi, C. and Falotico, E.

Open-loop Control of a Soft Arm in Throwing Tasks.

DOI: 10.5220/0011267100003271

In Proceedings of the 19th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2022), pages 138-145

ISBN: 978-989-758-585-2; ISSN: 2184-2809

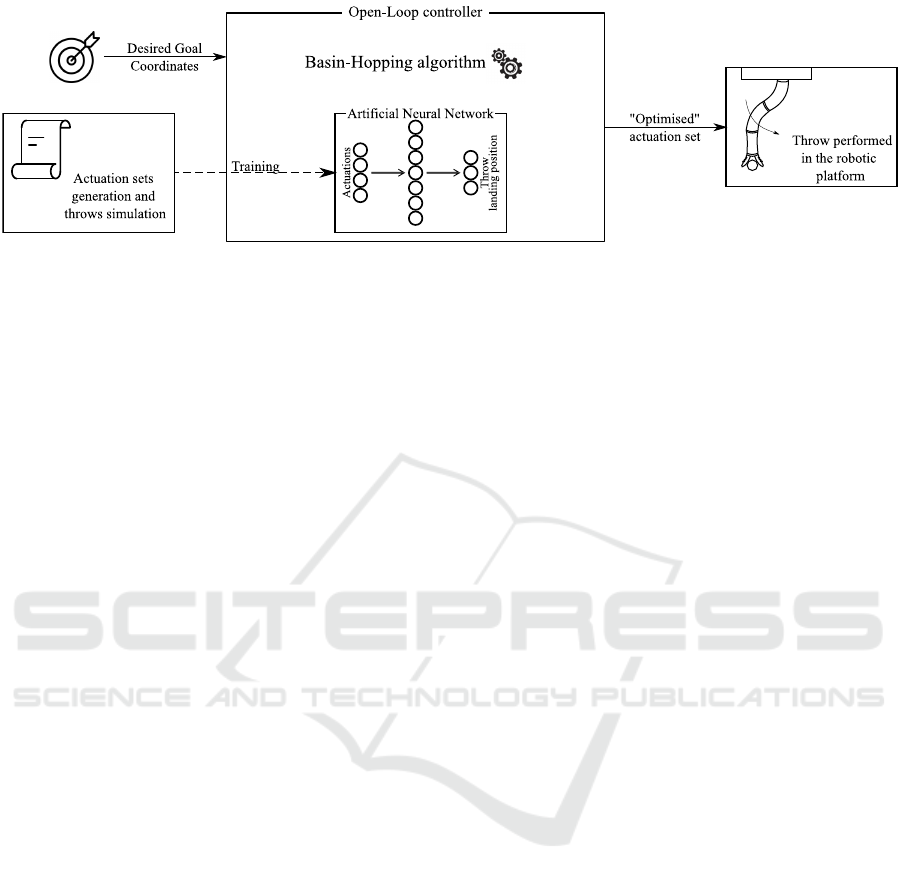
Figure 1: Methodology used in this work.

(Vannucci et al., 2014; Vannucci et al., 2015). How-

ever, this kind of controllers relies on the steady-state

assumption, which impedes the accurate and fast mo-

tion of a soft manipulators. In a dynamic scenario,

it is fundamental for a reliable controller to consider

all the dynamic effects associated with the different

sections of a manipulator. For this purpose, model-

free dynamic controllers have been developed. An

open-loop strategy is proposed by (Thuruthel et al.,

2018; Thuruthel et al., 2019) where a dynamic con-

troller is realized by running a trajectory optimisation

on a forward dynamic model obtained with a recur-

rent neural network. Even if it is characterised by

a low sensory requirement thanks to the model-free

approach, this strategy has been tested purely on a

trajectory tracking task. The same task is performed

in (Centurelli et al., 2021) in an open-loop controller

based on neural models and then extended in (Cen-

turelli et al., 2022) with a closed-loop dynamic con-

troller which has been trained by deep reinforcement

learning and it can deal with a payload attached to the

end-effector of the manipulator. A recent approach

considers the possibility to attach weights in differ-

ent positions of the manipulator to prove that a con-

tinual learning approach can be used to learn the dy-

namic models without forgetting (Piqu

e et al., 2022).

A comprehensive review on the control of soft ma-

nipulators can be found here (George Thuruthel et al.,

2018).

All the proposed approaches have been developed

for tracking tasks and are not suitable for ballistic

movements, where it is crucial to accurately reach the

point of release of the object with a predeﬁned speed:

these are the two parameters that determine the range

of the throw.

In this work, we present a methodology that, for

the ﬁrst time, allows a soft robot to perform ballistic

tasks, i.e., throwing an object towards the desired tar-

get. We developed the method presented in Section 2,

where also the soft robotic platform simulator is in-

troduced. In Section 3, each step of the methodology

is analysed on the platform and the results obtained

are shown. Section 4 concludes this work with some

considerations and some future improvements.

1.1 Related Works

This Section describes the principal work present in

literature about robots that perform throws with par-

ticular attention on the role of artiﬁcial intelligence

(AI). AI is used to increase the success rate of the

throws or, in general, the performance of a robot.

More speciﬁcally, in (Raptopoulos et al., 2020), the

authors propose to substitute the traditional pick-and-

place with the pick-and-toss for a cartesian robot em-

ployed in a waste sorting plant. It has been shown that

this substitution can expand the working space of the

robot, and in addition, they showed that this procedure

speeds up the sorting process increasing the speed by

15.3%. Here, AI is employed to classify the material

of the objects.

An interesting approach is presented in (Zeng

et al., 2020), where the authors present the Tossing-

Bot. This anthropomorphic robot can grasp an object

inside a drawer and toss it in a speciﬁc box placed

in front of it. In this case, a hybrid controller is

used. There is an analytical model which estimates

the control parameters of the robot. Then, a machine

learning-based controller is used to compensate for all

the phenomena that the numerical model cannot pre-

dict. These estimations are done with neural networks

that take input RGB images of the objects inside the

drawer and the target position coordinates. To make

the analytical model solvable, the authors imposed

some constraints to the movement by ﬁxing the re-

leasing height, the realising speed angle, and the dis-

tance between the releasing point and the robot base.

Both these strategies, implemented on rigid robots,

cannot be used since they rely on the analytical robot

model that is not available for the soft robot.

Open-loop Control of a Soft Arm in Throwing Tasks

139

2 METHODOLOGY

In Figure 1 the proposed method is summarised. It is

possible to identify four main steps:

1. Actuation Sets Generation and Throws Simula-

tion. Since the proposed approach is data-driven,

this stage is one of the most important of the work.

Let us imagine having a reference frame where the

z-axis passes through the soft manipulator back-

bone; we decided that each trajectory has to lay

in one of the planes of the sheaf of planes whose

intersecting line is the z-axis. Furthermore, to in-

crease its speed, we decided to divide the move-

ment into a run-up phase and a forward phase,

where the robot moves in the opposite direction

with respect to a hypothetical target (run-up) and

the towards it (forward). We established that the

sphere is released when it reaches the maximum

speed, i.e., when the manipulator passes toward

the resting position in the forward phase. The

dataset is generated by performing several throws

and collecting the landing positions.

2. Network Training. After the generation of the

dataset, an artiﬁcial neural network is trained to

approximate the relationship between the actua-

tion set, i.e., the commands sent to the robot, and

the resulting landing position. The actuation input

includes the commands responsible for the two

phases in which we divided the movement.

3. Deﬁnition of the Optimisation Problem. On the

previously trained network, a minimisation prob-

lem is deﬁned. We used the Basin-Hopping al-

gorithm to ﬁnd the actuation set necessary to per-

form a throw in the desired target. In this prob-

lem, we minimise the distance between the goal

and the landing position associated with the tenta-

tive actuation set, which corresponds to our value

function. We noted that the precision of this

method is highly dependent on the relationship

between the two actuation sets responsible for the

run-up and the forward movement.

4. Performing a Throw. Using the actuation input

previously found at point 3, the throw is per-

formed. Since a neural network approximates a

function, there is always an approximation error.

Moreover, the optimisation algorithm can fail to

ﬁnd the global minimum of the value function.

For these reasons, it is necessary to assess the ef-

fectiveness of the approach by comparing the ac-

tual landing position with the target one.

2.1 Soft Robotic Platform Simulator

The control strategy developed in this work has been

tested on an open-source simulator called Elastica

(Gazzola et al., 2018; Zhang et al., 2019). This

is based on Cosserat rods, and it takes into account

the bending, twisting, stretching, and shearing of the

modelled object. In particular, for our tests, we used

the Python version named PyElastica. This environ-

ment allows the simulation of soft robots, as shown

by the authors in (Naughton et al., 2021).

Figure 2: Elastica environment. In orange are shown the

directions in which are applied the internal torque to the

manipulator.

The soft arm is simulated by a single rod (whose

length is 1m), which has one extremity ﬁxed in the

position {0, 0,0} while the other one is free to move.

A horizontal plane (parallel to the xy plane) is placed

1.5m below the base of the robotic arm. The rod,

which points downward, is actuated by applying inter-

nal torques distributed continually along the module

body. These were deﬁned by ﬁrst assigning the mag-

nitudes of the torques to three points equally spaced

on the arm and then interpolating them using a spline.

The direction of the torques is established during the

deﬁnition of the arm. In particular, we decided to

use a bi-directional scenario where it is possible to

identify the normal direction d

, perpendicular to the

body and the binormal direction d

, perpendicular to

both d

and the body. In this case, even if allowed by

the simulator, we decided not to consider the twist-

ing of the rod. The inputs to the simulator are hence

three couples of torque, with magnitudes in the range

[−0.5, 0.5] for a total of 6 actuations. For the sake

of simplicity, the other characteristics of the soft arm,

such as the Young or Poisson’s modulus, have been

left to the defaults values since our aim is just to test

the controller and our methodology.

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

140

As for the tossed object, we assume it is massless

and attached to the soft arm end-effector, until it is

released. Once released, the sphere follows the law

of the projectile, and it lands on the horizontal plane

beneath the soft arm.

A stylised representation of the simulated arm and

the overall system can be seen in Figure 2, which rep-

resents one of the several trajectories and throws sim-

ulated for acquiring the dataset. It also shows the di-

rections, d

and d

, in which torques are applied.

Figure 3: A) Normalised trend of one of the actuation set

components. b) Movement of the soft arm end-effector

along the z-axis. c) Generated dataset.

3 EXPERIMENTS AND RESULTS

3.1 Dataset Generation

As described in Section 2, the ﬁrst step of our method-

ology is the dataset generation. Given an actuation set

τ, the respectively run-up actuation τ

is calculated

thanks to the (1) and then applied to the manipulator

for 0.1s.

= −τ (1)

Once this phase ends, the forward one starts where the

actual actuation set τ is applied for another 0.1s. To

avoid having a step torque on the robot, we used the

smooth-step function as shown in Figure 3a. As ex-

plained in Section 2.1, since the internal torques mag-

nitudes are evaluated by an interpolation of the torque

magnitudes deﬁned over three points by changing the

signs at the input values, we can obtain the same

movement in the opposite direction as described in

(1). In addition, we decided to apply each command

for 0.1 s because we wanted to avoid any undesired ef-

fect due to the transient response of the previous actu-

ation. Indeed, from Figure 3b, it is possible to notice

how the robot tends to reach a steady-state condition

if the actuation set does not change.

As for the throws, we assumed that the object

is released instantaneously at 0.105s since we ob-

served that around this instant, the manipulator pass

towards its initial resting position as represented in

Figure 3b. Moreover, the effect of the run-up phase

on the overall movement is visible. Even if the

end-effector steady-state response for the two phases

is the same in terms of displacement along the z-

axis, the transient responses are different; in fact,

during the forward stage, the manipulator has a

higher peak response compared to the previous pe-

riod. A collection of 6

= 46656 trajectories has

been generated by varying each torque value between

[0.5, 0.3, 0.1, −0.1, −0.3, −0.5]. For each of these

trajectories, the two actuation sets, the landing posi-

tion of the object and, for graphical reasons, also the

last position occupied by the end-effector are saved.

In particular, in Figure 3c, it is possible to compare the

difference between the workspace of the robot with

and without the ability to throw objects. In particu-

lar, the comparison of the farthest points in the two

cases shows that, thanks to the ability to throw an ob-

ject, the working space is increased of ∼ 260% with

a maximum distance ranging from 1.37m to 3.55 m.

3.2 Neural Network Comparison

The dataset, whose collection is shown in Section 3.1,

is used to derive the direct model of the task; with

an artiﬁcial neural network (ANN), we mapped the

input space with the resulting landing positions of the

thrown object as in (2).

x = f (τ

,τ) (2)

Here, (τ

,τ) are the actuation input of the run-up and

forward phase respectively and x represents the re-

sulting landing position. Different models of the same

Open-loop Control of a Soft Arm in Throwing Tasks

141

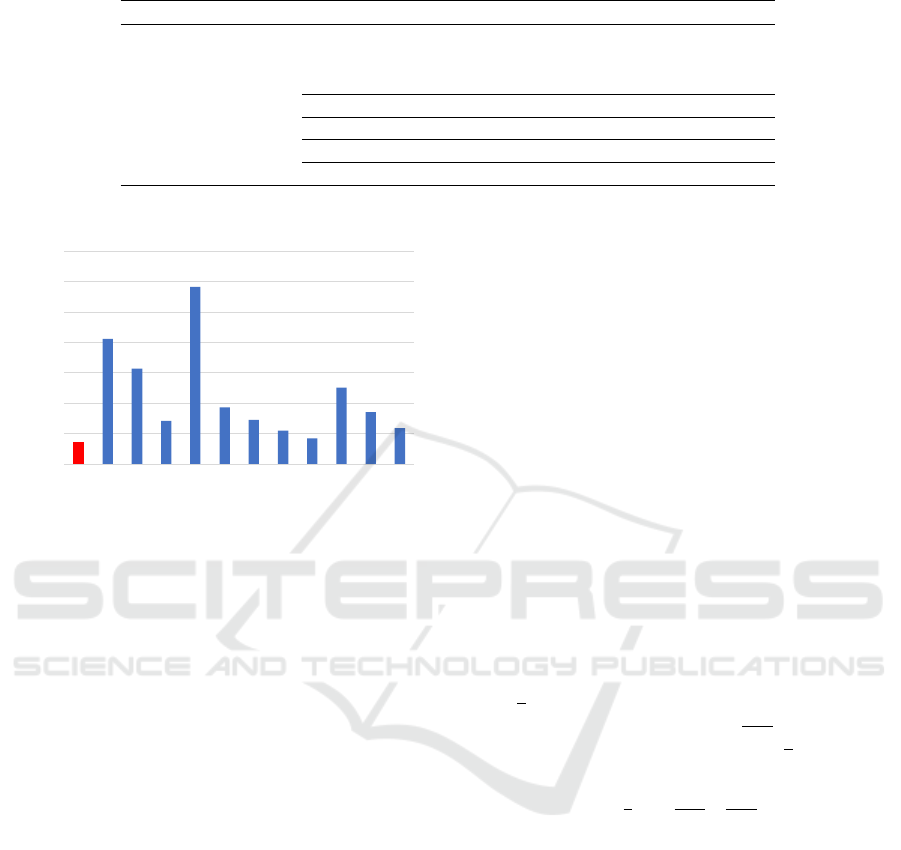
Table 1: Hyper-parameters - Elastica.

Hyper-parameters # Units Activation function Normalization

Changed

64 ReLU Z-score

128 Tanh Rescaling

Sigmoid

Fixed

Optimizer # Epochs Batch size

Adam 2500 64

Loss function Training set Learning rate

MSE 90% 0.001

0.0

1.0

2.0

3.0

4.0

5.0

6.0

7.0

64_ReLU_Z-score

64_Sigm_Z-score

64_Tanh_Z-score

128_ReLU_Z-score

128_Sigm_Z-score

128_Tanh_Z-score

64_ReLU_Rescaling

64_Sigm_Rescaling

64_Tanh_Rescaling

128_ReLU_Rescaling

128_Sigm_Rescaling

128_Tanh_Rescaling

Average distance [mm]

Neural Networks comparison

Figure 4: Best set of parameters selection.

robot were created and then compared to identify the

best one among them. The selection is made on the

test set by looking at the difference between the pre-

dicted landing position and the real one. Of course,

the best one is the model that achieves the lowest dis-

tance.

The soft arm model is represented by an artiﬁcial

neural network with one hidden layer. The hyper-

parameters that have been changed are the number of

units of the hidden layer, their activation function, and

the type of input normalisation. Default values have

been used for learning rate, partition between train-

ing, test set, and other parameters as reported in Table

1. To expedite the learning process, the early stopping

method has been considered. Furthermore, the input

layer of the network has twelve units while the output

one has three neurons which implement the linear ac-

tivation function. We decided to use for all the cases

a Z-score normalisation for the output values.

The results of the comparison are shown in Fig-

ure 4. Best performances are obtained with a Z-score

normalisation of the input and 64 units in the hidden

layer with a ReLU activation function.

3.3 Optimisation Problem

An optimization problem has been deﬁned to ﬁnd the

actuation set needed to throw an object in the desired

position. The idea is to gradually change the tentative

actuation set and compare the corresponding landing

position (generated by the neural network) with the

desired goal coordinates. To solve this problem, we

used the Basin-Hopping algorithm. This method, in-

spired by the Monte-Carlo minimisation and ﬁrstly

described in (Wales and Doye, 1997), is iterative, and

each cycle is composed of the following features:

1. Random perturbation of the input.

2. Local minimisation.

3. Based on the value function, the tentative input

can be marked as a reference or discarded.

In our case, as shown in Figure 5 which displays the

i-th iteration of the iterative algorithm, the input value

corresponds to the forward actuation set of the plat-

form τ

while the value function is represented by the

distance between the desired goal x

des

and the landing

point predicted by the neural network ˆx as described

by the equation (3).

f (τ) = ∥x

des

− ˆx(τ)∥ (3)

As anticipated in Section 2, the precision of this

method is highly dependent on the relationship be-

tween the actuation input used in the two phases of

the movement of the robotic arm. To increase the con-

troller performance, we decided to let the optimisa-

tion algorithm deal with just one of the two actuation

sets, in particular the one responsible for the forward

movement, while we derive the other since their rela-

tionship is known.

3.4 Results

With the proposed methodology, 1502 throws have

been completed. The goals are randomly chosen in-

side the working space shown in Figure 3c. In Figure

6 it is possible to appreciate the manipulator perform-

ing a throw towards one of the desired targets.

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

142

Table 2: Errors in different throws.

Category

Num.

Throws [-]

Maximum

error

Average

error

[mm] [%] [mm] [%]

A 260 1.36 0.11 0.49 0.04

B 741 5.97 0.47 0.81 0.06

C 501 10.47 0.83 1.25 0.10

Figure 5: Minimisation problem to ﬁnd the best actuation set: Basin-Hopping algorithm.

As represented in Figure 7, we classiﬁed the

throws in three categories based on the compari-

son between the distance of the goal from the base

of the robot and the characteristic dimension of the

workspace that is equal to d = 1.256 m, according to

the criteria (4).











category A : if dist < d/2,

category B : if d/2 < dist < d,

category C : otherwise

(4)

The results obtained are summarised in Table 2 where

are reported the number of trials for every category

and the distance from the desired goal. In particular,

the percentage values are obtained with respect to the

characteristic dimension of the workspace.

The error is due to the neural network predic-

tion inaccuracies and the optimisation algorithm that

might not ﬁnd the global optimum but a value close

to it. However, even with these sources of uncer-

tainties, the maximum error registered is equal to

∼ 10.5 mm. Considering that the arm length is 1 m

and the workspace maximum dimension is 3.55m (the

square diagonal), we can state that the error is negli-

gible.

4 CONCLUSIONS

This paper showed how an open-loop controller could

execute the throwing task for a soft manipulator. Even

if Elastica provides a soft robot model, we decided to

present a model-free approach to generalise the pro-

posed methodology that might be applied to any soft

manipulator since it does not require its model.

However, even if the error, in this case, is minimal

and related to the distance from the ﬁxed end of the

robot, there is still the problem of waiting for the op-

timisation process to obtain the actuation set to throw

an object in the desired target. For this reason, further

work in the future will be considering other strategies

to perform the same task, such as a neural network

or reinforcement learning. Then, testing this method

on a real platform will be necessary. In this case,

several challenges have to be faced. More speciﬁ-

cally, there could be a problem related to the trajec-

tories generation; while on this simulator ﬁnding the

relationship between the two phases in which we di-

vided the movement was relatively straightforward,

on a real platform we expect it to be more complex

because it will be related on the actuation systems of

the robot (ﬂuidic, tendon-driven, etc.) and how they

are placed inside it.

Open-loop Control of a Soft Arm in Throwing Tasks

143

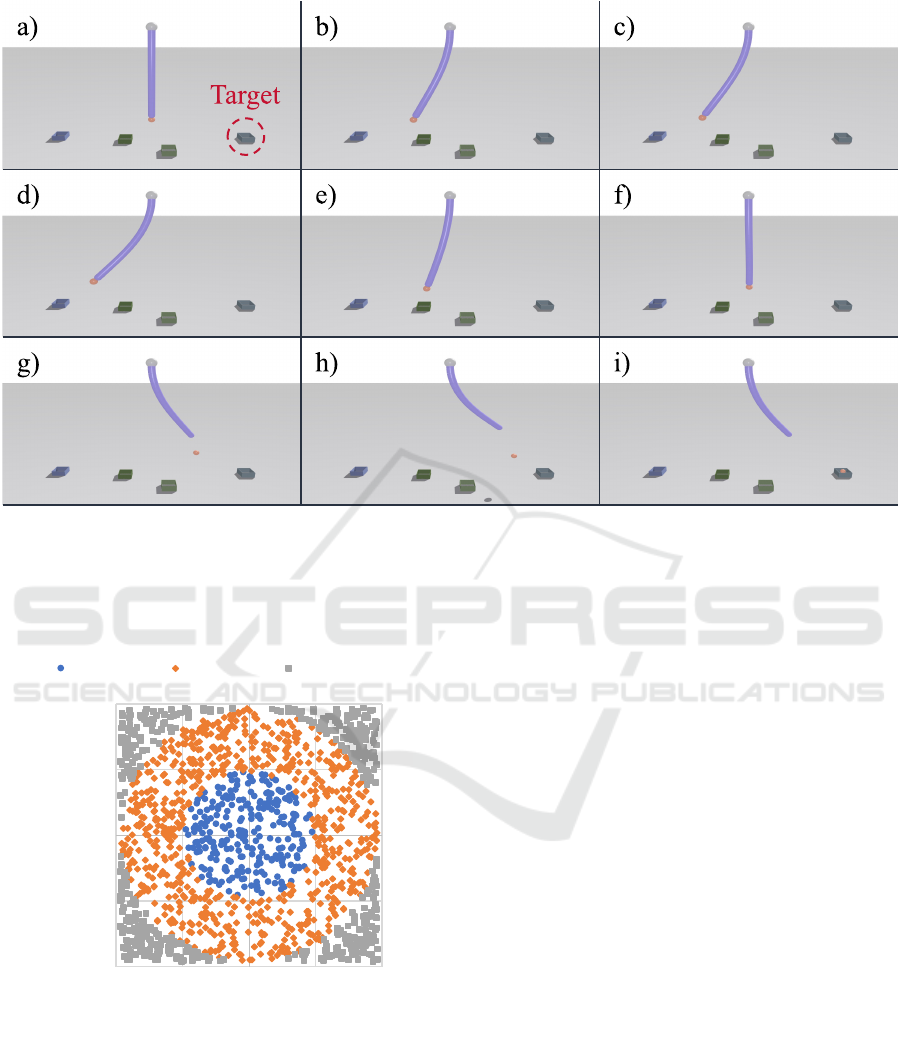
Figure 6: Soft robot manipulator while it is performing a throw toward the circled target in different time instants. The target,

here represented as a box without the lid, is 1.26 m distant from the projection of the ﬁxed-end of the arm on the ground.

Run-up phase from a) to d), the remaining frames present the forward stage in which the object, here represented as a sphere,

is launched. In the frame f) the sphere is released and it starts following the projectile motion till it reaches the target in the

frame i). Videos are available at the following link.

-1.3

-0.65

0.65

1.3

-1.3 -0.65 0 0.65 1.3

y [m]

x [m]

Category A Category B Category C

Figure 7: Desired targets divided in different categories.

In addition, the proposed method relies on a rich

dataset that allowed to reach a signiﬁcant accuracy in

the throwing tasks. In real application involving soft

robots, collecting such a consistent amount of data

could not be feasible leading to a decrease of perfor-

mances in terms of accuracy.

ACKNOWLEDGEMENTS

The authors would like to thank Andrea Centurelli

for the help provided during the development of

the proposed methodology and his comments on the

manuscript. The authors would like also to thank

Carlo Alessi for the support in the rendering of videos

available here.

This work was partially supported by the Euro-

pean Union’s Horizon 2020 FET-Open program under

grant agreement no. 863212 (PROBOSCIS project).

REFERENCES

Alqumsan, A. A., Khoo, S., and Norton, M. (2019). Robust

control of continuum robots using Cosserat rod theory.

Mechanism and Machine Theory, 131:48–61.

Centurelli, A., Arleo, L., Rizzo, A., Tolu, S., Laschi, C., and

Falotico, E. (2022). Closed-loop dynamic control of a

soft manipulator using deep reinforcement learning.

IEEE Robotics and Automation Letters, 7(2):4741–

4748.

Centurelli, A., Rizzo, A., Tolu, S., and Falotico, E. (2021).

Open-loop model-free dynamic control of a soft ma-

nipulator for tracking tasks. In 2021 20th Inter-

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

144

national Conference on Advanced Robotics (ICAR),

pages 128–133.

Chin, K., Hellebrekers, T., and Majidi, C. (2020). Machine

Learning for Soft Robotic Sensing and Control. Ad-

vanced Intelligent Systems, 2(6):1900171.

Cianchetti, M., Laschi, C., Menciassi, A., and Dario, P.

(2018). Biomedical applications of soft robotics. Na-

ture Reviews Materials, 3(6):143–153. Number: 6

Publisher: Nature Publishing Group.

Della Santina, C., Katzschmann, R. K., Biechi, A., and Rus,

D. (2018). Dynamic control of soft robots interact-

ing with the environment. In 2018 IEEE International

Conference on Soft Robotics (RoboSoft), pages 46–53.

Gazzola, M., Dudte, L. H., McCormick, A. G., and Ma-

hadevan, L. (2018). Forward and inverse problems in

the mechanics of soft ﬁlaments. Royal Society Open

Science, 5(6).

George Thuruthel, T., Ansari, Y., Falotico, E., and Laschi,

C. (2018). Control Strategies for Soft Robotic Ma-

nipulators: A Survey. Soft Robotics, 5(2):149–163.

Publisher: Mary Ann Liebert, Inc., publishers.

George Thuruthel, T., Falotico, E., Manti, M., Pratesi,

A., Cianchetti, M., and Laschi, C. (2017). Learning

closed loop kinematic controllers for continuum ma-

nipulators in unstructured environments. Soft robotics,

4(3):285–296.

Giorelli, M., Renda, F., Ferri, G., and Laschi, C. (2013). A

feed-forward neural network learning the inverse ki-

netics of a soft cable-driven manipulator moving in

three-dimensional space. In 2013 IEEE/RSJ Interna-

tional Conference on Intelligent Robots and Systems,

pages 5033–5039. ISSN: 2153-0866.

Kim, D., Kim, S.-H., Kim, T., Kang, B. B., Lee, M., Park,

W., Ku, S., Kim, D., Kwon, J., Lee, H., Bae, J., Park,

Y.-L., Cho, K.-J., and Jo, S. (2021). Review of ma-

chine learning methods in soft robotics. PLOS ONE,

16(2):e0246102. Publisher: Public Library of Sci-

ence.

Laschi, C., Mazzolai, B., and Cianchetti, M. (2016).

Soft robotics: Technologies and systems pushing

the boundaries of robot abilities. Science Robotics,

1(1):eaah3690. Publisher: American Association for

the Advancement of Science.

Mahl, T., Mayer, A. E., Hildebrandt, A., and Sawodny,

O. (2013). A variable curvature modeling approach

for kinematic control of continuum manipulators. In

2013 American Control Conference, pages 4945–

4950. ISSN: 2378-5861.

Naughton, N., Sun, J., Tekinalp, A., Parthasarathy, T.,

Chowdhary, G., and Gazzola, M. (2021). Elastica: A

Compliant Mechanics Environment for Soft Robotic

Control. IEEE Robotics and Automation Letters,

6(2):3389–3396. Conference Name: IEEE Robotics

and Automation Letters.

Piqu

e, F., Kalidindi, H. T., Fruzzetti, L., Laschi, C., Men-

ciassi, A., and Falotico, E. (2022). Controlling soft

robotic arms using continual learning. IEEE Robotics

and Automation Letters, 7(2):5469–5476.

Raptopoulos, F., Koskinopoulou, M., and Maniadakis, M.

(2020). Robotic Pick-and-Toss Facilitates Urban

Waste Sorting *. In 2020 IEEE 16th International

Conference on Automation Science and Engineering

(CASE), pages 1149–1154. ISSN: 2161-8089.

Rus, D. and Tolley, M. (2015). Design, fabrication and con-

trol of soft robots. Nature, 521:467–75.

Thuruthel, T. G., Falotico, E., Manti, M., and Laschi, C.

(2018). Stable Open Loop Control of Soft Robotic

Manipulators. IEEE Robotics and Automation Letters,

3(2):1292–1298. Conference Name: IEEE Robotics

and Automation Letters.

Thuruthel, T. G., Falotico, E., Renda, F., Flash, T.,

and Laschi, C. (2019). Emergence of behavior

through morphology: a case study on an octopus in-

spired manipulator. Bioinspiration & biomimetics,

14(3):034001.

Vannucci, L., Cauli, N., Falotico, E., Bernardino, A., and

Laschi, C. (2014). Adaptive visual pursuit involving

eye-head coordination and prediction of the target mo-

tion. In 2014 IEEE-RAS International Conference on

Humanoid Robots, pages 541–546.

Vannucci, L., Falotico, E., Di Lecce, N., Dario, P., and

Laschi, C. (2015). Integrating feedback and predic-

tive control in a bio-inspired model of visual pursuit

implemented on a humanoid robot. Lecture Notes in

Computer Science (including subseries Lecture Notes

in Artiﬁcial Intelligence and Lecture Notes in Bioin-

formatics), 9222:256–267.

Wales, D. J. and Doye, J. P. K. (1997). Global Opti-

mization by Basin-Hopping and the Lowest Energy

Structures of Lennard-Jones Clusters Containing up

to 110 Atoms. The Journal of Physical Chemistry A,

101(28):5111–5116. Publisher: American Chemical

Society.

Zeng, A., Song, S., Lee, J., Rodriguez, A., and Funkhouser,

T. (2020). TossingBot: Learning to Throw Arbitrary

Objects with Residual Physics. arXiv:1903.11239 [cs,

stat]. arXiv: 1903.11239.

Zhang, X., Chan, F. K., Parthasarathy, T., and Gazzola, M.

(2019). Modeling and simulation of complex dynamic

musculoskeletal architectures. Nature Communica-

tions, 10(1):undeﬁned–undeﬁned. Number: 1.

Zlatintsi, A., Dometios, A. C., Kardaris, N.,

Rodomagoulakis, I., Koutras, P., Papageorgiou,

X., Maragos, P., Tzafestas, C. S., Vartholomeos, P.,

Hauer, K., Werner, C., Annicchiarico, R., Lombardi,

M. G., Adriano, F., Asfour, T., Sabatini, A. M.,

Laschi, C., Cianchetti, M., G

uler, A., Kokkinos, I.,

Klein, B., and L

opez, R. (2020). I-Support: A robotic

platform of an assistive bathing robot for the elderly

population. Robotics and Autonomous Systems,

126:103451.

Open-loop Control of a Soft Arm in Throwing Tasks

145