Large-scale Randomness Study of Security Margins

for 100+ Cryptographic Functions

san Klinec

, Marek S

, Karel Kub

cek

, Petr

Svenda

and Vashek Maty

Masaryk Univesity, Brno, Czech Republic

ETH Zurich, Switzerland

ﬁ ﬁ

Keywords:

Randomness Analysis, Cryptographic Function, Security-margin.

Abstract:

The output of cryptographic functions, be it encryption routines or hash functions, should be statistically indis-

tinguishable from a truly random data for an external observer. The property can be partially tested automat-

ically using batteries of statistical tests. However, it is not easy in practice: multiple incompatible test suites

exist, with possibly overlapping and correlated tests, making the statistically robust interpretation of results

difﬁcult. Additionally, a signiﬁcant amount of data processing is required to test every separate cryptographic

function. Due to these obstacles, no large-scale systematic analysis of the the round-reduced cryptographic

functions w.r.t their input mixing capability, which would provide an insight into the behaviour of the whole

classes of functions rather than few selected ones, was yet published. We created a framework to consistently

run 414 statistical tests and their variants from the commonly used statistical testing batteries (NIST STS,

Dieharder, TestU01, and BoolTest). Using the distributed computational cluster providing required signiﬁcant

processing power, we analyzed the output of 109 round-reduced cryptographic functions (hash, lightweight,

and block-based encryption functions) in the multiple conﬁgurations, scrutinizing the mixing property of each

one. As a result, we established the fraction of a function’s rounds with still detectable bias (a.k.a. security

margin) when analyzed by randomness statistical tests.

1 INTRODUCTION

Truly random data are essential in many crypto-

graphic operations such as the generation of keys, un-

predictable nonces or padding schemes. Flawed ran-

dom generators producing partially predictable data

can lead to factorization of TLS server keys (Heninger

et al., 2012), compromise of RSA keys from elec-

tronic IDs (Bernstein et al., 2013) or theft of funds

from cryptocurrency wallets (Ketamine, 2018). Sim-

ilarly, cryptographic functions such as block ciphers

or hash functions are expected to produce output in-

distinguishable from the truly random data as long as

the attacker does not posses the key used, input data

or both. Producing data with detectable biases sug-

gests a susceptibility to linear or differential crypt-

analysis (Matsui, 1993; Biham and Shamir, 2012).

Multiple randomness test batteries exist, the

most common being NIST STS (Rukhin et al.,

2010), Dieharder (Brown et al., 2013) and

TestU01 (L’Ecuyer and Simard, 2007). How-

ever, when applied to pseudorandom generators,

human cryptanalysts typically do not consider

general-purpose statistical batteries to be a very

useful method for identifying weaknesses of crypto-

graphic functions. There are at least two reasons for

this:

Firstly, the use of statistical testing batteries is

far from easy in practice. Multiple test suites ex-

ist and with incompatible interfaces, using different

approaches for the test interpretation and difﬁcult to

computationally scale enough to analyze more than

a handful of analyzed functions. The results of sta-

tistical tests are also notoriously difﬁcult to interpret:

Research literature contains multiple examples of in-

valid results due to ﬂawed test interpretations. It is un-

clear how sensitive the separate tests included in the

different statistical batteries are and how well-suited

they are for the domain of testing the output of cryp-

tographic functions.

Secondly, existing tests are perceived as not sen-

sitive enough and signiﬁcantly falling behind the

human-performed cryptanalysis. However, there is

only limited empirical evidence for this – it holds

only for the well-studied functions such as ﬁnalists of

the AES or SHA-3 competitions. We aim to answer

134

Klinec, D., Sýs, M., Kubí

cek, K., Švenda, P. and Matyáš, V.

Large-scale Randomness Study of Security Margins for 100+ Cryptographic Functions.

DOI: 10.5220/0011267600003283

In Proceedings of the 19th International Conference on Security and Cryptography (SECRYPT 2022), pages 134-146

ISBN: 978-989-758-590-6; ISSN: 2184-7711

the question of whether automated analysis using ran-

domness testing batteries is useful for initial crypt-

analysis of round-reduced functions and how these

automatically found security margins compare with

the results found by human cryptanalysts.

A signiﬁcant amount of earlier work has tack-

led the problem of automatic randomness analysis of

cryptographic functions’ output using statistical tests.

However, they share the following limitations: 1)

Only a limited set of statistical tests is used for eval-

uation (usually a single battery) and test results in-

terpretation is often ﬂawed (ignoring correlated tests,

inappropriately adjusting the signiﬁcance level, etc.).

2) Only a very narrow set of different outputs is tested

(usually just a one or few functions).

Finally, but just as importantly, almost all these

studies are difﬁcult to replicate as the implementa-

tions are often not published and the computations

performed (e.g., seed used for data sequence produc-

tion) are not deterministic. The related work is revis-

ited in more detail at the end of the paper in Section 5.

To address the outlaid issues while avoiding the

common limitations, we designed and performed a

wide analysis of 109 different cryptographic functions

(or 130 different combinations of functions and their

parametrizations) by assessing their outputs with sta-

tistical tests. The output data is generated by Cryp-

toStreams

– our open-source framework for generat-

ing data from round-reduced cryptographic functions

in multiple input conﬁgurations. Testing was done us-

ing 414 statistical tests from four randomness testing

batteries (NIST STS (Rukhin et al., 2010), Dieharder

(Brown et al., 2013), TestU01 (L’Ecuyer and Simard,

2007) and BoolTest (S

ys et al., 2017)), uniﬁed into

a user-friendly tool called the Randomness Testing

Toolkit (RTT)

. The analysis is fully automatic and

replicable using these tools and the published starter

seeds.

Our paper brings the following contributions in

the areas of cryptographic function analysis and sta-

tistical testing of randomness:

1. Methodology for round-reduced function bias as-

sessment. We deﬁne a new methodology for test-

ing and deciding whether given round-reduced

function produces biased data using randomness

testing batteries with adjustable signiﬁcance level

α. The methodology aims to eliminate false posi-

tives and produce conservative results.

2. Security margins analysis of cryptographic func-

tions. For 109 distinct round-reduced functions,

we establish the security margin with respect to

https://github.com/ph4r05/CryptoStreams

https://github.com/ph4r05/rtt-deployment

the perceived randomness of produced outputs.

We then compare the results with manual crypt-

analysis, as shown in Subsection 3.2. To the best

of our knowledge, dataset being analyzed is supe-

rior in terms of number of functions, tested strate-

gies and amount of data being tested to previous

research in the ﬁeld.

2 RANDOMNESS TESTS AS

DISTINGUISHERS

Tests of randomness are proposed to detect speciﬁc

types of patterns (bias from randomness) in the anal-

ysed data. For example, a very simple test called

Monobit compares the counted frequency of binary

ones and zeroes, which shall be roughly equal in a

random stream. Each test can typically detect also

other types of patterns, but some others remain unde-

tected. For example, Monobit can detect bias from

randomness for the sequence (’011 011 011...’), but

the sequence (’01 01 01 ...’) will not be detected as

biased.

In practice, tests are grouped into testing suites

called batteries. We analyze tests belonging to com-

monly used batteries NIST STS, Dieharder, TestU01,

and recently introduced BoolTest. If tests are param-

eterized, the default settings from a battery are used.

Some tests in these batteries consist of more variants

(e.g., forward, backward, speciﬁc number of bits in

a searched pattern), resulting in 414 test variants in

total.

Randomness testing is based on statistical hypoth-

esis testing procedure that computes the statistical dis-

tance between the analyzed dataset and a synthetic

dataset produced by the idealized model (hypothesis).

Tests compute a certain type of statistic of bits and

evaluate how far is the computed statistic from the ex-

pected theoretical statistic for random data expressed

typically as the p-value (L’Ecuyer and Simard, 2007;

Marsaglia, 1995; Rukhin et al., 2010).

A small p-value below a chosen signiﬁcance level

α leads to the rejection of the hypothesis (bias de-

tected). In such a case, the test forms a distinguisher

as it can distinguish analysed data from random data.

We can commit two types of error. Type I error when

the test rejects the hypothesis and data being gener-

ated by an unbiased random generator. Type II error

when the hypothesis is accepted although generated

by a biased generator.

The probability of the Type I error is equal to α

and is directly controllable. The probability of the

Type II error β is unknown but related to α – larger/s-

Large-scale Randomness Study of Security Margins for 100+ Cryptographic Functions

135

maller α corresponds to smaller/larger β. Also, the

size of the data affects both α and β.

Randomness testing is used for the two main ar-

eas: 1) To detect systematic bias or physical failures

of the TRNGs (true random number generators) and

2) To demonstrate insufﬁcient confusion and diffusion

property (Menezes et al., 1996) of TRNGs. A physi-

cal device failure typically results in a constant or very

low variability output, which is easy to detect even by

simple tests like Monobit. A signiﬁcantly more com-

plex bias is present for TRNGs with an insufﬁcient

mixing property. The TRNG function designer typi-

cally improves the mixing property by increasing the

number of internal rounds (Menezes et al., 1996). It

should be noted that to conclude that a given gener-

ator is biased is a difﬁcult problem due to the proba-

bilistic nature of randomness test result. In practice,

this problem is solved by repeated testing with addi-

tionally generated data until the observed bias is con-

ﬁrmed or bias disappears and the generator is declared

unbiased. Besides the probabilistic nature of test re-

sults, there are other problems concerned with the set-

tings of tests (trade-off between Type I and II errors,

which is also affected by the volume of the analysed

data), approximation used to compute p-values and

incorrect assumptions about their uniform distribu-

tion, incorrect test implementation, etc. We discuss

these problems in more detail in Section 4.1.

2.1 Building Function Testing Set

Every sequence we analyse in our experiments de-

pends on a cryptographic function (and its parame-

terization) included in the benchmarking dataset and

a structure of input data (counter – CTR, Low Ham-

ming Weight counter – LHW, pair of inputs with one

bit ﬂipped and their parameterizations – SAC) pro-

cessed by the function. More details on these are pro-

vided below in Section 2.1.2. The sequences are pa-

rameterized by the following variables:

1. cryptographic function: a) the number of internal

rounds (on average, with range of ﬁve subsequent

rounds per function), b) key for stream and block

ciphers, seed for PRNG;

2. type (CTR, LHW or SAC) of processed input is

parameterized by: a) seed – deﬁnes seed of ﬁxed

PRNG used to generate random blocks in SAC,

b) offset – deﬁnes initial value of CTR or LHW

counter,

3. the length of the output data generated (10 MB,

100 MB and 1000 MB).

The combination of used parameters – crypto-

graphic function (deﬁned by a number of rounds and

a key in case of block ciphers), type of input (CTR,

LHW, SAC) and output data size (10, 100, 1000 MB)

– will be called conﬁguration (shortly cfg) of the (po-

tentially) detectable biased generator. Each conﬁgu-

ration is used to generate three different sequences by

using different values of seed, offset and byte.

The following two sections explain the selection

of cryptographic functions, type of inputs and usage

of their parameters in more details.

2.1.1 Round-reduced Cryptographic Functions

The basic set of cryptographic functions was collected

mainly from various cryptographic function competi-

tions like AES or SHA-3 with an addition of well-

known functions with available source-code. Out of

these, we included only functions with available test

vectors and such that contain some internal round-

based structure and can be therefore round-reduced

to produce a function with a reduced complexity.

The rounds used for a particular function were it-

eratively selected so that there are at least two rounds

before and after the last round for which at least one

test detects a bias. In total, we analyzed 52077 round-

reduced function conﬁgurations (complete list of an-

alyzed functions is shown in Table 1).

2.1.2 Parameterized Input Data Generation

Three different data generation strategies are used to

analyze confusion and diffusion properties of the tar-

get function output, namely CTR, LHW and SAC.

The CTR strategy generates blocks of a particu-

lar size, each containing the current block index. In-

tuitively, the high bits are set to zero while the low

bits are iterating until the required amount of data is

generated. Note that block ciphers with extremely

small blocks, like 32-bit version SIMON and SPECK

ciphers, can produce only 2

· 32 bits ≈ 17.2 GB.

However, even shorter streams are having issues with

a too high uniqueness of blocks.

The LHW stands for Low Hamming Weight as

it generates input blocks with a ﬁxed low Hamming

weight. The weight is derived from the block size as

it is required to avoid cycling of the generator, i.e.,

depleting all options on the block size. If the tested

function f has an input block size of 128 bits, and we

need to generate 100 MB of data, we set the Hamming

weight to 4, as 16



128



≈ 170 MB. The idea behind

the LHW strategy is to cover the whole input block

with small changes only, keeping the total Hamming

weight low, thus feeding the minimal possible entropy

to a function. Both CTR and LHW serve as low-

entropy input generators, allowing for inspection of

confusion properties of the cryptographic functions.

SECRYPT 2022 - 19th International Conference on Security and Cryptography

136

The SAC strategy aims to test the Strict Avalanche

Criterion (Webster and Tavares, 1985), where the

tested function shall generate two seemingly uncor-

related output blocks despite only a single bit ﬂip in

the corresponding input blocks. It generates pairs of

blocks, where the ﬁrst block in the pair is randomly

generated and the second one is almost the same ex-

cept for a single bit ﬂip at a randomly selected po-

sition. Both blocks are then used as an input to the

tested function f . This strategy inspects mainly diffu-

sion properties of the cryptographic functions.

The strongest generating strategy is rnd, which

generates a random block using a given seed, with

the PCG64 generator (O’Neill, 2014). Similarly, ornd

strategy generates a random value only once, then re-

peats it each time a value is needed. The ornd usage:

generate random plaintext block, then repeat the same

value with different keys.

Let’s deﬁne a function conﬁguration as a tuple

(function name, round). An input conﬁguration de-

ﬁnes input streams fed to the function being ana-

lyzed, e.g., plaintext, key, seed. Function generates

output sequence that is analyzed with randomness

testing batteries. We have analyzed basic function

types: block ciphers, stream ciphers, hash functions,

PRNGs. Each function type differs in input conﬁgu-

rations being used.

A hash function takes an input string and trans-

forms it to the output block. An input conﬁgura-

tion is thus a conﬁguration of an input stream of

blocks x

fed to the hash function. E.g., CTR con-

ﬁguration for function f generates a stream of values:

( f (x

), f (x

),···) = ( f (x

))

. Hash functions use con-

ﬁgurations: {ctr, lhw, sac}.

PRNG takes an input seed and generates long

stream of output data. One testing approach is to

generate a seed randomly and analyze a long out-

put sequence of the PRNG. However, it does not

yield useful results as PRNG internal state changes

when generating output sequences. It is difﬁcult to

spot randomness biases for randomness testing bat-

teries in this setting. Moreover, PRNGs usually do

not have internal round structure so it is not possible

to analyze weakened function versions, we have to

test PRNG in a full strength. We thus have two ap-

proaches when testing PRNGs. 1) Test N bytes with a

ﬁxed seed, 2) an alternative testing approach by re-

peating the following: reseed PRNG with an input

stream block, capture B output bytes, reseed and cap-

ture again: ( f (seed=s

)[: B])

. An input conﬁguration

deﬁnes seed stream. PRNGs testing strategies: {zero,

ctr.seed, lhw.seed, sac.seed, rnd.seed}.

Stream ciphers are similar to PRNGs in the test-

ing context. Feeding a speciﬁc plaintext to the stream

cipher does not bring beneﬁt from the testing perspec-

tive as it is only XORed with the keystream generated

by the stream function, adding unnecessary entropy.

We thus only test the keystream itself, feeding zero

vector plaintext to the function.

Stream ciphers usually have internal round struc-

ture that makes analysis of a long keystream from the

weakened cipher possible. Input strategy zero: gener-

ate a random key k

, generate a long keystream with

the k

. The output sequence is: ( f (key=r

)[: N]),

where N is the desired keystream length. A .key test-

ing strategy generates a sequence of ﬁrst B bytes of

the keystream for key k

: ( f (key=k

)[:B])

. Input

strategy deﬁnes how (k

) is generated. Stream func-

tion testing strategies: {zero, ctr.key, lhw.key, sac.key,

rnd.key}.

Block Ciphers: Take two inputs of a ﬁxed length:

key, plaintext and output a ﬁxed length block. We use

two different input conﬁguration types. Input conﬁg-

uration: ﬁx a random key k

, derived from a seed,

generate input blocks x

. ( f (key=k

))

. Testing

strategies: {zero, ctr, lhw, sac}.

Alternative approach is to change a key and ob-

serve the function behavior. This testing strategy can

reveal e.g. sensitivity to weak keys. Key conﬁgura-

tion deﬁnes how (k

) sequence is generated. The

tested output is then ( f (key=k

))

. The simplest

key strategy is to generate k

via CTR mode and keep

= 0. We call such strategy ctr.key..zero.inp. Block

cipher testing strategies: {zero, ctr, lhw, sac, rnd.key},

∪ {ctr.key, lhw.key, sac.key} ×{..zero.inp,..ornd.inp}.

A stronger strategies with ..ornd.inp sufﬁx gener-

ate a random plaintext block once and reuses the

same value with different keys, i.e., x

= x

randNext(seed).

Seeds: Using given strategies we obtain an out-

put sequence for a function and input conﬁguration.

Then randomness testing batteries are used to assess

whether the sequence contains statistical biases. If

enough biases are found (deﬁned later) we conclude

the hypothesis about an uniform output sequence dis-

tribution for the function conﬁguration being rejected,

in short, function at a round r was rejected.

In order to reduce false-positives we use 3 differ-

ent input conﬁgurations parameters per the function

conﬁguration F

. I.e., when using CTR generator,

we use an offset to generate 3 different counter se-

quences. Sequence 1 starts at offset 0, sequences 1,2

have offsets o

such that sequences do not over-

lap on the lengths used for testing. Technically, if

the output length per one block is B bytes, setting

offset O is done by setting the most signiﬁcant byte

of the counter to O, e.g., (S

)

= 2 ∗ 2

8∗8

,(S

)

2 ∗ 2

8∗8

+ 1,···

Large-scale Randomness Study of Security Margins for 100+ Cryptographic Functions

137

LHW generator offset is realized by setting ini-

tial LHW state so that the combination space is par-

titioned to 3 disjoint parts. Technically, we compute

a number of combinations for a weight w on B bits

as L =





. Offsets are then o

= L ∗

. Using rank-

ing algorithm we then compute o

th combination for





and use it as a starting position for LHW. As SAC

uses randomly generated values, we randomly gener-

ate seeds s

so that SAC generates sequences S

differ.

is rejected if at least 2 out of 3 output sequences

are rejected. The reason for the usage of three differ-

ent seeds is to make the likelihood of the (unwanted)

usage of a key with the value degrading the function

confusion and diffusion properties (called weak key)

very small. The weak keys are very infrequent or

shown to be non-existent for common cryptographic

functions with a full number of internal rounds. How-

ever, they are signiﬁcantly more likely to occur with

the reduced number of rounds we are using.

CryptoStreams is highly conﬁgurable; we pre-

conﬁgured more than ten additional general testing

strategies. We provide the list of all our strategies and

their description at the GitHub repository

. The total

number of the data conﬁgurations analyzed is: 6264x

10 MB, 6526x 100 MB and 4569x 1 GB. In total, we

analyzed 5160.4 GB of data.

3 RESULTS

The following section summarizes basic observations

from collected testing data.

3.1 Study Limitations

We used default settings of tests as such parame-

ters are commonly used in practice. Usage of other

non-standard parameters may provide a different re-

sult. Due to high computational costs only {10, 100,

1000} MB data sizes were tested. Using larger data

sizes could reveal more subtle biases and detect more

rounds. Also, some tests were not run as they require

more data for analysis, e.g., Test U01 BigCrush.

From all possible data generation strategies, we

used only a small subset that we deemed the most

promising, as deﬁned in Section 2.1.2. New genera-

tion strategies may reveal another unexpected biases.

Also, no detailed analysis of patterns found for par-

ticular cryptographic functions was performed.

https://github.com/ph4r05/SecurityMarginsPaper

3.2 Security Margins of Cryptographic

Functions

The number of rounds for which a distinguisher was

automatically constructed by at least one test can be

used to establish the security margin of a given cryp-

tographic function included in the CryptoStreams bat-

tery. We also performed an extensive literature survey

to identify the highest number of rounds for which

any distinguisher was published.

Classical techniques in cryptanalysis, such as lin-

ear or differential cryptanalyses, require determin-

ing some bias in the ciphertext, which then leads to

a recovery of (some) bits of key, plaintext or both.

The designers of cryptographic functions try to make

the function complex enough to hide any such bias,

usually by increasing the number of function’s inter-

nal rounds. For cryptographic functions now consid-

ered secure (like AES), neither the general-purpose

tests nor the custom tests by human cryptanalyst were

shown to detect bias in a function with a full number

of rounds as speciﬁed by its designers.

Still, we can weaken a function complexi-

ty/strength (e.g., in the number of rounds), while test-

ing the output for a bias presence. If the number of

rounds where the bias is detectable is too close to

the full number of rounds (unweakened function), the

function shall be considered less secure and in de-

mand for strength improvement (e.g., by increasing

the number of rounds). We deﬁne the security mar-

gin as the difference between the number of rounds,

for which a distinguisher can be still constructed and

the total number of rounds of that function. More pre-

cisely:

sec. margin( f ) = 1 −

max(i) : f

output is non-random

where f

stands for function f limited to i rounds and

n is the total number of rounds of the function f as

speciﬁed by its authors. For example, there exists a

distinguisher for a 3-round AES, but not for the 4-

round one. AES-128 has 10 rounds in total, so the re-

sulting security margin against analyzed randomness

tests is 70%.

Security Margins per Function Type. Results in

Table 2 indicate that security margins of all func-

tion types are similar when considering only input

type strategies. However, key type strategies reduce

security margins signiﬁcantly. Also, hash functions

have typically greater security margins than block and

stream ciphers using key strategies.

Measured security margins of MPC hash func-

tions are high, indicating that testing batteries might

SECRYPT 2022 - 19th International Conference on Security and Cryptography

138

Table 1: The security margin for each tested cryptographic function included in the CryptoStreams testbed. The table depicts

the maximal number of rounds for which some bias was reliably detected for at least one data conﬁguration used (red bar).

Additional rounds with a practical distinguisher published in research literature are shown as a pink bar (typically larger than

randomness tests). If no published and practical (complexity < 2

) attack is found, sign ”−” is used. The numerical value

of rounds is encoded as rounds by RTT/rounds by literature/rounds total. The average bar shows the median of observed

percentage security margin with ﬁrst and third quantile in the parentheses. MPC functions (Aly et al., 2020) are crypto-

graphic functions optimizing their arithmetic complexity (used for example in zero-knowlege proof systems or multi-party

computation protocols).

Function Security margin Function Security margin Function Security margin

Hash functions CAMELLIA 4/8/18 RECT.K80 8/18/25

Abacus 0/-/280 CAST 3/9/12 RECT.K128 8/14/25

ARIRANG 3/4/4 FANTOMAS 2/5/12 R.RUNNER.K80 3/8/10

AURORA 2/-/17 GOST 29/20/32 R.RUNNER.K128 5/8/12

BLAKE 1/4/14 IDEA 6/4/8 SPARX-B64 2/8/24

Blender 0/-/32 KASUMI 3/8/8 SPARX-B128 3/8/32

BMW 0/-/16 KUZNYECHIK 2/4/10 SPECK 10/15/32

Boole 3/16/16 LBLOCK 11/24/32 TEA 32/5/32

Cheetah 4/12/16 LEA 8/8/24 TWINE 9/23/35

CHI 0/-/20 LED 7/-/48 XTEA 8/8/32

CubeHash 0/-/8 MARS 0/8/16 MPC functions

DCH 1/4/4 MISTY1 1/6/8 GMiMC.S45a 1/-/121

DynamicSHA 10/-/16 NOEKEON 2/4/16 GMiMC.S128e 1/-/342

DynamicSHA2 17/17/17 PICCOLO 6/5/25 LowMC.S80a 4/-/12

ECHO 2/4/8 PRIDE 12/19/20 LowMC.S80b 4/-/12

ESSENCE 9/14/32 PRINCE 4/6/12 LowMC.S128a 4/-/14

Gost 1/5/32 RC5-20 5/17/20 LowMC.S128b 120/-/252

Grostl 2/-/10 RC6 5/5/20 LowMC.S128c 20/-/128

Hamsi 0/-/3 ROBIN 16/16/16 LowMC.S128d 16/-/88

JH 6/10/42 ROBIN

⋆

3/-/16 MiMC.S45 1/-/116

Keccak 4/5/24 SEED 2/-/16 MiMC.S80 1/-/204

Lesamnta 3/32/32 SERPENT 3/5/32 MiMC.S128 1/-/320

Luffa 7/8/8 SHACAL2 21/44/80 Poseidon.S80b 0/-/8

MCSSHA-3 0/-/1 SIMON 19/26/68 Poseidon.BLS12 0/-/8

MD5 25/-/64 DES 16/16/16 Rescue.S45a 0/-/10

MD6 10/16/104 TRIPLE-DES 16/-/16 Rescue.S128e 0/-/10

RIPEMD160 14/48/80 TWOFISH 3/16/16 RescueP.128a 0/-/27

Sarmal 0/-/16 Stream ciphers RescueP.128b 0/-/27

SHA-1 18/80/80 Chacha 3/6/20 RescueP.128c 0/-/14

SHA-2 14/31/64 DECIM 7/-/8 RescueP.128d 0/-/14

SHA-3 4/5/24 F-FCSR 5/5/5 RescueP.S80a 0/-/18

Shabal 0/-/1 Fubuki 0/-/4 RescueP.S80b 0/-/18

SHAvite3 2/-/12 Grain 11/13/13 RescueP.S80c 0/-/9

SIMD 0/-/4 HC-128 0/-/1 RescueP.S80d 0/-/9

Skein 4/17/72 Hermes 2/-/10 Starkad.S80b 1/-/8

Tangle 80/80/80 LEX 3/-/10 Starkad.S128e 1/-/8

Tangle2 80/-/80 MICKEY 0/-/1 Vision.S45a 0/-/10

TIB3 0/-/16 Rabbit 0/-/4 Vision.S128d 0/-/10

Tiger 2/19/23 RC4 1/-/1 PRNGs

Twister 6/9/9 Salsa20 2/6/20 Std.LCG 1/1/1

Whirlpool 1/10/10 SOSEMANUK 8/-/25 Std.MTwister 1/1/1

Block ciphers Trivium 3/5.8/8 Std.SubCarry 1/1/1

AES 3/6/10 TSC-4 14/-/32 U01.ULCG 1/1/1

ARIA 2/4/12 CHASKEY 3/7/16 U01.UMRG 1/1/1

BLOWFISH 5/4/16 HIGHT 11/18/32 U01.XorShift 1/1/1

not be directly usable for this function family. We

hypothesize this is due to usage of algebraic building

blocks which are difﬁcult to detect with randomness

testing batteries. To verify the claim, we tested a sim-

ple function f (x) = x

(mod p), where p is a 255-bit

prime. The function f was fed with a strongly biased

input distribution - normal distribution to produce 1

GB of output data. The output was tested with testing

batteries (after applying rejection sampling transfor-

mation, described in Section 4.2). There was no bias

detected in any of 10 tested streams. We thus con-

clude that even a simple algebraic function such as

Table 2: Aggregate security margins (SM, average and me-

dian values) for various function types and testing methods.

Function type

Input SM [%] Key SM [%]

avg med avg med

Hash 76.37 84.52 - -

Block cipher 78.84 80.62 68.86 74.64

Stream cipher 80.77 90 64.59 70

MPC 93.94 100 95.85 100

f can make the output indistinguishable from PRNG

stream for testing batteries. In fact, the described

function f is a basic building block of MiMC hash

function.

Large-scale Randomness Study of Security Margins for 100+ Cryptographic Functions

139

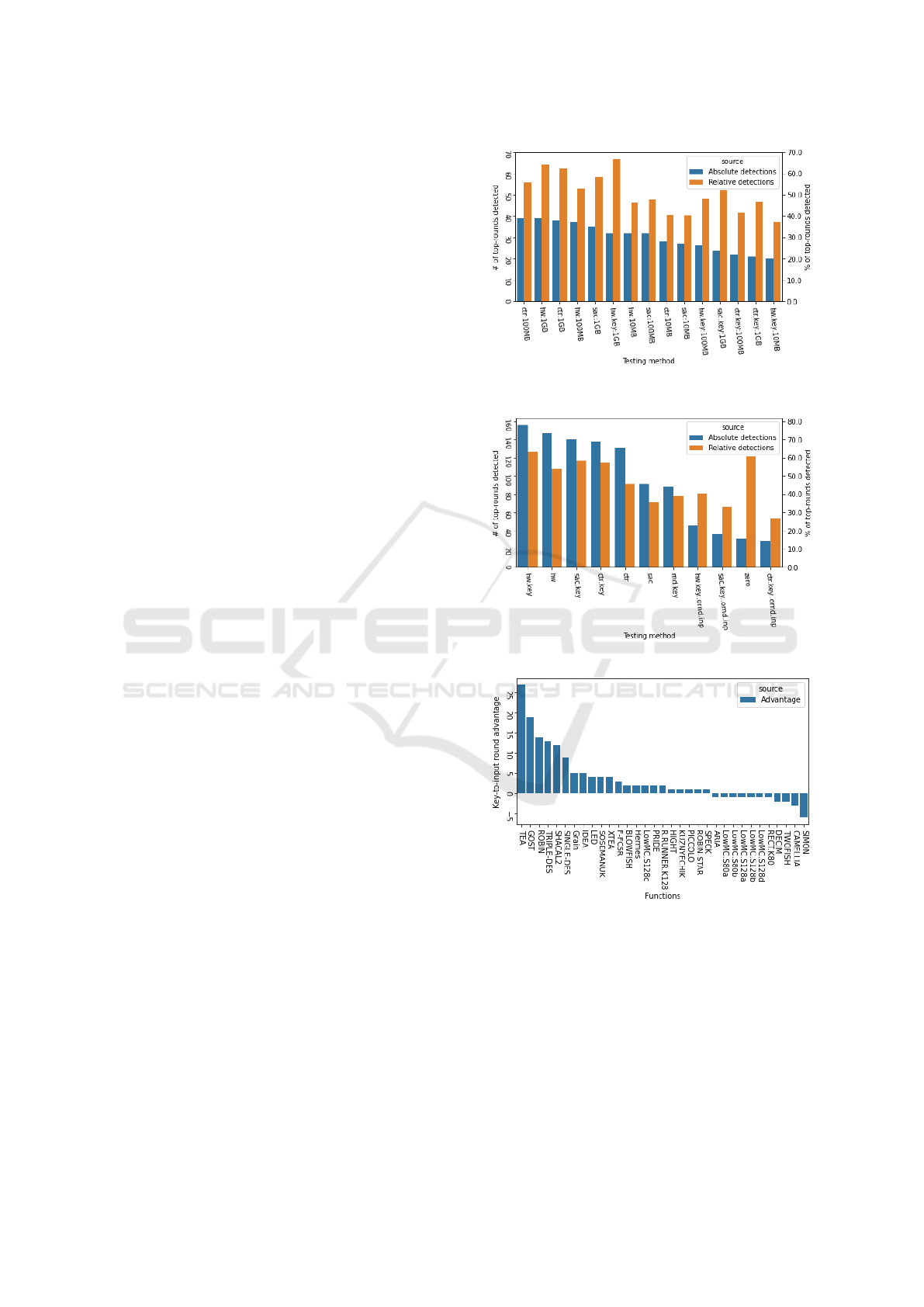
Used Methods. Figure 1 displays both absolute and

relative numbers per input generation methods for

breaking the highest broken round (top-round) of the

functions. From the results we can conclude that the

lhw strategy is very effective in breaking top-rounds,

both in input and key variants.

Also note that key variants have better relative suc-

cess rate than input variants, indicating that crypto-

graphic functions are more prone to biases when low-

entropy keys are used compared to low-entropy in-

puts. Also, strategy rnd.key is the most difﬁcult to

detect as the entropy fed to the key of the function is

high, it still managed to detect 37% of conﬁgurations

it was used on.

Note that strategy zero is used for all stream func-

tions with zero input as they generate long keystream

with ﬁxed random keys.

Considering input methods coupled with data

sizes we observe that large data set 1000 MB domi-

nate detection capabilities in all main methods {lhw,

ctr, sac}. Interestingly, {lhw, lhw.key} on 10 MB out-

perform ctr on 100 MB.

Key Method Dominance. We observed that in 24

(44.44%) cases the key variant was better than input

variant for given inputs, same performance was seen

in 19 cases (35.19%), input variant was better in 11

cases (20.37%). In some scenarios, the key to the in-

put advantage is quite signiﬁcant.

For example, Triple-DES is detected only to round

3 with input strategies, but the key strategy manages

to detect all 16 rounds, even rnd.key, which is the

most difﬁcult strategy to detect. That means there are

serious biases in Triple-DES output for some keys.

A hypothesis is that weak keys known for Triple-

DES were in the input stream, causing the cipher-

text to contain biases. On the other hand, the SI-

MON function was detected with key methods up to

14 rounds but input methods reached 19 rounds. Fig-

ure 1c shows key to input method advantage with re-

spect to the maximum round detected per given func-

tion.

RC4 is known to contain biases on the beginning

of the keystream. Experiments were not able to detect

biases using zero strategy, i.e., using keystream with

a random key. However, all tested key methods de-

tected biases with 100 MB of data and more, even the

most difﬁcult rnd.key strategy.

Data Size. This paragraph focuses on detection ca-

pabilities when all variables are ﬁxed, besides length

of the input data stream. We take results over all de-

tected rounds, not just a top-round detections. The

most observed event was that changing input data

(a) Testing methods breaking top-rounds, with

sizes.

(b) Figure 1a with aggregated sizes

breaking the highest round of the given function.

Methods axis shows number of test methods reject-

ing the same round. Entries with no advantages are

skipped for better readability.

Figure 1: Methods breaking top-level rounds and key-to-

input methods advantage in breaking the highest rounds.

stream did not increase detection capability, with

1694 detections (80.94%).

In general, one would assume that bigger the in-

SECRYPT 2022 - 19th International Conference on Security and Cryptography

140

put stream the easiest is to spot biases for the ran-

domness tests. In particular, it means that given con-

ﬁguration was not detected on lower input size but it

was detected by all higher data sizes. This turned out

to be the case for 397 detections (18.97%). For ex-

ample, AES round 3 using lhw.key strategy was not

detected on 10 MB input but since 100 MB. Similarly

for Blowﬁsh round 3 with sac strategy.

We also observed an inverse effect, i.e., detection

was successful on a lower data size, but higher data

sizes did not detect the stream. This happened in a

single case (0.05%). Our hypothesis is that that bias

was lost in a noise as data size increased, i.e., it was

probably a ﬂuke. The case is Kasumi round 3 with

the lhw.key strategy, bias was observed only in the

10 MB input stream. Considering no other strategy

could detect the same function conﬁguration, we can

assume the detection was a ﬂuke. Rest of the cases

are ﬂuctuations where bias was either observed or un-

detected on a 100 MB data size, observed in a single

case (0.05%).

Table 3 shows a result subset of a maximal de-

tected round depending on a chosen method and in-

creasing input size for the method. Apparently, the

highest detected round is strongly dependent on the

mentioned parameters.

Table 3: Maximal breaking rounds for selected (function :

method) pairs depending on different input sizes.

Function : method 10 MB 100 MB 1 GB

MD5 : lhw 17 20 25

: sac 13 16 20

DES : lhw 4 6 7

: rnd.key 16 16 16

SIMON: ctr 17 18 19

: lhw 15 17 17

: lhw.key 11 11 12

GOST : ctr.key 10 11 12

: lhw.key 21 25 29

: lhw.key..ornd.inp 20 22 27

: rnd.key 1 1 1

Function Publication Year. Figure 2 shows secu-

rity margin heat maps (the darker the more functions

belong to the bin) for particular function types based

on the year of a publication of the function. Note

that hash and stream function year variance is low as

majority of our function dataset comes from eStream

and SHA-3 competitions, thus many of the functions

were published in the same year. From the ﬁgures we

can conclude there is a high variance in security mar-

gins. Yet, we cannot conclude that older functions

have lower security margins.

(a) Security margin for hash functions

(b) Security margin for stream ciphers

ods

(d) Security margin for block ciphers, key methods

Figure 2: Security margin heat maps based on the publica-

tion year of the functions analyzed. The results generally

show increased number of published functions around the

related competitions (e.g., AES or SHA-3), better security

margin for the functions introduced later, but with excep-

tions of the broken ones.

Large-scale Randomness Study of Security Margins for 100+ Cryptographic Functions

141

Bias Strength Measure. There are several ways to

deﬁne a measured bias strength. E.g., ratio of ran-

domness tests detecting the sequence as biased on

a level α, minimal p-value observed, number of re-

jected seeds, etc. Intuitively, lower rounds of a cryp-

tographic function should have stronger biases com-

pared to higher rounds. Experiments conﬁrm that this

is true for majority of tested functions. To demon-

strate this, lets observe ratio of rejecting tests for the

SIMON function with the lhw input strategy on 100

MB of data, starting from round 11: 0.88, 0.83, 0.75,

0.68, 0.44, 0.37, 0.22, 0.07 (round 18), while round 19

is ﬁrst with no bias detected with only 3/735 rejecting

tests. On the other hand, there are functions which do

not have such smooth bias progression, for example

LED using lhw with 100 MB, rounds {1,2,3} are all

detected with 0.93 tests, round 4 has 0 test detections.

4 RANDOMNESS TESTING FOR

MASSES

We created a practical, generally usable tool for ran-

domness testing, the Randomness Testing Toolkit

(RTT), which integrates four randomness testing bat-

teries (NIST STS, Dieharder, TestU01, and BoolTest),

under simple and uniﬁed command-line and web-

based interface. The main beneﬁts are: a) the sim-

plicity of the randomness testing for the user, b) pre-

conﬁgured batteries and test conﬁgurations

c) uniﬁed

result interpretation, and d) signiﬁcant parallelization

to test large amounts of data.

4.1 Test Detection Evaluation

The goal of our evaluation is to correctly (with min-

imal Type I and II errors) identify biased genera-

tors deﬁned by the parameters (cryptographic func-

tion, round, key, strategy and size). P-values are

the only results of tests we use in our evaluation to

identify biased/unbiased generators. Interpretation of

a p-value (rejection/non-rejection of a hypothesis –

shortly fail/pass) is based on the signiﬁcance level α

chosen by a tester. P-value below α indicates biased

statistic that is interpreted as “generator of the anal-

ysed data fails the given test”. Choice of the signiﬁ-

cance level is crucial since it affects the probabilities

of both Type I and II errors.

Batteries use a conservative value α

FAIL

is used to

minimize Type I error, i.e. false-positive. Conserva-

E.g., TestU01 is a randomness testing library that re-

quires user to develop a testing program, choose which tests

to run, etc.

tive α determines a bigger Type II error as both errors

are related. The only way how to decrease Type II er-

ror, for ﬁxed Type I error, is to increase the volume of

analysed data.

Each test of the original batteries computes

two types of p-values: a) standard “ﬁrst-level” p-

value computed by a test for one sequence, b)

“second-level” p-value computed by uniformity test

(Kolmogorov-Smirnov, Anderson-Darling, etc.) for

a sequence of ﬁrst-level p-values, checking whether

ﬁrst level p-values are uniformly distributed on the

[0,1) interval.

In the RTT, the result of each test is a second-level

p-value. It is computed typically for several tens or

several hundreds of (ﬁrst-level) p-values computed by

the test. Some tests compute several second-level p-

values (over the same set of ﬁrst-level p-values) using

different uniformity tests. The p-values (ﬁrst-level or

second-level) computed by the original batteries (and

also by the RTT) are not exact due to approxima-

tion methods used in the tests. The sequence fails a

given test if at least one of the second-level p-values

is smaller than the signiﬁcance level. Approximation

of the null distribution is used in the computation of

ﬁrst-level p-values. This introduces some small errors

that are accumulated in the second-level p-values. To

ﬁnd suitable signiﬁcance level α, we analyzed refer-

ence random data produced by full-round AES-128 to

determine number of false positives, taking approxi-

mation errors into account.

The initial analysis of data showed that

three tests behave differently than others. The

smultin MultinomialBitsOver from the Rabbit

sub-battery of TestU01 has a signiﬁcantly biased

proportion of small p-values. Random Excursion and

Random Excursion Variant tests from the NIST STS

compute different numbers of ﬁrst-level p-values for

a ﬁxed size of the sequence hence signiﬁcance of

their results varies. We excluded the results of these

three tests from all our experiments (including one

with the reference data).

BoolTest (Sys et al., 2017) battery comes in two

versions. BoolTest2 returns directly a p-value and it

works without precomputations. BoolTest1 is eval-

uated using conﬁdence intervals of Z-scores from

empirically computed reference distibution (for each

BoolTest setting) using 10

of random sequences.

This gives the signiﬁcance level α

BT 1

= 10

−5

for the

BoolTest, for RTT we use the same α

RT T

= 10

−5

4.2 Function Bias Classiﬁcation

As mentioned in Section 2.1.2, we claim the input

conﬁguration is rejected if at least 2 of 3 tested seed

SECRYPT 2022 - 19th International Conference on Security and Cryptography

142

variants are rejected. This section describes the de-

cision methodology for a seed variant to be claimed

rejected. We set global α = 10

−7

to minimize false-

positives across our dataset.

Reference Runs, Cut-off Threshold. We ran RTT

tests on 75 000 reference input conﬁgurations, i.e.,

full 10 round AES-128 using ctr input mode with a

random key. The reference test data results show be-

haviour of statistical tests on a good-quality pseudo-

random input data, namely tests p-value distribution

on a reference data and distribution of number of si-

multaneously failing tests per analyzed sequence with

= 10

−5

. From the reference test data we can estab-

lish a cut-off criteria on a number of simultaneously

failing test per sequence run to be 5% of performed

test with α ≤ 10

−7

. Reference runs showed that the

maximal number of simultaneously failing tests with

for a single sequence is 3 out of 216 tests (1.38%,

such event occurred 9 times, 0.016%). As the number

of analyzed sequences in our cryptographic function

dataset is smaller (54 500), the cut-off limit is set con-

servatively enough to avoid false-positives. Ideally,

a further study of reference p-value distributions and

number of test rejections per tested sequence would

be needed to model the distribution and to avoid com-

putation of reference data in sizes of the tested set.

It would also help setting cut-off limit precisely for

given α. The reference data study is left for a future

work.

Hommel Correction. In the ideal case, the propor-

tion of failed sequences for a given test is given by

the signiﬁcance level α for an unbiased generator. In

such a case, the number of failed sequences is given

by n ∗ α for number of sequences n. It is clear that

the probability that a sequence (generated by an unbi-

ased or unbiased generator) fails one of the used tests

increases with the number of tests m. It is possible

to compute the actual signiﬁcance level α

(sequence

fails m tests if it fails at least of the tests) for m tests

although we used α as the signiﬁcance level for each

test using p-value correction methods.

If the number of tests rejecting the seed is below

the cut-off threshold, we apply the Hommel correc-

tion (Hommel, 1988) on all p-values collected from

the seed run, using given α to tell whether tested se-

quence is rejected. Hommel correction is used to de-

cide null-hypothesis rejection using set of positively-

correlated p-values representing results from ran-

domness tests and their associated alternate hypothe-

ses. The correction keeps the probability of a false-

positive of the p-value set below α. Note that p-values

are positively correlated as the tests test the same in-

put sequence and also due to overlap of features be-

ing assessed by the tests, i.e., a particular bias pattern

can cause multiple tests to reject the input stream. To

the best of our knowledge, this is a new method for

assessing biases in output of round-reduced crypto-

graphic functions using different positively-correlated

randomness tests.

BoolTest1 Rejection. BoolTest1 works with a pre-

computed reference distribution, thus the α

BT 1

ﬁxed to an inverse to a number of reference re-

sults. As α

BT 1

< α BoolTest1 would never help re-

ject the tested sequence. We thus use observation

from cut-off threshold analysis. There are always 36

BoolTest1 tests executed per tested sequence. From

the reference data we observed that BoolTest1 results

have negligible correlation and rejection happens in

36n ∗ α

BT 1

on average. BoolTest1 is thus removed

from Hommel correction and we use BoolTest1 cut-

off threshold 3 to consider output sequence rejected

with α ≤ 10

−7

. Due to small correlation among

BoolTest1 test fails, distribution of a number of simul-

taneously failing tests per input can be easily simu-

lated without need to run BoolTest1 and approximate

it with Beta-Binomial distribution.

Prime Order Functions. Randomness testing bat-

teries are suited to test byte-aligned data. However,

cryptographic functions used in context of MPC /

zero-knowledge proofs using algebraic construction

can work in prime ﬁelds F

, where p is a prime. Such

function F output vectors F

. Testing batteries thus

cannot be na

ıvely applied to output values x

< p, as

interval [p, 2

8⌈lg(p)/8⌉

) is not covered by the function

output. Thus batteries trivially reject the output even

though the output is uniformly distributed on the in-

terval [0, p). We thus need to apply an transforma-

tion T to the function output that transforms uniform

prime order elements x

to a uniform byte-aligned out-

puts x

′

before testing it with the batteries. The sim-

plest approach is to use a rejection sampling, i.e., ﬁnd

byte-aligned boundary M = 2

8⌊lg(p)/8⌋

− 1 ≤ p. Out-

put x is then ignored if x > M. Rejection sampling

strategy requires more data to be generated as portion

of the generated data is discarded. We also used more

advanced transformations based on inverse function

sampling, i.e., directly stretching uniform distribution

from [0, p) to [0,M] using auxiliary randomness so all

F output values are used.

Large-scale Randomness Study of Security Margins for 100+ Cryptographic Functions

143

5 RELATED WORK

In this section, we ﬁrstly discuss published works

in cryptanalytical statistical testing, secondly the

analysis of tests of randomness in RTT. There ex-

ist many other statistical batteries except for those

used in RTT (NIST STS, Dieharder and TestU01):

Donald Knuth (Knuth, 1969), Diehard (Marsaglia,

1995), Crypt-X suite (Caelli et al., 1998), Prac-

tRand (Doty-Humphrey, 2014), RaBiGeTe (Pi-

ras, 2004), CryptoStat (Kaminsky and Sorrell,

2013), YAARX (Biryukov and Velichkov, 2014),

ENT (Walker, 2008), SPRNG (Mascagni and Srini-

vasan, 2000), gjrand (Jones, 2007) and the BSI test

suite (Schindler and Killmann, 2002).

There are two cryptanalytic approaches that are

based on the randomness testing. In the ﬁrst approach,

a cryptographic function (hash, block or stream ci-

pher) is turned into a PRNG, and this PRNG is used

to generate a sequence of bits/bytes and a test of ran-

domness is applied to the sequence. In the second

approach, the cryptographic function (and its random-

ness) is analysed directly. Tests of randomness are ap-

plied here to check whether the given function forms

a random function or a random Boolean function.

Nice overview of papers covering both approaches

can be found in (Kaminsky, 2019), section “Related

Work”. Next, we will list only sources not included

in (Kaminsky, 2019) or papers that are the most rele-

vant to our approach.

One of the evaluation criteria for AES candidates

was “their demonstrated suitability as random number

generators.” Therefore, AES candidates were eval-

uated by NIST STS batteries under several testing

scenarios. Murphy in (Murphy, 2000) described the

methodology of testing and its weaknesses. Soto in

(Soto, 1999) reported randomness evaluation of ﬁf-

teen AES candidates under nine categories of data:

Key Avalanche, Plaintext Avalanche (SAC with zero

key), Plaintext/Ciphertext Correlation (RPC), Cipher

Block Chaining Mode, Random Plaintext/Random

Keys (stream consisting of key, plaintext and cipher-

text tuple), Low Density Plaintext (LHW), Low Den-

sity Keys, High Density Plaintext (inversed LHW),

and High Density Keys. In the succeeding work (Soto

and Bassham, 2000), Soto and Bassham expanded re-

cent results with a study of round reduced candidates

with longer keys and the same data types (LHW, SAC,

etc). Kubicek et al. analysed the round reduced TEA

using evolutionary algorithms (Kub

ıcek et al., 2016).

Hernandez-Castro and Barrero in (Hernandez-

Castro and Barrero, 2017) evaluate tests in the Ent

battery using genetic algorithms. Authors of NIST

STS analysed the correlation of tests results in or-

der to eliminate redundant tests. NIST performed a

study to determine the dependence between the NIST

STS tests (Rukhin et al., 2010). They applied princi-

pal components analysis of m (no value speciﬁed) p-

values and extracted 161 factors, equal to the number

of tests (default settings of tests were not used). They

claimed that “there is no large redundancy among our

tests”. Yet some other works also analysed the cor-

relation of NIST STS tests (e.g., (S

ys et al., 2015))

and showed a correlation between NIST STS’s tests

leading to an estimate of the higher number of failing

test needed for rejection of randomness hypothesis.

Eskandari et al. in (Eskandari et al., 2018) automati-

cally construct distinguishers for 30 crypto primitives

using bit division property method and a new Salva-

tore framework.

6 CONCLUSIONS

Our paper provides the most extensive analysis of the

power of the commonly used randomness statistical

tests and their variants on the data produced by 109

cryptographic hash functions and block ciphers pub-

lished to date. To perform the analysis of 414 tests,

we modiﬁed the code of every function to make the

number of internal rounds conﬁgurable and executed

it on three types of highly redundant input blocks to

produce a stream of testing data.

All the tests were integrated under the same in-

terface allowing for an efﬁcient evaluation using a

distributed computation cluster. We also designed a

uniﬁed framework for evaluating biases’ presence in

the output of a cryptographic function using differ-

ent randomness testing batteries. Our approach is re-

producible, and new functions can be later tested and

compared with existing results.

The security margin – as the ratio between the to-

tal number of function rounds and rounds with bias

still detectable (distinguisher) – was established for

all the tested functions and compared with the distin-

guishers published in the research literature. While

being around 77% on average (up to 23% of inter-

nal rounds still distinguishable), there is high vari-

ability among the functions analyzed. SHA-3 exhibits

a security margin of 83%, and ten functions, includ-

ing Blake, Gost, Skein, Mars, Serpent, Shacal2, and

XTEA have even more than 90%. Contrary to func-

tions with a large security margin, the functions de-

tected with a very small margin (Arirang, DCH, Dy-

namicSha2, Luffa, and Twister) were also shown to be

weak by existing research literature. The randomness

tests can be therefore seen as the simple automated

ﬁrst step in cryptanalysis.

SECRYPT 2022 - 19th International Conference on Security and Cryptography

144

All our tools and results, including tests results

from both reference runs and cryptographic function

dataset, are publicly available

ACKNOWLEDGEMENT

Authors were supported by Czech Science Founda-

tion project (GA20-03426S). This work was partially

supported by the European cybersecurity pilot Cy-

berSec4Europe. Computational resources were sup-

plied by the project ”e-Infrastruktura CZ” (e-INFRA

CZ LM2018140) supported by the Ministry of Educa-

tion, Youth and Sports of the Czech Republic. Com-

putational resources were provided by the ELIXIR-

CZ project (LM2018131), part of the international

ELIXIR infrastructure.

REFERENCES

Aly, A., Ashur, T., Ben-Sasson, E., Dhooghe, S., and Szepi-

eniec, A. (2020). Design of symmetric-key primitives

for advanced cryptographic protocols. IACR Transac-

tions on Symmetric Cryptology, 2020(3):1–45.

Bernstein, D. J., Chang, Y.-A., Cheng, C.-M., Chou, L.-P.,

Heninger, N., Lange, T., and Van Someren, N. (2013).

Factoring RSA keys from certiﬁed smart cards: Cop-

persmith in the wild. In International Conference on

the Theory and Application of Cryptology and Infor-

mation Security, pages 341–360. Springer.

Biham, E. and Shamir, A. (2012). Differential cryptanalysis

of the data encryption standard. Springer Science &

Business Media.

Biryukov, A. and Velichkov, V. (2014). Automatic search

for differential trails in ARX ciphers. In Cryptogra-

phers’ Track at the RSA Conference, pages 227–250.

Springer.

Brown, R. G., Eddelbuettel, D., and Bauer, D. (2013).

Dieharder: A random number test suite. Open Source

software library, under development.

Caelli, W. et al. (1998). Crypt-X suite.

Doty-Humphrey, C. (2014). Practically Random: Speciﬁc

tests in PractRand.

Eskandari, Z., Kidmose, A. B., K

olbl, S., and Tiessen, T.

(2018). Finding integral distinguishers with ease. In

IACR Cryptol. ePrint Arch.

Heninger, N., Durumeric, Z., Wustrow, E., and Halderman,

J. A. (2012). Mining your ps and qs: Detection of

widespread weak keys in network devices. In Pre-

sented as part of the 21st USENIX Security Sympo-

sium (USENIX Security 12), pages 205–220.

Hernandez-Castro, J. and Barrero, D. F. (2017). Evolution-

ary generation and degeneration of randomness to as-

sess the indepedence of the ent test battery. In 2017

https://crocs.ﬁ.muni.cz/public/papers/secmargins

secrypt22

IEEE Congress on Evolutionary Computation (CEC),

pages 1420–1427. IEEE.

Hommel, G. (1988). A stagewise rejective multiple

test procedure based on a modiﬁed bonferroni test.

Biometrika, 75:383–386.

Jones, G. (2007). gjrand random numbers.

Kaminsky, A. (2019). Testing the randomness of crypto-

graphic function mappings. IACR Cryptology ePrint

Archive, page 78.

Kaminsky, A. and Sorrell, J. (2013). CryptoStat: a Bayesian

Statistical Testing Framework for Block Ciphers and

MACs. Rochester Institute of Technology, Rochester,

NY.

Ketamine (2018). Multiple vulnerabilities in Se-

cureRandom(), numerous cryptocurrency products

affected. https://lists.linuxfoundation.org/pipermail/

bitcoin-dev/2018-April/015873.html.

Knuth, D. E. (1969). The Art of Computer Programming,

volume 2. Addison-Wesley Longman Publishing Co.,

Inc., Boston, MA, USA, ﬁrst edition.

Kub

ıcek, K., Novotn

y, J.,

Svenda, P., and Ukrop, M. (2016).

New results on reduced-round tiny encryption algo-

rithm using genetic programming. INFOCOMMUNI-

CATIONS JOURNAL, 8(1):2–9.

L’Ecuyer, P. and Simard, R. (2007). TestU01: A C Li-

brary for Empirical Testing of Random Number Gen-

erators. ACM Transactions on Mathematical Software

(TOMS), 33(4).

Marsaglia, G. (1995). Diehard: a battery of tests of random-

ness.

Mascagni, M. and Srinivasan, A. (2000). Algorithm 806:

SPRNG: A scalable library for pseudorandom num-

ber generation. ACM Transactions on Mathematical

Software (TOMS), 26(3):436–461.

Matsui, M. (1993). Linear cryptanalysis method for des ci-

pher. In Workshop on the Theory and Application of of

Cryptographic Techniques, pages 386–397. Springer.

Menezes, A. J., Van Oorschot, P. C., and Vanstone, S. A.

(1996). Handbook of applied cryptography. CRC

Press.

Murphy, S. (2000). The power of NIST’s statistical testing

of AES candidates. Preprint. January, 17.

O’Neill, M. E. (2014). Pcg: A family of simple fast

space-efﬁcient statistically good algorithms for ran-

dom number generation. Technical Report HMC-CS-

2014-0905, Harvey Mudd College, Claremont, CA.

Piras, C. (2004). RaBiGeTe Documentation.

Rukhin, A., Soto, J., Nechvatal, J., Smid, M., Barker,

E., Leigh, S., Levenson, M., Vangel, M., Banks, D.,

Heckert, A., Dray, J., and Vo, S. (2010). A Statisti-

cal Test Suite for Random and Pseudorandom Number

Generators for Cryptographic Applications.

Schindler, W. and Killmann, W. (2002). Evaluation crite-

ria for true (physical) random number generators used

in cryptographic applications. In International Work-

shop on Cryptographic Hardware and Embedded Sys-

tems, pages 431–449. Springer.

Soto, J. (1999). Randomness testing of the AES candi-

date algorithms. NIST. Available via csrc. nist. gov,

page 14.

Large-scale Randomness Study of Security Margins for 100+ Cryptographic Functions

145

Soto, J. and Bassham, L. (2000). Randomness testing of

the advanced encryption standard ﬁnalist candidates.

Technical report.

Sys, M., Klinec, D., and Svenda, P. (2017). The Efﬁcient

Randomness Testing using Boolean Functions. In

14th International Conference on Security and Cryp-

tography (Secrypt), pages 92–103. SCITEPRESS.

ys, M., Klinec, D., and

Svenda, P. (2017). The efﬁcient

randomness testing using boolean functions. In 14th

International Conference on Security and Cryptogra-

phy (Secrypt), pages 92–103. SCITEPRESS.

ys, M.,

ıha, Z., Maty

s, V., Marton, K., and Suciu, A.

(2015). On the interpretation of results from the NIST

statistical test suite. Romanian Journal of Information

Science and Technology, 18(1):18–32.

Walker, J. (2008). Ent: A Pseudorandom Number Sequence

Test Program.

Webster, A. and Tavares, S. E. (1985). On the design of s-

boxes. In Conference on the theory and application of

cryptographic techniques, pages 523–534. Springer.

SECRYPT 2022 - 19th International Conference on Security and Cryptography

146