Parallel and Distributed Implementations of the Wiedemann and the

Block-Wiedemann Methods over GF(2)

Rahul Roy, Abhijit Das and Dipanwita Roy Chowdhury

Crypto Research Lab, Department of Computer Science and Engineering, IIT Kharagpur, Kharagpur, India

Keywords:

RSA, Integer Factoring, GNFSM, Large Sparse Linear Systems, Wiedemann Method, Block-Wiedemann

Method, Multi-core Parallelization, Load Balancing, Distributed Parallelization, Computation-communication

Overlapping.

Abstract:

Finding the prime factors of large composite integers is the fundamental computational problem in number

theory. Currently, the fastest known integer-factoring algorithm is the General Number Field Sieve method

(GNFSM) which has been used by the research community to factor RSA moduli of sizes 500–800 bits. One

of the steps of this method involves ﬁnding non-zero solutions of the linear system available from the sieving

stage. Since the linear systems involved in GNFSM are necessarily sparse, special iterative system solvers

are used. One such solver is called the Wiedemann method. This paper reports our efﬁcient implementa-

tion of the Wiedemann method, and its block version. We start with a single-core sequential implementation,

and then make efforts to parallelize the implementation to run on multiple cores of a single machine. Spe-

cial load-balancing techniques are designed to reduce synchronization overheads after each iteration. Finally,

we distribute the computation across multiple computing nodes. Our load-balancing ideas are reﬁned, and

computation-communication overlapping techniques are explored in order to absorb the communication over-

heads. Speed-up ﬁgures achieved by the different improvements incorporated in our implementations are

reported. To the best of our knowledge, we are the ﬁrst to report distributed implementations of the Wiede-

mann method.

1 INTRODUCTION

Public-Key Cryptographic (PKC) algorithms like

RSA (Rivest et al., 1978) serve as the fundamental se-

curity primitives to ensure conﬁdentiality, authentic-

ity, and non-repudiation of Internet communications

and data storage. Like other public-key encryption

algorithms, RSA uses two keys: one public key or en-

cryption key available to all, and a private key or de-

cryption key which is kept secret. RSA involves four

signiﬁcant steps: (i) key generation, (ii) key distribu-

tion, (iii) encryption, and (iv) decryption. The secu-

rity of RSA depends on the difﬁculty of factoring the

product of two large prime numbers. Many general-

purpose integer-factoring algorithms are developed in

the last few decades. The fastest known such al-

gorithm is the General Number Field Sieve Method

(GNFSM) (Cowie et al., 1996; Case, 2003) which is a

generalization of another algorithm known as the Spe-

cial Number Field Sieve Method (SNFSM) (Lenstra

et al., 1993; Montgomery et al., 1997). Besides cryp-

tographic applications, factoring large composite in-

tegers is the fundamental computational problem in

number theory.

Many integer-factoring algorithms (including

GNFSM) require a linear-algebra step. A large lin-

ear system of equations is generated in the sieving

stage. Subsequently, multiple non-zero vectors in the

null space of this system are computed. The sys-

tems available from GNFSM are necessarily sparse.

Therefore, a study of sparse system solvers is impor-

tant from number-theoretic and cryptographic points

of view.

A way to solve linear systems of equations is

structured Gaussian elimination (SGE) (Bender and

Canﬁeld, 1999; Pomerance and Smith, 1992). SGE

can signiﬁcantly reduce the system size by eliminat-

ing many rows and columns, eventually leading to a

signiﬁcantly dense system which is then solved by a

general-purpose system solver. Although SGE can be

used as a precomputation to the ﬁnal system-solving

algorithm, it is not efﬁcient in practice for very large

systems. Current literature suggests that for solving

large sparse systems, iterative algorithms collectively

540

Roy, R., Das, A. and Roy Chowdhury, D.

Parallel and Distributed Implementations of the Wiedemann and the Block-Wiedemann Methods over GF(2).

DOI: 10.5220/0011267700003283

In Proceedings of the 19th International Conference on Security and Cryptography (SECRYPT 2022), pages 540-547

ISBN: 978-989-758-590-6; ISSN: 2184-7711

known as Krylov-space methods (Krylov, 1931) work

more efﬁciently than SGE. Two popular variants of

Krylov-space methods are the Lanczos method (Lanc-

zos, 1952) and the Wiedemann method (Wiedemann,

1986). Both these methods use a black-box model for

solving large sparse systems (unlike SGE which ex-

ploits the structural properties of the matrices). They

perform a linear number of matrix-vector products

and other vector operations. Their complexity is mea-

sured in terms of the dimensions of the input matrices.

Speeding up the performances of the sparse sys-

tem solvers involves several optimization techniques.

One such optimization technique introduces the con-

cept of blocking for both the methods in order to en-

hance parallelization possibilities and to get multiple

solutions simultaneously. (Coppersmith, 1994) intro-

duces the block version of the Wiedemann method,

and (Montgomery, 1995) introduces the block ver-

sion of the Lanczos method.

One step of the Wiedemann method ﬁnds a mini-

mal generating polynomial of a sequence of matrix-

vector products. The block version is extended to

minimal generating matrix polynomials (Kaltofen,

1995; Villard, 1997). To improve the efﬁciency of the

method, a particular effort is made by (Thom

e, 2002)

that focuses on optimizing the step of computing the

minimal generating matrix polynomial. An initial at-

tempt to implement the block-Wiedemann method in

a distributed environment is reported by (Kaltofen

and Lobo, 1999). However, the matrices considered

are smaller than those generated after the post-sieving

stages. In 2009, the block version of the method is im-

plemented in a grid platform by the team of interna-

tional researchers to break the 768-bit RSA challenge

key (Kleinjung et al., 2010). It is reportedly used

in the factorization of RSA keys of different other

lengths (Bai et al., 2012; Bai et al., 2016). The ef-

fort of (Yang et al., 2017) on the factorizations of

381-bit RSA keys is made on a cloud platform, and

also uses the block-Wiedemann method for the linear-

algebra step. Other papers focus on implementations

in multi-core environment (Penninga, 1998) or on lin-

ear systems generated over large prime ﬁelds (Bar-

bulescu et al., 2014). (Bhateja and Kannan, 2017)

propose a cache-optimized version of both the Lanc-

zos and the Wiedemann methods. (Cavallar et al.,

2000) and (Chen et al., 2008) both use the block-

Lanczos method in their efforts to factor 512-bit RSA

keys.

In this paper, we report optimized versions of the

Wiedemann and the block-Wiedemann methods, their

implementation details, and the experimental results

for the sequential, parallel (single-node), and dis-

tributed (multi-node) settings. The rest of the paper

is organized as follow. In Section 2, the Wiedemann

and the block-Wiedemann methods are described.

Section 3 describes our implementational details of

the Wiedemann and the block-Wiedemann methods,

where we describe our load-balancing strategies and

other practical optimizations. In section 4, experi-

mental setup and results achieved are shown. Section

5 concludes the paper after enumerating some scopes

of extending our study.

2 THE WIEDEMANN AND

BLOCK-WIEDEMANN

METHOD

This section starts with a detailed foundation of the

Wiedemann method, together with the Berlekamp–

Massey method which is used for ﬁnding the mini-

mal polynomial. This is followed by an introduction

to Coppersmith’s version of the block-Wiedemann

method.

2.1 The Wiedemann Method over GF(2)

Introduced by Douglas Wiedemann (Wiedemann,

1986) to solve large sparse linear systems over ﬁ-

nite ﬁelds, the Wiedemann method is a Krylov-space

method. It is a randomized Las Vegas algorithm

that always provides a correct output or reports fail-

ure. Unlike the Lanczos method (Lanczos, 1952),

it does not require the matrix to be symmetric or

positive deﬁnite. It involves only the arithmetic op-

erations of GF(2). The Wiedemann method uses

an external algorithm called the Berlekamp–Massey

method (Berlekamp, 1968; Massey, 1969) for ﬁnding

minimal polynomials.

Given a matrix B of size M × N over GF(2) with

M > N and a non-zero vector u, we want to solve the

linear system

Bx ≡ u (mod 2). (1)

The objective is to ﬁnd multiple solutions for the vec-

tor x. The Wiedemann algorithm requires the system

to be in the form

Ax = b, (2)

where A is an N × N matrix. In order to adapt the

algorithm, the input system (1) needs to be converted

to equation (2) as

A = B

B (3)

and

b = B

u, (4)

where B

is the transpose of the input matrix B. The

characteristic polynomial of A is deﬁned as χ

(x) =

Parallel and Distributed Implementations of the Wiedemann and the Block-Wiedemann Methods over GF(2)

541

det(xI − A), where I is the N ×N identity matrix. By

the Cayley–Hamilton theorem, A satisﬁes χ

(x), that

is, χ

(A) = 0. The minimal polynomial of A is the

monic non-zero polynomial of the smallest degree for

which µ

(A) = 0. It is known that µ

(x) divides the

characteristic polynomial χ

(x), that is, µ

(x) | χ

(x)

in GF(2)[x]. Wiedemann’s method computes the min-

imal polynomial of A as

(x) = x

+ u

d−1

+ u

d−2

+ ···+ u

x + u

(5)

Here, d = deg(µ

(x)) ≤ N. The coefﬁcients of µ

(x)

are solved using the Berlekamp–Massey algorithm.

This requires the computation of A

v for a non-zero

vector v, and for k = 0,1,2,..., 2d −1. Since µ

(A) =

0, for any k ≥ d, we have

v − u

d−1

k−1

v − · ·· − u

k−d+1

v − u

k−d

v = 0.

(6)

A solution for x is obtained by putting v = b as

x = −u

−1

d−1

b + u

d−1

d−2

b + u

d−2

k−3

b + u

Ab).

(7)

We consider the solution if x 6= 0 and Ax = 0. One

of the most time-consuming task here is computing

the matrix-vector product in each iteration of the two

loops.

2.2 The Block-Wiedemann Method over

GF(2)

Coppersmith (1994) introduces a block version of the

Wiedemann method to increase the scope of paral-

lelization. In the block method, the concept of the

scalar sequence by Wiedemann (1986) is replaced by

a linearly generated matrix sequence. Subsequently,

the minimal matrix polynomial is generated. In or-

der to compute the minimal matrix polynomial, the

concept of multivariate Berlekamp–Massey method

is introduced by (Coppersmith, 1994; Kaltofen and

Yuhasz, 2013). (Kaltofen and Lobo, 1999) uses a ho-

mogeneous block Toeplitz system. The Fast Power

Hermite-Pad

e Solver (FPHPS) algorithm of Becker-

mann et al. (Beckermann and Labahn, 1994) to com-

pute the minimal matrix polynomial is proposed by

(Villard, 1997). (Kaltofen and Saunders, 1991) de-

scribe an asymptotically faster algorithm than the bi-

nary search algorithm that Wiedemann proposes to

compute the rank of a black-box matrix over large

ﬁelds.

In Coppersmith’s version of the block-

Wiedemann method, The ﬁrst step (called BW1),

consists of computing the sequence

(i)

= (U

Z). (8)

This step starts with two random blocks U of size

N × m and V of size N × n. Multiplying succes-

sively by the input matrix A, it computes A

V , and

U is used to compute the projections U

V of size

N × n. To obtain kernel vectors, only the ﬁrst L co-

efﬁcients of the sequence are required, where L =

N/m + N/n + O(1).

In Step BW2, Coppersmith modiﬁes the

Berlekamp–Massey method as the matrix

Berlekamp–Massey method or block Berlekamp–

Massey method. It takes the sequence A

(i)

output by Step BW1, and deﬁnes the polynomial

(λ) ∈ GF(2)

(m×n)

of degree N/m + N/n + 1. It

generates a matrix sequence F(λ) of degree d

This is the main step of the Block Wiedemann

algorithm. Unlike the scalar version, this step is the

most complex.

Steps BW3 involves deg(F) matrix-block multi-

plications and block-vector multiplications. It also

performs δ(F) matrix-vector multiplications, and

δ(F) tests for the nullity of vectors.

3 IMPLEMENTATION DETAILS

OF THE WIEDEMANN AND

THE BLOCK-WIEDEMANN

METHODS OVER GF(2)

In this section, our implementational details of the

Wiedemann and the block-Wiedemann methods over

GF(2) are explained, including space optimizations,

introduction to new load-balancing strategies, and

other practical optimizations that help us gain im-

proved speed-up for both the methods.

3.1 Representing the Matrix

To store the sparse matrices, there are various possi-

bilities (Lin et al., 2003; Bhattacherjee and Das, 2010)

like the compressed column-storage format (CCS),

the compressed row-storage format (CRS), and the

linked-list representation. The CRS and the CCS

formats provide efﬁcient storage schemes because of

their low memory requirements, so we adopt these

formats.

The CRS representation maintains three arrays

value array, column index, and row pointer. We

scan the matrix A row-wise, and the value array

stores the non-zero elements of the matrix. The array

column index stores the column numbers of the non-

zero values stored in the value array, and row pointer

stores the number of non-zero values encountered be-

fore the current row of the original matrix A.

SECRYPT 2022 - 19th International Conference on Security and Cryptography

542

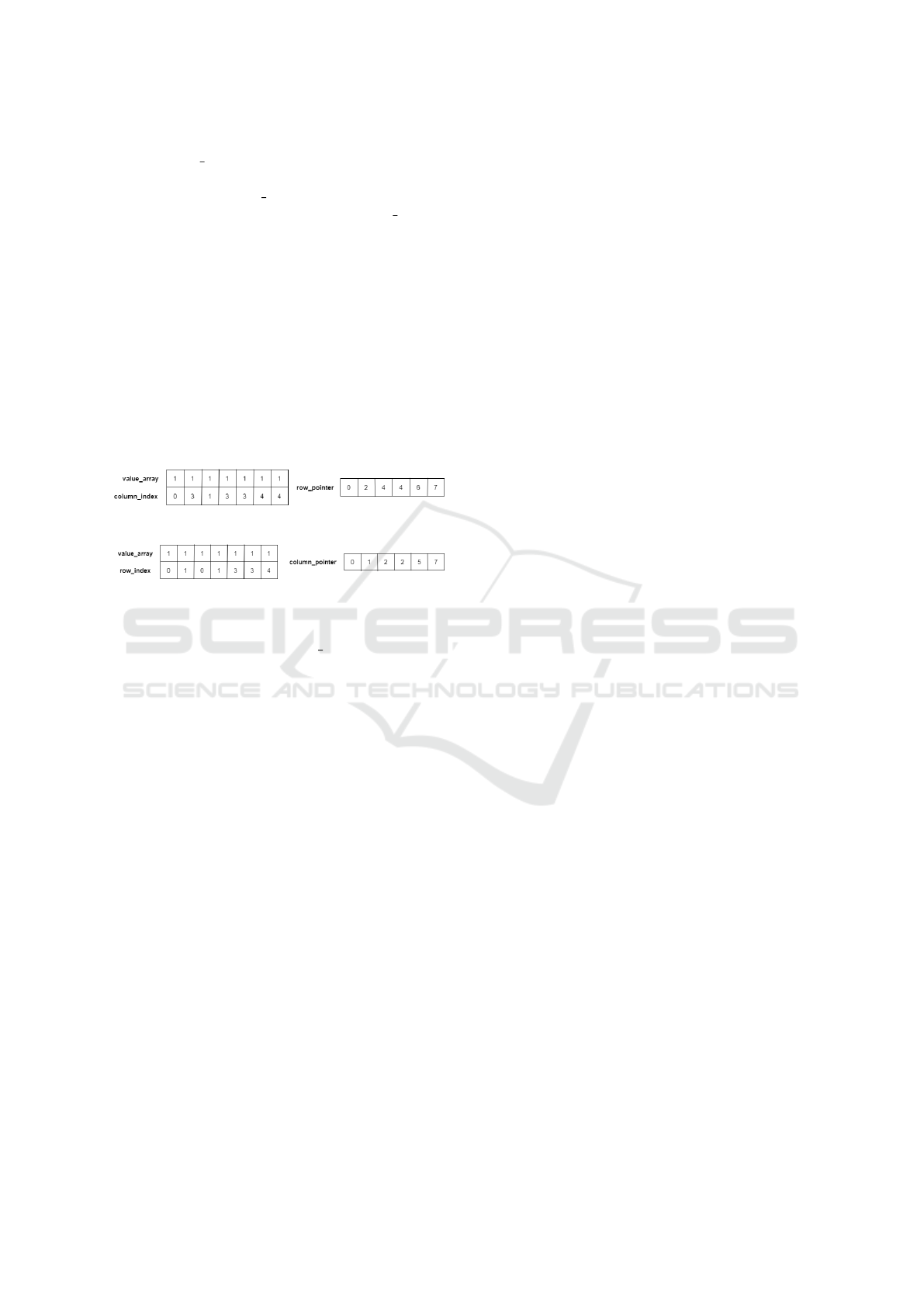
The value array in the CCS representation stores

the non-zero entries in the column-major order. It

maintains an array row index to store the row num-

bers of non-zero entries and an array column pointer

to store the number of non-zero values encountered

before the current column of the original matrix A.

If the number of non-zero entries in the matrices is

M, then both the CRS and the CCS representations re-

quire space proportional to M. The CRS and the CCS

representations of the following matrix A over GF(2)

are shown in Figure 2 and Figure 2, respectively. We

assume that array indexing starts from 0.

A =







1 0 0 1 0

0 1 0 1 0

0 0 0 0 0

0 0 0 1 1

0 0 0 0 1







Figure 1: CCS representation of the matrix A.

Figure 2: CRS representation of the matrix A.

For systems over GF(2) (as our case is), the only

non-zero entry is 1, so the value array list is not ex-

plicitly needed in both the representations.

The Wiedemann method requires a square system,

whereas those available from GNFSM sieves are not

square. We therefore work with the square matrix

A, and a matrix-vector product (A

A)v involves two

matrix-vector products v

= Av and A

. This is the

reason why we store the given matrix A in both repre-

sentations.

3.2 Parallelization using a Controlled

Load-balancing Technique

The ﬁrst step of the Wiedemann method involves

many matrix-vector multiplications. We take a ran-

dom vector v of dimension N × 1, and keep on pre-

multiplying v by the input matrix A. Iteratively it gen-

erates the sequence A

v for i = 0,1, ·· · ,2N −1. In the

i-th iteration, A

v is computed by multiplying the ma-

trix A with the vector A

i−1

v generated in the previous

iteration. In the third step, a random vector b of di-

mension N ×1 is taken, and repeatedly pre-multiplied

by the input matrix A for i = 0,1,· ·· , N −1. The num-

ber of iterations in the third step is half of that in the

ﬁrst step.

It is evident that the iterations behave very sequen-

tially, that is, the output A

i−1

v of one iteration should

be fully ready for feeding to the next one for com-

puting A

v = A × (A

i−1

v). The only way to optimize

an iteration of the method is to parallelize the basic

arithmetic operations like sparse matrix-vector multi-

plications. Such methods are not suitable for massive

multi-core parallelization. Moreover, it is essential to

ensure that every core (or processor) shares more or

less the same amount of computational load. Other-

wise, the synchronization step at the end of every it-

eration may keep many nodes waiting, thereby wast-

ing signiﬁcant (parallel) running time. To sum up, we

face two challenges. First, the parallelization is rather

ﬁne-grained, and second, beneﬁts of parallelization

are lost in absence of effective load balancing.

A third problem associated with matrices avail-

able from GNFSM sieves is that the sparse matrix

entries are not non-zero with a uniform probabil-

ity. Instead, such matrices have some distinct dis-

tributions of non-zero entries. In order to work

around these problems, an effective load-balancing or

loop-scheduling strategy is needed to compute sparse

matrix-vector multiplications. The load-balancing

constructs of OpenMP (OpenMP, 2016) are exploited

together with additional strategies derived from our

mathematical analysis. During the sparse matrix-

vector multiplication mul1 : v

= A

v, we use the CRS

representation of the matrix A. Since the rows fol-

low the same statistical distribution, we evenly dis-

tributed them among all the available P processors or

cores. Initially, no scheduling constructs are used.

For the second sparse matrix-vector multiplication

(mul2 : A

) (where v

= Av) in each Wiedemann it-

eration, we use the CCS representation of A (which is

the CRS representation of the transpose A

). We start

with no load-balancing or loop-scheduling strategies.

As already mentioned, the columns of A are not iden-

tically distributed in terms of counts of non-zero en-

tries. We therefore need to devise custom-made load-

balancing strategies alongside the constructs provided

by OpenMP. One such strategy is called controlled dy-

namic load balancing. Here, the matrix is initially an-

alyzed to extract information like the maximum and

the minimum numbers of non-zero entries in a col-

umn, the indices of the denser columns, the indices of

the columns with all zero entries, and so on. Based on

these information, we implement the concept of shar-

ing and stealing which work as follows. The available

cores are divided into smaller groups, and the range

of column indices are also divided. This groupings

are based on manual calculations based on column-

distribution data. The subgroups are assigned various

chunks or ranges of the columns, and then we use dy-

namic scheduling to process the chunks of columns.

The subgroup sizes and the column ranges are ex-

Parallel and Distributed Implementations of the Wiedemann and the Block-Wiedemann Methods over GF(2)

543

perimentally optimized by trying several possibilities.

In the controlled static load balancing scheme, the

static construct (circular scheduling) is used in con-

junction with the pre-analyzed grouping of the cores

and chunking of columns.

3.2.1 Distributed Implementation of the

Wiedemann Method

The implementations reported in the literature use

multi-core (more speciﬁcally, shared-memory) archi-

tecture. In addition to single-node implementations,

we also carry out multi-node implementations. We

need to handle inter-node communications efﬁciently

during the synchronization after every iteration of the

Wiedemann loop.

We investigate two ways of distributing the com-

putational load to multiple nodes. First, we note that

the Wiedemann method falls under the category of

Las Vegas algorithms that may report failure, and we

need multiple solutions in the null space of the given

matrix with the hope that at least one of these leads

to a non-trivial factoring of the input integer. So we

can let every node run the same algorithm with a dif-

ferent random vector v. Here, the parallel running

time remains the same as that of a single execution

of a single-node multi-core implementation. It only

helps in getting multiple non-zero solutions, thereby

increasing the probability of successful factoring. In

this approach, the communication overhead is essen-

tially absent, as every node runs independently of one

another. However, the degree of parallelization is re-

stricted by the number of independent runs required

to obtain a successful factoring (with high probabil-

ity). More precisely, each random vector can factor

with a probability of 1/2, so only a few independent

trials are needed for achieving high success proba-

bility. Having a larger number of nodes than this

requirement cannot be meaningfully exploited using

this idea.

A better option is to run the matrix-vector mul-

tiplications in the distributed setting. We need to

distribute the rows judiciously to the collaborating

nodes. For the matrix A, this can be done by equally

dividing the rows. However, during the multiplica-

tion by the transpose A

, we have an uneven dis-

tribution of non-zero entries in different columns of

A. A careful pre-planning is necessary before tak-

ing distribution decisions. More processors need to be

used for handling the denser columns than those han-

dling the sparser columns. We use the same trial-and-

optimize strategy as explained in connection with our

controlled load-balancing policy for single-node im-

plementations. This distribution idea is not arbitrarily

scalable, because each Wiedemann iteration requires

the full vectors v and v

for synchronization. These

vectors need to be communicated to all the participat-

ing nodes.

3.3 Implementational Details of the

Block-Wiedemann Method

This section explains our implementation and prac-

tical optimization details for the block-Wiedemann

method. We start with a single-node multi-core im-

plementation, and then port it to a distributed imple-

mentation. As before, we represent the matrices in

the CRS and CCS formats. A new load-balancing

technique is developed and reported for the block-

Wiedemann method.

3.3.1 Saving Operations

First suggested by (Thom

e, 2002), many operations

are repeated in the block Wiedemann method. Some

of the results can be saved to be reused when needed.

The saved computations particularly boost the perfor-

mance of BW3. In the steps BW1 and BW3, the prod-

ucts of the input sparse matrix A and the already com-

puted blocks A

V are required twice. These results

are saved during step BW1 for use in BW3. This re-

duces the number of matrix-block computations con-

siderably in BW3.

3.3.2 Choice of Parameters

To start with, we need to choose the block size m × n.

The number of useful coefﬁcients in the sequence

decreases with m and n, and the complexity of

the block operations increases with m and n. After

many experimental trials, we ﬁx these parameters as

m = 512 and n = 512. In the step BW2, two additional

parameters s and d need to be deﬁned. We notice that

ﬁxing s = 1 as it is suggested (s =

in (Thom

e, 2002)

or s = 1 in (Anand and II, 2007)) does not provide a

high probability of success. The assumption that the

coefﬁcient of degree zero in the sequence A

is of full

rank also often appears to be wrong. Therefore, we

decide to ﬁnd at each execution an appropriate value

of s, that is, the one for which the columns of the

matrices A

[0],.. ., A

[s − 1] form a basis of GF(2)

Moreover, we ﬁx d =





3.3.3 An Adaptive Load-balancing Technique

A scheduling approach for a multi-node cluster pro-

posed by (Bhattacherjee and Das, 2010) computes the

time for each unit operation. A runtime adaptive load-

balancing algorithm proposed by (Lee and Eigen-

mann, 2008) uses the cumulative time per core. Every

SECRYPT 2022 - 19th International Conference on Security and Cryptography

544

core loads the entire sparse representation of the ma-

trix under this approach. Following this approach, we

extend the controlled load-balanced scheduling, and

develop an adaptive load-balancing algorithm for dis-

tributing the load across multiple nodes. In this tech-

nique, we try to normalize the execution capacities

of the cores by ensuring that the average execution

time per core remains the same. Let N be the num-

bers of rows/columns that need to be processed, and

M the number of available cores. Initially,

num-

bers of rows/columns are distributed to each of the

M cores. The matrix-vector (or block vector) product

operation is executed, and the execution time for each

row/column is stored in an array/list. The average ex-

ecution time is calculated as

total execution time

, where

the total execution time is the sum of the execution

times of all rows/columns. Finally, the rows/columns

are redistributed to the cores in following manner.

• Compute the sum of the execution times for all

rows/columns in the range 0 to N − 1.

• Assign the row/column range i to j to the k-th core

such that the total execution time for the range i to

j is less than the average execution time.

• Record the starting and ending indices of

rows/columns for each core.

4 EXPERIMENTAL RESULTS

Our computations are carried out in Intel Xeon E5-

2683v4 16C/32T Linux machines. Each node has 32

cores clocked at 2.1 GHz, and there are eight worker

nodes, each having 128 GB RAM. These nodes are

connected via an InﬁniBand switch. The gcc com-

piler version 9.2.0 is used, OpenMP version 4.5 is

used for thread-level parallelism, and OpenMPI 3.1

is used for the distributed implementations. Pro-

grams are compiled with the –O2 optimization ﬂag.

We have considered two matrices A

and A

of sizes

3698651 ×2934621 and 2100000 × 1500000, respec-

tively. The speedup ﬁgures achieved by the single-

node implementations are listed in Table 1. Here, DS

and SS refer to dynamic and static scheduling without

any explicit load-balancing policy, whereas CDS and

CSS refer to dynamic and static scheduling with our

controlled load-balancing policy. Since the rows of

A are statistically identical, we do not apply our con-

trolled load-balancing strategy for the multiplication

mul1 (computation of Av). This is applied only for

the multiplication mul2 (computation of Av

). Static

scheduling (without load balancing) performs very

poorly for mul2 and is not listed in the table.

Table 1: Speed-up achieved by several single-node multi-

core implementations.

Number mul1 mul2

of cores DS SS DS CDS CSS

4 1.64 1.07 1.67 1.66 0.96

8 2.84 1.79 2.72 3.00 1.18

16 4.52 2.41 4.08 3.81 1.55

32 4.83 4.65 5.06 6.13 3.86

4 2.21 1.24 2.38 2.81 2.11

8 3.64 1.71 3.50 5.29 2.65

16 5.46 3.48 6.78 10.85 4.43

32 6.56 6.30 7.48 19.72 8.34

The effectiveness of our load-balancing strategy

is evident from the table. In general, the strategy per-

forms the best in tandem with dynamic scheduling.

A comparison with the reported implementation

of (Dumas and Villard, 2002) is shown in Table 2. For

meaningful comparisons, we use a 423360 × 423360

matrix with 23 non-zero entries per row, similar to as

reported in (Dumas and Villard, 2002). Our timing

ﬁgures pertain to the CDS strategy on 4 and 32 cores,

whereas Dumas et al. use only 4 cores. The times are

in hours.

Table 2: Comparison of load-balanced parallel Wiedemann

method.

Our time (4 cores) Our time (32 cores) Time by Dumas et al.

23.96 3.92 34.00

Table 3 compares the running times and speedup

achieved by distributed implementations with block-

ing communications (DB) and non-blocking commu-

nications (DNB) over our single-node implementa-

tion (SN). 32 cores are used in each node. The dis-

tributed implementations use eight identical nodes

(with 32 cores per node). In all these experiments,

controlled load-balancing with dynamic scheduling is

used. All times in the table are in seconds.

The table indicates that the blocking communica-

tion mode gives very little boost to the distributed im-

plementation. On the other hand, we are able to get

some decent speedup with the non-blocking commu-

nication mode.

For the block-Wiedemann method, we use a ma-

trix A

of size 6699191 × 6699181 with an average of

63 non-zero entries per row, a maximum of 101 non-

zero entries, and a minimum of 52 non-zero entries.

Table 4 demonstrates the beneﬁts of using the adap-

tive load-balancing (ALB) scheme over the controlled

load-balancing (CLB) scheme. The times are in sec-

onds. The ALB scheme applies only to the steps BW1

and BW3. For the step BW2, we only use dynamic

scheduling. All the distributed implementations run

Parallel and Distributed Implementations of the Wiedemann and the Block-Wiedemann Methods over GF(2)

545

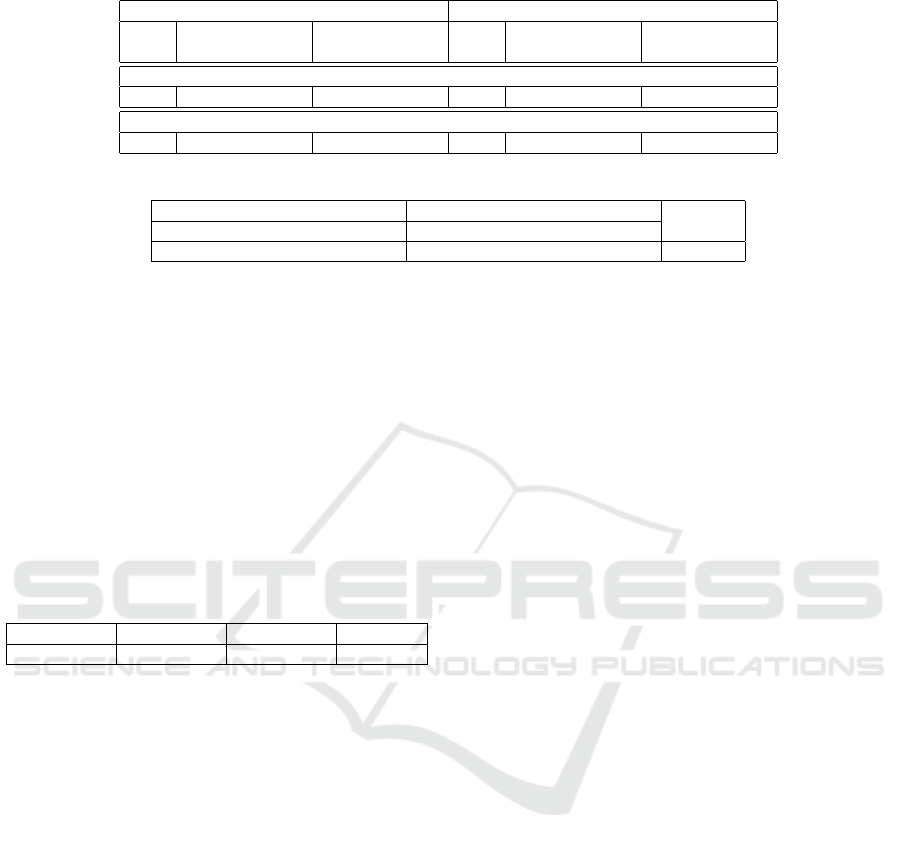
Table 3: Comparison of single-node and distributed implementations.

mul1 mul2

SN DB DNB SN DB DNB

Time Time Speedup Time Speedup Time Time Speedup Time Speedup

0.43 0.32 1.34 0.13 3.30 0.48 0.27 1.77 0.11 4.36

0.25 0.21 1.19 0.11 2.27 0.11 0.13 0.84 0.07 1.57

Table 4: Distributed running times of block Wiedemann with controlled and adaptive load balancing.

CLB ALB

BW1 BW2 BW3 Total BW1 BW2 BW3 Total Speed-up

54510 27975 14849 83974 33581 27975 11777 73333 1.14

on eight nodes, each utilizing 32 cores. The non-

blocking communication mode of MPI is used in all

the implementations reported in the table.

A comparison with the times reported in (Caval-

lar et al., 2000) and (Chen et al., 2008) is made in

Table 5. Although both these papers use the block-

Lanczos implementation, these target solving a linear

system of dimensions similar to A

, generated from

the sieving stage of RSA-512 factorization. The times

reported are in hours.

Table 5: Comparison with (Cavallar et al., 2000) and (Chen

et al., 2008).

CLB Strategy ALB Strategy Cavallar et al. Chen et al.

23.33 20.37 224 37.51

5 CONCLUSIONS

This paper deals with the parallel and distributed im-

plementations of the large sparse linear system solver

called Wiedemann’s method. The focus is on solv-

ing systems over GF(2) available from the sieving

stage of the general number ﬁeld sieve method for

factoring RSA moduli. In this paper, the Wiedemann

method is implemented in three settings: sequential

(single-core), parallel (single-node multi-core), and

distributed (multi-node multi-core). Effective load-

balancing ideas are proposed for the parallel and

distributed implementations. The block Wiedemann

method is also implemented, parallelized, and dis-

tributed. An adaptive load-balancing strategy is de-

signed for the block Wiedemann implementations.

Experimental results and speed-up ﬁgures are re-

ported extensively to illustrate the effectiveness of our

optimization steps.

ACKNOWLEDGEMENTS

This work is funded by Ministry of Electronics and

Information Technology, India. Project: Cryptanaly-

sis of cryptographic ciphers with an emphasis on AES

and RSA (CER).

REFERENCES

Anand, C. and II, S. (2007). Factoring of large numbers

using number ﬁeld sieve-the matrix step.

Bai, S., Gaudry, P., Kruppa, A., Thom

e, E., and Zimmer-

mann, P. (2016). Factorisation of rsa-220 with cado-

nfs.

Bai, S., Thom

e, E., and Zimmermann, P. (2012). Factori-

sation of rsa-704 with cado-nfs. Cryptology ePrint

Archive.

Barbulescu, R., Bouvier, C., Detrey, J., Gaudry, P., Jel-

jeli, H., Thom

e, E., Videau, M., and Zimmermann,

P. (2014). Discrete logarithm in gf (2 809) with ffs. In

International Workshop on Public Key Cryptography,

pages 221–238. Springer.

Beckermann, B. and Labahn, G. (1994). A uniform ap-

proach for the fast computation of matrix-type pad

approximants. SIAM Journal on Matrix Analysis and

Applications, 15(3):804–823.

Bender, E. A. and Canﬁeld, E. R. (1999). An approximate

probabilistic model for structured gaussian elimina-

tion. Journal of Algorithms, 31(2):271–290.

Berlekamp, E. (1968). Binary bch codes for correcting mul-

tiple errors. Algebraic Coding Theory.

Bhateja, A. and Kannan, V. (2017). Cache optimized so-

lution for sparse linear system over large order ﬁnite

ﬁeld. In International Conference on Mathematics

and Computing, pages 84–95. Springer.

Bhattacherjee, S. and Das, A. (2010). Parallelization of the

lanczos algorithm on multi-core platforms. In Interna-

tional Conference on Distributed Computing and Net-

working, pages 231–241. Springer.

SECRYPT 2022 - 19th International Conference on Security and Cryptography

546

Case, M. (2003). A beginner’s guide to the general number

ﬁeld sieve. Oregon State University, ECE575 Data

Security and Cryptography Project.

Cavallar, S., Dodson, B., Lenstra, A. K., Lioen, W., Mont-

gomery, P. L., Murphy, B., Te Riele, H., Aardal, K.,

Gilchrist, J., Guillerm, G., et al. (2000). Factoriza-

tion of a 512-bit rsa modulus. In International Confer-

ence on the Theory and Applications of Cryptographic

Techniques, pages 1–18. Springer.

Chen, J.-M., Yu, S.-I., Ou-Yang, Y., Wang, P.-H., Lin, C.-

H., Huang, P.-Y., Yang, B.-Y., and Laih, C.-S. (2008).

Improved factoring of rsa modulus. In Proceedings

of the 25th Workshop on Combinatorial Mathematics

and Computation Theory. Citeseer.

Coppersmith, D. (1994). Solving homogeneous linear

equations over gf(2) via block wiedemann algorithm.

Mathematics of Computation, 62(205):333–350.

Cowie, J., Dodson, B., Elkenbracht-Huizing, R., Lenstra,

A., Montgomery, P., and Zayer, J. (1996). A world

wide number ﬁeld sieve factoring record: On to 512

bits. In International Conference on the Theory and

Application of Cryptology and Information Security,

pages 382–394. Springer.

Dumas, J.-G. and Villard, G. (2002). Computing the rank

of large sparse matrices over ﬁnite ﬁelds. In Computer

Algebra in Scientiﬁc Computing (CASC) 2002, pages

47–62.

Kaltofen, E. (1995). Analysis of coppersmith’s block

wiedemann algorithm for the parallel solution of

sparse linear systems. Mathematics of Computation,

64(210):777–806.

Kaltofen, E. and Lobo, A. (1999). Distributed matrix-

free solution of large sparse linear systems over ﬁnite

ﬁelds. Algorithmica, 24(3):331–348.

Kaltofen, E. and Saunders, B. D. (1991). On wiedemann’s

method of solving sparse linear systems. In Interna-

tional Symposium on Applied Algebra, Algebraic Al-

gorithms, and Error-Correcting Codes, pages 29–38.

Springer.

Kaltofen, E. and Yuhasz, G. (2013). On the matrix

berlekamp-massey algorithm. ACM Transactions on

Algorithms (TALG), 9(4):1–24.

Kleinjung, T., Aoki, K., Franke, J., Lenstra, A. K., Thom

E., Bos, J. W., Gaudry, P., Kruppa, A., Montgomery,

P. L., Osvik, D. A., et al. (2010). Factorization of a

768-bit rsa modulus. In Annual Cryptology Confer-

ence, pages 333–350. Springer.

Krylov, A. N. (1931). On the numerical solution of the

equation by which the frequency of small oscillations

is determined in technical problems. Izv. Akad. Nauk

SSSR Ser. Fiz.-Mat, 4:491–539.

Lanczos, C. (1952). Solution of systems of linear equations

by minimized iterations. J. Res. Nat. Bur. Standards,

49(1):33–53.

Lee, S. and Eigenmann, R. (2008). Adaptive runtime tuning

of parallel sparse matrix-vector multiplication on dis-

tributed memory systems. In Proceedings of the 22nd

annual international conference on Supercomputing,

pages 195–204.

Lenstra, A. K., Lenstra, H. W., Manasse, M. S., and Pol-

lard, J. M. (1993). The number ﬁeld sieve. In The

development of the number ﬁeld sieve, pages 11–42.

Springer.

Lin, C.-Y., Chung, Y.-C., and Liu, J.-S. (2003). Efﬁ-

cient data compression methods for multidimensional

sparse array operations based on the ekmr scheme.

IEEE Transactions on Computers, 52(12):1640–1646.

Massey, J. (1969). Shift-register synthesis and bch de-

coding. IEEE transactions on Information Theory,

15(1):122–127.

Montgomery, P., Cavallar, S., and Te Riele, H. (1997). A

new world record for the special number ﬁeld sieve

factoring method. CWI Quaterly, 10(2):105–107.

Montgomery, P. L. (1995). A block lanczos algorithm for

ﬁnding dependencies over gf (2). In International

Conference on the Theory and Applications of Cryp-

tographic Techniques, pages 106–120. Springer.

OpenMP, A. (2016). The openmp api speciﬁcation for par-

allel programming, openmp arb.

Penninga, O. (1998). Finding column depedencies in sparse

matrices over f

2 by block wiedemann. Modelling,

Analysis and Simulation [MAS].

Pomerance, C. and Smith, J. W. (1992). Reduction of huge,

sparse matrices over ﬁnite ﬁelds via created catastro-

phes. Experimental Mathematics, 1(2):89–94.

Rivest, R. L., Shamir, A., and Adleman, L. (1978). A

method for obtaining digital signatures and public-

key cryptosystems. Communications of the ACM,

21(2):120–126.

Thom

e, E. (2002). Subquadratic computation of vector

generating polynomials and improvement of the block

wiedemann algorithm. Journal of symbolic computa-

tion, 33(5):757–775.

Villard, G. (1997). Further analysis of coppersmith’s block

wiedemann algorithm for the solution of sparse lin-

ear systems. In Proceedings of the 1997 international

symposium on Symbolic and algebraic computation,

pages 32–39.

Wiedemann, D. (1986). Solving sparse linear equations

over ﬁnite ﬁelds. IEEE transactions on information

theory, 32(1):54–62.

Yang, L. T., Huang, G., Feng, J., and Xu, L. (2017). Parallel

gnfs algorithm integrated with parallel block wiede-

mann algorithm for rsa security in cloud computing.

Information Sciences, 387:254–265.

Parallel and Distributed Implementations of the Wiedemann and the Block-Wiedemann Methods over GF(2)

547