Performance Evaluation of Call Admission Control Strategy in Cloud
Radio Access Network using Formal Methods
Maroua Idi
1,2 a
, Sana Younes
1,2 b
and Riadh Robbana
1,3 c
1
LIPSIC Laboratory, Faculty of Sciences of Tunis, University of Tunis El Manar, Tunis 2092, Tunisia
2
Faculty of Sciences of Tunis, University of Tunis El Manar, Tunis 2092, Tunisia
3
National Institute of Applied Sciences and Technology, University of Carthage, Tunis 1080, Tunisia
Keywords:
Cloud Radio Access Network, Virtual Machine, Hysteresis, Stochastic Model Checking, CTMC, PRISM.
Abstract:
For the fifth-generation (5G), Cloud Radio Access Network (C-RAN) has been proposed as a cloud archi-
tecture to provide a common connected resource pool management. In this regard, considering the rapidly
changing in network traffic load, the efficient management of radio resources is a challenge.
Call Admission Control (CAC) is a resource allocation mechanism to guarantee the Quality of Service (QoS)
to User Equipment (UE) in a mobile cellular network. This paper proposes a new CAC schema, based on
a hysteresis mechanism, named Virtual Machine Hysteresis Allocation Strategy (VMHAS) in the context of
C-RAN. We aim to provide a good QoS by improving the blocking probability of calls, adjusting the amount
of active VMs being provisioned for the current traffic load, and providing a load balancing in the considered
C-RAN. We use probabilistic model checking to evaluate the performance of the proposed strategy. First, we
model the VMHAS CAC schema with Continuous-Time Markov Chains (CTMCs). Then, we specify QoS
requirements through the CTMC using the Continuous-time Stochastic Logic (CSL). Finally, we quantify the
performance measures of the considered strategy by checking CSL steady-state and transient formulas using
the PRISM model checker.
1 INTRODUCTION
Cloud Radio Access Network (C-RAN) is a novel
mobile network architecture based on a virtualization
technology that has emerged as a promising architec-
ture to efficiently address the challenges of the fifth-
generation (5G) cellular networks, such as spectrum
efficiency and energy reduction. The concept was
first proposed by IBM in (Lin et al., 2010) with the
name of wireless network cloud to reduce network-
ing costs and achieve more flexible network capabil-
ities. Then this concept was described in detail by
China Mobile Research Institute in 2011 (Chen and
Duan, 2011). In contrast to the traditional access net-
works, the main idea behind C-RAN (Checko et al.,
2014) is to decompose the traditional Base Stations
(BS) into Base Band Units (BBUs) and Remote Ra-
dio Heads (RRHs) that are respectively responsible
for baseband and radio functionalities. Although the
a
https://orcid.org/0000-0002-6467-8887
b
https://orcid.org/0000-0002-4883-3381
c
https://orcid.org/0000-0001-5736-4137
RRHs are distributed and deployed with an antenna
at the cell site, the BBUs are grouped in a data cen-
ter called the BBU pool. The connection between the
BBUs and RRHs is referred to as the fronthaul links
and is done via optical transport network. In this ar-
chitecture, all BBUs functions could be implemented
on standard hardware and executed on Virtual Ma-
chines (VMs) (Bhamare et al., 2018). Hence, they
could serve each User Equipment (UE) by generat-
ing a VM to provide computing resources as common
data centers do in a cloud-based system (Urgaonkar
et al., 2010). In the BBU pool, each UE has its own
corresponding VM (Wang et al., 2017), (Haberland
et al., 2013). The number of VMs generated by each
BBU is restricted due to the limited processing ability
of each BBU. (Chen and Duan, 2011), which means
that each BBU can only support a certain number of
UEs.
Radio resource allocation always remains a big
challenge for all cellular networks; even for the C-
RAN, it is crucial to increase spectral efficiency while
guaranteeing a good Quality of Service (QoS). There-
fore, Call Admission Control (CAC) is one of the fun-
630
Idi, M., Younes, S. and Robbana, R.
Performance Evaluation of Call Admission Control Strategy in Cloud Radio Access Network using Formal Methods.
DOI: 10.5220/0011271300003266
In Proceedings of the 17th International Conference on Software Technologies (ICSOFT 2022), pages 630-640
ISBN: 978-989-758-588-3; ISSN: 2184-2833
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

damental strategies for radio resource management
that decides to accept or reject a new UE connection
demand based on the current cell load, the QoS of the
new UE demand, and of the ongoing traffic.
In existing works (Sigwele et al., 2014), (Sigwele
et al., 2015), all VMs of BBUs are always activated,
waiting for the arrival of calls in the case of high or
low traffic load. Whereas when a VM is activated, it
consumes energy. In fact, an idle VM, which is not
busy by call, consumes 60 to 80 percent of the energy
consumed by an occupied VM (Duan et al., 2015). In
this context, in order to preserve energy, a common
method makes non-occupying BBUs in sleep mode
(Sigwele et al., 2017a).
In our work, we use the sleep mode in the devel-
oped strategy but differently. In fact, we put VMs in
sleep mode, level by level in all BBUs, using the hys-
teresis mechanism. Moreover, let us note that it is es-
sential to take care of balancing the load between the
different BBUs through an appropriate VM allocation
strategy because the excessive or insufficient resource
utilization in the BBU impacts the virtual BBU’s per-
formance and the physical equipment’s maintenance
costs.
In this regard, we propose a new CAC scheme,
called Virtual Machine Hysteresis Allocation Strategy
(VMHAS). The proposed VMHAS, on the one hand,
adjusts the number of active VMs in BBUs by making
not using VMs in sleep mode and ensuring a low call
blocking probability. On the other hand, it guarantees
the load balancing between BBUs. To achieve this,
we propose using the hysteresis mechanism based on
the division of resources (VMs) to levels. Each level
will be activated when the used resource attains an ac-
tivated threshold. Similarly, the deactivation of level
is done when the using resources are less than a de-
activation threshold. Let us note that in the hystere-
sis mechanism, the deactivation threshold is always
strictly less than the activation threshold because the
fluctuations of the reserved resources from levels (ac-
tivation and deactivation of VMs) should be the min-
imum possible as the rapid switching between levels
has costs.
By applying the hysteresis mechanism in our VM
strategy, we propose to divide all BBUs into three lev-
els of VMs. In the first level of all BBUs, VMs are
always active and in idle mode, waiting for the ar-
rival of calls. However, in the remaining two levels
of all BBUs, VMs are deactivated and in sleep mode
and will be activated in need. In order to achieve a
load balancing between all BBUs, we propose to as-
sign, level by level, the UE calls by available VMs
in all BBUs, and we put the call to the least loaded
BBU. The second (resp.\ third) level of VMs will be
activated simultaneously in all BBUs when the num-
ber of occupied VMs attains the first (resp.\ second)
hysteresis activating threshold. When the current traf-
fic load in all BBUs decreases, we aim to reduce the
number of idle VMs. Hence, the third (resp.\ sec-
ond) level of VMs will be deactivated, simultaneously
in all BBUs, when the number of occupied VMs de-
creases and is lower than the descending thresholds.
Recall that we choose deactivation thresholds that are
lower than activation thresholds to reduce the switch-
ing operation between levels.
In this paper, we use Probabilistic Model Check-
ing (PMC) to analyze the performance of the pro-
posed VMHAS. PMC is a probabilistic extension
of the model checking formal verification technique,
used to analyze stochastic systems in different do-
mains (Kwiatkowska et al., 2005). It requires two in-
puts: a description of the system and a specification of
requirements under the system expressed in temporal
logics. In this work, we develop a Continuous-Time
Markov Chains (CTMC) model to describe our CAC
schema. We specify QoS requirements in terms of di-
minishing blocking probability, ensuring the load bal-
ancing between BBUs, and adjusting the number of
active VMs being provisioned for the current traffic
load. These requirements are expressed by checking
CSL steady-state and transient formulas of the system
using the PRISM model checker (Kwiatkowska et al.,
2011) to perform the VMHAS strategy.
The rest of the paper is organized as follows.
In section 2, we discuss the related work of CAC
schemes in the context of C-RAN and the use of the
hysteresis mechanism. In section 3, we give a brief
description of CTMC and CSL. Then, in section 4, a
performance model of the considered VMHAS is pre-
sented. In section 5, we present and discuss the results
of formal verification of QoS properties. Finally, we
conclude the paper.
2 RELATED WORK
In this section, we enumerate some works that present
CAC algorithms in the context of C-RAN. Then, we
focus on works that use the hysteresis mechanism in
order to ensure optimum reservation and utilization of
resources.
CAC is a mechanism that can play a key role in
providing guaranteed QoS and avoiding traffic con-
gestion in all cellular networks. In this context, pre-
vious works have been proposed in (Younes and Ben-
mbarek, 2017), (Younes and Idi, 2018) to treat CAC
schemes for the fourth generation, where the BS is not
shared.
Performance Evaluation of Call Admission Control Strategy in Cloud Radio Access Network using Formal Methods
631

In the context of C-RAN, Sigwele et al. proposed
in (Sigwele et al., 2014) an algorithm for CAC to en-
sure the QoS needs of the requested call. This algo-
rithm collects and uses traffic information to verify
the existence of sufficient resources, and it assigns
the incoming call to the less-load BBU in the clus-
ter of BBUs. When all BBUs are saturated, and the
QoS requirements are violated, the incoming calls are
blocked. To solve this problem, the authors take the
benefit of cloud elasticity to increase the processing
capacity of BBUs. In (Khan et al., 2015), the authors
proposed a self-organized C-RAN. The proposed net-
work architecture is formulated as an optimization
problem and can balance network traffic by reducing
the number of blocked calls and improving the QoS.
In (Sigwele et al., 2015), (Sigwele et al., 2017b)
and (Al-Maitah et al., 2018) authors proposed a CAC
schemes using Fuzzy Logic for heterogeneous traffic
classes. They evalute with simulation the call block-
ing probabilies.
To ensure efficient utilization of BBUs, the idea of
the model presented in (Sigwele et al., 2017a) is to act
with a fixed amount of BBUs and, according to the
demand, to deactivate the idle BBUs and reactivate
them only in case of overloading. In [(Gakhar et al.,
2006), (Levy et al., 2004), (Halberstadt et al., 1995)],
authors proposed CAC schemes based on hysteresis
mechanism in old cellular access networks. The al-
location mechanism in (Gakhar et al., 2006) was pro-
posed for traffic in IEEE 802.16 broadband wireless
network, and it dynamically modified the number of
resources reserved between a minimum and maxi-
mum number depending on the number of active con-
nections. It considers one, two, and multiple thresh-
olds in the three cases studied. In (Levy et al., 2004),
the authors consider multiple thresholds. Hence, the
reserved bandwidth varies from one to another thresh-
old until the number of channels being used reaches
a prefixed threshold. A mechanism to optimize re-
sources allocations in ATM networks was proposed in
(Halberstadt et al., 1995). In this model, the passage
of the bandwidth to a superior or inferior reservation
is attained as a function of the state of the client queue
at the ATM switch.
3 PRELIMINARIES
This section introduces the basic concepts of for-
malisms that we use to evaluate performance mea-
sures for the studied CAC scheme. We start by pre-
senting labelled CTMC, and then we recall the logic
CSL. For more details we refer to (Kulkarni, 2016)
for CTMC and to (Aziz et al., 2000) for CSL.
3.1 CTMC
A labelled CTMC M is a tuple (S,R,L) where S is
a finite set of states, R : S × S → R
+
is the rate ma-
trix and L : S → 2
AP
is the labelling function which
assigns to each state s ∈ S, the set L(s) of atomic
propositions a ∈ AP that are valid in s. The finite
set of atomic propositions is denoted by AP. Q, the
infinitesimal generator, can be deduced as Q(s,s
0
) =
R(s,s
0
) if s 6= s
0
and Q(s,s) = −
∑
s
0
∈S
R(s,s
0
).
A Path. Through a CTMC, a path is an alternating
sequence σ = s
0
t
0
s
1
t
1
··· with R(s
i
,s
i+1
) > 0 and t
i
∈
R
+
for all i ≥ 0. t
i
defines the amount of time spent
in state s
i
. Let’s call by path
s
the set of paths through
M starting from the state s.
State Probabilities. There are two types of state
probabilities in a CTMC: transient probabilities con-
sider the system at a time t and steady-state proba-
bilities when the system reaches an equilibrium if it
exists. Let us denote by Π
M
s
(t) the transient dis-
tribution at time t of M starting at t = 0 from the
initial state s. The probability to be in state s
0
at
time t starting initially from s will be denoted by
Π
M
s
(s
0
,t). The steady-state probability to be in state
s
0
is Π
M
s
(s
0
) = lim
t→∞
Π
M
s
(s
0
,t). If M is ergodic
(irreducible), Π
M
s
(s
0
) exists and it is independent of
the initial distribution that we will denote by Π
M
(s
0
).
Also, we denote by Π
M
the steady-state probability
vector. For S
0
⊆ S, we denote by Π
M
s
(S
0
,t) (resp.
Π
M
(S
0
)) the transient probability to be in states of S
0
,
Π
M
s
(S
0
,t) =
∑
s
0
∈S
0
Π
M
s
(s
0
,t) (the steady-state proba-
bility to be in states of S
0
, Π
M
(S
0
) =
∑
s
0
∈S
0
Π
M
(s
0
)).
3.2 CSL
This subsection presents CSL, which allows specify-
ing properties over CTMCs. CSL is an extension of
CTL (Computational Tree Logic) (Clarke et al., 1986)
with two probabilistic operators that refer to steady-
state and transient behaviors of the underlying system.
Let p be a probability threshold,  be a compar-
ison operator with  ∈ {≤,≥,<,>}, and I be an in-
terval of real numbers. The set of states that satisfy φ
property is denoted by S
φ
, and the satisfaction relation
is denoted by |=.
The syntax and semantic of CSL are defined
by:
s |= true for all s ∈ S
s |= a iff a ∈ L(s)
s |= ¬φ iff s 6|= φ
s |= P
p
(φ
1
U
I
φ
2
) iff Prob
M
(s,φ
1
U
I
φ
2
)  p
s |= S
p
(φ) iff Π
M
s
(S
φ
)  p
ICSOFT 2022 - 17th International Conference on Software Technologies
632

In this paper, we will use the probabilistic operators
P
p
(φ
1
U
I
φ
2
) and S
p
(φ) to define and quantify per-
formance measures of the studied system. In fact,
these operators are referring to transient and steady
state behavior of the considered system.
The operator P
p
(φ
1
U
I
φ
2
) asserts that the prob-
ability measure of paths satisfying φ
1
U
I
φ
2
meets
the bound given by p. Whereas, the path formula
φ
1
U
I
φ
2
asserts that φ
2
will be satisfied at some
time t ∈ I and that at all preceding time φ
1
holds.
Prob
M
(s,φ
1
U
I
φ
2
) denotes the probability measure
of all paths σ starting from s (σ ∈ paths
s
) satisfying
φ
1
U
I
φ
2
i.e.\ Prob
M
(s,φ
1
U
I
φ
2
) = Prob{σ ∈ paths
s
|
σ |= φ
1
U
I
φ
2
}.
Recall that the verification of time bounded un-
til formula P
p
(φ
1
U
I
φ
2
) for a CTMC M requires
the computation of Prob
M
(s,φ
1
U
I
φ
2
). This mea-
sure can be computed by transient analysis of another
CTMC M
0
which is derived from M . Let M [φ] be
the CTMC defined from M = (S,R,L), by making all
φ-states in M absorbing, i.e.\ M
0
= (S,R
0
,L) where
R
0
(s,s
0
) = R(s,s
0
) if s 6|= φ and 0 otherwise.
In this paper, we will use the formula
P
p
(true U
[t,t]
φ
2
) which is a particular case of
(φ
1
= true) and in a specific time t. In this particular
case M
0
= M , φ
1
∧ φ
2
= φ
2
and the verification of
this formula requires the computation of transient
distribution at time t of the considered model M
without doing any transformation.
s |= P
p
(true U
[t,t]
φ
2
) iff Π
M
s
(S
φ
2
,t) =
∑
s
0
|=φ
2
Π
M
s
(s
0
,t)  p (1)
The operator S
p
(φ) asserts that the steady-state
probability for φ-states meets the bound p. The veri-
fication of the steady-state operator requires the com-
putation the steady-state probability to be in φ-states.
s |= S
p
(φ) iff Π
M
s
(S
φ
) =
∑
s
0
|=φ
Π
M
s
(s
0
)  p (2)
In this work, we will also use two reward operators
from Continuous Stochastic Reward Logic (CSRL).
The CSRL (Haverkort et al., 2002) is an extension of
CSL by adding constraints over rewards. E
J
(φ), the
steady-state reward operator, asserts that the expected
reward rate for φ-states lies in J (J is an interval of
real numbers). The transient operator reward E
t
J
(φ)
asserts that the expected instantaneous reward rate at
time t for φ-states lies in J.
Let ρ : S → R
+
be a reward structure that as-
signs to each state s ∈ S a reward value ρ(s). The
verification of these reward formulas E
J
(φ) (resp.
E
t
J
(φ)) requires the computation of the steady-state
(resp.transient at t) distribution Π
M
s
of the considered
M .
s |= E
J
(φ) iff
∑
s
0
∈S
φ
Π
M
s
(s
0
) · ρ(s
0
) ∈ J
s |= E
t
J
(φ) iff
∑
s
0
∈S
φ
Π
M
s
(s
0
,t) · ρ(s
0
) ∈ J
(3)
4 SYSTEM DESCRIPTION AND
FORMAL MODEL OF VMHAS
In this section, we first describe the C-RAN archi-
tecture adopted in this paper. Then, we present the
VM Hysteresis Allocation Strategy (VMHAS) that
we propose. After that, we develop the algorithmic
description of VMHAS. Finally, we give the Marko-
vian model of the proposed VMHAS.
4.1 System Description
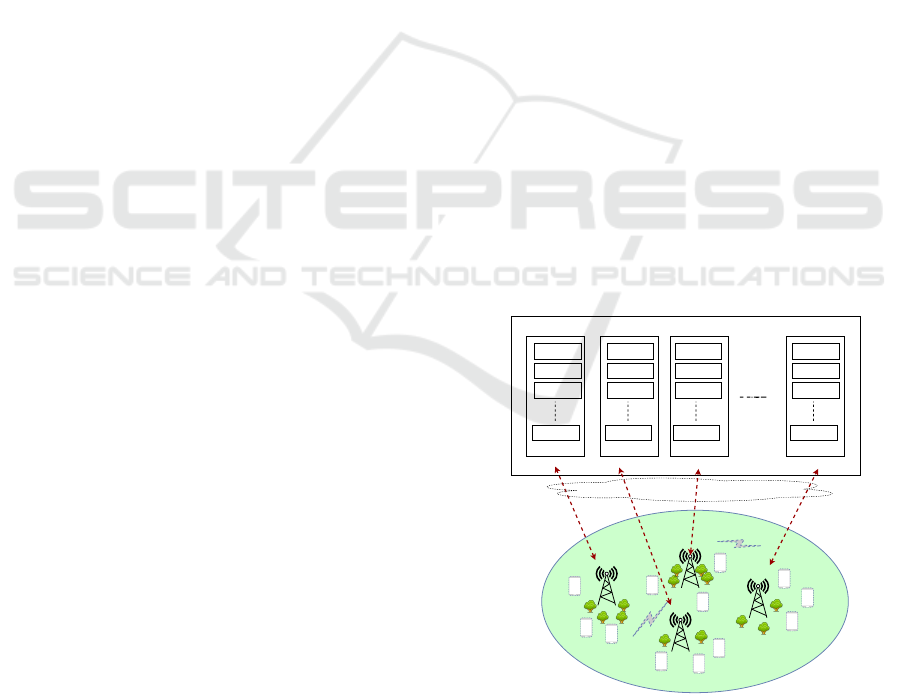
The C-RAN architecture that we consider in this pa-
per, as shown in Fig.
−
1, is composed of three main
components: a centralized BBU pool on the cloud
that contains a number of BBUs, a cell with a number
of distributed RRHs, and the fronthaul links used to
transmit baseband signals between the BBU pool and
RRHs. Given the adopted C-RAN architecture, each
BBU on the BBU pool is composed of a set of VMs,
and it can support one or more RRHs. We assume that
all BBUs are identical, they have the same number of
VMs, and a VM can only serve one UE.
VM1
BBU BBU BBU BBU
BBU Pool
UE
RRH
RRH
RRH
RRH
Fronthaul Links
K321
VM2
VM3
VMn
UE
UE
UE
UE
UE
UE
UE
UE
UE
UE
UE
VM1
VM2
VM3
VMn
VM1
VM2
VM3
VMn
VM1
VM2
VM3
VMn
Figure 1: C-RAN considered architecture.
Performance Evaluation of Call Admission Control Strategy in Cloud Radio Access Network using Formal Methods
633

4.2 Proposed VM Hysteresis Allocation
Strategy (VMHAS)
This subsection explains in detail the strategy that we
propose. Recall that we aim to achieve maximum ac-
cepted calls while adjusting the number of active VMs
in BBUs needed to serve all UE demands and ensure
a load balancing between BBUs.
In the proposed VMHAS, each BBU is divided
into three levels of VMs, as shown in Fig.
−
2. The
two hysteresis activating thresholds are V m
1
and V m
2
,
while the two hysteresis deactivating thresholds are T
1
and T
2
with T
1
< V m
1
, and T
2
< V m
2
. A VM can be
in an active or sleep mode, as shown in Fig.
−
3. When
a VM is activated, it can be in two different modes:
idle or busy. The idle mode is when the VM is acti-
vated but not occupied by a call. Whereas the busy
mode is when the VM is activated and occupied by a
call.
Initially, for all BBUs, all VMs in the first level,
containing V m
1
VMs, are always activated and in
idle mode, while the remaining VMs belonging to the
other two levels are deactivated and in sleep mode.
When a call arrives, it will be assigned to the avail-
able VM in the least load BBU. By default, when the
current traffic load is the same in all BBUs, the first
BBU will serve the incoming call.
The second level, containing (V m
2
−V m
1
) VMs,
will be activated when the first level in all BBUs
reaches the maximum capacity V m
1
. Therefore, when
a call arrives, and it is assigned to the last available
VM in the first level, all VMs in the second level will
be activated, simultaneously, in all BBUs and be in
idle mode waiting for the arrival of calls.
Similarly, the third level, containing (V max −
V m
2
) VMs, will be activated when the second level
reaches the maximum capacity V m
2
in all BBUs.
From the description above, it is clear that the acti-
vation of the second (resp.\ third) level of VMs in
all BBUs depends on traffic demands and the current
traffic load in the system. Therefore, when the cur-
rent traffic load decreases and in order to diminish
the number of VMs in idle mode, we adopt to de-
activate level by putting VMs to sleep mode. Note
that we talk about VMs deactivation when the system
is in the second or the third level. When the second
(resp.\ third) level is activated, and the current num-
ber of busy VMs in the system is strictly lower than T
1
(resp. T
2
) in all BBUs, then the corresponding VMs
of the second (resp.\ third) level will be deactivated
and be in sleep mode.
BBU
Vm2
Vm1
Vmax
Vmax-Vm2
Vm2-Vm1
T1
Vm1
Level1
Level2
Level3
T2
Figure 2: BBU with three
levels of VMs.
VM
Active mode Sleep mode
Idle mode Busy mode
Figure 3: VM−modes in a
BBU.
4.3 Proposed Algorithm of VMHAS
In this subsection, we present the algorithmic descrip-
tion of VMHAS in the case general of K-BBUs. We
use a Markovian process to model our strategy in
which the arrival of calls follows a Poisson process
and the service time (duration of the call) follows
an exponential distribution. Therefore, under these
Markovian hypotheses, the arrival of different calls
and the departure of ongoing calls cannot trigger si-
multaneously.
Algorithm 1: Proposed algorithm of VMHAS in the case of
K-BBUs.
K: Total number of BBUs;
V max: Max number of VMs in a BBU;
V m
2
: Hysteresis Level 3 activating threshold;
V m
1
: Hysteresis Level 2 activating threshold;
T
2
: Hysteresis Level 3 deactivating threshold;
T
1
: Hysteresis Level 2 deactivating threshold;
V
k
: Number of VMs in busy mode in the k
th
BBU where ( 1 ≤ k ≤ K);
/* Number of active VMs is initialized
to Vm
1
. */
L = V m
1
;
/* All BBUs are empty. */
for (1 ≤ k ≤ K) do
V
k
= 0
ActiveLevel2 ← False;
ActiveLevel3 ← False;
/* Two methods used to verify the
arrival (resp.\ the departure) of a
call. */
CallA = CallArrived();
CallD = CallDeparture();
While (CallA or CallD) do
if CallA then
/* Put the call in the first BBU.
*/
if (∀ 1 ≤ k ≤ K,V
1
= V
2
... = V
K
) then
V
1
= V
1
+ 1;
/* Put the call in the least
loaded BBU. */
else if (∀ 1 ≤ k ≤ K,V
k
< L) then
V
l
= min V
k
;
V
l
= V
l
+ 1;
ICSOFT 2022 - 17th International Conference on Software Technologies
634

Algorithm 1: Proposed algorithm of VMHAS in the case of
K-BBUs (cont.).
/* For each BBU, activate the
second level of VMs. */
if not ActiveLevel2 then
if (∀ 1 ≤ k ≤ K,V
k
= V m
1
) then
L = V m
2
;
ActiveLevel2 = True;
/* For each BBU, active the third
level of VMs. */
if not ActiveLevel3 then
if (∀ 1 ≤ k ≤ K,V
k
= V m
2
) then
L = V max;
ActiveLevel3 = True;
/* Reject the call because all
VMs in all BBUs are occupied.
*/
if (∀1 ≤ k ≤ K,V
k
= V
max
) then
reject call ;
if CallD then
/* Function returning a BBU from
which a call departed. */
k = departedcall();
V
k
= V
k
− 1;
/* For each BBU, deactivate the
second level of VMs */
if ActiveLevel2=True then
if (∀ 1 ≤ k ≤ K,V
k
< T
1
) then
L = V m
1
;
ActiveLevel2 = False;
/* For each BBU, deactivate the
third level of VMs */
if ActiveLevel3=True then
if (∀ 1 ≤ k ≤ K,V
k
< T
2
) then
L = V m
2
;
ActiveLevel3 = False;
CallA = CallArrived();
CallD = CallDeparture();
4.4 Model Analysis for 2-BBUs
The use of discrete-state approaches to model the per-
formance of large-scale systems is fundamentally pre-
vented by the state-space explosion problem, which
causes an exponential increase of the reachable state
space as a function of the number of components
which constitute the model. This is suitable for our
model, which is modeled by multidimensional CTMC
and consists of large numbers of components (each
dimension represents the number of active VMs in a
BBU). Therefore, in order to represent our VMHAS
model, we choose to discuss a labelled Markov model
in a special case of two BBUs (K = 2)
Let us remember that we assume that the arrival
processes of traffic are independent and follow a Pois-
son distribution with a rate equal to λ. We suppose
that the holding time of VMs is exponentially dis-
tributed with a mean 1/µ.
Based on these assumptions for arrival and ser-
vice rates, the proposed VMHAS can be modeled
by a multidimensional homogeneous CTMC M , pre-
sented in Fig.
−
4.
Obviously, the obtained M is composed of three
blocks relative to the number of levels in the hys-
teresis mechanism. The first (resp.\ second) contains
states of S
1
(resp.\ S
2
) (see Eq.
−
4 and Eq.
−
5) relative
to the activation of the second (resp.\ third) level of
VMs. The third block contains states of S
3
(see Eq.
−
6) where VMs are activated in all BBUs.
It is easily seen that the two transitions with con-
tinuous lines (marked in blue) represent the activation
for the second and the third level of VMs, while the
transitions with broken lines (marked in green) repre-
sent the deactivation for the second and the third level
of VMs.
The state space is given by:
S = S1 ∪ S2 ∪ S3
In state (i, j,l), i (resp.\ j) represents the number of
busy VMs in BBU
1
(resp.\ BBU
2
), and l represents
the activate level of VMs (1, 2 or 3):
S
1
=
{(i, j,1);1 ≤ i ≤ V m
1
and 0 ≤ j ≤ i − 1}
∪ {(i, j,1);0 ≤ j ≤ V m
1
− 1 and 0 ≤ i ≤ j}
(4)
S
2
=
{(i, j,2);T
1
≤ i ≤ V m
2
and 0 ≤ j ≤ i − 1}
∪ {(i, j,2);T
1
≤ j ≤ V m
2
− 1 and 0 ≤ i ≤ j}
(5)
S
3
=
{(i, j,3);T
2
≤ i ≤ V max and 0 ≤ j ≤ i − 1}
∪ {(i, j,3);T
2
≤ j ≤ V max and 0 ≤ i ≤ j}
(6)
By the particular structure of the obtained M , we can
calculate the number of states in S
1
, S
2
and S
3
which
is denoted respectively by N
1
, N
2
, and N
3
:
N
1
=
V
m1
∑
i=1
i +
V
m1
−1
∑
i=0
(i + 1) = 2
V
m1
∑
i=1
i
N
2
=
V
m2
∑
i=T
1
i +
V
m2
−1
∑
i=T
1
(i + 1) = 2
V
m2
∑
i=T
1
+1
i + T
1
Performance Evaluation of Call Admission Control Strategy in Cloud Radio Access Network using Formal Methods
635

0,0,1
λ
µ
1,0,1
λ
µ
1,1,1 0,1,1
µ
λ
λ
2µ
2,1,1 2,0,1
λ
µ
µ
2µ
λ 2µ
T1-1,T1-2,1 T1-1,T1-3,1 T1-1,0,1
λ
(T1-1)µ
λ
(T1-2)µ
λ λ
(T1-3)µ
µ
T1-1,T1-1,1
λ
(T1-1)µ
T1-2,T1-1,1 0,T1-1,1
λ
(T1-1)µ
λ λ
(T1-2)µ
µ
λ
λ
Vm1,Vm1-1,1 Vm1,Vm1-2,1 Vm1,0,1
λ
(Vm1-1)µ
λ λ
µ
(T1-1)µ (T1-1)µ
(T1-1)µ(T1-1)µ
T1µ
(Vm1-2)µ
Vm1µ
T1,T1-1,2 T1,T1-2,2 T1,0,2
(T1-1)µ (T1-2)µ
µ
T1,T1,2
λ
T1µ
T1-1,T1,2 0,T1,2
λ
T1µ
λ λ
(T1-1)µ
µ
λ
λ
Vm1,Vm1,2 Vm1-1,Vm1,2 0,Vm1,2
λ λ λ
µ
T1µ
(T1+1)µ
(Vm1-1)µ
Vm1µ
λ
Vm1µ
λ
λ
T2-1,T2-2,2 T2-1,T2-3,2 T2-1,0,2
λ λ λ
µ
T2-1,T2-1,2 T2-2,T2-1,2 0,T2-1,2
(T2-1)µ
(T1-2)µ
µ
(Vm1+1)µ
(T2-2)µ (T2-3)µ
(T2-1)µ (T2-1)µ
λ
λ
Vm2,Vm2-1,2
Vm2,Vm2-2,2 Vm2,0,2
λ λ λ
µ
Vm2µ
T2,T2-1,3 T2,T2-2,3 T2,0,3
λ
λ
λ
µ
T2,T2,3 T2-1,T2,3 0,T2,3
T2µ
(T2-1)µ
µ
(T2-1)µ
(T2-2)µ
λ
Vm2,Vm2,3
Vm2-1,Vm2,3 0,Vm2,3
λ
λ
µ
Vm2µ
Vm2µ
λ
(Vm2-1)µ
Vm2µ
λ
Vm2µ
λ
λλ
λ
T2µ
λ
Vmax,Vmax-1,3
Vmax,Vmax-2,3 Vmax,0,3
λ
λ
λ
(Vmax-2)µ
(Vm2+1)µ
Vmax-1,Vmax,3
0,Vmax,3
µ
λ
Vmaxµ
Vmaxµ
(Vmax-1)µ
λ
λ
λ
(Vmax-1)µ
Vmaxµ
Vmaxµ
Vmax,Vmax,3
Vmaxµ
µ
λ
Vmaxµ Vmaxµ
Vm1µ
Vm1µ
Vm1µ
Vm1µ
T1µ
T1µ
T1µ
T1µ
(T2-1)µ(T2-1)µ(T2-1)µ
λ
λλλ
(T2-1)µ
T2µ
Vm2µVm2µ
λλλ
(Vm2-1)µ
(Vm2-2)µ
λ
T2µ
T2µ
T2µ
T2µ
T2µ
S1
S2
S3
(T2+1)µ
Figure 4: CTMC of the proposed VMHAS.
N
3
=
V
max
∑
i=T
2
i +
V
max
∑
i=T
2
(i + 1) = 2
V
max
∑
i=T
2
i +V
max
− T
2
+ 1
The number of states N of the obtained M can be de-
duced by adding N
1
, N
2
and N
3
. It is given by Eq.
−
7.
N = V
2
m1
+V
2
m2
+ (V
max
+ 1)
2
+V
m1
+V
m2
−T
2
1
− T
2
2
(7)
Similarly, the number of the transitions can be
obtained by the Eq.
−
8.
T N = 3(V
2
max
+V
2
m2
+V
2
m1
) + 4V
max
+V
m2
+V
m1
− 3(T
2
1
+ T
2
2
) + 2(T
1
+ T
2
) − 2
(8)
5 NUMERICAL RESULTS
In this section, we present numerical results of the
performance evaluation of the proposed VMHAS.
These results are obtained by verifying CSL formu-
las under the VMHAS model that we proposed in the
subsection 4.2. Therefore, to check CSL formulas
that specify performances requirements, we label the
states of M , presented in Fig.
−
4, with atomic propo-
sitions which characterize the states. Let us consider
the following set of atomic propositions AP.
AP = {System
Sat,BBU
1
Sat,BBU
2
Sat}
The atomic proposition System Sat is assigned to
states in which the call is blocked in the system.
BBU
1
Sat (resp.\ BBU
2
Sat) is assigned to states in
which the call is blocked in BBU
1
(resp.\ BBU
2
).
The obtained satisfaction sets are marked in Fig.
−
4 and defined formally by:
S
System Sat
=
{(i, j,l) | i = V max & j = V max & l = 3}
S
BBU
1
Sat
=
{(i, j,l) | i = V max & 0 ≤ j ≤ V max & l = 3}
S
BBU
2
Sat
=
{(i, j,l) | 0 ≤ i ≤ V max & j = V max & l = 3}
Obviously:
S
System Sat
= S
BBU
1
Sat
∩ S
BBU
2
Sat
.
In order to construct and solve M , we use the
probabilistic model checker PRISM (Kwiatkowska
et al., 2011). This tool is a high-level modelling
language, and formulas are checked automatically.
Numerical results that we present in this section are
obtained with the parameters presented in Table 1.
The choice of the value of thresholds (T
1
< V m
1
and T
2
< Vm
2
) is justifiable because we need some
reserve VMs to avoid the rapid activating or deacti-
vating of the second (resp.\ third) level.
ICSOFT 2022 - 17th International Conference on Software Technologies
636

Table 1: Experimental Parameters.
Parameters Value
K:Total number of BBUs 2
V max:Max number of VMs in a BBU 100
V m
2
:Hysteresis Level 3 activating threshold 60
V m
1
:Hysteresis Level 2 activating threshold 40
T
2
: Hysteresis Level 3 deactivating threshold 56
T
1
:Hysteresis Level 2 deactivating threshold 36
1/µ: The mean VM holding time (per minute) 1
The size of the obtained M (states and transi-
tions number) is calculated by PRISM and is equal to
11069 and 32986. These results are equal to the math-
ematics formulas established by Eq.
−
7 and Eq.
−
8.
Now, we present the performance evaluation of
VMHAS obtained by checking steady-state and tran-
sient formulas.
5.1 Checking Steady-state Formulas
The verification of steady-state formulas needs the
computation of steady-state distribution Π
M
of the
considered M . It is clear that the obtained M of
VMHAS presented in subsection 4.4 is ergodic (ir-
reducible), so the steady-state probability vector Π
M
of M exists and is unique and it is independent of the
initial distribution.
5.1.1 S
=?
(φ)
The verification of this formula is presented by Eq.
−
2. In order to compute the steady-state call blocking
probability in the system, in BBU
1
and in BBU
2
, we
check the following formulas:
• S
=?
(System Sat): specifies the steady-state call
blocking probability for two BBUs (system). This
measure is equal to Π
M
(S
System−Sat
).
• S
=?
(BBU
1
Sat) (resp.\ S
=?
(BBU
2
Sat)): speci-
fies the steady-state call blocking probability for
BBU
1
(resp.\ BBU
2
). This measure is equal to
Π
M
(S
BBU
1
−Sat
) (resp.\ Π
M
(S
BBU
2
−Sat
)).
In order to evaluate the steady-state call blocking
probability in the system, in BBU
1
, and in BBU
2
by
considering different traffic loads, we vary the arrival
rate λ of calls from 110 to 180. It can be observ-
able through Fig.
−
5 that the increase of traffic load
does not influence the call blocking probabilities un-
til λ = 160, which is due to the resource availabil-
ity. Nevertheless, as the offered traffic increases, the
blocking probabilities also increase, but it remains ac-
ceptable despite using two BBUs and given the traffic
load that reaches 180 calls per minute. Therefore, we
can conclude that VMHAS has a higher acceptance
rate of connections request; hence more UEs can be
served. As observed, also, the call blocking probabil-
ity of BBU
2
is slightly lower than the call blocking
probability of BBU
1
. This slight difference between
these two BBUs is because when both BBUs have the
same current traffic load, the incoming call will be as-
signed to BBU
1
.
Figure 5: Steady-state call blocking probabilities.
5.1.2 E
=?
(true)
We use CSRL (Haverkort et al., 2002) logic to express
requirements related to the occupation rate for each
BBU, and the switching between levels. Hence, we
enrich PRISM M model with the reward functions.
Recall that the verification of this formula is given by
Eq.
−
3.
• Mean Occupation Rate: In order to check
that VMHAS ensures the load balancing between
BBUs which is important in the system, we eval-
uate the mean occupation rate for BBU
1
(resp.\
BBU
2
) by enriching our PRISM model with the
reward function ρ
BBU
1
(resp.\ ρ
BBU
2
). We as-
sign to each state s = (i, j,l) the reward val-
ues ρ
BBU
1
(s) = 100(i)/V max and, ρ
BBU
2
(s) =
100( j)/V max.
As observed in Fig.
−
6, when the traffic load in-
creases, the mean occupation rate for each BBU
increases. This is trivial because when the number
of calls increases, the number of occupied VMs
increases too. In addition, it can be observed that
the mean occupation rate attains a significant per-
centage (nearly 90%) because the arrival rate per
minute is significant (180 calls per minute) rela-
tive to the number of VMs in two BBUs. It is
also remarkable that the difference between the
two curves is very slight because when the call
arrives, it will be assigned to the available VM in
the least load BBU. By default, when the current
traffic load is the same in the two BBUs, the first
BBU will serve the incoming call. All that shows
that our VMHAS ensures the load balancing be-
tween BBUs.
Performance Evaluation of Call Admission Control Strategy in Cloud Radio Access Network using Formal Methods
637

Figure 6: Steady-state occupation rate for each BBU.
• Switching between Levels: In order to evaluate
the switching degree between levels depending on
the hysteresis deactivating thresholds and the traf-
fic load, we enrich the PRISM M model with the
reward function ρ
level
. We assign to each state
s = (i, j, l) the reward value:
ρ
level
(s) = l. (9)
We present in the steady-state the switching be-
tween the first and the second level while chang-
ing T
1
(see Fig.
−
7), and the switching between
the second and the third level while changing T
2
(see Fig.
−
8). Recall that according to Eq.
−
7 and
Eq.
−
8, the size of the obtained M (states and
transitions number) will change with the variation
of T
1
or T
2
. In fact, by decreasing T
1
, the size
of M increases which is confirmed by the exper-
iment results obtained in Table 2, and that is due
to the increase of state number in S
2
. Similarly,
the size of M increases too for decreasing values
of T
2
(see Table 3) because the number of states
increases in S
3
.
Table 2: The size of the model by varing T
1
.
T
1
States Transitions
6 12329 36706
14 12169 36242
22 11881 35394
30 11465 34162
38 10921 32546
In Fig.
−
7, we can observe that by decreasing T
1
,
the VMs of the second level stay active despite the
decrease in traffic load, which is observable in the
highest curve that still plates when λ is decreased
from 100 to 25. Whereas, in the lowest curve,
the second level is deactivated rapidly because the
value of T
1
is near to Vm
1
.
Now, in Fig.
−
8, we illustrate the switching from
the third to the second level by decreasing the traf-
fic load. Similarly, the transition from the third to
the second level is done quickly by values of T
2
near to Vm
2
. Whereas, by decreasing values of
Table 3: The size of the model by varing T
2
.
T
2
States Transitions
42 12441 37074
46 12089 36026
50 11705 34882
54 11289 33642
58 10841 32306
Figure 7: Steady-state switching between levels while
changing T
1
.
T
2
, the deactivation of level three will make more
time despite the decrease in traffic load.
Figure 8: Steady-state switching between levels while
changing T
2
.
5.2 Checking Transient-state Formulas
The verification of transient-state formulas at time t
needs the computation of transient-state distribution
Π
M
s
(t), which depends on the initial state s, of the
considered M .
5.2.1 P
=?
(true U
[t,t]
φ)
The verification of this formula is presented by
Eq.
−
1. We will compute probabilities for VMHAS
considering the initial state s = (0,0,1). We suppose
that at t = 0 all VMs are empty.
• P
=?
(true U
[t,t]
System
Sat): The verification of
this formula is performed by the computation of
the transient blocking probability of calls in two
ICSOFT 2022 - 17th International Conference on Software Technologies
638

BBUs at time t in the considered M . This mea-
sure is equal to Π
M
s
(S
System Sat
,t).
• P
=?
(true U
[t,t]
BBU
1
Sat): The verification of
this formula is performed by the computation of
the transient blocking probability of calls in BBU
1
at time t in the considered M . This measure is
equal to Π
M
s
(S
BBU
1
Sat
,t).
• P
=?
(true U
[t,t]
BBU
2
Sat): The verification of
this formula is performed by the computation of
the transient blocking probability of calls in BBU
2
at time t in the considered M . This measure is
equal to Π
M
s
(S
BBU
2
Sat
,t).
In order to evaluate the transient-state call blocking
probability in the system and in each BBU, we fix
λ = 160. It is observable through Fig.
−
9 that despite
the heavy traffic load, the values of blocking prob-
abilities (in the system, in BBU
1
and in BBU
2
) are
small. We note that the two BBUs saturation curves
have similar probabilities. Note that the difference be-
tween the two curves is explained by when the two
BBUs have the same number of occupied VMs, the
incoming call will be assigned to the first BBU.
Figure 9: Transient-state call blocking probabilities.
5.2.2 E
t
=?
(true)
We use the reward value presented in Eq.
−
9 in the
transient case to evaluate the activation level at time t,
depending on traffic load. this evaluation is illustrated
in Fig.
−
10.
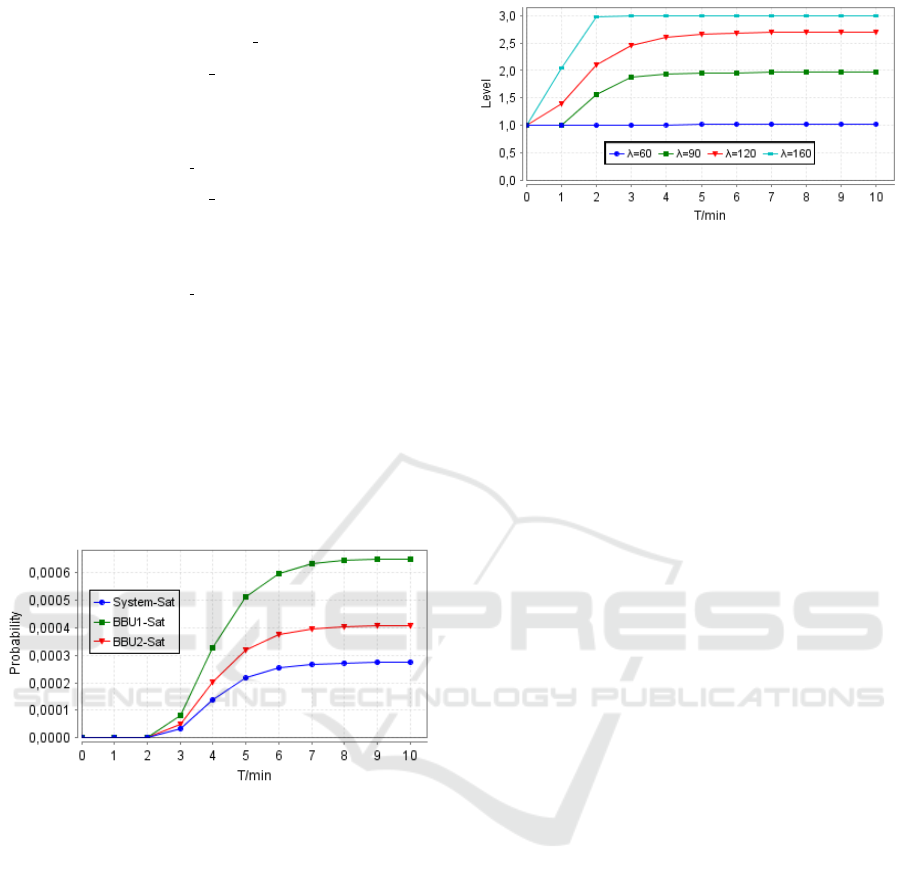
As observed, when the call arrival rate is light
(λ = 60 calls/min), only the first level of VMs in two
BBUs is activated to accept calls. However, the re-
maining two levels are deactivated because they are
not needed. Nevertheless, when the traffic load in-
creases (λ = 90 calls/min) and the number of occu-
pied VMs attains the first hysteresis activating thresh-
old, the second level of VMs will be activated in
the two BBUs. When the traffic load is very high
(λ = 160 calls/min), the third level of VMs will be
activated.
Figure 10: Transient-state activated level for BBUs.
6 CONCLUSION
In this paper, we have presented formal modelling and
verification of call admission control strategy in the
context of C-RAN. We have proposed a new CAC
scheme, called Virtual Machine Hysteresis Allocation
Strategy (VMHAS), based on two activation (resp.\
deactivation) hysteresis thresholds. We have devel-
oped the algorithmic description and the Markovian
model of the proposed VMHAS. Then, we have used
CSL logic to express the performance requirements
of calls in terms of diminishing blocking probability,
ensuring the load balancing between BBUs, and ad-
justing the number of active VMs being provisioned
for the current traffic load. The performance analysis
is performed using PRISM by checking CSL formulas
in the transient and the steady-state of the system. Re-
sults show that the proposed model could have an ac-
ceptable blocking probability considering a high call
arrival rate. Furthermore, it allowed load balancing
between the BBUs and an active number of VMs ac-
cording to the current traffic.
In the future, we will extend this work by perform-
ing additional performance measures to evaluate en-
ergy consumption and taking into account the even-
tual failure in the system by presenting a performabil-
ity model.
REFERENCES
Al-Maitah, M., Semenova, O. O., Semenov, A. O., Kulakov,
P. I., and Kucheruk, V. Y. (2018). A hybrid approach
to call admission control in 5G networks. Advances in
Fuzzy Systems, 2018.
Aziz, A., Sanwal, K., Singhal, V., and Brayton, R.
(2000). Model-checking continuous-time Markov
chains. ACM Transactions on Computational Logic
(TOCL), 1(1):162–170.
Bhamare, D., Erbad, A., Jain, R., Zolanvari, M., and
Samaka, M. (2018). Efficient virtual network function
Performance Evaluation of Call Admission Control Strategy in Cloud Radio Access Network using Formal Methods
639

placement strategies for cloud radio access networks.
Computer Communications, 127:50–60.
Checko, A., Christiansen, H. L., Yan, Y., Scolari, L.,
Kardaras, G., Berger, M. S., and Dittmann, L.
(2014). Cloud RAN for mobile networks—a tech-
nology overview. IEEE Communications surveys &
tutorials, 17(1):405–426.
Chen, K. and Duan, R. (2011). C-RAN the road towards
green RAN. China Mobile Research Institute, white
paper, 2.
Clarke, E. M., Emerson, E. A., and Sistla, A. P. (1986).
Automatic verification of finite-state concurrent sys-
tems using temporal logic specifications. ACM Trans-
actions on Programming Languages and Systems
(TOPLAS), 8(2):244–263.
Duan, L., Zhan, D., and Hohnerlein, J. (2015). Optimiz-
ing cloud data center energy efficiency via dynamic
prediction of CPU idle intervals. In 2015 IEEE 8th
International Conference on Cloud Computing, pages
985–988. IEEE.
Gakhar, K., Achir, M., and Gravey, A. (2006). Dynamic re-
source reservation in IEEE 802.16 broadband wireless
networks. In 200614th IEEE International Workshop
on Quality of Service, pages 140–148. IEEE.
Haberland, B., Derakhshan, F., Grob-Lipski, H., Klotsche,
R., Rehm, W., Schefczik, P., and Soellner, M. (2013).
Radio base stations in the cloud. Bell Labs Technical
Journal, 18(1):129–152.
Halberstadt, S., Kofman, D., and Gravey, A. (1995). A
congestion control mechanism for connectionless ser-
vices offered by ATM networks. In International
Workshop on Performance Modelling and Evaluation
of ATM Networks, pages 57–73. Springer.
Haverkort, B., Cloth, L., Hermanns, H., Katoen, J.-P., and
Baier, C. (2002). Model checking performability
properties. In Proceedings International Conference
on Dependable Systems and Networks, pages 103–
112. IEEE.
Khan, M., Alhumaima, R., and Al-Raweshidy, H. (2015).
Quality of service aware dynamic BBU-RRH map-
ping in cloud radio access network. In 2015 Interna-
tional Conference on Emerging Technologies (ICET),
pages 1–5. IEEE.
Kulkarni, V. G. (2016). Modeling and analysis of stochastic
systems. Chapman and Hall/CRC.
Kwiatkowska, M., Norman, G., and Parker, D. (2005).
Probabilistic model checking in practice: Case studies
with PRISM. ACM SIGMETRICS Performance Eval-
uation Review, 32(4):16–21.
Kwiatkowska, M., Norman, G., and Parker, D. (2011).
PRISM 4.0: Verification of probabilistic real-time sys-
tems. In International conference on computer aided
verification, pages 585–591. Springer.
Levy, H., Mendelson, T., and Goren, G. (2004). Dy-
namic allocation of resources to virtual path agents.
IEEE/ACM Transactions on networking, 12(4):746–
758.
Lin, Y., Shao, L., Zhu, Z., Wang, Q., and Sabhikhi, R. K.
(2010). Wireless network cloud: Architecture and sys-
tem requirements. IBM Journal of Research and De-
velopment, 54(1):4–1.
Sigwele, T., Alam, A. S., Pillai, P., and Hu, Y. F. (2017a).
Energy-efficient cloud radio access networks by cloud
based workload consolidation for 5G. Journal of Net-
work and Computer Applications, 78:1–8.
Sigwele, T., Pillai, P., Alam, A. S., and Hu, Y. F. (2017b).
Fuzzy logic-based call admission control in 5G cloud
radio access networks with preemption. EURASIP
Journal on Wireless Communications and Network-
ing, 2017(1):1–10.
Sigwele, T., Pillai, P., and Hu, Y. F. (2014). Call admission
control in cloud radio access networks. In 2014 Inter-
national Conference on Future Internet of Things and
Cloud, pages 31–36. IEEE.
Sigwele, T., Pillai, P., and Hu, Y. F. (2015). Elastic call
admission control using fuzzy logic in virtualized
cloud radio base stations. In International Confer-
ence on Wireless and Satellite Systems, pages 359–
372. Springer.
Urgaonkar, R., Kozat, U. C., Igarashi, K., and Neely, M. J.
(2010). Dynamic resource allocation and power man-
agement in virtualized data centers. In 2010 IEEE
Network Operations and Management Symposium-
NOMS 2010, pages 479–486. IEEE.
Wang, K., Zhou, W., and Mao, S. (2017). On
joint BBU/RRH resource allocation in heterogeneous
cloud-RANs. IEEE Internet of Things Journal,
4(3):749–759.
Younes, S. and Benmbarek, M. (2017). Performance analy-
sis of multi-services call admission control in cellular
network using probabilistic model checking. In Inter-
national Conference on Verification and Evaluation of
Computer and Communication Systems, pages 17–32.
Springer.
Younes, S. and Idi, M. (2018). Steady-state performability
analysis of call admission control in cellular mobile
networks. In International Conference on Model and
Data Engineering, pages 5–16. Springer.
ICSOFT 2022 - 17th International Conference on Software Technologies
640