Partially Oblivious Neural Network Inference

Panagiotis Rizomiliotis, Christos Diou, Aikaterini Triakosia, Ilias Kyrannas and Konstantinos Tserpes

Dep. of Informatics and Telematics, Harokopio University, Omirou 9, Athens, Greece

Keywords:

Homomorphic Encryption, Neural Network.

Abstract:

Oblivious inference is the task of outsourcing a ML model, like neural-networks, without disclosing criti-

cal and sensitive information, like the model’s parameters. One of the most prominent solutions for secure

oblivious inference is based on a powerful cryptographic tools, like Homomorphic Encryption (HE) and/or

multi-party computation (MPC). Even though the implementation of oblivious inference systems schemes has

impressively improved the last decade, there are still signiﬁcant limitations on the ML models that they can

practically implement. Especially when both the ML model and the input data’s conﬁdentiality must be pro-

tected. In this paper, we introduce the notion of partially oblivious inference. We empirically show that for

neural network models, like CNNs, some information leakage can be acceptable. We therefore propose a novel

trade-off between security and efﬁciency. In our research, we investigate the impact on security and inference

runtime performance from the CNN model’s weights partial leakage. We experimentally demonstrate that in

a CIFAR-10 network we can leak up to 80% of the model’s weights with practically no security impact, while

the necessary HE-mutliplications are performed four times faster.

1 INTRODUCTION

Artiﬁcial intelligence (AI), and in particular, machine

learning (ML) technology is transforming almost ev-

ery business in the world. ML provides the ability

to obtain deep insights from data sets, and to cre-

ate models that outperform any human or expert sys-

tem in critical tasks, like face recognition, medical di-

agnosis and ﬁnancial predictions. Many companies

offer such ML-based operations as a service (Ma-

chine learning as a service, MLaaS). MLaaS facili-

tates clients to beneﬁt from ML models without the

cost of establishing and maintaining an inhouse ML

system. There are three parties involved in the trans-

action; the data owner, the model owner and the in-

frastructure provider.

However, the use of ML models raises crucial se-

curity and privacy concerns. The data set used for

the ML model training and/or the MLaaS client’s in-

put in the inference phase can leak sensitive personal

or business information. To complete the scenery of

security threats, in several applications, like medical

or ﬁnancial, the ML models are considered as the

MLaaS provider’s intellectual property, and they must

be protected.

Oblivious inference is the task of running a

ML model without disclosing the client’s input, the

model’s prediction and/or by protecting the owner-

ship of the trained model. This ﬁeld of research is

also referred to as Privacy-preserved machine learn-

ing (PPML).

Several solutions for oblivious inference have

been proposed that utilize powerful cryptographic

tools, like Multi-party Computation (MPC) primitives

and the Homomorphic Encryption (HE) schemes.

MPC based protocols facilitate the computation of an

arbitrary function on private input from multiple par-

ties. These protocols have signiﬁcant communication

overhead as they are very interactive. On the other

hand, using HE cryptography we are able to perform

computations on encrypted data, but with signiﬁcant

computation and storage overhead.

Several PPML schemes have been proposed that

are either based solely on one of these technologies

or that they leverage a combination of them (hybrid

schemes). So far, literature has focused on two attack

models. It is assumed that either the model owner is

also the infrastructure provider or that the ML model

that it is used, it is publicly known. This is a rea-

sonable choice, as in both cases, the ML model’s

weights can be used in plaintext form. That is that, the

schemes designers avoid expensive computations be-

tween ciphertexts and thus, they introduce inference

systems that are practical.

158

Rizomiliotis, P., Diou, C., Triakosia, A., Kyrannas, I. and Tserpes, K.

Partially Oblivious Neural Network Inference.

DOI: 10.5220/0011272500003283

In Proceedings of the 19th International Conference on Security and Cryptography (SECRYPT 2022), pages 158-169

ISBN: 978-989-758-590-6; ISSN: 2184-7711

In this paper, we consider the use cases in which

the ML model’s conﬁdentiality must be protected.

The service provider wants to outsource the ML pre-

diction computation (for instance to a cloud provider

or to an edge device). However, the ML model con-

stitutes intellectual property and it’s privacy must be

preserved.

Protecting both the client’s input data and the

model’s privacy can increase prohibitively the com-

putational complexity as all the computations must be

performed between encrypted data. Just as a rough

estimation, the runtime of a single HE multiplication

increases ten times when it is performed between two

ciphertexts compared to HE multiplication between

a plaintext and a ciphertext. At the same time, HE

multiplications between encrypted data (ciphertexts)

increase signiﬁcantly the accumulative level of noise

and they limit the applicability of the HE schemes.

Thus, they must be avoided when possible.

Building on this observation, we introduce the no-

tion of partially oblivious (PO) inference. In a PO in-

ference system, the ML model owner decides to leak

some of the model’s weights in order to improve the

efﬁciency of the inference process. PO inference can

be seen as a generalization of oblivious inference that

offers a trade-off between security and efﬁciency. The

PO inference systems lie between the two extreme use

cases, the most secure but the less efﬁcient in which

all the ML model weights are encrypted and the less

secure and the most efﬁcient in which all the weights

are revealed. The optimal point of equilibrium be-

tween efﬁciency and security depends on the use case.

Our work is summarized as follows:

1. We introduce the notion of Partially Oblivious in-

ference for ML models.

2. We provide a security deﬁnition for the evaluation

of the information leakage impact. In our analy-

sis, the attacker is passive (”honest-but-curious”)

and she aims to compute a model that simulates

the protected one as accurately as possible. We

use accuracy improvement as our security metric.

3. As a proof-of-concept use case, we apply the

notion of PO inference to protect Convolutional

Neural Networks (CNN) inference.

4. We experimentally measure the security and per-

formance trade-off. We use two models trained

with the MINST (LeCun et al., ) and CIFAR-10

datasets (Krizhevsky, 2009), respectively. For the

PO inference implementation, Gazelle-like (Ju-

vekar et al., 2018) approach is used. Impressively,

it is shown that in some scenarios, leakage of more

than 80% of the model weight’s can be acceptable.

The paper is organized as follows. In Section 2,

the necessary background is provided. In Section 3,

we analyze our motivation, we introduce the security

attack model and the security deﬁnition for PO infer-

ence and we demonstrate the application of the PO

inference to CNN models. Finally, in Section 4, we

implement and evaluate the two CNN models and in

Section 5, we conclude the paper.

1.1 Related Work

There are several lines of work for PPML systems that

leverage advanced cryptographic tools, like MPC and

HE. The most promising solutions are hybrid, and

they are using HE to protect the linear and MPC to

protect the non-linear layers.

CryptoNet ((Gilad-Bachrach et al., 2016)) is the

ﬁrst scheme that deploys the HE primitive for PPML

on the MNIST benchmark. In the same research line,

CHET (Dathathri et al., 2019b), SEALion (van El-

sloo et al., 2019) and Faster Cryptonets (Chou et al.,

2018) use HE and retrained networks. There are

HE based schemes that use pre-trained networks, like

Chimera (Boura et al., 2020) and Pegasus (Lu et al.,

2020). In the pre-trained PPML category, we can ﬁnd

several proposals that use only MPC schemes, like

ABY3 (Mohassel and Rindal, 2018), and XONN (Ri-

azi et al., 2019).

The most promising type of PPML systems are

hybrid, i.e. the proposals that use both MPC and the

HE schemes. Hybrid HE-MPC schemes provide an

elegant solution for pre-trained networks. The MPC

is responsible for the non-linear part (activation func-

tion) and HE for the linear transformations (FC and

convolutional layers). Gazelle (Juvekar et al., 2018)

is a state-of-the-art hybrid scheme for CNN prediction

and several works have followed, like Delphi (Mishra

et al., 2020), nGraph-HE (Boemer et al., 2019b),

nGraph-HE2 (Boemer et al., 2019a), and PlaindML-

HE (Chen et al., 2019). All these schemes assume

that either the model owner runs the models locally or

that the ML model is publicly known.

There are several open source HE libraries that

implement the operations of a HE schemes and offer

higher-level API (Viand et al., 2021) and there is an

ongoing effort to standardize APIs for HE schemes

(sta, 2018). However, dealing directly with HE-

libraries and operations is still a very challenging task

for the developers. In order to facilitate developers

work, HE compilers have been proposed to offer a

high-level abstraction. There is a nice overview of

existing HE-compilers in (Viand et al., 2021).

Partially Oblivious Neural Network Inference

159

2 BACKGROUND

2.1 Homomorphic Encryption

In the last decade, the performance of HE schemes

has impressively improved up to several orders of

magnitude thanks to advances in the theory and

to more efﬁcient implementations. However, it is

still signiﬁcantly slower than plaintext computations,

while realizing HE-based computations is complex

for the non-expert.

Modern HE schemes belong into one of two main

categories. The schemes that compute logical gates

and thus, they are most efﬁcient for generic applica-

tions, and the schemes that operate nicely on arith-

metic or p-ary circuits and thus, they are used for

the evaluation of polynomial functions. The CKKS

(Cheon et al., 2017) scheme belongs in the second

category. As it operates to arithmetic circuits on com-

plex and real approximate numbers, CKKS is suitable

for machine learning applications. We are going to

use it in our experiments.

Following the last version of the HE Standard (sta,

2018), all the schemes must support the following

types of operations: key and parameters management,

encryption and decryption operation, HE evaluation

of additions and multiplications, and noise manage-

ment.

2.2 HE Evaluation Operations Cost

Practically, all the modern HE schemes are based on

the hardness of the Learning With Errors (LWE) prob-

lem (Regev, 2005) and its polynomial ring variant.

Depending on the scheme the plaintext, the keys, and

the ciphertexts are elements of Z

or Z

[X]/(X

+ 1),

i.e. they are either vectors of integers or polynomials

with integer coefﬁcients.

In order to protect a message m a randomly se-

lected vector (or polynomial) e is selected from a dis-

tribution and it is added to produce a noisy version of

m. The level B of this added noise must always be

between two bounds B

min

and B

max

. When B < B

min

the ciphertext cannot protect the message, while when

B > B

max

, the noise cannot be removed and the correct

message cannot be retrieved anymore.

Thus, it is crucial to manage the level of noise in-

duced by the HE operations. It has been demonstrated

that the best noise management approach is to treat

the ciphertext’s noise level B as an invariant. That is

that, after each HE operation, the level of noise must

remain close to B.

In the CKKS (Cheon et al., 2017) scheme, the

ciphertext is a pair of polynomials c = (c

) over

a ring of polynomials Z

[X]/(X

+ 1), for appropri-

ately selected integers q and N. The four main eval-

uation operations of CKKS scheme are summarized

as:

1. Plaintext-Ciphertext Addition.

Let m and m

′

be two plaintexts and c

′

= (c

′

)

be the encrypted value of m

′

. The output of the

addition is c

out put

= (m + c

′

) and decrypts to

m + m

′

and the noise level is B.

2. Ciphertext Addition.

Let c = (c

) and c

′

= (c

′

) be the encrypted

values of plaintexts m and m

′

. The output of the

addition is c

out put

= (c

+ c

′

+ c

′

) and it is the

ciphertext of m +m

′

(approximately with good ac-

curacy). The level of noise is upper bounded by

2B.

3. Plaintext-Ciphertext Multiplication.

Let m and m

′

be two plaintexts and c

′

= (c

′

)

be the encrypted value of m

′

. The output c

out put

(m ·c

′

,m ·c

′

) decrypts to m ·m

′

and the level of

noise is mB.

4. Ciphertext Multiplication.

Let c = (c

) and c

′

= (c

′

) be the encrypted

values of plaintexts m and m

′

. The output of the

multiplication is three polynomials, c

out put

= (c

′

·c

′

·c

′

) and the noise level is B

It is clear that the ciphertext multiplication is the

problematic one. The number of ciphertext polynomi-

als increases linearly (one more polynomial after each

multiplication) and the noise level increases exponen-

tially (it becomes B

, after L consecutive multiplica-

tions). To manage this size and noise increase, two

refresh type operations are applied. In order to bring

the dimension of the output ciphertext back to two,

the relinearlization algorithm is used. The resulting

ciphertext c

′′

out put

is an encryption of the m ·m

′

and the

level of noise is B

. For the noise management, an al-

gorithm called rescale (or modulo switching in other

HE schemes) is used. However, it can be applied only

a limited and predetermined number of times, usually

equal to the multiplicative depth L of the arithmetic

circuit.

Both algorithms, rescaling and relinearization, are

costly in terms of computational complexity and both

of them are applied after each multiplication between

two ciphertexts. Relinearization has approximately

the same computational cost with ciphertext multipli-

cation and an evaluation key is required. The evalua-

tions keys are created by the encryptor and passed to

the evaluator.

To summarize, the HE multiplication between

cipehrtexts is a very costly operation in terms of com-

SECRYPT 2022 - 19th International Conference on Security and Cryptography

160

putational overhead and noise management. Com-

pared to ciphertext multiplication, the other three HE

evaluation operations are practically for free.

2.3 Plaintext Packing

One of the main features of some HE schemes that

extremely improve performance is plaintext packing

(also referred to as batching). It allows several scalar

values to be encoded in the same plaintext. Thus, for

schemes with cyclotomic polynomial of degree N, it

is possible to store up to N/2 values in the same plain-

text (we refer to them as slots). Thus, homomorphic

operations can be performed component-wise in Sin-

gle Instruction Multiple Data (SIMD) manner. This

encoding has several limitations, since there is not

random access operation and only cyclic rotations of

the slots is allowed.

There are various choices for plaintext packing in

ML, i.e. how the input data and the model weights are

organized in plaintexts (or ciphertexts). Depending on

the workload two are the main packing approaches,

batch-axis-packing and inter-axis packing.

The batch-axis-packing is used by CryptoNets,

nGraph-HE and nGraph-HE2. It is used to a 4D ten-

sor of shape (B,C, H,W ), where B is the batch size, C

is number of channels and H, W the height and width

of input, along the batch axis. That is that, each plain-

text (or ciphertext) packing has B slots and C ·H ·W

are needed. This approach assumes that B inputs are

available for each inference operation.

On the other hand, inter-axis packing is used when

each input is processed separately, i.e. it is not neces-

sary to collect B inputs before performing a prediction

(this is common in medical diagnosis). There are sev-

eral packing choices, all of them encode scalars from

the same input. This approach is used by Gazelle in

which different packing is used for each type of linear

transformation. We will use inter-axis packing in our

analysis. In Section 3.4, we provide more details on

the different inter-axis packing choices.

2.4 CNN Models

The neural-network inference has been identiﬁed as

the main application area for privacy preserving tech-

nology, and especially for HE and MPC schemes, as

we have seen in Section 1.1. However, there are prac-

tical limits to the complexity of the use cases that can

be implemented (the unprotected computation must

be at most a few hundreds of milliseconds).

A CNN model consists of linear layers (like con-

volutional layer and fully connected layer) and non-

linear layers, like an activation function, usually a

ReLU functions or a pooling function, like max-

pooling. A very simple CNN appears in Fig. 1.

A fully connected (FC) layer with M inputs and N

Outputs is speciﬁed by a tuple (W,b), where W is an

M ×N weight matrix and b is a vector of length N,

called bias. This layer receives as input vector v

length M and computes the output as the linear trans-

formation of the input: v

out

= W

+ b.

The convolutional layer has c

number of input

channels with image dimension w

×h

each and pro-

duces c

output images with dimension w

×h

. The

Conv layer is parameterized by c

×c

many f

× f

ﬁlters.

3 PARTIALLY OBLIVIOUS

INFERENCE

3.1 Attack Model

The architecture of the neural network (number of

layers, type of neural network) is publicly known. On

the other hand, the network’s weights constitute in-

tellectual property of MLaaS provider and their con-

ﬁdentiality must be protected. We make no assump-

tions regarding the training data or the training pro-

cess. The training can be based on a private dataset as

well as on a partially public one. Also, the ML model

may has been trained from scratch or it may has been

based on publicly known pre-trained model.

All the model inference computations are out-

sourced to a cloud provider or an edge device (we re-

fer to both as the Server). We assume that the Server

is honest-but-curious, i.e. it executes the operations

correctly, but it wants to reveal any information that

it can. The goal of the attacker is to compute a ML

model that can simulate the original one as accurately

as possible.

Our scenario appears in Fig. 2. We make the as-

sumption that HE schemes are used at least for the

linear layers of the ML model. In our experiments,

we assume that the nonlinear layers are implemented

using an MPC protocol (in our case the Garbled Cir-

cuit from the Gazelle system). However, our attack

model is general and it can easily be adapted to other

privacy preserving technologies as well.

The model’s owner together with the data owner

produce the necessary HE keys, namely, the secret

key for the decryption, the public key for the encryp-

tion and the corresponding evaluation keys that are

sent to the server. In a simpliﬁed version of this sce-

nario, the model’s and data owner is the same entity.

The model’s weights and the input data are encrypted

with the public key and they are sent to the server.

Partially Oblivious Neural Network Inference

161

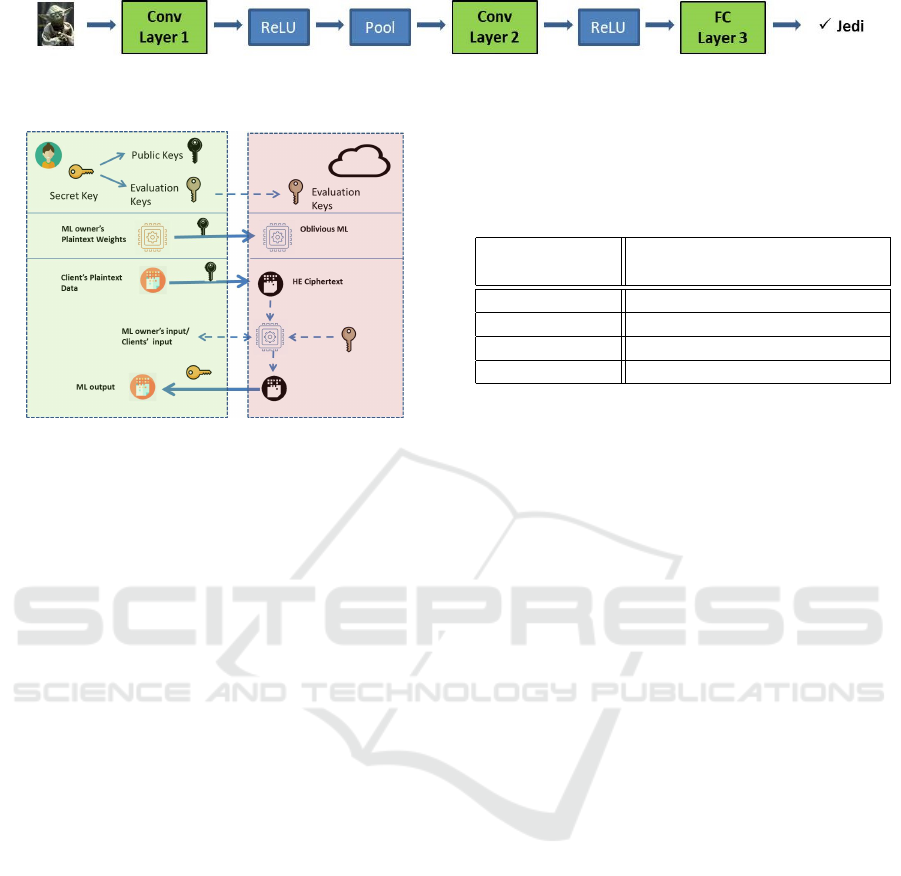
Figure 1: The example of a simple CNN. The green blocks are the linear layers (2 convolutional and one fully connected) and

blue blocks are the non-linear layers.

Figure 2: Oblivious Inference attack model.

The server runs the encrypted model on the en-

crypted input data, using the evaluation keys for the

HE protected linear layers and any other technology

for the nonlinear ones. The produced output is com-

puted encrypted and it is sent to the legitimate user (it

depends on the use case) who can decrypt it using the

secret key directly or an MPC protocol on secret key’s

shares.

Note that, in theory, we can even hide the archi-

tecture of the model, however this is prohibitively ex-

pensive and it is avoided in practice.

3.2 Motivation

The efﬁciency, and practicality, of a HE-based system

depends strongly on the type of operations that are

performed. Based on the analysis in Section 2.2, two

parameters are crucial:

1. Multiplicative Depth: The number of consecutive

ciphertext multiplications must remain small. As

the depth L increases, the modulo coefﬁcient q

must also increase and the HE scheme becomes

inefﬁcient.

2. Number of ciphertext multiplications: Even when

multiplications can be performed in parallel, the

computational complexity is signiﬁcant. The goal

is to reduce the number of ciphertext multiplica-

tions in total.

In the use cases under consideration the number

of ciphertext multiplications is very high since both

the system’s input values and the ML coefﬁcients are

HE-encrypted.

Table 1: CKKS operations for security level λ = 128-bit.

N is the degree of the polynomial (N/2 slots per plain-

text/ciphertetx) and L is the multiplicative depth. All the

parameters are deﬁned in SEAL from the HE standard (sta,

2018).

N = 2

L = 2 L = 4 L = 8

Plain Mult. 1 4 16

Ciph Mult. 2.7 12.3 60

Rescale 7.6 38.5 175.7

Relinearization 16.1 80 477

One of the main techniques used to reduce the

number of the multiplications between ciphertexts is

packing (see Section 2.3), i.e. to organize several

data in the same ciphertext and to compute in par-

allel all the computations with a single HE cipher-

text multiplication. Both the human expert and HE-

compilers use a pre-processing phase aiming to op-

timize the use of packing. For instace CHET, intro-

duced in (Dathathri et al., 2019a), is a compiler that

leverages the huge batching capacity and the rotations

of the CKKS scheme, to decrease the number of re-

quired ciphertext multiplications.

Our goal is to go beyond the capabilities of pack-

ing by building on the computational cost asymmetry

between HE ciphertext and HE plaintext multiplica-

tions. In Table 1, we can see an estimation of the run-

time cost for different HE-multiplication related op-

erations, i.e. plaintext multiplication, ciphertext mul-

tiplication, rescale and relinearization. The CKKS-

RNS is used implemented in the SEAL library.

Each entry of the Table 1 indicates how many

times lower is each operation compared to the plain-

text multiplication for N = 2

and multiplicative

depth L = 2. For instance for the same parameters N

and L the ciphertext multiplication is 2.7 times slower

and the relinearization is 16 times slower.

While we evaluate each operation separately, in

practice the ciphertext multiplication is always fol-

lowed by the relinearization operation. That it that,

it is almost 19 times slower in practice. Similarly, we

can argue for the rescale opeation.

From Table 1, it is clear that the multiplications

between a plaintext and ciphertext are much more ef-

ﬁcient. Based on this observation, we are motivated

to investigate the possibility of leaking information

that has limited impact on the security of the protected

scheme. The performance beneﬁts are pretty clear in

SECRYPT 2022 - 19th International Conference on Security and Cryptography

162

terms of runtime overhead as the revealed values can

be used in plaintext form.

Note. We need to have in mind that plaintext multi-

plication form leads also to limited noise growth and

as a result a larger variety of functions that can be HE

implemented. This is illustrate in Example 1. In this

paper, we don’t investigate this positive side-effect.

Example 1. Let f (x, y, z,w) = xy + zw be a bilin-

ear function that must be computed homomorphically.

The naive approach requires two ciphertext multipli-

cations, and a single ciphertext addition.

Let’s assume that any two of the four input val-

ues can be leaked, i.e. they can be used as plaintext.

There are





different combinations of two inputs, i.e.

6 in total. Due to the symmetry of the function they

belong into two equivalent classes, either both inputs

are the operands of the same multiplication (i.e. {x,y}

or {z,w}) or operands of different multiplications.

In the ﬁrst case, it requires one ciphertext multi-

plication, and one plaintext-ciphertext addition (the

multiplication between plaintexts is for free). In the

second case, it requires two plaintext-ciphertext mul-

tiplications, and one ciphertext addition. This is much

more efﬁcient.

3.3 Security Deﬁnition

In this section, we introduce the notion of Partially

Oblivious (PO) inference and we provide the corre-

sponding security deﬁnition.

Let W be the set of weights of a model M and let

L be a subset of W .

Deﬁnition 1. A model M is L-Partially Oblivious

(L-PO), when the model is FHE computed and only

the weights w ̸∈ L are HE-encrypted.

The deﬁnition implies that the model’s inference

is computed using HE while the weights that are in

the subset L are used unencrypted, i.e. these weights

are leaked.

When L =

0, all the weights are encrypted and

we have the standard deﬁnition of oblivious inference.

The model is

0-PO.

Next, we introduce a security deﬁnition to assess

the impact of the proposed information leakage. In

our attack scenario, we assume that the adversary’s

goal is to steal the model. That is that, the attacker

wants to produce a model

M that is equivalent to M .

Let

and

be the models that the attacker

computes when all the weights are encrypted and

when L are leaked, respectively. Also, let ACC

and

ACC

be the accuracy of each model.

Deﬁnition 2. A L-PO model M is λ-secure, if the

advantage of any polynomial-time adversary A,

Adv

(M ,L) = ACC

−ACC

(1)

is upper bounded by λ, i.e.

Adv

(M ,L) ≤ λ.

Ideally, λ = 0. In that case, the leaked weights

L do not improve the attackers capability to steal the

model.

3.4 CNN Mdel Partially Oblivious

Inference

In this section, we investigate the application of our

Partially Oblivious inference approach to the CNN

use case. From our attack model, the topology of the

network is publicly known, but the weights are conﬁ-

dential.

Our goal is to investigate trade-offs between secu-

rity and performance. This is expressed as informa-

tion leakage and more precisely as revealing model’s

weights. We will show that the model’s owner can

use some of the weights in plaintext in order to im-

prove inference runtime performance, while at the

same time this leakage gives a very limited advantage

to the attacker. These weights are only used in the

linear layers.

The linear layers (linear operations of fully con-

nected and convolutional layers) are implemented us-

ing an HE scheme. To simplify our analysis, we as-

sume that the non-linear layers (activation functions)

refresh the ciphertext noise. This is very common in

the hybrid schemes. For instance in Gazelle (Juvekar

et al., 2018), the non-linear layers are implemented

with MPC (using Garbled Circuits) and the output of

the layer is a ciphertext of with fresh noise (the same

applies with TEE based solutions).

The model owner can reveal a certain percentage

of the model’s weights. The higher the percentage

the more efﬁcient the inference process. At the same

time the security level is decreasing. The selection

of the weights is subject to the restrictions imposed

by the packing policy. The weights that are encoded

in the same polynomial must be treated as a group.

That is that, either they will all be revealed and used

in plaintext form or they must all be protected and

used in ciphertext form.

In our investigation, we follow the inter-axis pack-

ing (see Section 2.3) which is more common in medi-

cal diagnosis use cases and we analyze different pack-

ing techniques for the convolutional and fully con-

nected layers. For the fully connected layer, we an-

alyze the three packing techniques from Gazelle (Ju-

vekar et al., 2018), namely the naive approach, the

Partially Oblivious Neural Network Inference

163

diagonal and the hybrid. On the other hand, the two

packing techniques for the convolutional layer (called

in the paper padded and packed SISO) treat each ﬁlter

value independently. Thus, the model owner can de-

cide on the conﬁdentiality of the convolutional layer

weights without restrictions from the packing tech-

niques used.

The model owner selects a percentage of the

model weights to reveal following one of the foll-

woign strategies:

1. Random selection: The weight groups of the fully

connected layer and the individual ﬁlter values of

the convolutional layer are selected completely at

random.

2. Maximum weight: The weight groups of the fully

connected layer and the individual ﬁlter weights

of the convolutional layer with the largest mean

of absolute values are selected.

For example, consider a fully connected layer with

M inputs and N outputs. This layer is represented by

an M ×N weight matrix W. The linear output (logit)

is z = W

+ b, where h

is the input vector and b

the biases. The naive approach with rows as groups

will select ⌊pM⌋ rows of W for encryption. The ﬁrst

policy will randomly select the rows, while the second

will select rows i with the highest mean

M·N

∑

i j

In the case of a convolutional layer, the layer is

represented by a k ×k ×M ×N tensor W, where k

is the kernel size, M is the number of input channels

and N is the number of output channels. In this case, a

group can be a “ﬁlter” W

with dimensions k ×k ×M,

or each k ×k kernel W

i j

. For the maximum weight

strategy, the ﬁlters with the largest mean of absolute

weights are selected.

For both FC and convolutional layers, encrypting

the biases b is an additional option (the biases are also

encrypted as a group).

Regarding the attacker, we assume that she is try-

ing to produce a model from the leaked information.

We assume that the attacker has a very small set of

data just for the evaluation, but not sufﬁcient data to

train or ﬁne-tune a model. The attacker follows one of

the following policies for the prediction of the miss-

ing weights.

1. Constant (0.0): All the weights are replaced by

the constant value (zero, in the case of our exper-

iments).

2. Mean (µ): The mean value of the known weights

of the same layer is used. If no weights of the

current layer are known, then the constant policy

is used for that layer.

3. Normal (N (0,1)): The values are sampled from

a standard normal distribution.

Table 2: Neural network architectures used in the

experiments with MNIST and CIFAR-10 datasets.

“conv 3 ×3 X” denotes a convolutional layer with X ﬁlters

and a 3 ×3 kernel. FC-Y is a fully connected layer with Y

neurons, while “batchnorm” denotes batch normalization

(Ioffe and Szegedy, 2015). The ReLU activation function is

used in all layers except the output FC layer.

model for MNIST model for CIFAR-10

Input: (28 ×28 ×1) Input: (32 ×32 ×3)

conv 3 ×3 32 conv 3 ×3 32

maxpool 2 ×2 batchnorm

conv 3 ×3 64 conv 3 ×3 32

maxpool 2 ×2 batchnorm

FC-10 maxpool 2 ×2

softmax conv 3 ×3 64

batchnorm

conv 3 ×3 64

batchnorm

maxpool 2 ×2

conv 3 ×3 128

batchnorm

conv 3 ×3 128

batchnorm

maxpool 2 ×2

FC-128

Dropout (p = 0.5)

FC-10

softmax

4. Fitted normal (N (µ, σ)): Same as the Normal

policy, but the values are sampled from a nor-

mal distribution that is estimated from the known

weights of the same layer (i.e., with mean equal

to the known weight mean, and standard devia-

tion equal to the unbiased estimate of the standard

deviation of the known weights).

In the following section, we empirically evaluate

the tradeoffs between computational efﬁciency and

security of the proposed L-PO inference.

4 EXPERIMENTS

4.1 Experimental Setup

For our experiments we have used the MNIST (LeCun

et al., ) and CIFAR-10 (Krizhevsky, 2009) data sets,

using the standard train/test splits. The architecture

of the networks used in each dataset are outlined in

Table 2.

These architectures are used for empirical evalu-

ation of the security and computational efﬁciency of

the different L-PO strategies.

SECRYPT 2022 - 19th International Conference on Security and Cryptography

164

4.2 L-PO Security

To evaluate the security of L-PO for CNN networks

we initially train both network architectures of Table

2 using the Adam optimizer (Kingma and Ba, 2014)

with a learning rate of 0.001 and categorical cross-

entropy loss. The MNIST network is trained for 10

epochs without the use of a validation set, while the

CIFAR-10 network is trained for 20 epochs, with 20%

validation set and early stopping if no reduction in

loss is observed for more than 3 epochs.

Then, we apply an “encoding” step, where

weights of the neural network are selected accord-

ing to the strategies described in Section 3.4. In

this step we simulate L-PO by storing the indices

of the weights that would be selected for encryption.

Then, we evaluate the accuracy that an attacker would

achieve in a “decoding” step, for different policies

(also described in Section 3.4).

Both the original model M , the model

M that

is estimated by the attacker, as well as the fully en-

crypted model M

are evaluated in the test set of each

dataset and the resulting accuracies are used to assess

the security of L-PO in terms of Adv

(M ,L) deﬁned

in Section 3.3.

In each experiment we deﬁne the percentage p of

the weights to be selected for encryption, the weight

selection strategy, whether to select biases for encryp-

tion, as well as the attacker policy. Since some of the

policies applied by the attacker are stochastic, we re-

peat each experiment 10 times and report the average

and standard deviation of Adv

(M ,L). For each ex-

periment (i.e., combination of these options), the orig-

inal network is trained only once and is used in all 10

iterations. Training a network for each different ex-

periment (instead of using the same network across all

experiments of the same datasets) helps take into ac-

count randomness introduced by model training (e.g.,

due to weight initialization).

Results of the experiments are shown in Table

3, for both datasets and for some combinations of

p, weight selection strategies and attacker prediction

policies. For each experiment, the table provides the

average and standard deviation of the attacker advan-

tage observed in the 10 experiment runs. In all exper-

iments, bias weights have been selected for encryp-

tion.

Note also that, after encrypting all weights (p =

1.0) the model accuracy is roughly equal to the class

prior (i.e., the accuracy of the random classiﬁer). This

ascertains our knowledge of the model architeture by

itself does not lead to any attacker advantage.

An important observation from these results is that

for both datasets and models, the attacker advantage

0.0 0.2 0.4 0.6 0.8 1.0

Percentage of weights in L

0.0

0.1

0.2

0.3

0.4

Diﬀerence in advantage from revealing bias weights

Constant

N(µ, σ)

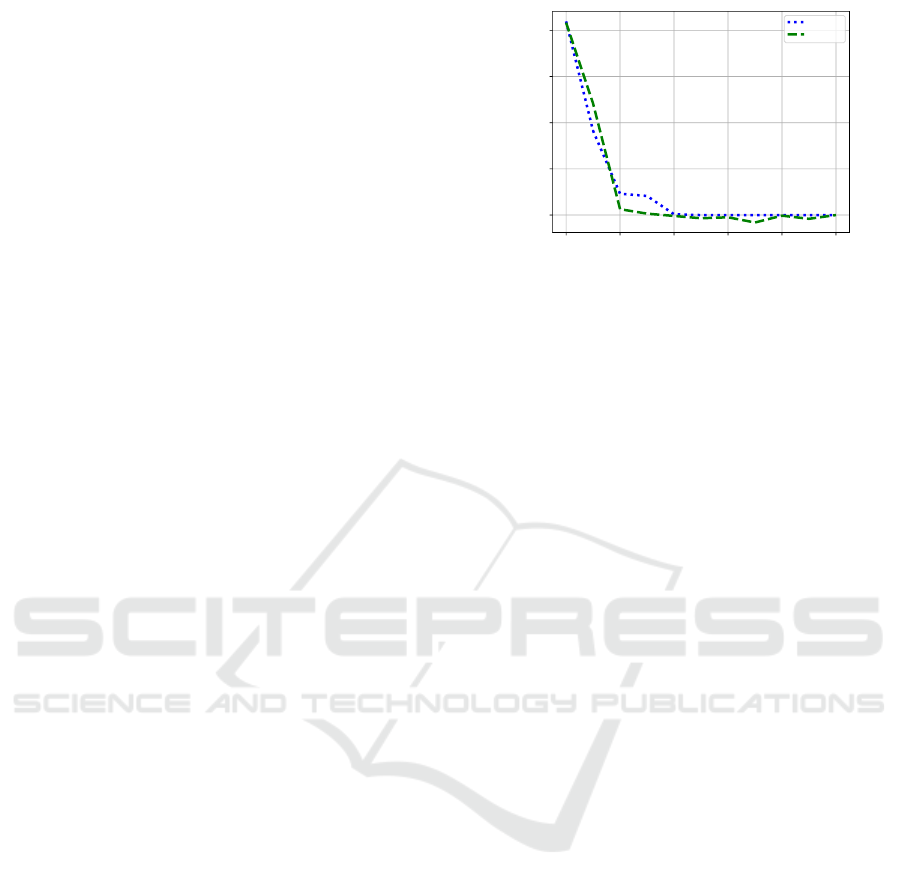
Figure 3: Difference in Adv

(M , L) achieved by an at-

tacker by when biases are not included in L, for the max

weight selection strategy. For very small p, the attacker can

beneﬁt from observing the biases, however as p grows this

advantage quickly becomes insigniﬁcant.

quickly diminishes as more weights are encrypted.

This is more pronounced in the more complex model

of the CIFAR-10 dataset, where for p > 0.2, the at-

tacker advantage is zero for both weight selection

strategies. But even for a small number of hidden

weights, e.g., p = 0.1, the maximum attacker advan-

tage (obtained with the constant policy) is only 47.9,

as opposed to 70.5 if she or he had access to the full

model. In this case, the attacker would achieve ap-

proximately 0.58 accuracy, while with the full model

she would achieve approximately 0.8. For the max

weight selection strategy the advantage is even lower.

Another interesting observation is that the weight

selection strategy plays an important role especially

for the CIFAR-10 dataset. Max weight selection

seems to be the most effective for both datasets. On

the other hand, random ﬁlter and random weight se-

lection conveys the minimum information about how

weights were selected to an adversary. It seems that

the optimal weight selection strategy depends on the

model and more sophisticated methods could be ex-

plored. This is not further discussed in this paper and

is left as future work. In the ideal case, one should

evaluate different weight selection strategies and use

the one that seems to provide the best results for each

model.

Regarding the different attacker weight estimation

policies, replacing all weights with zero leads to very

good results for both datasets, while using weights

from a ﬁtted normal distribution seems to be a good

policy as well. On the other hand, the mean and stan-

dard normal polices do not seem to be as effective.

In all experiments, the biases have been selected

for encryption, since the addition is relatively cheap,

computationally. Figure 3 illustrates the effect of in-

cluding biases in L for the CIFAR dataset for the ran-

dom and the best two weight estimation policies for

Partially Oblivious Neural Network Inference

165

Table 3: Results of experiments. Values are average and standard deviation across 10 runs, in 100Adv

(M , L) (a similar table

with the corresponding accuracy values is provided in the appendix). All runs include hidden biases, while the asterisk ‘*’

indicates the model without any hidden weights. Columns const = 0.0, N (0, 1), N (µ, σ) and µ correspond to the different

weight estimation policies of the attacker.

Random weight selection

MNIST CIFAR10

p const = 0.0 N (0, 1) N (µ, σ) µ const = 0.0 N (0, 1) N (µ, σ) µ

* 89.2 88.7 87.8 89.2 70.5 70.9 70.5 70.5

0.0 89.1 (0.0) 27.4 (19.5) 86.6 (0.9) 89.1 (0.0) 47.9 (0.0) 3.1 (2.3) 39.9 (12.5) 40.6 (0.0)

0.1 88.3 (0.6) 0.7 (3.1) 82.2 (4.9) 88.4 (0.6) 33.3 (11.2) 0.0 (0.7) 11.6 (9.5) 18.4 (13.2)

0.2 85.6 (3.1) 0.6 (3.0) 62.2 (12.0) 83.8 (4.6) 18.2 (5.7) 0.8 (0.7) 5.2 (4.1) 9.2 (4.5)

0.3 83.8 (2.1) 0.7 (1.0) 47.0 (13.7) 83.1 (3.3) 0.4 (1.0) 0.7 (0.8) 1.2 (1.7) 0.5 (1.4)

0.4 78.3 (4.3) 0.1 (2.0) 29.8 (13.8) 73.4 (6.0) 0.6 (1.1) 0.9 (1.2) -0.2 (1.4) 1.2 (1.5)

0.5 72.0 (9.0) -0.8 (3.2) 19.1 (7.9) 67.9 (7.6) -0.0 (0.5) 0.7 (1.5) 0.3 (1.9) -0.0 (1.5)

0.6 47.6 (15.3) 0.3 (1.8) 8.8 (4.5) 40.5 (13.4) -0.4 (0.6) 0.4 (0.3) -0.3 (0.6) 0.0 (0.0)

0.7 28.3 (9.9) 0.6 (1.7) -0.0 (4.3) 14.3 (3.8) 0.0 (0.0) 0.7 (1.1) 0.1 (1.1) 0.0 (0.0)

0.8 9.6 (7.2) -0.8 (2.7) 2.0 (3.0) 9.6 (6.6) -0.1 (0.4) -0.1 (0.7) -0.1 (0.7) 0.0 (0.0)

0.9 4.6 (5.9) 0.4 (3.3) -1.2 (2.9) -0.2 (1.5) 0.0 (0.0) -0.2 (1.5) 0.6 (1.0) 0.0 (0.0)

1.0 0.0 (0.0) 0.0 (1.8) 0.0 (4.5) 0.0 (0.0) 0.0 (0.0) 0.0 (0.7) 0.0 (1.3) 0.0 (0.0)

Max weight selection

MNIST CIFAR10

p const = 0.0 N (0, 1) N (µ, σ) µ const = 0.0 N (0, 1) N (µ, σ) µ

* 89.0 87.8 89.3 89.0 69.7 69.7 69.9 69.7

0.0 88.8 (0.0) 16.5 (10.9) 86.7 (3.8) 88.7 (0.0) 28.0 (0.0) 2.5 (3.6) 27.7 (14.2) 17.9 (0.0)

0.1 75.5 (0.0) 0.2 (2.6) 71.0 (8.6) 79.9 (0.0) 22.2 (0.0) 0.1 (0.3) 13.4 (10.0) 19.8 (0.0)

0.2 77.9 (0.0) -1.2 (2.6) 60.2 (10.0) 76.9 (0.0) 8.2 (0.0) -0.2 (1.0) 3.5 (2.3) 8.9 (0.0)

0.3 67.4 (0.0) -2.3 (2.6) 25.9 (14.7) 43.1 (0.0) 0.3 (0.0) 0.4 (0.4) 0.9 (1.8) 1.8 (0.0)

0.4 52.1 (0.0) -0.5 (3.8) 14.3 (4.3) 24.1 (0.0) 0.0 (0.0) 0.0 (1.0) 0.2 (0.9) 0.6 (0.0)

0.5 33.4 (0.0) -2.5 (2.3) 3.6 (3.3) 3.9 (0.0) 0.0 (0.0) 0.3 (0.8) -0.2 (0.9) 0.0 (0.0)

0.6 39.4 (0.0) -0.7 (2.9) 1.6 (2.7) 3.5 (0.0) 0.0 (0.0) -0.2 (0.8) 0.4 (0.5) 1.4 (0.0)

0.7 15.9 (0.0) -1.9 (1.2) 1.9 (3.1) 2.5 (0.0) 0.0 (0.0) 0.3 (0.8) 0.4 (1.1) 0.0 (0.0)

0.8 10.3 (0.0) -0.6 (2.7) 1.1 (2.7) 8.1 (0.0) 0.0 (0.0) -0.1 (0.7) 0.4 (0.9) 0.0 (0.0)

0.9 6.2 (0.0) -0.4 (3.3) 1.0 (3.2) 6.9 (0.0) 0.0 (0.0) -0.1 (0.3) 0.3 (1.0) 0.0 (0.0)

1.0 0.0 (0.0) 0.0 (2.3) 0.0 (2.4) 0.0 (0.0) 0.0 (0.0) 0.0 (0.6) 0.0 (1.3) 0.0 (0.0)

0.0 0.2 0.4 0.6 0.8 1.0

Percentage of weights in L

0.0

0.1

0.2

0.3

0.4

0.5

0.6

Adv

(M, L)

Random ﬁlter selection

Random weight selection

Max weight selection

Figure 4: Worst-case across 10 runs, between random ﬁlter

selection, random weight selection and max weight selec-

tion on the CIFAR-10 dataset, for varying percentages of

the weights included in L. In all cases, the reference accu-

racy is approximately ACC

= 0.1, (achieved when setting

all weights and biases equal to zero). As p grows, the at-

tacker advantage quickly diminishes.

that dataset.

Figure 4 illustrates the worst-case in the CIFAR-

10 dataset. For each value of p, the plot shows the

maximum advantage Adv

(M ,L) achieved by the at-

tacker across 10 runs and across all different weight

estimation policies. Ever when encrypting a small

percentage p of the weights, the model effectiveness

drops signiﬁcantly. For example, the maximum ad-

vantage for p = 0.1 and the max weight selection

strategy is 0.34, leading to a model accuracy of ap-

proximately 0.44, which is signiﬁcantly worse than

the accuracy of the original model (close to 0.8).

When encrypting more than 20% of the weights, the

attacker advantage becomes insigniﬁcant, even in the

worst case.

Overall, these results indicate that it is possible to

only encrypt a portion of the weights of a neural net-

work without enabling an attacker to infer the model

weights. In addition, a signiﬁcant drop in model ef-

fectiveness is observed even when hiding 10% of the

weights. Finally, the security was higher for the more

complex CIFAR-10 model, compared to the simpler

MNIST model, especially for smaller percentages of

hidden weights.

SECRYPT 2022 - 19th International Conference on Security and Cryptography

166

4.3 CNN Linear Layer

Micro-benchmarks

In this section, we evaluate the impact that the selec-

tion of the model weights type (i.e. plaintext or ci-

phertext) has on the inference performance. We as-

sume that a hybrid inference system is used and more

precisely, a system similar to Gazelle.

As the model weights are only used in the lin-

ear layers, and in order to isolate the impact of the

weights leakage to the system’s performance, we have

implemented only the linear layers using the CKKS

scheme from SEAL (SEAL, 2020). Regarding the

nonlinear layers, we assume that the privacy preserv-

ing techniques, used to implement the nonlinear func-

tions, refresh the noise induced by the HE operations

of the linear layer. Such an implementation is used

in Gazelle that leverages MPC protocols like Garbled

Circuits. Thus, we can further isolate the impact of

the leakage selection, as the multiplicative depth per

linear layer is very small (usually L = 1 or L = 2) and

we avoid expensive noise refreshing operations.

The linear layer weights (convolutional and fully

connected) are homomorphicaly encrypted and differ-

ent packing techniques can be used. For our analy-

sis we use the packing techniques from Gazelle. For

more details on these techniques please refer to the

original paper (Juvekar et al., 2018).

All these techniques mainly perform ciphertext

and/or plaintext HE multiplications between the layer

input and the model weights. The resulting prod-

ucts are always ciphertexts. Depending on the pack-

ing technique, some additions and rotations on these

ciphertxts are needed to produce the layer’s output.

However, these last operations (additions and rota-

tions) and their runtime overhead doesn’t depend on

the initial type of the model weights, as they always

operate on ciphertexts. That is that, only the initial

HE multiplications performance reﬂects the weight’s

leakage impact. Thus, we will only consider these

multiplications in our experiments.

For all both the FC and the convolutional layers,

the input of length is encrypted in a single cipher-

text. In the FC layer with M inputs and N outputs,

the matrix W is partially encrypted up to percent-

age p. Depending on the packing used, the entries of

W are grouped together in cipheretexts or plaintexts.

In the naive packing, each row constitutes a different

group of M elements and there are N groups. Thus,

we need N ·(1 −p) plaintext multiplications and N ·p

ciphertext multiplications. In the diagonal packing,

the number of multiplications depends on the inputs

M. Similarly, we need M ·(p −1) plaintext and M · p

ciphertext multiplications. Finally, the hybrid pack-

Table 4: Naive and diagonal packing for the FC layer. The

multiplicative factor of runtime overhead compared to the

all weights in plaintext computation.

p (128,10) (2048,128) (128,10) (2048, 128)

0.0 1 1 1 1

0.1 2.9 4.4 2.8 4.7

0.2 4.8 7.9 4.7 8

0.3 6.7 11.6 6.6 11.8

0.4 8.7 15.1 8.8 15.3

0.5 10.4 18.3 10 18.5

0.6 12.5 22.1 12.3 22

0.7 14.3 25.3 14.2 25.5

0.8 15.9 29.2 16 30

0.9 18.2 32.5 18 32.8

1.0 19.8 35.7 20.1 36.2

ing needs the same number of multiplications as the

naive techniques.

We evaluate the overhead of using a partially

encrypted matrix W in Table 4. The overhead is

computed a multiplicative factor compared to the all

weights in plaintext form case. Since after each linear

layer the HE noise is refreshed, we avoid the rescale

operation. Each ciphertext multiplication is followed

by a relinearization operation.

In Table 5, we investigate the impact of the rescale

operation. Since this operation is used after both

the plaintext and the ciphertext operations, the rela-

tive performance gain from the weights leakage is re-

duced.

Finaly, in the convolutional layer, each entry of the

3 ×3 ﬁlters are stored in a different ciphertext and al-

most all the slots are ﬁlled with the corresponding en-

try’s value. Thus, for each ﬁlter application we need 9

ciphertext or 9 plaintext multiplications. That is that,

we assume that the whole ﬁlter is either encrypted or

in plaintext form. Each convolutional layer input is

and RGB image 32 ×32 ×3. The result appears in

Table 6.

In our experiments we use the convolutional and

fully connected layers computed in Section 4.2 and

we compute the performance of the linear layers for

different values of the weights leakage percentage p.

5 CONCLUSIONS

This paper initiates a new line of research regarding

the oblivious outsourcing of ML models computation.

More speciﬁcally, we investigate the trade-offs be-

tween security and efﬁciency, when some information

leakage is acceptable.

Our work serves mainly as a proof of concept us-

ing CNNs. We have shown that the model owner

of a CIFAR-10 network can reveal 80% of selected

model’s weights in order to reduce the linear lay-

Partially Oblivious Neural Network Inference

167

Table 5: Naive packing for the FC layer using the rescale

operation after the plaintext multiplication and using both

the rescale and relinearization after the ciphertext multipli-

cation. The multiplicative factor of runtime overhead com-

pared to the all weights in plaintext computation.

p (128, 10) (2048,128)

0.0 1 1

0.1 1.3 4.4

0.2 1.55 7.9

0.3 1.7 11.6

0.4 1.9 2.2

0.5 2.15 2.5

0.6 2.3 2.9

0.7 2.5 25.3

0.8 2.7 3.252

0.9 2.95 3.7

1.0 3.11 4.1

Table 6: The convolutional layer using the relinearization

operation after the ciphertext multiplication. All the 9 mul-

tiplications for a ﬁlter application are either all ciphertext or

all plaintext. The multiplicative factor of runtime overhead

compared to the all weights in plaintext computation.

p (3,3)

0.0 1

0.1 4.5

0.2 8

0.3 11.7

0.4 15

0.5 18.15

0.6 22.3

0.7 25.5

0.8 29.7

0.9 32.55

1.0 36.11

ers cost of multiplications by a factor of 4. While

similar security-performance trade-offs are very com-

mon in applied cryptography (in searchable symmet-

ric schemes for instance), it is the ﬁrst time that such

approach is proposed in ML model inference.

Further research will follow. New attack models

must be proposed and new more ﬁne-grained security

deﬁnitions must be introduced per use case. At the

same time, the efﬁciency gain per use case must be

evaluated both theoretically (complexity asymptotic)

as well as experimentally. Our goal will be to leverage

the results of this research and provide new design

guidelines for efﬁcient HE-compilers.

ACKNOWLEDGEMENTS

This work was supported by the project COLLABS,

funded by the European Commission under Grant

Agreements No. 871518. This publication reﬂects

the views only of the authors, and the Commission

cannot be held responsible for any use which may be

made of the information contained therein.

REFERENCES

(2018). Homomorphic encryption standardization.

https://homomorphicencryption.org/standard/.

Boemer, F., Costache, A., Cammarota, R., and Wierzynski,

C. (2019a). ngraph-he2: A high-throughput frame-

work for neural network inference on encrypted data.

In Brenner, M., Lepoint, T., and Rohloff, K., editors,

Proceedings of the 7th ACM Workshop on Encrypted

Computing & Applied Homomorphic Cryptography,

WAHC@CCS 2019, London, UK, November 11-15,

2019, pages 45–56. ACM.

Boemer, F., Lao, Y., Cammarota, R., and Wierzynski, C.

(2019b). ngraph-he: a graph compiler for deep learn-

ing on homomorphically encrypted data. In Palumbo,

F., Becchi, M., Schulz, M., and Sato, K., editors, Pro-

ceedings of the 16th ACM International Conference

on Computing Frontiers, CF 2019, Alghero, Italy,

April 30 - May 2, 2019, pages 3–13. ACM.

Boura, C., Gama, N., Georgieva, M., and Jetchev, D.

(2020). CHIMERA: combining ring-lwe-based fully

homomorphic encryption schemes. J. Math. Cryptol.,

14(1):316–338.

Chen, H., Cammarota, R., Valencia, F., and Regazzoni, F.

(2019). Plaidml-he: Acceleration of deep learning

kernels to compute on encrypted data. In 37th IEEE

International Conference on Computer Design, ICCD

2019, Abu Dhabi, United Arab Emirates, November

17-20, 2019, pages 333–336. IEEE.

Cheon, J. H., Kim, A., Kim, M., and Song, Y. (2017). Ho-

momorphic encryption for arithmetic of approximate

numbers. In International Conference on the Theory

and Application of Cryptology and Information Secu-

rity, pages 409–437. Springer.

Chou, E., Beal, J., Levy, D., Yeung, S., Haque, A., and

Fei-Fei, L. (2018). Faster cryptonets: Leveraging

sparsity for real-world encrypted inference. CoRR,

abs/1811.09953.

Dathathri, R., Saarikivi, O., Chen, H., Laine, K., Lauter,

K., Maleki, S., Musuvathi, M., and Mytkowicz, T.

(2019a). Chet: an optimizing compiler for fully-

homomorphic neural-network inferencing. In Pro-

ceedings of the 40th ACM SIGPLAN Conference on

Programming Language Design and Implementation,

pages 142–156.

Dathathri, R., Saarikivi, O., Chen, H., Laine, K., Lauter,

K. E., Maleki, S., Musuvathi, M., and Mytkowicz,

T. (2019b). CHET: an optimizing compiler for fully-

homomorphic neural-network inferencing. In McKin-

SECRYPT 2022 - 19th International Conference on Security and Cryptography

168

ley, K. S. and Fisher, K., editors, Proceedings of the

40th ACM SIGPLAN Conference on Programming

Language Design and Implementation, PLDI 2019,

Phoenix, AZ, USA, June 22-26, 2019, pages 142–156.

ACM.

Gilad-Bachrach, R., Dowlin, N., Laine, K., Lauter, K. E.,

Naehrig, M., and Wernsing, J. (2016). Cryptonets:

Applying neural networks to encrypted data with high

throughput and accuracy. In Balcan, M. and Wein-

berger, K. Q., editors, Proceedings of the 33nd In-

ternational Conference on Machine Learning, ICML

2016, New York City, NY, USA, June 19-24, 2016, vol-

ume 48 of JMLR Workshop and Conference Proceed-

ings, pages 201–210. JMLR.org.

Ioffe, S. and Szegedy, C. (2015). Batch normalization: Ac-

celerating deep network training by reducing internal

covariate shift. In International Conference on Ma-

chine Learning, pages 448–456. PMLR.

Juvekar, C., Vaikuntanathan, V., and Chandrakasan, A.

(2018). GAZELLE: A low latency framework for

secure neural network inference. In Enck, W. and

Felt, A. P., editors, 27th USENIX Security Symposium,

USENIX Security 2018, Baltimore, MD, USA, August

15-17, 2018, pages 1651–1669. USENIX Association.

Kingma, D. P. and Ba, J. (2014). Adam: A

method for stochastic optimization. arXiv preprint

arXiv:1412.6980.

Krizhevsky, A. (2009). Learning multiple layers of features

from tiny images. Technical report, CIFAR.

LeCun, Y., Cortes, C., and Burges, C. J. MNIST handwrit-

ten digit database.

Lu, W., Huang, Z., Hong, C., Ma, Y., and Qu, H. (2020).

PEGASUS: bridging polynomial and non-polynomial

evaluations in homomorphic encryption. IACR Cryp-

tol. ePrint Arch., 2020:1606.

Mishra, P., Lehmkuhl, R., Srinivasan, A., Zheng, W., and

Popa, R. A. (2020). Delphi: A cryptographic in-

ference service for neural networks. IACR Cryptol.

ePrint Arch., 2020:50.

Mohassel, P. and Rindal, P. (2018). Aby

: A mixed protocol

framework for machine learning. In Lie, D., Mannan,

M., Backes, M., and Wang, X., editors, Proceedings of

the 2018 ACM SIGSAC Conference on Computer and

Communications Security, CCS 2018, Toronto, ON,

Canada, October 15-19, 2018, pages 35–52. ACM.

Regev, O. (2005). On lattices, learning with errors, ran-

dom linear codes, and cryptography. In Gabow, H. N.

and Fagin, R., editors, Proceedings of the 37th Annual

ACM Symposium on Theory of Computing, Baltimore,

MD, USA, May 22-24, 2005, pages 84–93. ACM.

Riazi, M. S., Samragh, M., Chen, H., Laine, K., Lauter,

K. E., and Koushanfar, F. (2019). XONN: xnor-

based oblivious deep neural network inference. In

Heninger, N. and Traynor, P., editors, 28th USENIX

Security Symposium, USENIX Security 2019, Santa

Clara, CA, USA, August 14-16, 2019, pages 1501–

1518. USENIX Association.

SEAL (2020). Microsoft SEAL (release 3.6).

https://github.com/Microsoft/SEAL. Microsoft

Research, Redmond, WA.

van Elsloo, T., Patrini, G., and Ivey-Law, H. (2019).

Sealion: a framework for neural network inference on

encrypted data. CoRR, abs/1904.12840.

Viand, A., Jattke, P., and Hithnawi, A. (2021). Sok: Fully

homomorphic encryption compilers. arXiv preprint

arXiv:2101.07078.

Partially Oblivious Neural Network Inference

169