
An Ensemble-based Dimensionality Reduction for Service Monitoring
Time-series
Farzana Anowar
1,2 a
, Samira Sadaoui
1 b
and Hardik Dalal
2
1
University of Regina, Regina, Canada
2
Ericsson Canada Inc., Montreal, Canada
Keywords:
Service Monitoring, High-dimensional Time-series, Dimensionality Reduction, Incremental Dimensionality
Reduction, Clustering Quality, Data Reconstruction.
Abstract:
Our work introduces an ensemble-based dimensionality reduction approach to efficiently address the high
dimensionality of an industrial unlabeled time-series dataset, intending to produce robust data labels. The en-
semble comprises a self-supervised learning method to improve data quality, an unsupervised dimensionality
reduction to lower the ample feature space, and a chunk-based incremental dimensionality reduction to further
increase confidence in data labels. Since the time-series dataset is massive, we divide it into several chunks
and evaluate each chunk’s quality using time-series clustering method and metrics. The experiments reveal
that clustering performances increased significantly for all the chunks after performing the ensemble approach.
1 INTRODUCTION
In industry, an incredible amount of data is produced
daily, and in many applications, data need to be pro-
cessed and analyzed in real-time. Even though ma-
chine learning algorithms can handle a vast quan-
tity of data, their performances worsen as the fea-
ture space becomes larger (Van Der Maaten et al.,
2009), (Spruyt, 2014). The predictive models become
more complex as the dataset’s size and dimension-
ality increase (Verleysen and Franc¸ois, 2005), (Jin-
dal and Kumar, 2017). Decision models trained on
a large feature space become reliant on the data and
may over-fit (Hawkins, 2004), (Anowar et al., 2021).
Additionally, the models’ accuracy declines due to
the presence of similar or irrelevant features (Jindal
and Kumar, 2017). This problems get worse when
high-dimensional time-series data is produced. Reg-
ular machine learning algorithms cannot handle the
continuous time-series data (Losing et al., 2018). Our
study emphasizes an industrial application on service
availability, which allows users to check what our
servers are up to. Hence, data are crawled continu-
ously or periodically with higher data dimensionality
for monitoring services’ availability. A robust Service
Monitoring dataset was developed in (Anowar et al.,
a
https://orcid.org/0000-0002-1535-7323
b
https://orcid.org/0000-0002-9887-1570
2022), which is temporal, unlabeled, and highly di-
mensional.
Furthermore, many machine learning methods fail
to perform efficiently in real-world scenarios because
of having inadequate target labels. Hence, it is crucial
achieving the highest confidence for the class labels.
For this purpose, we introduce an ensemble-based di-
mensionality reduction approach to efficiently pro-
cess an industrial use case’s high dimensional, non-
linear, and unlabeled time-series dataset with two ob-
jectives: 1) to better the data quality and 2) to produce
highly confident data labels. For the experimental
purpose, we have taken the new Service Monitoring
dataset from (Anowar et al., 2022), and we partition
the dataset into six week-by-week chunks.
The ensemble approach combines four methods
to handle this particular time-series dataset: a self-
supervised learning method, an unsupervised dimen-
sionality reduction, an incremental dimensionality re-
duction, and a time-series clustering. As a self-
supervised method, we adopt Autoencoder to recon-
struct the chunks in better data spaces by ignoring dis-
turbances, such as noisy and insignificant data. Sub-
sequently, we utilize the Kernel PCA (KPCA), an un-
supervised dimensionality reduction method, to re-
duce the ample feature spaces of the reconstructed
chunks into much shorter representations. Fewer di-
mensions mean less computation, faster training, eas-
ier data visualization, and less storage. The ulti-
Anowar, F., Sadaoui, S. and Dalal, H.
An Ensemble-based Dimensionality Reduction for Ser vice Monitoring Time-series.
DOI: 10.5220/0011273700003277
In Proceedings of the 3rd International Conference on Deep Learning Theory and Applications (DeLTA 2022), pages 117-124
ISBN: 978-989-758-584-5; ISSN: 2184-9277
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
117

mate goal of this research is to obtain the highest
level of confidence in the data labels for the Service
Monitoring dataset. For this purpose, we employ a
chunk-based incremental KPCA, an unsupervised in-
cremental dimensionality reduction method proposed
in (Tokumoto and Ozawa, 2011). We apply the incre-
mental learning method to each of the previously re-
duced chunks to improve the clustering performance
so that the cluster’s labels are accurate. We utilize the
cluster’s labels as the target data labels. We do not
consider the incremental KPCA to reduce the dimen-
sionality of the chunks; instead, we improve the data
quality.
To the best of our knowledge, there are minimal
incremental dimensionality reduction methods avail-
able for the supervised setting in the literature. This
limitation is even worse when dealing with non-linear
and unlabeled data (i.e., unsupervised). The chunk-
based incremental KPCA proposed in (Tokumoto and
Ozawa, 2011) is the only incremental dimensionality
reduction method that is chunk-based as opposed to
the instance-based incremental dimensionality reduc-
tion methods, and this is why we choose it.
Experimental results disclose that we obtain high
clustering performances with the ensemble-based
chunks. The latter outperforms the performances of
the initial chunks in all cases. Better clustering per-
formances ensure that the clusters are of better quality
where intra-cluster distances are maximized and inter-
cluster distances are minimized. In addition to that,
we will attain higher confidence in the target labels
for the further decision-making task for the industrial
partner.
We organize our paper as follows. Section 2 dis-
cusses recent literature on the efficacy of Incremen-
tal KPCA. Section 3 summarizes the characteristics
of the Service Monitoring dataset and then divides
it into multiple weekly chunks. Section 4 details
the proposed ensemble-based dimensionality reduc-
tion framework to produce accurate data labels. Sec-
tion 5 presents the experiments to assess the effec-
tiveness of the ensemble method in terms of clusters’
quality. Section 6 concludes our study and highlights
some future works.
2 RELATED WORKS
The very few incremental, unsupervised dimension-
ality reduction techniques have been defined in (Kim
et al., 2005), (Chin and Suter, 2007), (Takeuchi et al.,
2007), (Tokumoto and Ozawa, 2011). However, most
of them are instance-based where incoming data are
processed instance by instance. One of the very
first Incremental KPCA was proposed in (Kim et al.,
2005), which is based on the ‘Generalized Hebbian
Algorithm’ presented as an online algorithm for linear
PCA in (Sanger, 1989), (Oja, 1992). The hybrid algo-
rithm iteratively estimates the kernel principal com-
ponents using only a linear order memory complexity,
which makes it suitable for large datasets. However,
until an adequate accuracy is achieved, this Incremen-
tal KPCA necessitates a high number of learning iter-
ations.
(Chin and Suter, 2007) developed an incremental
KPCA that is based on the incremental linear PCA
introduced in (Lim et al., 2004). The Eigen-feature
space is incrementally updated instance by instance
in this proposed Incremental KPCA by performing
Singular Value Decomposition on the incoming train-
ing data. However, the Eigen-space model is updated
without learning all of the training data repeatedly,
this approach can be called a one-pass incremental
learning algorithm. Furthermore, higher memory and
computation costs are required to construct a reduced
dataset. The time and memory complexities are O(n
3
)
and O(n
2
), respectively for this algorithm.
The study (Takeuchi et al., 2007) proposed an in-
cremental KPCA where an eigen-feature space is rep-
resented by a combination of linearly independent
data, allowing it to learn from new data incremen-
tally without having to remember previous training
data. However, an open problem remains in this pro-
posed algorithm, is that an eigen-feature space should
be updated by solving an eigen value problem only
when new training data is received, which means that
eigen-value decomposition should perform for each
data in the chunk individually to update the eigen-
feature space, which leads to higher time and mem-
ory complexity, and it can only update eigen-vectors
quickly with a small set of linearly independent data
(lower dimensionality). Additionally, if the chunk
size is larger, real-time online feature extraction may
be impossible.
Later, the research (Tokumoto and Ozawa, 2011)
proposed a chunk-based incremental KPCA that con-
ducts the Eigen-feature space learning by only exe-
cuting the Eigen value decomposition once for each
chunk of incoming training data. The cumulative pro-
portion is used to choose linearly independent data
whenever a new chunk of training data becomes avail-
able. Then, the Eigen-space augmentation is per-
formed by measuring the coefficients for the chosen
linearly independent data, and the Eigen-feature space
is rotated based on the rotation matrix generated by
solving a kernel Eigen value problem. So far, this
proposed chunk-based algorithm is the most efficient
Incremental KPCA.
DeLTA 2022 - 3rd International Conference on Deep Learning Theory and Applications
118

The authors in (Joseph et al., 2016) proposed an
incremental KPCA by extending the algorithm de-
fined in (Takeuchi et al., 2007) to make it work for
the chunk setting. In this incremental KPCA, first,
a chunk of data is split into several smaller chunks
since author considered that retaining a suitable size
of data chunk is vital for fast learning. Then, from
the divided data chunks, only important features are
selected using regular KPCA, because not all data in
a chunk are valuable for learning. In the proposed in-
cremental KPCA, an Eigen-feature space is spanned
by Eigen vectors that are presented by a linear com-
bination of independent data. Later, a rotation matrix
to update the Eigen vectors and an Eigen value matrix
is attained by solving an Eigen value decomposition
problem only once for given data chunk. However, re-
ducing a chunk twice and keeping only few data from
a chunk is not practical always when processing real-
world dataset like time-series.
3 AN INDUSTRIAL TIME-SERIES
DATASET
Our past study (Anowar et al., 2022) developed a
Service Monitoring time-series, a new highly di-
mensional and unlabeled dataset derived from an in-
dustrial application, so developers can monitor ser-
vice availability, react to changes in service-wide
performance, and optimize service allocation. The
dataset was constructed from 48 sub-servers that used
Prometheus to collect data every 15 seconds for var-
ious services for over six weeks in the year 2020.
The chunks, containing information over six weeks
(39 days), come in different sizes and feature sets. A
dataset sample denotes the service’s availability, UP
or DOWN, for a given point of time. For example,
one instance may show that the service is up at 12.01
a.m., while another instance may suggest that the ser-
vice is down at 5.00 a.m. The Service Monitoring
data can be of two types: 1) Counter type indicating
a monotonically growing counter whose value can ei-
ther increase or be reset to zero on the restart, and 2)
Gauge type denoting a single numerical value that can
arbitrarily go up and down (Anowar et al., 2022). A
detailed description of this dataset is provided in past
work (Anowar et al., 2022).
The Service Monitoring dataset is large, compris-
ing 53,953 data and 3100 features. Hence, it requires
enormous memory space to be processed, particularly
when performing the KPCA method. The latter ne-
cessitates a sizeable short-term memory to perform
the kernel function and store the large kernel matrix
to project data to higher feature space so that data can
be linearly processed (Goel and Vishwakarma, 2016).
Hence, it is impossible to perform the kernel on the
whole dataset. Therefore, we split the dataset into six
chunks, one chunk for each week. This split enables
processing chunks in an incremental manner.
The first chunk possesses 9,099 data, the sixth
chunk has 4,534 data, and the four others have 10,080
data. These chunks have the same size because they
have the same amount of time for seven days, starting
at midnight and ending at 11.59 pm. The data collec-
tion for the first day of the first week began at 4.21
pm, and the last week has only four days. Table 1
presents the size and dimensionality for each chunk.
Table 1: Size and Dimensionality of Weekly Chunks.
Chunk Size Dimensionality
#1 9,099 3,100
#2 10,080 3,100
#3 10,080 3,100
#4 10,080 3,100
#5 10,080 3,100
#6 4,534 3,100
4 ENSEMBLE-BASED
DIMENSIONALITY
REDUCTION
When data come with high dimensionality, the train-
ing process for machine learning algorithms becomes
difficult, resulting in over-fitting the decision models
and lowering their performances (Jindal and Kumar,
2017). These problems are even worse when process-
ing complex data like time series. To this end, we
propose an ensemble-based dimensionality reduction
approach to manage unlabeled, non-linear, and high-
dimensional time-series chunks, intending to improve
each chunk’s quality and increase its labeling confi-
dence.
We first utilize a self-supervised learning method
on each time-series chunk to reconstruct its data and
improve its quality. Then, we adopt an unsupervised
dimensionality reduction technique to efficiently re-
duce the ample feature space. The reduced chunk is
then passed to an incremental, unsupervised dimen-
sionality reduction method not to lower the dimen-
sionality but to improve the data quality further and
increase the chunk labels’ confidence. Lastly, we as-
sess the quality of the final chunks by checking their
clustering performances to decide on the cluster la-
bels and show the necessity of our approach. The fol-
lowing section describes each phase of the ensemble-
based dimensionality reduction approach.
An Ensemble-based Dimensionality Reduction for Service Monitoring Time-series
119

4.1 Data Reconstruction of Each Chunk
We adopt a deep autoencoder model (named DAE)
as a pre-processing phase to increase data quality
by removing noisy data without changing the feature
space. Besides, DAE can process non-linear data,
like ours, efficiently by adopting non-linear activa-
tion functions in hidden and output layers (Almotiri
et al., 2017). DAE consists of two parts: 1) the en-
coder compresses the input data to a smaller encoding
with a latent space, and 2) the decoder reconstructs
the compressed data as closely as possible (Wang
et al., 2016). DAE learns from data when back-
propagating through the neural network and exclud-
ing irrelevant discrepancies during encoding, result-
ing in an accurately reconstructed dataset (Lawton,
2020). The DAE aims to minimize the reconstruc-
tion loss; the smaller the loss, the reconstructed data is
more likely to be the original data (Wang et al., 2016).
We first train DAE with the whole time-series dataset
to tune the hyper-parameters (hidden layers, weight
optimizer, loss function, batch size, epoch number,
and stopping criterion) and also determine the optimal
architecture. This DEA configuration will be utilized
for each weekly chunk.
4.2 Dimensionality Reduction of Each
Chunk
We make use of the popular feature extraction tech-
nique KPCA to manage each available chunk. The
KPCA method uses the “kernel trick” to project data
into a higher feature space so that data can be linearly
separable (Hoffmann, 2007). We employ RBF as the
kernel function for KPCA to better handle the non-
linearity of data. PCA uses the Eigen decomposition
to produce the Eigen vectors and values (Fan et al.,
2014). The Eigen vectors represent the new obtained
features called Principal Components (PCs).
Before applying KPCA, we search for the best
number of PCs by maximizing the “Total Explained
Variance Ratio” metric (TEVR) to ensure no signifi-
cant lose of information after reconstructing a chunk.
TEVR accumulates the explained variances of all the
PCs. The explained variance of a PC represents
the overall information contained by the PC (Kumar,
2020).
4.3 Incremental Dimensionality
Reduction of Each Chunk
Our objective is to perform the incremental KPCA on
each chunk to improve the clustering performances
and achieve the most confident cluster labels. We
adopt the chunk-based incremental KPCA algorithm
introduced in (Tokumoto and Ozawa, 2011) and dis-
cussed in Section 2 (related work). This study
(Tokumoto and Ozawa, 2011) provided only the the-
oretical framework. Another work (Hallgren and
Northrop, 2018) implemented this sophisticated al-
gorithm, which is capable of handling the training
chunks sequentially.
No direct library or package is available for incre-
mental KPCA in Python, Matlab, or R programming
languages. To use the incremental KPCA in Jupyter
Notebook, we first clone a Git repository from Github
where the implementation of the chunk-based incre-
mental KPCA (Hallgren and Northrop, 2018) was
provided. For using this Git repository efficiently,
Python 3.6 or higher versions, Numpy, and Scipy
must be installed. The Git module must be placed in
the same folder as the Python script to invoke the in-
cremental KPCA algorithm. Moreover, the input data
must be passed as an array for this implementation.
Additionally, to extract the desired principal compo-
nents, we have to conduct the dot product of the input
data matrix with the updated Eigen vectors returned
from the incremental KPCA program each time sep-
arately for all the chunks. Moreover, unlike conven-
tional KPCA implementations, this method returns all
the Eigen vectors (PCs) in decreasing order, allowing
users to select the desired PCs (the new features).
4.4 Clustering Evaluation of Each
Chunk
We employ a time-series clustering algorithm for each
ensemble chunk to produce the clusters. We uti-
lize the TS-Kshape method since Service Monitor-
ing dataset is temporal. TS-KShape is a domain-
independent and shape-based time-series clustering
technique (Paparrizos and Gravano, 2015). In each
iteration, TS-Kshape provides the similarity between
two time-series data based on the normalized cross-
correlation to update the cluster assignments (Paparri-
zos and Gravano, 2015). To efficiently determine
the centroid of each cluster, TS-Kshape considers the
centroid computation as an optimization problem by
minimizing the sum of the squared distances to all the
other data points from the centroid.
In addition, we consider two as the cluster num-
ber since the Service Monitoring dataset will have
two target labels (Up and Down). We evaluate the
cluster quality of the ensemble chunks using two per-
formance metrics: Davies-Bouldin (named DB) Index
and the Variance Ratio Criterion (named VRC). The
DB Index calculates how similar each cluster is on av-
erage, implying that the intra-cluster distance should
DeLTA 2022 - 3rd International Conference on Deep Learning Theory and Applications
120

be kept to a minimum, and VRC is a criterion that re-
turns the ratio of between-cluster and within-cluster
dispersion (Pedregosa et al., 2011), (Zhang and Li,
2013). The lower, the better for DB Index, and the
higher, the better for VRC (Pedregosa et al., 2011).
5 EXPERIMENTS
5.1 Autoencoder Configuration
To find the optimal architecture for DAE, we perform
grid search over multiple hyper-parameters. The best
DEA architecture is composed of six hidden layers
for both encoder and decoder, 1032 for batch size,
Adadelta for the weight optimization, Relu activation
function for all the hidden layers, Sigmoid function
for the output layer, and MSE for the loss function.
For the encoder part, we sequentially provide 3100
(original), 2500, 1650, 1032, 500, 100 and 5 features
using the six hidden layers, and again, we reconstruct
the features from 5, 100, 500, 1032, 1650,2500 and
3100. We utilize five epochs with no reduction in the
reconstruction loss by 0.0001 as the stopping criterion
for training. We use this optimal DAE configuration
for each incoming chunk individually.
5.2 First Chunk Transformation
We first describe the entire transformation process on
chunk #1 to improve the understandability. We train
the optimal DAE configuration on the first chunk until
the model’s loss is not converging anymore, intending
to build the best-reconstructed data. After reconstruc-
tion, the chunk will have the same dimensionality as
the initial one but with much better data quality. The
maximum TEVR and optimal PCs for chunk#1 are
0.999920 and 75, respectively. We, therefore, utilize
75 PCs when executing the KPCA algorithm to re-
duce the dimension space and the incremental KPCA
algorithm to produce better quality of data.
We note that the chunks obtained after utilizing
DAE+KPCA are denoted as ”reduced chunks”, and
after applying chunk-based incremental KPCA they
are named ”ensemble chunks”. From Table 2, we ob-
serve that the reduced chunk (DAE+KPCA) outper-
forms the initial chunk with a large margin. The ini-
tial chunk has DB and VRC of 1.552 and 3,455.962,
respectively, whereas the reduced chunk returns DB
of 0.5248 and VRC of 4,352.035. After utilizing
the incremental KPCA, we achieve much better DB
for chunk#1, though VRC under-performs with a tiny
gap.
After utilizing the chunk-based incremental
KPCA, we have one metric (DB) outperforming and
one metric slightly underperforming for chunk#1.
Hence, it is vital to decide which (reduced or ensem-
ble) chunk to use for the next decision-making task,
such as chunk labeling. For this purpose, we illustrate
the initial, reduced, and ensemble representations of
chunk#1 in Figure 1 to decide which chunk to uti-
lize. From Figure 1-(a, b), we observe that the two
clusters are very closely located. If two centroids are
very close, then there could be a possibility that an
instance can be mis-clustered, whereas, in 1-(c), two
clusters are sparsely located and can be differentiated
easily. Hence, we choose the ensemble chunk over
the reduced one for chunk#1. Also, we will select the
ensemble chunk when a similar scenario happens be-
tween reduced and ensemble representations for the
subsequent chunks.
Table 2: Cluster Performances of Chunk#1.
TEVR (in %)
Optimal
PCs
99.9920 75
Chunk DB VRC
Initial 1.552 3,455.962
Reduced 0.5248 4,352.035
Ensemble 0.5238 4,321.608
5.3 Remaining Chunks Transformation
By maximizing the TEVR metric for each chunk in-
dividually, we acquire the optimal PCs that is used for
the feature reduction method KPCA. Thus, we ensure
that the obtained PCs for a chunk hold most of the
information from its initial representation, and also
the same number of PCs is used with the chunk-based
incremental KPCA to improve the data quality. For
instance, for chunk#2, we attain the count of PCs of
100 with the maximum TEVR of 99.8900%.
Table 3 exposes the clustering quality for each
weekly chunk in terms of DB and VRC metrics be-
tween the initial and ensemble chunks. We perform
TS-Kshape clustering technique with two clusters on
all the chunks. We can see that the cluster quality has
improved significantly with a large gap for both met-
rics for all the chunks after applying the ensemble-
based dimensionality reduction approach. For exam-
ple, with the the initial data of chunk#3, DB and VRC
are 0.4546 and 1,499.436, respectively, whereas, the
ensemble chunk produced DB and VRC of 0.0851
and 447,828.401, respectively.
An Ensemble-based Dimensionality Reduction for Service Monitoring Time-series
121
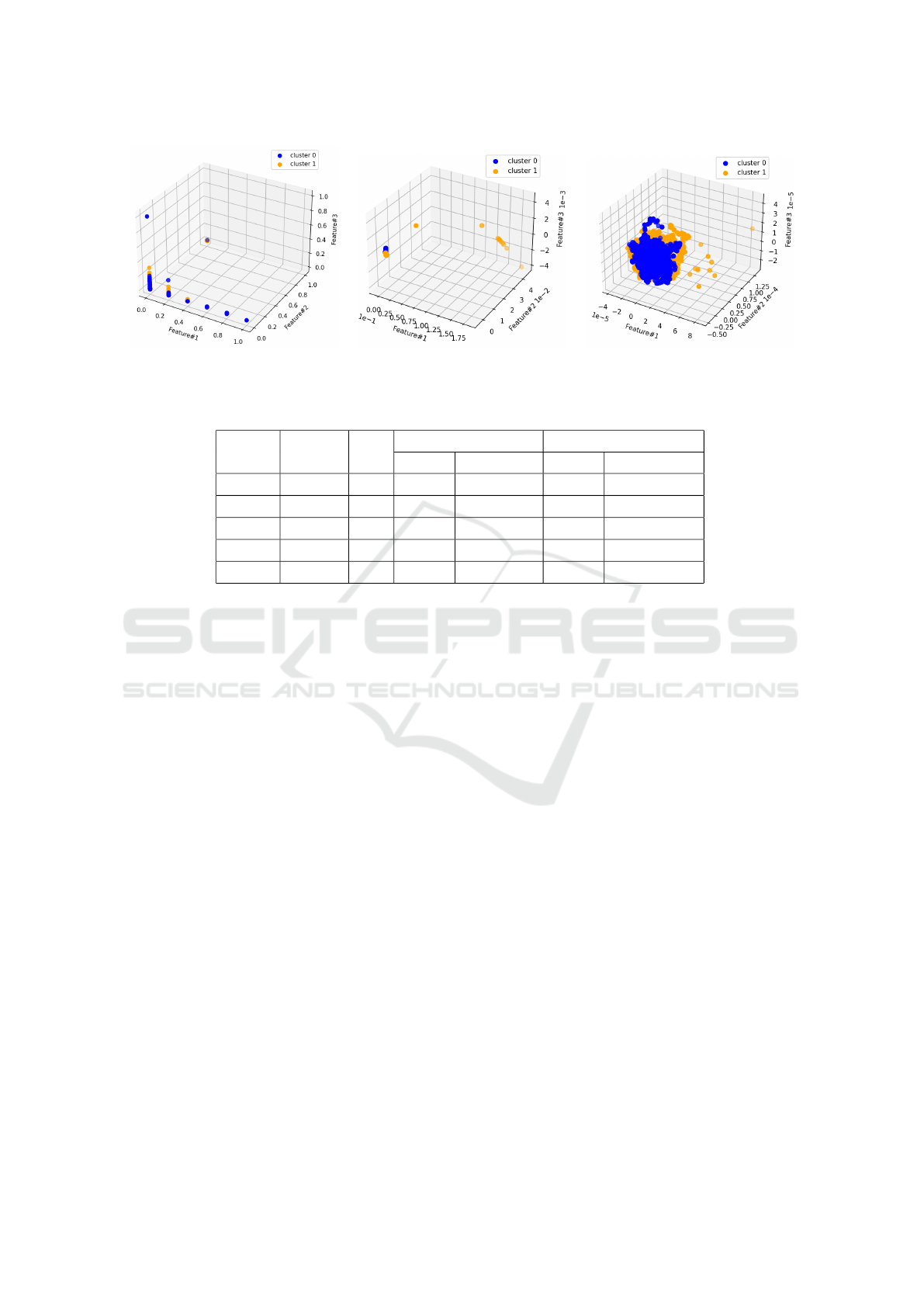
(a) Initial Chunk. (b) Reduced Chunk. (c) Ensemble Chunk.
Figure 1: First Chunk: Comparison of Initial and Transformed Chunks.
Table 3: Clustering Performances of Remaining Chunks.
Chunk TEVR PCs
Initial Ensemble
DB VRC DB VRC
#2 99.8900 100 0.7446 17,361.61 0.5424 24,166.550
#3 99.9998 117 0.4546 1,499.436 0.0851 447,828.401
#4 99.9992 76 0.5948 22,167.308 0.0807 882,006.425
#5 99.9000 100 5.6940 1,110.825 0.6086 14,621.410
#6 99.9100 120 3.256 388.953 0.6528 6,654.930
Next, in Table 4, we also compare the clustering
performances of the reduced and ensemble chunks for
the remaining weeks of data. We notice that the clus-
ter quality has improved significantly for the ensem-
ble chunks in most cases, particularly for chunks#3,
#4, and #5. Also, chunk#6 outperforms for VRC
using the ensemble-based dimensionality reduction.
However, ensemble chunk#2 under-performs for both
metrics compared to the reduced chunk#2. The differ-
ences between reduced and ensemble chunks are the
following:
• For chunk#3, #4, and #5, the ensemble-based
chunks outperform with a huge gap in terms of
VRC, whereas, DB outperform with a small gap.
• For chunk#6, only one metric outperforms. VRC
increased with a medium gap for chunk#6 com-
pared to the reduced chunk.
• The ensemble-based dimensionality reduction
under-performs for chunk#2 compared to the re-
duced chunk#2, but with a small and medium gaps
for DB and VRC, respectively.
5.4 Data Labeling
Table 5 presents the number of instances for the two
clusters for the initial and ensemble chunks. As an ex-
ample, regarding chunk#1, out of 9099 instances, we
have 4315 and 4784 instances for clusters 0 and 1, re-
spectively. On the other hand, we have 3733 and 5366
instances for clusters 0 and 1, respectively, for the
ensemble-based initial chunk. Since the ensemble-
based dimensionality reduction approach provided
superior clustering performances for most chunks, we
intend to use its cluster labels as the data labels for all
the chunks.
We also show the mismatch between initial and
ensemble clusters in Table 5. For instance, for chunk
#1, we have 1164 instances from the ensemble chunk
that do not belong to the same cluster as the initial
chunk. We attain the highest mismatch of 1530 in-
stances for chunk #5. For chunk#4, both initial and
ensemble chunks have exact instances for the two
clusters. Moreover, the class distribution is moder-
ately balanced for all the chunks using the ensemble-
based dimensionality reduction method. The highest
imbalance ratio is ≈ 1:3 for chunk #3.
In the future, we will pass only the mismatched
instances of chunk#1 to the human experts to ana-
lyze them and provide us with the ground truth. The
first chunk will be used to build the initial classifica-
tion model for service monitoring. Based on an incre-
mental learning approach introduced in (Anowar and
Sadaoui, 2021), we will develop the decision model
gradually using the chunks’ labels.
DeLTA 2022 - 3rd International Conference on Deep Learning Theory and Applications
122
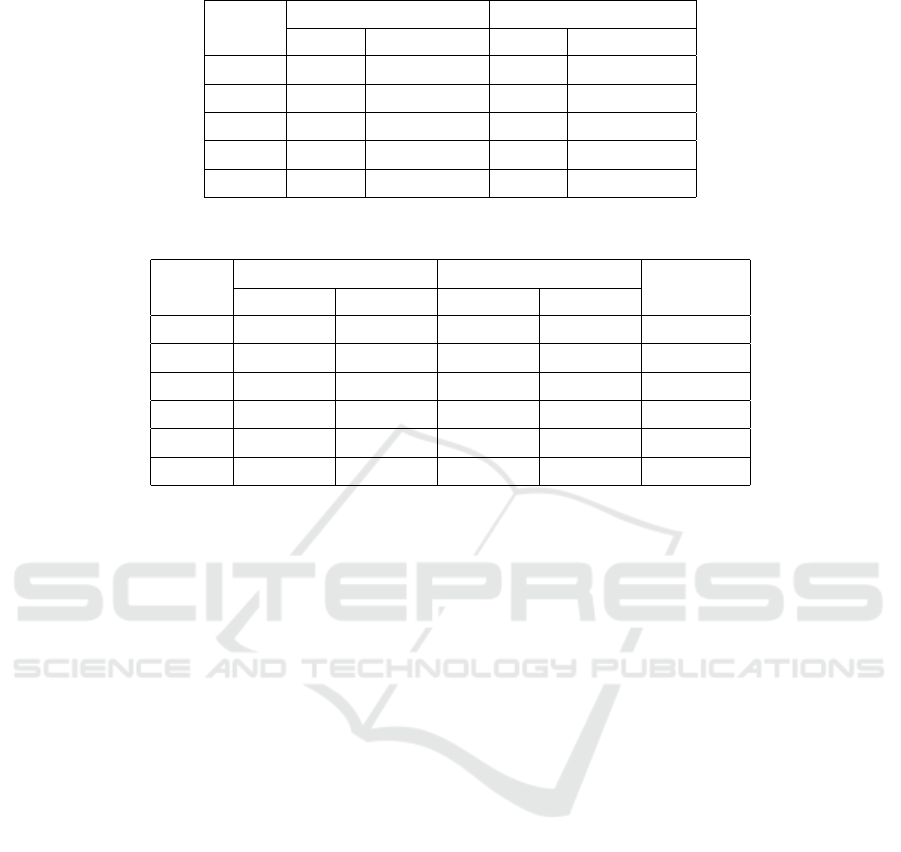
Table 4: Clustering Performances of Reduced and Ensemble Chunks.
Chunk
Reduced Ensemble
DB VRC DB VRC
#2 0.5147 25,727.25 0.5424 24,166.550
#3 0.0906 395,121.06 0.0851 447,828.401
#4 0.0808 881,211.368 0.0807 882,006.425
#5 0.6126 14,294.565 0.6086 14,621.410
#6 0.6420 6,631.924 0.6528 6,654.930
Table 5: Instances in Each Cluster for Each Weekly Chunk.
Chunk
Initial Ensemble
Mismatch
Cluster 0 Cluster 1 Cluster 0 Cluster 1
#1 4315 4784 3733 5366 1164
#2 4144 5936 4310 5770 332
#3 2299 7781 2313 7767 28
#4 4525 5555 4525 5555 0
#5 4791 5289 5556 4524 1530
#6 2702 1832 2306 2228 792
6 CONCLUSIONS AND FUTURE
WORKS
Service monitoring is vital because it allows users
to make proactive decisions when problems arise by
fixing issues and reducing server downtime. The
proposed framework addressed the problems of real-
world data: unlabeled, non-linear and high dimen-
sional time-series data. Nevertheless, service mon-
itoring applications generate time-series data with a
soaring feature space. For this purpose, we devised an
ensemble-based dimensionality reduction approach
based on 1) self-supervised learning to better data
quality, 2) unsupervised dimensionality reduction to
reduce the high data dimensionality, and 3) incremen-
tal dimensionality reduction to improve data labeling.
While implementing this ensemble approach, we
also verified that a minimal amount of information
was lost throughout the reduction process of the fea-
ture space. We further utilized a time-series data clus-
tering method to assess and compare the quality of
the initial, reduced, and ensemble chunks. The ex-
perimental results showed that higher-quality clusters
(maximum intra-cluster and minimum inter-cluster
distances) had been attained using the ensemble ap-
proach. These high-performing clusters and cluster
labels will be utilized for subsequent decision-making
tasks for the industrial partner.
This current work leads to other research direc-
tions for the same industrial application, as follows:
• Based on the data labels obtained in this study,
we will devise an adaptive ensemble learning ap-
proach to update gradually the service monitoring
classifier with incoming chunks.
• We are also interested in incorporating the
clustering-based outlier detection methods within
the ensemble-based dimensionality reduction ap-
proach to remove outliers from the data.
ACKNOWLEDGEMENTS
We want to express our gratitude to Global AI Ac-
celerator (GAIA) Ericsson, Montreal for collaborat-
ing with us on this research work, the Observability
team for allowing us to access the data, and Fredrik
Hallgren, University College London, UK, for provid-
ing us with the partial implementation of Incremental
KPCA.
REFERENCES
Almotiri, J., Elleithy, K., and Elleithy, A. (2017). Com-
parison of autoencoder and principal component anal-
ysis followed by neural network for e-learning us-
ing handwritten recognition. In 2017 IEEE Long Is-
An Ensemble-based Dimensionality Reduction for Service Monitoring Time-series
123

land Systems, Applications and Technology Confer-
ence (LISAT), pages 1–5. IEEE.
Anowar, F. and Sadaoui, S. (2021). Incremental learn-
ing framework for real-world fraud detection environ-
ment. Computational Intelligence, 37(1):635–656.
Anowar, F., Sadaoui, S., and Dalal, H. (2022). Cluster-
ing quality of a high-dimensional service monitoring
time-series dataset. In 14th International Conference
on Agents and Artificial Intelligence (ICAART), pages
1–11.
Anowar, F., Sadaoui, S., and Selim, B. (2021). Conceptual
and empirical comparison of dimensionality reduction
algorithms (pca, kpca, lda, mds, svd, lle, isomap, le,
ica, t-sne). Computer Science Review, 40:1–13.
Chin, T.-J. and Suter, D. (2007). Incremental kernel princi-
pal component analysis. IEEE transactions on image
processing, 16(6):1662–1674.
Fan, Z., Wang, J., Xu, B., and Tang, P. (2014). An
efficient kpca algorithm based on feature correla-
tion evaluation. Neural Computing and Applications,
24(7):1795–1806.
Goel, A. and Vishwakarma, V. P. (2016). Gender classifica-
tion using kpca and svm. In 2016 IEEE International
Conference on Recent Trends in Electronics, Informa-
tion & Communication Technology (RTEICT), pages
291–295. IEEE.
Hallgren, F. and Northrop, P. (2018). Incremental ker-
nel pca and the nystrom method. arXiv preprint
arXiv:1802.00043, pages 1–9.
Hawkins, D. M. (2004). The problem of overfitting. Jour-
nal of chemical information and computer sciences,
44(1):1–12.
Hoffmann, H. (2007). Kernel pca for novelty detection. Pat-
tern recognition, 40(3):863–874.
Jindal, P. and Kumar, D. (2017). A review on dimension-
ality reduction techniques. International journal of
computer applications, 173(2):42–46.
Joseph, A. A., Tokumoto, T., and Ozawa, S. (2016). Online
feature extraction based on accelerated kernel princi-
pal component analysis for data stream. Evolving Sys-
tems, 7(1):15–27.
Kim, K. I., Franz, M. O., and Scholkopf, B. (2005). Iter-
ative kernel principal component analysis for image
modeling. IEEE transactions on pattern analysis and
machine intelligence, 27(9):1351–1366.
Kumar, A. (2020). Pca explained variance concepts with
python example. https://vitalflux.com/pca-explained-
variance-concept-python-example/. Last accessed 12
March 2022.
Lawton, G. (2020). Autoencoders’ example
uses augment data for machine learning.
https://searchenterpriseai.techtarget.com/feature
/Autoencoders-example-uses-augment-data-for-
machine-learning. Last accessed 12 March 2022.
Lim, J., Ross, D. A., Lin, R.-S., and Yang, M.-H. (2004).
Incremental learning for visual tracking. In Advances
in neural information processing systems, pages 793–
800. Citeseer.
Losing, V., Hammer, B., and Wersing, H. (2018). Incre-
mental on-line learning: A review and comparison of
state of the art algorithms. Neurocomputing, Elsevier,
275(1):1261–1274.
Oja, E. (1992). Principal components, minor compo-
nents, and linear neural networks. Neural networks,
5(6):927–935.
Paparrizos, J. and Gravano, L. (2015). k-shape: Efficient
and accurate clustering of time series. In The 2015
ACM SIGMOD International Conference on Manage-
ment of Data, pages 1855–1870.
Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V.,
Thirion, B., Grisel, O., Blondel, M., Prettenhofer,
P., Weiss, R., Dubourg, V., Vanderplas, J., Passos,
A., Cournapeau, D., Brucher, M., Perrot, M., and
Duchesnay, E. (2011). Scikit-learn: Machine learning
in Python. Journal of Machine Learning Research,
12:2825–2830.
Sanger, T. D. (1989). Optimal unsupervised learning in a
single-layer linear feedforward neural network. Neu-
ral networks, 2(6):459–473.
Spruyt, V. (2014). The curse of dimensionality in classifi-
cation. Computer vision for dummies, 21(3):35–40.
Takeuchi, Y., Ozawa, S., and Abe, S. (2007). An efficient
incremental kernel principal component analysis for
online feature selection. In 2007 International Joint
Conference on Neural Networks, pages 2346–2351.
IEEE.
Tokumoto, T. and Ozawa, S. (2011). A fast incremental ker-
nel principal component analysis for learning stream
of data chunks. In The 2011 International Joint Con-
ference on Neural Networks, pages 2881–2888. IEEE.
Van Der Maaten, L., Postma, E., and Van den Herik, J.
(2009). Dimensionality reduction: A comparative re-
view. J Mach Learn Res, 10(66-71):13.
Verleysen, M. and Franc¸ois, D. (2005). The curse of dimen-
sionality in data mining and time series prediction.
In International work-conference on artificial neural
networks, pages 758–770. Springer.
Wang, Y., Yao, H., and Zhao, S. (2016). Auto-encoder
based dimensionality reduction. Neurocomputing,
184:232–242.
Zhang, Y. and Li, D. (2013). Cluster analysis by vari-
ance ratio criterion and firefly algorithm. International
Journal of Digital Content Technology and its Appli-
cations, 7(3):689–697.
DeLTA 2022 - 3rd International Conference on Deep Learning Theory and Applications
124
