Comparison of Different Excitation Strategies for Fault Diagnosis of Belt

Drives: Industrial Application Scenarios

Moritz Fehsenfeld

1 a

, Johannes K

uhn

, Zygimantas Ziaukas

1 b

and Hans-Georg Jacob

1 c

Leibniz University Hannover, Institute of Mechatronic Systems, An der Universit

at 1, Garbsen, Germany

Lenze SE, Hameln, Germany

Keywords:

Fault Diagnosis, Machine Learning, Industrial Application, Belt Drives, Mechatronics Systems.

Abstract:

Machine learning (ML) has received a lot of attention in solving fault diagnosis (FD) tasks. As a result, more

and more advanced machine learning algorithms have been developed to increase accuracy. But the system’s

excitation has likewise a high impact on the diagnosis performance and applicability. For this purpose, we

describe different industrial application scenarios and the related set trajectory. They are divided into passive

FD, where normal operation data serves as the input, and active FD, where an optimized excitation is injected.

All scenarios are investigated concerning achievable accuracy and data requirement based on comprehensive

measurements. We demonstrate that in active scenarios a high accuracy of 97.6% combined with a small

number of measurements are obtained by very basic algorithms like a one-nearest neighbor with Euclidean

distance. In passive scenarios, where the FD task is generally harder, the demand for large datasets and more

advanced ML methods increases. In this way, we illustrate how intelligent use of an optimized excitation

strategy leads to feasible, reliable, and accurate fault diagnosis with a broad industrial application spectrum.

1 INTRODUCTION

Fault diagnosis (FD) has seen increasing attention in

the last years. It has the potential to recognize faults

at an early stage and guarantee optimal operation con-

ditions. By this, downtime is decreased, maintenance

costs are reduced and safe operation is ensured. Fol-

lowing this trend, many FD applications of compo-

nents in electromechanical motion systems have been

published in the past. Besides the motor as a major fo-

cus (Kande et al., 2017) other drive elements such as

bearings (AlShorman et al., 2020) and gears (Sharma

and Parey, 2016) are likewise subject to FD.

Belts are a popular drive solution with a wide va-

riety of applications. A proper belt pretension is in-

evitable to operate with high efﬁciency and low wear.

It is adjusted while commissioning but decreases dur-

ing operation due to changing environments and wear.

For that reason, continuous pretension monitoring en-

sures optimal working conditions. Nevertheless, FD

applications targeting belt drives are rare. (Kang

et al., 2018) predict belt cracks and (Hu et al., 2016)

https://orcid.org/0000-0003-2639-7838

https://orcid.org/0000-0001-9161-0709

https://orcid.org/0000-0001-5605-9704

monitor belt oscillations. The majority of tension

monitoring applications utilize external sensors like

strain gauges (Musselman and Djurdjanovic, 2012;

Bzinkowski et al., 2022) or optical lasers (Khazaee

et al., 2017). These additional sensors are often un-

desired in practice given their extra costs and com-

missioning effort. (Picot et al., 2017) analyze motor

current which does not necessitate extra equipment to

discriminate four tension levels. Consequently, our

proposed FD system to detect a faulty belt tension re-

lies only on standard sensors.

Many contributions in the ﬁeld of FD focus on the

diagnosis methods. Recently, machine learning (ML)

has attracted great attention. Procedures are catego-

rized into conventional ML and deep learning (DL)

approaches. Conventional ML follows a two-stage

procedure. During feature engineering different sig-

nal processing techniques are applied to facilitate di-

agnosis. These features are handed over to a conven-

tional classiﬁcation method such as a support vector

machine (Gangsar and Tiwari, 2017) or random for-

est (Toma et al., 2020). Meaningful features are cru-

cial for successful FD, however, require high domain

knowledge. DL approaches omit extensive feature ex-

traction but follow an end-to-end approach where fea-

Fehsenfeld, M., Kühn, J., Ziaukas, Z. and Jacob, H.

Comparison of Different Excitation Strategies for Fault Diagnosis of Belt Drives: Industrial Application Scenarios.

DOI: 10.5220/0011274100003271

In Proceedings of the 19th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2022), pages 177-184

ISBN: 978-989-758-585-2; ISSN: 2184-2809

177

tures are learned during training. An outline is pro-

vided by (Thoppil et al., 2021).

Besides the choice of algorithm, the input data

is even more important. A high information content

about the considered task within the data is a basic

prerequisite for successful FD. The selection of ap-

propriate sensors has already been addressed. Mo-

tor current signature analysis (MCSA) and vibrational

analysis are popular among other FD approaches for

electrical drives. An overview of techniques is given

by (Nandi et al., 2005). The restriction to standard

sensor technology does not leave much choice. In

this context, the motor’s motion during diagnosis has

not been considered yet. Generally, passive and ac-

tive FD is distinguished with respect to the set mo-

tion. Passive FD takes normal operation data as input.

The disadvantage is that potential faults can not be

properly diagnosed because the information content is

low. One reason is that high excitations are undesired

during operation. Active FD overcomes this prob-

lem by injecting an additional excitation designed to

maximize diagnosability. It is reported that active FD

yields signiﬁcantly better performance while it has the

drawback of interfering with the system (Heirung and

Mesbah, 2019). Nevertheless, real-world applications

are rare. Therefore, this work provides an extensive

overview of application scenarios for FD systems.

Our main contributions are: (1) We describe four

typical fault diagnosis scenarios of electromechanical

motion systems without external sensors. (2) We em-

phasize the importance of the set trajectory selection

regarding achievable accuracy and data requirements

for three commonly applied FD algorithms. (3) We

carry out a comprehensive investigation in all scenar-

ios based on measurement data using the example of

belt drives.

The remainder of this work is structured as fol-

lows: Section 2 gives an overview of three common

machine learning algorithms used for fault diagnosis.

Section 3 introduces the belt pretension monitoring

as an example of FD commonly encountered in the

automation industry. Different real-world application

scenarios are described and the testbed used for gath-

ering measurement data is presented. All scenarios

are assessed on extensive datasets in section 4. Con-

clusions and further research directions are given in

section 5.

2 FAULT DIAGNOSIS

ALGORITHMS

ML-based FD is achieved by supervised classiﬁca-

tion of available sensor data x = (x

,. ..,x

) into

healthy and faulty classes y. For this task, a lot of al-

gorithms are proposed in the ﬁeld of time series clas-

siﬁcation (TSC). We select three methods for bench-

marking the classiﬁcation accuracy in different ap-

plication scenarios. te attempt was made to cover a

broad range of algorithms from basic to advanced.

This section gives insights into all methods.

2.1 One-nearest Neighbor with Distance

Measure

The one-nearest neighbor (1-NN) with a distance

measure is considered a simple baseline approach

which is hard to beat by more advanced methods

(Bagnall et al., 2016). It classiﬁes the data without

transformation. All data are simply stored and a dis-

tance measure assesses the similarity of a new se-

quence to all training samples. The closest sample’s

label is used as prediction following a one-nearest

neighbor approach. Dynamic time warping (DTW)

is an elastic distance measure that accounts for time

shifts and has proven to be suitable for the classiﬁca-

tion of sequential data. Further details can be taken

from (Bagnall et al., 2016). In this work, input data

stems from time and frequency domain. If no data

shift occurs, a simple Euclidean distance (ED) is like-

wise sufﬁcient. A shift can be avoided e.g. in the fre-

quency domain or by restricting the input data. For

the sake of simplicity, we choose 1-NN ED as the

baseline algorithm.

2.2 Statistical Features

Conventional classiﬁcation algorithms are not suit-

able for raw time series data. Therefore, features are

extracted in the ﬁrst step. Feature engineering aims to

ﬁnd features that are as informative as possible with

regard to the target variable. This step is crucial for

high accuracy. Statistical features that summarize cer-

tain characteristics of the underlying time series are

a frequently chosen possibility (Fulcher and Jones,

2014). A collection of common statistical features ap-

plied in this work is given in Table 1. The advantage

of simple feature functions such as mean F

, maxi-

mum F

minimum F

, or energy F

is a decent level

of interpretability. The classiﬁer’s decision is thereby

comprehensible promoting the general acceptance of

machine learning in the industry.

A random forest classiﬁer has proven to be effec-

tive in combination with statistical features (Fehsen-

feld et al., 2020). It consists of multiple Classiﬁcation

and Regression Trees (CART) described by (Breiman,

2001). Decision trees are trained from the root to mul-

tiple leaves connected by nodes. At each node, the

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

178

Table 1: Overview of feature functions F

. In the time do-

main the sequence consist of a value x

and a related time t

at each step ∀i ∈ {1, ..., L}. Transformed by FFT into fre-

quency domain the sequence comprises of an amplitude a

and a related frequency f

for ∀i ∈ {1,. .., K}.

Time domain Frequency domain

∑

i=1

∑

i=1

∑

i=1

− F

)

∑

i=1

− F

)

∑

i=1

−F

)

L·F

∑

i=1

−F

)

k·F

∑

i=1

−F

)

L·F

∑

i=1

−F

)

K·F

= min(x) F

∑

i=1

= max(x) F

∑

i=1

· f

∑

i=1

∑

i=1



∑

i=1



feature space is further split until regions exist where

classiﬁcation can be done. (Breiman, 2001) gives de-

tailed information about the method. This approach is

further referred to as SF+RF.

2.3 Minirocket

Minirocket (MINImally RandOm Convolutional

KErnel Transform) proposed by (Dempster et al.,

2021) is a fast classiﬁcation algorithm which achieves

state-of-the-art performance on a wide variety of TSC

problems in the UCR time series classiﬁcation archive

(Dau et al., 2018). The time series is transformed by a

large (by default n

= 10000) number of random con-

volutional kernels. The feature space K = (k

,. ..k

)

is obtained by calculating the proportion of positive

values for each kernel transformation. Details on the

kernels are reported in (Dempster et al., 2021). A lin-

ear ridge regression classiﬁer is used as recommended

by the authors. For this purpose, the linear regression

ˆy = β

+ β

+ ... + β

(1)

is utilized, where ˆy is the predicted target variable.

The coefﬁcients β

are estimated based on available

target variables y

β = min

obs

∑

i=1



− β

−

∑

j=1

i, j



+ λ

∑

j=1

, (2)

where the ﬁrst term is the residual sum of squares and

the second term is a shrinkage penalty forcing β

be close to zero. λ is the tuning parameter trading off

the two terms. (James et al., 2014)

belt

roller

powered pulley

servo motor

(belt tension)

Figure 1: Belt drive used for evaluation of different appli-

cation scenarios of belt pretension fault diagnosis.

3 FAULT DIAGNOSIS OF BELT

DRIVES

Electromechanical motion systems are applied in

many industrial ﬁelds. High reliability and efﬁciency

of all components involved are vital for safe and ef-

ﬁcient operation. Toothed belts are popular drive el-

ements because they combine the capability of high

acceleration, smooth running characteristics, and high

precision for point-to-point motions (Perneder and

Osborne, 2012). Diagnosing a belt drive’s pretension

serves as an FD example to introduce real-world ap-

plication scenarios. At this point, it is highlighted that

the selection of input data is not restricted to this case

but should be considered for every FD system.

The validation of all scenarios is based on mea-

surement data. Therefore, the experimental setup is

introduced ﬁrst. After that, we demonstrate how to

realize active and passive FD in this example.

3.1 Experimental Setup

A belt drive with adjustable pretension is used to

gather measurement data. It is depicted in Figure

1. There are four pulleys connected by a toothed

belt with AT-5 proﬁle and a total length of l = 2 m.

The upper pulley is powered by a servomotor with

a rated torque of M

= 1.2 Nm and a rated power of

= 1.2kW. The servomotor is equipped with stan-

dard sensors that are available in real-world applica-

tions:

• position ϕ

act

(and derivatives

act

• torque M

act

• temperature ϑ.

Comparison of Different Excitation Strategies for Fault Diagnosis of Belt Drives: Industrial Application Scenarios

179

Consequently, broad applicability is ensured by in-

volving only standard sensors.

Another servo motor adjusts the belt tension that

moves a roller attached to a linear axis. The servo-

motor’s position correlates with the belt pretension.

A characteristic curve between the servomotor’s po-

sition and the belt tension force F

belt

is created which

is only used to label the measurement data and not

for prediction. The pretension force ranges from

belt,min

= 40 N to F

belt,max

= 200 N. Afterwards, it

is discretized into n

= 5 equally-spaced classes.

3.2 Application Scenarios

The diagnosis solely relies on the input data gathered

from the machine regardless of the downstream algo-

rithm. Obviously, the input data has a high impact on

the diagnosis performance. In many real-world appli-

cations, there is a certain amount of freedom in de-

signing the FD system which will be carved out in the

section below. Set trajectories for passive and active

scenarios are deﬁned and measurements are gathered.

Random samples of each class are shown in Figure 2

and discussed below.

3.2.1 Passive Fault Diagnosis

Passive FD takes only normal operation data as in-

put to the algorithm. During normal operation, the

servo motor fulﬁlls speciﬁc tasks by following point-

to-point motions. Jerk-limited trajectories (JLT) are

the industrial standard for this purpose. The trajec-

tory between the start ϕ

start

and end position ϕ

end

designed in advance during path planning. Matching

set position ϕ

set

(t) and set velocity

set

(t) are calcu-

lated. A rectangular-shaped and thereby limited set

jerk

...

set

(t) and the associated trapezoidal set acceler-

ation is characteristic for JLT. The shape is deﬁned by

the maximum values of jerk

...

max

, acceleration

max

velocity

max

and the distance d = ϕ

end

− ϕ

start

. The

outcome is a smooth trajectory between ϕ

start

and x

end

hereby limiting the excitation of oscillations initiated

by the set trajectory.

In the case of passive FD, it is inevitable to analyze

JLT whether a fault has occurred. Two scenarios have

been chosen which are feasible in practice.

Random Test Trajectory. During operation a large

variety of JLT can be the result to fulﬁll the designated

tasks. Therefore, all kind of JLT must be analyzed

to be capable of fault diagnosis at any time. In this

scenario, a dataset is created where all characteristic

JLT parameters are chosen randomly and uniformly

distributed as follows:

d ∼ U(100 deg,2000 deg),

max

∼ U(1000deg /s,7000 deg/s),

max

∼ U(1000deg /s

,6000 deg/s

...

max

∼ U(6000deg /s

,60 000 deg/s

). (3)

Consequently, the input data of the FD algorithm has

a high variety. Random sections of the trajectories

are selected to cut all samples to equal length. In this

manner, a sliding window with ﬁxed size of t

win

= 1s

is imitated. Examples are shown in Figure 2a. All set

trajectories differ making it hard to recognize patterns

between the classes with the naked eye.

Fixed Test Trajectory. During operation, a motion

can occur regularly when accomplishing a repeating

task e.g. moving a lifting station from the ground to

the ﬁrst level. By choosing a certain JLT the vari-

ety of the input data is eliminated. The characteris-

tic pattern of the FD target is now potentially better

visible because the input variety signiﬁcantly drops.

The drawback is that potential faults can only be de-

tected during this typical motion. In the case of faulty

belt tension, this drawback seems acceptable since the

pretension reduces gradually due to wear. But a sud-

den loss remains possibly undetected.

There are many potential trajectories for this sce-

nario. Two JLT are compared to evaluate the impor-

tance of trajectory selection. Trajectory T

is chosen

to be comparatively fast, while trajectory T

has re-

duced velocity. The parameters are chosen as follows:

= 700deg,

max,1

= 7000deg /s,

max,1

= 50000 deg/s,

...

max,1

= 200000 deg/s

= 2500deg,

max,2

= 1000deg /s,

max,2

= 50000 deg/s,

...

max,2

= 200000 deg/s

Trajectory T

is visualized in Figure 2b. The set tra-

jectory is the same for all runs which can be seen in

the rotational speed signal. No big differences are vis-

ible between the classes indicating that the controller

is able to follow the set value. The torque acts as the

control variable. Slight deviations between the classes

can be detected. All ﬁndings apply for trajectory T

as well.

3.2.2 Active Fault Diagnosis

In an active FD scenario, input data is not restricted to

JLT but every motion is possible. Therefore, the ﬁrst

task is designing an optimal input sequence leading

to an easy diagnosis of the considered faults. In the

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

180

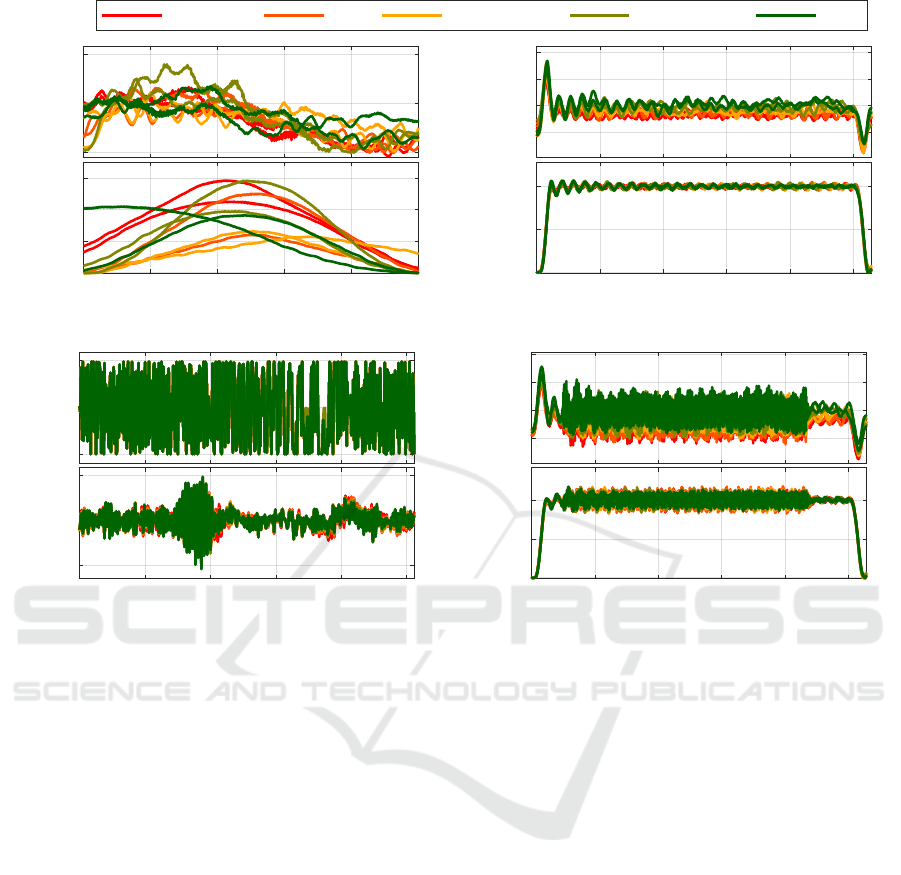
very loose loose slightly loose slightly tight tight

0.2

0.4

act

in Nm

0 0.2 0.4 0.6 0.8

time in s

1000

2000

3000

act

in deg/s

(a) Random test trajectory.

0.2

0.4

0.6

act

in Nm

0 0.5 1 1.5 2 2.5

time in s

500

1000

act

in deg/s

(b) Fixed test trajectory (T

-0.2

0.2

act

in Nm

0 0.1 0.2 0.3 0.4 0.5

time in s

-1

act

in deg/s

0.2

0.4

0.6

act

in Nm

0 0.5 1 1.5 2 2.5

time in s

500

1000

act

in deg/s

(d) Superposition during operation.

Figure 2: The actual torque M

act

and the actual rotational speed

act

are shown for all scenarios in the time domain. Random

observations for each class (n

= 5) are drawn.

case of belt drives, multi-frequency excitations (MFE)

have proven successful (Fehsenfeld et al., 2020). It is

a superposition of n

freq

sine signals

add

(t) = A ·

freq

∑

i=0

sin(2π f

t + φ

), (4)

having different frequencies f

and phases φ

. All

sine signals are phase-shifted to avoid extreme values

making the signal as compact as possible. The each

phase φ

is chosen according to (Schroeder, 1970).

The MFE can further be optimized by adjusting the

amplitude A and the frequency content f

Two different application scenarios are considered

for active FD using an MFE as an auxiliary signal by

adding it as torque offset M

add

. First, the MFE is in-

jected at standstill. In the other scenario, it is applied

during operation.

Optimized MFE at Standstill. In practice, there

might be natural stops of production overnight or dur-

ing waiting periods until the next motion is triggered.

In these situations, the test excitation can easily be

applied. Since the normal operation is not affected,

constraints regarding the auxiliary signal are small.

As long as the servo drive and the mechanics are not

damaged, the impact is irrelevant.

A heuristic tuning of all MFE parameters is car-

ried out in the design stage. The frequency content

is observed to be optimal with n

freq

= 256 frequen-

cies ranging from f

min

= 1.9531 Hz to f

max

= 500 Hz.

The length of the MFE is set to t

max

= 0.512 s ensur-

ing an integral multiple of the period duration of each

frequency to avoid spectral leakage when transform-

ing to frequency domain. The amplitude of all sines

is set to A = 0.015Nm. The optimized MFE is shown

in Figure 2c as torque signal M

act

. There are no dif-

ferences between the belt classes since it is a set sig-

nal. The rotational speed

act

includes the system’s

response. In the time domain, only slight deviations

are visible. A fast Fourier transform (FFT) is applied

to obtain the frequency domain. A small but highly

reproducible shift of characteristic frequencies across

the classes can be observed in Figure 3.

While the possibilities to design an appropriate

auxiliary signal are many, the biggest drawback is

Comparison of Different Excitation Strategies for Fault Diagnosis of Belt Drives: Industrial Application Scenarios

181

very lo os e loose slightly loose

slightly tight tight

0 100 200 300 400

frequency in Hz

-80

-60

-40

-20

amplitude in dB

Figure 3: Frequency domain of rotational speed

act

when

excited by optimized MFE at standstill.

the fact that the operation must be interrupted. If

no pauses in the process are possible or desired, the

auxiliary signal must be injected during operation to

make active FD viable in this case.

Optimized MFE during Operation. If the auxil-

iary signal is injected into a motion it is desirable to

keep its impact at a minimum. Especially the ampli-

tude A has a high effect and must be chosen as small

as possible. This leads to a trade-off between perfor-

mance and disturbance since a higher amplitude nor-

mally leads to better diagnosability. A heuristic tun-

ing is done to balance this trade-off. The frequency

content is found to be optimal with n

freq

= 4 from

min

= 100 Hz to f

max

= 300 Hz. The amplitude is

set to A = 0.02Nm and the total excitation length is

max

= 1.921 s. This MFE superposes the normal op-

eration in the phase of constant velocity. The ﬁxed

trajectory T

is chosen for direct comparison to a pas-

sive scenario. The superposition is visible in both

torque and rotational speed signals in Figure 2d start-

ing at t ≈ 0.2 s. The maximum speed error

set

−

act

is increased by approximately 9 % due to superposi-

tion compared to the original motion. If no task is

performed that requires high path accuracy this seems

acceptable in many real-world applications.

4 EXPERIMENTAL RESULTS

For all scenarios training and test datasets are created.

Both datasets are independently recorded. The train-

ing and test dataset size for the random trajectory sce-

nario is n

obs,1

= 10000, for all other scenarios it is

obs,2

= 1000.

All datasets are used to evaluate two different as-

pects of FD. The ability to reliably recognize faults

is the key factor for successful FD. The classiﬁca-

tion accuracy is hence assessed in the ﬁrst step. Fur-

thermore, a big problem in real-world applications is

that datasets are usually scarce because data gathering

and labeling are associated with large human effort.

The number of required measurements is desirably as

small as possible and therefore additionally investi-

gated. An overview of all results on the test dataset is

given in Table 2 and will be further discussed subse-

quently.

4.1 Achievable Accuracy

The classiﬁcation results of all algorithms introduced

in section 2 can be seen in Table 2. As expected, the

accuracy in active FD scenarios is higher compared

to passive FD scenarios. In both active scenarios, the

accuracy is notably above 90% accomplishing a near-

perfect outcome. In a passive scenario, the accuracy

drops signiﬁcantly. When considering a ﬁxed test tra-

jectory the achievable performance depends on its se-

lection. Trajectory 2 is more suitable for FD than tra-

jectory 1 regardless of the algorithm. In the case of

random trajectories by deﬁnition no selection is nec-

essary. All kinds of trajectories are present whereby

some are better suitable than others. The result is a

maximum accuracy of approximately 90% requiring

a massive amount of measurements.

The comparison of selected FD algorithms yields

expectable results. The state-of-the-art classiﬁer

minirocket outperforms 1-NN ED and SF+RF in all

scenarios. It can be concluded that the ﬁndings in

both active scenarios do not differ much and basic

algorithms perform equally well. In the passive sce-

narios where classiﬁcation is more difﬁcult minirocket

shows its capabilities.

4.2 Data Requirements

The required amount of data is determined by grad-

ually reducing the training dataset size. The results

Table 2: Maximum achievable test accuracy Acc

max

(top)

and minimum dataset size n

min

(below). The belt tension is

discretized into n

= 5 classes.

Scenario 1-NN ED SF + RF Minirocket

MFE

97.6 %

143

98 %

143

99.7%

484

Superposed

traj.

89.8 %

725

95.6 %

310

99.2%

502

Fixed test

traj. 1

74.7 %

660

87.8 %

690

97.4%

930

Fixed test

traj. 2

80.5 %

660

93.8 %

725

99.1%

930

Random

traj.

50.1 %

8860

81.5 %

7860

89.7%

7970

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

182

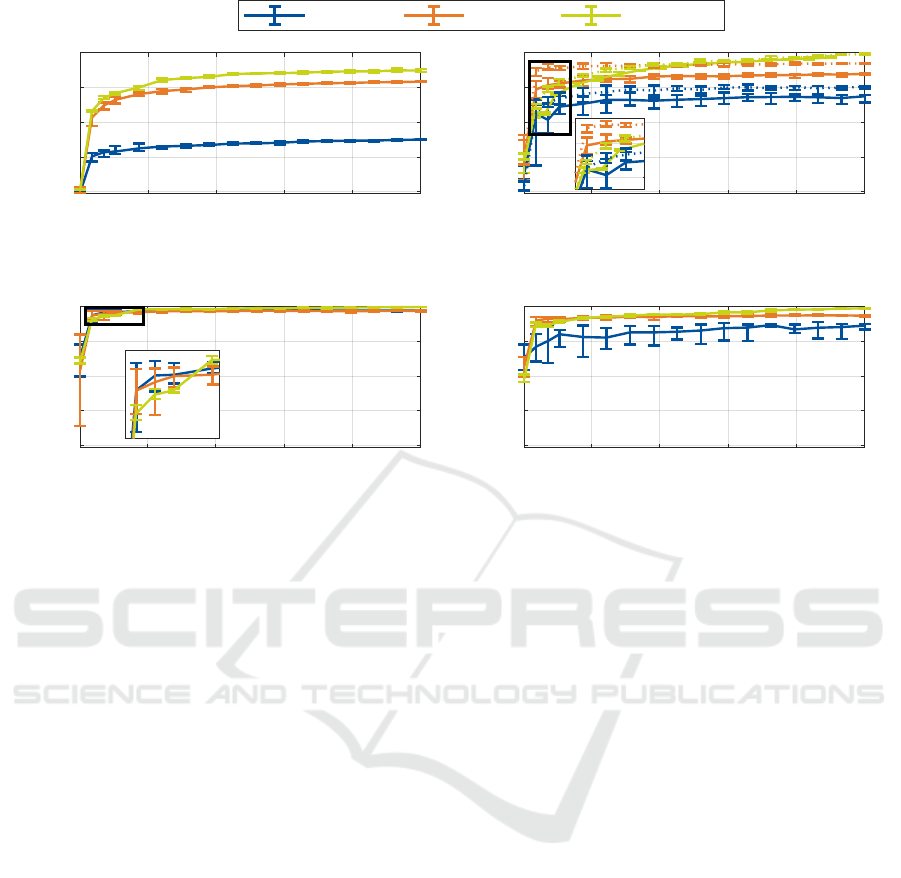
1-NN ED SF + RF minirocket

2000 4000 6000 8000 10000

number of ob servations

100

accuracy in %

(a) Random test trajectory.

200 400 600 800

number of ob servations

100

accuracy in %

(b) Fixed test trajectory. The solid line is trajectory 1

and dashed line is trajectory 2.

200 400 600 800

number of ob servations

100

accuracy in %

200 400 600 800

number of ob servations

100

accuracy in %

(d) Superposition during operation.

Figure 4: Test accuracy over number of training observations in all scenarios and FD algorithms. The training dataset is drawn

ﬁve times independently from all training samples while test dataset is kept constant. Errorbars show the scattering.

for data requirements are depicted in Figure 4. In all

cases, a convergence behavior towards the maximum

achievable test accuracy is observed. It can be con-

cluded that enough data was gathered. The required

dataset size n

min

is calculated as the smallest number

of observations needed to achieve 99 % of maximum

test accuracy in each scenario. The results are added

to Table 2.

Again, active FD scenarios show advantageous

properties. Small datasets are sufﬁcient to reach

a high accuracy regardless of the algorithm. Ba-

sic methods generally require fewer data while

minirocket tends to require more data. It can be no-

ticed in Figure 4c and Figure 4b that SF+RF even out-

performs minirocket on small dataset sizes n

obs

< 200.

The superposition of a JLT has a positive effect com-

pared to the original motion. The data requirement

notably decreases and the accuracy improves in par-

ticular for 1-NN ED, while for SF+RF and minirocket

it is already on a high level.

In passive FD scenarios, the selection of the al-

gorithm is of greater importance as large differences

are observed. 1-NN ED shows worst results followed

by SF+RF, whereas minirocket yields a high accu-

racy for both ﬁxed trajectories. A random trajectory

scenario seems infeasible in practical applications be-

cause of the massive amount of data (n

obs

> 7500)

needed.

5 CONCLUSIONS AND FUTURE

WORK

In this work, different FD application scenarios of

electromechanical drive systems are described and

examined. They are divided into passive scenarios

which rely on jerk-limited trajectories and active sce-

narios where an MFE is injected. We demonstrate

how an additional excitation leads to several advan-

tages: By using an optimized MFE at standstill, even

a very basic algorithm like 1-NN ED achieves a high

accuracy of 97.6% while only n

obs

≈ 143 number

of training samples are required. Furthermore, the

applicability of basic methods promotes secondary

objectives like interpretability. In passive scenarios

classiﬁcation becomes more difﬁcult. The accuracy

drops below 90% in many cases. In this case, the

state-of-the-art classiﬁer minirocket stands out with

high accuracy, but requiring a signiﬁcantly increased

amount of data (n

obs

> 800). A random trajectory

scenario seems practically infeasible due to low ac-

curacy (Acc < 90 %) and massive data requirement

obs

> 7500). As a result, active FD is preferred over

passive FD. The intelligent use of optimized excita-

tions leads to feasible, reliable, and accurate fault di-

agnosis in a broad application spectrum.

Comparison of Different Excitation Strategies for Fault Diagnosis of Belt Drives: Industrial Application Scenarios

183

Active fault diagnosis is lacking practical exam-

ples. The design of appropriate auxiliary signals for a

broad range of FD applications is still open. Further

research in this direction has the potential to enable

safe and economical FD in real-world applications.

ACKNOWLEDGEMENTS

The authors of the Institute of Mechatronic Systems

would like to thank Lenze SE for enabling the coop-

erative project.

REFERENCES

AlShorman, O., Irfan, M., Saad, N., Zhen, D., Haider, N.,

Glowacz, A., and AlShorman, A. (2020). A Review

of Artiﬁcial Intelligence Methods for Condition Mon-

itoring and Fault Diagnosis of Rolling Element Bear-

ings for Induction Motor.

Bagnall, A., Lines, J., Bostrom, A., Large, J., and Keogh,

E. (2016). The great time series classiﬁcation bake

off: a review and experimental evaluation of recent

algorithmic advances. Data Mining and Knowledge

Discovery.

Breiman, L. (2001). Random forests. Machine Learning,

45(1):5–32.

Bzinkowski, D., Ryba, T., Siemiatkowski, Z., and Rucki,

M. (2022). Real-time monitoring of the rubber belt

tension in an industrial conveyor. Reports in Mechan-

ical Engineering, 3(1):1–10.

Dau, H. A., Keogh, E., Kamgar, K., Yeh, C.-C. M., Zhu,

Y., Gharghabi, S., Ratanamahatana, C. A., Yanping,

Hu, B., Begum, N., Bagnall, A., Mueen, A., Batista,

G., and Hexagon-ML (2018). The ucr time series

classiﬁcation archive. URL:https://www.cs.ucr.edu/

∼

eamonn/time series data 2018/.

Dempster, A., Schmidt, D. F., and Webb, G. I. (2021).

MINIROCKET: A Very Fast (Almost) Determinis-

tic Transform for Time Series Classiﬁcation. Pro-

ceedings of the 27th ACM SIGKDD Conference on

Knowledge Discovery & Data Mining, pages 248–

257. arXiv: 2012.08791.

Fehsenfeld, M., K

uhn, J., Wielitzka, M., and Ortmaier,

T. (2020). Tension Monitoring of Toothed Belt

Drives Using Interval-Based Spectral Features. IFAC-

PapersOnLine, 53(2):738–743.

Fulcher, B. D. and Jones, N. S. (2014). Highly comparative

feature-based time-series classiﬁcation. IEEE Trans-

actions in Knowledge and Data Engineering, pages

3026–3037.

Gangsar, P. and Tiwari, R. (2017). Comparative investiga-

tion of vibration and current monitoring for prediction

of mechanical and electrical faults in induction mo-

tor based on multiclass-support vector machine algo-

rithms. Mechanical Systems and Signal Processing,

94:464–481.

Heirung, T. A. N. and Mesbah, A. (2019). Input design

for active fault diagnosis. Annual Reviews in Control,

47:35–50.

Hu, Y., Yan, Y., Wang, L., and Qian, X. (2016). Non-

contact vibration monitoring of power transmission

belts through electrostatic sensing. IEEE Sensors

Journal, 16(10):3541–3550.

James, G., Witten, D., Hastie, T., and Tibshirani, R. (2014).

An Introduction to Statistical Learning: With Applica-

tions in R. Springer, New York, NY, 1 edition.

Kande, M., Isaksson, A., Thottappillil, R., and Taylor, N.

(2017). Rotating electrical machine condition moni-

toring automation—a review. Machines, 5(4):24.

Kang, T., Yang, C., Park, Y., Hyun, D., Lee, S. B., and

Teska, M. (2018). Electrical monitoring of mechanical

defects in induction motor-driven v-belt–pulley speed

reduction couplings. IEEE Transactions on Industry

Applications, 54(3):2255–2264.

Khazaee, M., Banakar, A., Ghobadian, B., Mirsalim, M. A.,

Minaei, S., and Jafari, S. M. (2017). Detection of

inappropriate working conditions for the timing belt

in internal-combustion engines using vibration signals

and data mining. Proceedings of the Institution of Me-

chanical Engineers, Part D: Journal of Automobile

Engineering, 231(3):418–432.

Musselman, M. and Djurdjanovic, D. (2012). Tension mon-

itoring in a belt-driven automated material handling

system. CIRP Journal of Manufacturing Science and

Technology, 5(1):67 – 76.

Nandi, S., Toliyat, H. A., and Li, X. (2005). Condition

monitoring and fault diagnosis of electrical motors—a

review. IEEE Transactions on Energy Conversion,

20(4):719–729.

Perneder, R. and Osborne, I. (2012). Handbook Timing

Belts. Springer Berlin Heidelberg.

Picot, A., Fournier, E., R

egnier, J., TientcheuYamdeu, M.,

Andr

ejak, J., and Maussion, P. (2017). Statistic-

based method to monitor belt transmission looseness

through motor phase currents. IEEE Transactions on

Industrial Informatics, 13(3):1332–1340.

Schroeder, M. (1970). Synthesis of low-peak-factor sig-

nals and binary sequences with low autocorrelation

(corresp.). IEEE Transactions on Information Theory,

16(1):85–89.

Sharma, V. and Parey, A. (2016). A Review of Gear Fault

Diagnosis Using Various Condition Indicators. Pro-

cedia Engineering, 144:253–263.

Thoppil, N. M., Vasu, V., and Rao, C. S. P. (2021). Deep

Learning Algorithms for Machinery Health Prognos-

tics Using Time-Series Data: A Review. Journal of

Vibration Engineering & Technologies.

Toma, R. N., Prosvirin, A. E., and Kim, J.-M. (2020).

Bearing Fault Diagnosis of Induction Motors Using a

Genetic Algorithm and Machine Learning Classiﬁers.

Sensors, 20(7):1884.

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

184