Federated Naive Bayes under Differential Privacy

Thomas Marchioro

1 a

, Lodovico Giaretta

2 b

, Evangelos Markatos

1 c

and

Sar

unas Girdzijauskas

2 d

Institute of Computer Science, Foundation for Research and Technology Hellas, Heraklion, Greece

Division of Software and Computer Systems, KTH Royal Institute of Technology, Stockholm, Sweden

Keywords:

Federated Learning, Naive Bayes, Differential Privacy.

Abstract:

Growing privacy concerns regarding personal data disclosure are contrasting with the constant need of such

information for data-driven applications. To address this issue, the combination of federated learning and

differential privacy is now well-established in the domain of machine learning. These techniques allow to

train deep neural networks without collecting the data and while preventing information leakage. However,

there are many scenarios where simpler and more robust machine learning models are preferable. In this paper,

we present a federated and differentially-private version of the Naive Bayes algorithm for classiﬁcation. Our

results show that, without data collection, the same performance of a centralized solution can be achieved on

any dataset with only a slight increase in the privacy budget. Furthermore, if certain conditions are met, our

federated solution can outperform a centralized approach.

1 INTRODUCTION

The emergence of the Internet of Things and the per-

vasive use of Internet-enabled technologies have fa-

cilitated the process of gathering and collecting data,

from a myriad of sources and with ever-increasing

granularity. This in turn has led to the development

and deployment of a vast array of data-driven tech-

nologies ranging from smart home products to medi-

cal wearable devices (Shafagh et al., 2017).

However, this has sometimes come at the detri-

ment of personal privacy. Many organizations col-

lect sensitive personal information about their users

or customers, and thanks to the high granularity and

broad scope of many data gathering processes, track-

ing individual users across data collections is danger-

ously feasible (Marchioro. et al., 2021). Due in part

to high-proﬁle data misuse incidents and to the ever-

increasing threat of data exﬁltration attacks (Ullah

et al., 2018), many users and regulators have grown

aware of the importance of ensuring a certain degree

of personal privacy in the handling of user data.

In the context of machine learning, this has led

to the growing popularity of Federated Learning

(McMahan et al., 2017), a paradigm in which a group

https://orcid.org/0000-0003-3353-102X

https://orcid.org/0000-0002-0223-8907

https://orcid.org/0000-0003-3563-7733

https://orcid.org/0000-0003-4516-7317

of data owners can train a model on their private data,

without the need to disclose it or gather it into a cen-

tral storage. In each iteration of the process, every

participant computes local updates of the model pa-

rameters, which are sent to a central aggregator and

merged.

While Federated Learning removes the need to di-

rectly share private data, it may still leak sensitive in-

formation to third parties. The most obvious leak is

given by the fact that the central aggregator, by com-

paring the previous model version and the update pro-

vided by a participant, may reconstruct the training

data used by that participant (Zhu et al., 2019). How-

ever, even assuming that the aggregator is trusted, re-

search has shown that it is sometimes possible to re-

construct data used during training just by inspecting

or querying the resulting trained model (Salem et al.,

2018).

A robust approach to prevent these leaks is the use

of Differential Privacy (Ji et al., 2014), a family of

techniques that consists of injecting into the compu-

tation process noise sampled from speciﬁcally-crafted

distributions. Thanks to its strong mathematical guar-

antees, Differential Privacy has become a de-facto

standard in privacy-preserving machine learning.

Most work combining Federated Learning and

Differential Privacy has focused on deep neural net-

works, trained using stochastic gradient descent tech-

niques. However, not all applications require this

170

Marchioro, T., Giaretta, L., Markatos, E. and Girdzijauskas, Š.

Federated Naive Bayes under Differential Privacy.

DOI: 10.5220/0011275300003283

In Proceedings of the 19th International Conference on Secur ity and Cryptography (SECRYPT 2022), pages 170-180

ISBN: 978-989-758-590-6; ISSN: 2184-7711

level of model complexity and capacity. In many

cases, extremely simple but very robust models, such

as Naive Bayes classiﬁers, are preferable (Zhang,

2004).

Therefore, in this paper we develop and evalu-

ate the ﬁrst (to our knowledge) implementation of a

differentially-private Naive Bayes classiﬁer in a fed-

erated setting for horizontally-partitioned data. Con-

trary to typical federated learning, federated Naive

Bayes is trained with a single communication step,

without requiring multiple iterations, thus being fast

and efﬁcient.

Our results show that the federated approach

can reach the same accuracy as a centralized,

differentially-private implementation, but requires a

slightly higher privacy budget (i.e. slightly higher

chance of information leakage). Furthermore, we

show that, when the local sensitivity in each federated

data partition is much lower than the sensitivity of the

whole dataset, our approach outperforms a centralized

one. Thus, overall, switching to a federated solution

to avoid central data collection incurs minimal or no

cost in terms of accuracy or privacy budget.

The contributions of this work are as follows:

• We provide an algorithmic implementation for

Federated Naive Bayes under Differential Pri-

vacy;

• We extensively evaluate how the accuracy of the

model varies under different choices of privacy

budget and data distribution;

• We discuss several potential extensions to our

algorithm, including online parameter updates,

byzantine resilience and full decentralization.

2 BACKGROUND

In this section we introduce the core concept of the

original Naive Bayes algorithm, along with the deﬁ-

nition and some useful properties of differential pri-

vacy, which will serve as a background to understand

the rest of the paper. The symbols used through the

discussion are summarized in Table 1.

Naive Bayes. The Naive Bayes algorithm is used

to train a model for sample classiﬁcation, meaning

that it leverages a training dataset (X,Y ) ∈ X

× Y

to learn a function ˆg : X → Y that maps an exam-

ple x ∈ X to a class y ∈ Y . The classiﬁcation rule is

based on the maximum a posteriori probability crite-

rion (MAP), which chooses the class maximizing the

posterior probability p

Y |X

(y|x). This is computed ac-

Table 1: Notation used in the paper.

ε Privacy budget

n Size of the training set

Number of training examples in class y

f vy

Number of training examples in class y

with categorical feature f equal to v

f y

Mean value of feature f for class y

f y

Second moment of feature f for class y

f y

Variance of feature f for class y

□

(i)

Value □ computed on the i-th partition

□[k] k-th sample of □

N Number of dataset partitions

C Number of classes

cat

Number of categorical features

num

Number of numerical features

cat

Set of categorical features

num

Set of numerical features

cording to the Bayes rule (hence the name):

ˆy = argmax

y∈Y

Y |X

(y|x) = argmax

y∈Y

(x)p

X|Y

(x|y) (1)

where the term p

(x) at the denominator is neglected

as independent from y. A simplifying assumption

made in Naive Bayes is that the features f = 1,. ..,F

are independent, leading to

ˆy = argmax

y∈Y

(y)

∏

f =1

|y) (2)

The prior class probabilities p

and the conditional

probabilities p

for categorical features are esti-

mated from the training data as ratios of counts, i.e.,

(y) =

∑

′

∈Y

′

, p

(v|y) =

f vy

. (3)

For numerical features, the standard method to esti-

mate the conditional distribution is to assume p

be normal with density

|y) =

2πσ

f y

exp

−

− µ

f y

)

2σ

f y

(4)

where

f y

∑

k:y[k]=y

[k]

,σ

f y

∑

k:y[k]=y

[k] − µ

f y

)

(5)

This method of estimating the conditional distribution

is know as Gaussian Naive Bayes.

Differential Privacy. The main idea of differential

privacy is to perturb aggregate queries in order to pre-

vent information leakage. The formal deﬁnition is

that a randomized mechanism q

: D

→ Q provides

Federated Naive Bayes under Differential Privacy

171

ε-differential privacy (ε-DP) if for any pair of adja-

cent datasets D,D

′

(i.e., differing by one single entry)

it holds

Pr[q

(D) ∈ Q] ≤ e

Pr[q

′

) ∈ Q],∀Q ⊆ Q , (6)

meaning that the output distribution of q

should not

differ “too much” by changing a single entry. The

maximum variation allowed in the distribution is de-

termined by the parameter ε, which takes the name of

privacy budget. Intuitively, to a lower ε corresponds

a higher level of privacy. Two useful properties that

are used throughout the discussion are the following

(McSherry, 2009):

• P1: If m independent

-DP queries are computed

on a same dataset D, then any function of these

queries provides ε-DP.

• P2: If ε-DP queries are computed on disjoint sub-

sets of a dataset D

(1)

,. ..,D

(N)

(i)

∩D

( j)

0,i ̸=

j, then any function of these queries provides ε-

DP.

For numerical queries such as count or average,

a well-established method to provide ε-DP is the

Laplace mechanism L

. The Laplace mechanism L

for a query q computed on a dataset D consists in

simply adding Laplace noise to the query with scale

inversely proportional to ε:

(D,q) = q(D) + ξ, ξ ∼ Lap(0,

∆

). (7)

The value ∆

is the maximum variation of the query

between adjacent datasets, also called the sensitivity

of the query. In this paper, we make use of two deﬁ-

nitions of sensitivity:

• The global sensitivity of a query q

∆

= max

D,D

′

|q(D) − q(D

′

)| (8)

which is deﬁned for any possible pair of adjacent

datasets D,D

′

. This implies that the global sensi-

tivity is always the same, regardless of the dataset

on which the query is computed.

• The local sensitivity of a query q for a dataset D

∆

(D) = max

′

|q(D) − q(D

′

)| (9)

which is instead deﬁned for datasets that differ by

one row from D

. The local sensitivity depends

on the dataset on which the query is computed.

In practice, to compute the local sensitivity, we con-

sider the maximum variation obtained by removing one row

from the dataset.

The Laplace mechanism provides ε-DP using both

deﬁnitions of sensitivity. The main difference be-

tween the two is that global sensitivity requires to ap-

ply always the same amount of noise. For example,

counting queries have a global sensitivity of 1, mean-

ing that the required amount of noise is Lap(0,

However, other queries such as sum and mean over

the samples of a dataset depend on the dataset itself,

so it is not possible to compute the global sensitiv-

ity. In such cases, we settle for using local sensitivity,

which leads to different amounts of noise depending

on the dataset.

Sensitivity of the Queries. As we discuss in later

sections, our algorithm makes use of two types of

queries: “count” and “sum”. It is easy to compute the

global sensitivity of a “count” query, since if you re-

move a row from a dataset, the count can change by at

most 1. For sums, instead, we compute the local sen-

sitivity, as per the above discussion. Supposing the

data we are trying to sum is v

(1)

,. ..,v

(N)

, the maxi-

mum variation in the sum is given by max

i=1,...,N

(i)

3 RELATED WORK

Differentially Private Machine Learning. Differ-

ential privacy has become a de facto standard to

compute statistics on sensitive data (Dwork, 2008).

Among its many applications, privacy-preserving ma-

chine learning is probably the most prominent and

studied (Ji et al., 2014). Differentially private SGD is

now a well-established training method (Abadi et al.,

2016) for neural networks, and outside the domain of

deep learning many studies have also explored classi-

cal models such as support vector machines, decision

trees, and Naive Bayes (Lopuha

a-Zwakenberg et al.,

2021). The original algorithm for a differentially pri-

vate Naive Bayes, which we extend in this paper, was

proposed in (Vaidya et al., 2013).

Naive Bayes on Partitioned Data. Albeit simple

in its design, Naive Bayes has proven to be an ef-

fective machine learning algorithm for classiﬁcation,

which is virtually immune to overﬁtting (Rish et al.,

2001; Zhang, 2004). Because of its efﬁcacy and pop-

ularity, a number of efforts have been put into mak-

ing it usable also on personal data. In (Kantarcıoglu

et al., 2003), the authors designed an algorithm to

train Naive Bayes on horizontally partitioned data

(i.e., each node possesses different samples), while

(Vaidya and Clifton, 2004) proposed solution for ver-

tically partitioned data (i.e., each node possesses dif-

ferent features from the same samples). Both solu-

SECRYPT 2022 - 19th International Conference on Security and Cryptography

172

tions, however, rely on cryptographic methods that

protect the data during the training procedure, but do

not provide guarantees that information is not leaked

from the resulting model. Another method to pro-

tect horizontal data partitions during training relies

on semi-trusted mixers (Yi and Zhang, 2009). An al-

gorithm that combines homomorphic encryption and

differential privacy was proposed in (Li et al., 2018).

However, the algorithm estimates conditional proba-

bilities of numerical features using histograms, rather

than with the standard Gaussian Naive Bayes ap-

proach. Furthermore, the paper does not report how

the accuracy is affected by the privacy budget and dis-

tribution of the data among the nodes.

Federated Learning and Differential Privacy.

Federated Learning was proposed in (McMahan et al.,

2017) as general framework for training deep mod-

els using gradient-based optimization techniques on

private data that are massively distributed in horizon-

tal partitions. It consists of an iterative process in

which, at each step, the data-owning devices compute

the gradient of the model on a batch of local data, and

forward it to a central aggregator. This will in turn av-

erage the gradients from all devices, update the model

weights accordingly, and then communicate the new

weights to each device to initiate the next iteration.

While Federated Learning ensures that the training

data never leaves the device of its owning entity, it

does not prevent data leakage from either the trained

model (Salem et al., 2018) or from the gradients that

are shared at each step (Zhu et al., 2019). There-

fore, (Wei et al., 2020) incorporates differential pri-

vacy in each shared gradient to protect the individ-

ual data points in each private partition. On the other

hand, (Geyer et al., 2017) employs differential privacy

within the central aggregator, thus protecting not the

identity of an individual data point, but rather of an

entire data-owning entity participating in the proto-

col.

Most studies of Federated Learning present two key

differences compared to our work. First, Feder-

ated Learning focuses on iterative gradient-based op-

timization of model weights, while Naive Bayes mod-

els are trained in a single step from simple aggre-

gate statistics of the dataset. Second, most works fo-

cus on massively-decentralized Federated Learning,

in which the number of nodes is very large and each

contains little data, typically from a single user (e.g.

next word prediction applications from the typing his-

tory stored on smartphones). On the other hand, few

works, such as (Geyer et al., 2017) and (Bernal et al.,

2021), focus on the scenario where a relatively small

number of entities, each owning datapoints from mul-

tiple individuals, cooperate to train a model.

In (Islam et al., 2022), the authors studied how dif-

ferential privacy affects the accuracy of Naive Bayes,

in a federated setting where data are vertically par-

titioned. The contribution of our work can be con-

sidered complementary, since we consider a federated

setting where data are horizontally partitioned.

4 FEDERATED SETTING

In this work, we consider a federated setting, in which

the dataset is composed of N partitions D

(1)

,. ..,D

(N)

each held by a different entity, i.e., an organization or

an individual. Each entity stores its partition on its

own appliances and is unwilling to share these data

due to privacy concerns. Data points within a parti-

tion may, for example, represent individual users of

a service provided by the organization owning that

partition and may therefore carry sensitive personal

information. The entities wish to take part in the col-

laborative training of a joint predictive model, namely

a Naive Bayes model, as long as the following condi-

tions are satisﬁed:

1. each data partition D

(i)

never leaves the appli-

ances of the owning entity, and

2. it is not possible, from the trained model, to glean

sensitive information about individual data points

within each partition that is not already inferrable

from the rest of the data.

The ﬁrst condition is met by having each entity com-

puting aggregated queries locally on its data partition,

while the second condition is met by applying the ε-

DP Laplace mechanism to the queries before disclos-

ing them. These queries are collected by a central

aggregator and used to estimate the parameters of the

Naive Bayes model. The participating entities are also

referred as of an overlay network that is used to com-

municate with the central aggregator, and they are de-

noted by their data partition (i.e., the i-th node is de-

noted by D

(i)

5 ALGORITHM DESIGN

In order to train a federated Naive Bayes model, the

central aggregator should be able to collect informa-

tion that allows to compute the prior and conditional

probabilities for each feature and class. Indeed, all

the query results must be disclosed after applying the

Laplace mechanism in order to guarantee differential

privacy. The parameter ε

′

of the Laplace mechanism

is decided according to the privacy budget ε and to the

Federated Naive Bayes under Differential Privacy

173

number of queries asked to each node

Mirroring eq. (3), prior probabilities p

(1),. .. , p

(C)

can be simply estimated by collecting from each node

(i)

the number of samples per each class n

(i)

,. ..,n

(i)

and by computing

(y) =

∑

i=1

(i)

∑

i=1

∑

′

(i)

. (10)

Similarly, conditional probabilities for categorical

features are estimated according to

X|Y

(v|y) =

∑

i=1

(i)

f vy

∑

i=1

(i)

(11)

where m

(i)

f vy

is the number of samples with feature

f ∈ F

cat

equal to v for node D

(i)

. For numerical fea-

tures, Gaussian Naive Bayes requires to compute the

parameters µ

f y

,σ

f y

of the assumed normal distribu-

tion of each feature for each class. The mean µ

f y

can

be derived by querying the sample sum

(i)

f y

∑

k:y

[k]=y

(i)

[k] (12)

for feature f ∈ F

num

and class y from each node D

(i)

f y

∑

i=1

(i)

f y

∑

i=1

(i)

. (13)

For the variance σ

f y

, a straightforward solution would

be to calculate it by having each node computing the

sum of squared deviations from the sample average

f y

, i.e.,

∑

k:y

(i)

[k]=y

(i)

[k] − µ

f y

)

. (14)

However, this solution would require two exchanges

between each node and the central aggregator, since

f y

would need to be sent back to the nodes to com-

pute the squared deviations. A solution that enables

the central aggregator to compute means and vari-

ances with a single exchange leverages the relation

between second moment, mean, and variance, i.e.,

= ς − µ

. Therefore, in our algorithm the nodes

are asked to compute the sum of the squared samples

(i)

f y

∑

k:y

[k]=y



(i)

[k]



(15)

and the variance is obtained by the centralized aggre-

gator as

f y

∑

i=1

(i)

f y

∑

i=1

(i)

− µ

f y

. (16)

In principle, each node may have a different privacy

budget, but herein we assume there is a common value of ε

for all the nodes.

Achieving ε-differential Privacy. In order to guar-

antee ε-DP to each node D

(i)

, all queries must be pro-

tected with the Laplace mechanism L

′

. The parame-

ter ε

′

is determined according to properties (P1) and

(P2) described in section 2. Since queries on differ-

ent classes are computed on disjoint subsets of D

(i)

sample cannot belong to multiple classes at the same

time), from a privacy perspective they count as a sin-

gle query. On the other hand, queries on different

features of D

(i)

are counted separately, since they in-

volve the same entries. Therefore each node overall

is asked:

• 1 class counting query, i.e, n

(i)

;

• F

cat

category counting queries, i.e., m

(i)

f vy

, f ∈ F

cat

;

• 2F

num

sum queries on numerical features, i.e.,

(i)

f y

(i)

f y

, f ∈ F

num

Therefore, in order to guarantee a privacy budget

of ε, the parameter ε

′

of the Laplace mechanism to be

applied to each query is given by

′

1 + F

cat

+ 2F

num

, (17)

in congruence with the centralized ε-DP Naive Bayes

(Vaidya et al., 2013). However, in our case the mecha-

nism must be applied locally at each node, and there-

fore the overall noise applied to the parameters will

not follow a Laplace distribution, as will be shown in

section 6.3.

Training Procedure. As mentioned in the discus-

sion above, the training procedure consists of a single

exchange for each node with the central aggregator.

Each node i computes locally the counting and sum

queries on its own partition according to Algorithm 1.

The query results ˜n

(i)

, ˜m

(i)

are sent to the

central aggregator, which collects them across all

nodes and computes the overall parameters of the

model according to Algorithm 2.

The inference of a sample’s class is done according

to the computed parameters as in the original Naive

Bayes (see equation 2).

6 EVALUATION

6.1 Datasets

We test our approach on 6 standard datasets, all taken

from the UCI repository

. The statistics of each

datasets are listed in table 2. For those datasets that

https://archive.ics.uci.edu/ml/datasets.php

SECRYPT 2022 - 19th International Conference on Security and Cryptography

174

Algorithm 1: Local queries computed by i-th node.

Require: Data partition D

(i)

= (X

(i)

), privacy

budget ε

1: for y = 1,. ..,C do

2: ε

′

←

1 + F

cat

+ 2F

num

3: ˜n

(i)

← L

′

(|{k : y

(i)

[k] = y}|)

4: for f ∈ F

cat

5: ˜m

(i)

f vy

← L

′

(|{k : x

(i)

[k] = v ∧ y

(i)

[k] = y}|)

6: end for

7: for f ∈ F

num

(i)

f y

← L

′

(

∑

k:y

(i)

[k]=y

(i)

[k])

(i)

f y

← L

′

(

∑

k:y

(i)

[k]=y

(i)

[k])

)

10: end for

11: end for

12: return ˜n

(i)

, ˜m

(i)

Algorithm 2: Centralized aggregation.

Require: ˜n

(i)

, ˜m

(i)

for i = 1,..., N

1: for y = 1,. ..,C do

2: ˜p

(y) ←

∑

i=1

˜n

(i)

∑

i=1

∑

′

˜n

(i)

3: for f ∈ F

cat

4: ˜p

(v|y) ←

∑

i=1

˜m

(i)

f vy

∑

i=1

˜n

(i)

5: end for

6: for f ∈ F

num

7: ˜µ

f y

←

∑

i=1

(i)

f y

∑

i=1

˜n

(i)

f y

←

∑

i=1

(i)

f y

∑

i=1

˜n

(i)

− ˜µ

f y,ℓ

9: end for

10: end for

11: return ˜p

, ˜p

X|Y

, ˜µ,

do not provide a standardadized train/test split, we

perform a 9:1 split with a random seed that is kept

ﬁxed across the entire work.

6.2 Setup

We implement three variants of Naive Bayes:

1. a “vanilla” Naive Bayes based on eqs. (2) to (5)

that has access to the entire centralized dataset

2. a differentially-private centralized Naive Bayes

based on (Vaidya et al., 2013)

3. our differentially-private federated Naive Bayes

based on the algorithm in section 5.

We test each variant on all datasets through

a Monte Carlo analysis, using logarithmically-

spaced values of ε between 10

−2

and 10

for the

differentially-private variants. For the federated ap-

proach, we test with number of data partitions N ∈

[1,10, 100,1000] whenever possible, skipping the

higher values of N on small datasets, based on the

condition that each partition should include at least 2

data points.

We repeat each experiment 1000 times to account

for the randomness in both the data partitioning across

federated entities and the sampling of Laplace noise.

Unless otherwise stated, we report the mean of those

1000 trials.

All the code and data used in this work are avail-

able on GitHub

6.3 Results

Basic Behaviour. Figure 1 plots the accuracy of the

differentially-private Naive Bayes models as a func-

tion of the privacy budget ε, including both the cen-

tralized approach, and the federated approach with

different choices of N. The score obtained by a

non-differentially-private model is shown as an upper

bound of attainable performance.

On most datasets, the centralized model presents a

typical S-shaped curve, being no better than a random

guess for very small values of ε, but quickly grow-

ing towards the baseline accuracy as the privacy bud-

get increases. The federated model tends to follow

the same curve, but with a “delay” proportional to the

number of partitions. This behaviour is most clear in

the Mushroom and Congressional Voting datasets, al-

though in the former ε = 10

−2

is not sufﬁcient to fully

appreciate the left-hand tail. Due to its large sample

count, Skin Segmentation only shows the right-hand

tail of the S-shape, with the federated models dipping

below the maximum performance only for very small

values of ε. SPECT Heart, on the other hand, shows a

long left-hand tail and peaks at an accuracy only just

above that of a random guess, likely due to the small

size of the training set and the non-independence of

its features.

Impact of Local Sensitivity. Two datasets, how-

ever, show a different behaviour. In Adult, the ex-

pected pecking order is present on the right hand side

of the spectrum, but a reversed order can be seen for

small values of ε, where federated Naive Bayes is

more accurate than the centralized variant and further

https://github.com/thomasmarchioro3/

FederatedNaiveBayesDP

Federated Naive Bayes under Differential Privacy

175

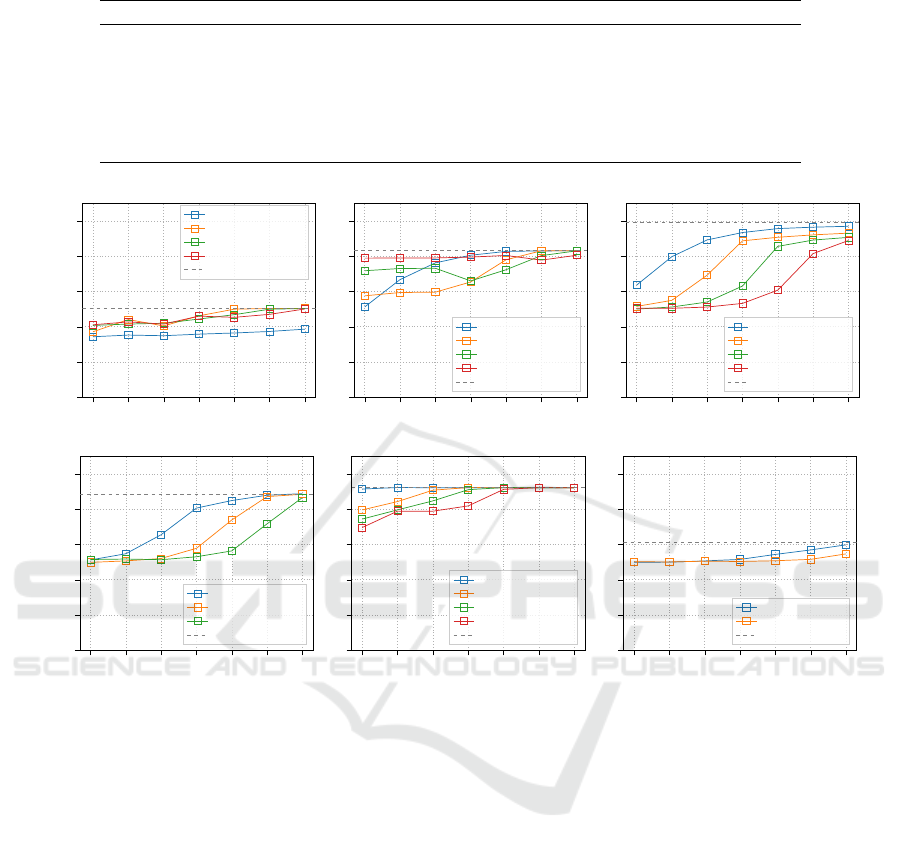
Table 2: Datasets used in the evaluation.

Dataset Samples Labels F

num

cat

Predeﬁned train/test split

Accelerometer 153,000 3 3 0 no

Adult 48,842 2 6 8 yes (2:1)

Congressional Voting 435 2 0 16 no

Mushroom 8,124 2 0 22 no

Skin Segmentation 245,057 2 3 0 no

SPECT Heart 267 2 0 22 yes (3:7)

0.01 0.1 0.03 0.32 1.0 3.16 10.0

0.2

0.4

0.6

0.8

Accuracy

Accelerometer

Centralized

Federated (N = 10)

Federated (N = 100)

Federated (N = 1000)

Non-private

0.01 0.03 0.1 0.32 1.0 3.16 10.0

0.2

0.4

0.6

0.8

Adult

Centralized

Federated (N = 10)

Federated (N = 100)

Federated (N = 1000)

Non-private

0.01 0.03 0.1 0.32 1.0 3.16 10.0

0.2

0.4

0.6

0.8

Mushroom

Centralized

Federated (N = 10)

Federated (N = 100)

Federated (N = 1000)

Non-private

0.01 0.03 0.1 0.32 1.0 3.16 10.0

0.2

0.4

0.6

0.8

Accuracy

Congressional Voting

Centralized

Federated (N = 10)

Federated (N = 100)

Non-private

0.01 0.03 0.1 0.32 1.0 3.16 10.0

0.2

0.4

0.6

0.8

Skin Segmentation

Centralized

Federated (N = 10)

Federated (N = 100)

Federated (N = 1000)

Non-private

0.01 0.03 0.1 0.32 1.0 3.16 10.0

0.2

0.4

0.6

0.8

SPECT Heart

Centralized

Federated (N = 10)

Non-private

Figure 1: Comparison of centralized and federated ε-DP Naive Bayes for different privacy budgets.

improves as the number of participants N increases.

On Accelerometer, the federated variant is always bet-

ter than the centralized one, with N having a negligi-

ble impact.

This is likely caused by a decrease in the sen-

sitivity of the queries in each local partition. With

a centralized approach, the variance of the laplacian

noise is proportional to the sensitivity of the whole

dataset. In addition, a single additive noise contribu-

tion is sampled for each parameter of the model. On

the other hand, in a federated setting, the noise added

by each participant has variance proportional to the

sensitivity of its local partition. This is never bigger

than that of the full dataset and may decrease dramat-

ically as the partition gets smaller. Furthermore, the

ﬁnal estimate of each model parameter is obtained by

summing the contributions – and thus the noises – of

each partition. The sum of many low-variance noise

contributions is likely closer to zero compared to a

single contribution with high variance.

On Adult and Accelerometer, this drop in local

sensitivity is sufﬁcient to reduce the generally higher

noise level of the federated model below that of the

centralized model, thus leading to better results. For

other datasets, such as Skin, the sensitivity does not

decrease much with more partitions. We can see this

difference in ﬁg. 2, which compares the sensitivity of

the sum query

(i)

for all numerical features on Adult

and Skin.

On Adult, the ε range of our experiments per-

fectly captures the threshold at which this effect be-

comes signiﬁcant. On Accelerometer, the ε range

only captures the very left-hand side of the behaviour.

This can be deduced by the fact that the centralized

approach is far from the accuracy ceiling and only

barely starting to improve.

Susceptibility to the Privacy Budget. These re-

sults highlight how the threshold at which the differ-

ential privacy mechanism starts severely affecting ac-

curacy is highly dependent on the dataset and should

be evaluated domain by domain. They also show how

SECRYPT 2022 - 19th International Conference on Security and Cryptography

176

switching to a federated setting, and thus avoiding the

data collection phase, only requires a small increase

to the privacy budget in order to achieve the same ac-

curacy, with the possibility of even surpassing a cen-

tralized solution in certain limited scenarios.

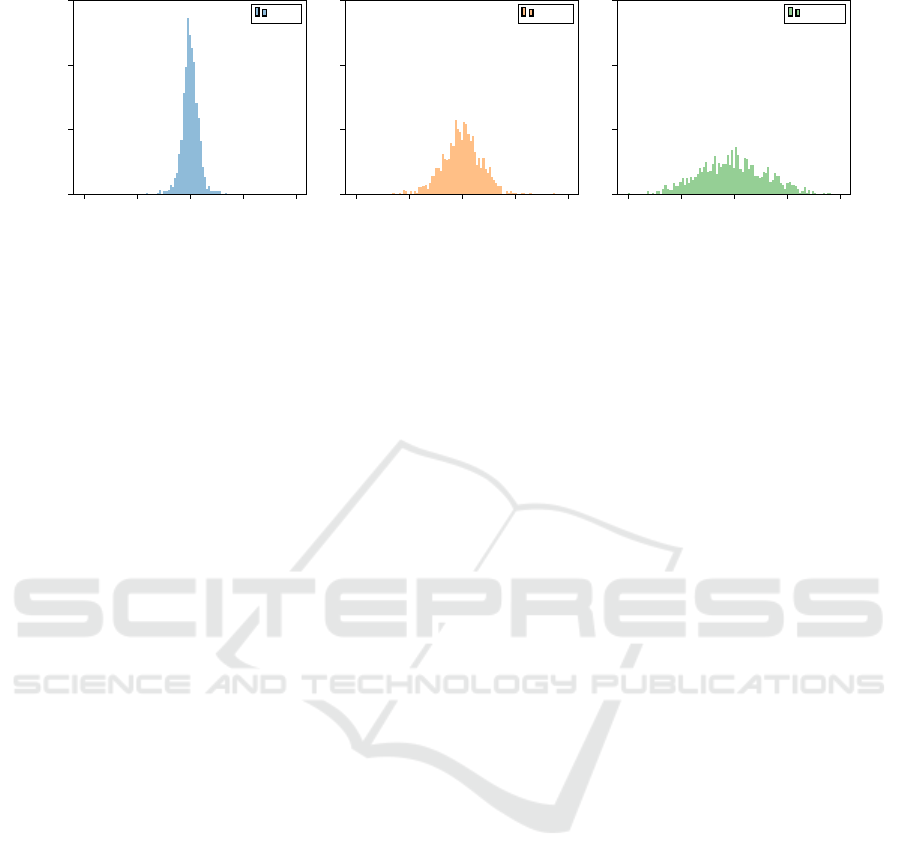
Noise Distribution. Figure 3 compares the error

distribution of ˜µ, as computed with algorithm 2, on

Adult, for different number of partitions N. While

each noise contribution added to the individual ˜n

(i)

and

(i)

parameters follows a Laplace distribution,

their combination by the central aggregator (eq. (13))

approaches a normal distribution as the number of in-

dividual contributions increases.

7 POSSIBLE EXTENSIONS AND

FUTURE WORK

The differentially-private algorithm for federated

Naive Bayes introduced in section 5 is simple at its

core, leaving room for possible extensions and adap-

tations to new use cases. In this section, we describe

some of such extensions that can be added in order

to increase the efﬁciency and security of the training

procedure. Furthermore, we discuss an open prob-

lem, i.e., Byzantine resilience, which we leave to be

addressed by future work.

0.2

0.4

0.6

0.8 1

Sensitivity

Adult

N = 1

N = 10

N = 100

0.2 0.4

0.6

0.8 1

Sensitivity

Skin

N = 1

N = 10

N = 100

Figure 2: Distribution of the sensitivity for the sum query

(i)

, for different choices of N, on Adult and Skin.

Online Updates. Algorithm 2 takes as input the

query results from all nodes. In reality, we expect the

training procedure to be executed in an asynchronous

fashion, with each participant sending its results at a

different time and the aggregator performing subse-

quent updates to the Naive Bayes parameters. This

also allows new nodes to join the overlay network

and collaborate in training the model. One straight-

forward way to make this possible is to store the re-

sponses of each node, and recompute the model pa-

rameters every time a new set of query responses is

sent by a node. However, this is inefﬁcient and re-

quires the central aggregator to store unnecessary in-

formation.

An alternative consists in storing the following ag-

gregated information:

• the total number

of samples for each class;

• the total counters of categorical features

f vy

for

each class;

• the values of mean and variance of all the numer-

ical features ˜µ

f y

for each class.

Notice that the parameters ˜p

(y) and ˜p

(v|y) can

be computed from

and

f vy

˜p

(y) =

∑

′

, ˜p

X|Y

(v|y) =

f vy

, (18)

so the stored variables completely characterize the

model. The complete procedure for updating such

parameters is described in Algorithm 3, and the for-

mulas employed for each of them are derived in the

appendix.

Algorithm 3: Online update.

Require: current parameters

(t)

, ˜µ

(t)

]

(t)

update ˜n

(i)

, ˜m

(i)

from D

(i)

1: for y = 1,. ..,C do

(t+1)

←

(t)

+ ˜n

(i)

3: for f ∈ F

cat

(t+1)

f vy

←

(t)

f vy

+ ˜m

(i)

f vy

5: end for

6: for f ∈ F

num

7: ˜µ

(t+1)

f y

←

(t)

(t+1)

˜µ

(t)

f y

(i)

f y

(t+1)

f y

←

(t)

(t+1)

([

f y

]

(t)

+ [˜µ

(t)

f y

]

) +

(i)

f y

(t+1)

9: [

f y

]

(t+1)

←

(t+1)

f y

− [˜µ

(t+1)

f y

]

10: end for

11: end for

12: return

(t+1)

, ˜µ

(t+1)

]

(t+1)

Federated Naive Bayes under Differential Privacy

177

−0.4 −0.2 0 0.2 0.4

100

150

(˜µ − µ)/µ

N = 1

−0.4 −0.2 0 0.2 0.4

100

150

(˜µ − µ)/µ

N = 10

−0.4 −0.2 0 0.2 0.4

100

150

(˜µ − µ)/µ

N = 100

Figure 3: Distribution of the relative error between the noisy estimate of the mean ˜µ and the true value µ, averaged across all

the features and classes. As N increases, the shape looks less like a Laplace distribution and more like a normal one.

Fully-decentralized Naive Bayes. While our main

implementation of differentially-private federated

Naive Bayes achieves its goal of protecting data pri-

vacy, it still presents certain limitations that are related

to the use of a central aggregator. First, since this ag-

gregator is uniquely responsible for merging the con-

tributions of individual entities, it must be trusted to

do so in a fair and correct manner. Second, the aggre-

gator may represents a bottleneck in terms of compu-

tation and/or network communication in the process.

One promising alternative is the use of Gossip

Learning techniques (Orm

andi et al., 2013), where the

central aggregator is replaced by peer-to-peer model

exchanges. Therein, participants update their local

state based on the information received from a peer,

and later broadcast their own information to another

random participant. These peer-to-peer communica-

tions eventually lead to the convergence of the lo-

cal state of all participants. While these techniques

have not been studied to the same extent as Feder-

ated Learning, recent work has shown that they can

compete with it in terms of performance (Heged

et al., 2021) and that they can be quite robust to dif-

ferent data distributions and network conditions (Gia-

retta and Girdzijauskas, 2019).

To apply Gossip Learning in the context of Naive

Bayes, each entity still computes the statistics of its

partition according to algorithm 1. Then, the gossip-

based aggregation scheme detailed in (Jelasity et al.,

2005) is used which, upon reaching convergence, pro-

vides every entity with the sums of each statistic

across all partitions. Each entity is then able to per-

form algorithm 2 locally and independently, thus ob-

taining the full Naive Bayes model without any need

for central orchestration.

Byzantine Resilience. One important research

topic in the area of Federated Learning is byzan-

tine resilience, i.e., the ability to converge to a high-

quality model even when some of the entities involved

are malicious and may take arbitrary actions to pre-

vent this outcome. We refer the reader to (Lyu et al.,

2020) and (Awan et al., 2021) for a thorough intro-

duction to the topic.

This issue is most signiﬁcant in a massively-

distributed, crowd-sourced setting, where participa-

tion in the protocol is open to any entity and the total

number of participants can reach millions. However,

it can also affect smaller, closed settings: it might not

be possible to establish trust relationships between the

entities in the system, or there may be a concern that

some otherwise honest entities may at some point be

compromised by an external malicious actor.

One well-studied approach to achieve byzantine

resilience consists of median-based aggregation rules,

such as Krum (Blanchard et al., 2017) and Bulyan

(Guerraoui et al., 2018). However, there are chal-

lenges that need to be addressed when applying these

techniques to Naive Bayes. First, the query re-

sults ˜n

(i)

, ˜m

(i)

are not suitable for median-

based aggregation, as their magnitude depends on

the amount of the data (overall and per class) within

each partition. Instead, local Naive Bayes parame-

ters ˜p

(i)

(y), ˜p

(i)

(v|y), ˜µ

(i)





(i)

need to be input to

the median-based aggregation rule. This works well

when the partitions are large and the data IID dis-

tributed among them. However, it may not be suitable

when certain classes or feature values are underrepre-

sented in certain partitions, causing the local parame-

ters to be very inaccurate if not undeﬁned. Thus, one

key strength of the sum- and count-based aggregation

approach is lost.

Additionally, these byzantine resilience ap-

proaches, like most others, are designed for iterative

training processes, in which new updates from each

entity are computed and aggregated at each time step,

thus slowly tuning the model parameters over time. In

a single-step process, as is the training of Naive Bayes

models, such approaches may fail to capture sufﬁcient

information.

SECRYPT 2022 - 19th International Conference on Security and Cryptography

178

8 CONCLUSION

We introduced the ﬁrst implementation of a federated

Naive Bayes classiﬁer under differential privacy. The

relative performance of our approach to its centralized

counterpart varies depending on the characteristics of

the dataset. According to our Monte Carlo analysis,

in most cases, a small privacy penalty must be paid

to achieve the same accuracy level. However, when

the local sensitivity in each federated data partition is

much lower than the sensitivity of the whole dataset,

we show that the federated Laplace mechanism better

estimates the true parameters of the model.

Moreover, we demostrated that our algorithm can

be easily extended to incorporate additional features

such as online updates and full decentralization, while

more research is needed to achieve byzantine re-

silience.

ACKNOWLEDGEMENTS

This project has received funding from the Euro-

pean Union’s Horizon 2020 research and innovation

programme under the Marie Skłodowska-Curie grant

agreement No 813162: RAIS – Real-time Analytics

for the Internet of Sports. The content of this paper

reﬂects the views only of their author (s). The Eu-

ropean Commission/ Research Executive Agency are

not responsible for any use that may be made of the

information it contains.

REFERENCES

Abadi, M., Chu, A., Goodfellow, I., McMahan, H. B.,

Mironov, I., Talwar, K., and Zhang, L. (2016). Deep

learning with differential privacy. In Proceedings of

the 2016 ACM SIGSAC conference on computer and

communications security, pages 308–318.

Awan, S., Luo, B., and Li, F. (2021). Contra: Defending

against poisoning attacks in federated learning. In Eu-

ropean Symposium on Research in Computer Security,

pages 455–475. Springer.

Bernal, D. G., Giaretta, L., Girdzijauskas, S., and Sahlgren,

M. (2021). Federated word2vec: Leveraging feder-

ated learning to encourage collaborative representa-

tion learning. arXiv preprint arXiv:2105.00831.

Blanchard, P., El Mhamdi, E. M., Guerraoui, R., and

Stainer, J. (2017). Machine learning with adversaries:

Byzantine tolerant gradient descent. Advances in Neu-

ral Information Processing Systems, 30.

Dwork, C. (2008). Differential privacy: A survey of results.

In International conference on theory and applica-

tions of models of computation, pages 1–19. Springer.

Geyer, R. C., Klein, T., and Nabi, M. (2017). Differentially

private federated learning: A client level perspective.

arXiv preprint arXiv:1712.07557.

Giaretta, L. and Girdzijauskas,

S. (2019). Gossip learning:

Off the beaten path. In 2019 IEEE International Con-

ference on Big Data (Big Data), pages 1117–1124.

IEEE.

Guerraoui, R., Rouault, S., et al. (2018). The hidden vul-

nerability of distributed learning in byzantium. In In-

ternational Conference on Machine Learning, pages

3521–3530. PMLR.

Heged

us, I., Danner, G., and Jelasity, M. (2021). Decentral-

ized learning works: An empirical comparison of gos-

sip learning and federated learning. Journal of Paral-

lel and Distributed Computing, 148:109–124.

Islam, T. U., Ghasemi, R., and Mohammed, N. (2022).

Privacy-preserving federated learning model for

healthcare data. In 2022 IEEE 12th Annual Com-

puting and Communication Workshop and Conference

(CCWC), pages 0281–0287. IEEE.

Jelasity, M., Montresor, A., and Babaoglu, O. (2005).

Gossip-based aggregation in large dynamic networks.

ACM Trans. Comput. Syst., 23(3):219–252.

Ji, Z., Lipton, Z. C., and Elkan, C. (2014). Differential pri-

vacy and machine learning: a survey and review. arXiv

preprint arXiv:1412.7584.

Kantarcıoglu, M., Vaidya, J., and Clifton, C. (2003). Pri-

vacy preserving naive bayes classiﬁer for horizontally

partitioned data. In IEEE ICDM workshop on privacy

preserving data mining, pages 3–9.

Li, T., Li, J., Liu, Z., Li, P., and Jia, C. (2018). Differen-

tially private naive bayes learning over multiple data

sources. Information Sciences, 444:89–104.

Lopuha

a-Zwakenberg, M., Alishahi, M., Kivits, J., Klaren-

beek, J., van der Velde, G.-J., and Zannone, N. (2021).

Comparing classiﬁers’ performance under differential

privacy. In International Conference on Security and

Cryptography (SECRYPT).

Lyu, L., Yu, H., Ma, X., Sun, L., Zhao, J., Yang, Q., and

Yu, P. S. (2020). Privacy and robustness in feder-

ated learning: Attacks and defenses. arXiv preprint

arXiv:2012.06337.

Marchioro., T., Kazlouski., A., and Markatos., E. (2021).

User identiﬁcation from time series of ﬁtness data. In

Proceedings of the 18th International Conference on

Security and Cryptography - SECRYPT,, pages 806–

811. INSTICC, SciTePress.

McMahan, B., Moore, E., Ramage, D., Hampson, S., and

Arcas, B. A. y. (2017). Communication-Efﬁcient

Learning of Deep Networks from Decentralized Data.

In Singh, A. and Zhu, J., editors, Proceedings of

the 20th International Conference on Artiﬁcial Intelli-

gence and Statistics, volume 54 of Proceedings of Ma-

chine Learning Research, pages 1273–1282. PMLR.

McSherry, F. D. (2009). Privacy integrated queries: an ex-

tensible platform for privacy-preserving data analysis.

In Proceedings of the 2009 ACM SIGMOD Interna-

tional Conference on Management of data, pages 19–

30.

Federated Naive Bayes under Differential Privacy

179

Orm

andi, R., Heged

us, I., and Jelasity, M. (2013). Gossip

learning with linear models on fully distributed data.

Concurrency and Computation: Practice and Experi-

ence, 25(4):556–571.

Rish, I. et al. (2001). An empirical study of the naive bayes

classiﬁer. In IJCAI 2001 workshop on empirical meth-

ods in artiﬁcial intelligence, volume 3, pages 41–46.

Salem, A., Zhang, Y., Humbert, M., Berrang, P., Fritz,

M., and Backes, M. (2018). Ml-leaks: Model and

data independent membership inference attacks and

defenses on machine learning models. arXiv preprint

arXiv:1806.01246.

Shafagh, H., Burkhalter, L., Hithnawi, A., and Duquennoy,

S. (2017). Towards blockchain-based auditable stor-

age and sharing of iot data. In Proceedings of the 2017

on cloud computing security workshop, pages 45–50.

Ullah, F., Edwards, M., Ramdhany, R., Chitchyan, R.,

Babar, M. A., and Rashid, A. (2018). Data exﬁltra-

tion: A review of external attack vectors and counter-

measures. Journal of Network and Computer Appli-

cations, 101:18–54.

Vaidya, J. and Clifton, C. (2004). Privacy preserving naive

bayes classiﬁer for vertically partitioned data. In Pro-

ceedings of the 2004 SIAM international conference

on data mining, pages 522–526. SIAM.

Vaidya, J., Shaﬁq, B., Basu, A., and Hong, Y. (2013). Dif-

ferentially private naive bayes classiﬁcation. In 2013

IEEE/WIC/ACM International Joint Conferences on

Web Intelligence (WI) and Intelligent Agent Technolo-

gies (IAT), volume 1, pages 571–576. IEEE.

Wei, K., Li, J., Ding, M., Ma, C., Yang, H. H., Farokhi, F.,

Jin, S., Quek, T. Q. S., and Poor, H. V. (2020). Fed-

erated learning with differential privacy: Algorithms

and performance analysis. IEEE Transactions on In-

formation Forensics and Security, 15:3454–3469.

Yi, X. and Zhang, Y. (2009). Privacy-preserving naive bayes

classiﬁcation on distributed data via semi-trusted mix-

ers. Information systems, 34(3):371–380.

Zhang, H. (2004). The optimality of naive bayes. Aa,

1(2):3.

Zhu, L., Liu, Z., and Han, S. (2019). Deep leakage from

gradients. Advances in Neural Information Processing

Systems, 32.

APPENDIX

Deriving the Formulas for Online

Updates

In order to derive the the online updates of our model,

we consider a time-varying model where all the pa-

rameters ν

(t)

,µ

(t)

,σ

(t)

are deﬁned at the t-th ex-

change between the central aggregator and one node

of the network. According to this deﬁnition, denot-

ing with τ

the time at which iteration with node D

(i)

happens, the parameters of the model at time t should

satisfy

(t)

∑

i:τ

(i)

, M

(t)

f vy

∑

i:τ

(i)

f vy

, (19)

(t)

f y

∑

i:τ

(i)

f y

∑

i:τ

(i)

, [σ

f y

]

(t)

∑

i:τ

(i)

f y

∑

i:τ

(i)

− µ

(t)

f y

(20)

Counting parameters such as ν

(t)

and M

(t)

are simply

updated by adding the new counts n

(i)

of the i-th

node which is sending updates at time t + 1

(t+1)

= ν

(t)

+ n

(i)

, M

(t+1)

f vy

= M

(t)

f vy

+ m

(t)

f vy

. (21)

The mean µ

(t)

f y

, instead, can be updated by observing

that

(t+1)

f y

∑

′

:τ

′

<t+1

′

)

f y

∑

′

:τ

′

<t+1

′

)

(22)

∑

′

:τ

′

)

∑

′

:τ

′

<t+1

′

)

∑

′

:τ

′

)

f y

∑

′

:τ

′

)

(i)

f y

∑

′

:τ

′

<t+1

′

)

(23)

(t)

(t+1)

(t)

f y

(i)

f y

(t+1)

, (24)

where S

(i)

is the sample sum submitted by node D

(i)

at time t. Analogously, the estimated second moment

at time t + 1 is obtained as

(t+1)

f y

(t)

(t+1)

(t)

f y

(i)

f y

(t+1)

. (25)

The variance can be obtained by replacing ς

(t)

f y

[σ

f y

]

(t)

+ [µ

(t)

f y

]

, which leads to

[σ

f y

]

(t+1)

(t)

(t+1)

([σ

f y

]

(t)

+[µ

(t)

f y

]

(i)

f y

(t+1)

−[µ

(t+1)

f y

]

(26)

SECRYPT 2022 - 19th International Conference on Security and Cryptography

180