Mason Vulnerability Scoring Framework: A Customizable Framework
for Scoring Common Vulnerabilities and Weaknesses
Ibifubara Iganibo
1 a
, Massimiliano Albanese
1 b
, Kaan Turkmen
1
, Thomas R. Campbell
1
and Marc Mosko
2 c
1
Center for Secure Information Systems, George Mason University, Fairfax, U.S.A.
2
Palo Alto Research Center, U.S.A.
Keywords:
Vulnerability Analysis, Security Metrics, Software Weaknesses.
Abstract:
One of the first lines of defense against cyberattacks is to understand and evaluate the weaknesses and vul-
nerabilities that a system exposes to malicious users. To address this need, several scoring systems have been
developed, providing security analysts and practitioners with a means of quantifying the severity of common
weaknesses and vulnerabilities found in software. However, these scoring systems rely on predefined no-
tions of risk, use fixed equations to compute numerical scores, and do not provide users with the flexibility to
fine-tune such equations or factor in new variables altogether. Furthermore, official scores and rankings are
updated infrequently, making them less valuable in a rapidly evolving cybersecurity landscape. In this paper,
we present the Mason Vulnerability Scoring Framework, a comprehensive and customizable framework for
scoring vulnerabilities and ranking common weaknesses that gives users significant control over the scoring
and ranking process.
1 INTRODUCTION
Over the years, different organizations, including
NIST (Mell et al., 2006) and MITRE (Christey, 2008),
have tried to establish software vulnerability scoring
systems, metrics, and best practices as critical tools
to help security administrators make informed deci-
sions about vulnerability prioritization, remediation,
and mitigation (Black et al., 2018). Some of the tools
that were developed were intended to serve as check-
lists for security administrators during security audits
and compliance procedures. However, all these so-
lutions rely on predefined notions of risk and impact,
use predefined and fixed equations to compute numer-
ical scores, and do not provide users with the flexibil-
ity to fine-tune the equations or factor in new variables
altogether. For these tools to be effective in support-
ing security-related decisions, administrators should
be given the opportunity to tailor the scoring and rank-
ing processes to the specific needs of the environment
in which they operate, and have up-to-date informa-
tion about the current vulnerability landscape.
MITRE and OWASP have tried to address the
a
https://orcid.org/0000-0003-1321-8554
b
https://orcid.org/0000-0002-2675-5810
c
https://orcid.org/0000-0002-3270-8738
need to provide up-to-date information by publish-
ing yearly rankings of software weaknesses. How-
ever, these solutions are limited because the vulner-
ability landscape evolves at a much more rapid pace
than the pace at which these official rankings are pub-
lished. The National Vulnerability Database is up-
dated roughly every two hours to keep up with infor-
mation about new vulnerabilities and updates about
known vulnerabilities, but their scoring system has
proven to be unable to keep up with these constant
changes, as demonstrated by the many vulnerabili-
ties that are added to the database and have not been
scored yet. As shown in Figure 1, as of May 11, 2022,
there were over 2,000 recently discovered vulnerabili-
ties that were either awaiting or undergoing analysis
1
.
We addressed these gaps by establishing the Ma-
son Vulnerability Scoring Framework (MVSF), a
framework that allows users to generate custom rank-
ings by tuning several parameters used to calcu-
late vulnerability and weakness scores. The frame-
work publishes monthly rankings of Common Weak-
nesses Enumeration (CWE) categories based on a
standard parameter configuration, but can also gen-
erate monthly, weekly, or even daily rankings on de-
1
The live NVD Dashboard can be accessed at
https://nvd.nist.gov/general/nvd-dashboard.
Iganibo, I., Albanese, M., Turkmen, K., Campbell, T. and Mosko, M.
Mason Vulnerability Scoring Framework: A Customizable Framework for Scoring Common Vulnerabilities and Weaknesses.
DOI: 10.5220/0011277400003283
In Proceedings of the 19th International Conference on Security and Cryptography (SECRYPT 2022), pages 215-225
ISBN: 978-989-758-590-6; ISSN: 2184-7711
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All r ights reser ved
215

Figure 1: Screenshot of the NVD Dashboard as of 1:00am EDT on May 11, 2022.
mand, based on a user’s needs. This work builds
upon and expand our previous work on vulnerabil-
ity metrics (Iganibo et al., 2021), and aggregates
vulnerability-level metrics to compute weakness-
level scores and enable ranking of common weak-
nesses. The framework has been implemented as a
web-based application and has been made available
to the general public
2
.
The remainder of the paper is organized as fol-
lows. Section 2 discusses related work. Section 3 de-
scribes the vulnerability-level metrics used as a foun-
dation for the work presented here and the proposed
common weakness score. Then, Section 4 describes
the architecture of the framework and provides details
about its four main components. Finally, Section 6
compares MVSF against MITRE’s and OWASP’s so-
lutions, and Section 7 provides concluding remarks
and a roadmap for future work.
2 RELATED WORK
Scoring software vulnerabilities and ranking different
vulnerability categories are not novel concepts. The
National Vulnerability Database (NVD) is the U.S.
government repository of vulnerability information
that is maintained by the National Institute of Stan-
dards and Technology (NIST). NVD is built upon and
fully synchronized with MITRE’s Common Vulner-
abilities and Exposures (CVE) List, and augments it
2
MVSF can be accessed at https://mvsf.gmu.edu/. The
system is password protected, but anyone interested in using
the system can request an account following the instructions
on the login screen.
with severity scores, and impact ratings based on the
Common Vulnerability Scoring System.
Common Weakness Enumeration (CWE) is a sys-
tem that provides a structured list of clearly defined
software and hardware weaknesses
3
. MITRE’s Com-
mon Weakness Scoring System (CWSS) provides a
mechanism for prioritizing software weaknesses that
are present within software applications in a consis-
tent and flexible manner
4
. MITRE publishes annual
rankings of the Common Weakness Enumeration Top
25 Most Dangerous Software Weaknesses
5
(CWE
Top 25), which is intended to be a demonstrative list
of the most common and impactful issues experienced
over the previous two calendar years. To create this
list, MITRE leverages CVE data from NVD as well
as the CVSS scores associated with each CVE record.
Each weakness is scored based on prevalence and
severity. Similarly, the Open Web Application Secu-
rity Project (OWASP) releases its Top 10 Web Appli-
cation Security Risks list yearly
6
. A limitation of this
ranking is that there is no published quantitative ap-
proach backing it, making this ranking subjective and
difficult to replicate by users.
Several recent metrics (Mukherjee and Mazum-
dar, 2018; Wang et al., 2019) use scores from the
Common Vulnerability Scoring Systems (CVSS) or
the Common Weakness Scoring Systems (CWSS) in
isolation or as the dominant factor in determining the
severity of a vulnerability. Even the approaches that
consider the effect of multiple variables on the over-
3
https://cwe.mitre.org/
4
https://cwe.mitre.org/cwss/
5
https://cwe.mitre.org/top25/
6
https://owasp.org/Top10/
SECRYPT 2022 - 19th International Conference on Security and Cryptography
216

all scores assigned to vulnerabilities cannot be easily
extended if one wants to consider additional variables
that were not originally taken into account – such as
the age of a vulnerability or the set of IDS rules as-
sociated with it – and do not allow one to change the
relative weights of these variables.
The proposed framework was designed to address
all these limitations, by allowing users and adminis-
trators to control several aspects of the scoring and
ranking process and obtain real-time rankings based
on current vulnerability information. To develop
comprehensive cyber situational awareness (Jajodia
and Albanese, 2017), and in line with more traditional
risk analysis approaches, we also distinguish between
the likelihood that a vulnerability might be exploited
and the impact a successful exploitation would cause.
Furthermore, all details have been disclosed to make
this process reproducible by others.
3 METRICS
In this section, we first briefly review two vulnera-
bility metrics that we introduced in (Iganibo et al.,
2021), namely the exploitation likelihood and the ex-
posure factor and further generalize the definition of
exposure factor compared to its original formulation.
Then, building upon these metrics, we define a com-
mon weakness score that is semantically equivalent
to MITRE’s CWE scores, but presents several key ad-
vantages compared to current solutions.
3.1 Exploitation Likelihood
The exploitation likelihood of a vulnerability is de-
fined as the probability that an attacker will attempt to
exploit that vulnerability when certain preconditions
are met. In our analysis, we identified three main
factors that influence the likelihood that an attacker
will exploit a given vulnerability v: (i) the vulnera-
bility’s exploitability score as determined by CVSS,
Exploitability(v); (ii) the amount of time elapsed
since the vulnerability was made public, t(v); and
(iii) the number of known IDS rules associated with
the vulnerability, |IDS
k
(v)|. Thus, the likelihood of v
is defined by Equation 1, where α, β, and γ are tunable
parameters.
ρ(v) =

1 −e
−α·
√
t(v)

·

1 −e
−β·Exploitability(v)

e
γ·|IDS
k
(v)|
(1)
Intuitively, if a vulnerability has been known for
a long time, it is likely that more exploits have been
developed by the hacker community, making that vul-
nerability easier to exploit. On the other hand, the ex-
istence of know IDS rules associated with a vulnera-
bility may discourage an attacker from exploiting that
vulnerability in favor of less detectable exploits.
The reader can refer to (Iganibo et al., 2021) for a
more detailed discussion about the rationale for this
choice of variables. We argue that these may not
be the only variables influencing the likelihood, and
we have designed this metric to be easily extended
to include any additional variables that administra-
tors deem appropriate. Additionally, by considering
multiple variables, we avoid relying on a single data
source, which might be incomplete or occasionally
unavailable. For instance, as we mentioned earlier, at
any point in time, there might be hundreds or thou-
sands of vulnerabilities that have been reported to
NVD but have not been analyzed yet, therefore they
do not yet have assigned CVSS scores. In such sce-
narios, Equation 1 allows us to ignore the effect of a
variable and assess or compare vulnerabilities based
on any other available data.
Each variable contributes to the overall likelihood
as a multiplicative factor between 0 and 1 that is for-
mulated to account for diminishing returns. A fac-
tor corresponding to a variable x that contributes to
increasing the likelihood is of the form 1 −e
−c·f (x)
,
where f (x) is a monotonically increasing function
7
of x and c is a constant parameter. Similarly, a factor
corresponding to a variable x that contributes to de-
creasing the likelihood is of the form e
−c·f (x)
=
1
e
c·f (x)
.
This formulation provides several practical advan-
tages: (i) the resulting likelihood is normalized be-
tween 0 and 1; (ii) accounting for the effect of addi-
tional independent variables is straightforward; and
(iii) ignoring the effect of a variable simply entails set-
ting the constant c such that the corresponding factor
evaluates to 1 (i.e., c = +∞ for factors increasing the
likelihood and c = 0 for factors decreasing the likeli-
hood).
In summary, this formulation allows administra-
tors to easily add or remove variables in Equation 1
and control the relative weight of each variable by
tuning the corresponding parameter. Note that, based
on the mathematical formulation of each multiplica-
tive factor, the tunable parameters allow us to control
how quickly each factor converges to 1. Once a factor
converges to 1, variables corresponding to the other
factors gain more discriminating power.
7
In most cases, f (x) can be simply defined as the linear
function f (x) = x, but we use f (x) =
√
x for the time since
publication and f (x) = |x| for the set of IDS rules.
Mason Vulnerability Scoring Framework: A Customizable Framework for Scoring Common Vulnerabilities and Weaknesses
217

3.2 Exposure Factor
The exposure factor of a vulnerability represents the
relative damage that would result from its exploita-
tion. In our analysis, we identified two main factors
that influence the exposure factor of a given vulnera-
bility v: (i) the vulnerability’s impact score as deter-
mined by CVSS, Impact(v); and (ii) the number of
deployed IDS rules associated with the vulnerability,
|IDS
d
(v)|. Thus, the exposure factor of v is defined
by Equation 2, where λ and δ are tunable parameters.
e f (v) =
1 −e
−λ·impact(v)
e
δ·|IDS
d
(v)|
(2)
The set of deployed IDS rules can be determined
by analyzing local IDS rules files. Intuitively, de-
ployed IDS rules can mitigate the impact of a success-
ful exploit by allowing timely detection and response.
The reader can refer again to (Iganibo et al., 2021) for
a more detailed discussion about the rationale for this
choice of variables. As for the likelihood metric, we
argue that these may not be the only variables influ-
encing the exposure factor, and we have designed this
metric to be easily extended to include any additional
variables that administrators deem appropriate.
The formulation of Equation 2 is more general
than the original formulation in (Iganibo et al., 2021),
which was simply normalizing the CVSS impact
score, instead of using it in a multiplicative factor of
the form 1 −e
−c·f (x)
. This more generic formulation
allows us to easily and intuitively extend the expo-
sure factor metric with additional variables, similarly
to what we described for the likelihood metric.
3.3 Common Weakness Score
As mentioned in Section 2, CWE provides a struc-
tured list of clearly defined software and hardware
weaknesses, and MITRE’s Common Weakness Scor-
ing System (CWSS) provides a mechanism for priori-
tizing weaknesses in a consistent and flexible manner.
CWSS is organized into three metric groups: Base
Finding, Attack Surface, and Environmental. Each
group includes multiple metrics that are used to com-
pute a CWSS score for a weakness. However, we fo-
cus our attention on the method MITRE uses to rank
the most dangerous weaknesses, and refer the reader
to its documentation for further details on CWSS.
Equation 3 defines the set of CVEs mapped to
each CWE, and Equation 4 defines the number of
times each CWE is mapped to a CVE entry
8
.
8
We slightly abuse notation and use CWE
i
∈ NV D to
denote a CWE that is mapped to at least one CVE entry in
NVD.
C(CWE
i
) =

CV E
j
∈ NV D, CV E
j
→CWE
i

(3)
Freqs =
{
|C(CWE
i
)|, CW E
i
∈ NV D
}
(4)
Then, Equations 5 and 6 respectively compute a
frequency and a severity score for each CWE, where
the severity is based on the average CVSS score of all
CVEs in that CWE category. Frequency and severity
scores are both normalized between 0 and 1.
Fr(CWE
i
) =
|C(CWE
i
)|−min(Freqs)
max(Freqs) −min(Freqs)
(5)
Sv(CW E
i
) =
avg
CWE
i
(CVSS) −min(CV SS)
max(CV SS) −min(CVSS)
(6)
Finally, Equation 7 defines the overall score that
MITRE assigns to a CWE as the product of its fre-
quency and severity scores, normalized between 0 and
100.
S
MIT RE
(CWE
i
) = Fr(CWE
i
) ·Sv(CWE
i
) ·100 (7)
In summary, MITRE scores each weakness based
on its prevalence – which is a function of the num-
ber of vulnerabilities mapped to that weakness – and
severity – which is assumed to be the average sever-
ity of the vulnerabilities mapped to that weakness.
To compute our own score for common weaknesses,
we follow a similar approach, but, instead of relying
solely on CVSS scores, we define the severity score
of a CWE based on the vulnerability-level metrics de-
scribed in Sections 3.1 and 3.2. This allows users and
administrators to control the ranking by fine-tuning
the underlying vulnerability metrics. Additionally, we
do not normalize our scores in order to speed up real-
time computation of CWE rankings, as normaliza-
tion has no impact on the rankings other than putting
scores on a different scale.
We define the severity of a weakness CWE
i
as the
product of the average likelihood ρ(CW E
i
) of vulner-
abilities mapped to CWE
i
and the average exposure
factor e f (CW E
i
) of such vulnerabilities.
Sv
MV SF
(CWE
i
) = ρ(CWE
i
) ·e f (CWE
i
) (8)
where ρ(CWE
i
) and e f (CWE
i
) are defined by Equa-
tions 9 and 10 respectively.
ρ(CWE
i
) =
avg
v∈C(CW E
i
)
ρ(v) (9)
e f (CWE
i
) =
avg
v∈C(CW E
i
)
e f (v) (10)
Finally, we can define the proposed common
weakness score through Equation 11, where the fre-
quency Fr(CWE
i
) in Equation 7 is replaced by
SECRYPT 2022 - 19th International Conference on Security and Cryptography
218

S
MV SF
(CWE
i
) = |C(CWE
i
)|·
avg
v∈C(CW E
i
)

1 −e
−α·
√
t(v)

·

1 −e
−β·Exploitability(v)

e
γ·|IDS
k
(v)|
·
avg
v∈C(CWE
i
)
1 −e
−λ·impact(v)
e
δ·|IDS
d
(v)|
Figure 2: MVSF Common Weakness Score.
|C(CWE
i
)| and the average severity Sv(CW E
i
) is re-
placed by Sv
MV SF
(CWE
i
).
S
MV SF
(CWE
i
) = |C(CWE
i
)|·Sv
MV SF
(CWE
i
) (11)
Combining Equations 1, 2, 9, 10, and 11, we can
expand S
MV SF
(CWE
i
) as shown in Figure 2.
4 SYSTEM ARCHITECTURE
Having described our technical approach to scoring
and ranking, we now discuss MVSF’s architecture,
which is comprised of a data ingestion module, a
metrics computation module, a ranking module, and
a graphical user interface. This high-level architec-
ture is shown in Figure 3, which also shows the data
sources used by the system. The individual modules
are discussed in detail in the following subsections.
The data ingestion, metrics computation, and
ranking modules form the backend of the system and
are application-independent. The backend has been
implemented as a set of containerized services, and
the graphical user interface has been implemented as
a web-based application, which has been made avail-
able to the general public. As part of our future work,
we plan to make APIs available for third-party appli-
cations to access MVSF-generated scores and rank-
ings in a programmatic way.
4.1 Data Ingestion Module
MVSF currently ingests vulnerability information
from the the National Vulnerabilities Database (NVD)
and Intrusion Detection System (IDS) rules from pub-
lic repositories and local rule files, but can be eas-
ily extended to ingest any additional vulnerability-
specific data.
The data ingestion module periodically
9
fetches
data from NVD data feeds, and stores it in an inter-
nal database. Data fetched from NVD includes the
CVE-ID, description, CVSS exploitability and impact
scores, and CWE mappings for each known vulnera-
bility.
9
The frequency is currently set to once every 4 hours,
but we are considering making it dynamic, based on the vol-
ume of updates to NVD at different times of the day or on
different days of the week.
Additionally, the data ingestion module periodi-
cally fetches IDS rules from public repositories man-
aged by the major providers of intrusion detection
systems (e.g., Snort
10
and Suricata
11
), and searches
for rules that are explicitly mapped to CVE entries.
As discussed in (Iganibo et al., 2021), the existence
of IDS rules for detecting attempts to exploit a given
CVE may deter attackers from targeting that CVE and
incentivize them to opt for less detectable exploits.
Thus, we consider the number |IDS
k
(v)| of known
IDS rules as one of the variables influencing the ex-
ploitation likelihood of a vulnerability v.
The data ingestion module also processes local
rule files and looks for rules that are not only explic-
itly mapped to CVE entries but also currently used by
the IDS. Intrusion detection systems typically come
with a predefined set of rules, but not all of them are
necessarily enabled, and users have the ability to en-
able or disable rules based on their specific needs and
the characteristics of the environment in which they
are deployed.
As discussed in (Iganibo et al., 2021), attackers
have no knowledge about which specific rules are in
use in a given system, but deployed rules can help
mitigate the consequences of an exploit, as timely de-
tection may help defenders take appropriate mitiga-
tion actions early on. Thus, we consider the number
|IDS
d
(v)| of deployed IDS rules as one of the vari-
ables influencing the exposure factor of a vulnerabil-
ity v. Deployed rules may include a subset of known
rules and custom rules developed by the system’s ad-
ministrators. As the set of deployed IDS rules differs
across IDS installations, when administrators provide
copies of local rule files as input, the resulting rank-
ings are customized and different for different users
12
.
The ability to generate custom rankings is what
sets our approach apart, and the use of deployed IDS
rules is just one example of how users can control the
scoring process and customize the rankings by pro-
viding system-specific information.
10
https://www.snort.org/
11
https://suricata.io/
12
While our formal model and the backend system both
allow us to factor in deployed IDS rules, the graphical user
interface does not have yet an option to submit local rules
files as inputs.
Mason Vulnerability Scoring Framework: A Customizable Framework for Scoring Common Vulnerabilities and Weaknesses
219

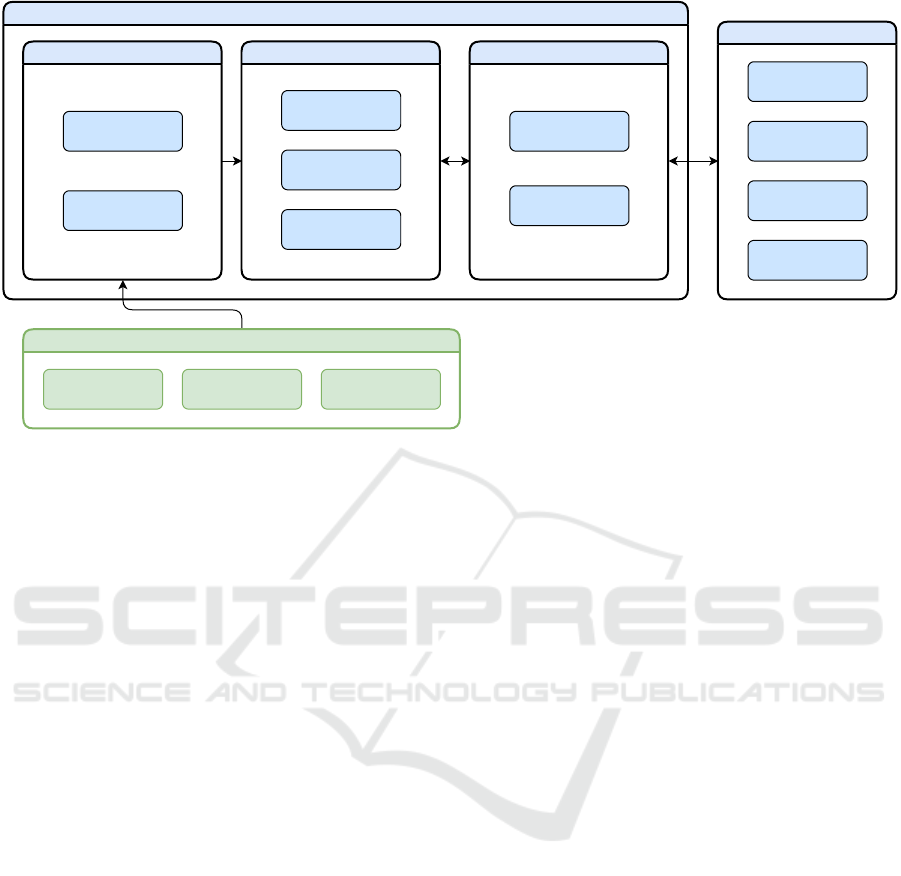
Backend
Data Ingestion Module
IDS Rules
Submodule
NVD Submodule
Metrics Computation Module
Exploitation
Likelihood
Exposure Factor
Common Weakness
Score
Ranking Module
Standard Ranking
Custom Ranking
Input Data
Public IDS Rules
Repository
Local IDS Rules
Files
NVD Data Feeds
Graphical User Interface
Historical Rankings
Live Rankings
Custom Rankings
CVE Search
Figure 3: Architecture of the Mason Vulnerability Scoring Framework.
4.2 Metric Computation Module
The metrics computation module implements a suite
of algorithms to compute all the metrics discussed in
Section 3. As a reminder, MVSF generates and pub-
lishes official monthly rankings of all CWEs using
predefined values for all the tunable parameters, and
allows the user to generate rankings on demand, based
on custom values of the parameters. Thus, the algo-
rithms in this module can be triggered by either the
data ingestion module or the ranking module.
Every time the data ingestion module fetches new
data, these algorithms are executed to compute (i) the
likelihood and exposure factor of any newly discov-
ered vulnerability; (ii) updated scores for any vulner-
ability for which new information has become avail-
able (e.g., updated CVSS scores, new IDS rules); and
(iii) updated common weakness scores. When their
execution is triggered by the data ingestion module,
these algorithms use predefined values for all the tun-
able parameters. Results of these computations are
stored in the internal database, as they form the basis
for the generation of official CWE rankings.
Execution of these algorithms is also triggered
when a user requests CWE rankings with custom pa-
rameters. In this case, the results are not cached, as
caching CVE and CWE scores for all possible val-
ues of the parameters would be unfeasible. However,
we plan to collect and analyze usage data, and define
effective caching strategies to reduce the need to com-
pute CVE and CWE scores in real time. For instance,
it is reasonable to assume that once a user has cho-
sen values of the parameters that are suitable for their
environment, they will request future rankings based
on the same set of parameters. If such hypothesis is
verified, then scores could be cached on a per-user ba-
sis, and an offline cache refresh could be triggered by
the data ingestion module, so that up-to-date custom
scores would be readily available to users when they
need them.
4.3 Ranking Module
The ranking module generates ranked lists of CWEs
both periodically and on demand. The module in-
cludes a process that, on the first day of every month,
automatically generates a ranking of all CWEs based
on data from the previous 24-month period, using
predefined and fixed values of the parameters. This
process is extremely efficient because, by the time
it is executed, all the vulnerability-level scores have
already been computed by the metrics computation
module, triggered by the data ingestion module every
time new data is fetched. Once computed, a monthly
ranking is saved to the database and becomes an his-
torical ranking, thus it is not updated even if the data
used for its computation is updated later.
When a user requests a custom ranking, with non-
standard values of the parameters, the ranking module
needs to invoke algorithms in the metrics computa-
tion module to compute CVE and CWE scores based
on the provided values of the parameters. This pro-
cess is slower because we cannot predict what values
of the parameters a user will choose, thus we cannot
precompute the scores offline. However, as discussed
in the previous section, it may be possible to define
SECRYPT 2022 - 19th International Conference on Security and Cryptography
220

Mason CWE Ranking for February 2022
Rank CWE-ID Name Overall Score Change in Rank
1 CWE-79 Improper Neutralization of Input During Web Page Generation ('Cross-site Scripting') 3806 0
2 CWE-787 Out-of-bounds Write 2666 0
3 CWE-20 Improper Input Validation 1266 0
4 CWE-89 Improper Neutralization of Special Elements used in an SQL Command ('SQL Injection') 1178
1
5 CWE-125 Out-of-bounds Read 1146
-1
6 CWE-269 Improper Privilege Management 932
1
7 CWE-416 Use After Free 906
-1
8 CWE-78 Improper Neutralization of Special Elements used in an OS Command ('OS Command Injection') 822
1
9 CWE-22 Improper Limitation of a Pathname to a Restricted Directory ('Path Traversal') 807
-1
10 CWE-352 Cross-Site Request Forgery (CSRF) 762 0
11 CWE-120 Buffer Copy without Checking Size of Input ('Classic Buffer Overflow') 739 0
12 CWE-287 Improper Authentication 661
1
13 CWE-863 Incorrect Authorization 628
-1
14 CWE-200 Exposure of Sensitive Information to an Unauthorized Actor 556
1
15 CWE-77 Improper Neutralization of Special Elements used in a Command ('Command Injection') 537
-1
16 CWE-434 Unrestricted Upload of File with Dangerous Type 522 0
17 CWE-476 NULL Pointer Dereference 468 0
18 CWE-400 Uncontrolled Resource Consumption 423 0
19 CWE-190 Integer Overflow or Wraparound 411 0
20 CWE-119 Improper Restriction of Operations within the Bounds of a Memory Buffer 396 0
21 CWE-862 Missing Authorization 375 0
22 CWE-502 Deserialization of Untrusted Data 358 0
23 CWE-276 Incorrect Default Permissions 325 0
24 CWE-74 Improper Neutralization of Special Elements in Output Used by a Downstream Component ('Injection') 307 0
25 CWE-798 Use of Hard-coded Credentials 306 0
Note: N/A indicates that this CWE was not present in the previous month's ranking.
Mason Vulnerability Scoring Framework
HISTORICAL RANKINGS
Figure 4: MVSF homepage showing the most recent monthly ranking.
suitable caching strategies to improve the efficiency
of this process.
5 USER INTERFACE
The framework’s graphical user interface has been
implemented as a web-based application that can be
accessed at https://mvsf.gmu.edu/. The system is cur-
rently password protected, but anyone interested can
request an account following the instructions on the
login screen. In the following, we describe the differ-
ent functionalities offered by the web application.
5.1 Homepage
The Homepage displays the most recent monthly
ranking of the top 150 CWEs, based on data from the
previous 24-month period, and it is automatically up-
dated on the first day of every month. Figure 4 shows
how the Homepage appeared in March 2022, after the
ranking for the 24-month period ending on February
28, 2022 was computed. For each ranked CWE, the
system is showing (i) its rank, (ii) its CWE ID with
a link to the official entry maintained by MITRE,
(iii) a brief description, (iv) its MVSF score, and (v) the
change in rank compared to the previous month.
5.2 Historical Rankings
The Historical Rankings view shows the last 12
monthly rankings calculated by the ranking module
and saved to the database. As mentioned before, once
these monthly rankings are computed, they are never
updated as they are intended to capture a snapshot of
the vulnerability landscape at a given point in time.
For instance, if the CVSS Exploitability and Impact
scores of a vulnerability published in February 2022
are updated in NVD on March 2, 2022, the ranking
computed on March 1, 2022 for the 24-month period
ending in February 2022 will not be updated to re-
flect this change. In principle, the Historical Rankings
have the same objective of MITRE’s Top 25 yearly
rankings, but they are published more frequently –
monthly vs. yearly – and include more CWEs – 150
vs. 25.
Figure 5 shows the Historical Rankings view as of
March 2022. By default, this view shows the last 12
monthly rankings, but the user can navigate through
time by using the Previous and Next buttons. This
view also shows the change in rank of each CWE
compared to 12 months before. Being able to identify
trends enables users to learn, predict, plan, and build
their security measures (Aigner et al., 2007). To help
achieve this level of security awareness, the Historical
Rankings view includes a feature that allows a user
to highlight trends in the rank of CWEs. When hover-
ing over a CWE ID, the interface highlights that CWE
through the entire 12-month period to visually show
the trend. Also, the checkboxes on the left side of the
table can be used to make the highlight permanent,
allowing the visualization of multiple CWE trends si-
multaneously. The checkbox at the top of the table
allows the user to clear the selection of highlighted
CWEs and reset to the original view. For instance, the
screenshot in Figure 5 shows that the rank of CWE-79
did not change in the last 12 months, whereas CWE-
Mason Vulnerability Scoring Framework: A Customizable Framework for Scoring Common Vulnerabilities and Weaknesses
221

Historical Rankings
Click on month headers for more information
Rank 2021-03 2021-04 2021-05 2021- 06 2021-07 2021-08 2021-09 2021-10 2021-11 2021-12 2022-01 2022-02 Rank Change
1
CWE-79 CWE-79 CWE-79 CWE-79 CWE-79 CWE-79 CWE-79 CWE-79 CWE-7 9 CWE-79 CWE-79
1 0
2
CWE-787 CWE-787 CWE-787 CWE-787 CWE-787 CWE-787 CWE-787 CWE-787 CWE-787 CWE-787 CWE-787 CWE-787
2 0
3
CWE-20 CWE-20 CWE-20 CW E-20 CWE -20 CWE- 20 CWE-2 0 CWE-20 CWE-20 CWE-20 CWE-2 0 CWE-20
3 0
4
CWE-125 CWE-125 CWE-125 CWE-125 CWE-125 CWE-125 CWE-125 CWE-125 CWE-125 CWE-89 CWE-89 CWE-125
4 0
5
CWE-89 CWE-89 CWE-89 CW E-89 CWE -89 CWE- 89 CWE-8 9 CWE-89 CWE-89 CWE-125 CWE-125 CWE-89
5 0
6
CWE-78 CWE-78 CWE-78 CW E-78 CWE -78 CWE-416 CWE-416 CWE-416 CWE-416 CWE-416 CWE-269 CWE-416
6 2
7
CWE-352 CWE-352 CWE-416 CWE-416 CWE-416 CWE-78 CWE-78 CWE-78 CWE-269 CWE-269 CWE-416 CWE-269
7 7
8
CWE-416 CWE-416 CWE-352 CWE-352 CWE-352 CWE-352 CWE-22 CWE-269 CWE-78 CWE-78 C WE-78 CWE-22
8 1
9
CWE-22 CWE-22 CWE-22 CW E-22 CWE -22 CWE- 22 CWE-352 CWE-22 CWE-22 CWE-22 CWE-22 CWE- 78
9 -3
10
CWE-200 CWE-200 CWE-200 CWE-200 CWE-269 CWE-269 CWE-269 CWE-352 CWE-352 CWE-352 CWE-352 CWE-352
10 -3
11
CWE-287 CWE-287 CWE-120 CWE-269 CWE-200 CWE-120 CWE-120 CWE-120 CWE-120 CWE-120 CWE-120 CWE-120
11 2
12
CWE-119 CWE-120 CWE-269 CWE-1 20 CWE-120 CWE-200 CWE-287 CWE-287 CWE-287 CWE-287 CWE-287 CWE-863
12 9
13
CWE-120 CWE-269 CWE-287 CWE-287 CWE-287 CWE-287 CWE-200 CWE-200 CWE-863 CWE-863 CWE-863 CWE-287
13 -2
14
CWE-269 CWE-119 CWE-119 CWE-119 CWE-434 CWE-863 CWE-863 CWE-863 CWE-200 CWE-200 CWE-200 CWE-77
14 14
15
CWE-434 CWE-434 CWE-434 CWE-434 CWE-863 CWE-434 CWE-434 CWE-434 CWE-434 CWE-434 CWE-77 CWE-2 00
15 -5
16
CWE-862 CWE-190 CWE-190 CWE-863 CWE-119 CWE-119 CWE-476 CWE-476 CWE-476 CWE-476 CWE-434 CWE -434
16 -1
17
CWE-306 CWE-862 CWE-863 CWE-190 CWE-190 CWE-190 CWE-190 CWE-119 CWE-77 CWE-77 CWE-476 CWE-47 6
17 2
18
CWE-190 CWE-306 CWE-476 CWE-862 CWE-476 CWE-476 CWE-119 CWE-77 CWE-400 CWE-400 CWE-400 CWE-400
18 2
PREVIOUS NEXT
CWE-79
Mason Vulnerability Scoring Framework
Figure 5: Historical Rankings as of March 2022.
78 moved down 3 positions in the ranking.
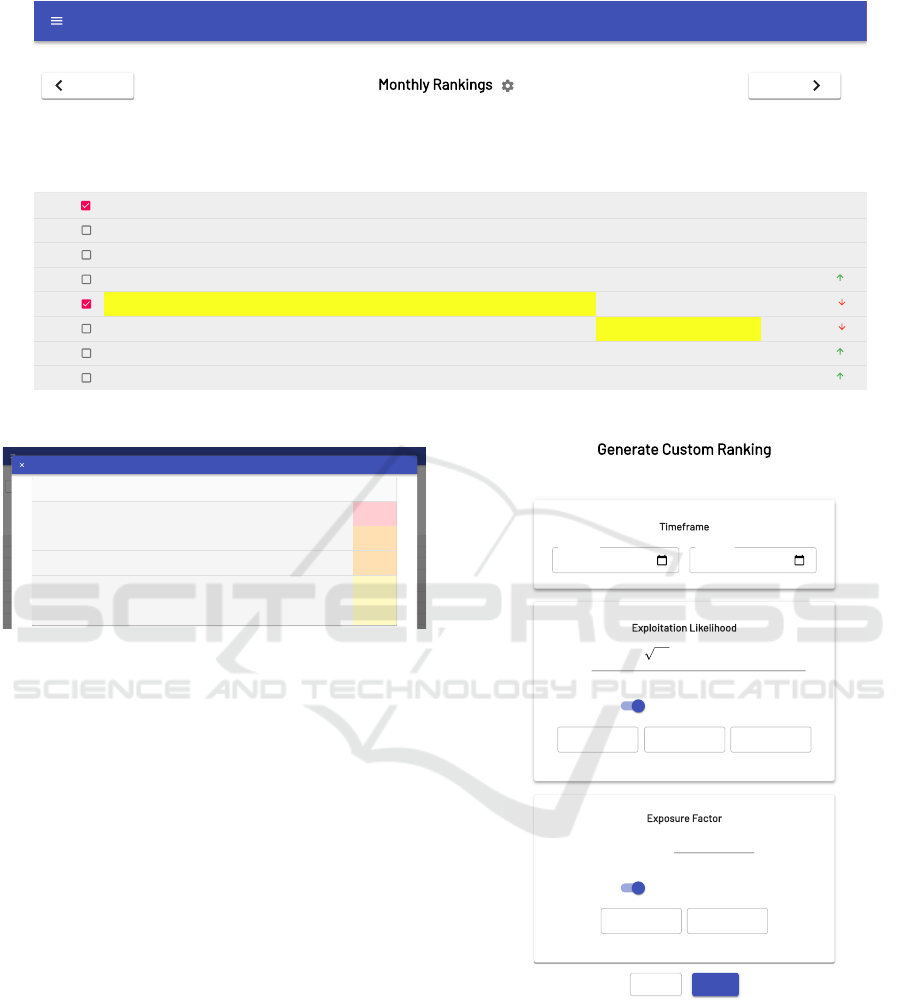
5.3 Live Rankings
The Live Rankings view shows the same type of in-
formation as the Historical Rankings view, but in this
case each monthly ranking reflects changes to the data
that occurred after the corresponding historical rank-
ing was computed. For instance, when MVSF com-
puted and published the monthly ranking for Febru-
ary 2022, the rank of CWE-125 had not changed over
the previous 12 months. However, as shown in Fig-
ure 6, the live ranking for February 2022, as of March
25, 2022, indicates that, based on new information
that become available after the historical ranking was
computed on March 1, CWE-125 is down one posi-
tion in the ranking.
Additionally, the live monthly rankings are com-
puted based on the values of the tunable parameters
selected by the user, which are clearly indicated in
the header section of the Live Rankings view, along
with information about the update frequency and the
last update. The user can change the value of the pa-
rameters by clicking on the gear icon in the header.
Similar to the historical rankings, these rankings are
computed based on data from the previous 24-month
period.
The ability of a user to examine the CVEs that
make up a CWE is also critical to understanding the
nature of a weakness and how it would affect their
systems. To this aim, the Live Rankings view includes
a feature that allows the user to access the list of CVEs
that are mapped to a CWE, sorted by their severity un-
der the MVSF scoring system (the severity of a vul-
nerability v is ρ(v) ·e f (v)). Selecting a CWE in the
Live Rankings view triggers the visualization of an in-
formation panel which contains several key statistics,
a link to the official MITRE entry for that CWE, and a
button to access the CWE Composition panel shown
in Figure 7. This panel shows all the CVEs mapped to
the selected CWE in decreasing order of severity and
color-coded based on the level of severity. For each
vulnerability, values of all the key vulnerability-level
metrics are also shown.
5.4 Custom Rankings
The Custom Rankings functionality is used to create
fully-customized rankings. Instead of returning a col-
lection of monthly rankings like the Historical Rank-
ings and Live Rankings views, this process returns a
single ranking, based on data in an arbitrary time-
frame specified by the user, as opposed to the standard
24-month period, and based on the parameter values
specified by the user. Figure 8 shows the entry form
for specifying the settings to be used in the generation
of a custom ranking.
As discussed earlier, MVSF considers different
variables in the computation of scores. In order to
provide better insights into how CWE scores are cal-
culated, the web application gives access to the sub-
scores of each CWE in both the Custom Rankings and
Live Rankings views. The list of subscores includes:
number of CVEs, average CVSS Exploitability score,
average Days Since Published, average CVSS Im-
pact score, average Exposure Factor, and average Ex-
SECRYPT 2022 - 19th International Conference on Security and Cryptography
222

Monthly Rankings
This information is updated every 4 hours.
Latest Update: Fri Mar 25 2022 20:00:02 GMT-0400 (Eastern Daylight Time)
Settings: : 0.75 : 0.25 : 0 : 0 : 0.5
Rank 2021-03 2021-04 2021-05 2021-06 2021-07 2021-08 2021-09 2021-10 20 21-11 2021-12 2022-01 2022-02 Rank Change
1
CWE-79 CWE-79 CWE-79 CWE-79 CWE-79 CWE-79 CWE-79 CWE-79 CWE -79 CWE-79 CWE-79 CWE-79
1 0
2
CWE-787 CWE-787 CWE-787 CWE-787 CWE-787 CWE -787 CWE-787 CWE-787 CWE-787 CWE-787 CWE-787 CWE -787
2 0
3
CWE-20 CWE-20 CWE-20 CWE-20 CWE-20 CWE-20 CWE-20 CWE-20 CWE -20 CWE-20 CWE-20 CWE-89
3 2
4
CWE-125 CWE-125 CWE-125 CWE-125 CWE-125 CWE -125 CWE-125 CWE-125 CWE-125 CWE-89 CWE-89 CWE-20
4 -1
5
CWE-89 CWE-89 CWE-89 CWE-89 CWE-89 CWE-89 CWE-89 CWE-89 CWE -89 CWE-125 CWE-125 CWE-125
5 -1
6
CWE-78 CWE-78 CWE-78 CWE-78 CWE-78 CWE-416 CWE-416 CWE-416 CWE-416 CWE-416 CWE-416 CWE-416
6 3
7
CWE-352 CWE-352 CWE-352 CWE-352 CWE-352 CWE-78 CWE-78 CWE-78 CWE-78 CWE-78 CWE-269 CWE-269
7 8
8
CWE-22 CWE-416 CWE-416 CWE-416 CWE-416 CWE-352 CWE-22 CWE-22 CWE-22 CWE-22 CWE-22 CWE-22
8 0
9
CWE-416 CWE-22 CWE-22 CWE-22 CWE-22 CWE-22 CWE-352 CWE-352 CWE-352 CWE-269 CWE-78 CWE-352
9 -2
10
CWE-200 CWE-200 CWE-200 CWE-200 CWE-200 CWE -120 CWE-269 CWE-269 CWE-269 CWE-352 CWE-352 CWE-78
10 -4
11
CWE-287 CWE-287 CWE-120 CWE-120 CWE-120 CWE -269 CWE-120 CWE-120 CWE-120 CWE-120 CWE-120 CWE -120
11 2
12
CWE-119 CWE-120 CWE-287 CWE-287 CWE-269 CWE-200 CWE-287 CWE-287 CWE-287 CWE-287 CWE-287 CWE-287
12 -1
13
CWE-120 CWE-119 CWE-269 CWE-269 CWE-287 CWE -287 CWE-200 CWE-200 CWE-863 CWE-863 CWE-863 CWE -863
13 9
14
CWE-434 CWE-269 CWE-119 CWE-434 CWE-434 CWE-434 CWE-863 CWE-863 CWE-200 CWE-200 CWE-200 CWE-77
14 14
15
CWE-269 CWE-434 CWE-434 CWE-119 CWE-863 CWE -863 CWE-434 CWE-434 CWE-434 CWE-434 CWE-434 CWE -200
15 -5
16
CWE-306 CWE-190 CWE-190 CWE-863 C WE-119 CWE-119 CWE-476 CWE-476 CWE-476 CWE-77 CWE-77 CWE-434
16 -2
PREVIOUS NEXT
α β γ δ c
Mason Vulnerability Scoring Framework
SELECT YEAR SETTINGS
Figure 6: Live Rankings as of March 25, 2022.
Monthly Rankings
This information i s updated every 4 ho urs.
Latest Update: Fri Mar 25 2022 20:00:0 2 GMT-0400 (Eastern Daylight Time)
Setti ngs: : 0.75 : 0 .25 : 0 : 0 : 0.5
Rank 2021-03 2021-04 202 1-05 2021-0 6 2021-07 2021-08 20 21-09 2021- 10 2021-11 2021 -12 2022 -01 2022-02 Rank Chan ge
1
CWE-79 CWE-79 CWE-79 CWE-79 CWE-79 CWE-79 CW E-79 CWE- 79 CWE-79 CWE-79 CWE -79 CWE-79
1 0
2
CWE-787 CWE-787 CWE-787 CWE-787 CWE- 787 CW E-787 CWE-787 CWE-787 CWE-787 CWE-787 CWE-787 CWE-787
2 0
3
CWE-20 CWE-20 CWE-20 CWE-20 CWE-20 CWE-20 CW E-20 CWE- 20 CWE-20 CWE-20 CWE -20 CWE-89
3 2
4
CWE-125 CWE-125 CWE-125 CWE-125 CWE- 125 CW E-125 CWE-125 CWE-125 CWE-125 CWE-89 CWE-89 CWE-20
4 -1
5
CWE-89 CWE-89 CWE-89 CWE-89 CWE-89 CWE-89 CW E-89 CWE- 89 CWE-89 CWE-125 CWE-125 CWE-125
5 -1
6
CWE-78 CWE-78 CWE-78 CWE-78 CWE-78 CWE-4 16 CWE- 416 CWE -416 CWE-41 6 CWE-416 CWE-416 CWE-416
6 3
7
CWE-352 CWE-352 CWE-352 CWE-352 CWE- 352 CWE-78 C WE-78 CWE-78 CWE-7 8 CWE-78 CW E-269 CWE-269
7 8
8
CWE-22 CWE-416 CWE-416 CWE-416 CWE-416 CWE -352 C WE-22 CWE -22 CWE-2 2 CWE-22 CWE-22 CWE-22
8 0
9
CWE-416 CWE-22 CWE-22 CWE-22 CWE-22 CWE- 22 CWE- 352 C WE-352 CWE- 352 CWE-269 C WE-78 CWE-352
9 -2
10
CWE-200 CWE-200 CWE-200 CWE-200 CWE- 200 CW E-120 CWE-269 CWE-269 CWE-269 CWE-352 CWE-352 CWE-78
10 -4
11
CWE-287 CWE-287 CWE-120 CWE-120 CWE- 120 CW E-269 CWE-120 CWE-120 CWE-120 CWE-120 CWE-120 CWE-120
11 2
12
CWE-119 C WE-120 C WE-287 CWE-287 CWE-269 CWE-200 CWE-287 CW E-287 CWE-2 87 CWE-28 7 CW E-287 CWE-2 87
12 -1
13
CWE-120 CWE-119 CWE-269 CWE-269 CWE- 287 CW E-287 CWE-200 CWE-200 CWE-863 CWE-863 CWE-863 CWE-863
13 9
14
CWE-434 CWE-269 CWE-119 CWE-434 CWE- 434 CW E-434 CWE-863 CWE-863 CWE-200 CWE-200 CWE-200 CWE-77
14 14
15
CWE-269 CWE-434 CWE-434 CWE-119 CWE- 863 CW E-863 CWE-434 CWE-434 CWE-434 CWE-434 CWE-434 CWE-200
15 -5
16
CWE-306 CWE-190 CWE-190 CWE-863 CWE-119 CWE-119 CWE-476 CWE-476 CWE-476 CWE-77 CWE-77 CWE-434
16 -2
17
CWE-862 CWE-306 CWE-863 CWE-19 0 CWE-1 90 CWE- 190 CWE-119 CWE-119 C WE-77 CWE- 476 CWE-476 CWE -476
17 2
18
CWE-190 CWE-862 CWE-476 CWE-86 2 CWE-4 00 CWE- 476 CWE -190 CW E-77 CWE -400 CWE-40 0 CW E-400 CWE-4 00
18 2
19
CWE-476 CWE-476 CWE-306 CWE-40 0 CWE-4 76 CWE- 400 CWE -400 CW E-400 CW E-119 C WE-190 CWE-190 CWE-190
19 -1
20
CWE-400 CWE-863 CWE-862 CWE-47 6 CWE-8 62 CWE- 862 CWE -77 C WE-190 CW E-190 CWE-119 CWE-119 CWE-119
20 -8
21
CWE-502 CWE-400 CWE-400 CWE-30 6 CWE-3 06 CWE- 502 CWE -502 CW E-502 CWE-8 62 CWE-502 CW E-862 CWE-86 2
21 -4
22
CWE-863 CWE-502 CWE-502 CWE-50 2 CWE-5 02 CWE -77 CWE -862 CWE-862 CW E-502 CWE -862 CWE-502 CW E-502
22 -1
23
CWE-798 CWE-798 CWE-798 CWE-77 CWE-77 C WE-306 CWE-306 CWE-306 CWE-306 CWE-74 CWE-798 CWE-276
23 3
24
CWE-732 CWE-732 CWE-77 CWE-798 CWE-79 8 CWE- 276 C WE-276 CWE-276 CW E-276 CWE -798 CWE-74 CWE-74
24 1
25
CWE-74 CWE-77 CWE-732 CWE-2 76 CWE- 276 CWE -798 CW E-798 CW E-798 CWE -798 CWE- 276 CWE-276 CWE -798
25 -2
26
CWE-276 CWE-74 CWE-276 CWE-74 CWE-74 CWE-7 4 CWE-74 CWE-74 CWE-74 CWE-306 CWE -306 CWE-668
26 23
27
CWE-522 CWE-276 CWE-74 CWE-732 CWE-73 2 CWE- 732 C WE-732 CWE-732 CW E-732 CWE -918 CWE-918 CW E-918
27 6
28
CWE-77 CWE-522 CWE-522 CWE-522 CWE-5 22 CWE- 918 CWE -918 CW E-918 CWE-9 18 CWE-94 CWE-94 CWE-3 06
28 -12
29
CWE-295 CWE-611 CWE-295 CWE-94 CWE-91 8 CWE- 522 C WE-522 CWE-522 CW E-522 CWE -522 CWE-668 CW E-94
29 3
30
CWE-601 CWE-295 CWE-94 CWE-295 CWE-29 5 CWE- 295 C WE-295 CWE-295 C WE-94 CW E-668 CWE-522 C WE-732
30 -6
31
CWE-611 C WE-601 C WE-601 CWE-601 CWE-94 CWE-94 CWE-94 CWE-94 CWE- 295 CWE-7 32 C WE-732 CWE- 522
31 -4
32
CWE-94 CWE-94 CWE- 611 CWE-918 CWE- 601 CWE -601 CW E-601 CW E-601 CWE -601 CWE- 295 CWE-601 CWE -601
32 -2
33
CWE-918 CWE-918 CWE-918 CWE -611 CWE-611 CWE-611 CWE -611 CW E-611 CWE-668 CWE-601 CWE -295 CWE-295
33 -4
34
CWE-362 CWE-362 CWE-362 CWE-36 2 CWE-3 62 CWE- 362 CWE -362 CW E-362 CW E-611 CWE-611 CWE-6 11 CWE -611
34 -3
35
CWE-319 CWE-319 CWE-319 CWE-31 9 CWE-3 19 CWE- 319 CWE -668 CW E-668 CWE-3 62 CWE-362 CW E-362 CWE-36 2
35 -1
36
CWE-59 CWE-59 CWE-401 CWE-4 01 CWE- 401 CWE -401 CW E-401 CW E-401 CWE -401 CWE- 319 CWE-427 CWE -427
36 2
37
CWE-401 CWE-401 CWE-59 CWE-59 CWE-59 CWE-4 27 CW E-319 CW E-319 CWE -319 CWE- 427 CWE-319 CWE -319
37 -2
38
CWE-427 CWE-427 CWE-427 CWE-42 7 CWE-4 27 CWE- 668 CWE -427 CW E-427 CWE-4 27 CWE-312 CW E-312 CWE-31 2
38 2
39
CWE-532 CWE-312 CWE-312 CWE-31 2 CWE-3 12 CWE -59 CWE -312 CWE-755 CW E-312 CWE -843 CWE-755 CW E-843
39 4
40
CWE-312 CWE-755 CWE-755 CWE-53 2 CWE-6 68 CWE- 312 CWE -59 C WE-59 CWE-59 CWE-401 CWE -843 CWE-755
40 1
41
CWE-755 CWE-532 CWE-532 CWE-75 5 CWE-5 32 CWE- 755 CWE -755 CW E-312 CWE-7 55 CWE-755 CW E-327 CWE-40 1
41 -4
PREVI OUS NEXT
α β γ δ c
Mason Vulnerability Scoring Framework
SELEC T YEA R SETT INGS
CWE ID: CWE-37 7
CWE Details
Number of CVEs : 10
Avg Exploitabili ty V2: 4.77
Avg Days Since P ublished: 411.80
Avg Impact Score V2: 5.56
Avg Exposure Fac tor: 0.90
Avg Base Score: 4.43
Avg Exploitation Likelihood: 0. 64
Known IDS Rule s: 0
Deployed IDS R ules: 0
Overall Score: 6
VIEW CVE COMPOS ITION
1 CVE-2012-2 666 NETWORK 2021/07/09 2 60 0.99 10 0.96 6.4
0.95
2 CVE-2011-4119 NETWORK 2021/10/26 151 0.99 10 0.96 6.4
0.95
3 CVE-20 20-8027 LOCAL 2021/02/11 408 0.86 3.9 0.96 6.4
0.82
4 CVE-2021-20202 LOCAL 2021/05/12 318 0.86 3.9 0.96 6.4
0.82
5 CVE-2020 -8032 LOCAL 2021/02/25 394 0.82 3.4 0.99 10
0.81
6 CVE-2020- 8030 LOCAL 2021/02/11 408 0.86 3.9 0.91 4.9
0.78
7 CVE-2021-2 5316 LOCAL 2021/04/14 346 0 .86 3.9 0.77 2.9
0.66
8 CVE-2020- 1740 LOCAL 2020/03/16 740 0.82 3.4 0.77 2. 9
0.63
9 CVE-2021-2942 9 LOCAL 2021/04/12 348 0 .82 3.4 0. 77 2.9
0.63
10 CVE-2020-1733 LOCAL 2020/03/11 745 0.61 1.9 0 .96 6.4
0.59
Currently displaying: 50 CVE's out of 10
LOAD MORE
LOAD ALL
Index CVE ID
Attack
Vector
Publish
Date
Days Since
Published
Exploitation
Likelihood
Exploitabili ty
Score
Exposure
Factor
Impact
Score
MVSF Overall
Score
CVE Composition of CWE-377 (2022-02)
Figure 7: CWE Composition panel.
ploitation Likelihood.
Once the user has generated a ranking tailored to
their needs, they can download it as a read-only Excel
spreadsheet. This allows users to save and store their
rankings for later review and possible use for their se-
curity assessment.
5.5 CVE Search
The CVE Search functionality allows the user to re-
trieve information that MVSF has ingested for each
CVE, along with the vulnerability metrics computed
by MVSF. Figure 9 shows the results of searching the
database for CVE-1999-0199.
6 DISCUSSION
In this section, we briefly compare MVSF against
MITRE Top 25 CWEs and OWASP Top 10 and sum-
marize its benefit over these two solutions. MVSF
rankings and MITRE CWE rankings serve a similar
purpose. However, there are significant differences
that deserve attention.
Generate Custom Ranking
To get the ranking for a specific timeframe, please specify the parameters below.
Timeframe
Exploitation Likelihood
Use default values
Exposure Factor
Use default values
Contact Us
Research
Hall, Suite
[e-mail]
+1 (703) 993-
12/01/2018
12/01/2020
ρ(v) =
e
γ⋅∣I DS (v)∣
k
1− e ⋅ 1− e(
−α⋅ t(v)
) (
−β⋅Exploitability(v)
)
[0, +∞)
0.75
α
[0, +∞)
0.25
β
[0, 1]
0
γ
ef(v, h) =
e
δ⋅∣IDS (v)∣
d
1 − e
−c⋅impact(v)
[0, +∞)
0.5
c
[0, 1]
0
δ
RESET RANK
Home
Start Date End Date
Mason Vulnerability Scoring Framework
Figure 8: Custom ranking definition.
The main difference is the static and non-
customizable nature of MITRE CWE rankings. In the
ever-changing cyberspace, new vulnerabilities are in-
troduced and discovered very frequently. This chang-
ing ecosystem can render such annual rankings obso-
lete in a short period of time. To adapt to this rate of
change, MVSF offers rankings that are updated dy-
namically through the day as new vulnerability infor-
Mason Vulnerability Scoring Framework: A Customizable Framework for Scoring Common Vulnerabilities and Weaknesses
223

CVE Search
Please Note: All searches must be in the format of "CVE-XXXX-XXXXX", other formats will not be submitted.
Data Range Rating
0.1 - 0.39 LOW
0.40 - 0.69 MEDIUM
0.70 - 0.89 HIGH
0.90 - 1.0 CRITICAL
Settings: : 0.75 : 0.25 : 0 : 0 : 0.5
CVE-1999-0199
MVSF Score: 0.95 | Rating: CRITICAL
CVE Data:
CVE ID: CVE-1999-0199
CWE Category: CWE-252
Base Score: 7.50
Exploitability Score: 10.00
Impact Score: 6.40
Publication Date: 2020/10/06
Days Since Publication: 1 Year(s) 171 Days
Known IDS Rules: 0
CVE Metrics:
Exploitation Likelihood: 0.99
Exposure Factor: 0.96
Overall MVSF Score: 0.95
Contact Us
Research Hall, Suite 417
George Mason University
4400 University Dr.
Fairfax, VA 22030
United States of America
[e-mail]
[phone]
csis.gmu.edu
Disclaimer: CVE and CWE are trademarks of The MITRE Corporation.
α β γ δ c
CVE-1999-0199
SEARCH
Home
About
Historical Rankings
Live Rankings
Custom Rankings
Mason Vulnerability Scoring Framework
Figure 9: Search results for CVE-1999-0199.
mation becomes available. To this aim, it is important
to consider that MVSF filters CVE information by
publication date, whereas MITRE filters CVE infor-
mation by CVE year. This is a fundamental difference
because it enables us to generate rankings based on
data from an arbitrary time interval – such as the 24-
month moving window used for computing monthly
rankings – whereas MITRE can only compute rank-
ings with data from one or more consecutive calendar
years.
In addition to the difference in the frequency at
which rankings are published and the way we look
at raw vulnerability data (CVE year vs. publication
date), MVSF and MITRE rankings of CWEs differ for
the type of information they factor in the computation
of the rankings. While MITRE only considers CVSS
scores, MVSF considers a larger set of variables, in-
cluding system-specific ones, and defines an approach
for factoring in additional variables as needed. Last
but not least, MITRE’s rankings are limited to the top
25 CWEs, whereas we list the top 150 CWEs.
The Open Web Application Security Project
(OWASP) Foundation is another organization that
publishes rankings of software security flaws, and
their reports are standard awareness documents for
developers and web application security engineers.
Nonetheless, these rankings have their shortcomings.
Internet and network environments are rapidly chang-
ing and becoming more dynamic and security mecha-
nisms have to adapt to this rate of change (Fernandes
et al., 2014). Just like MITRE’s Top 25 CWEs rank-
ing, OWASP Top 10 rankings fail to keep up with this
large rate of change as they are published annually.
Similar to MITRE’s rankings, OWASP rankings are
static and do not allow any level of customization.
6.1 Evaluation
To validate the quality of our scoring system, we an-
alyzed the correlation between the CWE scores com-
puted through MVSF and those computed by MITRE
for the top 40 CWEs
13
. For this evaluation, the MVSF
scores were computed using settings of the parame-
ters that best approximate MITRE’s ranking. Under
these conditions, the correlation between MVSF and
MITRE scores is 0.962 (R
2
= 0.926), as shown in Fig-
ure 10. In other words, a CWE ranking that approxi-
mates MITRE’s ranking can be generated as a special
case of MVSF ranking, but our framework is more
general and can adjust rankings based on other inputs
not considered by MITRE.
R² = 0.926
100
200
400
800
1,600
3,200
2 4 8 16 32 64
MVSF Score
MITRE Score
Figure 10: Correlation between MVSF and MITRE scores.
7 CONCLUSIONS
The Mason Vulnerability Scoring Framework
(MVSF) is a customizable framework for scoring
common vulnerabilities and weaknesses that offers
numerous advantages over the static and predefined
scoring systems that are available today. MVSF
could become an essential resource for security ad-
ministrators, software developers, or anyone who is
interested in mitigating security vulnerabilities found
in their systems. We have extensively described the
key features of the framework, with respect to both
its theoretical foundations and its architecture, and
have discussed the current implementation of the
system. In these concluding remarks, we want to
highlight some current limitations of the framework
and discuss the roadmap for future developments.
As mentioned earlier, current limitations of the
framework include the incomplete integration with in-
13
MITRE publishes the scores for additional 15 weak-
nesses that scored just outside of the final Top 25.
SECRYPT 2022 - 19th International Conference on Security and Cryptography
224

trusion detection systems (end users do not currently
have a way to submit information about deployed IDS
rules) and the lack of caching mechanisms for reduc-
ing the cost of computing live and custom rankings on
demand. In addition to addressing these limitations,
we plan to work in three major directions, namely
(i) investigating predictive analytics approaches to an-
ticipate future trends in the severity of vulnerabili-
ties and weaknesses; (ii) developing APIs to make
the functionality of the framework available for in-
tegration with third-party applications; and (iii) inte-
gration with vulnerability scanning to enable further
customization of the rankings based on the specific
vulnerabilities that exist in a given system.
ACKNOWLEDGEMENTS
This work was funded in part by the US Department
of Defense under the DARPA ConSec program, in
part by the National Science Foundation under award
CNS-1822094, and in part by the Commonwealth Cy-
ber Initiative (CCI). Any opinions expressed herein
are those of the authors and do not necessarily reflect
the views of the U.S. Department of Defense or any
other agency of the U.S. Government.
REFERENCES
Aigner, W., Miksch, S., M
¨
uller, W., Schumann, H., and
Tominski, C. (2007). Visualizing time-oriented data
— A systematic view. Computers & Graphics,
31(3):401–409.
Black, L., Scala, N. M., Goethals, P. L., and Howard, II,
J. P. (2018). Values and trends in cybersecurity. In
Proceedings of the 2018 Industrial and Systems Engi-
neering Conference, pages 2009–2014, Orlando, FL,
USA. IISE.
Christey, S. (2008). The evolution of the CWE development
and research views. Technical report, The MITRE
Corporation.
Fernandes, D. A. B., Soares, L. F., Gomes, J. V., Freire,
M. M., and In
´
acio, P. R. M. (2014). Emerging Trends
in ICT Security, chapter A Quick Perspective on the
Current State in Cybersecurity, pages 423–442. Mor-
gan Kaufmann.
Iganibo, I., Albanese, M., Mosko, M., Bier, E., and Brito,
A. E. (2021). Vulnerability metrics for graph-based
configuration security. In Proceedings of the 18th In-
ternational Conference on Security and Cryptography
(SECRYPT 2021), pages 259–270. SCITEPRESS.
Jajodia, S. and Albanese, M. (2017). Theory and Models
for Cyber Situation Awareness, volume 10030 of Lec-
ture Notes in Computer Science, chapter An Integrated
Framework for Cyber Situation Awareness, pages 29–
46. Springer.
Mell, P., Scarfone, K., and Romanosky, S. (2006). Com-
mon Vulnerability Scoring System. IEEE Security &
Privacy, 4(6):85–89.
Mukherjee, P. and Mazumdar, C. (2018). Attack difficulty
metric for assessment of network security. In Proceed-
ings of 13th International Conference on Availability,
Reliability and Security (ARES 2018), Hamburg, Ger-
many. ACM.
Wang, L., Zhang, Z., Li, W., Liu, Z., and Liu, H.
(2019). An attack surface metric suitable for het-
erogeneous redundant system with the voting mech-
anism. In Proceedings of the International Confer-
ence on Computer Information Science and Applica-
tion Technology (CISAT 2018), volume 1168 of Jour-
nal of Physics: Conference Series, Daqing, China.
IOP Publishing.
Mason Vulnerability Scoring Framework: A Customizable Framework for Scoring Common Vulnerabilities and Weaknesses
225