Triangular Expansion Revisited: Which Triangulation Is The Best?

Jan Mikula

1,2 a

, Miroslav Kulich

2 b

Department of Cybernetics, Faculty of Electrical Engineering, Czech Technical University in Prague,

Karlovo n

est

ı 13, 12135 Praha 2, Czech Republic

Czech Institute of Informatics, Robotics and Cybernetics, Czech Technical University in Prague,

Jugosl

avsk

ych partyz

u 1580/3, 16000 Praha 6, Czech Republic

Keywords:

Autonomous Agents, Visibility Region, Triangular Expansion Algorithm, Triangulation, TriVis.

Abstract:

Visibility region is a classic structure in computational geometry that ﬁnds use in many agent planning prob-

lems. Triangular expansion algorithm (TEA) is the state-of-the-art algorithm for computing visibility regions

within polygons with holes in two dimensions. It has been shown that it is two orders of magnitude faster

than the traditional rotation sweep algorithm for real-world scenarios. The algorithm triangulates the under-

lying polygon and recursively traverses the triangulation while keeping track of the visible region. Instead

of the constraint Delaunay triangulation used by default, this paper introduces the idea of optimizing the

triangulation to minimize the expected number of triangle edges expanded during the TEA’s traversal while

assuming that every point of the input polygon is equally likely to be queried. The proposed triangulation is

experimentally evaluated and shown to improve TEA’s mean query time in practice. Furthermore, the TEA is

modiﬁed to consider limited visibility range of real-life sensors. Combined with the proposed triangulation,

this adjustment signiﬁcantly speeds up the computation in scenarios with limited visibility. We provide an efﬁ-

cient open-source implementation called TriVis which, besides the mentioned, includes determining visibility

between two points and other useful visibility-related operations.

1 INTRODUCTION

Visibility is a fundamental concept in computational

geometry, security, and mission planning for mobile

robots. In general, we say that a point is visible by

an agent from its conﬁguration if the agent is phys-

ically capable of seeing the point. All points visi-

ble from that particular conﬁguration form a visibil-

ity region. Visibility regions are useful when one

needs to guard an art gallery by a set of static ob-

servers (O’Rourke, 1987), establish a watchman’s

route from which the whole boundary or interior of

an area is visible (Ntafos, 1992; Mikula and Kulich,

2022), or provide a guarantee that a room is free of

intruders (Guibas et al., 1997). The classic formu-

lation assumes the conﬁguration is a point in poly-

gon with holes W ⊂ R

, also called polygonal do-

main or polygonal map, and two points q, p ∈ W are

visible to each other if segment qp ⊂ W . The vis-

ibility region usually takes the form of star-shaped

polygon, but in some exceptional cases, the polygon

https://orcid.org/0000-0003-3404-8742

https://orcid.org/0000-0002-0997-5889

can have attached one-dimensional antennae (Bungiu

et al., 2014). However, the antennae can be often

neglected; thus, visibility region V (q) ⊂ W is fre-

quently denoted just as visibility polygon.

Although computing visibility polygon V (q) for

given query point q ∈ W can be done in polynomial

time, frequent employment of this computation as a

sub-routine in algorithms often solving NP-hard prob-

lems (such as those mentioned earlier) causes the im-

mense need for an efﬁcient implementation. The cur-

rent state of the art is the triangular expansion algo-

rithm (TEA) by (Bungiu et al., 2014). TEA’s worst-

case query time complexity is O(n

), where n denotes

the number of W ’s vertices. However, the authors

show that in real-world scenarios the TEA can be

by two orders of magnitude faster than the rotational

sweep algorithm (RSA) by (Asano, 1985) which runs

in O(n logn) in the worst case. The reason is that ba-

sic operations performed by the TEA are extremely

fast compared to the RSA’s, and the polygonal map

on which TEA actually runs in O(n

) has a unique

structure quite dissimilar to practical scenarios.

The TEA is based on a simple idea of triangulat-

ing the underlying polygonal map in a preprocess-

Mikula, J. and Kulich, M.

Triangular Expansion Revisited: Which Triangulation Is The Best?.

DOI: 10.5220/0011278700003271

In Proceedings of the 19th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2022), pages 313-319

ISBN: 978-989-758-585-2; ISSN: 2184-2809

313

Figure 1: An example of a visibility region computed by

the TEA. Borders and holes of the input polygon W are

black. The query point q is green. Triangle edges (not) ex-

panded by the TEA are (orange) red. (Un)visited triangles

are (gray) white. The restricted views around q are translu-

cent blue and form the output visibility polygon V (q).

ing phase and then using the triangulation structure

in the query phase to ﬁnd requested visibility regions.

Having the structure, TEA’s answer to a query starts

by locating triangle △

containing the query point q.

This can be done by a simple walk, as the authors

suggest. A recursive procedure is then initiated by

expanding the view of q through every edge e

, i ∈

{1,2,3}, of △

to the neighboring triangle (unless e

is part of W ’s border) and restricting the view by e

’s

endpoints. As the recursion proceeds only the edges

that are at least partially in the current restricted view

are expanded and the view can be further restricted

by the endpoints of next expanded edges. A branch

of the recursion ends when either all edges that are

candidates for expansion are part of the W ’s border

or the restricted view angle is reduced to zero (may

lead to creating an antenna). After all branches of the

recursion have ended, the resulting V (q) is the col-

lection of all the restricted views around q acquired

up to that time. See Figure 1 for illustrations of some

of these concepts.

TEA’s query time is clearly proportional to the

number of edge expansions η during the computation

of V (q). In some sense, the TEA is output-sensitive

because η partially depends on the complexity of the

output, but as the authors state, not strictly because the

algorithm may traverse an edge even though the edge

does not contribute to the boundary of V (q) (Bungiu

et al., 2014). Preprocessing, i.e., constructing the tri-

angulation of W , can be done at best in O(n log n) by

efﬁcient construction of the constraint Delaunay tri-

angulation (CDT) as suggested by (Shewchuk, 2002),

although TEA’s authors use a CDT implementation

that runs in O(n

). The TEA will work correctly with

any valid triangulation. However, the inﬂuence of

particular triangulation choice on η and thus TEA’s

query time has escaped researchers’ attention so far.

Yet, assuming every point in W is equally likely to be

queried, it can be shown that certain triangulations are

less or more suited for usage in the TEA than others.

The best triangulation is clearly the one minimiz-

ing the expected (mean) number of edge expansions

during the progress of the algorithm. In this paper, we

design a simple heuristic procedure to obtain a good

approximation of such triangulation. The proposed

procedure is run on several benchmark instances to

obtain the new type of triangulation for each. These

triangulations are then experimentally evaluated in

the query phase of the TEA and compared to the CDT

shown to signiﬁcantly reduce mean number of expan-

sions

η and thus mean query times for all studied

cases and one million random query points.

This work does not evaluate TEA’s preprocessing

time, signiﬁcantly increased by the triangulation opti-

mization, which is partially caused by a naive imple-

mentation of some of its sub-procedures. Instead, the

primary purpose of this work is to draw attention to

the interesting observation that the particular triangu-

lation matters to TEA’s query times.

Overall, the contribution of this work is three-fold.

1. We propose a new type of triangulation to improve

TEA’s query time,

2. modify the TEA to efﬁciently cope with more re-

alistic visibility regions, and lastly,

3. provide an efﬁcient open-source TEA’s imple-

mentation tailored for some of the most common

visibility-related tasks, e.g., computing visibility

regions, ﬁnding all W ’s vertices visible from q,

and determining visibility between two queries.

2 PROBLEM DEFINITION

In this section, we formalize the search for a trian-

gulation that approximately minimizes the expected

number

η of edge expansions done by the TEA while

assuming that query points are drawn from a known

probability distribution. The approximation is based

on a further assumption that the number of edge ex-

pansions η is the same as that of expanded edges µ.

In general, the assumption is not valid because TEA

can expand some triangle edges more than once. (See

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

314

Figure 1, where the six left-most expanded (red)

edges are actually expanded twice because they are

visible through two of the (blue) restricted views.)

However, as we show in our experiments, the assump-

tion makes a good approximation because in real-

world scenarios the two values are similar, i.e., η ∼ µ.

Note that exactly those triangle edges that are (at

least partially) visible from query point q but do not

contribute to the boundary of W are expanded by

the TEA (see Figure 1). Therefore, the number of

edges expanded by the TEA at least once given query

point q and triangulation T can be computed as

µ(q,T ) =

∑

e∈E(T ) : e /∈∂W

Visible(e,q), (1)

where E(T ) denotes the set of T ’s edges, ∂W the

border of W , and

Visible(uv,q) =











1 if exists any p ∈ uv

visible from q,

0 else.

(2)

Let the location of the query point be described by

random variable Q with a known two-dimensional

probability density function (PDF). Then, the ex-

pected number of expanded edges is given by

¯µ(T ) =

∑

e∈ E(T ) : e /∈∂W

P(Visible(e,Q) = 1), (3)

where P(Visible(e,Q) = 1) is the probability that seg-

ment e is visible from the point value taken by Q.

The optimal triangulation T

⋆

is the one minimizing

¯µ(T ), i.e.,

⋆

= argmin

T ∈T (W )

¯µ(T ), (4)

where T (W ) denotes the set of all possible triangu-

lations of W .

Let us further assume that every point in W

is equally likely to be queried. This assumption

known in the literature as the principle of indif-

ference (Keynes, 1921) implies modeling the query

point’s location by random variable Q following PDF

that is uniform inside W and zero outside. This yields

a speciﬁc formula for computing the probability of

segment e being visible from the value taken by Q:

P(Visible(e,Q) = 1) =

Area(V (e))

Area(W )

, (5)

where Area(V (e)) is the area of a region visible

from e, and Area(W ) is the area of the whole polyg-

onal map. An example of region V (e) visible from

segment e is shown in Figure 2. Substituting (5)

into (3) and the result into (4) while removing the con-

stant factor 1/Area(W ) from the optimization, we get

⋆

= argmin

T ∈T (W )

∑

e∈ E(T ) : e /∈∂W

Area(V (e))

. (6)

Figure 2: Regions visible from segment e while assuming

different maximal visibility ranges. Borders and holes of

the input polygon W are black. Segment e is green. The re-

gion visible from e is white, while the unvisible part of W is

gray. Borders of the d-visible regions for restricted visibil-

ity ranges d = 3, 6, and 12 meters are red, blue, and orange,

respectively.

We call the resulting T

⋆

minimum visibility triangu-

lation (MinVT).

3 SOLUTION APPROACH

3.1 Constructing the New Triangulation

Finding the MinVT is a special case of ﬁnding a tri-

angulation minimizing the sum of values (weights) on

its edges; a problem known as the minimum weight

triangulation (MWT), which is NP-hard for a gen-

eral set of points on a plane and arbitrarily deﬁned

weights (Mulzer and Rote, 2008). For the proposed

MinVT, the weight of candidate edge e is w(e) =

Area(V (e)) (see (6)).

Unlike the triangulation of a set of points, a tri-

angulation of polygonal map W always contains the

edges that contribute to the boundary of W . In ad-

dition, a segment is an edge candidate only if its

endpoints are vertices of W and are visible to each

other. Although there are known methods for com-

puting the MWT of a simple (without holes) poly-

gon P (Grantson et al., 2008), the MWT of a poly-

gon with holes W was not yet addressed in the lit-

erature. Therefore, we approximate the MWT of W

by an iterative improvement of its CDT. Starting with

T ← CDT(W ), in each iteration i, random triangle

Triangular Expansion Revisited: Which Triangulation Is The Best?

315

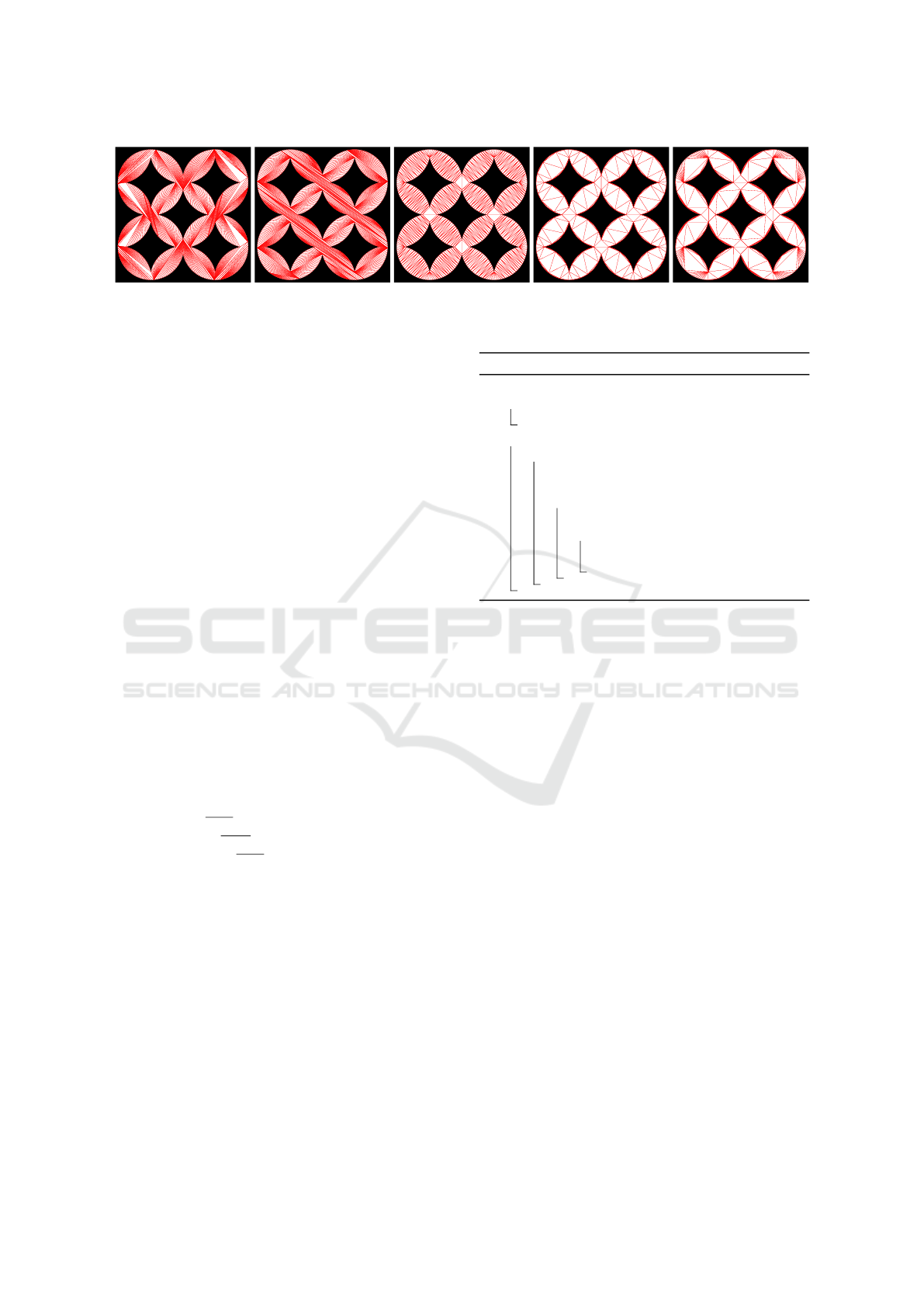
(a) MaxVT (b) MaxLT (c) CDT (d) MinLT (e) MinVT

Figure 3: Different triangulations of the same input polygon ordered according to their (increasing) efﬁciency in the TEA.

△

∈ T is selected ﬁrst. A simple polygon P

is then

generated from △

by gradually adding random adja-

cent triangles from T . The process of forming P

ﬁnished when no triangle can be added to it, i.e., when

adding an arbitrary triangle violates simplicity of the

polygon (i.e., adds a hole). Triangles forming P

are

then substituted in T by the MWT of P

. This process

converges typically in less than 10 iterations.

The MWT of simple polygon P has a recursive

substructure, which allows to employ dynamic pro-

gramming (Grantson et al., 2008) depicted in Algo-

rithm 1. Assuming that polygon vertices are num-

bered consecutively around the polygon boundary,

i.e., P = ⟨p

,.. ., p

⟩, a tree of weights W

i, j

of sub-

polygons with vertices between p

and p

is build

starting from triangles and ending when W

1,n

is deter-

mined. Weights of non-trivial sub-polygons deﬁned

by pair of indices (i, j) are evaluated considering all

possible triangles △

i, j,k

. Each triangle divides the

polygon into three parts: the triangle itself, the sub-

polygon to the left, and to the right. Weight W

i, j

the minimal sum of weights of these parts and k is

stored in K

i, j

. The weight of triangle △

i, j,k

is com-

puted as

Weight(△

i, j,k

) =

···













w(p

) +

w(p

) +

w(p

)



if p

, p

are

pairwise visible

to each other,

∞ else.

(7)

Finally, the MWT of P is reconstructed from K in

linear time. Starting with pair (1,n) we recursively

traverse matrix K. In each step, pair (i, j) determines

the base of the triangle △

i, j,K

i, j

, which is reported and

the reconstruction is called subsequently for its edges

(i,K

i, j

) and ( j,K

i, j

The construction procedure described above can

be employed to generate various triangulations of in-

put polygon with holes W depending on the used

weights:

• MinVT : w(e) = Area(V (e)),

• MinLT : w(e) = Length(e),

Algorithm 1: MWT for simple polygon P .

1 Let P = ⟨p

,..., p

⟩.

2 for i = 2,...,n do

3 W

i−1,i

← 0

4 for δ = 2,...,n − 1 do

5 for i = 1,...,n − δ do

6 j ← i + δ

7 W

i, j

← ∞

8 for k = i + 1,..., j − 1 do

9 val ← W

i,k

k, j

+ Weight(△

i, j,k

)

10 if val < W

i, j

then

11 W

i, j

= val

12 K

i, j

= k

• MaxVT : w(e) = −Area(V (e)),

• MaxLT : w(e) = −Length(e);

see Figure 3 for examples of these triangulations and

CDT, all computed on the same input.

3.2 d-TEA Modiﬁcation

Visibility regions are a general concept to model

agent’s ability to visually cover part of the environ-

ment in which it operates. So far, we have consid-

ered the most idealized case of omnidirectional vision

with an unlimited visibility range. However, in real-

life applications, visibility regions can be subject to

some additional constraints. Take robotics, for exam-

ple. Although omnidirectional sensors are common

in robotics, their resolution over longer distances is

limited to ﬁnite range d. A straightforward solution,

in this case, is to compute the standard visibility re-

gion V (q) by the TEA and then intersect the result

with a circle of radius d centered in q to obtain re-

gion V (q,d). Nevertheless, if the area of V (q,d) is

much smaller than the area of the original V (q) this

approach is highly inefﬁcient because the TEA ex-

pands many edges that do not contribute to the output.

To be more efﬁcient with a limited visibility range,

we suggest an early exit strategy for the TEA, called

d-TEA. During the recurring procedure, only edges

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

316

Table 1: Properties of the polygonal maps.

map n h x [m] y [m] a [m

] comment

ar 938 11 45.1 43.7 782 AR0018SR (MAI)

c4 632 5 31.6 31.6 623 artiﬁcial

de 362 4 25.2 30.8 391 den312d (MAI)

dr 864 14 57.2 47.8 692 dr_ dungeon (MAI)

e1 483 1 18.8 18.9 153 expl. data (sim.)

ec 1126 7 24.4 19.7 212 expl. data (real)

jh 278 9 20.6 23.2 460 real

la 331 35 40.0 40.0 1153 artiﬁcial

pb 92 3 133.3 104.9 1504 real

ph 153 23 20.0 20.0 367 artiﬁcial

ta 87 2 39.7 46.9 731 real

ar de dr e1 ec

jh la pb ph ta

Figure 4: Polygonal maps used in the experiments.

that either are inside or intersect the circle of radius

d centered in q are expanded, and those that do not

are added to the boundary of output region V

′

(q,d).

To obtain the requested V (q,d) ⊂ V

′

(q,d), the circle

intersection is computed efﬁciently by rotating around

q utilizing the star shape of V

′

(q,d).

Although the extension from TEA to d-TEA may

seem trivial, we need to contemplate that the pro-

posed early exit strategy directly affects how many

edges are expanded by the algorithm and thus also

the criterion optimized when constructing the pro-

posed triangulation MinVT. The best triangulation for

TEA may not be the same for d-TEA with various

values of d. Therefore, we need to adapt MinVT’s

edge weight w(e) from Area(V (e)) to Area(V (e,d)),

where V (e,∞) = V (e) and region V (e,d) is d-visible

from segment e for d ∈ (0,∞). d-visibility extends the

concept of visibility, whereas two points are visible

to each other if and only if the line segment between

them lies entirely in W and is no longer than d. Fig-

ure 2 shows examples of d-visible regions from par-

ticular segment e in 20 m × 20 m W for d = 3, 6, and

12 meters. Considering d-visibility, the MinVT trian-

gulation is denoted as d-MinVT.

3.3 TriVis: The Implementation

C++ implementation of the TEA, d-TEA, and MWT

is publicly available along with the data and conﬁgu-

ration ﬁles that we used in our experiments.

The im-

plementation is available in many variants tailored for

computing visibility regions, ﬁnding all environment

vertices that are visible from a query point, or deter-

mining visibility between two query points. For com-

puting the CDT, TriVis uses Triangle (Shewchuk,

1996).

4 EXPERIMENTAL EVALUATION

The proposed triangulation (MinVT) has been eval-

uated on 11 polygonal maps obtained from various

sources. The maps and some of their properties are

listed in Table 1. Here, n denotes the number of map’s

vertices, h the number of its holes, x and y its dimen-

sions, and a its area. Maps ar, de, and dr are based

on 2D grid maps from Moving AI (MAI) Lab web-

sites

(Sturtevant, 2012) that we converted into polyg-

onal representation. Full names of the MAI maps are

in the comment column of the table. Maps e1, and

ec are based on mobile robot exploration data (Kulich

et al., 2018) obtained from simulation, and real robot,

respectively. Maps jh, pb, ta, la, and ph are robot

mission planning benchmarks from which the ﬁrst

three are inspired by real indoor environments, an the

last two are artiﬁcial. All maps mentioned so far are

shown in Figure 4 (not in scale). Finally, c4 is the

map designed speciﬁcally for this paper to manifest

differences between the considered triangulations and

is shown in Figure 3.

The MinVT, CDT, and the other triangulations

discussed in Section 3 have been constructed for all

the considered maps. Then, the triangulations were

tested in the query phase of the TEA. One million

uniformly random query points were generated in-

side each map, and then visibility regions for all these

points were computed by the TEA using the stored

triangulations. During the computations, the num-

bers of expansions were stored and then averaged to

obtain metric

η. The results in Table 2 show the

values of

η and average computational times

t for

all the triangulations and maps. In addition, for the

MinVT, the table displays the estimated value of

η,

¯µ, computed solely from the triangulation (according

to (3) and (5)) and the percentage improvement over

the CDT (

CDT

imp

). The best value of

t and

η per line

http://imr.ciirc.cvut.cz/Research/TriVis

https://movingai.com/benchmarks/grids.html

Triangular Expansion Revisited: Which Triangulation Is The Best?

317

Table 2: Efﬁciency of computing visibility regions by the TEA with different underlying triangulations.

map

MaxVT MaxLT CDT MinLT MinVT

t [ns]

η ¯µ

CDT

imp

[%]

ar 13,331 299.0 12,167 259.7 10,086 179.3 9,308 173.6 8,804 157.8 155.5 12.0

c4 10,147 206.3 8,818 175.4 9,019 137.1 7,437 104.3 5,615 99.1 98.0 27.7

de 3,460 69.5 3,293 63.4 2,888 46.6 2,719 46.1 2,666 43.4 42.6 6.9

dr 5,338 105.7 5,103 97.3 4,602 72.1 4,232 71.7 4,123 66.0 64.3 8.5

e1 8,200 185.9 8,087 175.7 7,540 127.4 6,673 119.2 6,260 111.1 109.6 12.8

ec 30,096 723.6 27,713 620.5 22,590 383.6 19,715 356.3 18,898 336.8 325.6 12.2

jh 4,299 102.7 4,147 95.6 3,227 60.5 3,126 61.2 3,027 55.2 52.6 8.8

la 2,957 64.5 2,861 60.0 2,406 42.3 2,303 40.3 2,245 38.4 37.3 9.3

pb 974 18.1 959 17.6 849 12.5 817 12.4 822 11.8 11.7 5.3

ph 7,273 180.2 7,207 180.4 5,665 119.0 5,404 113.7 5,401 111.6 105.1 6.1

ta 1,474 29.9 1,441 28.1 1,339 22.0 1,279 23.1 1,237 20.5 20.3 7.0

is shown in bold. Note that all the best values ex-

cept one value of

t belong to the MinVT. On aver-

age, the MinVT is by 10.6%, and 6.6% more efﬁcient

than the CDT, and MinLT, respectively. The results

for MaxVT and MaxLT triangulations are the worst,

which is not surprising. We evaluated them to show a

counterpoint to those good triangulations and empha-

size triangulation choice’s importance. Since MaxVT

and MaxLT are not expected to provide any good re-

sults, these two triangulations are excluded from fur-

ther experiments.

Next, we evaluated the remaining triangulations

the same way as before but in scenarios with more re-

alistic visibility regions that are constrained by ﬁnite

visibility range d ∈ {12, 6,3}m. Limited range d was

also considered during the MWT construction as dis-

cussed in Section 3.2 in the case of d-MinVT. There-

fore, the d-MinVT must have been recomputed for

every value of d. The TEA was run in two versions:

1. the standard, and 2. with early exit considering lim-

ited visibility range d (recall Section 3.2). The results

are shown in Table 3. All values in the table corre-

spond to the metric

η except for the ﬁrst two columns.

We emphasize the four most important observations.

First, the early exit strategy helps to reduce the num-

ber of expansions for all cases signiﬁcantly. Second,

the proposed d-MinVT triangulation is the best in all

cases with early exit as shown in bold. Third, since

d-MinVT assumes early exit during its own construc-

tion, it may not be the best for the standard TEA, as

observed in the results. Fourth, the effectiveness of

MinLT gets very close to MinVT with smaller visibil-

ity ranges. The last observation can be explained us-

ing Figure 2. It is apparent that as the visibility range

gets smaller, the visible area around segment e is more

and more proportionally dependent on the segment’s

length.

Table 3: Results for limited visibility range d. All values

correspond to the

η metric except for the ﬁrst two columns.

map

[m]

standard TEA d-TEA (with early exit)

CDT MinLT MinVT d-MinVT CDT MinLT d-MinVT

12 162.9 101.1 95.2 92.1

6 179.3 173.6 157.8 167.8 53.0 49.4 48.3

3 171.6 26.9 24.9 24.5

12 104.0 95.4 80.6 78.6

6 137.1 104.3 99.1 107.4 59.3 53.5 52.6

3 105.4 29.2 25.7 25.5

12 43.8 42.2 41.9 39.8

6 46.6 46.1 43.4 44.9 30.3 30.1 29.2

3 46.2 17.8 17.4 17.1

12 66.8 64.5 64.4 61.4

6 72.1 71.7 66.0 69.0 47.3 42.6 41.6

3 71.4 25.1 22.5 22.2

12 111.4 119.0 112.0 105.2

6 127.4 119.2 111.1 114.0 83.7 80.5 77.6

3 120.9 46.4 45.2 43.9

12 339.7 336.5 314.2 301.5

6 383.6 356.3 336.8 347.6 194.9 181.3 175.6

3 354.7 80.5 73.9 72.4

12 55.7 53.2 53.7 49.3

6 60.5 61.2 55.2 58.1 31.6 31.5 30.0

3 59.1 17.0 16.8 16.4

12 38.9 31.9 31.0 30.1

6 42.3 40.3 38.4 40.1 20.9 20.4 20.0

3 40.6 12.2 11.9 11.8

12 12.2 8.0 7.9 7.8

6 12.5 12.4 11.8 12.5 6.1 6.0 6.0

3 12.6 4.7 4.6 4.6

12 112.6 98.3 95.0 94.0

6 119.0 113.7 111.6 113.4 51.6 50.2 49.7

3 113.0 23.9 23.3 23.1

12 21.1 17.1 17.9 16.3

6 22.0 23.1 20.5 21.6 11.0 10.8 10.5

3 22.7 6.7 6.2 6.1

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

318

5 CONCLUSION

We have shown that when computing visibility re-

gions by the triangular expansion algorithm (TEA),

the choice of the triangulation type matters. Choos-

ing the right or lousy triangulation can shift the av-

erage query performance of the TEA signiﬁcantly in

both directions. We have also shown that the con-

straint Delaunay triangulation (CDT), although it is

commonly used, is not optimal for the TEA in the

sense that it does not minimize the expected number

of edge expansions done by the algorithm. This pa-

per contributes by designing a new type of triangula-

tion called MinVT that approximately minimizes the

above criterion and improves the TEA query perfor-

mance compared to CDT by about 5-28%, depending

on the input map. In addition, the proposed triangula-

tion can adapt to TEA with early exit strategy, called

d-TEA, used when computing visibility regions con-

strained by limited visibility range d.

In future work, we plan to address the preprocess-

ing time, i.e., the time needed for constructing the

proposed triangulation, which was not addressed here

but appeared slow due to naive approaches used in

some of the sub-procedures. Furthermore, a promis-

ing direction for future research is generalizing from a

triangulation optimization to an optimization of gen-

eral collection of convex polygons, also called a nav-

igation mesh. A computation similar to TEA’s com-

putation of visibility regions but using a general nav-

igation mesh appears in (Shen et al., 2020). Here,

Polyanya (Cui et al., 2017), a state-of-the-art optimal

solver for computing geometric shortest paths in nav-

igation meshes, was adapted to compute all convex

obstacle vertices visible from a query mesh vertex.

Adapting the ideas of this paper to navigation meshes

used in Polyanya may result in a similar average im-

provement of query times as for TEA with optimized

triangulation.

ACKNOWLEDGMENTS

This work was supported by the European Regional

Development Fund under the project Robotics for In-

dustry 4.0 (reg. no. CZ.02.1.01/0.0/0.0/15003/000

0470) and by the Grant Agency of the Czech Tech-

nical University in Prague, grant No. SGS21/185/OH

K3/3T/37.

REFERENCES

Asano, T. (1985). An efﬁcient algorithm for ﬁnding the

visibility polygon for a polygonal region with holes.

IEICE Transactions, 68(9):557–559.

Bungiu, F., Hemmer, M., Hershberger, J., Huang, K., and

oller, A. (2014). Efﬁcient Computation of Visibility

Polygons. arXiv:1403.3905.

Cui, M., Harabor, D. D., and Grastien, A. (2017).

Compromise-free pathﬁnding on a navigation mesh.

In Proceedings of the Twenty-Sixth International Joint

Conference on Artiﬁcial Intelligence, IJCAI-17, pages

496–502.

Grantson, M., Borgelt, C., and Levcopoulos, C. (2008).

Fixed parameter algorithms for the minimum weight

triangulation problem. International Journal of Com-

putational Geometry & Applications, 18(03):185–

220.

Guibas, L. J., Latombe, J.-C., Lavalle, S. M., Lin, D.,

and Motwani, R. (1997). Visibility-based pursuit-

evasion in a polygonal environment. In Dehne, F.,

Rau-Chaplin, A., Sack, J.-R., and Tamassia, R., ed-

itors, Algorithms and Data Structures, pages 17–30,

Berlin, Heidelberg. Springer Berlin Heidelberg.

Keynes, J. M. (1921). The Principle of Indifference. In A

Treatise on Probability, volume 4, chapter IV, pages

41–64. Macmillan and Co.

Kulich, M., Koz

ak, V., and P

reu

cil, L. (2018). An inte-

grated approach to autonomous environment model-

ing. In Modelling and Simulation for Autonomous Sys-

tems (MESAS 2017), volume 10756 of Lecture Notes

in Computer Vision. Springer International Publishing

AG.

Mikula, J. and Kulich, M. (2022). Towards a continuous

solution of the d-visibility watchman route problem in

a polygon with holes. IEEE Robotics and Automation

Letters, 7(3):5934–5941.

Mulzer, W. and Rote, G. (2008). Minimum-weight triangu-

lation is np-hard. J. ACM, 55(2).

Ntafos, S. (1992). Watchman routes under limited visibility.

Computational Geometry: Theory and Applications,

1(3):149–170.

O’Rourke, J. (1987). Art Gallery Theorems and Algorithms.

Oxford University Press.

Shen, B., Cheema, M. A., Harabor, D., and Stuckey, P. J.

(2020). Euclidean pathﬁnding with compressed path

databases. In Proceedings of the Twenty-Ninth Inter-

national Joint Conference on Artiﬁcial Intelligence,

IJCAI-20, pages 4229–4235.

Shewchuk, J. R. (1996). Triangle: Engineering a 2d qual-

ity mesh generator and delaunay triangulator. Applied

Computational Geometry Towards Geometric Engi-

neering, 1148:203–222.

Shewchuk, J. R. (2002). Delaunay reﬁnement algorithms

for triangular mesh generation. Computational Ge-

ometry, 22(1):21–74.

Sturtevant, N. (2012). Benchmarks for grid-based pathﬁnd-

ing. Transactions on Computational Intelligence and

AI in Games, 4(2):144 – 148.

Triangular Expansion Revisited: Which Triangulation Is The Best?

319