
Near-collisions and Their Impact on Biometric Security
Axel Durbet
1
, Paul-Marie Grollemund
2
,
Pascal Lafourcade
1
and Kevin Thiry-Atighehchi
1
1
Universit
´
e Clermont-Auvergne, CNRS, Mines de Saint-
´
Etienne, LIMOS, France
2
Universit
´
e Clermont-Auvergne, CNRS, LMBP, France
Keywords:
Biometric Transformations, Biometric Authentication, Biometric Identification, Closest-string Problem,
Machine Learning, Near-collisions.
Abstract:
Biometric recognition encompasses two operating modes. The first one is biometric identification which
consists in determining the identity of an individual based on her biometrics and requires browsing the entire
database (i.e., a 1:N search). The other one is biometric authentication which corresponds to verifying claimed
biometrics of an individual (i.e., a 1:1 search) to authenticate her, or grant her access to some services. The
matching process is based on the similarities between a fresh and an enrolled biometric template. Considering
the case of binary templates, we investigate how a highly populated database yields near-collisions, impacting
the security of both the operating modes. Insight into the security of binary templates is given by establishing
a lower bound on the size of templates and an upper bound on the size of a template database depending on
security parameters. We provide efficient algorithms for partitioning a leaked template database in order to
improve the generation of a master-template-set that can impersonates any enrolled user and possibly some
future users. Practical impacts of proposed algorithms are finally emphasized with experimental studies.
1 INTRODUCTION
With the continuous growth of biometric sensor mar-
kets, the use of biometrics is becoming increasingly
widespread. Biometric technologies provide an effec-
tive and user-friendly means of authentication or iden-
tification through the rapid measurements of physical
or behavioral human characteristics. For biometric
identification and authentication schemes, biometric
templates of users are registered with the system. The
first operating mode consists in determining the iden-
tity of an individual based on similarity scores calcu-
lated from all the enrolled templates and the fresh pro-
vided template. The latter corresponds to the verifica-
tion of the claimed identity based on a similarity score
calculated from the assigned enrolled template and a
fresh template. As a consequence, service providers
need to manage biometric databases in a manner sim-
ilar to managing password databases.
The leak of biometric databases is more dramatic
since, unlike passwords, biometric data serve as long
term identifiers and cannot be easily revoked. The
consequences of stolen biometric templates are im-
personation attacks and the compromise of privacy.
Essential security and performance criteria that must
be met by biometric recognition systems are identi-
fied in (ISO, 2011) and (ISO, 2018): Irreversibility,
unlinkability, revocability and performance preserva-
tion.
Biometric templates are generated from biomet-
ric measurements (e.g., a fingerprint image). They
result from a chain of treatments, an extraction of
the features (e.g., using Gabor filtering (Manjunath
and Ma, 1996; Jain et al., 2000)) followed eventu-
ally by a Scale-then-Round process (Ali et al., 2020)
to accommodate better handled representations, i.e.,
binary or integer-valued vectors. These templates
are then protected either through their mere encryp-
tion, or using a Biometric Template Protection (BTP),
e.g., a cancelable biometric transformation such as
Biohashing (Jin et al., 2004; Lumini and Nanni,
2007) or any other salting method. For more de-
tails on BTP schemes, the reader is referred to the
surveys (Nandakumar and Jain, 2015; Natgunanathan
et al., 2016; Patel et al., 2015). The use of a BTP
scheme is in general preferred since its goal is to
address the aforementioned criteria. However, note
that cancelable biometric transformations are prone
to inversion attacks, at least in the sense of second-
preimages (Durbet et al., 2021). They even lead
sometimes to the compromise of privacy with a good
approximation of a feature vector (Lacharme et al.,
2013; Ghammam et al., 2020).
Recent works have also demonstrated that recog-
382
Durbet, A., Grollemund, P., Lafourcade, P. and Thiry-Atighehchi, K.
Near-collisions and Their Impact on Biometric Security.
DOI: 10.5220/0011279200003283
In Proceedings of the 19th International Conference on Security and Cryptography (SECRYPT 2022), pages 382-389
ISBN: 978-989-758-590-6; ISSN: 2184-7711
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

nition systems are vulnerable to dictionary attacks
based on master-feature vectors (Roy et al., 2017;
Bontrager et al., 2018). A master-feature vector is a
set of synthetic feature vectors that can match with a
large number of other feature vectors. This can natu-
rally be extended to the problem of generating master-
templates and masterkeys. The notion of masterkey
has recently been addressed in (Gernot and Lacharme,
2021) to produce backdoors with the aim of imple-
menting biometric-based access rights. In the same
topic, the present paper analyses the security of bio-
metric databases by making some recommandations,
and by proposing attacks using the notions of master-
template, master-feature and masterkey.
Contributions. Our main contribution is an effi-
cient partitioning algorithm which accelerates attacks
aiming to generate master-key or master-feature vec-
tor. Numerical studies on implementations of the pro-
posed algorithm show a reduction of the computa-
tional time by a factor of up to 38 in certain settings.
In addition, we show a link with the closest string
problem with an arbitrary number of words, for which
we provide a solution using Simulated ANNealing
(SANN). Moreover, we determine a bound on the size
of a database in function of the template space di-
mension and the decision threshold, thus preventing
near-collisions with a high probability. Specifically,
for a secure database, the recommanded template size
is n = 512 bits with a threshold of the order of 10% of
n, i.e., around 50 bits. Setting these paramaters in this
way rules out attacks based on master-templates and
ensures a good recognition accuracy. Finally, some
indications are provided for handling basic database
operations such as addition or deletion of users.
Outline. In Section 2, we introduce some nota-
tions, background material as well as definitions of
new notions such as master-template and ε-covering-
template. In Section 3, we describe an algorithm
which provides a segmentation of a database in order
to focus on potential master-templates. In Section 4,
we show how this algorithm can be used to improve
the computation of masterkey-set and master-feature-
set. Moreover, we describe how near-collisions can
be used to define a secure parameter k which depends
on the template space dimension and a threshold. We
also explain why the secure parameter is a counter-
measure and, the case of a user which is added or re-
moved from the database are studied. In Section 5, we
provide some experimentations in order to assess the
performance of the proposed algorithm and to detail
in practice how the near string problem is solved. All
proofs are in the long version of this paper.
2 PRELIMINARIES
A biometric system is a method of authentication
or identification based on biometric data. The main
idea is to transform the biometric data into a tem-
plate to match the four aforementioned criteria, i.e.,
irreversible, unlinkable, revocable and performance
preservation. It must be able to compare template and
determine if they belong to the same person. The tem-
plate is constructed by combining a feature vector de-
rived from the biometric data and a secret parameter
named token which can be for example a password. A
biometric authentication or identification system al-
ways starts by using a feature extraction scheme to
extract some information from the biometric image
to construct a feature vector (Ratha et al., 2001). A
database partitioning method can be applied to each
biometric system for this. In this paper, we focus on
templates expressed as binary vectors, but the results
below can be adapted to every template representa-
tions.
In the following, we let (M
I
,Dist
I
), (M
F
,Dist
F
)
and (M
T
,Dist
T
) be three metric spaces, where M
I
,
M
F
and M
T
represent the image space, the feature
space and the template space, respectively; and Dist
I
,
Dist
F
and Dist
T
are the respective distance functions.
Note that Dist
I
and Dist
F
are instantiated with the Eu-
clidean distance, while Dist
T
is instantiated with the
Hamming distance.
Definition 2.1 (Feature Extraction Scheme). A bio-
metric feature extraction scheme is a pair of determin-
istic polynomial time algorithms Π := (E,V ), where:
• E is the feature extractor of the system, that takes
biometric data I ∈ M
I
as input, and returns a fea-
ture vector F ∈ M
F
.
• V is the verifier of the system, that takes two fea-
ture vectors F = E(I), F
0
= E(I
0
), and a threshold
τ
F
as input, and returns True if Dist
F
(F,F
0
) ≤ τ
F
,
and returns False if Dist
F
(F,F
0
) > τ
F
.
For the sake of privacy, biometric data (the feature
vector) should be designed in a such way that it pre-
vents information leakage. This motivates the use of
a cancelable biometric transformation scheme.
Definition 2.2 (Cancelable Biometric Transformation
Scheme). Let K be the token (seed) space, represent-
ing the set of tokens to be assigned to users. A cance-
lable biometric scheme is a pair of deterministic poly-
nomial time algorithms Ξ := (T ,V ), where:
• T is the transformation of the system, that takes
a feature vector F ∈ M
F
and the token parameter
P ∈ K as input, and returns a biometric template
T = T (P,F) ∈ M
T
.
Near-collisions and Their Impact on Biometric Security
383

• V is the verifier of the system, that takes
two biometric templates T = T (P,F), T
0
=
T (P
0
,F
0
), and a threshold τ
T
as input; and re-
turns True if Dist
T
(T,T
0
) ≤ τ
T
, and returns False
if Dist
T
(T,T
0
) > τ
T
.
In this paper, the template space is, unless oth-
erwise specified, F
n
2
=
Z
2Z
n
, equipped with the
Hamming distance denoted by d
H
. As the template
space is a metric space, we denote it as (F
n
2
,d
H
). In
our case, the verifier is the Hamming distance, but the
transformation does not need to be specified. As we
work on a set of template, we denote it as Template
DataBase (TDB).
Definition 2.3 (Template Database or TDB). Let
(Ω,d) be the template space equipped with the dis-
tance d. A subset L ⊂ Ω such that L 6=
/
0 and L 6= Ω is
a template database (TDB), or just a database.
As with hash functions, an antecedent of a trans-
form can be searched in order to steal a password or a
pass tests using this hash function. This preimage can
be the exact feature vector or a nearby preimage.
Definition 2.4 ({Nearby} Template Preimage). Let
I ∈ M
I
be a biometric image, a threshold ε
B
,
and T = Ξ.T (P,Π.E(I)) ∈ M
T
for some secret pa-
rameter P. A template preimage of T with re-
spect to P is a biometric image I
∗
such that T =
Ξ.T (P,Π.E(I
∗
)), and a nearby template preimage is
such that d(T,Ξ.T (P,Π.E(I
∗
))) < ε
B
.
The goal of an attacker can be to create a
masterkey-set. This is a set of tokens that allow to
build all the templates of a targeted database using the
same feature vector. Another goal of an attacker can
be to create a master-feature-set. This is a set of fea-
ture that allow to build all the templates of a targeted
database using preferably the same token.
Definition 2.5 (Masterkey and Master-feature). Let
D =
{
v
i
}
i=1,...,n
be a template database where
v
i
:= Ξ.T (x
i
,s
i
) generated with distinct tokens S =
{
s
i
}
i=1,...,n
and distinct biometric features X =
{
x
i
}
i=1,...,n
, and let τ
B
be a threshold. Then,
m is a masterkey for D, with respect to τ
B
, if
∀i ∈ J1,nK ,Ξ.V (Ξ.T (x
i
,m),Ξ.T (x
i
,s
i
),τ
B
) = True,
and in addition, m is a master-feature if ∀i ∈
J1,nK ,Ξ.V (Ξ.T (m, s
i
),Ξ.T (x
i
,s
i
), τ
B
) = True.
Targeting random template to find a masterkey are
often not efficient, thus, to maximize the efficiency
of the research of a masterkey-set, we suggest to fo-
cus on ε-covering templates and ε-master-templates
(ε-MT).
Definition 2.6 (ε-cover-template and ε-master-
template). Let (Ω, d) be the template space and D be
a template database. An ε-cover-template of D is x
such that d(x, a) ≤ ε,∀a ∈ D. Moreover, a template
t ∈ Ω is an ε-master-template if ∀t
0
∈ D,d(t,t
0
) ≤ ε.
Note that, there are cases for which there is no
possible ε-cover-template. In addition, an ε-master-
template-set is a non-empty set: D is an ε-master-
template-set of itself but an ε-master-template of D
could be empty. Moreover, an ε-cover-template is
an ε-master-template and an ε-master-template-set is
a set of ε-cover-templates which are not in the same
ε-cover-template-set. We define a near-collision and
more precisely multiple-near-collision.
Definition 2.7 (Near Collision). Let (Ω, d) be the
template space and a threshold ε . There exists a near-
collision if ∃a,b ∈ Ω | d(a,b) ≤ ε.
Thus, the search of an ε-cover-template of D a
database corresponds to the search of an at least |D|-
near-collision for which each template of D is related
to the collision.
3 DATABASE PARTITIONING
The aim of this part is to determine the smallest ε-
covering-template-set for a given database D.
3.1 Agglomerative Clustering
Consider M
D
the dissimilarity matrix of a template
database D, for the Hamming distance. The dissimi-
larity matrix M
D
is used to compute template clusters,
denoted by C
ε
, for which the distance between two
templates in the same cluster is at most s. To perform
this clustering, we use the agglomerative clustering
method which is a type of the hierarchical clustering.
This method consists in successively agglomerating
the two closest groups of templates. It begins with
|D| groups, one for each template, and it terminates
when all the groups are merged as a unique one.
A standard post-processing is required to define
at which iteration the algorithm should be termi-
nated so that a relevant set of template clusters is ob-
tained. However, we define a termination condition
so that the clustering algorithm stop when it is not
possible anymore to obtain templates cluster verifying
the following required property: ∀i ∈ J1,nK, ∀a,b ∈
C
i
,max(d
H
(a,b)) ≤ s. The Agglomerative Cluster-
ing algorithm we used then corresponds to a slight
variation of the HACCLINK (Hierarchical Agglom-
erative Clustering Complete LINK) presented in (De-
fays, 1977).
By using the aforementioned clustering method,
we obtain a set of template clusters, for which the
inner-cluster distance suggests that it could exist at
SECRYPT 2022 - 19th International Conference on Security and Cryptography
384

least one master-template for these templates. An ad-
ditional step is described below whose aim is to deter-
mine potential master-templates, if there exists some.
3.2 Master-template of a Template
Group
We consider having a group of templates verifying
∀i ∈ J1,nK, ∀a,b ∈ C
i
, max(d
H
(a,b)) ≤ s, and for
which we aim at finding a master-template. We em-
phasize that this problem can be formulated as a mod-
ified case of closest-string problem which is defined
as follows.
Definition 3.1 (Modified Closest-string Problem).
Given S = {s
1
,s
2
,..., s
m
} a set of strings with length
n and d a distance, find a center string t of length m
such that for every string s in S, d
H
(s,t) ≤ d.
The closest-string problem is known as an NP-
hard problem (Frances and Litman, 1997), and there
exist algorithms to solve that kind of problem, see
among others (Meneses et al., 2004; Gramm et al.,
2001). According to the link between both problems,
we can establish that the issue addressed in this paper
is a hard problem, which is specified in the following
theorem.
To the best of our knowledge, this problem has
not been addressed in the literature, then we propose
an algorithm to solve it. Moreover, with regards to
the hardness of MCSP, we deem that relying on brute
force type algorithm could not be efficient and that
more parsimonious algorithm must be investigated,
notably stochastic algorithms. However, more effi-
cient upcoming methods could replace this part with-
out affecting the remainder of the database partition-
ing method proposed in Section 3.
We consider D = {v
1
,..., v
k
} be a template
database and C the ε-cover-template-set for D (a set
of ε-cover-template such that all points of D are in a
ball around a point of C). The approach described
below provides a constructive definition of the ele-
ments of C , if C 6=
/
0. In particular, the following
result emphasizes the link between C and the balls
B
i
= {u ∈ F
n
2
|d
H
(u,v
i
) ≤ ε}.
Theoreme 3.1 (C Is the Intersection of the Balls
of Radius ε). Let D = {v
1
, . ..,v
k
} be a template
database and C the ε-cover-template-set for D.
Then, C = ∩
i∈{1,...,k}
B
i
.
We denote by p ∈ C a master-template, and The-
orem 3.1 indicates that determining all the master-
template p reduces to determining the intersection of
k Hamming balls, which turns out to be formulated as
the solutions of the following system:
d
H
(p,v
i
) ≤ ε, ∀i ∈ {1, .. .,k}. (1)
Notice that System 1 is a linear system, hence we can
rely on a binary ILP (Integer Linear Programming) to
solve it and then to compute C.
However, solving this system could be time-
consuming in real world cases since there are as many
parameters as the length of p, i.e., the dimension n of
F
n
2
. Therefore, we suggest reducing System 1 by re-
moving dependent variables and below are introduced
necessary notations:
• For K = {k
1
,..., k
|K|
} ⊂ {1, .. .,n}, the Hamming
distance over K is denoted by: ∀u, v ∈ F
n
2
,d
K
=
d
H
((u
k
1
,..., u
k
|K|
),(v
k
1
,..., v
k
|K|
)).
• Let P
D
(K) a statement about K ⊂ {1, ...,n},
P
D
(K) holds if ∀u, v ∈ D, d
K
(u,v) ∈
{
0,|K|
}
.
• The smallest partition {(K
1
,..., K
|I|
),K
i
⊂
{
1,..., n
}
| ∀i ∈
{
1,..., | I |
}
} such that P
D
(K
i
)
holds for all i ∈ {1,. ..,n} is noted I. As I is the
smallest possible partition, System 1 is reduced
as much as it is possible.
• For p ∈ F
n
2
and v ∈ D, n
v,i
denotes d
K
i
(p,v) and
n
I
v
denotes the parameters vector (n
v,1
,..., n
v,|I|
),
written N = (n
1
,..., n
|I|
) for short when the con-
text is clear.
• The distance vector
d
H
(v
1
,v),... ,d
H
(v
|D|
,v)
is
denoted by d(v) with v ∈ D and D = (v
1
,..., v
|D|
).
Then, with these notations, Theorem 3.2 can be estab-
lished, specifying a smaller version of System 1.
Theoreme 3.2. For a given template database D
and for a given v ∈ D, consider L = {p ∈ F
n
2
|AN ≤
ε − d(v)} with N = n
I
v
, ε = (ε, ...,ε)
T
,n
v,i
de-
notes d
K
i
(p,v), n
I
v
denotes the parameters vector
(n
v,1
,..., n
v,|I|
) and A = (a
i, j
) a matrix of size |I|× |D|
whose the (i, j)
th
element is
a
i, j
=
(
1 if d
K
j
(v
1
,v
i
) = 0
−1 if d
K
j
(v
1
,v
i
) = |K
j
|
Then, L = C the ε-cover-template-set for D.
As I is required to reduce System 1, we assure
with Lemma 3.1 that I 6=
/
0, whatever the configura-
tion of the set D is.
Lemme 3.1 (I Is Not Empty). ∀D ⊂ F
n
2
such that |
D |> 1, I 6=
/
0.
In the same vein, one can determine that |I| ≤ n.
As |I| corresponds to the number of parameters, the
system described in Theorem 3.2 is always smaller or
equivalent to System 1.
Theorem 3.2 indicates that determining the ε-
cover-template-set for D (which corresponds to an in-
tersection of |D| balls in F
2
n
can be reduced to solving
Near-collisions and Their Impact on Biometric Security
385

a potentially small linear system. While the resolu-
tion of the aforementioned system can be done with
powerful tools (like GUROBI (Pedroso, 2011)), we
deem that simpler algorithms should be used in this
case. In particular, according to the configuration of
D, it is possible to obtain a such system linear that it
is straightforward to determine the space of the poten-
tial solutions and to find a solution with any Marko-
vian scanning algorithm. More precisely, if N de-
notes the set of the possible solutions N for the lin-
ear system described in Theorem 3.2, we have: N =
∏
|I|
k=1
{0,..., min(ε,|K
k
|)} since, for k ∈ {1,. .. ,|I|},
n
v,k
corresponds to the distance d
K
k
(v
k
,v), which can
not be greater than |K
k
|, and in the other hand if
d
K
k
(v
k
,v) > ε then, N does not belong to L. One can
then be aware that depending on the dimension of N ,
finding a solution N can be efficiently done via either
a brute force algorithm in case of small dimensional
set N , or via a more parsimonious algorithm if the
dimension is high. As the dimension of N depends
among other factors on D, we consider that the use of
one of the both approaches should be determined with
regards to pratical context-specific consideration. In
this paper, we only describe an algorithm to use in
case of high dimensional N set. We propose to rely
on an efficient and simple algorithm: the Simulating
Annealing algorithm (Kirkpatrick et al., 1983). Nev-
ertheless, even if we illustrate the proposed method-
ology with this algorithm, it could be replaced by any
optimization algorithm based on scanning the space.
Below we detail features of Simulating Annealing al-
gorithm that we tune in order to obtain good perfor-
mances in our numerical study. It is composed of the
following parameters:
• Energy: We define the following energy so that
larger it is, the closer N is to solve the linear sys-
tem: E(N) =
∑
|I|
i=1
f ((ε − d(v)− AN)
i
) where f is
a ReLU type function: f (x) = min(0, x).
• Cooling Schedule: In practice, we observe that
finding a solution is not sensitive to the cooling of
the system, see Section 5.2. Then, we propose to
choose a linear decreasing temperature. The start-
ing temperature is fixed so that at the initial iter-
ation, all potential move must be accepted, what-
ever the chosen initial point is.
• Proposal distribution: According to computa-
tional considerations and for the sake of numerical
performance, we define a proposal distribution for
which the support is the neighbors set. Moreover,
we choose a non-symmetric proposal that prefer-
entially promotes neighbors that increases the en-
ergy.
• Termination: The algorithm is terminated either
it reaches the maximum iteration number (about
200k iterations), or if a solution is found, which
corresponds to a vector N with a null energy.
The experimentations of this part are presented in
Section 5.2.
3.3 Database Partitioning Algorithm
Using the developments of the sections 3.1 and 3.2,
we propose Algorithm 1 to partition the template
database. It takes as inputs D a template database and
a threshold ε and returns an ε-MTS.
Algorithm 1: Database partitioning algorithm.
Data: D, ε
Result: MTS
1 Set s to 2ε.
2 Set MTS to [ ].
3 while D 6=
/
0 do
4 Compute cluster Cls using D and s.
5 foreach cluster c in Cls do
6 Search the cover template t for c.
7 if a cover template t is found for
c ∈ C then
8 Set D to D\c and add t to MTS.
9 end
10 Set s to s − 1.
11 end
12 end
13 return MT S.
4 ATTACK SCENARIO,
COUNTERMEASURE AND
CASE STUDIES
The aim of this section is to show that the method
described Section 3 eases the computation of a
masterkey-set or a master-feature-set. Their com-
putations are straightforward in the absence of BTP
scheme and are still possible if an invertible transfor-
mation is employed, like Biohashing or some other
salting transformations. Moreover, that kind of at-
tack is analyzed, and a security bound is established
in Section 4.2.
4.1 Attack Scenario
Consider a pair of functions T
−1
1
and T
−1
2
defined as
follows :
Definition 4.1 (Token (resp. Feature) Transforma-
tion Inversion Function). The token (resp. feature)
SECRYPT 2022 - 19th International Conference on Security and Cryptography
386

transformation inversion function denoted by T
−1
1
(resp. T
−1
2
) takes v ∈ M
F
a feature vector (resp. a
token) and t ∈ Ω a template and gives p a token such
that T (v, p) = t.
Note that we focus on frameworks for which T
−1
1
and T
−1
2
can be computed in a reasonable time: at
least linear and at most subexponential. These func-
tions must be determined case-by-case according to
the used biometric transformation. Furthermore, an
attacker seeking to create a master-feature-set (resp.
a masterkey-set) can do it using k calls to the inverse
transformation function T
−1
1
(resp. T
−1
2
), where k is
the number of templates. However, the method devel-
oped in Section 3 can be used to reduce the compu-
tation complexity. Actually, the attacker can compute
a master-feature-set or a masterkey-set in only ` step
with ` ≤ k, where l is the number of clusters.
4.2 Countermeasure: Managing the
Database Size
Consider a biometric system set with a template space
of size n and a threshold ε. Moreover, suppose that
the biometric system is unbiased i.e., each template is
randomly chosen in the template space. There exists
a maximum size for a database at n and ε fixed which
minimizes the gain of an attacker with the method
presented in Section 3 and which maximizes the size
of that database. Notice that the following approach
can be applied to any biometric system.
Prevent an Advantage. An advantage of an at-
tacker is significant when our database partitioning
method (Section 3) reduces the complexity of the ini-
tial attack by at least one. Let k be the number of
clients allowed in a database and, F
n
2
the template
space. If k ≥
2
n
∑
ε
i=0
n
i
then, there is at least one
cluster containing two or more templates, according
to the Dirichlet’s box principle. In our case, c is at
most:
2
n
∑
ε
i=0
n
i
and there are two scenarios:
1. There are enough clients to find a coverage of F
n
2
by using their clusters and any other enrollment is
already compromised.
2. There is not enough clients to find a coverage of
F
n
2
and the attacker obtains an advantage for the
computation.
By using birthday problem, more particularly the
probability of a near collision (Lamberger et al.,
2012; Lamberger and Teufl, 2012), we can establish
that, the average number of template must be about
2
(n+1)/2
S
ε
(n)
−1/2
so that a cluster contained two tem-
plates, where,
∑
ε
i=0
n
i
= S
ε
(n). Furthermore, the
number of near collisions is N
C
(ε) and its expected
value E(N
C
(ε)) is equal to
k
2
S
ε
(n)2
−n
with k the
number of templates. Thus, the number k of templates
which give a collision with a probability of 50% is
≈ 2
n/2
S
ε
(n)
−1/2
.
Figure 1 provides numerical and graphical rep-
resentations based on experimentations, enlightening
on how k behaves relatively to n and ε. They show
that the size of a database which can provide colli-
sions is wide smaller than the size of n. Furthermore,
if ε is bigger than 20% of n, this size dramatically de-
creases. To keep enough room in a safe database, n
must be larger than 512 and ε smaller than 51.
5 ATTACK EVALUATION
In this section we provide some experimental evalua-
tions of Algorithm 1 and, we discuss our results. In
our experiments, the passwords are assumed unique
for each individual. The hashed passwords serve as
seeds for the generation of the matrices. Thus, the
produced templates are uniformly distributed.
To compare the efficiency of our proposal with a
baseline, we propose a naive algorithm based on a
greedy strategy. First, a template is picked from the
template database. Then, all templates in the template
database which are at a distance of at most ε from
the chosen template are removed. These steps are re-
peated as long as there are templates in the database.
As a result, the chosen templates form the MTS.
5.1 Evaluation of the Database
Partitioning
Templates are randomly drawn from F
n
2
. For each
configuration, experimentations are replicated 10k
times and averaged results are computed. The av-
erage results are presented in Table 1 and Table 2
with the following notations: n: the space dimension,
ε: the threshold, #clients: the number of templates
in the TDB, #clust: the number of clusters found
with Algorithm 1, #clust(G): the number of clusters
found using the greedy Algorithm 5, E f f iciency is
the ratio #clust(G)/#clust, Time is the running time
of Algorithm 1, Time(G) is the running time of the
greedy Algorithm 5. As the computation of the ε-
cover-template 3.2 is the most expensive part of Al-
gorithm 1, an experimentation Table 2 is dedicated to
the ε-cover-template search 3.2. In fact, we remark
that the gain of the attacker is greater when the value
of k is greater that what we recommend in Section 4.2.
Near-collisions and Their Impact on Biometric Security
387
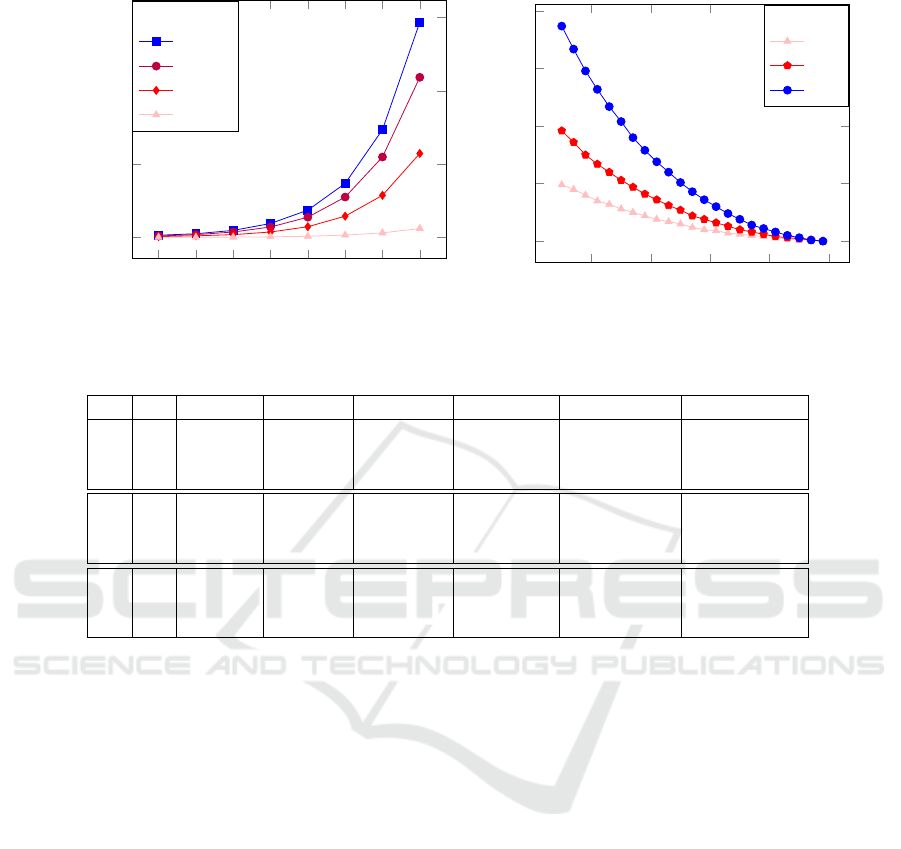
(a) log
2
n in function of log
2
k for ε.
5 6
7 8 9 10 11 12
0
500
1,000
1,500
log
2
n
log
2
k
ε in %
10%
20%
40%
5%
(b) ε in % in function of log
2
k for n.
10 20 30 40
50
0
50
100
150
200
ε in %
log
2
k
n
128
256
512
Figure 1: Link between k and n or ε.
Table 1: Summary of the experiments of the space partitioning algorithm.
n ε #clients #clust #clust(G) Efficiency Time (ms) Time G (ms)
20 2.700 35.433 ×13.12 8 415.270 10.714
30 10 50 8.709 48.977 × 5.70 8775.802 18.940
40 18.087 49.986 × 2.77 6417.596 23.762
5 200.000 200.000 × 1.00 43.969 449.166
70 15 200 90.000 200.000 × 2.22 47016.050 337.082
25 22.109 198.982 × 9.00 222386.614 346.420
90 89.67 90 136.572 137.186
50 10 130 129.30 130 ×1.00 428.885 251.221
170 168.79 170 531.363 434.727
5.2 Evaluation of Simulated Annealing
Keeping the same notations, the average experimen-
tations are stored in Table 3. In the case where the
simulated annealing is used as a sub-routine of the al-
gorithm 1, this latter is slower and less efficient. The
main reason of this loss of performance is the error
rate of the simulated annealing which forces doing
more calculations. However, it is quicker and more
efficient than solving a system to answer to the near
string problem given in Section 3.1.
Moreover, we use several cooling functions (Aarts
et al., 2005; Kirkpatrick et al., 1983) to determine
what is preferable and we remark that finding a so-
lution is not strongly sensitive to the cooling method.
6 CONCLUDING REMARKS
In this paper, we have performed an in-depth analy-
sis of the Hamming space as template space. We first
have introduced some formal definitions such as mul-
tiplicative near-collision, master-template, ε-covering
template and some technical terms and concepts. We
then have proposed an algorithm to perform a par-
tition of the set of templates. This partitioning can
be used to improve either the masterkey-set search
or the master-feature-set search. The proposed cen-
ter search algorithm using simulated annealing is also
a result of independent interest for solving the near-
string-problem.
By relying on the properties of near-collisions and
the partitioning algorithm, we have also shown there
exists a security bound on the size of a database that
depends on both the space dimension and the decision
threshold. Beyond that limit on the size, there is a
high probability of a near collision that impacts both
security and efficiency.
ACKNOWLEDGEMENT
The authors acknowledges the support of the French
Agence Nationale de la Recherche (ANR), under
grant ANR-20-CE39-0005 (project PRIVABIO).
SECRYPT 2022 - 19th International Conference on Security and Cryptography
388

Table 2: Summary of the experiments of the ε-cover-template search algorithm ILP version.
n ε #clients Time (ms)
20 1592.213
30 10 50 2428.682
40 3887.738
n ε #clients Time (ms)
5 24949.724
70 15 200 20978.806
25 29089.280
n ε #clients Time (ms)
90 11087.893
70 10 130 18330.508
170 20887.950
Table 3: Summary of the experiments of the ε-cover-template search algorithm SANN version.
n ε #clients Error Time
in % (ms)
20 0.64 17
30 10 50 0.00 1
40 0.05 1
n ε #clients Error Time
in % (ms)
5 0.00 36
70 15 200 0.00 36
25 0.00 40
n ε #clients Error Time
in % (ms)
90 0.14 12
70 10 130 0.00 22
170 0.00 31
REFERENCES
(2011). ISO/IEC24745:2011: Information technology – Se-
curity techniques – Biometric information protection.
Standard, International Organization for Standardiza-
tion.
(2018). ISO/IEC30136:2018(E): Information technology
– Performance testing of biometrictemplate protec-
tion scheme. Standard, International Organization for
Standardization.
Aarts, E., Korst, J., and Michiels, W. (2005). Simulated
Annealing, pages 187–210.
Ali, S., Karabina, K., and Karagoz, E. (2020). Formal accu-
racy analysis of a biometric data transformation and
its application to secure template generation. In SE-
CRYPT 2020, pages 485–496.
Bontrager, P., Roy, A., Togelius, J., Memon, N., and Ross,
A. (2018). Deepmasterprints: Generating master-
prints for dictionary attacks via latent variable evolu-
tion. In 2018 IEEE 9th International Conference on
Biometrics Theory, Applications and Systems (BTAS),
pages 1–9. IEEE.
Defays, D. (1977). An efficient algorithm for a complete
link method. The Computer Journal, 20(4):364–366.
Durbet, A., Lafourcade, P., Migdal, D., Thiry-Atighehchi,
K., and Grollemund, P.-M. (2021). Authentica-
tion attacks on projection-based cancelable biometric
schemes.
Frances, M. and Litman, A. (1997). On covering problems
of codes. Theory of Computing Systems, 30(2):113–
119.
Gernot, T. and Lacharme, P. (2021). Biometric masterkeys.
Ghammam, L., Karabina, K., Lacharme, P., and Thiry-
Atighehchi, K. (2020). A cryptanalysis of two cance-
lable biometric schemes based on index-of-max hash-
ing. IEEE Transactions on Information Forensics and
Security, PP:1–12.
Gramm, J., Niedermeier, R., and Rossmanith, P. (2001). Ex-
act solutions for closest string and related problems.
pages 441–453.
Jain, A., Prabhakar, S., Hong, L., and Pankanti, S. (2000).
Filterbank-based fingerprint matching. IEEE Trans-
actions on Image Processing, 9(5):846–859.
Jin, A. T. B., Ling, D. N. C., and Goh, A. (2004). Biohash-
ing: two factor authentication featuring fingerprint
data and tokenised random number. Pattern Recog-
nition, 37(11):2245–2255.
Kirkpatrick, S., Gelatt, C. D., and Vecchi, M. P. (1983).
Optimization by simulated annealing. Science,
220(4598):671–680.
Lacharme, P., Cherrier, E., and Rosenberger, C. (2013).
Preimage Attack on BioHashing. In SECRYPT 2013,
pages 363–370.
Lamberger, M., Mendel, F., Rijmen, V., and Simoens, K.
(2012). Memoryless near-collisions via coding theory.
Designs, Codes and Cryptography, 62(1):1–18.
Lamberger, M. and Teufl, E. (2012). Memoryless near-
collisions, revisited.
Lumini, A. and Nanni, L. (2007). An improved BioHash-
ing for human authentication. Pattern Recognition,
40(3):1057 – 1065.
Manjunath, B. S. and Ma, W. Y. (1996). Texture features for
browsing and retrieval of image data. 18(8):837–842.
Meneses, C., Lu, Z., Oliveira, C., and Pardalos, P. (2004).
Optimal solutions for the closest string problem via
integer programming. Informs Journal on Computing
- INFORMS, 16:419–429.
Nandakumar, K. and Jain, A. K. (2015). Biometric tem-
plate protection: Bridging the performance gap be-
tween theory and practice. IEEE Signal Processing
Magazine, 32:88–100.
Natgunanathan, I., Mehmood, A., Xiang, Y., Beliakov, G.,
and Yearwood, J. (2016). Protection of privacy in bio-
metric data. IEEE Access, 4:880–892.
Patel, V. M., Ratha, N. K., and Chellappa, R. (2015). Can-
celable biometrics: A review. IEEE Signal Processing
Magazine, 32(5):54–65.
Pedroso, J. P. (2011). Optimization with gurobi and python.
INESC Porto and Universidade do Porto, Porto, Por-
tugal, 1.
Ratha, N. K., Connell, J. H., and Bolle, R. M. (2001).
An analysis of minutiae matching strength. In Bi-
gun, J. and Smeraldi, F., editors, Audio- and Video-
Based Biometric Person Authentication, pages 223–
228, Berlin, Heidelberg. Springer Berlin Heidelberg.
Roy, A., Memon, N., and Ross, A. (2017). Masterprint: Ex-
ploring the vulnerability of partial fingerprint-based
authentication systems. IEEE Transactions on Infor-
mation Forensics and Security, 12(9):2013–2025.
Near-collisions and Their Impact on Biometric Security
389
