A Model based on 2-tuple Linguistic Model and CRITIC Method for
Hotel Classification
Ziwei Shu
1a
, Ramón Alberto Carrasco González
2b
, Javier Portela García-Miguel
1c
and
Manuel Sánchez-Montañés
3d
1
Department of Statistics and Data Science, Faculty of Statistics, Complutense University of Madrid,
Avenida Puerta de Hierro, s/n, 28040 Madrid, Spain
2
Department of Management and Marketing, Faculty of Commerce and Tourism, Complutense University of Madrid,
Avenida de Filipinas, 3, 28223 Madrid, Spain
3
Department of Computer Science, Universidad Autónoma de Madrid, 28049 Madrid, Spain
Keywords: Hotel Classification, Weighted K-means Clustering, 2-tuple Linguistic Model, CRITIC Method,
Multi-criteria Decision Making.
Abstract: Hotel classification is critical for both customers and hotel managers. It can help hotel managers better
understand their customers' needs and improve their various aspects by implementing relevant strategies.
Moreover, it can assist customers in recognizing different hotel aspects and making a more informed decision.
This paper categorizes hotels on TripAdvisor based on their six aspects. The 2-tuple linguistic model is applied
to solve the problem of information loss in linguistic information fusion. The CRiteria Importance Through
Intercriteria Correlation (CRITIC) approach is employed to generate objective weights to calculate the overall
score of each hotel, as this method does not require any human participation in the weighting computation.
Finally, various hotels segments are obtained with Weighted K-means clustering. This proposal has been
evaluated by a use case with more than fifty million TripAdvisor hotel reviews. The results demonstrate that
the proposed model can increase the linguistic interpretability of clustering results and provide customers with
a more understandable objective overall hotel score, which can assist them in selecting a better hotel.
Moreover, these classification results aid hotel managers in designing more effective tactics for acquiring a
new competitive advantage or enhancing those aspects that require improvement.
1 INTRODUCTION
Accommodation is one of the most important aspects
of the tourism industry, in which online hotel
reservations account for a significant portion of the
market. TripAdvisor and Booking receive millions of
visits per month, by 2023, 700 million individuals
will be reserving hotel rooms online (Deane, 2022).
The classification of hotels is an essential component
of hotel development and is also critical for customers
as it allows them to choose the appropriate
accommodation based on their demands.
In recent years, different approaches to exploring
hotel classification have been developing, such as
a
https://orcid.org/0000-0001-6788-1111
b
https://orcid.org/0000-0001-7365-349X
c
https://orcid.org/0000-0002-5284-5123
d
https://orcid.org/0000-0002-5944-0532
(Beracha et al., 2018), (Mody et al., 2019), (Nilashi et
al., 2019), (Ali et al., 2020), (Çınar et al., 2020), and
so on. Among them, Nilashi et al. presented a hybrid
method for analyzing online opinions through multi-
criteria decision-making and Machine Learning
techniques to examine the relevance of aspects
influencing visitors' decision-making in choosing
hotels. Although K-means clustering has been
commonly utilized in the literature (El Khediri et al.,
2020; Abdullah et al., 2021; Chowdhury et al., 2021;
Jahangoshai Rezaee et al., 2021; Zhao et al., 2021),
few studies have taken into account that the different
quantity of information contained in the variables will
affect the clustering results.
Shu, Z., González, R., García-Miguel, J. and Sánchez-Montañés, M.
A Model based on 2-tuple Linguistic Model and CRITIC Method for Hotel Classification.
DOI: 10.5220/0011298700003269
In Proceedings of the 11th International Conference on Data Science, Technology and Applications (DATA 2022), pages 127-134
ISBN: 978-989-758-583-8; ISSN: 2184-285X
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
127

Therefore, this paper presents a segmentation of
hotels on TripAdvisor through a Weighted K-means
clustering based on the 2-tuple model and the
CRiteria Importance Through Intercriteria
Correlation (CRITIC) method. The CRITIC approach
is used in this proposal as it can generate objective
weights for distinct hotel aspects without the
requirement of expert evaluations. And the 2-tuple
linguistic model is applied to solve the problem of
information loss in linguistic information fusion. In
this way, this proposal allows weighting the aspects
of the hotel, considering the different quantities of
information included in each of them, and increasing
the linguistic interpretability of clustering results.
The rest of this paper is structured as follows.
Section 2 introduces the key concepts that will be
utilized to build the proposed model. Section 3
demonstrates a use case with more than fifty million
TripAdvisor hotel reviews to evaluate the proposed
model. Section 4 presents some conclusions and
future work.
2 THEORETICAL FRAMEWORK
In this section, the essential concepts on which this
proposal is based are presented: 2-tuple linguistic
model, CRITIC method, 2T-CRITIC model and
Weighted K-means clustering.
2.1 The 2-tuple Linguistic Model
In the fuzzy linguistic approaches, linguistic terms are
employed to assist computation and identify the
variety of each assessment item (Herrera & Martinez,
2000; Ju et al., 2012). To solve the problem of
information loss in linguistic information fusion,
Herrera and Martínez introduced the 2-tuple
linguistic model (Herrera & Martinez, 2000).
Numerous authors have utilized it to model customer
reviews with fuzzy linguistic scales, which provides
more understandable results than using solely
numerical scales (Liu & Chen, 2018; Carrasco et al.,
2018; Sohaib et al., 2019; Díaz et al., 2021).
The 2-tuple linguistic model expresses the
linguistic information through a pair of values called
2-tuple value
(
𝑠

,𝛼
)
, where 𝑠

∈𝑆 is a linguistic
term, and 𝛼∈[−0.5,0.5) is a numeric value that
represents the distance to the central value of 𝑠

. The
definition is as follows.
Definition 1. Let 𝑆=𝑠

,…,𝑠

 be a linguistic term
set, and 𝛽∈
[
0,𝑔

be a value that represents the result
of an operation of symbolic aggregation. The function
∆:
[
0,𝑔

→
〈
𝑆
〉
=𝑆𝑥∈[−0.5,0.5) is used to convert
β to 2-tuple value
(
𝑠

,𝛼
)
as the Equation (1):
() ( )



−∈−=
=
=Δ
)5.0,5.0[,
)(
,,
αβα
β
αβ
i
roundi
withs
i
(1)
where round(·) is the rounding operation; 𝑠

has the
nearest index label to β; and α is a numerical value of
the symbolic translation. The function ∆

:
〈
𝑆
〉
=
𝑆𝑥∈[−0.5,0.5)→
[
0,𝑔

is the inverse function of ∆,
so that a 2-tuple value can be converted into its
equivalent numerical value as ∆

(
𝑠

,𝛼
)
=𝑖+𝛼=
𝛽. The negation operator of a 2-tuple value is defined
as 𝑛𝑒𝑔
(
𝑠

,𝛼
)
=∆𝑔−∆

(
𝑠

,𝛼
)
=∆
(
𝑔−𝛽
)
.
The comparison and aggregation operators for 2-
tuple linguistic computation are described in (Herrera
et al., 2004). In this paper, the arithmetic mean is used
to aggregate 2-tuple values, which is defined as
follows.
Definition 2. Let 𝑇

=

(𝑠

,𝛼

),...,(𝑠

,𝛼

)

be a
set of 2-tuple values of the vth criterion, whose
arithmetic mean is calculated using Equation (2):






Δ=






ΔΔ=

==
−
n
i
i
n
i
iiv
n
s
n
T
11
1
1
),(
1
βα
(2)
2.2 CRiteria Importance Through
Intercriteria Correlation (CRITIC)
Method
Introduced by Diakoulaki et al., the CRiteria
Importance Through Intercriteria Correlation
(CRITIC) method is one of the weighting methods for
determining objective weights for each criterion
(Diakoulaki et al., 1995). This method is extremely
useful when the correlation between variables is high,
as it employs correlation analysis to determine the
differences between various criteria. Furthermore,
human intervention such as expert evaluations is not
required in the weight calculation process, as CRITIC
is an objective weighting approach.
The CRITIC method consists of four steps:
1) Calculate the standard deviation of each criterion.
2) Compute the linear correlation matrix to obtain
the correlation coefficient between the two
criteria.
3) Obtain the quantity of information on each
criterion.
4) Determine the objective weights for each
criterion.
The definition is as follows.
Definition 3. Let 𝑆

be the standard deviation of the
vth criterion out of a total of m criteria, and 𝑟

be the
DATA 2022 - 11th International Conference on Data Science, Technology and Applications
128

correlation coefficient between vth and fth criterion.
The quantity of information contained in the vth
criterion is calculated using Equation (3):

=
−=
m
f
vfvv
rSC
1
)1(
(3)
where v=1,2,...,m and f=1,2,...,m.
Definition 4. The weight of the vth criterion is
calculated using Equation (4):

=
=
m
f
f
v
v
C
C
w
1
(4)
where 𝐶

represents the quantity of information
contained in the vth criterion;
∑
𝐶



represents the
quantity of information contained in these m criteria.
The larger 𝐶

is, the more weight given to the vth
criterion.
2.3 2T-CRITIC Model
The 2T-CRITIC model consists of aggregating the
scores of different criteria into an overall score. The
definition is as follows.
Definition 5. Based on the 2-tuple value aggregated
for each criterion and the weights defined in Equation
(4), the overall score of these m criteria is calculated
using Equation (5):






Δ⋅Δ=
−
=
−

)(
1
1
2 v
m
v
vCRITICT
TwR
(5)
2.4 Weighted K-means Clustering
Traditional K-means clustering is computationally
efficient and works well with large datasets.
However, it assigns all observations identical weight,
ignoring the relevance of each feature attribute in the
dataset (Yu et al., 2020).
Weighted K-means clustering is a K-means
clustering extension that allows for user-defined
weighting. This method takes into account the
weights associated with each criterion or dimension
when computing the cluster centroid. It can be applied
to improve the clustering scalability (Kerdprasop
et al., 2005), and clustering results (Baswade et al.,
2012). The definition is as follows.
Definition 6. Let k be the the optimal number of
clusters, the weighted Euclidean distance of each
object to the cluster centroid is calculated using
Equation (6):
()

=
−−
Δ−Δ=
m
v
cvmvv
kxwcmd
1
2
11
)()(),(
(6)
where 𝑤

represents the weight of the vth criterion, as
defined in Equation (4).
For more details on the Weighted K-means
clustering processing steps, see (Yu et al., 2020).
The following is an example of how to calculate
the weighted Euclidean distance.
Let 𝑆=

𝑠

=𝑇,𝑠

=𝑃,𝑠

=𝐴,𝑠

=𝑉𝐺,𝑠

=
𝐸

be a linguistic term set, W=
(
0.2,0.3,0.5
)
be
the vector to represent the weight of three criteria
determined by the Equation (4), and 𝑋

=

(𝐴,0),(𝑃,−0.2),(𝐴,+0.3)

be a set of 2-tuple
values to represent the ratings of object A on three
different criteria. Let 𝑘=3 , so that the centroid of
Cluster 1 is 𝐶

=

(𝐴,+0.03),(𝑃,−0.2),(𝐴,+0.1)

,
the centroid of Cluster 2 is 𝐶

=

(𝑉𝐺,0),(𝑉𝐺,+0.1),(𝐴,+0.1)

, and the centroid of
Cluster 3 is 𝐶

=

(𝐴,0),(𝑉𝐺,−0.1),(𝐴,+0.11)

.
The weighted Euclidean distance between hotel A
and the centroid of Cluster 1 is determined as:
d
(
X

,C

)
=

0.2∆

(
A,0
)
−∆

(
A,+0.03
)


+0.3∆

(
𝑃, −0.2
)
−∆

(
𝑃,−0.2
)


+0.5∆

(
A,+0.3
)
−∆

(
A,+0.1
)


=

0.2
(
2 − 2.03
)

+0.3
(
0.8 − 0.8
)

+0.5
(
2.3−2.1
)

=0.1421
In the same way,
d
(
X

,C

)
= 1.3442 and
d
(
X

,C

)
= 1.158 are the weighted Euclidean
distance between object A and the centroid of Cluster
2 and 3, respectively. As the distance between object
A and the centroid of Cluster 1 is the smallest
(
d
(
X

,C

)
< d
(
X

,C

)
< d
(
X

,C

)
), it will be given a
cluster number 1.
3 PROPOSED MODEL AND
APPLICATION TO THE
SEGMENTATION OF
TRIPADVISOR HOTELS
This section explains how the proposed model was
developed, as well as its application in the hotel
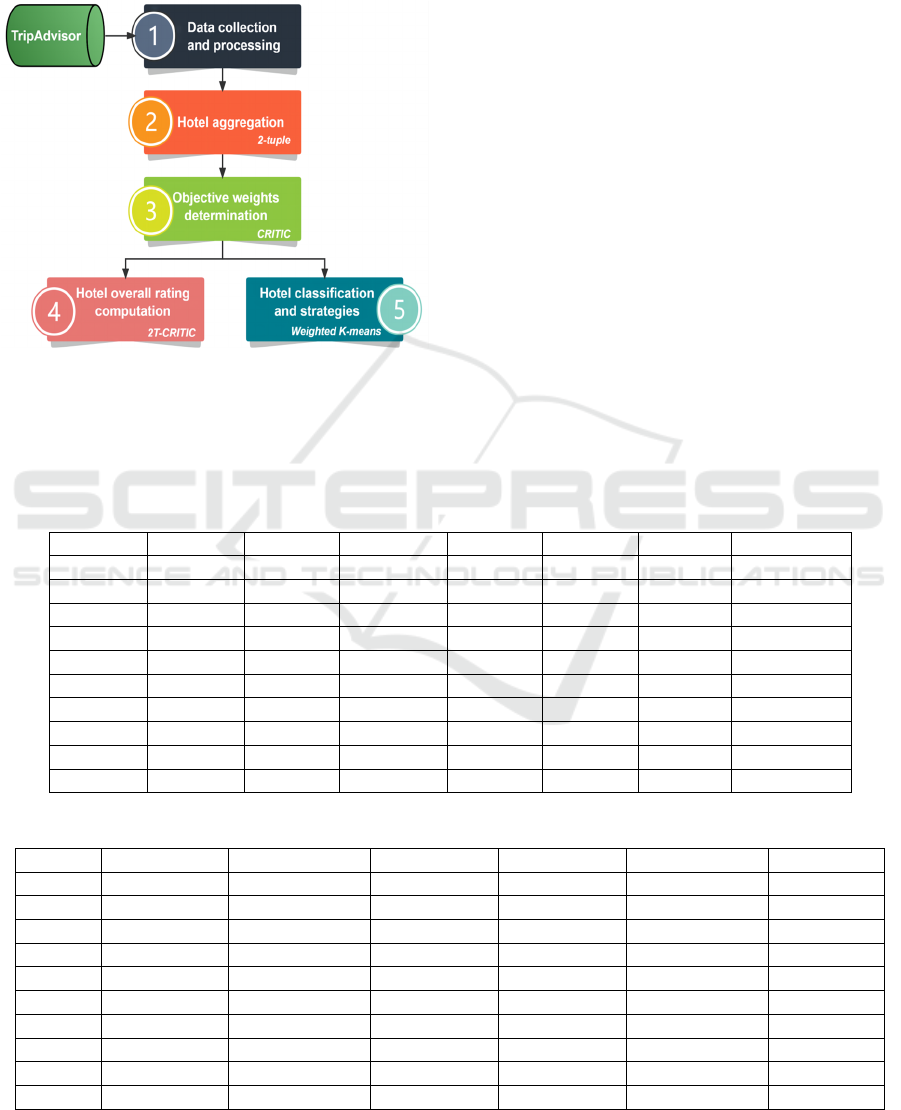
classification. This model is divided into five steps,
as shown in Figure 1.
Step 1. Data Collection and Processing
In this step, the dataset provided by (Antognini &
Faltings, 2020) has been applied in this paper. This
dataset contains more than fifty million TripAdvisor
hotel reviews from 21.89 million users that
commented from February 1, 2001, to May 14, 2019.
A Model based on 2-tuple Linguistic Model and CRITIC Method for Hotel Classification
129

This dataset contains both textual reviews and
numerical ratings of hotels. However, considering the
purpose of this paper is to classify hotels based on
their various aspects, the textual reviews have been
eliminated.
Figure 1: Steps of the proposed model.
Furthermore, as TripAdvisor's sub-ratings are
optional, not all aspects (up to eight) are assessed by
users. Most sub-ratings are evaluated in groups of
three or six aspects, with Check-In and Business
Service being the two aspects that are rarely scored.
Therefore, in this study, only those hotels that
have been scored in all six aspects are included,
obtaining a dataset of 228,339 hotels with the
following variables: user ID, hotel ID, Service aspect
rating, Cleanliness aspect rating, Value aspect rating,
Location aspect rating, Rooms aspect rating, and
Sleep quality aspect rating. Table 1 shows an example
of the dataset after data processing.
Step 2. Hotel Aggregation with the 2-tuple
Linguistic Model
This step is to aggregate the various user evaluations of
the hotel's six aspects into 2-tuple values.
The linguistic term set S used by TripAdvisor to
rate hotels has five terms: Terrible (T), Poor (P),
Average (A), Very Good (VG) and Excellent (E).
Thus, let 𝑆=𝑠

,…,𝑠

 with g=4: 𝑠

=𝑇𝑒𝑟𝑟𝑖𝑏𝑙𝑒=
𝑇, 𝑠

=𝑃𝑜𝑜𝑟=𝑃, 𝑠

=𝐴𝑣𝑒𝑟𝑎𝑔𝑒=𝐴, 𝑠

=
𝑉𝑒𝑟𝑦 𝐺𝑜𝑜𝑑=𝑉𝐺, y 𝑠

=𝐸𝑥𝑐𝑒𝑙𝑙𝑒𝑛𝑡=𝐸, as shown
in Figure 2. Based on the Equation (2), the ratings of
customers on hotel aspects have been aggregated into
2-tuple values. Table 2 shows an example of
aggregation of hotel aspect ratings expressed in 2-tuple
values.
Table 1: Example of hotel aspect ratings.
User ID Hotel ID Service Cleanliness Value Rooms Location Sleep quality
204966 54046
E E E E E E
12459774 54046
A A A A A A
7622513 193760
E E E E E E
3868105 152011
E E E E E E
17640662 33026
VG VG VG VG VG VG
8954809 177981
A A A A A A
3583774 177981
VG VG VG VG VG VG
288708 177981
T T T T T T
9010318 203518
VG VG VG VG VG VG
16145194 227714
P P P P P A
Table 2: Example of aggregation of hotel aspect ratings expressed in 2-tuple values.
Hotel ID Service Cleanliness Value Rooms Location Sleep quality
54046 (A, +0.0384) (P, -0.248) (A, +0.2616) (A, +0.1449) (P, -0.243) (A, +0.0685)
190291 (A, -0.01) (P, +0.0659) (A, -0.117) (P, +0.236) (P, +0.0588) (A, +0.009)
193760 (VG, +0.046) (VG, +0.0602) (A, +0.0577) (VG, +0.0174) (VG, -0.0323) (A, +0.1155)
152011 (E, -0.4444) (A, +0.49) (E, -0.25) (VG, +0.4286) (E, -0.1) (A, -0.14)
33026 (VG, -0.141) (VG, +0.0198) (A, +0.0986) (VG, +0.0375) (VG, -0.0647) (A, +0.0957)
177981 (A, -0.035) (P, -0.1279) (A, -0.3904) (P, -0.0668) (A, +0.0872) (A, +0.056)
203518 (A, +0.001) (VG, +0.0755) (A, +0.1075) (VG, -0.0589) (VG, +0.109) (A, +0.037)
227714 (VG, -0.1333) (VG, +0.0267) (A, +0.0806) (VG, +0.0502) (VG, -0.0489) (A, +0.107)
113986 (A, -0.0302) (VG, +0.0513) (A, -0.0685) (VG, +0.0921) (A, +0.152) (A, +0.0509)
44257 (A, +0.0135) (VG, -0.01) VG (A, +0.07) (A, +0.1) (A, +0.0278)
DATA 2022 - 11th International Conference on Data Science, Technology and Applications
130

Figure 2: Definition of linguistic term set S.
Figure 3: Correlation matrix for each pair of criteria.
Step 3. Determination of the Objective Weights for
each Aspect of Hotel with the CRITIC Method
This step is to obtain the objective weights for the
hotel's six aspects using the CRITIC method.
In the previous step, the arithmetic mean has been
used to aggregate the 2-tuple values of different
customer ratings for distinct aspects of the hotel,
resulting in the 2-tuple value for each hotel aspect.
Using the function ∆

to transform the 2-tuple value
into its numerical value, so that correlation
coefficients have been obtained as shown in Figure 3.
These six aspects are highly correlated since their
correlation coefficients are all more than 0.7. Their
objective weights are derived by using Equations (3)
and (4), as shown in Table 3.
Table 3: Weights for each hotel aspect.
Aspect
Standard
Deviation
Quantity of
information
weights
Service 0.479 0.0326 10.97%
Cleanliness 0.486 0.0807 27.16%
Value 0.492 0.0418 14.08%
Rooms 0.497 0.0447 15.06%
Location 0.495 0.0436 14.67%
Sleep quality 0.511 0.0537 18.06%
Step 4. 2T-CRITIC Hotel Overall Rating
Computation
This step is to aggregate the scores of six aspects of
the hotel into an overall score by using Equation (5).
The results of the calculations for some hotels are
shown in Table 5.
The example below shows how to calculate
overall score for hotel 152011:
()
)0187.0,(0187.3
%06.1886.1%67.149.3
%06.154286.3%08.1475.3
%16.2749.2%97.105556.3
%06.18)14.0,(
%67.14)1.0,(
%06.15)4286.0,(
%08.14)25.0,(
%16.27)49.0,(
%97.10)4444.0,(
1
1
1
1
1
1
2
+=Δ=








×+×+
×+×+
×+×
Δ=














×−Δ+
×−Δ+
×+Δ+
×−Δ+
×+Δ+
×−Δ
Δ=
−
−
−
−
−
−
−
VG
A
E
VG
E
A
E
R
CRITICT
Step 5. Hotel Classification and Strategies
In this step, Weighted K-means clustering has been
applied to create homogeneous groups of hotels. It
entails utilizing Equation (6) to categorize hotels
based on their weighted Euclidean distance.
As the Elbow Method reveals that k=8 is the
optimal number of clusters, 8 distinct groups of hotels
have been obtained. Table 4 demonstrates the results
of the hotel clusters expressed in the 2-tuple value and
the number of hotels included in each cluster.
Ten distinct hotels are presented in Table 5, with
their relation to the cluster characteristics indicated in
Table 6.
Table 4: Results of clusters expressed in 2-tuple value.
Cluster ID
Number
of hotels
Service Cleanliness Value Rooms Location
Sleep
qualit
y
1 31,566
(
VG, -0.12
)
(
VG, +0.01
)
(
A, +0.1
)
(
VG, +0.04
)
(
VG, -0.02
)
(
A, +0.12
)
2 29,869
(
A, +0.01
)
(
P, +0.17
)
(
A, -0.12
)
(
P, +0.2
)
(
P, +0.19
)
(
A, +0.01
)
3 28,993 (E, -0.21) (A, +0.05) (VG, +0.1) (A, -0.05) (E, -0.08) (A, -0.13)
4 25,627 (A, -0.03) (VG, +0.06) (A, -0.05) (VG, +0.08) (A, +0.17) (A, +0.06)
5 29,656 A (VG, +0.08) (A, +0.11) (VG, -0.07) (VG, +0.08) (A, +0.02)
6 30,815
(
A, +0.03
)
(
P, -0.21
)
(
A, +0.13
)
(
A, +0.15
)
(
P, -0.07
)
(
A, +0.07
)
7 25,295
(
A, -0.04
)
(
P, -0.15
)
(
A, -0.07
)
(
P, -0.06
)
(
A, +0.02
)
(
A, +0.05
)
8 26,518 A
(
VG, -0.05
)
(
VG, +0.01
)
(
A, +0.09
)
(
A, +0.11
)
(
A, +0.06
)
All_Data* 228,339 (A, +0.03) (A, +0.13) (A, +0.09) (A, +0.2) (A, +0.1) (A, +0.02)
*The average level of these 228,339 hotels is shown by All Data.
A Model based on 2-tuple Linguistic Model and CRITIC Method for Hotel Classification
131

Table 5: 2T-CRITIC Overall Score and Cluster ID for some
hotels.
Hotel ID 2T-CRITIC Overall Score Cluster ID
54046
(A, -0.4461) 6
190291
(P, +0.2966) 2
193760
(VG, -0.2731) 1
152011
(VG, +0.0187) 3
33026
(VG, -0.3042) 1
177981
(P, +0.4971) 7
203518
(VG, -0.3959) 5
227714
(VG, -0.2977) 1
113986
(A, +0.4685) 4
44257
(A, +0.4414) 8
Therefore, based on their objective overall score
aggregated by six hotel aspects, customers could
choose a hotel that is more relevant to their needs. For
example, as shown in Table 5, the hotels in cluster 1
(193760, 33026, 227714) have a similar 2T-CRITIC
overall score, indicating that this cluster consists of
upper-midscale hotels. Combined with the
information demonstrated in Table 6, it can be
concluded that this group of hotels is appropriate for
customers who desire particularly good cleanliness,
service, rooms, and location, but cannot afford the
price of a first-class hotel (cluster 3, such as hotel
152011).
Likewise, hotel managers could take suitable
actions to fix their weaknesses based on the
descriptions in Table 6 for each cluster. For instance,
as the cleanliness, service, rooms, and location of
cluster 1 are already very good, it might be beneficial
to increase the value or sleep quality of this sort of
hotel to gain a new competitive advantage.
Table 6: Description for each group of hotels.
Cluster
ID
Cluster Name Description
1
Hotel with a very good
cleanliness, service, rooms,
and location.
It consists of hotels with a very good level of cleanliness, service, and rooms.
The quality of sleep in this sort of hotel is superior to that of other hotels, but it
is still average level. Despite not having as good a location as clusters 3 and 5,
they are still better than the rest of the hotels.
2
Hotel with poor cleanliness,
location, and rooms.
It consists of hotels with much lower-than-average cleanliness, rooms, and
location. Their value is a touch below average. The other two aspects are nearly
identical to the average.
3
A first-class hotel with an
excellent location, very
good service, and value.
It consists of hotels that are well-known for their outstanding location, which
sets them apart from the rest of the hotels. Their service and value are also better
than the rest of the hotels, although the sleep quality in this type of hotel is lower
than the average level. The other two aspects are nearly identical to the average.
4
Hotel with very good
cleanliness and rooms.
It consists of hotels with higher-than-average cleanliness and rooms, although
the other four aspects are nearly identical to the average.
5
Hotel with very good
cleanliness, rooms, and
location.
It consists of hotels with very good cleanliness, rooms, and location, although
the other three aspects are almost as same as average. Despite not having as
excellent a location as cluster 3, their rooms and cleanliness are superior to those
of it.
6
Hotel with poor cleanliness
and bad location.
It consists of hotels that are less hygienic and have a worse location than the
other hotels. The other four aspects are nearly identical to the average.
7
Hotel with poor cleanliness
and rooms.
It consists of hotels with a poor level of cleanliness and rooms. Their rooms are
inferior to those of the other hotels. The other four aspects are nearly identical
to the average.
8
Hotel with very good
cleanliness and value.
It consists of hotels with higher-than-average cleanliness and value. Although
the other four aspects are roughly comparable to the average, the service level
of this group of hotels is the same as cluster 5, and its sleep quality is the same
as cluster 4.
DATA 2022 - 11th International Conference on Data Science, Technology and Applications
132

4 CONCLUSIONS AND FUTURE
WORK
In this paper, a new method for segmenting hotels
based on the 2T-CRITIC model and Weighted K-
means clustering is presented. Unlike standard K-
means clustering, this proposed model assigns
different weights to variables in the clustering process
as it considers the quantity of information included in
variables is different. A use case with more than 50
million TripAdvisor hotel reviews has been employed
to evaluate its functionality.
The results show that the proposed model can
improve clustering results by considering objective
weights for each criterion and make clustering results
more linguistically interpretable by using the 2-tuple
linguistic model. By interpreting these linguistic
scores of each hotel, hotel managers can develop
more effective strategies to improve their hotel
ranking. In fact, these results of classification aid
hotel managers in developing appropriate strategies
for gaining a new competitive advantage or
improving those aspects that they need to make a
change, so that they can attract more customers from
the other clusters. Furthermore, combined with the
objective overall hotel score, these results can help
customers choose a hotel that is more appropriate for
their needs.
Despite all the benefits of the proposed model in
this study, certain shortcomings should be pointed
out. First, as this proposal uses CRITIC method to
calculate the objective weight of each hotel aspect, it
ignores that the customers evaluated hotels with
different subjective feelings and levels of perception.
For example, perhaps 3 is very high (total score of 5)
for a very demanding customer, but for a less
demanding customer, 3 is only a medium score.
Another weakness is that this approach still relies on
the traditional 2-tuple model. It cannot be applied to
those variables without linguistic scales, such as sex,
hair color, country, etc., which are nominal variables.
Therefore, for future work, some practical
problems of the proposed model should be addressed.
This model could be extended by applying some
methods that allow calculating the subjective weights
of variables, such as the analytic hierarchy process
(AHP) method, Delphi method, Point allocation
method, etc. It could also develop a model that
combines subjective and objective weights into a
single function. Other variables like travel country,
duration of stay, hotel price, reservation number,
cancel number, etc., could also be included in the
hotel segmentation to get an all-round understanding
of the hotel.
ACKNOWLEDGEMENTS
The co-author Manuel Sánchez-Montañés was
funded by Agencia Estatal de Investigación
AEI/FEDER Spain, Project PGC2018-095895-B-I00,
and Comunidad Autónoma de Madrid, Spain, Project
S2017/BMD-3688.
REFERENCES
Abdullah, D., Susilo, S., Ahmar, A. S., Rusli, R., &
Hidayat, R. (2021). The application of K-means
clustering for province clustering in Indonesia of the
risk of the COVID-19 pandemic based on COVID-19
data. Quality & Quantity.
Ali, A., TAMBY CHIK, C., Sulaiman, S., Salman, W., &
Mohd Shahril, A. (2020). Measuring Tourist
Satisfaction And Revisit Intention Using Lodgeserv In
Boutique Hotel. EPRA International Journal of
Economic and Business Review, pages 16-25.
Antognini, D., & Faltings, B. (2020). HotelRec: A Novel
Very Large-Scale Hotel Recommendation Dataset.
http://arxiv.org/abs/2002.06854
Baswade, A. M., Joshi, K. D., & Nalwade, P. S. (2012). A
Comparative Study Of K-Means And Weighted K-
Means For Clustering. International Journal of
Engineering Research, 1(10), 4.
Beracha, E., Hardin, W. G., & Skiba, H. M. (2018). Real
Estate Market Segmentation: Hotels as Exemplar. The
Journal of Real Estate Finance and Economics, 56(2),
pages 252-273.
Chowdhury, K., Chaudhuri, D., & Pal, A. K. (2021). An
entropy-based initialization method of K-means
clustering on the optimal number of clusters. Neural
Computing and Applications, 33(12), pages 6965-6982.
Çınar, K., Yetimoğlu, S., & Uğurlu, K. (2020). The Role of
Market Segmentation and Target Marketing Strategies
to Increase Occupancy Rates and Sales Opportunities
of Hotel Enterprises. Strategic Innovative Marketing
and Tourism, pages 521-528.
Deane, S. (2022). Over 60 Online Travel Booking Statistics
(2022). https://www.stratosjets.com/blog/online-travel-
statistics/
Diakoulaki, D., Mavrotas, G., & Papayannakis, L. (1995).
Determining objective weights in multiple criteria
problems: The critic method. Computers & Operations
Research, 22(7), pages 763-770.
Díaz, G., Carrasco, R., & Gómez, D. (2021). RFID: A
Fuzzy Linguistic Model to Manage Customers from the
Perspective of Their Interactions with the Contact
Center. Mathematics, 9, page 2362.
El Khediri, S., Fakhet, W., Moulahi, T., Khan, R.,
Thaljaoui, A., & Kachouri, A. (2020). Improved node
localization using K-means clustering for Wireless
Sensor Networks. Computer Science Review, 37, page
100284.
Herrera, F., & Martinez, L. (2000). A 2-tuple fuzzy
A Model based on 2-tuple Linguistic Model and CRITIC Method for Hotel Classification
133

linguistic representation model for computing with
words. IEEE Transactions on Fuzzy Systems, 8(6),
pages 746-752.
Herrera, F., Herrera-Viedma, E., Martinez, L., Torres, J., &
López-Herrera, A. G. (2004). Incorporating Filtering
Techniques in a Fuzzy Linguistic Multi-Agent Model
for Information Gathering on the Web. Fuzzy Sets and
Systems, 148, pages 61-83.
Jahangoshai Rezaee, M., Eshkevari, M., Saberi, M., &
Hussain, O. (2021). GBK-means clustering algorithm:
An improvement to the K-means algorithm based on
the bargaining game. Knowledge-Based Systems, 213,
page 106672.
Ju, Y., Wang, A., & Liu, X. (2012). Evaluating emergency
response capacity by fuzzy AHP and 2-tuple fuzzy
linguistic approach. Expert Systems with Applications,
39, pages 6972-6981.
Kerdprasop, K., Kerdprasop, N., & Sattayatham, P. (2005).
Weighted K-Means for Density-Biased Clustering.
Data Warehousing and Knowledge Discovery, 3589,
pages 488-497.
Liu, P., & Chen, S.-M. (2018). Multiattribute group
decision making based on intuitionistic 2-tuple
linguistic information. Information Sciences, 430-431,
pages 599-619
MA, Y., & ZHANG, C. (2019). Research on the Division
of the Take-Out Order Region Based on Improved
Weighted K-Means Clustering. Statistics and
Application, 8(2), pages 203-217.
Mody, M., Suess, C., & Lehto, X. (2019). Using
segmentation to compete in the age of the sharing
economy: Testing a core-periphery framework.
International Journal of Hospitality Management, 78,
pages 199-213.
Nilashi, M., Mardani, A., Liao, H., Ahmadi, H., Manaf, A.
A., & Almukadi, W. (2019). A Hybrid Method with
TOPSIS and Machine Learning Techniques for
Sustainable Development of Green Hotels Considering
Online Reviews. Sustainability, 11(21), page 6013.
Sohaib, O., Naderpour, M., Hussain, W., & Martinez, L.
(2019). Cloud computing model selection for e-
commerce enterprises using a new 2-tuple fuzzy
linguistic decision-making method. Computers &
Industrial Engineering, 132, pages 47-58.
Yu, Y., Velastin, S. A., & Yin, F. (2020). Automatic
grading of apples based on multi-features and weighted
K-means clustering algorithm. Information Processing
in Agriculture, 7(4), pages 556-565.
Zhao, D., Hu, X., Xiong, S., Tian, J., Xiang, J., Zhou, J., &
Li, H. (2021). K-means clustering and kNN
classification based on negative databases. Applied Soft
Computing, 110, page 107732.
DATA 2022 - 11th International Conference on Data Science, Technology and Applications
134