
Verification of PUF-based IoT Protocols with AVISPA and Scyther
Tom
´
a
ˇ
s Rabas
a
, R
´
obert L
´
orencz
b
and Ji
ˇ
r
´
ı Bu
ˇ
cek
c
Faculty of Information Technology, Czech Technical University, Thakurova, Prague, Czech Republic
Keywords:
Authentication, PUF, IoT, Formal Verification.
Abstract:
Paper from 2020 (Buchoveck
´
a et al., 2020) suggests protocols suitable for lightweight IoT Devices. They are
based on physical unclonable functions (PUF) which among others simplify the problem of key management
on simple hardware devices and microcontrollers. These protocols are supposed to authenticate a device and
distribute keys safely so that only the intended parties can know the key. We analysed suggested protocols
using two automated verification tools AVISPA and Scyther. The analysis shows that there are several issues
concerning the authentication property. We demonstrate the results from the tools and describe several attacks
that exploit this vulnerability. Finally, we provide modified versions of these protocols that are resistant to
those attacks and satisfy authentication as desired.
1 INTRODUCTION
Related Work
Physical Unclonable Functions (PUFs) allowed for
the introduction of new cryptographic schemes and
protocols that intend to be used in special constrained
environments where standard protocols are too expen-
sive in terms of space, energy or power consumption.
Such protocols were introduced for example in (Ma-
jzoobi et al., 2012), (Idriss and Bayoumi, 2017) or
(Chatterjee et al., 2017).
Unfortunately, not all of such proposals indeed
satisfy the intended security properties as shown for
example in (Braeken, 2018).
Therefore, the need for formal verification is clear.
Such analysis can be done by several tools. One of
them is called AVISPA and it was used in (Zargar
et al., 2021) or (Nimmy et al., 2021). Another one
called Scyther was used in (Ray et al., 2016).
Organization of the Paper
We divided the paper into the following sections.
First, we give the necessary background on for-
mal verification, automated tools, physical unclonable
functions and our formal model of PUF in section
2. Then, we describe original protocols from (Bu-
a
https://orcid.org/0000-0002-0924-359X
b
https://orcid.org/0000-0001-5444-8511
c
https://orcid.org/0000-0003-1359-4285
choveck
´
a et al., 2020) in Section 3. We do the analy-
sis and describe found attacks in section 4. Finally, we
suggest corrections and modifications of the original
protocols that are necessary to fulfill desired security
properties in section 5.
2 BACKGROUND KNOWLEDGE
AND TERMINOLOGY
2.1 Dolev-Yao Model
The Dolev-Yao model is named after its authors D.
Dolev and A. Yao. It is a formal model used to prove
the security properties of cryptographic protocols.
Both verification tools we used follow the Dolev-Yao
model. This model represents cryptographic primi-
tives as abstract operators with certain properties and
it specifies intruder capabilities as follows.
The intruder cannot decrypt a message without the
key and he cannot guess a secret key or a nonce. In
other words, it says that cryptography is safe.
Then, we assume that the intruder has full con-
trol over the network, specifically he can read, store,
block every message, he can build and send mes-
sages, he can compose/decompose messages, he can
encrypt/decrypt if he has the key, he knows all the
public data of the protocol, and he has all the privi-
leges/keys of corrupted agents.
In general, the Dolev-Yao model allows treating
cryptography in automated tools, because it abstracts
Rabas, T., Lórencz, R. and Bu
ˇ
cek, J.
Verification of PUF-based IoT Protocols with AVISPA and Scyther.
DOI: 10.5220/0011299000003283
In Proceedings of the 19th International Conference on Security and Cryptography (SECRYPT 2022), pages 627-635
ISBN: 978-989-758-590-6; ISSN: 2184-7711
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
627

cryptography by deterministic operations on abstract
terms and simple cancellation rules. This simplifica-
tion enables the tools to treat larger overall systems
automatically than with more detailed models of cryp-
tography (Backes et al., 2006).
2.2 AVISPA+SPAN
AVISPA (Armando et al., 2005) is a tool for auto-
mated verification of protocols (Vigano, 2006). It in-
troduces High-Level Protocol Specification Language
(HLPSL) in which you implement the protocol as in-
put for AVISPA. You can choose from four different
back-ends included in AVISPA to verify the imple-
mented protocol. In case that the back-end finds an
attack, Security Protocol ANimator (SPAN) produces
a message sequence chart that graphically describes
the attack. Otherwise, the back-end evaluates that the
protocol is safe.
2.3 Scyther
Similarly as AVISPA, Scyther (Cremers, 2008) is a
push-button tool for verification, falsification, and
analysis of protocols. It provides a graphical inter-
face for verifying and understanding of a protocol.
It also provides a command line and scripting inter-
faces for large-scale protocol verification tests. It of-
fers state-of-the-art performance and novel features
like multi-protocol analysis. It accepts the description
of a protocol in easy-to-read language SPDL based on
C/Java-like syntax.
We used Scyther as a tool of second-opinion since
we encountered some bugs and questionable behav-
ior of AVISPA which slightly undermined our confi-
dence in that tool. Specifically, the results of different
back-ends contradicted each other. We describe that
in section 5.1.
2.4 Physical Unclonable Function
Physical Unclonable Functions (Herder et al., 2014)
offer a physically-based digital fingerprint of a de-
vice. The fingerprint is unpredictable and unique for
every device and every challenge if used in challenge-
response mode. Unfortunately, PUFs are not error-
free which can be mitigated by many techniques, and
one of them is Error Correcting Codes (ECC).
There are many different types of PUFs. One of
them is called SRAM PUF (B
¨
ohm et al., 2011). It is
based on the behavior of Static Random Access Mem-
ory (SRAM) that is available in any digital chip. Each
SRAM cell provides a zero or a one after powering
the circuit. The subset of such SRAM cells defines
the output of the SRAM PUF. Since each cell tends to
be in its preferred state, we get quite stable, yet ran-
domly looking, patterns of 0s and 1s that work as a
fingerprint of the chip and the concrete subset of cells
on the chip. We can refer to this subset of SRAM cells
as a challenge C.
2.5 Security Properties
Let us define several terms that we will use to describe
properties of the protocols. Although different for-
mal verification tools may use slightly different def-
initions, definitions described below should provide
as much insight and level of formalism as needed for
understanding the attacks. Especially in case of au-
thentication, there are many ways of formal definition
with different strength. For more information we re-
fer reader to (Cremers and Mauw, 2012) chapters 4.3
and 8.2 or (Lowe, 1997) – Lowe’s article from 1997
Hierarchy of Authentication Specifciations.
We say that protocol ensures secrecy of message
s if an adversary cannot syntactically deduce s. An
agent B authenticates a message m if B knows which
agent builds m. An agent A authenticates an agent
B if, after the successful session of the protocol, A
knows that he has run the protocol with B. During a
protocol session, a message is fresh if this message
has specifically been built for this protocol session.
2.6 Compromising Adversary
In 1978 (Needham and Schroeder, 1978) Needham-
Schroeder Protocol was proposed that achieves mu-
tual authentication of both parties. It was assumed to
be secure for over 20 years. In 1989 (Burrows et al.,
1989) Burrows, Abadi and Needham confirmed its se-
curity using formal methods of verification which was
seen as a formal proof of an intuitively straightfor-
ward protocol. Surprisingly in 1996 (Lowe, 1995) an
attack was found by Gavin Lowe. The reason for that
is not a more powerful analysis method but rather ex-
tended possibilities of the adversary.
In the eighties, users in the network were assumed
to be honest. Later, the view of networks changed.
Not all users were necessarily trusted, and so network
protocols in a formal analysis should assume that an
intruder can play one part in the protocol (or, the in-
truder has compromised a regular user). We say that
a protocol is safe with (resp. without) presence of a
compromising adversary (or internal intruder) if we
(do not) add this extra possibility to the intruder.
The verification tool Scyther during its analysis
automatically assumes the presence of a compromis-
ing adversary.
SECRYPT 2022 - 19th International Conference on Security and Cryptography
628

3 ORIGINAL PROTOCOLS
Here we describe three protocols and a unique enrol-
ment phase that is supposed to be exchanged through
a secure channel before the start of each protocol,
which were published in (Buchoveck
´
a et al., 2020)
(and later in extended form also in (Buchoveck
´
a et al.,
2022)). We denote Authentication Authority as AA
and its public key as PK
AA
.
3.1 Enrolment Phase
During the Enrolment phase where the AA commu-
nicates with some device D1, see Fig. 1, a database
DB
D1
is created and securely stored at the AA. It con-
tains challenge/response pair(s) (C, R) that are mea-
sured from the targeted device D1. Specifically for
Protocol 1, public key PK
AA
is stored in the device
D1 (lines 5 and 6).
Common for Protocols 1-3:
1. AA → D1: Challenges (C1, C2, ...)
2. D1: R1 = PUF(C1), R2 = PUF(C2), ...
3. D1 → AA: Responses (R1, R2, ...)
4. AA: Store (C
i
,R
i
) to DB
D1
Specific only for Protocol 1:
5. AA → D1: Public key PK
AA
6. D1: Store(PK
AA
)
Figure 1: Enrolment phase – stores the database of chal-
lenge response pairs at authentication authority.
3.2 Protocol 1 Description
Protocol 1 provides authentication of a device D1 to
authority AA. See Fig. 2. The authentication au-
thority chooses a challenge-response pair (C, R) from
DB
D1
and sends the challenge C together with a fresh
nonce N to device D1. It creates a response R’=
PUF(C) and concatenates it with N. Then, the device
encrypts R’||N with the public key PK
AA
as CR =
E
PK AA
(R’|| N) and sends it to AA. In the end, AA
decrypts the message and checks if the accepted re-
sponse R’ corresponds to the response R from the
database DB
D1
and it checks that the accepted nonce
is the same as the sent one.
Note that R’ and R are responses that are from
their very nature probabilistic values meaning there is
a chance of having a false negative in the protocol.
In our formal analysis, we disregard this probabilistic
nature and we assume that our PUF construction is
perfect. Therefore, instead of symbol
∼
=
in step 5,
we could have used just equality =, yet we left the
description as it was published in the original article.
0. Enrolment phase (secure environment)
1. AA: Choose (C,R) from DB
D1
2. AA → D1: Challenge C, Nonce N
3. D1: R’ = PUF(C)
4. D1 → AA: CR = E
PK AA
(R’||N)
5. AA: (R’, N’) = D
SK AA
(CR)
Compare(R
∼
=
R’), Compare(N = N’)
Figure 2: Protocol 1 provides authentication of a device D1
to authority AA.
3.3 Protocol 2 Description
Protocol 2 is described in Fig. 3. It provides authenti-
cation of the device D1 to the authority AA as Proto-
col 1, but on top of that, it establishes shared symmet-
ric key K for future encrypted communication starting
from step 10.
In the beginning, device D1 notifies the author-
ity that it would like to start protocol 2 by sending
the message Call(D1) (step 1). Then, authority gener-
ates a random data r, chooses challenge-response pair
(C,R) from its database DB
D1
, creates helper string
H = R xor Encode(r) and derives K by key derivation
function as K = KDF(r) (steps 2-5). Authority sends
the challenge C and the helper string H to the device
(step 6). The device creates the response R’ from the
accepted challenge as R’ = PUF(C). It obtains the se-
cret random data r = Decode(R’ xor H) and derives
the shared key K = KDF(r) (steps 7-9).
Usage of helper data in protocols is described for
example in (Delvaux et al., 2014), (Merli et al., 2013)
or (Maes et al., 2009).
Notice that it is a key distribution protocol and not
a key agreement protocol, since the random data r are
generated solely by the AA and distributed to the de-
vice xored with the response so that one can deter-
mine the value r only with knowledge of the response.
Since we assume that our PUF is perfect, the En-
code and Decode functions are in our case just identi-
ties. Yet, in real implementation, they implement the
usage of Error Correction Code that makes otherwise
very probabilistic PUF constructions useful. There-
fore, we left them in the description.
3.4 Protocol 3 Description
The last protocol provides mutual authentication be-
tween devices D1 and D2 and establishes shared sym-
metric key K between those devices for future en-
crypted communication starting from step 19. Sim-
ilarly, as in protocol 2, it is in fact distribution pro-
tocol and authentication authority takes an essential
role. See Fig. 4 for the description.
Let us assume that device D1 wants to connect
to device D2. It initiates the protocol by sending
Verification of PUF-based IoT Protocols with AVISPA and Scyther
629

0. Enrolment phase (secure environment)
1. D1 → AA: Call(D1)
2. AA: r = TRNG()
3. Choose (C,R) from DB
D1
4. H = R xor Encode(r)
5. K = KDF(r)
6. AA → D1: Challenge C, Helper string H
7. D1: R’ = PUF(C)
8. r = Decode(R’ xor H)
9. K = KDF(r)
10. D1 ↔ AA: Authentication + Encryption with K
Figure 3: Description of Protocol 2 that authenticates a de-
vice to the authority and distributes the shared key from the
authority to the device.
message Call(D1, D2) to authority AA which iden-
tifies both devices in step 1. Authority generates
two random components r
D1
and r
D2
from the set of
preimages of ECC and encodes them, thereby form-
ing randomly chosen codewords. In our case, ECC
is just identity since our PUF is error-free. Never-
theless, the code length should in reality correspond
to the PUF response length. Then, authority creates
helper strings H
D1
and H
D2
by xoring the expected
PUF responses R
D1
and R
D2
to the corresponding
codewords. In step 8, both random components are
hashed and xored together resulting in r = Hash(r
D1
)
xor Hash(r
D2
).
Authority then sends triplet with the correspond-
ing challenge, helper data and r to both devices in
steps 9 and 10. In addition, it relays the initial re-
quest for communication Call(D1, D2) from D1 to
D2. Both devices then create their responses to the ac-
cepted challenges as R’
Di
= PUF(C
Di
). Devices xor it
with helper data H
Di
and decode it, so they get the ran-
dom component r
Di
which they are entitled to (steps
12 and 16). Let us note that they are not able to recre-
ate the random component for the other device. Nev-
ertheless, they can compute its hash (by xoring r with
the hash of its own random component), and use it
to recover the final shared secret key K (steps 14 and
18).
4 ANALYSIS AND ATTACKS
In this section, we will discuss the results of our anal-
ysis and elaborate on found attacks. You can see sum-
marization in Table 1. You can see Just before that, we
explain how we model PUF in the verification tools.
4.1 Model of PUF
The aim of AVISPA and Scyther is to verify the logic
of protocols and they are abstracted away from im-
plementation details. Therefore, it is not possible to
0. Enrolment phase (secure environment)
1. D1 → AA: Call(D1, D2)
2. AA: r
D1
= TRNG()
3. r
D2
= TRNG()
4. Choose (C
D1
, R
D1
) from DB
D1
5. Choose (C
D2
, R
D2
) from DB
D2
6. H
D1
= R
D1
xor Encode(r
D1
)
7. H
D2
= R
D2
xor Encode(r
D2
)
8. r = Hash(r
D1
) xor Hash(r
D2
)
9. AA → D1: (C
D1
, H
D1
, r)
10. AA → D2: Call(D1,D2), (C
D2
, H
D2
, r)
11. D1: R’
D1
= PUF(C
D1
)
12. r
D1
= Decode(R‘
D1
xor H
D1
)
13. Hash(r
D2
) = Hash(r
D1
) xor r
14. K = KDF(Hash(r
D1
) || Hash(r
D2
))
15. D2: R‘
D2
= PUF(C
D2
)
16. r
D2
= Decode(R‘
D2
xor H
D2
)
17. Hash(r
D1
) = Hash(r
D2
) xor r
18. K = KDF(Hash(r
D1
) || Hash(r
D2
))
19. D1 ↔ D2: Authentication + Encryption with K
Figure 4: Description of Protocol 3 that provides mutual au-
thentication between devices D1 and D2 using central au-
thentication authority which also distributes shared secret
key K between both devices for further communication.
Table 1: Table summarizing our results of verification of
each protocol without a compromising adversary.
Protocol
1 2 3 1 ext. 2 corr.
secrecy X X X X X
authent. of D1 X × × X X
authent. of AA × × × X X
implement PUF with its errors and we made an as-
sumption that our PUF is perfect, ergo no Error Cor-
rection Codes are needed. Also, our perfect PUF has
the same formal properties like MAC
K
with unique K
for every device.
This way, we are able to model the one-wayness
property of PUF (MAC is one-way with respect to its
input), and also the unclonability property (MAC is
also one-way with respect to the key). The per-device
unique key represents the uniqueness property of PUF
that would normally be derived from manufacturing
process variations.
Protocol verification tools usually implement
only encryption/decryption algorithms and hash algo-
rithms. Others, like the MAC algorithm, verification
tools derive from these two. The most popular way is
to concatenate secret key K to the message M and then
apply hash, i.e. MAC
K
(M) = Hash(M||K). For ex-
ample, this model of MAC was also used by Cas Cre-
mers during its analysis of IKE protocols in (Cremers,
2011). It also corresponds to the way how HMAC is
constructed. Let us note that in our case the message
M will be in fact a challenge C.
SECRYPT 2022 - 19th International Conference on Security and Cryptography
630
4.2 Protocol 1 Verification
We run the OFMC back-end of AVISPA on Protocol
1. The result of the analysis without a compromising
adversary has shown that the protocol is safe. When
we assumed the presence of a compromising adver-
sary, AVISPA showed a theoretical attack. Only real-
ization of the theoretical attack that we could think of
are the following:
Let us say that the adversary plays the role of au-
thority in one run of the protocol. After accepting the
message from device with the secret response, he im-
mediately knows the secret response and is able to in-
terpersonate the device in future runs. It is described
in Fig. 5.
This attack could happen for example if authority
is compromised (during one session) or if we let an
adversary inject his PK
Intruder
and the device trusts the
adversary in one session.
Nevertheless, these scenarios are unrealistic and
this type of protocols where the authority knows the
secret material of the device cannot resist these types
of attack.
% session 1 - between device and
intruder as an authority:
% i -> D1: C,Ni
% D1 -> i: {R,Ni}_pki
%
% session 2 - compromising
authentication of the device:
% AA -> i(D): C,Naa
% i -> AA: {R,Naa}_pkAA
Figure 5: Attack trace of an attack on Protocol 1 in the pres-
ence of a compromising adversary. He runs session 1 as the
authority which gives him knowledge of R and then he can
impersonate device in session 2 being authenticated by hon-
est authority.
We would like to also point out that in this proto-
col a device authenticates to the authority, but not the
other way around. In other words, the devices can-
not know if the first message was sent by the author-
ity, therefore an adversary can easily pretend to be the
authority. We suggest an extension of the protocol 1
providing mutual authentication in next section.
4.3 Protocol 2 Verification
This protocol correctly protects the confidentiality of
intended secret messages, but unfortunately, it does
not provide the assumed authentication of the device.
We found an attack on authentication property when
we analysed it with AVISPA. Screenshot of AVISPA
with an attack is in Fig. 6. According to definitions
from (Lowe, 1997), the attack breaks aliveness – the
weakest form of authentication.
Figure 6: Screenshot from AVISPA with an attack on Pro-
tocol 2 breaking authentication property – aliveness.
We then analysed it and constructed two different
approaches how intruder could take advantage of this
vulnerability. Description of the first variant is in Fig.
7. Here, the device is not part of the communication
at all. Yet the authority trusts the other participant to
be the device. The problem is that the device does not
prove itself to the authority in any way (it does not
even reply), hence the authority cannot really authen-
ticate the device.
Another way how to exploit this error is by com-
pleting the protocol with both roles (authority and de-
vice) but ending up with different keys for each of
them. See Fig. 8. The problem is that at the end of
the protocol both roles will think they have the same
key, but they do not verify it.
Let us also note, that if a key is distributed in a
protocol, it is essential to authenticate the party that
the key comes from or at least authenticate the key.
Otherwise, the accepting party cannot trust this key
(and its origin). In other words, one cannot achieve
safe key distribution if the accepting role does not au-
thenticate the key and does not verify his freshness
(otherwise replay attack might be possible). Unfor-
tunately, the original protocol is not (actually it was
not supposed to be) constructed in that way, that these
properties are also achieved. In the next section, we
suggest a correction of the protocol fulfilling these
properties.
4.4 Protocol 3 Verification
After modeling Protocol 3 in AVISPA, we quickly
found an attack on authentication properties. Screen-
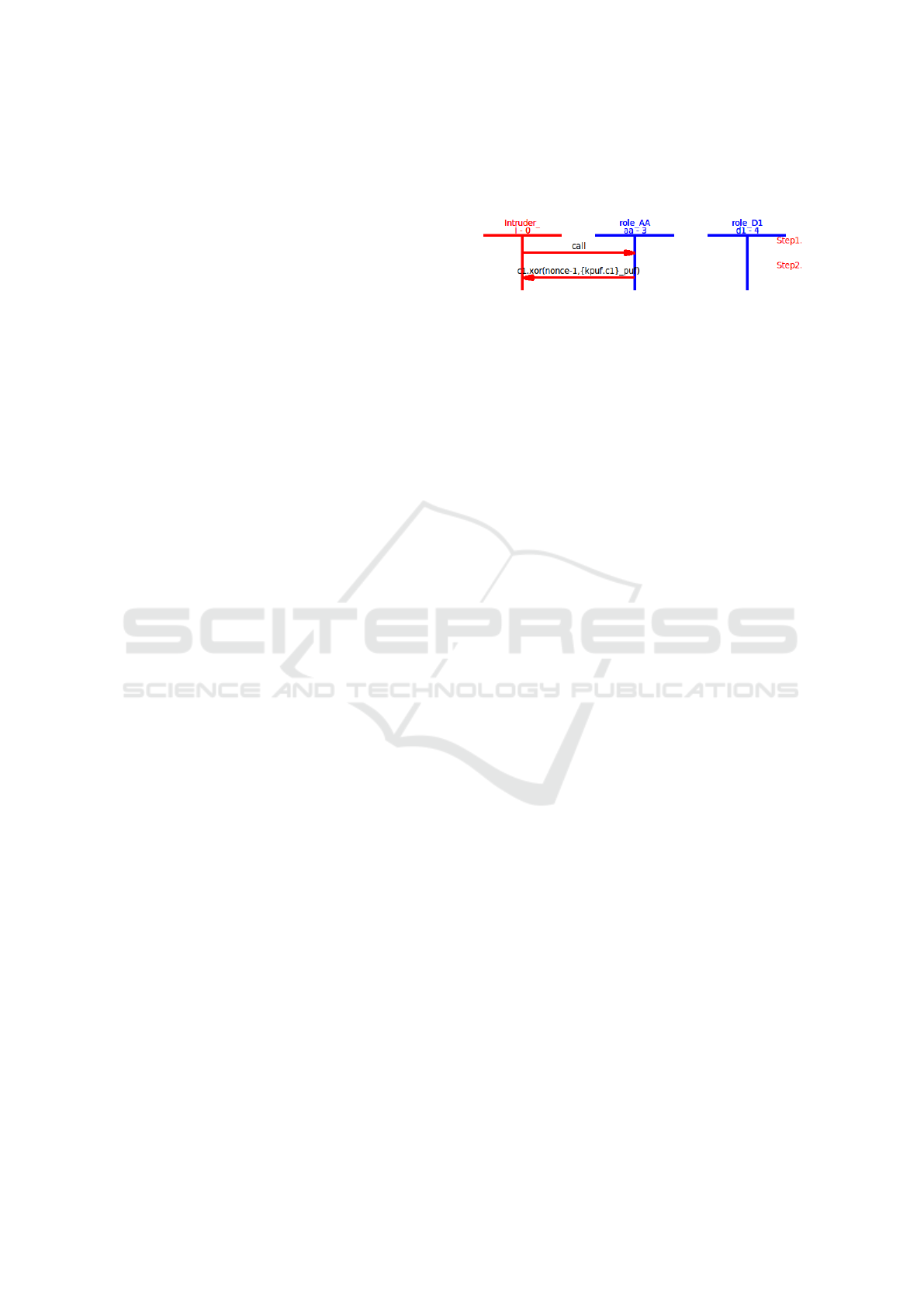
0. Enrolment phase (secure environment)
1. I → AA: Call(D1)
2. AA: r = TRNG()
3. Choose (C,R) from DB
D1
4. H = R xor Encode(r)
5. K = KDF(r)
6. AA → I(D1): Challenge C, Helper string H
Figure 7: Attack v1 on Protocol 2 by capturing.
Verification of PUF-based IoT Protocols with AVISPA and Scyther
631
0. Enrollment phase (secure environment)
1. D1 → AA: Call(D1)
2. AA: r = TRNG()
3. Choose (C,R) from DB
D1
4. H = R xor Encode(r)
5. K = KDF(r)
6a. AA → I(D1): Challenge C, Helper string H
6b. I → D1: Challenge C, Helper string H
tampered
7. D1: R‘ = PUF(C)
8. r
tampered
= Decode(R‘ xor H
tampered
)
9. K
tampered
= KDF(r
tampered
)
10. D1 6↔ AA: Authentication + Encryption with K
Figure 8: Attack v2 on Protocol 2 by tampering.
shot is in Fig. 9. Again, according to formal defini-
tions from (Lowe, 1997), the attack breaks aliveness
of D1 – the weakest form of authentication.
Figure 9: Screenshot from AVISPA with an Attack on Pro-
tocol 3 breaking authentication property – aliveness of D1.
Subsequent analysis of the results provided by
AVISPA showed that Protocol 3 suffers from a sim-
ilar error as protocol 2. After receiving public infor-
mation from a device, authority responds to both de-
vices. The necessary information to derive the shared
key lies in these responses. Unfortunately, that does
not authenticate the messages and also it does not en-
sure its freshness.
The original protocol means to achieve mutual au-
thentication of devices, but there is no stated commu-
nication between them. How can devices know that
they have the same distributed key? How can one of
them know that the other one obtained some key at
all?
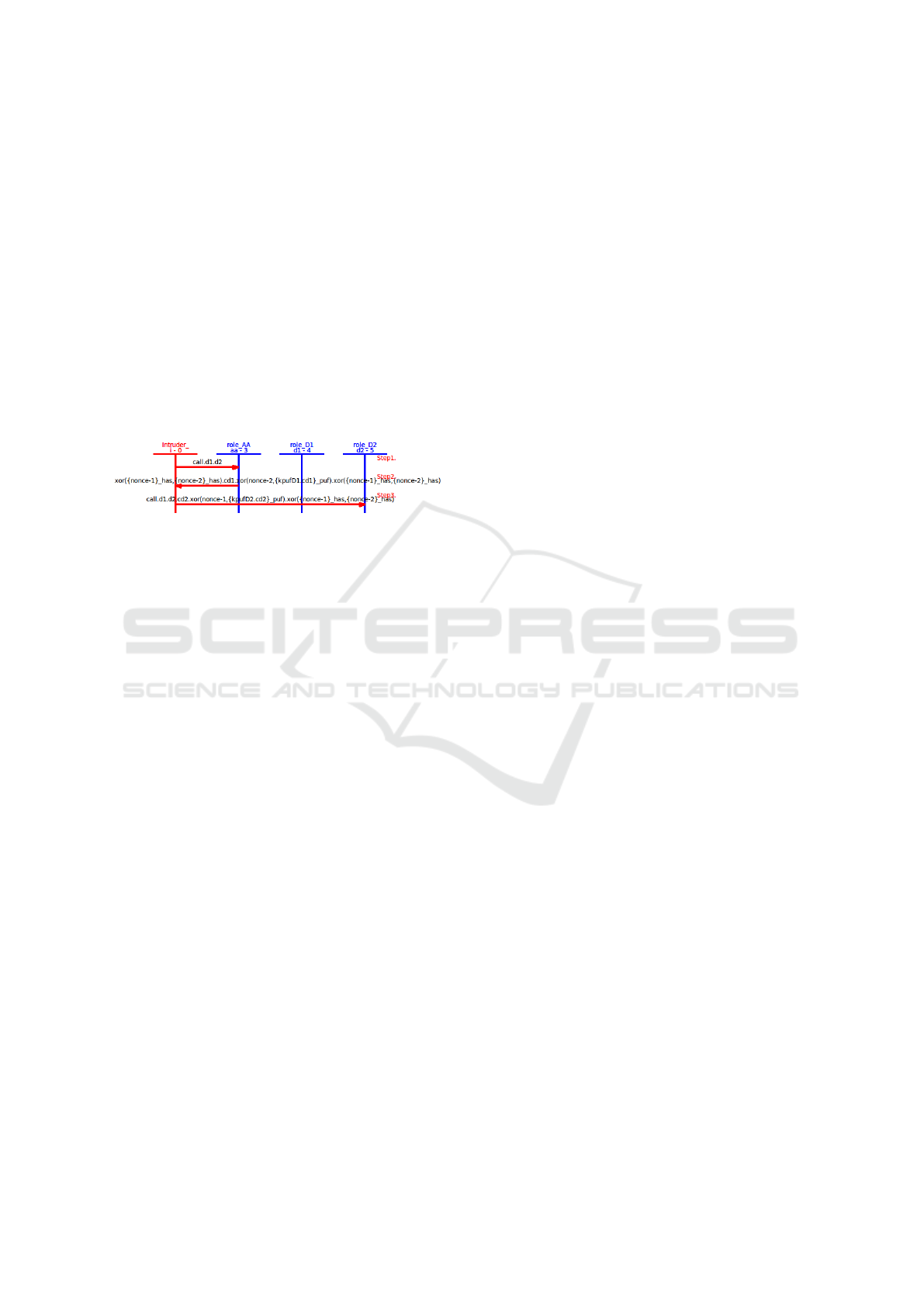
The first variant of an attack on Protocol 3, see
Fig. 10, consists of impersonating D1 by sending ini-
tial constant Call to authority by adversary and cap-
turing the message for device D1. Since message for
device D2 would be correct, device D2 would assume
it successfully shares the fresh secret key K ready to
safely communicate with device D1, but device D1
won’t be even participating in the communication.
In the second variant of an attack, see Fig. 11, an
adversary tampers one of the messages, making one
of the devices accept a false key. Of course, an adver-
sary could tamper with messages for both devices as
well. Since devices do not authenticate the messages,
both devices blindly believe that they share the same
secret key K at the end of the protocol, which is not
true.
0. Enrolment phase (secure environment)
1. I(D1) → AA: Call(D1, D2)
2. AA: r
D1
= TRNG()
3. r
D2
= TRNG()
4. Choose (C
D1
, R
D1
) from DB
D1
5. Choose (C
D2
, R
D2
) from DB
D2
6. H
D1
= R
D1
xor Encode(r
D1
)
7. H
D2
= R
D2
xor Encode(r
D2
)
8. r = Hash(r
D1
) xor Hash(r
D2
)
9. AA → I(D1): (C
D1
, H
D1
, r)
10. AA → D2: Call(D1,D2), (C
D2
, H
D2
, r)
11. D2: R‘
D2
= PUF(C
D2
)
12. r
D2
= Decode(R‘
D2
xor H
D2
)
13. Hash(r
D1
) = Hash(r
D2
) xor r
14. K = KDF(Hash(r
D1
) || Hash(r
D2
))
15. D1 6↔ D2: Authentication + Encryption with K
Figure 10: Attack v1 on Protocol 3 by capturing.
0. Enrolment phase (secure environment)
1. D1 → AA: Call(D1, D2)
2. AA: r
D1
= TRNG()
3. r
D2
= TRNG()
4. Choose (C
D1
, R
D1
) from DB
D1
5. Choose (C
D2
, R
D2
) from DB
D2
6. H
D1
= R
D1
xor Encode(r
D1
)
7. H
D2
= R
D2
xor Encode(r
D2
)
8. r = Hash(r
D1
) xor Hash(r
D2
)
9. AA → D1: (C
D1
, H
D1
, r)
10a. AA → I(D2): Call(D1,D2), (C
D2
, H
D2
, r)
10b. I(AA) → (D2): Call(D1,D2), (C
D2
, H
D2
, r
tampered
)
11. D1: R‘
D1
= PUF(C
D1
)
12. r
D1
= Decode(R‘
D1
xor H
D1
)
13. Hash(r
D2
) = Hash(r
D1
) xor r
14. K = KDF(Hash(r
D1
) || Hash(r
D2
))
15. D2: R‘
D2
= PUF(C
D2
)
16. r
D2
= Decode(R‘
D2
xor H
D2
)
17. Hash(r
D1
)
tampered
=
Hash(r
D2
) xor r
tampered
18. K
tampered
=
KDF(Hash(r
D1
)
tampered
|| Hash(r
D2
))
19. D1 6↔ D2: Authentication + Encryption with K
Figure 11: Attack v2 on Protocol 3 by tampering.
5 SUGGESTED IMPROVEMENTS
In this section, we suggest extension of Protocol 1 that
offers mutual authentication (without a compromising
adversary), since in many cases unilateral authentica-
tion may not be enough, and we analyse this protocol
by verification tools AVISPA and Scyther. Then we
suggest correction and extension of Protocol 2 provid-
ing mutual authentication. Former protocol offered
just unilateral authentication, but we argued that mu-
tual authnetication is needed since it is necessary to
authenticate the key from authority as well. You can
see the results of different back-ends in Table 2.
SECRYPT 2022 - 19th International Conference on Security and Cryptography
632
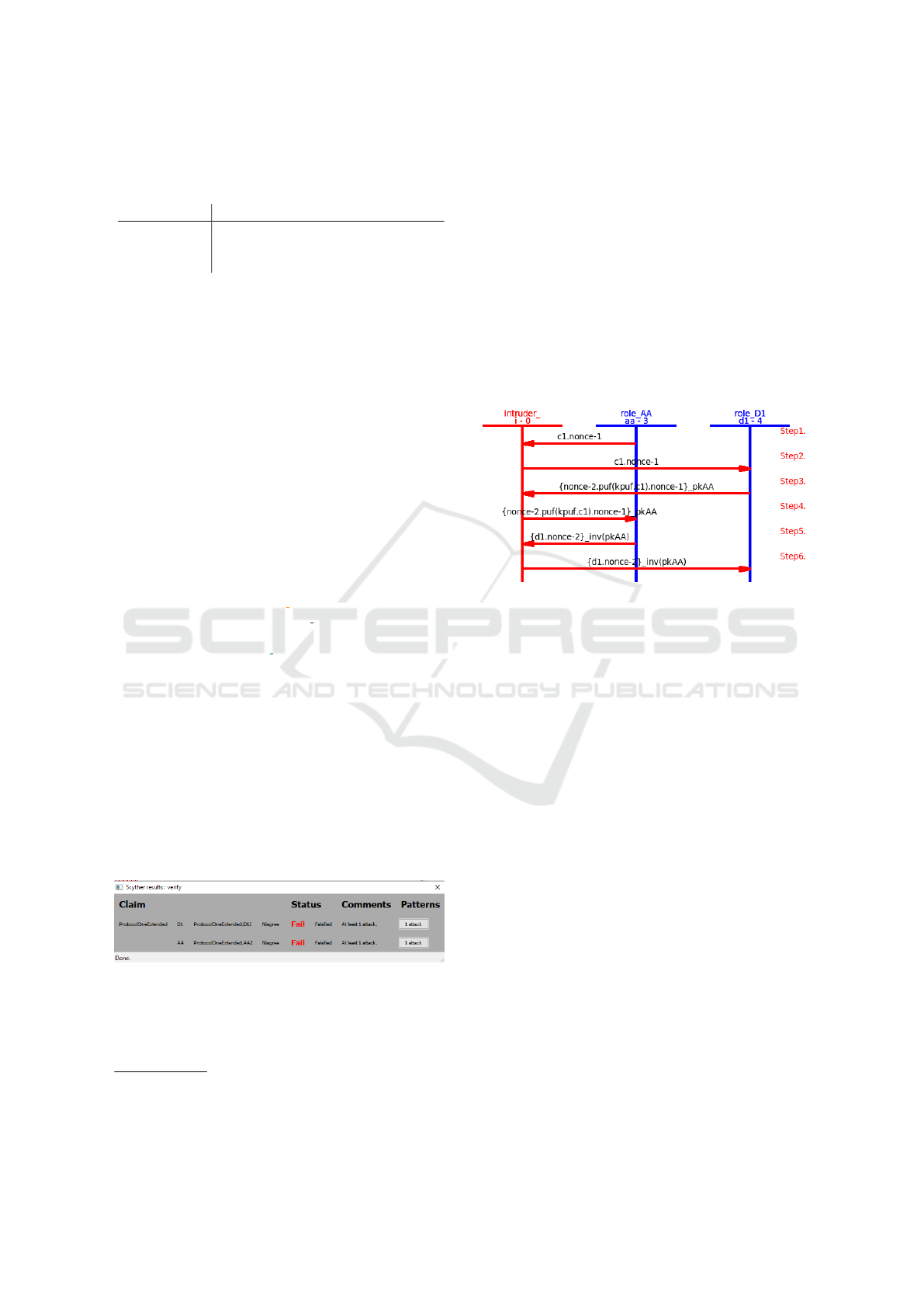
Table 2: Table summarizing concrete results of different
back-ends of our suggested protocols without a compromis-
ing adversary.
Back-end Protocol 1 – ext. Protocol 2 – corr.
OFMC-64bit UNSAFE
1
SAFE
OFMC-32bit SAFE SAFE
Cl-ATSE SAFE SAFE
5.1 Protocol 1: Extension
Here we suggest extension of the protocol 1 pro-
viding mututal authentication in Fig. 12. We add
creating random nonce Nb by device D1 that is sent
to authority AA in step 4. Authority signs it and
sends it back to the device with its identity in step 6.
Thanks to randomness (in verification tools modeled
as uniqueness) of this nonce generated by the device,
it would be sure that the message is fresh and could
not be replayed from later runs. Result of its analysis
by AVISPA back-ends Cl-ATSE and OFMC-32bit
says it is safe.
0. Enrolment phase (secure environment)
1. AA: Choose (C,R) from DB
D1
2. AA → D1: C, N
3. D1: R‘ = PUF(C)
4. D1 → AA: CR = E
PK AA
(Nb || R‘|| N)
5. AA: (R‘,N‘) = D
SK AA
(CR)
Compare(R
∼
=
R‘), Compare(N=N‘)
6. AA → D1: Sign
SK AA
(D1||Nb)
Figure 12: Extension of the protocol 1 that provides mutual
authentication without a compromising adversary.
This protocol does not offer safe mutual authen-
tication with compromising adversary. If Intruder
would play a role of authority in one session, he
would (similarly as in Protocol 1 Fig. 5) obtain the
secret response R. Then it could imitate the device
in another future session. Note that for this reason
its safety could not be fully proved by the verification
tool Scyther that automatically takes into account a
compromising adversary. It can be seen in Fig. 13.
Figure 13: Screenshot of Scyther results when verifying
Protocol 1 – extension with presence of a compromising
adversary.
When we tested Protocol 1 – extension with
AVISPA, we came across an interesting problem. Dif-
1
As we comment later, the result (i.e. unsafe) is most
probably caused by a mistake in the back-end OFMC 64-bit
version.
ferent back-ends gave us different results contradict-
ing each other. Cl-ATSE returned that the protocol is
SAFE and no attack was found. The same result came
from OFMC-32bit version. Surprisingly, OFMC-64
bit version returned an attack that assumed just one
session of the protocol and it consisted of just for-
warding messages between the device and authority
by an intruder, see Fig. 14. Since we follow Dolev-
Yao model in which ”intruder is the network”, this
cannot be seen as valid attack. Therefore, we believe
that it is caused by a bug in the program and our pro-
tocol 1 - extension is secure without a compromisign
adversary as Cl-ATSE and OFMC-32 bit version con-
firmed.
Figure 14: Screenshot of AVISPA with the (False?) Attack
on Protocol 1 – extension by OFMC-64 bit version (contra-
dicting the result of Cl-ATSE and OFMC-32 bit version).
5.2 Protocol 2: Correction
We tried to modify original protocol 2 in such a way
that it will, in fact, provide authentication of the de-
vice D1 and on top of that authentication of the au-
thority AA as well. Our suggested modification of
Protocol 2 can be seen in Fig. 15.
We added random nonce Nd created by D1 and
sent to AA in step 1. In step 6, AA creates random
nonce NA and among the challenge C and Helper
string H it also sends data (AA,D1,Nd,Na) encrypted
by symmetric key K = KDF(r). Lastly, we added
new step number 10, where D1 sends a nonce Na en-
crypted with the key K to AA.
Nonce Na gives assurence to AA that D1 owns the
key K and that D1 recently (after Na was generated)
used this key to encrypt Na freshly generated by AA.
Similarly, nonce Nd gives assurance to D1 that AA
owns the key K and recently used this key to encrypt
Nd freshly generated by D1.
We analysed our correction of Protocol 2 with
backends OFMC-64 bit version, OFMC-32 bit ver-
sion, and Cl-ATSE. All of them returned the same re-
sult that the protocol is safe.
Similarly to extension of Protocol 1, this protocol
is not safe with assumption of compromising adver-
Verification of PUF-based IoT Protocols with AVISPA and Scyther
633

0. Enrolment phase (secure environment)
1. D1 → AA: Call(D1,Nd)
2. AA: r = TRNG()
3. Choose (C,R) from DB
D1
4. H = R xor Encode(r)
5. K = KDF(r)
6. AA → D1: Challenge C, Helper string H,
Enc
K
(AA,D1,Nd,Na)
7. D1: R‘ = PUF(C)
8. r = Decode(R‘ xor H)
9. K = KDF(r)
10. D1 → AA: Enc
K
(Na)
11. D1 ↔ AA: Authentication + Encryption with K
Figure 15: Description of Protocol 2 – correction that pro-
vides mutual authentication without compromising adver-
sary.
sary. If one session is run with Intruder as authority, it
gains the response R. Thanks to that, it can interper-
sonate the device in another run of the protocol.
5.3 Compromising Adversary as Too
Strong for PUF-based Protocols
We believe that no small change of any of the proto-
cols would make it safe with presence of a compro-
mising adversary, since the safety of both protocols
utterly rely on the fact that the response is known just
to the device and the authority.
Compared to Diffie-Hellman key-exchange proto-
col that provides forward secrecy, our key-distribution
PUF-based protocol does not. Since the response is
the only long-term secret between device and author-
ity and this response is the only protection of session
secrets like r or K=KDF(r), protocol does not satisfy
(weak) perfect forward secrecy. If the response is
compromised, all the communication is then public
if the adversary just recorded the messages.
Even more of a concern is the fact that compro-
mising just the session secret r from just one recorded
session makes the long-term secret response R deriv-
able, and consequently all other session keys as well.
Nevertheless, we believe that the model (i.e. in the
presence of compromising adversary) is too strong for
this type of protocol. The discussion was motivated
by Scyther that does assume the model automatically,
and therefore returned negative results even for other-
wise safe protocols.
6 CONCLUSION
We explained the security problems with original pro-
tocols, and we showed the results of formal analysis.
This analysis was done with two tools for formal ver-
ification AVISPA and Scyther. We also constructed
several attacks exploiting the vulnerabilities.
Then, we proposed new protocols that intend to
achieve security property mutual authentication and,
in the second protocol, also secrecy of the distributed
key. We successfully verified these protocols with the
tool AVISPA. During this analysis, we encountered
wrong behavior of AVISPA whose back-ends contra-
dicted each other. That was caused probably due to a
bug.
To compensate this discrepancy we also con-
ducted formal verification by another verification tool
Scyther whose natural behavior is to apply the model
with compromising adversary. After consideration we
concluded that this model is unreasonably strong for
our case where authority must know the secret re-
sponses of the device.
To conclude our paper, we repaired and strength-
ened original protocols that now provides all desired
security properties.
ACKNOWLEDGEMENTS
The authors acknowledge the support of the OP VVV
MEYS funded project CZ.02.1.01/0.0/0.0/16 019/
0000765 ”Research Center for Informatics”. The re-
search was partly carried out under the project of
NCISA of the Czech Republic – Software tools for
cryptographic security assessment – therefore, we
would like to thank them for their support. Also, we
would like to thank Thomas Genet for his advice with
the AVISPA tool.
REFERENCES
Armando, A., Basin, D., Boichut, Y., Chevalier, Y., Com-
pagna, L., Cu
´
ellar, J., Drielsma, P. H., H
´
eam, P.-
C., Kouchnarenko, O., Mantovani, J., et al. (2005).
The avispa tool for the automated validation of in-
ternet security protocols and applications. In Inter-
national conference on computer aided verification,
pages 281–285. Springer.
Backes, M., Pfitzmann, B., and Waidner, M. (2006). Sound-
ness limits of dolev-yao models. In Workshop on For-
mal and Computational Cryptography (FCC 2006).
B
¨
ohm, C., Hofer, M., and Pribyl, W. (2011). A microcon-
troller sram-puf. In 2011 5th International Confer-
ence on Network and System Security, pages 269–273.
IEEE.
Braeken, A. (2018). Puf based authentication protocol for
iot. Symmetry, 10(8):352.
SECRYPT 2022 - 19th International Conference on Security and Cryptography
634

Buchoveck
´
a, S., L
´
orencz, R., Bucek, J., and Kod
´
ytek, F.
(2020). Lightweight authentication and secure com-
munication suitable for iot devices. In ICISSP, pages
75–83.
Buchoveck
´
a, S., L
´
orencz, R., Bu
ˇ
cek, J., and Kod
´
ytek,
F. (2022). Symmetric and asymmetric schemes for
lightweight secure communication. In Information
Systems Security and Privacy, Basel, CH. Springer
Nature Switzerland AG.
Burrows, M., Abadi, M., and Needham, R. M. (1989). A
logic of authentication. Proceedings of the Royal So-
ciety of London. A. Mathematical and Physical Sci-
ences, 426(1871):233–271.
Chatterjee, U., Chakraborty, R. S., and Mukhopadhyay, D.
(2017). A puf-based secure communication protocol
for iot. ACM Transactions on Embedded Computing
Systems (TECS), 16(3):1–25.
Cremers, C. (2011). Key exchange in ipsec revisited: For-
mal analysis of ikev1 and ikev2. In European Sympo-
sium on Research in Computer Security, pages 315–
334. Springer.
Cremers, C. and Mauw, S. (2012). Security properties.
In Operational Semantics and Verification of Security
Protocols, pages 37–65. Springer.
Cremers, C. J. (2008). The scyther tool: Verification, falsi-
fication, and analysis of security protocols. In Inter-
national conference on computer aided verification,
pages 414–418. Springer.
Delvaux, J., Gu, D., Schellekens, D., and Verbauwhede, I.
(2014). Helper data algorithms for puf-based key gen-
eration: Overview and analysis. IEEE Transactions
on Computer-Aided Design of Integrated Circuits and
Systems, 34(6):889–902.
Herder, C., Yu, M.-D., Koushanfar, F., and Devadas,
S. (2014). Physical unclonable functions and ap-
plications: A tutorial. Proceedings of the IEEE,
102(8):1126–1141.
Idriss, T. and Bayoumi, M. (2017). Lightweight highly se-
cure puf protocol for mutual authentication and secret
message exchange. In 2017 IEEE International Con-
ference on RFID Technology & Application (RFID-
TA), pages 214–219. IEEE.
Lowe, G. (1995). An attack on the needham- schroeder
public- key authentication protocol. Information pro-
cessing letters, 56(3).
Lowe, G. (1997). A hierarchy of authentication specifica-
tions. In Proceedings 10th Computer Security Foun-
dations Workshop, pages 31–43. IEEE.
Maes, R., Tuyls, P., and Verbauwhede, I. (2009). A soft
decision helper data algorithm for sram pufs. In 2009
IEEE international symposium on information theory,
pages 2101–2105. IEEE.
Majzoobi, M., Rostami, M., Koushanfar, F., Wallach, D. S.,
and Devadas, S. (2012). Slender puf protocol: A
lightweight, robust, and secure authentication by sub-
string matching. In 2012 IEEE Symposium on Security
and Privacy Workshops, pages 33–44. IEEE.
Merli, D., Stumpf, F., and Sigl, G. (2013). Protecting puf
error correction by codeword masking. Cryptology
ePrint Archive.
Needham, R. M. and Schroeder, M. D. (1978). Using en-
cryption for authentication in large networks of com-
puters. Communications of the ACM, 21(12):993–999.
Nimmy, K., Sankaran, S., and Achuthan, K. (2021). A
novel lightweight puf based authentication protocol
for iot without explicit crps in verifier database. Jour-
nal of Ambient Intelligence and Humanized Comput-
ing, pages 1–16.
Ray, B. R., Chowdhury, M. U., and Abawajy, J. H. (2016).
Secure object tracking protocol for the internet of
things. IEEE Internet of things Journal, 3(4):544–553.
Vigano, L. (2006). Automated security protocol analysis
with the avispa tool. Electronic Notes in Theoretical
Computer Science, 155:61–86.
Zargar, S., Shahidinejad, A., and Ghobaei-Arani, M.
(2021). A lightweight authentication protocol for iot-
based cloud environment. International Journal of
Communication Systems, 34(11):e4849.
Verification of PUF-based IoT Protocols with AVISPA and Scyther
635
