Line-up Optimization Model of Basketball Players

and the Simulation Evaluation

Wang Yichen

and Haruka Yamashita

Graduated School of Science and Technology, Sophia University, 7-1, Kioicho, Chiyoda-ku, Tokyo, Japan

School of Science and Technology, Sophia University, 7-1, Kioicho, Chiyoda-ku, Tokyo, Japan

Keywords: Basketball Games, Game Strategy, Deep Neural Network, Game Simulation.

Abstract: This study aims to maximize the offensive capabilities of the basketball team by optimizing the line-up of

players at an arbitrary time. We construct a highly accurate prediction model when the members are

changed considering the situation in the game and then propose a model to determine the optimal line-up.

The Recursive Neural Network model analyzes time series data, and the Neural Network model

incorporates player combinations and game conditions as conditions are combined. The model enables an

analysis of the past scores and game conditions and the construction of a predictive model of scores that

takes the line-up into account and determines the optimal line-up by calculating the prediction of the offense

capabilities with changing the line-up. Furthermore, to demonstrate the validity of the proposed model, this

study evaluates the accuracy of the prediction of the score using data accumulated from the actual baseball

game. Moreover, because it is difficult to use this method in actual games, we applied the proposed model

to the play data of a basketball simulation game. We conducted a simulation experiment where members

were successively optimized and showed that the score was better than the experiment without the

optimization.

This

paper is the revised version of Lineup Optimization Model of Basketball Players Based on the Prediction of Recursive

Neural Networks (Wang and Yamashita, 2021). this paper includes the outcomes of the further research of the previous

paper. Specifically, this research derived the simulational study of the player lineup optimization using the video game.

1 INTRODUCTION

In recent years, decisions on game members and

strategies based on the analysis of accumulated data

have been widely attempted in sports. One of the

famous leagues of sports games NBA (National

Basketball Association), has many teams analyzing

the play data for each game. Therefore, each team

has a dedicated team of analysts, and various data

analyses exist to win games.

Here, the game situation in a basketball game is

rapid changes in each game. This feature makes

decision-making based on analysis difficult. In

addition, recent rule changes in the NBL (Homepage

of the NBA) have resulted in more diverse team

line-up compositions (Nourayi, 2019). For example,

the Los Angeles Lakers (Homepage of Los Angels

Lakers) discuss the specific team line-up called

Small Ball, which overwhelmed offensive power

with the aggressive use of shorter players. Some

teams have strengthened their offense and have won

many league championships in recent years.

However, the Small Ball strategy does not apply to

all teams and may not be appropriate depending on

the game situation. Therefore, each team must

analyze both team and player post-game analysis

and real-time play data to determine the line-up of

players in the team's strategy to improve their

offensive capabilities.

Here, it is necessary to determine the members of

the line-up of players for whom the results are

favourable. In other words, determining the

combination of members to optimize the results

while considering the real-time game situation is

required. Therefore, to maximize the offensive

capability of the team, this study (1) constructs a

highly accurate prediction model for changing the

members considering the situation at any given time,

and (2) proposes a model to determine the optimal

492

Yichen, W. and Yamashita, H.

Line-up Optimization Model of Basketball Players and the Simulation Evaluation.

DOI: 10.5220/0011307900003269

In Proceedings of the 11th International Conference on Data Science, Technology and Applications (DATA 2022), pages 492-499

ISBN: 978-989-758-583-8; ISSN: 2184-285X

line-up composition in real-time. In this study, we

construct a model that uses score data per gameplay,

which indicates the contribution of the line-up to the

game as output in time-series data and the line-up

and situation of the players as input. We apply a

Recurrent Neural Network (RNN) model (Mikolov,

et al., 2011) that can analyze time-series data as a

basis and combine a Neural Network (NN) model

(Mccullagh, 2010) that incorporates player

combinations and game conditions as conditions,

past scores, and game conditions. The modeling

enables to take line-ups into account for the score

prediction. Furthermore, when optimizing a line-up,

calculating the score's prediction for each

combination of players is required; however, the

number of combinations is vast, and often not

enough data is available. Therefore, we set up a line-

up of candidates for each strategy in advance and

optimize the line-ups among them.

Furthermore, to demonstrate the validity of the

proposed model, this study evaluates the accuracy of

prediction using data collected from actual games. In

addition, it is not easy to use this method in actual

games. Therefore, to verify the model's reliability,

we applied the proposed model to the play data of a

basketball simulation game and conducted a

simulation experiment in which members were

successively replaced.

2 PRELIMINARIES

2.1 Data Description

To examine the validity of the proposed method, this

study conducts an analysis using basketball game

data and game data for simulation, which enables the

evaluation of effects in real-time. Specifically, the

basketball game data was collected by watching the

2019-20 Los Angeles Lakers (Homepage of Los

Angels Lakers) game, recording the game conditions

(referred to as Lakers data), and training the model.

The game data for the simulation records using the

game simulation function of NBA2k21 (Homepage

of NBA2k21) while optimizing the members using

the proposed model. The data for the analysis

consists of 11 variables in Table 1.

For the analysis, the first ten variables are the

model's input variables, and the 11th time series

variable is for both the input and output (objective)

variables. The scores of the former 5 points are the

input variables, and the score of one end is the

output variable.

Table 1: Variables and description of the Lakers data.

Variable Description

Position Uniform number of candidates

Quarter Categorical data for the

uarte

Time Time of the timing

Score difference The scoring offense of each

Fouls Number of Fouls

Consecutive wins /

losses

The number of Consecutive

wins/losses before the

ame

Length difference The difference in the sum of

the length of players for each

tea

Main defender The main defender of the

onent

Average score The average score of the last

season

Home/ away Home/ away (binary data)

Score A score of each play

2.2 Related Works

In this subsection, we describe the related works

from two viewpoints: the research of basketball

analysis and the research approach using RNN.

Considering the study of basketball analysis,

researchers are using the statistical methods;

factor model for the factors of a ball in basketball

rebounding situations (Hojo, et al., 2019),

illustrating a model of the crucial players in each

game using graph structure (Piette, et al., 2016), and

the transition of the ball during the offense is

proposed (Fewell, et al., 2012). In this study, the

proposal considers individual scoring prediction and

the whole line-up scoring prediction. The

conventional analysis methods have not been

focusing on the viewpoint.

Recently, several studies using the deep NN

model (Rajiv, et al., 2016; Wang, et al., 2016) for

analyzing basketball data have been proposed.

Primarily, basketball analysis based on the RNN

model, which is the high-performance model for the

time series data prediction, is derived (Clemente, et

al. 2015; Luong, et al, 2013) Therefore, constructing

the prediction model of the team should be required.

2.3 Recursive Neural Network Model

Recursive neural network model (RNN) (Mikolov;

2011) is one of the neural network models and has

the feature that the output from the

Line-up Optimization Model of Basketball Players and the Simulation Evaluation

493

Figure 1: Outline of the proposed model intermediate layer

at one time is used in the intermediate layer at the next

time for the time-series information. Figure 1 shows the

structure of an RNN with one middle layer.

Here, we describe the structure of the basic RNN

model, which has only one middle layer. Let

𝒙

𝒕





𝑥



,…, 𝑥





be an input vector of time series data

at the time，

𝑦



be an output of time. Let 𝑊



the weight matrix of edges from the input to the

middle layer, 𝑊



is the weight matrix of edges

from the middle layer to the output layer. RNN has a

feature that the message passing of the output from

middle layers at each time. We denote 𝒉



as the

output vector from the middle layer, 𝑊 as the

weight matrix from the intermediate layer at time 𝑡

output, and is the weight matrix of the input of 𝒉



the middle layer at the next point in time 𝑡 .

Parameter estimation is based on backpropagation.

The RNN model does not work well when the

period is extended. Therefore, In the case of long-

term prediction, Long Short Term Memory network

(Greff, 2016; Zhao, 2018) is used.

3 PROPOSED METHOD

Basketball is a fast-paced, multiplayer sport.

Therefore, it is difficult for all teams to know what

line-ups to change (or not change) in an arbitrary

game to perform well. To solve this problem, we

propose two-step models.

We propose (1) a highly accurate model for

predicting scores of upcoming five plays when line-

ups are changed at arbitrary times during a game and

(2) an optimization model for line-ups to maximize

scores for upcoming five plays using the obtained

model. A schematic diagram is shown in Figure 2.

(1) Score prediction model

5 points Game situation Line-up data

Score data data

(2) Line-up optimization

Figure 2: Outline of the proposed model.

3.1 Score Prediction Model

The situation of the play in the game can be a

significant cause for a team's offense. To predict the

score while considering the team situation, we

consider the score from the current point in time to 5

plays back in time-series data and input it into the

RNN model. Next, the line-up of players on the field

and the current game situation are given as input

variables to the NN model. Furthermore, the RNN

and the NN output are combined and input into

another NN model that considers the game situation

and the flow. The output is the total points scored by

the team in the five plays from that point.

Moreover, this model enables us to predict scores

even in situations and line-ups that do not appear.

First, we describe the RNN model in Figure 3. Let

𝒙

𝒕𝟏





𝑥



,…, 𝑥





be an input vector of the

score of 5 past offensive plays at time 𝑡1, and let

𝒛

𝒕

𝑧





,…,𝑧





 be the input vector of the game

situation denoted in Table 1 without the score, and

𝑦



be the upcoming score of 5 plays. Here, letting

the RNN function whose input vector is 𝒙

𝒕𝟏

𝑓





𝒙

𝒕𝟏



considering the activation functions and

NN function whose input is 𝒛

𝒕

activation functions

are 𝑓



𝒛

𝒕

), the score prediction function

𝑓



of 𝑦



can be represented as follows:

𝑦



𝑓



𝑐𝑜𝑛𝑓



𝒙

𝒕𝟏

, 𝑓



𝒛

𝒕

, (1)

where let () be the combining function of the output

of both RNN and NN. Parameters are estimated

through a backpropagation algorithm. Note that,

because the settings of the detailed structure of the x

(2) an optimization model for line-ups to maximize

scores for upcoming five plays using the obtained

Score Maximization

Lineu

DATA 2022 - 11th International Conference on Data Science, Technology and Applications

494

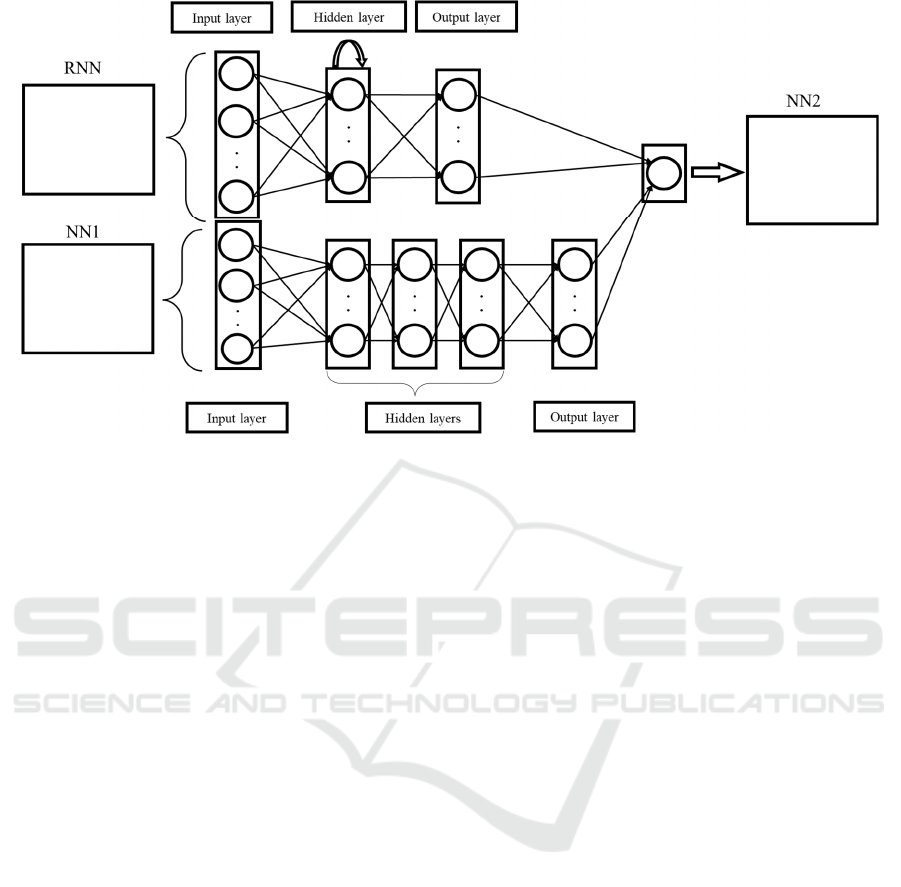
Figure 3: Structure of the score prediction model.

model. A schematic diagram is shown in Figure

2.considers only five plays and uses the data of 5

plays; we use the RNN approach.

3.2 Line-up Optimization

The score prediction model predicts the expected

score for the upcoming five plays in the target

basketball team. In this study, we indicate the

optimal team line-up at an arbitrary time by

changing the team line-up; however, because the

number of combinations of team line-up considering

position is enormous (9040 patterns), enough

learning data is challenging to be accumulated. Note

that the information of the top defender is used for

the prediction, the lack of learning data can be the

problem in the model. Therefore, in this study, we

restrict the combination of line-ups as the finite set

and find the optimal line-up from the set.

Considering the possible combination of line-ups,

we focus on the three kinds of line-ups: Normal ball

line-ups, small ball line-ups, and Bench line-ups. A

normal ball line-up is the essential combination of

players. We focus on the three normal line-ups for

the finite set. A small ball line-up is a specific

pattern that focuses on offense instead of defense.

This strategy has been tried in many teams recently;

however, the experts still discuss the effectiveness is

not the line-up. We focus on the three line-ups

which are well used in the actual game. The last kind

of line-up is the bench line-up which uses bench

start players (i.e., not the starting members). Because

basketball is a challenging sport, how to give players

rests is one of the crucial strategies. We focus on

four patterns that are well used in actual games.

Then, the number of the elements in a finite set 𝑈 is

10 (

𝑈

0. We find the line-up 𝑢 from 𝑈, which

maximizes the score

calculated by (1) as follows:

𝑢

∗

argmax

∈

𝑦



. (2)

In this study, we applied straight-forward approach

for finding the solution of 𝑢.

4 EVALUATION PREDICTION

MODEL USING REAL

BASKETBALL GAME DATA

In this section, we evaluate the accuracy of the

prediction of the proposed data using the actual

baseball game data. The data is accumulated from

the NBA league held from 2019th to 2020th. The

information is accumulated by watching videos of

the games of the Los Angeles Lakers, which is one

of the favored teams in the NBA league.

4.1 Detailed Setting of the Score

Prediction Model

The detailed setting of the model is represented

follows:

- RNN model has 3 layers, each layer has 32 nodes

Input data of

the score of 5

offensive past

plays

Input data of

game situations

Upcoming

score of 5 plays

Line-up Optimization Model of Basketball Players and the Simulation Evaluation

495

- NN model has 3 hidden layers, 24, 16, 16oki

nodes are set in each layer

- The concatenate function

- The activation function used was a combination

of three activation functions: sigmoid, tanh

(hyperbolic tangent), and ReLu function.

- The number of epochs is 40, and the batch size is

24.

- Optimization by Adam with a learning rate of 0.1.

- Evaluation is the mean absolute error (MAE) and

the correlation between the data and prediction.

- Learn the model using the offensive play data of

81 games and testing the last 50 plays in the last

game.

- For the evaluation, we used simple RNN (the

setting of the model is the same as the proposed

model) and compared the accuracy.

4.2 Prediction Result

The relationship between the predicted data and the

prediction of the proposed is represented in Figure 4.

The result shows that although some points are not

better than the simple RNN model, the proposed

model records better overall performance. The

evaluation indices: RMSE, and the correlation are as

Table 2. From the result, the proposed method is

superior to the simple RNN method; this result

shows that the line-up optimization should be

derived from the proposed method.

Figure 4: Indices of plays (x-axis) and the point (y-axis) of

the data, RNN prediction, and Proposed method

prediction.

Table 2: Evaluation indices of the proposed and simple

RNN method prediction.

Method RMSE Correlation

Proposed 1.8 0.68

Simple RNN 3.8 0.26

5 EVALUATION PREDICTION

MODEL USING SIMULATION

VIDEO GAME DATA

In the last section, we showed that the score's

prediction using the proposed method is more

accurate than the simple RNN model. However, the

objective of this study is to find the optimal line-up

in terms of the score at an arbitrary time.

Table 3: Results of the getting points for each quarter of

proposed and conventional (Automatically) optimization.

Proposed optimization

No qtr1 qtr2 qtr3 qtr4 Sum Gap

1 33 27 35 31 126 -12

2 32 31 29 55 147 1

3 33 30 30 43 136 38

4 30 25 31 36 122 28

5 27 23 24 37 111 -1

6 44 29 28 30 131 38

7 39 29 33 37 138 43

8 37 21 30 24 112 3

9 33 33 29 23 118 -2

10 25 42 22 36 125 3

Automatic optimization

No qtr1 qtr2 qtr3 qtr4 Sum Gap

1 28 35 28 29 120 8

2 36 27 33 29 125 -6

3 26 24 36 24 110 -7

4 26 20 25 37 108 15

5 25 32 39 34 130 3

6 26 25 39 29 119 2

7 22 37 28 30 117 -7

8 30 37 26 32 125 -4

9 23 28 29 19 99 -9

10 38 26 32 21 117 7

Table 4: Average of the getting points for each quarter of

proposed and conventional (Automatically) optimization.

Opt. qtr1 qtr2 qtr3 qtr4 Sum Gap

Win

Proposed 33.3 29 29.1 35.2 126.6 13.9 7

Automatic 28 29.1 31.5 28.4 117 0.1 5

Data

Simple RNN

Proposed method

DATA 2022 - 11th International Conference on Data Science, Technology and Applications

496

Therefore, the effectiveness of the proposed method

should be evaluated by the effect of the actual

basketball game data with changing players based on

the proposed method.

5.1 Accumulation of the Simulation

Video Game Data

In this section, we describe the experiments of the

line-up optimization using NBA2k21(Homepage of

NBA2k21), the basketball simulation video game

developed by Visual Concepts and published by 2K

Sports, based on the games played in 2020-2021 in

the NBA league.

This game has two playing modes: the mode

with the function that video game players can

change basketball players in arbitrary time, and the

mode that the computer (system) changes the

basketball players automatically for the number of

times that video game players set as parameters in

advance. Note that the timing of the change follows

the timing of NBA regulation. In this experiment,

we accumulate simulation video game data by

playing NBA2k21 by changing the basketball player

using the proposed method (score prediction model

and line-up optimization) for 7 times following the

NBA rule. We set the same home and away team

and same basketball game stadium. We played the

game, as well as the situations of each data, were

common during the games. We evaluate the results

by the sum of the getting points and the gap

(difference) between the getting points and losing

points. Comparing each quarter's results for the two

optimizations and the better result is represented by

the bold number. The results indicate that the

proposed optimization is superior than automatic

optimization.

5.2 Result of the Experiment

The results of the simulation experiments using the

video games for each quarter and the sum of the

obtained scores and the gap points are in Table 3.

We describe the result in Table 3. As shown in Table

4, in some quarters proposed optimization method is

superior, and quarters the automatic optimization;

however, the proposed method tends to be better.

The summary of the result (average score and the

number of game wins for each quarter for each

optimization) is shown in Table 3. Note that the

t-test shows differences in each average value

without quarter 3. From the result, we see that the

proposed method can lead to the offense ability of

the team by the player optimization at an arbitrary

time, and we indicate the effectiveness of our

proposal.

5.3 Discussion

In this study, our objective is to optimize the

basketball players in a game. Moreover, using our

proposal, the discussion of optimal line-ups for each

situation can be considered. However, because the

simulation data is accumulated for only ten times,

and the game situation is different, it is difficult to

summarize the data. Here, we show the score

predictions for the line-ups optimization in Figure 5

and indicate the features and problems of our

method.

The figure shows that our method tends to

predict that the small ball strategy is the best in the

first half of the game, and the bench line-up strategy

is best in the second half. Also, the normal ball

strategy tends to be not selected as the best strategy.

In terms of strengthening the offensive ability, these

decisions should be reasonable; however,

considering the offensive perspective, we should

consider the getting score and losing score. For

example, learning the gap score can be the solution

by setting the output as the gap score. Moreover,

because this game data has only the result of 10

games, discussion of the members' strategy is not

capable. We need more data for the detailed

consideration of the experiment.

Nevertheless, there are some difficulties; the

results indicate that our method can improve the

team strength, and these results showed the

effectiveness of our approach. Improving the model

and increasing the dataset to learn the model lead the

better game strategy.

6 CONCLUSION

In this study, to determine the combination of

basketball members in terms of the offensive ability,

the real-time game situation is considered. We (1)

constructed a highly accurate prediction model for

changing the members considering the situation at

any given time, and (2) proposed a model to

determine the optimal line-up composition in real-

time. For constructing the model, we applied a RNN

model that analyses time-series data as a basis and

combined a NN model that incorporates player

combinations, and game conditions, past scores as

the factor for deciding the upcoming score for the

five plays.

Line-up Optimization Model of Basketball Players and the Simulation Evaluation

497

Figure 5: Quatre indices (x-axis) and the predicted score (y-axis) of each combination of members for 10 games.

DATA 2022 - 11th International Conference on Data Science, Technology and Applications

498

The modeling considers to take line-ups into

account for the score prediction. Furthermore, to

demonstrate the validity of the proposed model, this

study evaluated the accuracy of prediction using data

collected from real games, and effectiveness of the

model using play data of a basketball simulation

game and conducted a simulation experiment in

which members were successively replaced.

There remains future works about the data

constructions. First future work is to expand the data

not only for focusing the Lakers. The data

accumulation needs enormous time, the support

system is required. The next future work is to

increase the number of input variables for more

reasonable prediction. Also, the consideration of the

objective value should be the future work.

Furthermore, we restricted the line-ups in advance.

In the real situation, we should consider every

pattern. Therefore, the effective optimization

algorithm such as branch cutting method should be

considered. Finally, the preferable model evaluation

is to use the method in the real basketball games,

and evaluate the performance of our method can be

derived.

REFERENCES

Homepage of National Basketball League,

https://nbl.com.au/

Nourayi, M. M. "Strategically Driven Rule Changes in

NBA: Causes and Consequences." The Sport Journal ,

Vol.2, published online, 2019.

Homepage of Los Angels Lakers: https://www.nba.com/

lakers

Wang, Y., Yamashita, H. "Lineup Optimization Model of

Basketball Players Based on the Prediction of

Recursive Neural Networks", International Journal of

Economics and Management Engineering Vol:15,

No:3, 2021.

Mikolov, T., Kombrink, S., Burget, L., Černocký, J., &

Khudanpur, S., Extensions of recurrent neural network

language model. In: 2011 IEEE international

conference on acoustics, speech and signal processing

(ICASSP). IEEE, pp. 5528-5531, 2011.

Mccullagh, J., "Data mining in sport: A neural network

approach." International Journal of Sports Science and

Engineering. Vol.4, no. 3: 131-138, 2010.

NBA2k2, https://nba2k.jp/nba2k21/

Hojo, M., Fujii, K., and Kawahara, Y. "Analysis of

factors predicting who obtains a ball in basketball

rebounding situations," International Journal of

Performance Analysis in Sport, Vol.19, no.2, pp.192-

205.

Piette, J., Anand, S., and Pham, L. "Evaluating basketball

player performance via statistical network modeling."

The 5th MIT Sloan Sports Analytics Conference.,

published online, 2011.

Fewell, J. H., Armbruster, D., Ingraham, J., Petersen, A.,

and Waters, J. S., "Basketball teams as strategic

networks," PloS one, Vol. 7, no.11, e47445, 2012.

Rajiv, S., and Romijnders, R.. "Applying deep learning to

basketball trajectories." arXiv preprint

arXiv:1608.03793, published online, 2016.

Wang, K, and Zemel, R. "Classifying NBA offensive

plays using neural networks." Proceedings of MIT

Sloan Sports Analytics Conference. Vol. 4., published

online, 2016.

Clemente, F. M., Martins, F. M. L., Kalamaras, D., and

Mendes, R. S. "Network analysis in basketball:

Inspecting the prominent players using centrality

metrics." Journal of Physical Education and Sport, Vol.

15, no.2, p.212, 2015.

Luong, M. T., Socher, R., and Manning, C. D. “Better

word representations with recursive neural networks

for morphology,” In Proceedings of the seventeenth

conference on computational natural language learning

pp. 104-113, 2013.

Greff, K., Srivastava, R. K., Koutník, J., Steunebrink, B.

R., and Schmidhuber, J.. “LSTM: A search space

odyssey, ” IEEE transactions on neural networks and

learning systems, Vol. 28, no. 10, pp. 2222-2232, 2016.

Zhao, Y., Yang, R., Chevalier, G., Shah, R. C., and

Romijnders, R.. Applying deep bidirectional LSTM

and mixture density network for basketball trajectory

prediction. Optik, 158, pp. 266-272, 2018.

Yin, W., Kann., K., Yu, M., and Schütze, H.,

"Comparative research of CNN and RNN for natural

language processing." arXiv preprint

arXiv:1702.01923, published online, 2017.

APPENDIX

This study is supported by JSPS grant number

21K14369.

Line-up Optimization Model of Basketball Players and the Simulation Evaluation

499