
Intelligent Control of Construction Manufacturing Processes using
Deep Reinforcement Learning
Ian Flood
1
and Paris D. L. Flood
2
1
Rinker School, University of Florida, Gainesville, FL 32611, U.S.A.
2
Dept. of Computer Science and Technology, University of Cambridge, Cambridge, U.K.
Keywords: Construction Manufacturing, Construction Simulation, Decision Agents, Deep Artificial Neural Networks,
Precast Reinforced Concrete Production, Reinforcement Learning, Rule-of-thumb Policies.
Abstract: This paper is concerned with the development and evaluation of a reinforcement learning approach to the
control of factory based construction operations. The unique challenges associated with controlling
construction work is first discussed: uneven and uncertain demand, high customization, the need to fabricate
work to order, and a lack of opportunity to stockpile work. This is followed by a review of computational
approaches to this problem, specifically those based on heuristics and machine learning. A description is then
given of a model of a factory for producing precast reinforced concrete components, and a proposed
reinforcement learning strategy for training a neural network based agent to control this system. The
performance of this agent is compared to that of rule-of-thumb and random policies for a series of protracted
simulation production runs. The reinforcement learning method was found to be promising, outperforming
the two competing strategies for much of the time. This is significant given that there is high potential for
improvement of the method. The paper concludes with an indication of areas of proposed future research.
1 INTRODUCTION
Achieving operational efficiency in construction is
challenging, more so than most other manufacturing
industries. This results in part because construction
work does not lend itself to the methods of mass
production. The arrival of work is random and
sporadic, the work can be diverse and extensive in
scope, and the products are rarely reproduced.
Consequently, work has to be made to order with little
or no potential for stockpiling, and with large
fluctuations in resource demand.
These complexities make it difficult to derive a
simple policy for controlling construction operations
that is likely to be near optimal. A potentially
promising approach to this problem is assisted control
of operations by artificial intelligence (AI) agents.
These agents would act like an advisor (in a human-
in-the-loop system) or a controller (in an automated
environment) offering solutions whenever an
operational decision is needed.
The use of AI based decision agents to control
operations in the field of construction is limited.
Shitole et al. (2019) developed an agent for
optimizing a simulated earth-moving operation based
on artificial neural networks (ANNs) and
reinforcement learning (RL), and found it worked
better than previously published hand-designed
heuristics. RL is a broad class of learning techniques
based on discovery and rewards that has
demonstrated much success in recent years (Sutton
and Barto, 2018). Their earth-moving system
comprised two excavators serving a fleet of dump-
trucks. The function of the agent was to direct the
trucks to one or other of the excavators at a junction
in the return road, with the goal of optimizing the
overall production rate of the system. An issue with
this approach to control is its lack of extensibility.
That is, the agent can only be applied to the earth-
moving system considered in the study. Applying the
agent to a new situation with a different site layout
and/or equipment combination would require its
redevelopment. Although this could be achieved prior
to the start of the new construction operation, it would
nevertheless be a significant burden on planning.
Clearly, there is a need for more work in the area of
ANN extensibility.
An alternative application area to site-based
construction, with more immediate application given
current technology, is factory based manufactured
112
Flood, I. and Flood, P.
Intelligent Control of Construction Manufacturing Processes using Deep Reinforcement Learning.
DOI: 10.5220/0011309600003274
In Proceedings of the 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2022), pages 112-122
ISBN: 978-989-758-578-4; ISSN: 2184-2841
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

construction. In this situation, the life-span of an
agent should be relatively long, lasting at least until
any reconfiguration of the factory system is required
or a change occurs in its operating environment. This
study will be focused on factory based construction
manufacture, specifically for precast reinforced
concrete (PRC) component production.
Optimization of customized PRC component
production has been considered by several
researchers (Leu & Hwang, 2001; Chan & Hu, 2002;
Benjaoran & Dawood, 2005), using genetic
algorithms (GAs) to improve production
performance. Although the approach was shown to
be successful, heuristic search methods such as GAs
are computationally expensive. Therefore, they are
not well suited to situations where decisions have to
be made quickly.
RL solutions based on a learned model, such as
that developed by Shitole et al. (2019), will generate
rapid solutions to a decision problem, once trained. A
number of authors have applied this method to the
control of factory operations (Waschneck et al., 2018;
Zhou et al., 2020; Xia et al., 2021) and found results
to be promising when compared to more conventional
approaches such as rules-of-thumb. Unfortunately,
applications have been outside construction
manufacturing, and therefore do not address many of
the challenges of this industry, although Waschneck
et al. (2018) did address the problem of customization
within the semiconductor industry.
The objective of this paper is to explore the
potential of RL based modelling as a means of
controlling factory based construction
manufacturing, given the unique demands of
construction projects.
2 DYNAMIC SYSTEM CONTROL
2.1 Decision Agents
The future path of a construction manufacturing
system is determined by both controllable and
uncontrollable events. The controllable events
provide an opportunity to steer this path along a line
that is favourable to the manufacturer, optimizing
performance in terms of, say, productivity and/or
profit. This is achieved through the selection of an
appropriate sequence of decisions wherever options
exist. Examples of such decisions include prioritizing
jobs in a queue, deciding when to take an item of
equipment offline for maintenance, and selecting the
number of machines to allocate to a process.
These decisions are made by one or more agents,
as illustrated in Figure 1, which operate dynamically
throughout the life of the system. An agent monitors
relevant variables defining the state of the system and
its environment (both current and possibly past states,
and even predictions about future states) then uses
these insights to decide on appropriate future actions
to implement. Typically, these actions will concern
events in the immediate future (given that the most
relevant, accurate, and valuable information is
available at the time of the decision) but can also be
applied to events later in the future for decisions that
have a long lead time.
Figure 1: Decision agent control of dynamic system.
An important dichotomy of decision agents is
search based versus experience based systems.
Search based agents, which include blind and
heuristic methods, use a systematic exploration of the
solution space looking for the best action attainable.
They tailor a solution to the specific instance of the
problem at hand. As such, they may find better
optimized solutions than experience based agents,
although that needs to be tested. Search based agents
are also highly extensible, meaning they can be easily
adapted to new versions of the problem. On the
downside, they can be computationally expensive and
thus not suited to situations requiring rapid decision
making.
In contrast, experience based agents, which
include rules-of-thumb and artificial neural networks
(ANNs), make decisions based on exposure to similar
situations from the past. Once developed, an
experience based agent can output decisions rapidly.
However, because the solutions they offer are generic
rather than tailored to each situation, their decisions
may not be as well optimized as those of search based
agents. Furthermore, experience based agents tend to
lack extensibility; each new version of the problem
requires redevelopment of the agent, which in turn
requires the acquisition and assimilation of large
volumes of new information on system behaviour.
Intelligent Control of Construction Manufacturing Processes using Deep Reinforcement Learning
113

A hybrid of these agent types is also possible. For
example, an experience based agent can be used to
make the first attempt at a solution and then a search
based agent can be used to improve on this result.
Conversely, a search based agent could be used to
acquire examples for development of an experience
based agent.
A longer term objective for this study is to
quantify and compare the benefits of search and
experience based approaches to controlling
construction production systems. This paper,
however, focuses on experience based approaches
applied to construction manufacturing. Two
experience based methods will be considered, a rule-
of-thumb and a deep artificial neural network
(DANN), representing two extremes in functional
complexity. DANNs are variants of ANNs that
include multiple hidden layers or recursion between
units. The additional structure offers a corresponding
increase in functional complexity, although model
development has additional challenges. Although a
DANN is an experience based approach, its
development will involve the use of search techniques
to gather good training solutions, specifically using
RL techniques.
2.2 DANN Agent Development
Strategies
For a construction manufacturing environment,
optimal solutions to decision problems are not easily
attained a priori or from direct observation of the real
system. Simulating the manufacturing system has the
potential to explore a broader range of scenarios than
direct observation of the real system, but it similarly
fails to provide good labels (near optimal solutions)
to problems. This excludes the direct use of
supervised training techniques for development of the
DANN. There are many ways around this problem,
including using a strategy of hindsight whereby the
agent explores alternative decision paths (through
simulation), then selects those that are most
successful, effectively learning by trial-and-error.
For DANNs, there are two broad approaches to
hindsight model development. The first is to explore
adjustments to the structure and/or weights of the
DANN model (such as random perturbations), and to
select those that result in a better performing decision
path. This was the strategy investigated by Flood
(1989) for selecting sequences for construction jobs
in an offline optimization problem. The second
approach is to explore adjustments to the values
generated at the output from the DANN model, then
to evaluate their impact on the performance of the
decision path and to feed this back to the model in a
supervised manner. A method for implementing this
is detailed in section 3.3.3 below. This is in essence
the RL method.
3 MODELLING
A key function of RL is the exploration of alternative
decision paths and their impact on the performance of
the system. This experience is used to shape the
decisions made by the agent, mapping from system
state to action. This mapping is referred to as the
decision policy.
In construction production (including factory-
based construction manufacturing) it is not
practicable to experiment with alternative decision
policies using the real system. Construction work is
rarely reproduced making it almost impossible to
compare the effectiveness of alternative strategies.
Artificially reproducing work is also not viable given
the cost and time required to manufacture a
construction component. One way around this
problem is to build a simulation model of the
construction production system, and then to use this
to experiment with alternative policies. This concept
is illustrated in Figure 2, where the blue line
represents the historic path taken by the real system,
and the orange lines represent alternative future paths
Figure 2: Historic path of the real system followed by alternative future paths of a simulated version of the system.
SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
114

explored by different policies in a simulated version
of the system. The horizontal axis shows the state of
the system through time. Information about the real
system and its past behaviour would be used to
develop and validate the simulation model. The
information gathered from the simulated system is
used to develop and validate the policy, as described
in section 4.1. For this study, a conceptual design was
chosen for the simulation model, as specified in
section 3.1, designed to test the feasibility of the
approach.
3.1 Production Simulator
Figure 3 shows the production model of the system
considered, representing the manufacture of precast
reinforced concrete (PRC) components such as walls,
floors, beams, and column units. The system is
designed to capture the challenging and somewhat
unique features of construction manufacturing,
namely:
•
orders arrive in a sparse random manner, must be
made to order and cannot be stockpiled;
•
each order consists of a batch of components
variable in number;
•
many if not all components are unique in design
both within a batch and between batches, and
therefore have variable handling times at each
process;
•
all components have uncertainty in the handling
times at each process; and
•
all components must be delivered by a given date
in accordance with a site assembly schedule.
In addition, the study includes the following
assumptions about the logic of the PRC
manufacturing system:
•
the processes are executed sequentially by all
components, in the order shown in Figure 3;
•
the order in which components are served can
change between processes; and
•
each process has only sufficient resources to serve
one component at a time, except the Cure process
which can handle an unlimited number of
components.
The stochastic time related data adopted for this
study, including their distribution types, are given in
Table 1. The dynamics of the system are given by the
relative values of these data (rather than by their
absolute values) and therefore units not included. The
triangular distribution was adopted because it is
computationally inexpensive and yet provides a
versatile way of approximating a wide range of
distribution shapes, including those with skew.
Incoming orders consist of a batch of PRC
components. The number of components in a batch is
sampled from a positively skewed triangular
distribution, rounded to a positive integer. The arrival
of orders is considered to be a Poisson process, with
an arrival rate, λ, selected so that the work demand
and the productivity of the system would balance over
time. Each PRC component is considered to have a
different design and therefore their process durations
(for Forms, Rebar, Concrete, Strip, and Delivery) are
sampled separately. Curing time is considered to be
the same for all PRC components.
On site delivery of a PRC component is measured
as a contingency time beyond the sum of the
component’s process durations, and is also sampled
from a triangular distribution.
Table 1: Modelling the time-related variables.
SYSTEM
VARIABLE
FORM OF
UNCERTAINTY
PARAMETERS
Order arrival time Poisson process
Arrival rate (λ)
1
/
5,000
Batch size
Discretized
triangular
distribution
Min Mode Max
1 20 100
Processes
d
urations
Triangular
distribution
Min Mode Max
50 100 150
Cure
d
uration Fixe
d
~
Contingency time
relative to site
assembly time
Triangular
distribution
Min Mode Max
0 100 200
Figure 3: Production model for precast reinforced concrete (PRC) components.
Intelligent Control of Construction Manufacturing Processes using Deep Reinforcement Learning
115

3.2 Policy Types Considered
The control of the system is undertaken by a decision
agent as shown in Figure 3. Whenever a vacancy
arises at a process, the agent will select a PRC
component for processing from the corresponding
queue, using its current policy. Three alternative
types of policy were considered:
1. A DANN based policy developed using the RL
method described in section 4. The selection of a
PRC component is based on the current state of
the system and predictions about the handling
times for all the PRC components at each of the
processes.
2. A rule-of-thumb policy in which the PRC
component with the least remaining contingency
time in the queue is selected. Note, negative
contingencies (delays) are possible. This type of
policy was included as a performance benchmark
for comparison with the DANN based policy.
3. A random policy strategy in which the PRC
component is selected from a queue using a
uniformly distributed random variate. Again,
this was included as a benchmark for comparison
with the DANN policy.
3.3 DANN Structure
The DANN has a layered feedforward structure as
shown in Figure 4.
3.3.1 Input Layer
The input layer receives both temporal and spatial
information about the state of the system and the work
to be completed. The input values specify the
remaining process durations and the remaining
contingencies for the PRC components currently in
the system. These data are normalized for each
process, so that the values range between 0.0 and 1.0
for each input variable. The location of the values at
the input indicates the relevant queue, the position in
the queue, and the relevant process.
An issue with this approach stems from the fact
that the structure of the inputs to the DANN is fixed
(DANNs are structurally rigid) yet the number of
PRC components in the system that need to be
evaluated is variable. To get around this, the DANN
was designed to allow up to a stipulated number (N)
of PRC components to be evaluated in each queue: if
the number of PRC components in a queue is less than
N then the spare input values are set to 0.0; and if the
number of PRC components in a queue is greater than
N then only the first N PRC components will be
evaluated. Furthermore, the N PRC components
evaluated are those with the least contingency (or
greatest delay), and in this sense this the DANN is a
hybrid with the rule-of-thumb policy. For this study,
N was set to 20 PRC components since the queue
lengths were rarely found to extend beyond this value
for the systems considered. Future work will treat this
as an experimental parameter.
3.3.2 Hidden Layers
The number of hidden layers was set to 6 and the
number of hidden units per layer was set to 64. These
values were found to have the best performance in the
DANN training phase (see section 4.2) in a
preliminary search. A more thorough sensitivity
analysis ranging these parameters is planned for
future work.
All hidden units adopted the ReLU (rectified
linear unit) activation function due its computational
efficiency and avoidance of the vanishing gradient
problem (Glorot et al., 2011).
3.3.3 Output Layer
The DANNs output layer is where the PRC
components are selected from the queues for
processing. All output units use a sigmoid activation
function, thereby limiting their activation to values
between 0.0 and 1.0. The output units are arranged
into groups, with each group representing a different
queue, and with each unit in a group representing a
position in the queue. The number of units in a group
is limited to N, the number of PRC components to be
evaluated in each queue (see section 3.3.1 above).
The current length of a queue or N, whichever is
smallest, determines the number of units that are
active in its group. The values generated at the active
output units in a group are normalized to sum to 1.0.
This allows the output values to be treated as
probabilities for selecting PRC components from a
queue.
Figure 4: Policy implemented as a DANN.
SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
116

The DANN based policy has two modes of
operation:
• Exploration. This mode is used to steer the
simulation through alternative partially-random
paths, to gathering high-reward input-output
pattern pairs for training the DANN. Monte Carlo
sampling is used to select PRC components based
on the values generated at the relevant output
units. The higher the value generated at an output,
the more likely the corresponding PRC
component will be selected. The broader strategy
adopted for learning is given in section 4 below.
• Implementation. This mode operates by selecting
a PRC component from a queue based on the
output unit that generates the highest value within
its group. The operation is entirely deterministic.
It is used to control the simulated system in non-
training mode, to validate the performance of the
current policy. In addition, this is the mode that
would be adopted when using the policy to control
the real system.
4 DANN LEARNING STRATEGY
DANN development is a deeply nested process, as
shown in Figure 5. The outer level of this process
comprises two main phases: the collection of training
patterns through the exploration of alternative
decision paths; and the training of the DANN. These
phases are cycled through a number of times until
learning converges, each occasion using the most
recent version of the DANN to control the simulation.
Each time the system cycles back to Phase I, the
simulation is reset to the beginning using a new seed
for the random number generator. These phases are
described in detail in the following two sections.
4.1 Collection of Training Patterns
Collecting training patterns is undertaken in a series
of stages ‘s’, as illustrated in the upper blue section of
Figure 5. Each stage experiments with a predefined
number of trials ‘t’ simulating the fabrication of a set
of PRC components. The trial with the best
production performance (see section 4.1.1 below) is
selected for later training of the DANN, and as the
lead-in for the next stage in the simulation. The
training patterns collected are the mappings from
input to output for each state transition in the selected
trial.
This process continues until a specified number of
stages have been completed, each time collecting
training patterns from the best performing trial. For
future studies, parameters that can be investigated in
terms
of optimizing performance are the number of
Figure 5: DANN Development Cycle.
Intelligent Control of Construction Manufacturing Processes using Deep Reinforcement Learning
117

trials per stage, the number of PRC components to be
fabricated per trial (this could be variable between
stages), and the number of stages in the phase.
After completion of this phase, the system moves
to DANN training before returning for another round
of collecting training patterns. The intent is that by
cycle between Phases I and II in this manner, the
policy will move towards a better solution
incrementally.
4.1.1 Production Performance
Production performance is measured in terms of
delays to the delivery of PRC components. The delays
are offset relative to a base value in the cost function
to account for the square component which would
otherwise treat early and late deliveries the same. The
basis of the cost function is the root-mean-square
(RMS) of these delays:
𝑐𝑜𝑠𝑡 =
∑
𝑑
−𝑏
𝑛
(1
)
where:
d is the delay for the i
th
PRC component at its
completion;
n is the number of PRC components completed
at the current trial;
b is the base value against which the delays are
offset - this value is the maximum
contingency time possible for a PRC
component.
4.1.2 Rewards
The learning strategy presented here collects training
patterns based on their success in improving system
performance. For this reason, a training pattern’s
output values are modified from that produced by the
DANN to increase the probability of making the same
selection in a similar circumstance. The modification
(a reward) is to move the selected output value closer
to 1.0, and to move the other relevant output values
closer to 0.0, remembering that the output values are
treated as probabilities of selecting an RC component
from the queue. The extent of the modification will
be treated as an experimental hyper-parameter,
although for this study the rewards will be set to 0.0
and 1.0 without any discount.
4.2 DANN Training
The training patterns collected in Phase I are used to
train the DANN, or to further train it in repeat cycles,
as illustrated in the lower orange section of Figure 5.
The DANN was implemented in Python (Van
Rossum, 1995) and PyTorch (Paszke et al., 2019),
using the optimizer RMSProp (root-mean-square
propagation) and the loss function MSELoss (mean-
squared-error) with reduction set to ‘mean’. Data
loading used a mini-batch size of 64 (with a training
set size typically between 2,000 and 6,000) with
shuffling switched on. The learning rate was set to
0.001.
Training was conducted until the output from the
loss function had converged, which was typically
within 1,000 epochs. Validation of the system was
undertaken after the learning cycle had plateaued.
This involved running the simulation in
implementation mode (see section 3.3.3) using a start
point not used for learning.
5 RESULTS AND DISCUSSION
A series of experiments were undertaken to evaluate
the ability of the DANN to learn, and to compare its
performance with both the rule-of-thumb and random
policies outlined in section 3.2.
The work demand (given by the batch size
distribution for orders and their arrival rate, λ) and the
system’s productivity (determined in part by the
handling times for the processes) were designed to be
in balance for these experiments. The relevant
parameters are given in section 3.1.
5.1 Short Term Reward Approach
The first experiment was designed to test the
performance of the DANN using a short term strategy
for collecting rewards, monitoring delivery delays in
cycles of 20 PRC components (the mode batch size
used for one order of PRC components).
Training data was collected over a 2,000 PRC
component production run, divided into 100 stages of
20 components each and with 100 trials per stage (see
Figure 5 and section 4.1). Learning was undertaken
for six cycles of Phase I and II, at which point no
further improvement in performance was found. Each
cycle generated around 2,000 training patterns.
After development of the DANN, the simulation
model was reset and run for a 10,000 PRC component
production run for validation purposes. The results of
this experiment are presented in Figure 6, plotting the
RMS of the shifted delays in the delivery of the PRC
components (the Phase I objective function, see Eq.
1) against the component sequence number. Note, the
measure of delay is presented as the rolling average
(the average delay from the first to the n
th
component)
SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
118
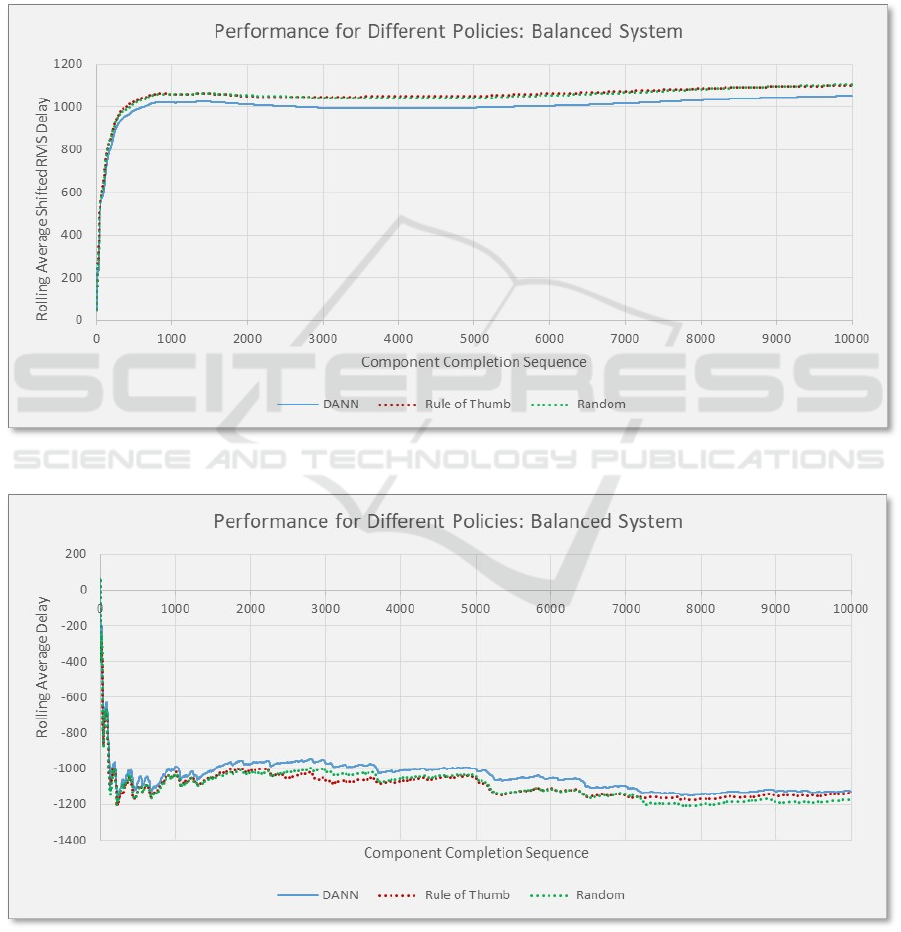
to capture the collective performance over the
production run. The initial rise in delay in the graph
(over approximately the first 700 components) is due
to start-up conditions in the production system. The
performance of the rule-of-thumb and random
policies are also shown in the figure for the same
production run.
The DANN demonstrated a slightly better
performance than the two alternative policies, settling
at approximately a 5% reduction on this measure of
delay. Interestingly, the rule-of-thumb and random
polices had very similar performance histories
throughout the run. This was found to be generally
true for all experiments undertaken.
Figure 7 presents the same results but for delays
rather than RMS delays. Noting that delays are
measured as negative quantities, a similar conclusion
is found to that drawn from Figure 6, except that the
rule-of-thumb policy becomes more competitive in
the latter stages of the experiment.
Figure 6: Validation run for a short term rewards strategy: shifted RMS delay versus PRC components.
Figure 7: Validation run for a short term rewards strategy: delay versus PRC components.
Intelligent Control of Construction Manufacturing Processes using Deep Reinforcement Learning
119

5.2 Mixed Term Reward Approach
The second experiment was designed to test the
performance of the DANN using a mixture of short,
medium, and long term strategies for collecting
rewards. In this case, delivery delays were monitored
in cycles of 20, 40 and 200 PRC components using
separate production runs which were then aggregated
into a single training set.
Training data was collected over three 2,000 PRC
component production runs, divided into stages as
follows:
•
100 stages of 20 components each, with 100 trials
per stage;
•
50 stages of 40 components each, with 100 trials
per stage; and
•
10 stages of 200 components each, with 100 trials
per stage.
Learning was undertaken for five cycles of Phase I
and II, at which point no further improvement in
performance was found. Each cycle generated around
6,000 training patterns.
As in the first experiment, the simulation model
was reset and run for a 10,000 PRC component
production run for validation purposes. The results of
this experiment are presented in Figure 8 for delays.
The DANN generally outperformed the rule-of-
thumb and random policies, except there was a period
(starting around 2,700 components) where its
performance regressed. It is not clear what caused
this, although the DANN appeared to make gains
relative to the other policies when the average delays
were increasing. The DANN does seem to be able to
learn good solutions, but this success is mixed. It
could be addressed by a broader and more
comprehensive set of training runs.
There was no obvious difference between the
learning abilities of the short and mixed term rewards
strategies. Clearly, a thorough analysis of this idea is
required for a range in the term lengths of the rewards.
Figure 9 shows the performance of the DANN at
each of the five learning cycles in the 10,000
production run. As expected, the lines higher on the
graph were produced by the later learning cycles,
indicating convergence on a solution. An important
observation from this, however, is that most of the
learning occurred in the region where the DANN
outperformed the rule-of-thumb and random policies
(compare Figures 8 and 9). In other words, the
DANN’s superior performance over its competitors
correlates very strongly with its ability to learn. The
question to be resolved is: what gives rise to the
differences in learning? For example, there could be
a lack of training examples similar to the situation
arising at the reduced performance regions in the
production run - this could be addressed by expanding
training. Alternatively, it could be that there are
situations where improvement in performance is
unattainable, perhaps because the default solution is
already optimal or near optimal. Indeed, the DANN
seemed to learn more when the delays were
increasing in the production run.
Figure 8: Validation run for a mixed term rewards strategy: delay versus PRC components.
SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
120

Figure 9: DANN learning progress over the first five cycles of Phase I and II.
6 CONCLUSION AND FUTURE
WORK
The work presented in this paper was concerned with
evaluating the potential of RL trained DANNs to
provide high-performance control of factory based
construction processes. The problem is particularly
challenging given the nature of construction projects:
uneven and uncertain demand, high customization,
the need to fabricate work to order, and a lack of
opportunity to stockpile work.
A preliminary series of experiments showed the
approach to be promising. The DANN outperformed
both a rule-of-thumb policy and a random policy in
the control of long production runs. Although the
improved performance was not maintained for the
entire duration of the production runs, there are many
opportunities for significant further development of
the technique. This is in contrast to the rule-of-thumb
and random policies which have no capacity for
further improvement - they are fixed strategies.
Future work will be aimed at improving the
performance of the RL approach, and increasing the
applicability of the technique to a more diverse range
of construction manufacturing problems.
The following work is planned for performance
improvement of the approach:
•
Increasing the length and diversity of production
runs used for training, thereby increasing the size
and scope of the training dataset.
•
Undertaking sensitivity analyses on the RL hyper-
parameters such as the reward term lengths, the
rewards discount rate, the number of trials per
stage, and the number of stages in a cycle.
•
Undertaking sensitivity analyses on the structure
and architecture of the DANN, including the
number of PRC components to be sampled at the
input (N), the number of hidden layers, the number
of hidden units per layer, and the inclusion of an
ensemble of models.
•
Consideration of the use of alternative RL
algorithms, and the use of heuristic search
techniques to solve the same problem.
The following work is planned to increase the scope
of application of the approach:
•
Case studies aimed at identifying detailed
performance data, logistics, and the practical
issues associated with day-to-day control of
construction manufacturing systems.
•
Increasing the range of state data used for input
and the scope of the type of decisions made by the
decision agent.
REFERENCES
Benjaoran, V., Dawood, N., (2005). An application of
Artificial Intelligence Planner for bespoke precast
concrete production planning: a case study. (ISSN:
2706-6568), http://itc.scix.net/paper/w78-2005-a11-5-
benjaoran.
Intelligent Control of Construction Manufacturing Processes using Deep Reinforcement Learning
121

Chan, W.T., and Hu, H., (2002). Production scheduling for
precast plants using a flow shop sequencing model.
Journal of Computing in Civil Engineering, 16 (3), pp.
165-174.
Flood, I., (1989). A Neural Network Approach to the
Sequencing of Construction Tasks. In proceedings of
the 6th ISARC, San Francisco, USA, IAARC, pp. 204-
211.
Glorot, X., Bordes, A., Bengio, Y., (2011). Deep Sparse
Rectifier Neural Networks. In proceedings of the
Fourteenth International Conference on Artificial
Intelligence and Statistics, Proceedings of Machine
Learning Research, 15, pp. 315-323.
https://proceedings.mlr.press/v15/glorot11a.html.
Leu, S., and Hwang, S., (2001). Optimal repetitive
scheduling model with sharable resource constraint.
Journal of Construction Engineering and Management,
127 (4), pp. 270-280.
Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J.,
Chanan, G., … Chintala, S., (2019). PyTorch: An
Imperative Style, High-Performance Deep Learning
Library. In Advances in Neural Information Processing
Systems, 32, pp. 8024–8035.
Shitole, V., Louis, J., Tadepalli, P., (2019). Optimizing
Earth Moving Operations via Reinforcement Learning,
In 2019 Winter Simulation Conference (WSC), pp.
2954-2965.
Sutton, R., Barto, A. (2018). Reinforcement Learning: An
Introduction, The MIT Press. London, 2
nd
edition.
Van Rossum, G., & Drake Jr, F. L., (1995). Python
reference manual. Centrum voor Wiskunde en
Informatica Amsterdam.
Waschneck, B., Reichstaller, A., Belzner, L., Altenmüller,
T., Bauernhansl, T., Knapp, A., & Kyek, A. (2018).
Optimization of global production scheduling with
deep reinforcement learning. In proceedings of 51
st
Conference on Manufacturing Systems, CIRP, 72, pp.
1264-1269.
Xia, K., Sacco, C., Kirkpatrick, M., Saidy, C., Nguyen, L.,
Kircaliali, A., Harik, R., (2021). A digital twin to train
deep reinforcement learning agent for smart
manufacturing plants: Environment, interfaces and
intelligence, Journal of Manufacturing Systems, Vol.
58, Elsevier, pp. 210-230.
Zhou, L., Zhang, L., Horn, BKP., (2020). Deep
reinforcement learning-based dynamic scheduling in
smart manufacturing. In proceedings of 53
rd
Conference on Manufacturing Systems, CIRP, 93, pp.
383-388.
SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
122
