Optimization of the Bottleneck Caused by Stacker Cranes in Dynamic

Hybrid Pallet Warehouses and Investigation of the Influence of the

Input/Output Area on Performance

Giulia Siciliano

, Anna Durek-Linn

and Johannes Fottner

Chair of Materials Handling, Material Flow, Logistics, Technical University of Munich,

Boltzmannstraße 15, Garching bei München, Germany

Keywords: Stacker Crane-based Warehouse, Discrete Event, Control Strategies, Route Optimization.

Abstract: The need for ever-higher performance in pallet storage systems has led to the development of Dynamic Hybrid

Pallet Warehouses (DHPW). DHPWs are created by either hybridizing a stacker crane-based warehouse with

shuttles, or by hybridizing a shuttle-based warehouse with stacker cranes. One limiting factor in both

categories is the bottleneck caused by having multiple stacker cranes in a single aisle. In this paper, we

demonstrate that, by using the proper control algorithms, the stacker crane bottleneck can be alleviated in

relation to the second DHPW category – almost to the point of reaching the performance that would be

obtained by introducing an additional stacker crane. Finally, we illustrate how the design of the loop on the

base tier has an increasing influence on the range of bottleneck improvement as the number of shuttles

increases.

1 INTRODUCTION

DHPWs are new systems which make it possible to

take advantage of the flexibility in the connection

between shuttles and stacker cranes in order to

achieve higher throughputs of the non-hybridized

base models on which they are based. The type called

Layout 1 is obtained by hybridizing an automated

storage and retrieval system (AS/RS) composed of

channel storage and stacker cranes with a shuttle base

tier (Eder, Klopfenstein, and Gebhardt 2019;

Siciliano, Lienert, and Fottner 2020). The types called

Layout 2 and Layout 3 are obtained by hybridizing a

warehouse based on shuttles with stacker cranes used

to connect the different levels (Malik 2014; Siciliano,

Yu, and Fottner 2022), as in Figure 1. The structure

of their base tier is shown in Figure 2. The difference

between Layout 2 and Layout 3 is that, in the latter,

the shuttles are free to move among the levels, which

strongly affects the performance of the warehouse as

the number of shuttles varies (Siciliano, Yu, and

Fottner 2022).

https://orcid.org/0000-0002-8438-9409

https://orcid.org/0000-0002-1247-6132

https://orcid.org/0000-0001-6392-0371

Layout 1, having a single base of shuttles, is much

more economical than Layouts 2 and 3, but it cannot

achieve as high a throughput as these (Siciliano, Yu,

and Fottner 2022). In Layout 1, it is possible to

increase the performance by using appropriate order

assignment strategies (Siciliano and Fottner 2021), or

through particular configurations and control

algorithms aimed at improving the impact of the

stacker crane bottleneck on performance (Siciliano,

Durek-Linn, and Fottner 2022).

Figure 1: Structure of Layouts 2 and 3 (Siciliano, Yu, and

Fottner 2022).

Siciliano, G., Durek-Linn, A. and Fottner, J.

Optimization of the Bottleneck Caused by Stacker Cranes in Dynamic Hybrid Pallet Warehouses and Investigation of the Inﬂuence of the Input/Output Area on Performance.

DOI: 10.5220/0011313600003274

In Proceedings of the 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2022), pages 123-130

ISBN: 978-989-758-578-4; ISSN: 2184-2841

123

In the following sections, we will conduct a brief

literature review of methodologies for improving the

performance of stacker cranes and then propose

several configurations and control algorithms for

optimizing multiple stacker cranes in a single aisle in

Layouts 2 and 3.

Figure 2: Structure of the base tier for Layouts 2 and 3

(Siciliano, Yu, and Fottner 2022).

2 LITERATURE REVIEW

Unlike DHPWs in which stacker cranes can exchange

pallets at transfer buffer locations along the entire

aisle, conventional AS/RSs include an input and an

output location only at the ends of the aisle. The

length of the aisle can be shortened in order to

increase the throughput of such systems (Lantschner

2015). Alternatively, a second stacker crane can be

introduced on separate rails (Hino, et al. 2009; Kung,

et al. 2012; Kung, et al. 2014). Another option for

improving performance is to coordinate more than

two stacker cranes on the same common rail, doing

which requires a specific control strategy (Kung, et

al. 2014). In addition, the development of analytical

methods (e.g., genetic coding for optimizing stacker

crane routes) can also provide an increase in terms of

throughput (Zhang and Zheng 1995). In (Siciliano,

Durek-Linn, and Fottner 2022) as regards Layout 1,

we developed several strategies for improving the

stacker crane bottleneck not only for the basic

configuration of Layout 1 having one satellite per

stacker crane, but also for the case in which more

satellites are assigned to each stacker crane, and in

which each stacker crane has two satellite positions

instead of one. In the following section, we illustrate

the optimization strategies applicable to Layouts 2

and 3.

3 OPTIMIZATION

ALGORITHMS

We apply the same stacker crane optimization

strategies to Layouts 2 and 3. In each layout,

however, it is necessary to employ adaptations of

varying extent when implementing these strategies.

In the event that the stacker cranes are equipped

with one pallet- or shuttle-position, we denote as One

Direction the algorithm we propose for improving the

stacker crane bottleneck. The purpose of this

algorithm is to reduce the time needed for a stacker

crane to serve shuttles by requiring that as many

orders as possible - up to a maximum of n - be

executed in the same aisle direction. For sake of

simplicity, the retrieval case is illustrated in Figure 3.

P2 denotes the location on the transfer buffer of one

of the levels where the stacker crane picks up the

pallet for Layout 2 or the shuttle for Layout 3 to be

retrieved to the transfer buffer of the base tier. The

control logic for the storage process is easily deduced

from that for the retrieval, so it is omitted here for the

sake of brevity. In the double cycle process, retrieval

and storage orders are chosen alternately up to a

maximum of 2n, i.e., n double cycles in the same

direction. In fact, a double cycle is defined as the

combination of a storage and a retrieval carried out by

the stacker crane. It is important to note that, in the

algorithm, the |x| coordinate of P2 must be greater

than and not equal to that of the last selected location

on the transfer buffer, because the stacker crane might

otherwise get stuck satisfying orders all having the

same x coordinate, but on different levels.

If the stacker cranes are equipped with two pallet-

or shuttle-positions, then we used the Double

algorithm to improve the throughput. We introduced

this algorithm for Layout 1 in an earlier contribution

(Siciliano, Durek-Linn, and Fottner 2022), and the

aim of this strategy is to combine two orders together

in order to reduce the total time taken by the stacker

crane to execute them. We then modified and further

developed the algorithm so as to fit Layouts 2 and 3.

In fact, each action is accomplished for each pallet or

shuttle, transported by the stacker crane, before

executing the next action.

As always in the case of stacker cranes comprising

two pallet- or shuttle-positions, an alternative to

Double is the Succession algorithm. We have

proposed this algorithm for Layout 1 in an earlier

paper (Siciliano, Durek-Linn, and Fottner 2022). Its

purpose is to find the order of operations allowing the

stacker crane to minimize its cycle time after

evaluating all of the possible combinations of

operations thereby. We then adapted it to be applica-

SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

124

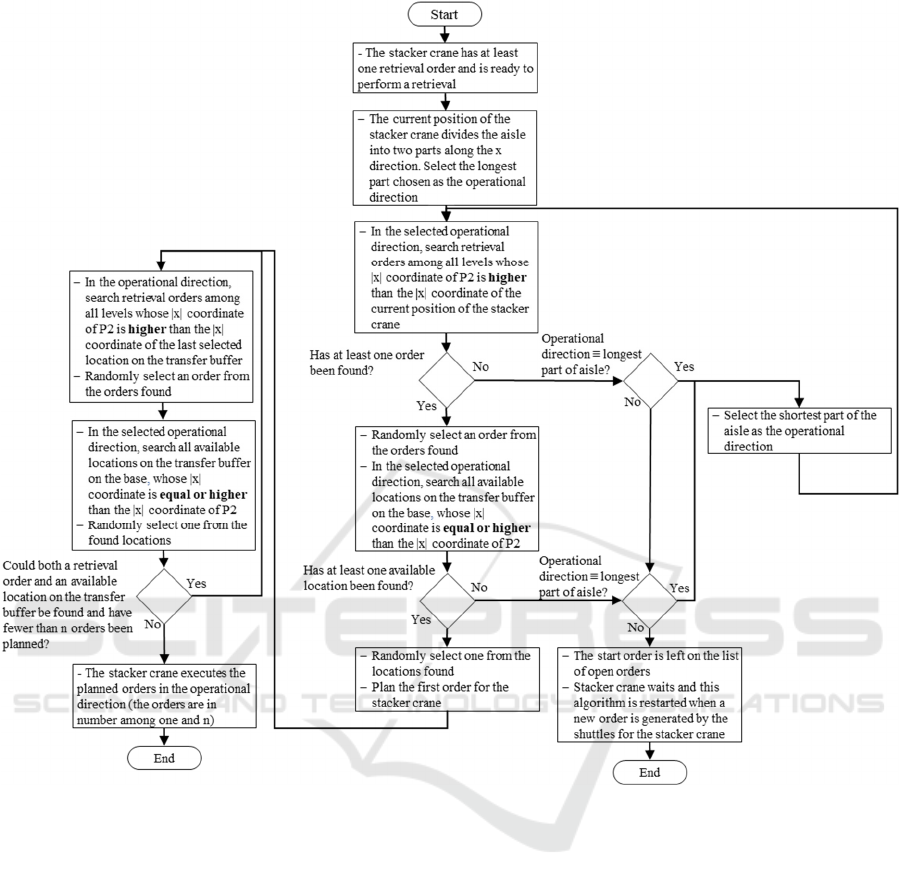
Figure 3: One Direction control strategy: Control logic for the stacker crane in Layouts 2 and 3.

ble for Layout 2 and 3 as well. In contrast to Layout

1, the presence of shuttles on all levels in Layouts 2

and 3 introduces additional boundary conditions

regarding coordination of the stacker crane. As a

result, in the process of double cycles, it is often

impossible for at least one retrieval or storage order

to be found. In such a case, in order to avoid reducing

the throughput of the warehouse, it becomes

necessary to perform two single cycles of the same

type, thus optimizing the succession of operations in

this case as well.

The following sections illustrate the experiments

performed and evaluate the effectiveness of each of

the algorithms described in Layouts 2 and 3.

4 SIMULATION STUDY

The purpose of this section is to identify which

control algorithms most improved the throughput

bottleneck caused by stacker cranes, and to

demonstrate the strong influence of loop or I/O area

design on throughput as the number of shuttles

increases. To this end, we performed experiments in

the discrete event simulation environment Plant

Simulation Tecnomatix. Given the small level of

variance, five repetitions of 24 hours each per

experiment were sufficient. We compared the

analytically calculated single shuttle cycle time with

the simulated cycle time to verify the model

(Siciliano, Lienert, and Fottner 2020). For validation,

we compared the simulated times for the shuttles and

Optimization of the Bottleneck Caused by Stacker Cranes in Dynamic Hybrid Pallet Warehouses and Investigation of the Inﬂuence of the

Input/Output Area on Performance

125

stacker crane with those of the real subsystem

prototypes (Siciliano, Schuster, and Fottner 2021).

The warehouse under consideration had 56 locations

distributed along the aisle for each of the transfer

buffers on the right and on the left. Every level was

similar to the base of Figure 2, except for the absence

of the I/O areas, and was equipped with 512 storage

locations. These storage locations were divided by

three storage aisles on each side of the warehouse and

two cross aisles used to ensure the movement of the

shuttles. There were three levels in addition to the

base. The base had one I/O area for each of the

extremes of the aisle. Every I/O area was equipped

with two I/O locations, which were used both for the

pallet entering from an extreme of the aisle as well as

those exiting from the other. The parameters we used

were provided by the manufacturer and are provided

in Tables 1 and 2. The maximum number of orders

for the strategy One Direction is set at four, because

the simulation experiments we executed have shown

that this number is rarely reached. Therefore, it would

not be efficient to set a higher maximum number of

orders. The abbreviations used in the experiments are

provided in Appendix.

Table 1: Stacker crane parameters.

Parameter Value

Travel speed x

4.0





Travel acceleration x

0.5







Lifting speed y

1.0





Lifting acceleration y

1.0







Time of pallet handover

6.0 𝑠

Time for positioning

efore channel

1.0 𝑠

Table 2: Shuttle parameters.

Parameter Value

Speed (loaded)

0.6





Speed (empty)

1.0





Acceleration (loaded)

0.3







Acceleration (empty)

0.6







Turning time 6.6 s

Handover time 10.0 s

4.1 Advantages of Optimization

Algorithms for Layout 2

We first evaluated the effectiveness of the

optimization strategies on Layout 2 in the case of

Figure 4: Effects of optimization strategies on the

throughput of Layout 2 for retrieval process.

retrieval. Figure 4 shows that, if only one stacker

crane is used, it is possible to achieve a significant

increase in throughput by applying the One Direction

strategy (blue solid line with rhombus), as compared

to the non-optimized base case (red solid line with

circles), in which the stacker cranes are bottle-

necking the system (i.e., for 32 or more shuttles).

Double strategy does not result in any throughput

improvement in comparison to the non-optimized

base case for Layout 2. Figure 4 demonstrates that the

Succession strategy (blue solid line with triangles)

provides a very high throughput improvement against

the non-optimized base case when the stacker crane

bottleneck occurs. This improvement amounts to

nearly 20 additional retrievals per hour. It should be

noted that, in the case of two stacker cranes, the

stacker crane bottleneck does not occur until at least

80 shuttles. Therefore, none of the strategies for

bottleneck improvement provided results better than

the non-optimized base case for two stacker cranes.

Figure 4 reveals the strong influence of the design

of the I/O area on performance when a high number

of shuttles is used. In fact, in the case of more than 80

shuttles, it is clear from the sudden decrease in

performance that deadlocks occur and, observing the

simulation, the reason is that they are creating

congestion in the I/O area. To avoid deadlocks, we

developed a new I/O area in Figure 5. The

performance achieved using the new loop is

represented in Figure 4 for 88 or more shuttles by the

yellow lines, which show that, even in the bottleneck

with two stacker cranes, the One Direction and

Succession strategies provided a slight throughput

SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

126

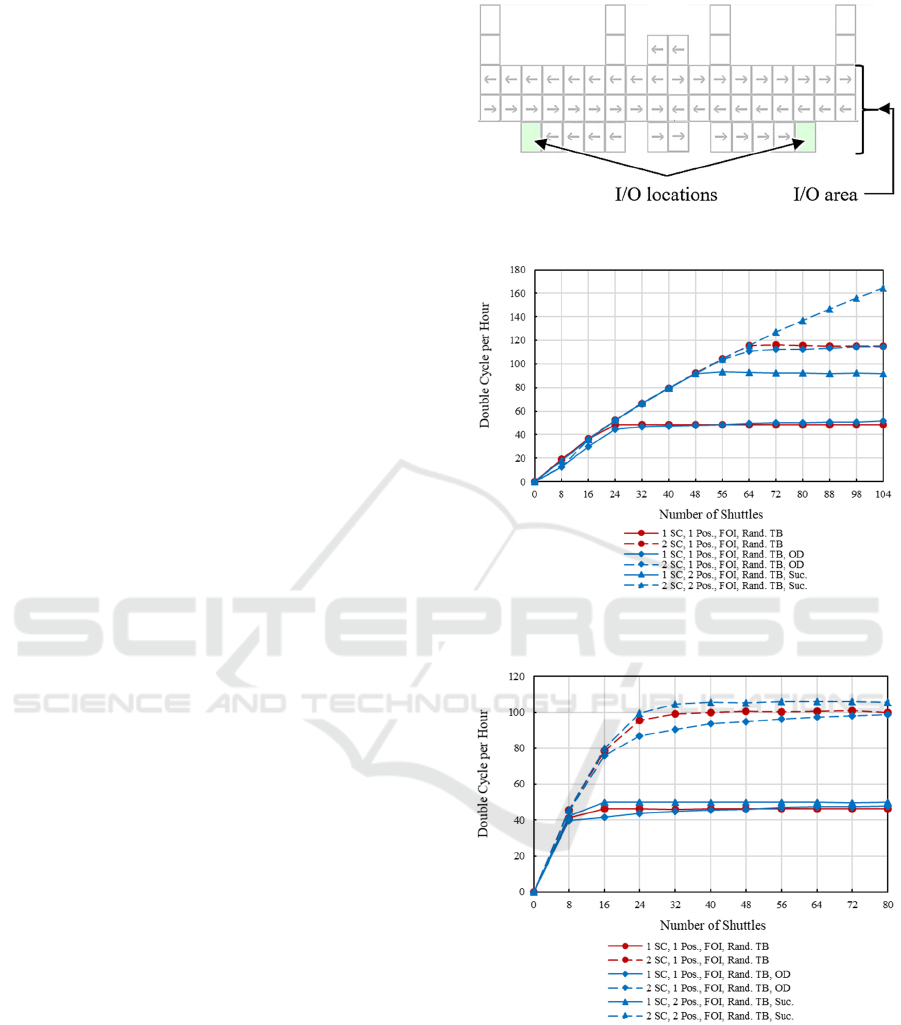
improvement compared to the non-optimized base

case. However, this improvement was limited by a

new bottleneck, i.e., the one caused by the number of

I/O locations present in the area.

Figure 6 shows the results of the optimization

strategies for Layout 2 in the case of double cycles.

For one stacker crane, the Succession strategy (blue

solid line with triangles) provided a very high

throughput improvement compared to the non-

optimized base case (red solid line with circles). For

48 shuttles, this amounted to about 40 additional

pallets retrieved and 40 additional pallets stored per

hour. It is important to note that this brought the

performance of the system quite near to that obtained

when using two stacker cranes in the non-optimized

base case (red dotted line with circles). This allowed

a very high level of throughput to be obtained without

the investment of an additional stacker crane, thus

reducing investment and operating costs. In addition

to improving throughput, the Succession strategy

improved the throughput, but it also postponed the

bottleneck of the stacker cranes from 24 to 48

shuttles, which represented a significant contribution

to the improvement of the systems scalability.

In case of two stacker cranes, the Succession

control algorithm (blue dotted line with triangles)

guaranteed an even higher throughput improvement,

which amounted to about 50 additional pallets

retrieved and 50 additional pallets stored per hour

compared to the non-optimized base case. Moreover,

the stacker crane bottleneck was postponed from 64

to at least 104 shuttles.

We were surprised to see that no relevant

improvement was provided by the One Direction and

Double strategies. It should be noted that, in Layout

1, the Double strategy was good at enabling

bottleneck improvement in the double cycles

(Siciliano, Durek-Linn, and Fottner 2022).

4.2 Advantages of Optimization

Algorithms for Layout 3

Figure 7 illustrates the behaviour of Layout 3 when

applying retrieval process optimization strategies.

Regarding the cases of both one and two stacker

cranes in the aisle, the Succession control algorithm

(blue solid and dotted lines with triangles) was the

only one that increased throughput against the non-

optimized base case (red solid and dotted lines with

circles). However, this was an increase of only about

5 retrievals per hour.

The One Direction strategy (blue solid and dotted

lines with rhombus) interfered with the rigid co-

ordination of the stacker crane, which has to move

Figure 5: New design for the I/O area.

Figure 6: Effects of optimization strategies on the

throughput of Layout 2 for the double cycles process.

Figure 7: Effects of optimization strategies on the

throughput of Layout 3 in the retrieval process.

shuttles between levels in Layout 3, and caused a

decrease of throughput when using a low or medium

number of shuttles compared to the non-optimized

base case.

The Double strategy did not provide any relevant

increase or decrease of throughput against the non-

optimized base case.

Optimization of the Bottleneck Caused by Stacker Cranes in Dynamic Hybrid Pallet Warehouses and Investigation of the Inﬂuence of the

Input/Output Area on Performance

127

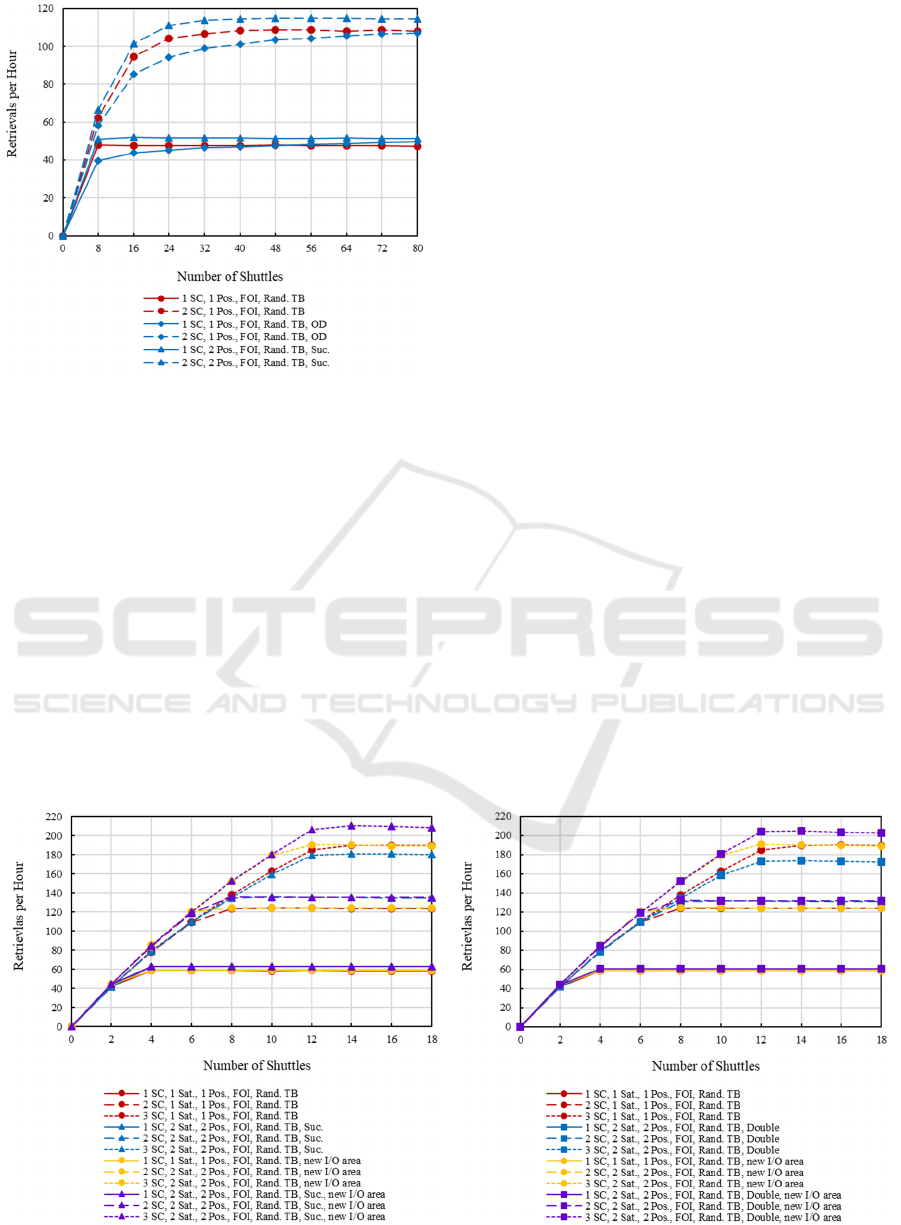
Figure 8: Effects of optimization strategies on the

throughput of Layout 3 for the double cycles process.

Figure 8 represents the results obtained when

simulating the double cycles process using

optimization strategies for Layout 3. In this case, as

was true of the retrieval process, only the Succession

control algorithm (blue solid and dotted lines with

triangles) provided, for both one and two stacker

cranes in the aisle, a slight improvement in

throughput compared to the non-optimized base case

(red solid and dotted lines with circles). In the One

Direction and Double strategies, like the retrieval

process, brought no improvement in performance.

The reason why the optimization strategies were more

effective for Layout 2 than for Layout 3 was that the

stacker crane bottleneck in the latter had a very strong

impact, because the stacker cranes were serving many

more order types than in Layout 2 in order to be able

to move the shuttles between levels.

4.3 Influence of I/O Area Design on

Performance

As illustrated in section 4.1, we noticed while

studying the behaviour of Layout 2 that a small

change in I/O area design led to an increasing

influence on performance, along with the increase of

the number of shuttles and stacker cranes. In our

previous article (Siciliano, Durek-Linn, and Fottner,

2022), we investigated the influence of several

strategies used to optimize the bottleneck caused by

the stacker crane in Layout 1. The results discussed in

this section are shown in Figure 9. The Double

strategy, in the case of retrieval for three stacker

cranes (blue small dotted line with squares), reached

a throughput level even lower than those for the non-

optimized base case (red small dotted line with

circles). After studying Layout 2, we concluded that

this effect was caused by the design of the I/O area.

Therefore, we applied the new I/O area design (see

Figure 5) to Layout 1 for the retrieval process. We

then noticed that, in addition to the non-optimized

base case for two and three stacker cranes (yellow

dotted lines with circles) reaching a higher throughput

using the new I/O area, the Double control algorithm

for three stacker cranes (violet small dotted line with

squares) also thus achieved a throughput about 10

retrievals per hour higher than that of the non-

optimized base case for 12 or more shuttles. We then

decided to also adapt the Succession strategy to the

retrieval process in Layout 1 with the old I/O area

Figure 9: Effects of optimization strategies on the throughput of Layout 3 for the double cycles process.

SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

128

used in (Siciliano, Durek-Linn, and Fottner, 2022).

As a result, we obtained a similar behaviour to that of

Double: For three stacker cranes, the throughput

obtained by Succession (blue small dotted line with

triangles) was lower than that of the non-optimized

base case (red small dotted line with circles).

However, also in this case, when using the new I/O

area of Figure 5, for three stacker cranes, the

throughput of Succession (violet small dotted line

with triangles) became almost 20 retrievals per hour

higher than those of the non-optimized base case for

12 or more shuttles. This outcome demonstrated the

strong influence of the I/O area on the behaviour of

DHPWs.

5 CONCLUSIONS

In this article, we examined how to improve the

bottleneck caused by stacker cranes for DHPWs

obtained by hybridizing a shuttle-based warehouse

with stacker cranes. The obtained results are valid for

DHPWs of Layout 2 and Layout 3. We demonstrated

through discrete event simulation that the One

Direction algorithm makes it possible to improve the

performance of Layout 2 for the retrieval case of one

stacker crane having just one pallet position.

However, if two pallet positions are used, Succession

provided the highest throughput for retrieval and

double cycles. Specifically, the improvement in

performance obtained using Succession for one

stacker crane was close to that which would be

obtained using an additional stacker crane in the

absence of any optimization strategy. As a result,

Succession makes it possible to achieve a high level

of throughput while keeping costs low. For Layout 3,

only the Succession strategy provided a slight

alleviation of the bottleneck caused by stacker cranes

because the latter bottleneck was stronger than in

Layouts 1 and 2. Finally, we demonstrated the strong

influence of I/O area design when the warehouse is

operating within the realm of high dynamics, i.e., for

a high number of shuttles, and for more than one

stacker crane per aisle.

Future research should work on developing

control algorithms able to significantly improve the

bottleneck caused by stacker cranes for Layout 3 as

well. Moreover, a systematic method should be

developed which is able to determine the optimal

configuration of the I/O area.

ACKNOWLEDGEMENTS

We would like to thank Joerg Eder and Thomas

Klopfenstein from the firm Gebhardt Fördertechnik

GmbH for the fruitful collaboration.

REFERENCES

Eder, J., Klopfenstein, T., Gebhardt, M., 2019.

“Lagersystem zur Speicherung und Abgabe von

Ladungsträgern”. Patent DE102019211804, German

Patent and Trade Mark Office (DPMA).

Hino, H., Kobayashi, Y., Higashi, T., Ota, J., 2009.

“Control methodology of stacker cranes for collision

avoidance considering dynamics in a warehouse”. In

Proceedings of the IEEE International Conference on

Robotics and Biomimetics, pp. 983–988. Piscataway,

New Jersey, Institute of Electrical and Electronics

Engineers, et al.

Kung, Y., Kobayashi, Y., Higashi, T., Ota, J., 2012.

“Motion planning of two stacker cranes in a large-scale

automated storage/ retrieval system”. In Journal of

Mechanical Systems for Transportation and Logistics 5

(1): 71 –85.

Kung, Y., Kobayashi, Y., Higashi, T., Sugi, M., Ota, J.,

2014. “Order scheduling of multiple stacker cranes on

common rails in an automated storage/retrieval

system”. In International Journal of Production

Research, Jg. 52 (2014) Nr. 4, pp. 1171–1187.

Lantschner, D., 2015. “Spielzeit automatischer

Lagersysteme mit mehreren Übergabepunkten”.

Dissertation, Lehrstuhl für Fördertechnik Materialfluss

Logistik, Technische Universität München, Garching.

Malik, O., 2014. Patent Application Publication:

Automated warehousing systems and method.

US20140086714A1, US Patent and Trademark Office

(USPTO).

Siciliano, G., Lienert, T., Fottner, J., 2020. “Design,

simulation and performance of a highly-dynamic,

hybrid pallet storage and retrieval system”. In

Proceedings of the 19th International Conference on

Modeling & Applied Simulation (MAS 2020), pp. 68-

75, https://doi.org/10.46354/i3m.2020.mas.009

Siciliano, G., Fottner, J., 2021. “Concept development and

evaluation of order assignment strategies in a highly-

dynamic, hybrid pallet storage and retrieval system”. In

Proceedings of the 11th International Conference on

Simulation and Modeling Methodologies, Technologies

and Applications (SIMULTECH 2021), ISBN 978-989-

758-528-9, ISSN 2184-2841, pp. 360-368.

Siciliano, G., Schuster, C. U., Fottner, J., 2021. “Analytical

method to determine the test positions for validation of

a two-dimensional shuttle system model”. In

Proceedings of the 20th International Conference on

Modeling & Applied Simulation (MAS 2021). pp. 21-

28, https://doi.org/10.46354/i3m.2021.mas.003

Optimization of the Bottleneck Caused by Stacker Cranes in Dynamic Hybrid Pallet Warehouses and Investigation of the Inﬂuence of the

Input/Output Area on Performance

129

Siciliano, G., Durek-Linn, A., Fottner, J., 2022.

“Development and Evaluation of Configurations and

Control Strategies to Coordinate Several Stacker

Cranes in a Single Aisle for a New Dynamic Hybrid

Pallet Warehouse”. In: Shi X., Bohács G., Ma Y., Gong

D., Shang X. (eds) LISS 2021. Lecture Notes in

Operations Research. Springer, Singapore.

https://doi.org/10.1007/978-981-16-8656-6_54

Siciliano, G., Yu, Y., Fottner, J., 2022. “Synergy between

Shuttles and Stacker Cranes in Dynamic Hybrid Pallet

Warehouses: Control Strategies and Performance

Evaluation”. In Proceedings of the 36th International

ECMS Conference on Modelling and Simulation

(ECMS 2022). In Press.

Zhang, L., Zheng, W., 1995. “Genetic coding for solving

both the stacker crane problem and its k-variant”. In

Proceedings of the IEEE International Conference on

Systems, Man and Cybernetics. Intelligent Systems for

the 21st Century, pp. 1061–1066.

APPENDIX

List of abbreviations used in the graphs containing the

results of simulation:

SC = stacker crane;

Pos. = pallet- or shuttle-position, on each stacker

crane in Layouts 2 and 3, respectively;

FOI = fixed operating intervals for each stacker crane;

Rand. TB = locations on transfer buffer are randomly

chosen among available ones;

OD = optimization strategy One Direction;

Double = optimization strategy Double;

Suc. = optimization strategy Succession;

New I/O area = use for experiments of the model with

I/O area as in Figure 5 instead of as in Figure 2.

SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

130