Towards Automatic Block Size Tuning for Image Processing Algorithms

on CUDA

Imene Guerﬁ

, Lobna Kriaa

and Leila Azouz Saidane

CRISTAL Laboratory, RAMSIS Pole, National School for Computer Sciences (ENSI), University of Manouba, Tunisia

Keywords:

GPU Computing, Parallel Programming, Program Optimization, Auto-tuning, and Face Detection.

Abstract:

With the growing amount of data, computational power has became highly required in all ﬁelds. To satisfy

these requirements, the use of GPUs seems to be the appropriate solution. But one of their major setbacks

is their varying architectures making writing efﬁcient parallel code very challenging, due to the necessity to

master the GPU’s low-level design. CUDA offers more ﬂexibility for the programmer to exploit the GPU’s

power with ease. However, tuning the launch parameters of its kernels such as block size remains a daunting

task. This parameter requires a deep understanding of the architecture and the execution model to be well-

tuned. Particularly, in the Viola-Jones algorithm, the block size is an important factor that improves the

execution time, but this optimization aspect is not well explored.

This paper aims to offer the ﬁrst steps toward automatically tuning the block size for any input without having

a deep knowledge of the hardware architecture, which ensures the automatic portability of the performance

over different GPUs architectures. The main idea is to deﬁne techniques on how to get the optimum block

size to achieve the best performance. We pointed out the impact of using static block size for all input sizes

on the overall performance. In light of the ﬁndings, we presented two dynamic approaches to select the best

block size suitable to the input size. The ﬁrst one is based on an empirical search; this approach provides

the optimal performance; however, it is tough for the programmer, and its deployment is time-consuming. In

order to overcome this issue, we proposed a second approach, which is a model that automatically selects a

block size. Experimental results show that this model can improve the execution time by up to 2.5x over the

static approach.

1 INTRODUCTION

Recent years have seen a signiﬁcant explosion in

Graphics Processing Units (GPUs) use in several aca-

demic and industrial ﬁelds (Tran et al., 2017). Mod-

ern GPUs have considerable computational power

due to their many cores, providing new opportunities

to accelerate data-intensive applications like image

processing, virtual reality, and deep learning. How-

ever, such applications are (1) challenging to be par-

allelized and (2) demand much effort from program-

mers to be optimized due to the GPU’s complex mem-

ory system and massive thread-level parallelism.

NVIDIA developed Compute Uniﬁed Device Ar-

chitecture (CUDA) which is a platform for mas-

sive data parallelism. The programmer should set

the launch conﬁguration parameters before launch-

ing parallel kernels (functions) onto the GPU. Once

https://orcid.org/0000-0002-2886-1713

https://orcid.org/0000-0002-2112-7807

established with a static number, the conﬁguration

parameters can’t be changed till the end of the exe-

cution. More precisely, the programmers select the

number of threads (block size) and the number of

blocks (grid size). Thus, an efﬁcient parallel imple-

mentation needs to be well-tuned, which often com-

plicates the task for programmers. These parame-

ters need to be tuned repeatedly, and sometimes parts

of the code must be rewritten to reach considerable

speedup compared to the original code. Moreover,

any change of the used GPU architecture implicates

that all the tuning work must be redone.

The block size to choose was a concern encoun-

tered in our previous work. To clarify, we have pro-

posed an efﬁcient GPGPU-based implementation of

the face detection algorithm (Guerﬁ et al., 2020).

In this previous work, we parallelize and optimize

the Viola-Jones face detection algorithm using the

CUDA programming model. The Viola-Jones algo-

rithm combines four kernels: 1) Nearest neighbor to

Guerﬁ, I., Kriaa, L. and Saidane, L.

Towards Automatic Block Size Tuning for Image Processing Algorithms on CUDA.

DOI: 10.5220/0011314800003266

In Proceedings of the 17th International Conference on Software Technologies (ICSOFT 2022), pages 591-601

ISBN: 978-989-758-588-3; ISSN: 2184-2833

591

resize the image, 2) Integral image, 3) Computing the

image coordinates for each feature, and 4) Scaling and

detecting faces. The main idea of the algorithm is to

resize the image until it is equal to or smaller than the

detection windows 25x25, and search faces in each re-

sized image. At each iteration, the four kernels will be

executed by the GPU with different input sizes. The

problem remains in choosing the block size at each

iteration; if the programmer determines the suitable

block size for each kernel’s initial image, this number

will probably not be the best for the other resized im-

ages. Moreover, the block size that can be adequate

for all image sizes doesn’t exist.

In order to solve this problem, this paper presents

two different approaches, an empirical search for the

block size and a model-based selection strategy. Be-

fore that, the impact of selecting a static block for

all the input images was studied. A considerable de-

crease in performance was noticed between different

block sizes, reaching 90.5%. After that, empirical re-

search was performed to dynamically select the opti-

mal block size for each input size. The founded val-

ues have been saved to a ﬁle and called at the execu-

tion time. However, empirical research is hard for the

programmer. And its deployment is time-consuming

because there is a vast range of possible values for

the block size, and any change in the input image or

the used GPU implies that all the work must be re-

done. Furthermore, a tuning model for the block size

was proposed. This model relies on understanding

the CUDA execution model and considering the in-

put image size, which automatically selects the block

size that provides nearly the optimal execution time

without requiring any interaction with the program-

mer. We show that auto-tuning the block size can im-

prove performance by up to 2.5x over the static con-

ﬁguration.

The rest of this paper is organized as follows:

The following section gives an overview of the re-

lated work. Section 3 presents a brief overview of

the NVIDIA GPUs, the CUDA execution model, and

the Viola-Jones algorithm. In the next section, we de-

scribe all the used methods and the processes of tun-

ing the block size. Section 5 elaborates on experi-

mental results and discussion, and ﬁnally. Section 6

concludes the paper.

2 RELATED WORKS

Many works proposed a parallelized and optimized

version of the Viola-Jones algorithm. These works

claim to recorded interesting results; unfortunately,

none of them explained how they tune the launch con-

ﬁguration. The nature of the Viola-Jones algorithm

makes adjusting the block size indispensable. Since

all kernels are executed multiple times with differ-

ent input sizes for the same image, the tuning method

should choose the block size that gives the best exe-

cution time without affecting the performance.

In the context of tuning CUDA performance,

many works exist on tuning different GPU parameters

for other applications. We are interested in the works

that tuned the block size. There are three types of tun-

ing: empirical, model-based, and predictive model-

based tuning (Alur et al., 2018).

- Empirical search-based approach: Several recent

studies have tackled the tuning problem through em-

pirical search-based approaches. The idea is to do an

exhaustive search for all candidate values in order to

ﬁnd the optimal block size. Among the signiﬁcant

number of works, we cite some relevant ones. Tor-

res et al. (Torres et al., 2012) presented an analy-

sis of the performance variation caused by selecting

the block size for the Fermi architecture. They stud-

ied the impact of block size on global memory ac-

cess performance and introduced a general approach

for block size choice by using some performance cri-

teria such as memory access pattern and total work-

load per thread. After that, they developed a suite

of micro-benchmarks (uBench) (Torres et al., 2013)

that explore the impact on the performance of the

thread-block geometry choice. In (Liu and Andelﬁn-

ger, 2017), Liu et al. presented a GPU-based parallel

discrete-event simulator based on the Time Warp syn-

chronization algorithm. They study the effectiveness

of parameter tuning, and they perform measurements

and adaptation at run-time. Brandt et al. (Brandt

et al., 2019) use a performance prediction model at the

compile time to select the thread block conﬁgurations

for the CUDA kernel. They tested the selection tool

using the Poly-bench/GPU benchmark kernels. They

reported good results; however, they precise that the

time for the selection process ranges between 30 sec-

onds and 2 minutes (Mohajerani, 2021); this delay is

not affordable for Viola-Jones algorithms in each iter-

ation and each kernel. Empirical tuning helps to ﬁnd

the optimal launch conﬁguration. However, applying

it takes a lot of time and effort from the programmers

or the compilers.

- Model-based approaches: Using the model-

based tuning, the programmer creates model-based

rules to select the optimal launch conﬁguration. We

cite some relevant work that considers the model-

based approach as a solution to the tuning problem.

Mukunoki et al. (Mukunoki et al., 2016) proposed

a method to adjust the thread-block size for several

memory-bound BLAS kernels. The proposed model

ICSOFT 2022 - 17th International Conference on Software Technologies

592

can calculate the block size by extracting the amount

of register and shared memory needed for the ker-

nel. These calculations are done at execution time

before executing the kernel. Tran et al. (Tran et al.,

2017) presented a tuning model based on the warp-

occupancy, which can calculate a set of options for

block size. However, the ﬁnal choice and its deploy-

ment in the code weren’t presented. Hu et al. (Hu

et al., 2020) proposed an automatic selection strat-

egy of block size based on the warp-occupancy, where

the model selects the block size with the highest oc-

cupancy at compile time. This model considers the

kernel’s amount of register and shared memory. The

model-based approach was not tested on the Viola-

Jones algorithm, where the choice of the block size

should not add much overhead to execution time.

- Predictive model-based approaches: For the pre-

dictive model-based tuning, in these approaches, the

tuning model is trained via machine learning algo-

rithms. Connors et al. (Connors and Qasem, 2017)

presented a supervised machine learning approach

that automatically selects proﬁtable block size. The

proposed model predicts if a change in block size

will improve the performance. Cui et al. (Cui and

Feng, 2021) designed an approach based on statistical

analysis and iterative machine-learning; this approach

automatically determines nearly optimal settings for

the GPU block size. In Viola-Jones case, the tuning

should not add too much overhead.

3 BACKGROUND

This section provides an overview of the NVIDIA

GPUs and the CUDA execution model. Then we

present the Viola-Jones Face Detection Algorithm.

3.1 A Brief Overview of NVIDIA GPUs

and CUDA Execution Model

GPU is a multicore system that consists of a set of

Streaming Multiprocessors (SMs). Each SM contains

several cores over which hundreds of threads can be

executed simultaneously, and there are multiple SMs

in a GPU. NVIDIA uses the term Compute Capa-

bility (CC) to describe hardware versions of GPUs,

which represents general speciﬁcations and available

features in these GPUs (NVIDIA, 2021b).

CUDA is a parallel computing platform and pro-

gramming model developed by NVIDIA. CUDA em-

ploys a Single Instruction Multiple Thread (SIMT) ar-

chitecture to leverage the parallelism provided by the

multiple cores, where threads are executed in a group

of 32 called warps.

CUDA code is formulated in kernels, which can

be called from the CPU. For each kernel, the pro-

grammer should specify the number of threads and

blocks that will execute it. Threads are grouped into

blocks, and blocks are grouped into grids. Blocks

and grids have a multidimensional aspect. When a

kernel is launched, its blocks are distributed among

available SMs based on the availability of resources.

Once a block is scheduled to an SM, it remains there

till the end of its execution; however, the SM can

execute multiple blocks simultaneously. After that,

the threads will be divided into warps that the SM

scheduler will distribute for execution on existing re-

sources. The resources (registers and shared memory)

used by threads limit the number of warps that can

physically be executed simultaneously. Shared mem-

ory is partitioned among blocks resident on the SM,

and registers are partitioned among threads (Cheng

et al., 2014)(NVIDIA, 2021b). Deep knowledge of

the hardware architecture and the execution model is

indispensable for conﬁguring kernel execution to get

the best performance.

3.2 Viola-Jones Face Detection

Algorithm

The viola-Jones face detection algorithm is an algo-

rithm created by Paul Viola and Michael Jones in

2001 (Viola and Jones, 2001). The detection process

begins with resizing the input image with a scale fac-

tor of 1.2 until the image is equal to or smaller than

the detection windows 25x25; the nearest neighbor al-

gorithm will be used. After that, the resized image

will be transformed into an integral image, used to

reduce the massive calculation caused by identifying

Haar features. Then the image positions for each Haar

feature will be computed, which are the relative coor-

dinates of Haar features in a 25x25 detection window

to prepare for shifting. After that, each moved de-

tection window will go through the cascade classiﬁer

stages; at each stage, if the integral sum is less than

the threshold, this window is rejected. Otherwise, the

window passes to the next stage. It will be accepted

as a face if a window passes all stages.

There will be four kernels for the GPU paral-

lelized version of this algorithm. The ﬁrst kernel re-

sizes the image and calculates the ﬁrst part of the inte-

gral image, where each thread will calculate one row,

so there will be as many threads as the height of the

image. The second kernel calculates the second part

of the integral image, where each thread will calculate

one column, so the total number of threads will equal

the image’s width. The third kernel for computing the

image coordinates for Haar features, each thread will

Towards Automatic Block Size Tuning for Image Processing Algorithms on CUDA

593

calculate one feature for this kernel, so there will be

2913 threads. And the fourth kernel for the cascade

classiﬁer and detecting faces which has the most in-

tensive work, this kernel needs (height x width) – (24

x 24) threads. For more information about the par-

allelized algorithm, we refer to (Guerﬁ et al., 2020).

Since the basic idea of the algorithm is to resize the

image, each kernel will deal with multiple image sizes

with a different total number of threads, for that using

static block size will lead to a degradation of the per-

formance. Next, we will prove that static block size

is a wrong decision for the programmer and how can

using a dynamic block size improve the performance.

After that, we will present our model, which will cal-

culate the block size for any image without interaction

with the programmer.

4 TUNING BLOCK SIZE

The optimal block size differs according to the lim-

its imposed by the GPU architecture, such as the max

threads per SM, and software factors such as the used

tion describes our methods to determine the optimal

block size. First, we will illustrate the impact of pass-

ing over the tuning step and choosing a static block

size for all image sizes. After that, we present how

making a dynamic block size selection according to

the input size could improve the performance. The

dynamic block size gives us the optimal performance;

however, it’s tough for the programmer and takes too

much time. For that, we present a model that automat-

ically selects the block size. The block sizes selected

by the model provide near-optimal performance.

4.1 Static Block Size

When writing the kernels of the Viola-Jones algo-

rithm, the block size should be speciﬁed; however,

that number could not suit all the input image sizes.

Moreover, due to the nature of the Viola-Jones algo-

rithm, for the same input, the image should be resized

multiple times. This section will show how choos-

ing one ﬁxed block size over another could consider-

ably decrease performance. We will execute ten dif-

ferent image sizes with all possible block sizes. How-

ever, since the search space for the block size (B

size

)

is vast, we need to reduce it; we will use some ba-

sic knowledge of the CUDA programming model that

any beginner should know and some hardware limits

(NVIDIA, 2021a)(Cheng et al., 2014).

• The blocks may contain a maximum of 1024

threads per block (MaxT

), which is the maximum

block size. Regardless of the block’s dimensions,

their product should not exceed this limit (equation

1).

size

≤ MaxT

(1)

• Since the hardware allocates threads for a block in

units of 32, which is the warp size (W

size

), so it makes

sense to choose a block size multiple of 32 (equation

2).

size

= W

×W

size

(2)

where (W

) is the number of warps per block. This

condition maximizes the performance and avoids

wasting resources; simultaneously, it ﬁxes a lower

boundary for the block size. From (equation 1) and

(equation 2), we found the limits of block size:

32 ≤ B

size

≤ 1024

Consequently, because the number of threads per

block should be multiple of 32 (equation 2), the

search space is restricted to:

size

∈ {32, 64, 96, 128, 160, 192, 224, 256, 288, 320,

352, 384, 416, 448, 480, 512, 544, 576, 608, 640, 672,

704, 736, 768, 800, 832, 864, 896, 928, 960, 992, 1024}

After decreasing the search space of the block size,

we claim that even the block size that gives the better

performance between these choices is not sufﬁcient;

we will provide an example to explain the problem.

We suppose that the input image size is 1024 x 1024.

in the Integral image kernel (we will focus on the inte-

gral image; however, this example applies to all used

Kernels). The total number of threads needed for ex-

ecution will equal the image’s width (as explained in

the previous section). After an empirical search, we

assume that the programmer found that 128 is the best

block size. After launching the face detection algo-

rithm, it will resize the image 21 times. The total

number of executed threads for the integral image in

each iteration is {1024, 853, 711, 592, 493, 411, 342,

285, 238, 198 165, 137, 114, 95, 79, 66, 55, 46, 38,

32, 26} respectively. After some iterations, we can

see that 128 will be bigger than the total number of

elements, which means we invoke more threads than

needed. That’s only one problem with the static block

size because it’s sure that one ﬁxed block size could

not ﬁt all the input sizes. Next, we attempt to tune

the best block size for the ten used input sizes and all

resized images.

4.2 Empirical Block Size Tuning

(Dynamic Block Size)

Since it’s clear that tuning is indispensable, the obvi-

ous way to tune that comes to mind is an empirical

ICSOFT 2022 - 17th International Conference on Software Technologies

594

search to examine all the possible block sizes with all

the input sizes and pick the best for each input, which

is the idea of empirical tuning. For that, several steps

are needed and explained below.

The ﬁrst step is to conduct a series of empirical

searches in the block size space introduced in the pre-

vious section. The program stores the performance

data and program input in a database during the in-

vestigation. This step aims to show the relationship

between the block size and the performance by per-

forming multiple sampling executions. In the second

step, we use collected data to select the best block

size; then, we save it to a new database. After that,

whenever we have to treat the exact image size, the

program will use the database to recognize the rela-

tion between input image size and the corresponding

suitable block sizes for all resized images. We call

this a dynamic block size since the block size changes

during the execution to adapt the input; ﬁgure 1 shows

the block size selection process using the dynamic

empirical approach. We assume that empirical tun-

ing provides the best overall performance because we

selected the block size by actual execution, consider-

ing the hardware architecture and the used resources.

However, this approach takes a lot of time and effort;

moreover, all the work must be redone if the GPU

changes or a new input image is used. Due to these

difﬁculties, we will next present our model that auto-

matically tunes the block size.

Figure 1: The block size selection process using the dy-

namic empirical approach for one image.

4.3 Model-based Block Size Tuning

This sub-section proposes a method for providing

near-optimal performance based on input size and

GPU architecture by automatically determining the

best block sizes. The model’s motivation is the need

for an automatic selection of the block size without

adding too much overhead. The model should se-

lect the block size ofﬂine and consider the input size

and GPU architecture. The CUDA best practice guide

indicates that keeping the multiprocessors on the de-

vice busy is the key to good performance (NVIDIA,

2021a); our idea is based on that. We select the block

size which makes the GPU work the maximum at all

levels. To build the model, we need to deﬁne three

types of occupancy that will be the key for the block

size selection.

4.3.1 Warp Occupancy

The warp occupancy represents the concurrence be-

tween the warps executed on SM; low occupancy re-

sults in performance degradation. On CUDA, the

number of threads, blocks, and warps performed per

SM is limited by the used resources and certain phys-

ical limits (the maximum number of resident threads,

blocks, and warps per SM). The SMs have to work

maximum so that it provides better performance.

When choosing a block size (B

size

), the number of

warps per block (W

) is calculated by (equation 3)

size

(3)

The block size limits the number of possible blocks

per SM (B

); in addition, B

is also bounded by

physical limits like the maximum number of resident

threads per SM (MaxT

) and the maximum number

of resident block per SM (MaxB

) (equation 4)

(

f loor(

MaxT

size

) ,if

MaxT

size

≤ MaxB

MaxB

,otherwise

(4)

The function f loor(x) rounds x down to the ﬁrst near-

est integer more minor than the argument passed (x).

Using equations (3) and (4), we can calculate the

maximum possible warps per SM (W

) (equation 5)

= W

× B

(5)

Before calculating the warp occupancy, we need to

add a condition to the input data to ensure that the

model will never pick a block size bigger than the to-

tal number of elements to be executed (Nb

ele

). We

deﬁne the warp occupancy (O

) as (equation 6):

(

MaxW

,if Nb

ele

> B

size

0 ,otherwise

(6)

Where MaxW

is the maximum number of resident

warps per SM. We note that the MaxT

, MaxB

and MaxW

depend on the GPU architecture, where

each CC has its values.

There are multiple block sizes for some kernels

that can reach maximum O

. The warp occupancy

is a theoretical value that decides the upper limit for

occupancy imposed by the launch conﬁguration and

the device’s capabilities; however, it illustrates only

Towards Automatic Block Size Tuning for Image Processing Algorithms on CUDA

595

the SM level concurrency and does not consider the

actual inputs. On the other side, the block size, the to-

tal number of blocks, and the total executed elements

affect the performance at the device level. We claim

that warp occupancy is not sufﬁcient to build a ro-

bust model. To solve this problem, we strengthen our

model with block occupancy and SM occupancy to

answer two questions How many SMs work? And

how much does each one work?

4.3.2 Block Occupancy

This part of the model has the role of making sure that

all the SMs have enough work. We calculate the real

number of blocks (grid size G

size

), which consider the

input size. Gsize can be calculated using the block

size and the total number of elements using the for-

mula (equation 7):

size

= f loor(

ele

+ B

size

− 1

size

) (7)

We have calculated the number of possible blocks per

SM (B

) in the previous sub-section. Now, since

we are at the device level, we know that the device

has multiple SMs. We can calculate the number of

possible blocks per device (B

device

) (equation 8):

device

= B

× Nb

(8)

Where Nb

is the number of SMs in the device. The

GPU can indeed carry out hundreds of threads; how-

ever, there is a limit for parallelism. We can imagine

the GPU execution as a sequential series of parallel

execution, so we will calculate the number of itera-

tions needed to execute all the elements (Nb

) (equa-

tion 9):

= ceil(

size

× MaxB

) (9)

The function ceil(x) rounds x up to the ﬁrst nearest in-

teger greater than the argument passed (x). We deﬁne

the block occupancy O

as (equation 10):

size

device

× Nb

(10)

4.3.3 SM Occupancy

When choosing the block size, we need to ensure that

the work is divided between SMs. As we explained

before, keeping the SMs busy is the key to perfor-

mance. So, we reinforce our model with SM occu-

pancy to ensure that the maximum number of SMs

are working at any moment of the execution. The

SM scheduler assigns blocks to SMs in a round-robin

fashion. Ideally, we suppose that the SMs will per-

form the iterations simultaneously, so we need to en-

sure that the last iteration will have enough work for

all SMs. Thus, we have to determine the number

of active SMs in the last iteration (Nb

SMlast

) by cal-

culating the number of blocks for the last iteration,

which will indicate if all the SMs will work at that

time (equation 11):

SMlast











size

− (B

device

× (Nb

− 1))

,if G

size

− (B

device

× (Nb

− 1)) < Nb

,otherwise

(11)

We deﬁne the SM occupancy OSM as (equation

12):

SMlast

+ (Nb

− 1)

(12)

The SM occupancy shows how much SMs are work-

ing during all iterations. More O

means that more

SMs were working simultaneously.

4.3.4 The Model

Our model combines three different ways to enhance

performance. We choose the block size that affords

the maximum warp occupancy to have enough con-

currency between warps. At the same time, it ensures

that the maximum number of SMs are working and

each of them is working utmost. In order to be closer

to the real execution, our model considers the input

size and GPU architecture. We assume that the block

size that maximizes the three former occupancies is

the most likely optimal block size. Hence, the model

chooses the block size which maximizes the former

three occupancies most. We don’t want to add a lot

of overhead to the execution time of the Viola-Jones

algorithm. Since when we calculate the block sizes

of all the kernels for one image size, it will ﬁt all im-

ages with the same size. Also, the same size will often

be executed multiple times, especially when we treat

video frames. We decided to devise the tuning algo-

rithm into 2 phases. First, we train all the ten image

sizes and save the values for all kernels and iterations

in a dataset named ﬁle.txt. Second, at the time of de-

tection, the already saved values will be loaded at the

beginning when we load the cascade classiﬁer. In the

case of a new image size, we have to calculate its val-

ues only one time and save them to the dataset; Fig-

ure 2 shows the block size selection process using the

model approach.

We need to deﬁne the algorithm’s search space for

the ﬁrst phase. We determined the search space in

section 4.1; however, that one was straightforward, so

we must reﬁne it. As we have seen, there is a maxi-

mum limit on the resident threads and blocks per SM,

so to maximize the use of threads and blocks in the

ICSOFT 2022 - 17th International Conference on Software Technologies

596

Figure 2: The block size selection process using the model

approach.

SM, we deﬁne equation 13:

size

≥

MaxT

MaxB

(13)

Using a block size that doesn’t follow equation 13

limits the total number of threads that could be used

in the SM because the maximum block per SM will

inhibit it. There are guidelines for the grid and block

size provided by The CUDA C Best Practices Guide

(NVIDIA, 2021a), in which it is speciﬁed that the

use of many small blocks is better than the use of

one big block; for that, we will eliminate block sizes

that lead to the use of one block per grid. Since all

block threads should be executed on the same SM,

the block size is limited by the hardware capacity of

the SM. Available resources, such as registers and

shared memory, limits the number of resident threads,

blocks, and warps per SM. The use of a small block

size leads to reaching these limits before all resources

are fully utilized; for that, we will eliminate the block

sizes that lead to the use of maximum block per SM.

Using these guides and equation (13), we deﬁne the

new search space as:

size

∈ {32, 64, 96, 128, 160, 192, 224, 256, 288,

320, 352, 384, 416, 448, 480, 512}

The process to determine the block size is performed

on the host (CPU) side before launching the CUDA

kernel.

5 EXPERIMENTATION AND

DISCUSSION

5.1 Experimental Setup

The proposed tuning approaches were developed and

tested on Intel(R) Core (TM) i5-10300H 2.50 GHz

loaded with Windows 10 (64 bits) and NVIDIA

graphics processing unit GeForce GTX 1650Ti. The

development and testing have been done in Microsoft

Visual Studio 14.0.25431.01. The CUDA ﬁles are

compiled by the CUDA compiler of Release 11.1,

with the architecture support corresponding to com-

pute capability 7.5. Table 1 describes the speciﬁca-

tions for this GPU and its physical limits.

Table 1: The device information for the used GPU.

Compute capability CC 7,5

Warp size W

size

The maximum number of threads per block Max

T B

1024

The maximum number of resident threads per SM MaxT

1024

The maximum number of resident blocks per SM MaxB

The maximum number of resident warps per SM MaxW

The number of SMs SM 16

For the evaluation of our approaches, we use

frontal face images with 10 different sizes (100x100,

320x240, 480x240, 512x512, 640x480, 720x480,

600x800, 1280x720, 1024x1024, 1024x1280).

5.2 Results, Discussion, and Model

Evaluation

In this section, we present the performance results

with analyses. The best practice guide (NVIDIA,

2021a) indicates that the block’s multidimensional as-

pect allows easier mapping of multidimensional prob-

lems to CUDA and does not play a role in perfor-

mance. For the sake of simplicity, we use only one

dimension for blocks and grids. The multidimen-

sional aspect will be considered in the extended model

in future works. In order to evaluate the effects of

static block size, we conducted experiments where the

block size ranges from 64 to 1024 for all the kernels,

the grid size was generated using equation (7), and we

used ten different input sizes. To ensure accuracy, the

execution was done multiple times. Figure 3 shows

the overall execution time of each image size with

varying block sizes. The green and red lines repre-

sent the minimum and maximum time, respectively.

According to ﬁgure 3, it’s clear that there is am-

ple space between the representation of the minimum

and maximum in all sub-ﬁgures. We can deduce

that choosing the wrong block size can lead to a se-

vere performance decrease. The gap among execu-

tion times for different images varies between 59.6%

and 90.5%. We can see that there isn’t a rhythm

for the performance, so we can’t orientate the user

to choose a bigger or smaller block size for the ker-

nels of this algorithm. After that, we navigated the

different choices for block size, and we chose the one

that provided better performance for each kernel. This

time, our experiments are based on comparing static

and dynamic block sizes select approach. Figure 4

shows the static and dynamic approaches execution

time for each image size.

Towards Automatic Block Size Tuning for Image Processing Algorithms on CUDA

597

(a) (b) (c) (d)

(e) (f) (g) (h)

(i) (j)

Figure 3: The overall execution time of the ten image sizes with varying block sizes (static approach).

Figure 4: The execution time of the static and dynamic approaches for each image size.

Figure 4 shows that, in actual performance tests,

the dynamic approach outperforms the static one for

all the test images in varying degrees; these degrees

range from 1.65x to 2.52x. We claim that the dynamic

approach can provide the best performance because it

is based on real execution, and the chosen block size

is the one that has the best performance for each ker-

nel and image size separately. Although the dynamic

approach doesn’t need any deep understanding of the

GPU architecture and the programming model, it is

hard for a programmer, and its deployment requires a

lot of time. In addition, if the architecture changes, all

the tuning needs to be redone. From here comes the

need for an automatic way to tune block size. Next,

we apply our tuning model described above. Using

the device parameters, we calculate the three occu-

pancies as described in equations (6), (10), and (12).

This model automatically picks the block size that

provides near-optimal performance. Figure 5 shows

the performance obtained with block size determined

ICSOFT 2022 - 17th International Conference on Software Technologies

598

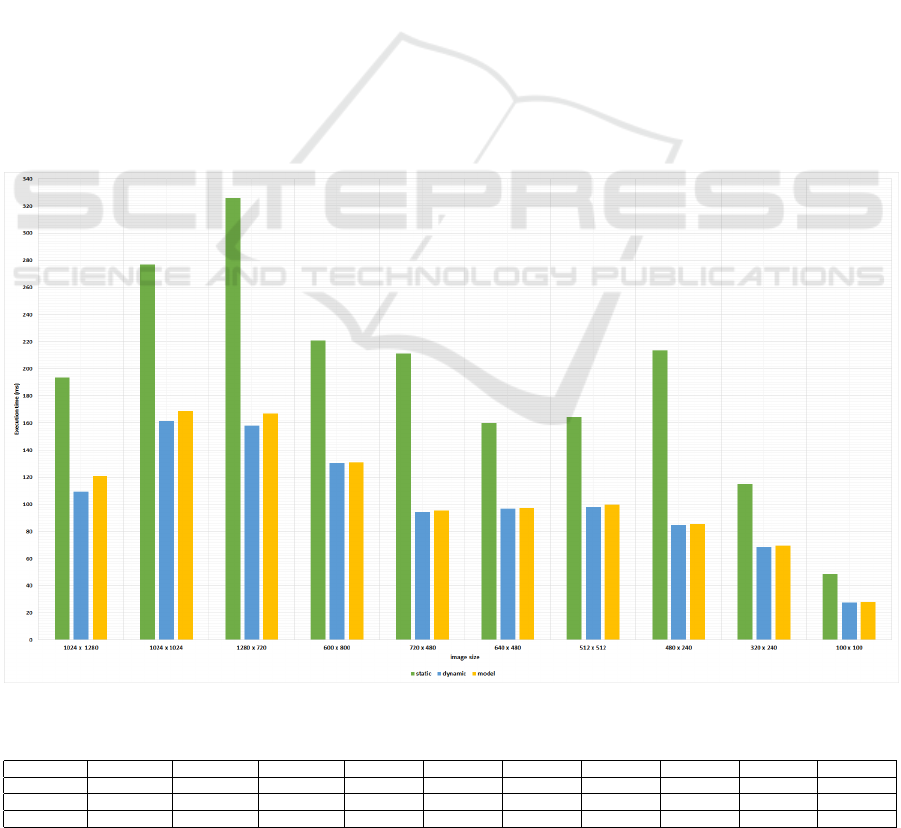
by our method in yellow and the one with the static

and dynamic approach in green and blue, respectively.

Figure 5 demonstrates how much the model out-

performs the static approach by a factor up to 2.5.

and gets nearly the same execution time as the dy-

namic one. The dynamic approach beats the model

with a difference that varies between 0.4 and 11.5 ms.

These results evaluate how precisely the model can

determine the optimal block size. We measured the

entire execution time of 10 different image sizes us-

ing the three above approaches. Table 2 summarizes

their execution time.

In order to evaluate the effects of our model, we

conducted experiments where we proﬁled all the ker-

nels to ﬁnd their achieved occupancies and their ex-

ecution time. Figures 6, 7, 8, and 9 show the result

of this experiment for the image size 1024x1280. (a)

for the real execution time and (b) for the model oc-

cupancy.

From ﬁgures 6, 7, and 8, we can see that the

model occupancy matches in reverse with the execu-

tion time, proving our model’s efﬁciency. However,

this doesn’t happen precisely in ﬁgure 9. We believe

that memory access is simple for the ﬁrst, second,

and third kernels and doesn’t need so many registers.

However, the fourth kernel executes more instructions

and consume more register.

Our model chooses the block size that maximizes

the occupancy, and from the ﬁgures 6, 7, 8 and 9, we

can see that the block size which has the highest oc-

cupancy is the one that has the lowest execution time.

These results further validate our model, and now we

will consider each ﬁgure separately. For the ”nearest

neighbor” kernel, the model chooses the block size 96

for the image size 1024x1280 because it has the best

occupancy, and in ﬁgure 6, this block size has the best

execution time. The same thing is for ﬁgure 7, which

presents the ”integral image” kernel, where the model

chooses 96 as the block size, and we can see that this

block size provides the best performance. For the ”Set

Image For Cascade Classiﬁer” kernel, 128 is the block

size chosen from the model, and it is the one that pro-

vides the best performance, as we can see in ﬁgure8.

In ﬁgure 9, it’s clear that a match doesn’t exist be-

tween execution time and the model. We believe that

the reason is its nature and the fact that it has a lot of

instruction and uses so much register. This issue will

be the subject of our extended model in future works.

Besides that, this example shows that the model chose

the best block size in most cases. We’ll dig a little

Figure 5: The performance of the 3 approaches with different image sizes.

Table 2: Summary of the execution time for the three approaches for selecting block size.

Image size 1024x1280 1024x1024 1280 x 720 600 x 800 720 x 480 640 x 480 512 x 512 480 x 240 320 x 240 100 x 100

Static 193,50 276,71 325,89 220,76 211,08 159,74 164,59 213,53 114,73 48,61

Dynamic 109,13 161,54 158,08 130,40 94,49 96,85 97,88 84,69 68,54 27,49

The model 120,67 168,63 166,64 130,86 95,36 97,26 99,63 85,43 69,34 27,89

Towards Automatic Block Size Tuning for Image Processing Algorithms on CUDA

599

(a) (b)

Figure 6: The nearest neighbor kernel.

(a) (b)

Figure 7: The integral image kernel.

(a) (b)

Figure 8: Set Image for Cascade Classiﬁer kernel.

(a) (b)

Figure 9: Scale Image Invoker kernel.

deeper in our future work by investigating the rela-

tionship between the three occupancies, the execution

time, and the used resources.

6 CONCLUSIONS

Performance is very important in image processing

applications running on GPUs, and it strongly de-

pends on GPU launch conﬁguration settings. In this

paper, we addressed the issue of block size tuning

for the image processing algorithms. We consider

this study as the ﬁrst step to facilitate parallel pro-

gramming by producing an analytical modeling tool

for tuning the algorithms and for the automatic porta-

bility of performance over different architectures. In

this paper, we considered the Viola-Jones algorithm.

Our study consists of three parts. First, we proved

the impact of using static block size on performance

degradation and that achieving the best performance

requires carefully tuning the block size. Second, we

tuned the block size empirically and made its selec-

tion dynamic based on the input size. This tuning

approach is very promising; however, it is hard and

takes a lot of time to be established. Third, we gen-

erate a model that automatically tunes the block size.

This model provides a near-optimal performance for

the Viola-Jones kernels in most cases. To evaluate our

work, we used ten different image sizes. The experi-

mental result shows that, for the ﬁrst part, the use of

static block size and choosing the wrong one can de-

crease performance down to 90.5%. For the second

part, using a dynamic tuned block size for each in-

put size decreased the execution time by up to 2.52x

comparing to the static block size. Because of the

hardness of employing the empirical dynamic tuning,

we considered the model-based tuning approach that

provides nearly the same performance as the dynamic

one with a difference of up to 11.5ms; however, it has

the advantage of being easier because it’s automatic.

In our future works, we will improve the model

by considering other factors that affect performance,

like registers and shared memory. And we will fo-

cus on the automatic portability of our model regard-

less of the hardware platform used. In addition, as

part of our ongoing works, we continue to validate

and reﬁne the model on additional kernels and algo-

rithms. We are convinced that, with further improve-

ments, our model will be able to tune any kernel on

any GPU architecture automatically. As another di-

rection of work, we will discover the impact of the

predictive model-based tuning on the image process-

ing algorithm’s performance.

REFERENCES

Alur, R., Devietti, J., and Singhania, N. (2018). Block-

size independence for gpu programs. In International

Static Analysis Symposium, pages 107–126. Springer.

Brandt, A., Mohajerani, D., Maza, M. M., Paudel, J., and

Wang, L. (2019). Klaraptor: A tool for dynamically

ﬁnding optimal kernel launch parameters targeting

cuda programs. ArXiv, Vol. CoRR abs/1911.02373.

ICSOFT 2022 - 17th International Conference on Software Technologies

600

Cheng, J., Grossman, M., and McKercher, T. (2014). Pro-

fessional CUDA c programming. John Wiley & Sons.

Connors, T. A. and Qasem, A. (2017). Automatically select-

ing proﬁtable thread block sizes for accelerated ker-

nels. In The 19th International Conference on High

Performance Computing and Communications; the

15th International Conference on Smart City; the 3rd

International Conference on Data Science and Sys-

tems (HPCC/SmartCity/DSS), pages 442–449. IEEE.

Cui, X. and Feng, W.-c. (2021). Iterml: Iterative machine

learning for intelligent parameter pruning and tuning

in graphics processing units. Journal of Signal Pro-

cessing Systems, 93(4):391–403.

Guerﬁ, I., Kriaa, L., and Sa

ıdane, L. A. (2020). An efﬁcient

gpgpu based implementation of face detection algo-

rithm using skin color pre-treatment. In The 15th In-

ternational Conference on Software Technologies (IC-

SOFT 2020), pages 574–585.

Hu, W., Han, L., Han, P., and Shang, J. (2020). Auto-

matic thread block size selection strategy in gpu par-

allel code generation. In International Symposium on

Parallel Architectures, Algorithms and Programming,

pages 390–404. Springer.

Liu, X. and Andelﬁnger, P. (2017). Time warp on the gpu:

Design and assessment. In Proceedings of the 2017

ACM SIGSIM Conference on Principles of Advanced

Discrete Simulation, pages 109–120.

Mohajerani, D. (2021). Parallel arbitrary-precision integer

arithmetic. Electronic Thesis and Dissertation Repos-

itory. 7674. https://ir.lib.uwo.ca/etd/7674.

Mukunoki, D., Imamura, T., and Takahashi, D. (2016).

Automatic thread-block size adjustment for memory-

bound blas kernels on gpus. In 2016 IEEE 10th Inter-

national Symposium on Embedded Multicore/Many-

core Systems-on-Chip (MCSOC), pages 377–384.

IEEE.

NVIDIA, C., editor (2021a). CUDA C++ BEST PRAC-

TICES GUIDE, volume Version 11.5. https:

//docs.nvidia.com/cuda/cuda-c-best-practices-guide/

index.htm.

NVIDIA, C., editor (2021b). CUDA C++ PRO-

GRAMMING GUIDE, volume Version 11.5.

https://docs.nvidia.com/cuda/pdf/CUDA\ C\

Programming\ Guide.pdf.

Torres, Y., Gonzalez-Escribano, A., and Llanos, D. R.

(2012). Using fermi architecture knowledge to speed

up cuda and opencl programs. In 2012 IEEE 10th

International Symposium on Parallel and Distributed

Processing with Applications, pages 617–624. IEEE.

Torres, Y., Gonzalez-Escribano, A., and Llanos, D. R.

(2013). ubench: exposing the impact of cuda block

geometry in terms of performance. The Journal of Su-

percomputing, 65(3):1150–1163.

Tran, N.-P., Lee, M., and Choi, J. (2017). Parameter

based tuning model for optimizing performance on

gpu. Cluster Computing, 20(3):2133–2142.

Viola, P. and Jones, M. (2001). Rapid object detection us-

ing a boosted cascade of simple features. In Proceed-

ings of the 2001 IEEE computer society conference on

computer vision and pattern recognition. CVPR 2001,

volume 1, pages I–I. IEEE.

Towards Automatic Block Size Tuning for Image Processing Algorithms on CUDA

601