Resilient Control of Interconnected Microgrids Under Attack

by Robust Nonlinear MPC

Sarah Braun

1 a

, Sebastian Albrecht

1 b

and Sergio Lucia

2 c

Siemens AG, Otto-Hahn-Ring 6, 81739 M

unchen, Germany

TU Dortmund University, August-Schmidt-Straße 1, 44227 Dortmund, Germany

Keywords:

Robust Control, Attack Identiﬁcation, Mathematical Modeling, Nonlinear Model Predictive Control,

Distributed Control.

Abstract:

With the growing share of renewable energy sources, the uncertainty in power supply is increasing, on the

one hand because of ﬂuctuations in the renewables, but on the other hand also due to the threat of deliberate

malicious attacks, which may become more prevalent due to the growing number of distributed generation

units. It is thus essential that local microgrids are controlled in a robust manner in order to ensure stability

and supply security even in the event of disturbances. To this end, we introduce a mathematical model for in-

terconnected, physically coupled microgrids with renewable generation that are exposed to the risk of attacks.

For optimal energy management and control, we present a resilient framework that combines a model-based

method to identify occurring attacks and a model predictive control scheme to compute robust control inputs.

We demonstrate the efﬁciency of the method for microgrid control in numerical experiments.

1 INTRODUCTION

In the course of the energy transition, power gener-

ation is undergoing a technological shift toward dis-

tributed generation, mainly from renewable energy

sources. This requires distributed control methods

that can be applied to safety-critical systems in real

time. Decentralized microgrids, combining local de-

mands, generation, and often storage units, increase

the security of supply within the microgrid area, but

create new challenges: Under the uncertainty of re-

newables, one has to address optimal control tasks

like economic generator dispatch, efﬁcient battery

use, or optimal power import and export strategies to

beneﬁt from ﬂuctuating energy prices, see (Olivares

et al., 2014; Mohammed et al., 2019). For the de-

sign of such control schemes, one has to be aware that

distributed systems with many local generators and

consumers provide attackers with many targets. Dis-

tributed control like the tertiary control tasks above

should thus be approached in a robust and secure

manner to provide viable solutions even under uncer-

tainty or in the event of an attack.

https://orcid.org/0000-0002-7032-6116

https://orcid.org/0000-0002-3647-4043

https://orcid.org/0000-0002-3347-5593

An important tool for ﬂexible energy management

in microgrids is model predictive control (MPC),

since it repeatedly computes optimal inputs to the sys-

tem based on measurements at each sampling time,

while it allows to include constraints and economic

costs into consideration. Robust MPC schemes ex-

plicitly take uncertainty into account and typically use

tube-based ideas, see (Mayne et al., 2005), or multi-

stage approaches, see (Lucia et al., 2013), which con-

sider a discrete set of possible scenarios. Robust

MPC cannot only be applied to parametric uncertain-

ties, but also to malicious attacks as illustrated in

(Braun et al., 2021a). Also distributed MPC schemes

for large systems under attack have been proposed,

e.g., in (Wang and Ishii, 2019; Braun et al., 2020).

While robust control can mitigate the impact of un-

known attacks, appropriate countermeasures require

detecting and identifying the attack. (Pasqualetti

et al., 2013) deﬁne attack detection and identiﬁca-

tion (ADI) as the tasks to uncover the presence of

an attack and localize all attacked components, re-

spectively. They also establish a widely used math-

ematical framework for control systems under attack.

An overview of physics-based ADI methods for both

linear and nonlinear dynamics is given by (Giraldo

et al., 2018; Arauz et al., 2021). Some approaches

like (Pasqualetti et al., 2013; Gallo et al., 2020) design

Braun, S., Albrecht, S. and Lucia, S.

Resilient Control of Interconnected Microgrids Under Attack by Robust Nonlinear MPC.

DOI: 10.5220/0011316500003271

In Proceedings of the 19th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2022), pages 58-66

ISBN: 978-989-758-585-2; ISSN: 2184-2809

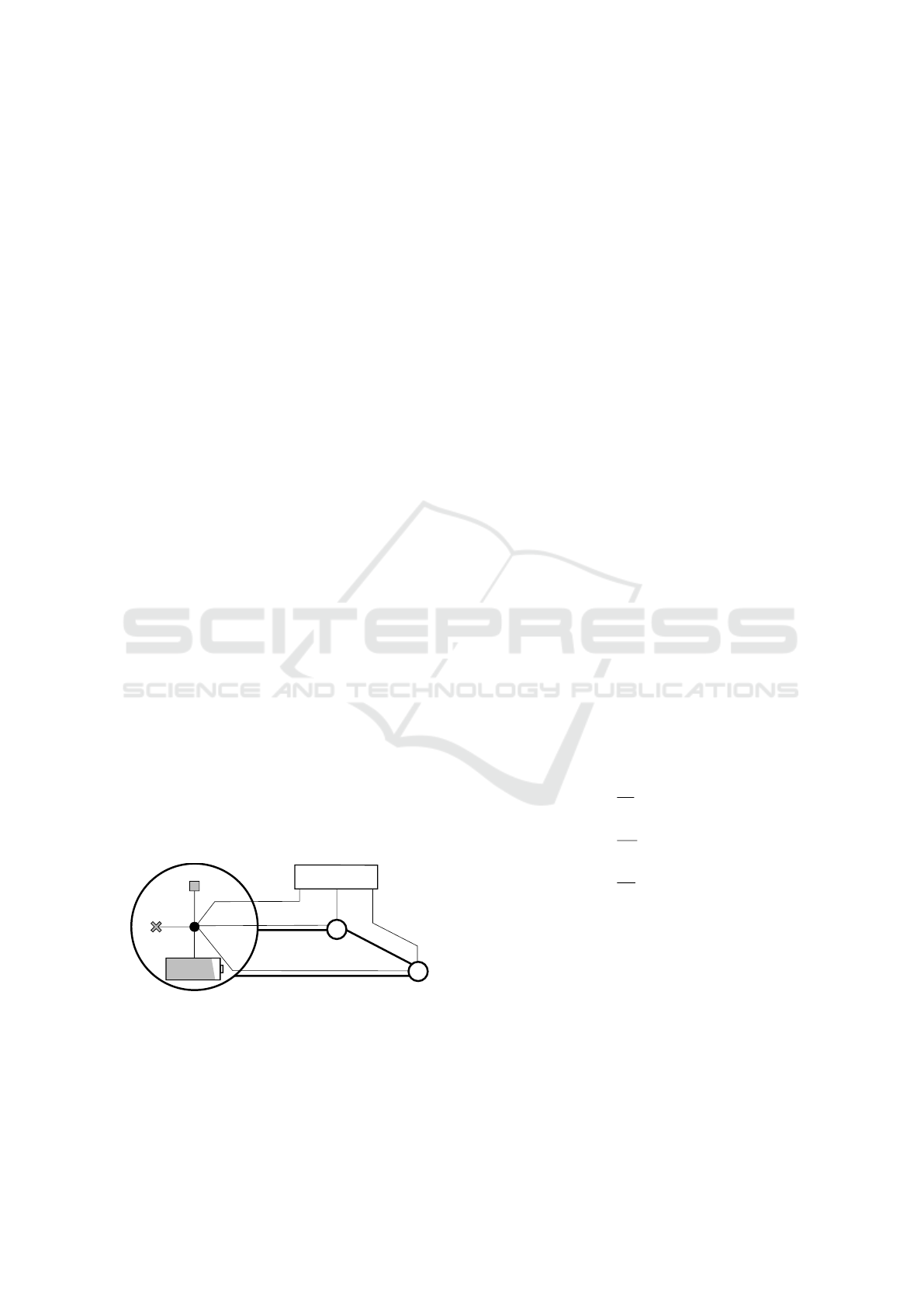
unknown-input observers for ADI, where identiﬁca-

tion typically requires the use of one observer for each

possible attack scenario. To avoid the resulting com-

binatorial nature, others propose optimization-based

methods and compute suspicious attackers by solving

sparse optimization problems like (Pan et al., 2015;

Braun et al., 2021b). Similar to the present work,

several authors examine their methods for robust con-

trol or ADI using the example of interconnected mi-

crogrids such as (Gallo et al., 2020; Ananduta et al.,

2020), which underlines the need for resilient meth-

ods in microgrid control. While (Gallo et al., 2020)

consider low-voltage control and focus on attack de-

tection, (Ananduta et al., 2020) solve economic dis-

patch problems similar to those in this work. They

propose an ADI method based on hypothesis testing

that, however, requires full enumeration of all possi-

ble attack scenarios, which again results in a combi-

natorial complexity. Both use linear dynamic models,

whereas we consider nonlinear battery dynamics.

The contribution of this work consists of a mathe-

matical model for tertiary control of interconnected

microgrids, a novel approach for local attack iden-

tiﬁcation, and a numerical case study to illustrate a

resilient control framework for attacked microgrids

with uncertain generation. The model, described in

Section 2, includes nonlinear battery dynamics, takes

into account the physical coupling of neighboring mi-

crogrids through dispatchable power exchange, and

covers the possible threat of attacks. To the new mi-

crogrid model, we apply the methods developed in

prior work for attack identiﬁcation based on sparse

optimization and for robust control against uncertain-

ties and already identiﬁed attacks. All approaches are

summarized in Section 3, where we also introduce a

new method for local ADI. We illustrate the potential

of these methods by numerical experiments in Sec-

tion 4, using an example of interconnected microgrids

with uncertain renewable generation under attack.

=-Σp

i j

Main grid

Figure 1: Schematic overview of the proposed model for

interconnected microgrids, showing the local model com-

ponents for microgrid i. Apart from internal power states,

each microgrid only requires knowledge of its neighboring

couplings (z

)

j∈N

. Storage units are used as a buffer to

maintain power balance.

2 A MODEL FOR

INTERCONNECTED

MICROGRIDS UNDER ATTACK

2.1 Microgrid Model

We consider a set of interconnected microgrids that

are represented by a graph G = (V ,E), where

each node i ∈ V corresponds to a microgrid and

each edge {i, j} ∈ E ⊆ V × V describes two phys-

ically coupled microgrids. Such pairs are called

neighbors and we denote the neighborhood of i as

{

j|{i, j} ∈ E

}

. Each microgrid contains dis-

patchable generation units, generating a total power

output p

≥ 0, and an aggregated load p

≤ 0. Mod-

eling uncertain load and nondispatchable generation

from renewable energy sources is postponed to Sec-

tion 2.3. Each microgrid is connected to the main

grid, from or to which it can import or export

power p

. Import is modeled by non-negative val-

ues p

≥ 0, export by negative values p

< 0. In

addition, we assume that neighboring microgrids i, j

with j ∈ N

can transfer power to each other. The

power that microgrid i sends to a neighbor j is de-

noted by p

i j

and vice versa, and the resulting directed

power ﬂow from i to j is given as p

ﬂow

i j

= p

i j

− p

Finally, each microgrid has a storage unit with state

of charge (SoC) s

∈ [0,1], from which power p

> 0

is taken when discharged and which can be charged

with power p

< 0. Unlike, e.g., (Ananduta et al.,

2020), we assume that generation cannot change in-

stantaneously and model p

and, similarly, p

and p

i j

as differential states, whose change over time is con-

trolled by inputs u

, u

, and u

i j

according to

˙p



− p



˙p

− p

˙p

i j



i j

− p

i j



(1)

The delay parameters T

, and T

i j

∈ R describe

how quickly a change in the input affects the state and

depend on technical characteristics. Compared to T

for power transfers with the main grid or neighboring

microgrids, typically smaller delay times T

and T

i j

are chosen as we will see in our numerical example in

Section 4. We assume that low-level controllers in all

units ensure that the computed set points are met at all

times. To make sure that the power balance in micro-

grid i is always satisﬁed, even when an attack occurs,

the storage is used as a buffer that provides the re-

quired power reserves. To this end, the storage power

Resilient Control of Interconnected Microgrids Under Attack by Robust Nonlinear MPC

is modeled as a dependent variable that is com-

puted from the states p

, p

and p

i j

and the load p

according to

= −p

− p

−

∑

j∈N



− p

i j



It should be noted here that for microgrid i, p

i j

is a

local state that can be controlled via u

i j

as in eq. (1),

whereas the neighboring state p

can neither be con-

trolled by microgrid i nor is its dynamic behavior

known to i. Instead, it represents a coupling vari-

able z

= p

, that models the physical connection

of neighboring microgrids and is treated locally as an

uncertain parameter as we will explain in more de-

tail in Section 3. Figure 1 illustrates that each mi-

crogrid only knows its local power variables and its

neighboring couplings, allowing for distributed con-

trol. According to the storage power p

, the storage

is charged or discharged and the resulting change in

the SoC s

is modeled as

˙s

= b

, p

with some function b

modeling the battery dynamics,

which is described in the next section.

2.2 Nonlinear Battery Model

If a microgrid is attacked, the battery may also be used

at SoCs close to 0 or 1, which is avoided during nor-

mal operation. Therefore, the goal of this section is to

derive a nonlinear function b

that describes the bat-

tery dynamics for all states of charge in [0,1] and not

only in the middle range, where a linear approxima-

tion is often sufﬁcient. With Q

denoting the maxi-

mum capacity of the battery and I

being the battery

current, the dynamics of the SoC are given as

˙s

= −

, (2)

see, e.g., (Mathieu and Taylor, 2016). With U

denot-

ing the battery voltage, the storage power p

is given

as p

= U

and U

, in turn, can be modeled as

= U

OCV

) + R

The ﬁrst term describes the open circuit voltage U

OCV

and the second the ohmic effect with resistance R

see (Mathieu and Taylor, 2016). For the storage

power p

, this results in the following equation,

which is quadratic in I

= U

OCV

+ R





Solving it for I

, the battery current I

is obtained

from s

and p

via I

= β

, p

) for some nonlin-

ear function β

. Together with eq. (2), this results

in a nonlinear function b

, p

) = −β

, p

)/Q

describing the dynamic behavior of the battery. It

remains open to specify U

OCV

). Models for the

open circuit voltage of batteries are typically obtained

from electrochemical analyses and often ﬁtted to lin-

ear curves. For low and high SoCs, however, this is

inaccurate, which is why we use the model by (Zhang

et al., 2016). With parameters A

, and N

that depend on the type of battery, their model in-

cludes a logarithmic, a linear, and an exponential

function

OCV

) = A

+ B

(−ln(s

))

+ D

−1)

2.3 Attack Model

In this work, we examine attacks on microgrid con-

trol and model an attack as an additional, unknown

input like, e.g., (Ananduta et al., 2020). In micro-

grid i, we consider the possibility of attacks on the

generation input u

, on the power exchange u

with

the main grid, and on power transfers u

i j

with any

neighbor j ∈ N

. If an attacker is present, the dynam-

ics in eq. (1) of the affected state p

∈ {p

, p

i j

}

with input u

∈ {u

i j

} and delay parameter

∈ {T

i j

} are changed to

˙p

+ a

− p

), (3)

where a

∈ {a

i j

} represents the modiﬁcation in

the dynamics caused by the attack. In other words, in

case of an attack, not the computed controller com-

mand u

is applied to the system, but some altered

input u

+ a

This model covers not only malicious attacks, but

uncertain disturbances in general. If microgrid i in-

cludes nondispatchable generation from renewables

or uncertain load, the input a

also models the power

difference between uncertain generation and load. We

deliberately make no difference in modeling, but con-

sider both attacks and renewable generation as uncer-

tain inﬂuences, since the resilient control framework

presented in Section 3 is robust against attacks as well

as ﬂuctuations in generation and load.

2.4 Cost Function

Each microgrid i is operated locally to meet the re-

spective load at the lowest possible cost. For a time

window [0,T ], we consider the following costs for

economic dispatch

(T ) =



, p



+ l



ﬂow

, p



dt + m

(T )),

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

that consist of quadratic stage costs q

, piecewise lin-

ear stage costs l

, and terminal costs m

. The costs q

are deﬁned as



, p



= C





∑

j∈N



i j







with cost values C

∈ R

≥0

. They describe the

per-unit costs of power generation, power transfers

to neighbors, and storage operations, and model the

costs that incur by the use of these units. The eco-

nomic proﬁt or loss from selling or buying energy in

trade with neighbors or the main grid is modeled by

piecewise linear costs l

. Based on the positive and

negative part functions

(x)

(

0 if x < 0,

x if x ≥ 0,

and

(x)

−

(

x if x < 0,

0 if x ≥ 0,

the piecewise linear cost function l

is deﬁned as



ﬂow

, p



∑

j∈N

ﬂow,ex



ﬂow



−

∑

j∈N

ﬂow,im



ﬂow



m,ex

)

−

m,im

)

for each microgrid i, with export and import per-unit

prices C

ﬂow,ex

, C

ﬂow,im

, C

m,ex

, C

m,im

∈ R

≥0

, which

may ﬂuctuate throughout the day. We will explic-

itly allow export prices to be considerably lower than

import prices since we focus on small producers, for

which in reality it is often more proﬁtable to gener-

ate power for their own demand than to import from

the main grid. To account for degradation costs of the

battery and to avoid that only the storage is discharged

to fulﬁll the load, we introduce terminal costs m

) = C

dis

(0) − s

(T ))

If the state of charge s

(T ) at the end of the consid-

ered horizon is smaller than s

(0) at the beginning,

each unit of power discharge is penalized by some

cost C

dis

∈ R

≥0

3 A FRAMEWORK FOR

RESILIENT CONTROL

In this section, we outline three methods for resilient

control of distributed systems under attack that have

been proposed in recently published work, see (Braun

et al., 2020; Braun et al., 2021b; Braun et al., 2021a):

First, we describe an approach for robust distributed

MPC in Section 3.1. Then, a global ADI method to

identify unknown attacks is outlined in Section 3.2,

and, ﬁnally, both methods are combined into an adap-

tively robust MPC scheme in Section 3.3 to compute

control inputs that are robust against previously iden-

tiﬁed attacks. We also propose a novel approach for

local ADI in Section 3.2. All methods are applica-

ble to distributed control systems with several subsys-

tems that behave according to discrete-time dynamics

of the form

k+1

= f



+ a



k+1

= h

k+1

= g

k+1

(4)

with local states x

, inputs u

, attacks a

, and system

outputs y

in subsystem i. The physical interconnec-

tion of subsystems is modeled through coupling vari-

ables z

, which depend on the local states. All func-

tions f

, and g

may be nonlinear and are assumed

to be sufﬁciently smooth. The microgrid model from

Section 2 is of the same form as eq. (4) when we de-

ﬁne local states



, p



i j



j∈N



local inputs





i j



j∈N



local attacks





i j



j∈N



and local couplings



i j



j∈N

and z





j∈N

The function f

is obtained from the dynamics in

eq. (1) by discretizing the equations in time, while the

function g

depends on the desired system output and

can for example model measurement data.

3.1 Contract-based Robust Distributed

MPC

An important aspect for the control of safety-critical

systems is to compute inputs that are robust against

uncertainties by ensuring that the constraints are ful-

ﬁlled in all possible cases. To this end, (Lucia et al.,

2013) propose a multi-stage scheme for robust MPC

that assumes a discrete set of possible scenarios and

Resilient Control of Interconnected Microgrids Under Attack by Robust Nonlinear MPC

represents all potential future states in a scenario tree.

Taking into account that in a closed-loop approach fu-

ture inputs can be adapted when new measurements

are available, they compute control inputs that achieve

constraint satisfaction in all scenarios and minimize a

cost function weighted over all scenarios.

Robust MPC can be employed to design also dis-

tributed MPC schemes since in a distributed setting

as in eq. (4), to the eyes of subsystem i, the neigh-

boring couplings z

behave in an uncertain manner.

Since multi-stage MPC requires knowledge about the

range of possible values for each uncertain quantity,

(Lucia et al., 2015) introduce so-called contracts Z

that contain predicted reachable values of the cou-

pling variables z

and are exchanged among neigh-

bors. In (Braun et al., 2020), approximations of these

contracts are proposed that can efﬁciently be obtained

from local scenario trees and have been proven to

work well in practice.

To apply multi-stage (distributed) MPC for robust

control also against attacks, one has to provide suit-

able uncertainty sets A

with possible values for local

attacks a

. To this end, one can choose suitable sam-

ples for attack values as in (Braun et al., 2020), or in a

more general approach use available knowledge about

the attackers gained from attack identiﬁcation. The

latter approach is introduced in (Braun et al., 2021a)

and summarized in Section 3.3.

3.2 Attack Identiﬁcation based on

Sparse Optimization

Robust MPC schemes provide an important tool to

manage the impact of a potential attack. Neverthe-

less, when an attack occurs, it is crucial to detect and

identify it quickly to initiate appropriate countermea-

sures in order to eliminate the attacker or mitigate

its impact. To avoid the combinatorial nature that

is inherent to most identiﬁcation methods relying on

unknown-input observers, one can solve a continuous

optimization problem to compute a suspected attack

from an unknown, possibly inﬁnite dimensional and

unbounded set of potential attacks. Taking advantage

of the observation that typical attacks in practical ap-

plications target only few network components, the

optimization reveals a sparsest possible attack that ex-

plains the observed system output.

In (Braun et al., 2021b), this idea is implemented

in a global ADI method with rigorous success guaran-

tees for nonlinear networked systems. Since in a dis-

tributed setting, model information about the subsys-

tems’ dynamics is available only locally and should

remain private, a linear approximation of the dynam-

ics at the current iterate is used for identiﬁcation. To

this end, each subsystem locally evaluates ﬁrst-order

derivatives and makes them publicly available. Then,

a global linear optimization problem is solved to iden-

tify a sparse suspected attack.

In this paper, we propose a novel identiﬁcation

problem for local attack identiﬁcation, which is also

based on sparse optimization. Since no information

on local dynamics is published in this decentralized

approach, the linearization from above is no longer

necessary. Instead, each subsystem locally solves the

following nonlinear identiﬁcation problem with mea-

surements

, and

of the output y

, the state x

and the neighboring couplings z

min

s.t.



− g

◦ f

(

+ a

)



≤ ε

(5)

where the ◦-operator denotes the function composi-

tion of g

and f

. A solution of problem eq. (5) locally

reveals a suspected attack, referred to as a

∗

, based on

which the local model in eq. (4) with functions g

, f

explains the observed output

up to an accuracy of

. The choice of the tolerance ε

is not trivial, even

if perfect measurements were assumed, since the dis-

tributed model in eq. (4) only approximates the dy-

namic behavior of the global system. More specif-

ically, the coupling variables z

in the local mod-

els represent differential states of neighboring subsys-

tems, but their dynamic behavior is unknown to sub-

system i. In ongoing research, we investigate how dif-

ferent parametrization schemes of the coupling vari-

ables inﬂuence the resulting error between centralized

and distributed numerical integration. Based on this

error, a suitable value ε

can be chosen. In the numer-

ical experiments in this work, we use a ﬁxed value,

which is given in Section 4.

3.3 Attack Mitigation using Adaptively

Robust MPC

In the previous sections, two important tools for dis-

tributed control systems under attack have been intro-

duced: For one thing, robust MPC can limit the im-

pact of a disturbance by ensuring satisﬁed constraints

in all scenarios, but requires information about the

uncertainty range. For another thing, attack identi-

ﬁcation provides suspicions about an attack, but is

not able to mitigate its effects. To combine the ad-

vantages of both, an adaptively robust MPC scheme

was proposed in (Braun et al., 2021a). It repeatedly

adjusts the uncertainty sets A

that involve possible

attacks a

at time k according to ﬁndings from attack

identiﬁcation. The method is designed for attacks that

obey a probability distribution with unknown, time-

invariant expected value µ and standard deviation σ,

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

which are estimated at each time k from solutions a

∗,l

of the identiﬁcation problem in earlier times l ≤ k.

The mean µ

and the sample standard deviation σ

all previously identiﬁed values a

∗,l

serve as estimates

for µ and σ according to

k + 1

∑

l=0

∗,l

and

∑

l=0



∗,l

− µ



The uncertainty of possible attacks a

is now repre-

sented by three scenarios for each component a

,µ

+ σ

,µ

− σ

. (6)

The total amount of scenarios considered in the multi-

stage control scheme results from the product of all

uncertainty sets A

for each identiﬁed component a

The interplay of all methods presented in Section 3 is

summarized in Algorithm 1.

Algorithm 1: A resilient control framework.

Input: Initial contracts Z

∀i, e.g., Z

= {h

(0))}

1: Set A

= {} ∀i

2: for time step k and microgrid i do

3: Set up local multi-stage problem and compute

input u

, robust against Z

k−1

and A

k−1

4: Derive new contract Z

and transmit to all

neighbors j ∈ N

5: Local ADI: Solve problem (5) to obtain a sus-

picion a

∗,k

6: Locally adapt uncertainty set A

as in eq. (6)

7: end for

4 NUMERICAL EXPERIMENTS

In this section, we perform a numerical case study to

analyze how economic dispatch for microgrids can

be achieved at minimum cost despite possible dis-

turbances, using the methods from Section 3. We

consider three microgrids with renewable generation

that may be exposed to attacks, each connected to the

other microgrids and the main grid as in Figure 1. Ac-

cording to Section 2, each microgrid i ∈ {1,2,3} is

modeled by ﬁve states s

, p

i j

and four control

inputs u

i j

for j ∈ {1,2,3} \ {i}. For all vari-

ables v

∈

, p

i j

, the initial val-

ues v

(0) and lower and upper bounds v

and v

are

Table 1: This table lists all model and cost parameters, vari-

able bounds, and initial values that are used in all experi-

ments presented in this work.

Parameters Values Unit

, T

i j

∀i, j 0.1, 0.001, 0.001 h

100, 200, 100 kAh

1.5, 2.0, 3.0 mΩ

∀i 2.23, -0.001 V

∀i -0.35, 0.6851 V

∀i

3.0, 1.6 -

0.2, 3.0, 2.0 -

dis

∀i

4.0, 1.0, 2000 -

ﬂow,im

i j

ﬂow,ex

i j

∀i, j 4.0, 0.04 -

, p

i j

∀i, j 0, 0, -1000, -100 -, kW

, p

i j

∀i, j 1, 1000, 2000, 100 -, kW

i j

∀i, j 0, -1000, -100 kW

i j

∀i, j 1000, 2000, 100 kW

(0),s

(0) 0.9, 0.5, 0.6 -

(0), p

(0) ∀i 0.0, 0.0 kW

i j

(0) ∀i, j 0.0 kW

∀i -2.0 kW

given in Table 1, which also contains the values of

all model parameters as in Section 2. The param-

eters A

, and N

in the model for open

circuit voltage by (Zhang et al., 2016) are chosen fol-

lowing their suggestion for LTO-batteries. During a

time window of two days, each microgrid locally ap-

plies MPC with step size 0.25h. At time t ∈ [0, 48] h,

the local cost function J

considers the time win-

dow [t,t + N

] with prediction horizon N

= 6 h and is

designed as in Section 2.4 with cost parameters from

Table 1. The values C

m,im

and C

m,ex

, that describe the

cost or revenue of power imports from or exports to

the main grid, vary in the course of the day. For all

microgrids i, we use the following ﬁctitious values,

which reﬂect typical market ﬂuctuations with rising

prices in the morning and evening hours, based on real

prices by (Bundesnetzagentur Deutschland, 2021):

m,im

(t) =











275 if t % 24 h ∈ [15,20)h,

200 if t % 24 h ∈ [6,9) ∪ [20,22)h,

150 if t % 24 h ∈ [9,15) ∪ [22,24)h,

100 otherwise,

m,ex

(t) =











15 if t % 24 h ∈ [15,20)h,

10 if t % 24 h ∈ [6,9) ∪ [20,22)h,

0 otherwise.

Resilient Control of Interconnected Microgrids Under Attack by Robust Nonlinear MPC

Here, % denotes the modulo operator and t %24h

indicates the time of day. One possible strategy

to maximize revenue is to store energy at times of

low prices for later export. Toward a resilient op-

eration, the system is controlled using the adap-

tively robust distributed MPC scheme described in

Algorithm 1. Based on the local control problems,

each microgrid computes contracts Z

for its cou-

pling variables z



i j



j∈N

at each time k and

shares them with its neighbors. To locally identify

the unknown attack, a nonlinear optimization prob-

lem of the form (5) is solved at each sampling time

to an accuracy of ε

= 10

−3

. Only partial observ-

ability of the states x



, p

i j

, p



with

) = diag(1, 1, 1, 0, 0)x

is assumed. That means,

for each microgrid i the outputs y

= (s

, p

)

are

considered by the local identiﬁcation process, but not

the transfer variables p

i j

, p

. Based on the suspected

attacks a

∗,k

, we approximate the uncertainty sets A

as in eq. (6). The local control problems are repeat-

edly adapted to new contracts and identiﬁcation re-

sults that become available in course of time. As a

consequence, the computed inputs at time k + 1 are

robust toward neighboring couplings in Z

and iden-

tiﬁed attacks in A

. For comparison, we repeat each

experiment with non-robust distributed MPC, where

neither contracts are exchanged nor attack identiﬁca-

tion is considered.

We examine the behavior of the system in two

attack scenarios, each with adaptively robust versus

non-robust control. First, we assume that all genera-

tion units are dispatchable and an attack a

= 10 kW

disturbs the generator dynamics in microgrid 1 as in

eq. (3). Later we will also consider uncertain re-

newable generation. The attack is present over the

entire time window [0,48]h and causes the gener-

ated power p

in the attacked microgrid to deviate

strongly from the control input u

, see Figure 2. The

local ADI method successfully identiﬁes the attack

in every time step, computing suspected attack val-

ues a

g,∗

≈ 9.9989, which allows the adaptively robust

MPC scheme to adjust its prediction. As a result, the

control inputs are adapted and the microgrid makes

use of the additionally generated power by storing it

into the battery and exporting it to the main grid dur-

ing times with high proﬁt. In contrast, in the solution

computed with non-robust MPC, the battery reaches

and violates its maximum state of charge of 1 af-

ter about 5 h, see Figure 2. This is because due to

the attack, more power than planned is generated and

charged into the storage to maintain power balance.

Since SoC values larger than 1 are invalid, the next

State of chargeGenerated powerImp./exp. powerTransferred power

1.00

0.96

0.92

0.88

-10

-20

-30

2.0

1.5

1.0

0.5

0.0

robust

non-robust

Time in hours

0 12 24 36 48

Figure 2: Selected state and input trajectories for micro-

grid 1 that is exposed to a generator attack, all powers

in kW. The different SoC trajectories, computed by adap-

tively robust versus non-robust MPC, show the beneﬁt of

the proposed resilient control framework.

MPC step starts with s

= 1, but as the attack is not

identiﬁed, the full battery continues to be charged, re-

sulting in bound violations in 171 of 192 steps.

It should be mentioned that power balance can

be ensured in other ways than using the storage as

a buffer. If power exchange with the main grid

is allowed at all times, using the main grid as a

buffer would not cause bound violations like the

above. However, this may result in very high costs

if, for instance, power has to be imported at ex-

pensive prices in the evening. The battery, on the

other hand, allows to store power until exports to the

main grid become proﬁtable. Indeed, over the en-

tire time window, robust MPC achieves total costs

of −5.2 · 10

, thus making proﬁt despite the attack,

while non-robust MPC yields total costs of 2.3 · 10

being orders of magnitudes larger.

In the second experiment, we modify the genera-

tor attack to a

= 10 kW + r

with renewable gener-

ation r

∼ N (0,8)kW, randomly drawn from a nor-

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

Actual attack a

Identiﬁed mean µ

Sample std. dev. σ

Time in hours

0 12 24 36 48

Disturbance a

in kW

-10

Figure 3: Course of the mean µ

of identiﬁed values a

∗,k

over time, with sample standard deviation σ

. The actual

disturbance a

g,k

at each time k is shown in orange.

mal distribution with mean 0 kW and standard devi-

ation 8 kW, independently at each time. Attack and

renewable generation together may cause more gen-

erated power than planned (if a

> 0) or less (a

< 0),

but are chosen such that the total input u

+ a

nonnegative. Due to the continually changing values

for a

, the ADI method identiﬁes different values a

∗,k

at each time step, but as Figure 3 shows, the mean

value µ

quickly settles at around 10 kW. Due to the

ﬂuctuating uncertainty, the three scenarios in multi-

stage MPC are further apart than in the ﬁrst experi-

ment. Adaptively robust MPC computes a solution,

shown in Figure 4, with total costs of 3.1 · 10

that

is admissible for all scenarios, using the storage as a

buffer to cope with the uncertainty. The non-robust

approach again proves to be unsuitable to control the

disturbed system as it computes a solution that vio-

lates state bounds in 113 steps and causes more than

ten times higher total costs of 3.2 · 10

5 CONCLUSION AND OUTLOOK

We introduced a distributed model for microgrids that

are interconnected by dispatchable power transfers

and inﬂuence neighboring systems through coupling

variables. The model considers possible disturbances

in the form of input attacks or uncertain renewable

generation. We applied a previously presented re-

silient control framework, combining multi-stage ro-

bust MPC with optimization-based methods to iden-

tify unknown attacks. It is designed for distributed

systems, where each component has (only) access to a

local dynamic model and transmits information about

predicted coupling values to its neighbors. In numer-

ical experiments, the method has proven to be suit-

able for microgrids under attack, even if renewables

State of chargeGenerated powerImp./exp. powerTransferred power

1.00

0.95

0.90

0.85

0.80

-10

-20

-30

-40

1.5

1.0

0.5

0.0

-0.5

-1.0

robust

non-robust

Time in hours

0 12 24 36 48

Figure 4: States and inputs in microgrid 1, which now con-

tains renewable generation as another source of uncertainty

in addition to the generator attack.

cause additional uncertainty. We plan to extend ex-

isting ADI methods toward distributed identiﬁcation

schemes, where the exchange of suitable information

allows microgrids to identify not only local distur-

bances, but even attacks on neighboring microgrids.

ACKNOWLEDGEMENTS

This work was supported by the German Federal

Ministry of Education and Research (BMBF) via the

funded research project AlgoRes (01S18066B).

REFERENCES

Ananduta, W., Maestre, J., Ocampo-Martinez, C., and Ishii,

H. (2020). Resilient distributed model predictive con-

trol for energy management of interconnected micro-

grids. Optimal Control Applications and Methods,

41:146–169.

Arauz, T., Chanfreut, P., and Maestre, J. (2021). Cyber-

Resilient Control of Interconnected Microgrids Under Attack by Robust Nonlinear MPC

security in networked and distributed model predictive

control. Annual Reviews in Control.

Braun, S., Albrecht, S., and Lucia, S. (2020). Hierarchical

attack identiﬁcation for distributed robust nonlinear

control. In 21st IFAC World Congress, pages 6191–

6198.

Braun, S., Albrecht, S., and Lucia, S. (2021a). Adaptively

robust nonlinear model predictive control based on at-

tack identiﬁcation. Accepted for publication in at-

Automatisierungstechnik, preprint at https://tu-dortm

und.sciebo.de/s/w8IPet5jfxJaEaW.

Braun, S., Albrecht, S., and Lucia, S. (2021b). Attack iden-

tiﬁcation for nonlinear systems based on sparse opti-

mization. IEEE Transactions on Automatic Control.

early access.

Bundesnetzagentur Deutschland (2021). SMARD Strom-

marktdaten for Germany in November 2021. https:

//www.smard.de/home/downloadcenter/download-

marktdaten. Online, last accessed: November 18

2021.

Gallo, A., Turan, M., Boem, F., Parisini, T., and Ferrari-

Trecate, G. (2020). A distributed cyber-attack detec-

tion scheme with application to DC microgrids. IEEE

Transactions on Automatic Control, pages 3800–

3815.

Giraldo, J., Urbina, D., Cardenas, A., Valente, J., Faisal, M.,

Ruths, J., Tippenhauer, N., Sandberg, H., and Candell,

R. (2018). A survey of physics-based attack detection

in cyber-physical systems. ACM Computing Surveys,

51:76:1–76:36.

Lucia, S., Finkler, T., and Engell, S. (2013). Multi-stage

nonlinear model predictive control applied to a semi-

batch polymerization reactor under uncertainty. Jour-

nal of Process Control, 23:1306–1319.

Lucia, S., K

ogel, M., and Findeisen, R. (2015). Contract-

based predictive control of distributed systems with

plug and play capabilities. IFAC-PapersOnLine,

48:205–211.

Mathieu, J. and Taylor, J. (2016). Controlling nonlinear

batteries for power systems: Trading off performance

and battery life. In IEEE Power Systems Computation

Conference, pages 1–7.

Mayne, D., Seron, M., and Rakovi

c, S. (2005). Robust

model predictive control of constrained linear systems

with bounded disturbances. Automatica, 41:219–224.

Mohammed, A., Refaat, S., Bayhan, S., and Abu-Rub, H.

(2019). AC microgrid control and management strate-

gies: evaluation and review. IEEE Power Electronics

Magazine, 6:18–31.

Olivares, D., Mehrizi-Sani, A., Etemadi, A., Ca

nizares, C.,

Iravani, R., et al. (2014). Trends in microgrid control.

IEEE Transactions on Smart Grid, 5:1905–1919.

Pan, W., Yuan, Y., Sandberg, H., Gonc¸alves, J., and Stan,

G. (2015). Online fault diagnosis for nonlinear power

systems. Automatica, 55:27–36.

Pasqualetti, F., D

orﬂer, F., and Bullo, F. (2013). Attack

detection and identiﬁcation in cyber-physical systems.

IEEE Transactions on Automatic Control, 58:2715–

2729.

Wang, Y. and Ishii, H. (2019). A distributed model pre-

dictive scheme for resilient consensus with input con-

straints. In IEEE Conference on Control Technology

and Applications, pages 349–354.

Zhang, C., Jiang, J., Zhang, L., Liu, S., Wang, L., and

Loh, P. (2016). A generalized SOC-OCV model for

lithium-ion batteries and the SOC estimation for LN-

MCO battery. Energies, 9:900:1–900:16.

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics