
Statistical Analysis of Color Differences on Iris Images for Supporting
Cluster Headache Diagnosis
Inmaculada Mora-Jim
´
enez
1 a
, Andr
´
es Iglesias-Rojano
1
, Mohammed El-Yaagoubi
1 b
,
Jos
´
e Luis Rojo-
´
Alvarez
1 c
and Juan Antonio Pareja-Grande
2 d
1
Department of Signal Theory and Communications, Telematics and Computing Systems,
Rey Juan Carlos University, Madrid, Spain
2
Department of Neurology, Hospital Universitario Fundaci
´
on de Alcorc
´
on, Madrid, Spain
Keywords:
Iris, Color Space, Color Similarity, Cluster Headache, Histogram Matching, Cross-correlation, Kullback-
Leibler Divergence, Image Analysis.
Abstract:
It is well known the existence of certain headaches in humans caused by the sympathetic hypofunction, either
congenital or developed at birth. These pathologies, called cluster headaches, are physically manifested by
the change in texture, color and/or intensity of the iris eye on the painful side. The automatic study of these
variations would make it possible to provide quantitative measures of the existence of such pathology from
color images of the left and right iris of a particular individual. In this context, this work analyzes the color of
the left and right irises to identify chromatic differences between the irises belonging to the same individual by
analyzing three color spaces. The iris color distribution in the same eye has been studied, as well as the degree
of similarity and divergence between the chromatic distributions of irises in both eyes. Cross-correlation
between color feature vectors exhibited low detection capabilities, whereas a relative measure based on the
Kullback-Leibler divergence provided good performance to show color differences in the irises. No color space
was identified as the most appropriate for evidencing color differences in all the scrutinized cases. The results
obtained are promising on a dataset with eight patients, and can be considered a proof of concept on which
it is necessary to extend the analysis with a larger database. From a practical viewpoint, this characterization
could help to discriminate patients who attend the neurology department suffering from headache.
1 INTRODUCTION
The iris is the colored part of the eye located be-
tween the pupil and the ciliary zone. It has a set of
grooves, ridges, and pigmented regions, all of them
situated within a ring bounded in the inner part by
the pupil, in such a way that the light penetrating
in the eye is tuned and adjusted to different environ-
mental situations. The iris coloration is known to be
produced by the concentration of melanin, which se-
cretion depends on the sympathetic nervous system
(Wielgus and Sarna, 2005). There are many factors
contributing the eye color and its variation, with iris
patterns being unique for each person. This unique-
ness of the human iris is used in iris scans for per-
a
https://orcid.org/0000-0003-0735-367X
b
https://orcid.org/0000-0003-0189-6075
c
https://orcid.org/0000-0003-0426-8912
d
https://orcid.org/0000-0002-3260-3880
sonal identification, with lower error rates than those
obtained with face and fingerprint recognition (Sang-
wine and Horne, 2008). This is the reason for one of
the most widespread applications related with the iris
being biometry, as far as the probability of two iris be-
ing similar has been estimated as 1 to 10
72
, and also
taking into account that it remains stable throughout
our life. Biometric systems have been proposed from
the digital segmentation and analysis of iris images,
from the use of the Hough transform to Gabor filters,
and local versus global image windows, among many
others (e.g., see (Ma et al., 2003)).
On the other hand, the presence of abnormal iris
coloration or texture has been related to some dis-
eases. For instance, trigeminal autonomic cephalal-
gias belong to group III of the International Headache
Society, and they share the clinical features of pain
felt in the area supplied by the first division (V-1)
of the trigeminal nerve (Pareja et al., 1997). Clus-
40
Mora-Jiménez, I., Iglesias-Rojano, A., El-Yaagoubi, M., Rojo-Álvarez, J. and Pareja-Grande, J.
Statistical Analysis of Color Differences on Iris Images for Supporting Cluster Headache Diagnosis.
DOI: 10.5220/0011318700003289
In Proceedings of the 19th International Conference on Signal Processing and Multimedia Applications (SIGMAP 2022), pages 40-47
ISBN: 978-989-758-591-3; ISSN: 2184-9471
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

ter headache (CH) is the most usual of this kind of
cephalalgias, being predominant in male with onset
often in the 20s, and it is often accompanied with se-
vere unilateral, orbital or periorbital pain, with several
autonomic features. As summarized in (El-Yaagoubi
et al., 2020), a sympathetic hypofunction remains la-
tent and subclinical between attacks, but it can be
shown by provocative tests with eye-drop substances.
If there is a persistent but subtle and constitutional
sympathetic hypofunction in the symptomatic side,
the iris of that side is expected to be less pigmented,
and this can likely happen during the first years af-
ter birth. Accordingly, one of the signs of CH could
be different iris coloration in a patient’s eyes, and this
difference could be subtle and not always noticeable
by simple visual inspection. These previous works
propose that the screening and early detection of CH
could be addressed by creating biomarkers from sub-
tle color changes in the iris of both eyes from a given
patient.
The use of machine learning techniques has been
proposed for providing the clinicians with methods
detecting color differences between both eyes (El-
Yaagoubi et al., 2020), with promising results. An
alternative way to create new biomarkers using statis-
tical tools to characterize iris image distributions, is
proposed in the present work, given the vast amount
of existing methods devoted to biometry using the iris.
For instance, a system was delivered in (Demirel and
Anbarjafari, 2008) using color histograms as pixel
statistic feature vectors for recognition of irises in
order to perform cross correlation between the his-
togram of a given iris and those from available indi-
viduals in a database, in which the final assignation
was assigned by a majority voting scheme. Specifi-
cally, our main contribution here was to scrutinize the
raw statistical distributions of colors and their differ-
ences between the eyes of a given subject, using his-
tograms of the iris color components in several color
spaces and the Kullback-Leibler divergence for their
comparison. This can represent a principled input fea-
ture space in machine learning systems designed to
provide neurologists with biomarkers in CH.
The rest of the paper is structured as follows. First,
color spaces characteristics are summarized, in partic-
ular for RGB, HSI, and CIELAB model spaces. Then,
the color feature vectors are described, as well as
the approaches using cross-correlation and Kullback-
Leibler divergence, for their comparison. Next, the
dataset used in our experiments is described, and the
results of comparisons are subsequently presented.
Finally, conclusions are drawn and directions for fu-
ture research are highlighted.
Figure 1: Color Iris image, captured with a high resolution
camera (Zeiss FF 450 plus Fundus IE).
2 COLOR SPACES
Color is the way the Human Visual System (HVS)
perceives radiation from part of the electromagnetic
spectrum, approximately between the wavelengths of
300 nm and 830 nm (Tkalcic and Tasic, 2003). Fig-
ure 1 shows the eye image (sclera, iris and pupil) cap-
tured with a high resolution camera in the department
of neurology of Hospital Universitario Fundaci
´
on de
Alcorc
´
on in Spain.
In the field of Image Processing, a color model
is an abstract mathematical model specifying the way
in which colors can be represented as a set of num-
bers (Gonz
´
alez and Woods, 2007). Thus, color spaces
aim to facilitate the specifications of colors in some
standard way, by creating a coordinate system such
that each color is mapped as a point onto it.
Some color spaces are hardware oriented (cam-
eras, monitors, printers), while others are more ade-
quate for color processing. In digital image process-
ing, the RGB (red, green and blue) space is mainly
used for cameras and monitors, CMY (cyan, magenta
and yellow) for printers and HSI (hue, saturation and
intensity) which is closer to the human eye percep-
tion, is usually convenient for image processing and
analysis because it separates color and intensity in-
formation. In this line, the CIELAB space (luminos-
ity, red-green and yellow-blue) or CIE L ∗a ∗ b∗, gen-
erally called L ∗ a ∗ b∗, is also interesting because it
separates intensity and colors in a way more similar
as the HVS performs (differences in colors are uni-
formly perceived).
In this work, the RGB, HSI and CIELAB models
have been considered.
2.1 RGB
The RGB (Red, Green, Blue) color model is a sensory
model characterized by representing each color by its
three primary spectral components of red (R), green
(G), and blue (B) (Gonz
´
alez and Woods, 2007). This
model is based on the Cartesian coordinate system,
with the color gamut forming a cube, where each of
the main axes quantifies the proportion of red, green
Statistical Analysis of Color Differences on Iris Images for Supporting Cluster Headache Diagnosis
41
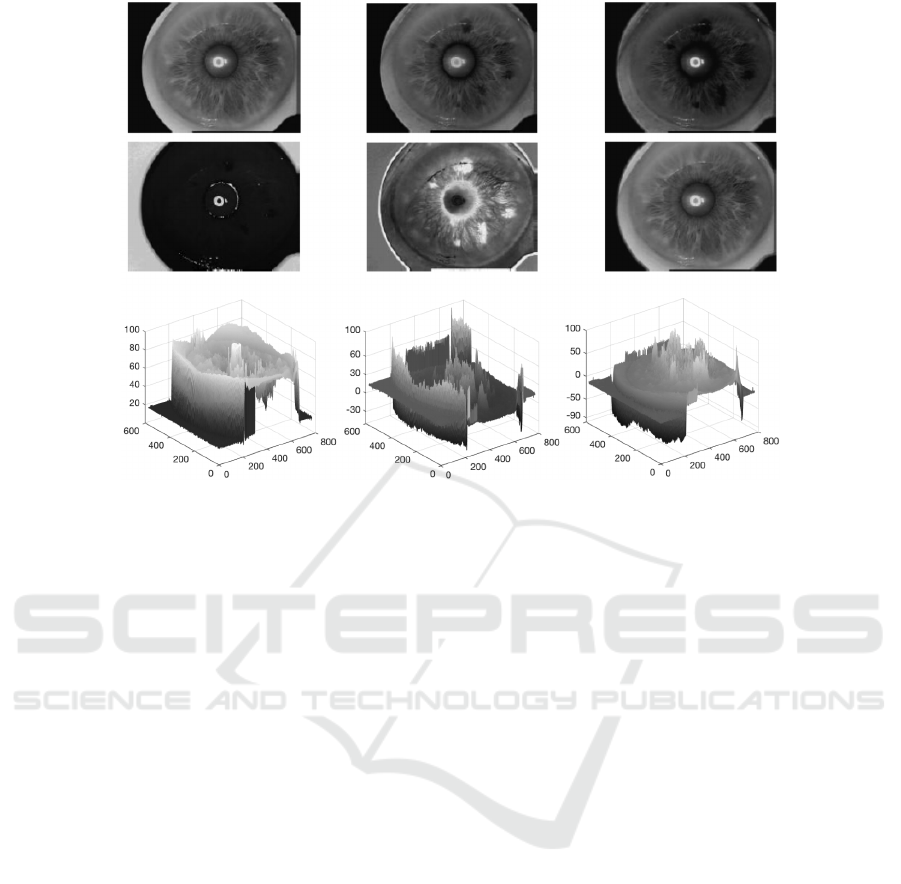
Figure 2: Color components of the image in Figure 1: upper panel (from left to right, R, G and B); middle panel (from left to
right, H, S and I); lower panel (from left to right, L∗, a∗ and b∗).
and blue light that has a specific color (Tkalcic and
Tasic, 2003). Thus, a color RGB image can be inter-
preted as a collection of three monochrome images,
one for each primary color. The upper panel in Fig-
ure 2 shows the R, G and B components associated
with the eye image displayed in Figure 1.
It is interesting to remark that the components in
the RGB color space present a high correlation be-
tween them, especially in natural images (Sangwine
and Horne, 2008).
2.2 HSI
Compared to the RGB model, the HSI model pro-
vides a more intuitive description of color for hu-
mans, describing color through three components;
hue (H), saturation (S) and brightness (I) (Gonz
´
alez
and Woods, 2007).
The HSI model, which decouples the intensity
component from the chromatic part (hue and satura-
tion), is defined through a non-linear transformation
of the RGB color space. This transformation modi-
fies the cube subspace of the RGB model, turning it
into two cones joined at their base. Geometrically,
the saturation component S corresponds to the radial
distance from the cone, quantifying the mixture with
white light. The component H describes the domi-
nant wavelength and is determined as the angle that
the particular color point makes with respect to the
angle of zero degrees (wavelength associated with a
red color). The range for H is [0, 360) degrees, with
an angular separation of 120 degrees between each
of the primary colors R, G and B. Lastly, the in-
tensity component I refers to the vertical axis of the
cones and incorporates achromatic information, with
low/high values of I corresponding to dark/light col-
ors. In general, both S and I take values in the interval
[0, 1], and H is usually normalized within [0, 1].
The middle panel in Figure 2 shows the H, S and I
components associated with the eye image displayed
in Figure 1.
2.3 CIELAB
The Commission Internationale d’Eclairage (CIE) is
a non-profit organization devoted to publish standards
related to science, technology and art in the fields of
light and lighting. In 1976, the CIE proposed the
CIELAB space to define a perceptually linear repre-
sentation of color, characterized by representing the
separation between colors proportionally to the visual
differences between them.
The L ∗ a ∗ b∗ components are obtained by apply-
ing a set of nonlinear transformations to the RGB
model (Sangwine and Horne, 2008), providing a sub-
space that corresponds to a sphere. The component
L∗ represents the brightness of the color and contains
the achromatic information. The range of variation
of L∗ is the interval [0, 100]: values close to 0 rep-
resent dark colors up to black, while high values in-
SIGMAP 2022 - 19th International Conference on Signal Processing and Multimedia Applications
42

dicate light colors up to white. On the other hand,
the a∗ and b∗ components can take positive and neg-
ative values, and define a measure of the amount that
certain color is magenta-green and yellow-blue, re-
spectively. For a better visualization of the a∗ and
b∗ components (potentially with negative values), a
three-dimensional representation has been chosen in
the lower panel of Figure 2 (the xy plane corresponds
to the spatial coordinates of the image).
3 STATISTICAL APPROACHES
FOR QUANTIFYING IRIS
COLOR DIFFERENCES
There are not two identical irises, including those of
twins and even the two irises of one and the same per-
son (Juniati et al., 2020). However, we are not inter-
ested in the iris texture pattern structure, mostly de-
termined by fibers, nerves and vessels. Instead, our
goal is to identify color differences in the eyes of the
same person, focusing on the global distribution of
the iris color. For this purpose, we consider the color
histograms (one histogram per color component) and
propose two techniques to quantify their differences.
3.1 Color Feature Vectors
The histogram of a monochrome image is a bar chart
representing the distribution of the pixel values in the
image (Gonz
´
alez and Woods, 2007). Each bar corre-
sponds to a group of values, determined by the width
of the bar (also named bin width), while the bar height
is the number of image pixels with values within the
bin. Regardless of the image size, values in the his-
togram are normalized to represent probability esti-
mations (calculated as relative frequencies).
Although the histogram discards information
about the spatial distribution of intensity levels, it is
a very useful tool in image analysis for image char-
acterization (Gonz
´
alez and Woods, 2007). Thus, his-
tograms allow the evaluation of image attributes such
as contrast and brightness. In general, a low con-
trast image will have the histogram bars clustered in
a narrow range, while an image with high contrast
will have a balanced histogram. In image process-
ing, histogram matching is used to transform the his-
togram of any image to a specific one. The histogram
equalization technique is a special case in which the
specified histogram is uniformly distributed. Though
we also consider histogram matching, our approach is
completely different, since no transformation is per-
formed, just a quantification of the similarity between
histograms to determine their matching degree.
The basis of our work is inspired by the biometric
recognition system proposed in (Demirel and Anbar-
jafari, 2008), where each color component of the iris
image is characterized by a feature vector F obtained
from the corresponding histogram. The length of F
depends on the number of considered bins. In color
images, a histogram is represented for each compo-
nent of the color model. Color histograms in this work
are computed only considering the pixels associated
with the iris (manually segmented from the whole im-
age).
Let us assume L bins in the histogram, denoted
as b
0
, b
1
, ··· , b
L−1
and uniformly distributed in the
whole range of the corresponding color component.
Considering the RGB model, three feature vectors
F
I
R
, F
I
G
and F
I
B
representing the the color histograms
of the image I, are obtained:
F
I
R
= [ f
I
R,b
0
, ··· , f
I
R,b
L−1
]
F
I
G
= [ f
I
G,b
0
, ··· , f
I
G,b
L−1
]
F
I
B
= [ f
I
B,b
0
, ··· , f
I
B,b
L−1
]
(1)
To make the iris characterization independent on
the image and iris size, note that each feature vector
can be normalized so that its L elements can be inter-
preted as probabilities.
3.2 Cross Correlation
In the signal processing field, cross-correlation allows
us to measure the similarity of two series as a function
of the displacement τ of one series relative to the an-
other one (Rabiner and Gold, 1975). Thus, the statis-
tical similarity between two images can be measured
by computing the cross-correlation between the his-
tograms of the respective images.
The authors of (Demirel and Anbarjafari, 2008)
propose to use the maximum absolute value of the
cross-correlation coefficient between the color his-
tograms of a given iris and those associated with indi-
viduals in a database for iris recognition. The idea is
to determine the identity of the individual as the one
in the database for which the maximum value of the
cross-correlation coefficient is obtained.
With a different approach, in this work we propose
to calculate the cross-correlation R between two fea-
ture vectors F obtained from histograms, see Eq.(1).
The feature vectors considered to compute R are as-
sociated with the same color component in each iris
(left and right, I
L
and I
R
) of the same individual I.
The mathematical formulation of cross-correlation is
dependent on the shift τ between sequences F
I
L
and
F
I
R
, as follows:
Statistical Analysis of Color Differences on Iris Images for Supporting Cluster Headache Diagnosis
43

Figure 3: Average cross-correlation between feature vectors of the R component when considering the left iris (left panels),
the right iris (middle panels) and the left and right iris (right panels) of two patients: healthy patient (upper panels) and patient
with CH (lower panels).
R(τ) =
∑
L+τ−1
k=0
( f
I
L
b
k−τ
−
¯
F
I
L
)( f
I
R
b
k
−
¯
F
I
R
)
r
h
∑
L−1
k=0
( f
I
L
b
k
−
¯
F
I
L
)
2
ih
∑
L−1
k=0
( f
I
R
b
k
−
¯
F
I
R
)
2
i
for τ < 0
∑
L−τ−1
k=0
( f
I
L
b
k
−
¯
F
I
L
)( f
I
R
b
k+τ
−
¯
F
I
R
)
r
h
∑
L−1
k=0
( f
I
L
b
k
−
¯
F
I
L
)
2
ih
∑
L−1
k=0
( f
I
R
b
k
−
¯
F
I
R
)
2
i
for τ ≥ 0
(2)
where
¯
F
I
L
and
¯
F
I
R
are the average values of sequences
F
I
L
and F
I
R
, respectively. The denominator in Eq. (2)
has a normalization effect in the series R(τ), so that
the cross-correlation values are within [−1, 1]. Note
that R(τ) = 0 indicates no correlation, while maxi-
mum correlation is obtained for |R(τ)| = 1.
When considering a specific color component C,
our hypothesis is that the maximum correlation value
between F
I
L
C
and F
I
R
C
should be centered at τ=0 (no
shift). This would show a similar distribution for the
C-th color component in both eyes (bin rates coin-
cide with respect to their positions). Note that this
statement would be true as long as the comparisons
are made with identical bin widths and positions be-
tween the two histograms. Therefore, when calculat-
ing the maximum cross-correlation value between the
eye feature vectors of a healthy patient, values close
to one should be obtained at τ=0. This would show
that both sequences have the same structure regarding
the distribution of the intensity levels in a particular
color component. For the case of patients with CH,
it is expected that the maximum value is obtained for
τ 6= 0.
For illustration, Figure 3 shows the average cross-
correlation as a function of the shift τ between se-
quences. Feature vectors linked to the histogram of
the R component of the two irises of the same per-
son have been considered for two cases: a healthy pa-
tient (upper panels) and a patient diagnosed with CH
(lower panels). The average is computed over four
disjoint subsets of pixels in the same iris image, as de-
tailed in Subsection 4.1. Note that the highest cross-
correlation value corresponds to τ = 0 when the his-
tograms of the same iris (left or right) are considered,
both for the healthy and for the patient with CH. How-
ever, when considering cross-correlation between his-
tograms of the left and right irises, the highest cross-
correlation value is located in τ = 0 for the healthy pa-
tient and in τ = −1 for the patient with CH. This result
shows statistical differences in the distribution of the
intensity levels of the red color component in the left
and right irises for the patient with CH. Though only
results for the R component are presented, similar out-
comes are obtained when considering components G
and B for these cases.
3.3 Kullback-Leibler Divergence
In contrast to cross-correlation, which measures simi-
larity between two probability distributions linearly,
the Kullback-Leibler Divergence or D
KL
(Kullback
and Leibler, 1951) provides a nonlinear measure of
the difference between two distributions.
Let be P and Q two probability distributions of
a discrete random variable with L possible values
in b
0
, ··· , b
L−1
, the Kullback-Leibler Divergence be-
tween P and Q is defined by
SIGMAP 2022 - 19th International Conference on Signal Processing and Multimedia Applications
44

D
KL
(P||Q) =
L−1
∑
i=0
P(b
i
)ln
P(b
i
)
Q(b
i
)
(3)
According to this measure, the closer the value of D
KL
is to zero, the more similar P and Q are. In our sce-
nario, P and Q correspond to two feature vectors as
those in Eq. (1).
4 EXPERIMENTS AND RESULTS
4.1 Image Dataset
A set of 16 iris images from 8 patients obtained in the
Ophthalmology Department of the Hospital Univer-
sitario Fundaci
´
on Alcorc
´
on (Madrid, Spain) is avail-
able. The high-resolution camera Zeiss FF 450 plus
Fundus IE, 768x576 pixels with 451 Visupac Digi-
tal version 3.2.1 digital file system was used. Im-
ages were taken under the same light conditions and
exposure parameters, counteracting the effect of the
flash by making the reflection on the pupil, trying
not to affect the iris brightness. The neurologist JA
Pareja-Grande performed the diagnosis of these pa-
tients, resulting in one healthy patient (HP), three pa-
tients who have some kind of pathology affecting the
iris color but it is not confirmed that such pathology
is CH (DP1, DP2 and DP3), and four individuals with
confirmed diagnosis of CH (CHP1, CHP2, CHP3 and
CHP4). Figure 4 and Figure 5 display the irises of
each patient in the study.
The iris segmentation is manually performed by
removing pupil and sclera. Subsequently, for a more
robust statistical analysis, the pixels of each iris are
separated into four disjoint subsets or patitions. Pix-
els for each partition were randomly distributed in
the iris, so that the values of cross-correlation and
Kullback-Leibler divergence presented in the follow-
ing tables are averaged.
4.2 Use of Histogram Cross-correlation
The average cross-correlation was computed consid-
ering each component of the three color subspaces.
Following the approach presented in Subsection 3.2,
just the healthy patient (HP) was correctly identified
by using the cross-correlation of each of the nine
color components. For patients identified as CHP2,
CHP3 and CHP4, the cross-correlation technique did
not identify color differences in any component of the
three color spaces. For the group of patients with no
confirmed CH diagnosis, cross-correlation of at least
one component of each color space revealed differ-
ences between both irises for two of the three patients
(DP1 and DP2) in Figure 4.
After analyzing these results, we concluded that
the histogram cross-correlation does not seem ade-
quate to identify most of the patients with CH in our
dataset. In fact, just the patient with the most evident
differences in the iris color (CHP1) is identified.
4.3 Use of Kullback-Leibler Divergence
We present now in Table 1 the average values of D
KL
computed when considering the same color feature
vectors as those in Subsection 4.2. Each row in Table
1 is associated with a color component, and each col-
umn refers to the D
KL
when considering probability
distributions (computed from Eq. (1)) within the same
eye and between both eyes of the same patient. Note
that the obtained values do not seem comparable be-
tween patients: for example, the D
KL
for the compo-
nent H when considering both irises of the healthy pa-
tient takes the value 0.01731, which is higher than that
associated with the component H of CHP1 (0.00384),
which in principle is contrary to our hypothesis (diver-
gence value closer to 0, more similar distributions).
Since there can also be significant differences
in absolute values when comparing estimates of the
mass probability function (obtained from the iris par-
titions) in the same iris, we propose to compute a rel-
ative measure. It is obtained by normalizing the D
KL
when considering feature vectors of both irises with
the D
KL
obtained using feature vectors of each of the
irises. The results are shown in Table 2 and Table 3,
i.e. two tables to consider all patients in our dataset.
As an example, the value 27.16 in the first column and
first row in Table 2 is obtained as the ratio between
0.00718 and 0.00026.
From Table 2, none of the D
KL
ratios exceeds two
orders of magnitude for the case of the healthy patient
(column HP). In contrast, for all patients with CH (Ta-
ble 3) there is always at least one component of the
three color spaces for which this ratio exceeds 100
(two orders of magnitude). For example, in the case of
CHP1, the RGB color space seems to be the most suit-
able for identifying differences between irises, with
high difference in the relative distributions between
irises for the the three components. The L ∗ a ∗ b∗
space seems best suited to show differences in the
case of CHP2, while only the component b∗ shows
a ratio greater than 100 (shown in bold). For CHP4,
the components H and S seem the least appropriate
for showing color differences in the irises. Again,
these two components offer the least relative differ-
ence for the patient DP3. It is interesting to remark
that, in general, patients with CH do not show in our
Statistical Analysis of Color Differences on Iris Images for Supporting Cluster Headache Diagnosis
45

Figure 4: Left and right iris images associated with: the healthy patient (left, identified as HP) and three patients with doubt
in the CH diagnosis (patients identified from right to left as DP3, DP2 and DP1).
Figure 5: Left and right iris images associated with patients diagnosed with CH, named: CHP1 (left), CHP2, CHP3 and CHP4
(right).
Table 1: Average D
KL
for each component of the RGB, HSI and L ∗ a ∗b∗ spaces when three patients are considered: HP, DP1
and CHP1. For each patient, only the left iris (column labeled “Left”), only the right iris (column labeled “Right”) and both
irises (column labeled “Both”) are considered.
HP DP1 CHP1
Left Right Both Left Right Both Left Right Both
R 0.00026 0.00059 0.00718 0.00086 0.00049 0.69376 0.00023 0.00024 0.20515
G 0.00036 0.00054 0.02151 0.00060 0.00067 1.58974 0.00014 0.00019 0.23238
B 0.00026 0.00059 0.02301 0.00039 0.00041 0.75488 0.00016 0.00019 0.26849
H 0.00109 0.00075 0.01731 0.00081 0.00056 0.13888 0.00044 0.00046 0.00384
S 0.00075 0.00084 0.05878 0.00061 0.00088 0.59718 0.00036 0.00047 0.19486
I 0.00084 0.00070 0.02580 0.00076 0.00071 1.24638 0.00042 0.00056 0.26411
L∗ 0.00024 0.00029 0.01895 0.00026 0.00032 1.15035 0.00022 0.00018 0.22983
a∗ 0.00011 0.00006 0.00172 0.00010 0.00004 0.61492 0.00001 0.00002 0.00102
b∗ 0.00010 0.00019 0.00281 0.00010 0.00006 0.04871 0.00006 0.00003 0.00558
Table 2: Ratio of the average D
KL
for each component of the RGB, HSI and L∗a∗b∗ spaces when four patients are considered:
HP, DP1, DP2 and DP3. For each patient and color component, the column labeled “Both/Left” contains the ratio of the
average D
KL
of both irises to that of the left irises, while column labeled “Both/Right” refers to the ratio of the average D
KL
of both irises to that of the right iris. Figures in bold indicate relative measures greater than 100.
HP DP1 DP2 DP3
Both/Left Both/Right Both/Left Both/Right Both/Left Both/Right Both/Left Both/Right
R 27.61 12.17 806.69 1415.83 270.32 273.66 1489.91 927.85
G 59.75 39.83 2649.57 2372.74 702.74 654.72 139.67 109.66
B 88.50 39.00 1935.59 1841.17 3027.95 2813.13 145.57 91.48
H 15.88 23.08 171.45 248.00 287.84 251.08 29.26 21.88
S 78.37 69.98 978.98 678.61 1858.27 1797.27 21.73 22.11
I 30.71 36.85 1639.97 1755.46 516.85 561.16 351.85 169.85
L∗ 78.95 65.34 4424.42 3594.84 604.06 667.40 616.42 416.77
a∗ 15.63 28.67 6149.20 15373.00 2779.63 2150.27 1577.93 1110.57
b∗ 28.10 14.78 487.10 811.83 3203.30 14092.98 2024.80 1589.49
(reduced) dataset the highest relative differences.
From the results, it could be concluded that inter-
mediate values of the proposed relative measure lead
to a clearer diagnosis of CH, while more pronounced
color differences (see results for DP1 and DP2) might
not be so closely related to the same stages of CH di-
agnosis, or even be related to other pathologies.
5 CONCLUSIONS AND FUTURE
WORK
In this work, we have addressed the suitability of the
cross-correlation series compared with the Kullback-
Leibler divergence in order to provide us with qual-
ity biomarkers for cluster headache. Whereas pre-
vious efforts had been devoted to design machine
learning schemes accounting for the differences in
SIGMAP 2022 - 19th International Conference on Signal Processing and Multimedia Applications
46

Table 3: Ratio of the average D
KL
for each component of the RGB, HSI and L ∗ a ∗b∗ spaces when the four patients diagnosed
with CH are considered. For each patient and color component, the column labeled “Both/Left” contains the ratio of the
average D
KL
of both irises to that of the left irises, while column labeled “Both/Right” refers to the ratio of the average D
KL
of both irises to that of the right iris. Figures in bold indicate relative measures greater than 100.
CHP1 CHP2 CHP3 CHP4
Both/Left Both/Right Both/Left Both/Right Both/Left Both/Right Both/Left Both/Right
R 891.95 854.79 384.47 355.80 20.01 21.03 575.23 306.46
G 1659.85 1223.05 235.53 115.95 24.80 21.25 1178.46 768.58
B 1678.06 1413.10 78.81 54.22 52.96 16.93 221.62 179.19
H 8.72 8.34 1351.64 267.01 29.01 28.05 28.18 43.88
S 541.27 414.59 136.11 98.56 20.50 18.61 83.89 96.73
I 628.83 471.62 545.83 525.34 17.53 23.45 654.68 418.55
L∗ 1044.68 1276.83 1135.23 401.34 17.36 35.80 1370.98 999.81
a∗ 102.00 51.00 692.14 454.07 8.43 12.84 135.49 196.85
b∗ 93.00 186.00 1048.50 518.60 135.27 222.59 984.58 1059.58
color of a given patient with direct representation of
color neighborhood of each pixel, here we focused on
building principled features based on color space his-
tograms.
Our results show that the difference between iris
coloration can be detected in terms of both luminance
and chrominance, as the color resulting from melanin
concentration is also dependent of brightness. In ad-
dition, cross-correlation based schemes seem to ex-
hibit low detection capabilities, whereas the relative
measure based on the Kullback-Leibler Divergence
seems to provide us with good results. That is, the
proposed procedure based on D
KL
provides moder-
ate fluctuations in healthy subjects, yielding increased
fluctuations in some (or even all) components of the
color spaces in the case of patients with CH.
The most evident limitation of our study is the re-
duced number of iris images, which also include pa-
tients with doubted diagnostic of CH. It is interesting
to remark that assembling this kind of images repre-
sents an additional workload for clinicians and hospi-
tal staff. In this sense, the present work evidences that
digital signal processing could provide us with suit-
able biomarkers for CH diagnosis and their use in the
clinical environment.
ACKNOWLEDGEMENTS
This work has been partly supported by the Spanish
Research Project PID2019-106623RB-C41.
REFERENCES
Demirel, H. and Anbarjafari, G. (2008). Iris recogni-
tion system using combined histogram statistics. In
Proceedings of the 23rd International Symposium on
Computer and Information. IEEE.
El-Yaagoubi, M., Mora-Jim
´
enez, I., Jabrane, Y., Mu
˜
noz-
Romero, S., Rojo-
´
Alvarez, J., and Pareja-Grande, J.
(2020). Quantitative cluster headace analysis for neu-
rological diagnosis support using statitical classifica-
tion. Information, 11(393):1–13.
Gonz
´
alez, R. and Woods, R. (2007). Digital Image Process-
ing. Pearson Prentice Hall, 3rd edition.
Juniati, D., Budayasa, I., and Khotimah, C. (2020). The
similarity of iris between twins and its effect on iris
recognition using box counting. Communications in
Mathematical Biology and Neuroscience, (90):1–13.
Kullback, S. and Leibler, R. (1951). On information
and sufficiency. Annals of Mathematical Statistics,
22(1):79–86.
Ma, L., Tan, T., Wang, Y., and Zhang, D. (2003). Personal
identification based on iris texture analysis. IEEE
Trans Pat An Mach Intel, 25:1519–33.
Pareja, J., Espejo, M., Trigo, M., and Sjaastad, O.
(1997). Congenital horners syndrome and ipsilateral
headache. Funct. Neurol., 12:123–31.
Rabiner, L. and Gold, B. (1975). Theory and Application of
Digital Signal Processing. Prentice Hall.
Sangwine, S. and Horne, R. (2008). The Colour Image Pro-
cessing Handbook, chapter 4, pages 67–90. Chapman
and Hall.
Tkalcic, M. and Tasic, J. (2003). Colour spaces: Perceptual,
historical and applicational background. In The Re-
gion 8 EUROCON 2003. Computer as a Tool. IEEE.
Wielgus, A. and Sarna, T. (2005). Melanin in human irides
of different color and age of donors. Pigment Cell
Res., 18:454–64.
Statistical Analysis of Color Differences on Iris Images for Supporting Cluster Headache Diagnosis
47
