Practical Formation Acquisition Mechanism for Nonholonomic

Leader-follower Networks

Kader Monhamady Kabore

and Samet G

uler

Dept. Electrical and Electronics Eng., Abdullah G

ul University, Barbaros, Kayseri, 38080, Turkey

Keywords:

Multi-robot Formation Control, Directed Graphs, Convolutional Neural Networks.

Abstract:

A grand challenge lying ahead of the realization of multi-robot systems is the lack of an adequate coordina-

tion mechanism with reliable localization solutions. In some workspaces, external infrastructure needed for

precise localization may not be always available to the MRS, e.g., GPS-denied environments, and the robots

may need to rely on their onboard resources without explicit communication. We address the practical forma-

tion control of nonholonomic ground robots where external localization aids are not available. We propose a

systematic framework for the formation maintenance problem that is composed of a localization module and

a control module. The onboard localization module relies on heterogeneity in sensing modality comprised of

ultrawideband, 2D LIDAR, and camera sensors. Particularly, we apply deep learning-based object detection

algorithm to detect the bearing between robots and fuse the outcome with ultrawideband distance measure-

ments for precise relative localization. Integration of the localization outcome into a distributed formation

acquisition controller yields high performance. Furthermore, the proposed framework can eliminate the mag-

netometer sensor which is known to produce unreliable heading readings in some environments. We conduct

several realistic simulations and real world experiments whose results validate the competency of the proposed

solution.

1 INTRODUCTION

There has been a long-standing interest in multi-robot

systems (MRS) to address complex tasks beyond the

ability of a single robot. While equipping a single

robot with excessive load and highly capable sen-

sor suits could be a viable option, swarming offers

a promising direction to handle challenging applica-

tions. A recent survey highlights the advances in

aerial swarms for critical tasks such as security and

surveillance, collaborative transportation, and envi-

ronment monitoring (Chung et al., 2018; Almadhoun

et al., 2016; Abdelkader et al., 2021). For instance,

in a dramatic search and rescue operation, a group of

drones can rapidly map and provide insights about an

area which may be hard to access (Tian et al., 2020).

In addition, multiple agents can easily operate in envi-

ronments which can be dangerous for humans. For in-

stance, an aerial robot team can inspect safely electri-

cal power lines or wind turbines (Silano et al., 2021).

Therefore, MRS will positively impact multiple work

ﬁelds. However, it is worth noticing that a safe re-

https://orcid.org/0000-0001-5388-9649

https://orcid.org/0000-0002-9870-166X

alization of these applications with MRS entails to

solve challenges in several subﬁelds such as forma-

tion control and multi-agent localization. Decades of

research have contributed to these ﬁelds, yet there is

still a long road ahead to reaching a complete decen-

tralized MRS.

On the formation control side, several studies have

focused on maintaining the desired shape pattern.

References (Anderson et al., 2008; Oh et al., 2015)

summarize various techniques on the formation ac-

quisition using the distances between agents only. In

the same direction, the authors of (Zhao and Zelazo,

2019; Trinh et al., 2018) demonstrate control laws

based on the bearing vectors among agents. Various

stable and convergent algorithms have been proposed

for single- or double-integrator kinematic agents in

primitive simulation environments by assuming al-

most perfect agent dynamics and sensing modalities.

However, these assumptions usually do not reﬂect the

real life experimental scenarios, particularly when the

robots employ onboard sensors only.

When it comes to localization, the primary ob-

jective is to design a decentralized system and lo-

calization methods without the reliance on infrastruc-

330

Kabore, K. and Güler, S.

Practical Formation Acquisition Mechanism for Nonholonomic Leader-follower Networks.

DOI: 10.5220/0011320200003271

In Proceedings of the 19th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2022), pages 330-339

ISBN: 978-989-758-585-2; ISSN: 2184-2809

tures such as Global Positioning System (GPS) or mo-

tion capture (mocap) cameras. Such infrastructures

can provide a MRS with positioning solutions with

millimeter-level precision. However, the MRS may

be desired to operate in critical environments, and the

positioning system should not stand as a barrier to

the operation. An agent should be able to maneuver

safely indoors and outdoors with the proposed local-

ization method. To address this challenge, previous

research have proposed to use additional markers as a

pattern for relative localization. The study in (Saska

et al., 2017) illustrates that a circular marker with

a predeﬁned diameter can be used with a ﬂood and

ﬁll image processing technique to estimate the rela-

tive position between two agents. Similarly, special

color markers could be placed on a speciﬁc agent to be

identiﬁed to extract the relative positions between the

agents (Fidan et al., 2012; Lin et al., 2020). Likewise,

this work (Walter et al., 2018) introduces ultraviolet

(UV) instead of markers and uses a UV recognizable

camera to process the blinking signals and compute

the relative positions. The marker approach is proven

effective to identify the relative location but offers a

solution solely constrained by the unique design of

the marker. Additionally, this approach scales poorly:

When the number of agents increases, different pat-

terns need to be presented to identify each agent in

the swarm (Saska et al., 2017; Fidan et al., 2012).

A novel approach presents an infrastructure-free

and completely onboard alternative for relative lo-

calization for a leader-follower scheme (Guler et al.,

2020; Nguyen et al., 2020). The follower is equipped

ultrawideband (UWB) sensors with known position

and estimates its relative position to a leader with a

single UWB sensor. The UWB distance measure-

ments are fused in a ﬁltering algorithm to extract an

estimate of the relative position. Besides range sen-

sors, cameras and the prospect of vision have been

implemented as well (Kabore and G

uler, 2021a; Ka-

bore and G

uler, 2021b; Liu et al., 2018). The authors

in (Vrba and Saska, 2020) apply a convolutional neu-

ral network (CNN) model to detect a leader drone and

use the camera intrinsic parameters to project the ob-

ject from 2D to 3D and obtain a moderate estimation

of the relative positions. These results demonstrate

the effectiveness of the distance and vision sensors

for reliable relative localization.

Currently, there is no generic practical localiza-

tion framework that can enable MRS to operate in

any environmental conditions. The proposed theo-

retical solutions usually remain insufﬁcient to reﬂect

the real-time characteristics of robotic systems. On

the other hand, most of the current practical solu-

tions rely on a central unit for computation and com-

munication among robots (De Queiroz et al., 2019;

Choi and Kim, 2021), which prevents to implement

further completely distributed formation control algo-

rithms. This work aims at proposing a relative local-

ization algorithm for MRS that does not depend on

a central computation unit and explicit communica-

tion among robots. Thus, the proposed solution al-

lows a distributed implementation of the entire sys-

tem. Particularly, we apply a heterogeneous sensing

model on three non-holonomic ground robots with

three sensor types, namely, UWB, camera, and 2D

LIDAR, which yields two sensing modalities. We im-

plement a CNN-based object detection to generate the

relative bearing between a group of robots. We show

that the heterogeneity of the sensing modalities leads

to high performance in the formation acquisition ob-

jective with the leader-ﬁrst follower-second follower

constraint graph. The main contributions of this work

are as follows:

• We propose a systematic framework comprising

a relative localization and distributed formation

control modules for MRS without explicit com-

munication and exchange of velocities between

robots.

• The proposed relative localization system with

heterogeneous sensing modalities relies on the on-

board units only, and no external infrastructure or

ground station is incorporated.

• We demonstrate the practicality of the framework

on a three-robot system in both realistic simula-

tions and real experiments.

• We propose a control method which eliminates

the magnetometer sensor which may perform un-

reliably in some environments.

The rest of the work is organized as follows. We

deﬁne our system model and the problem considered

in Section 2. We propose the localization and control

modules in Section 3 and Section 4, respectively. Sec-

tion 5 demonstrates the simulation and experimental

results, and Section 6 is on conclusions and future

works.

2 SYSTEM MODELING

In this section, we illustrate the mathematical model

of the robots used in our system, the underlying graph

in the network, and the main objective.

2.1 Preliminaries

We consider a swarm of non-holonomic ground

robots S = {R

, R

, ..., R

}, N ≥ 2. Each robot pos-

Practical Formation Acquisition Mechanism for Nonholonomic Leader-follower Networks

331

Figure 1: Illustration of agent R

and the frame constraints.

sesses the unicyle kinematics model as follows:

(t) = v

(t)cos(θ

(t))

(t) = v

(t)sin(θ

(t))

(t) = ω

(t) (1)

where x

, y

are the Cartesian coordinates and θ

(t)

is the heading angle of robot R

, v

and ω

are the

control inputs for linear velocity and the angular ve-

locity about the inertial z-axis, respectively (Fig. 1).

Each robot R

comprises onboard sensing and compu-

tational units, and the robots do not interact or com-

municate between each other or with a ground station

except for active sensing (e.g., distance sensing by ul-

trawideband (UWB) sensors).

The local sensing and communication interactions

among agents in a MRS can be described with a

graph. We deﬁne a leader-follower directed graph

G = (V, E) among the agents of the swarm S. Each

vertex i ∈ V represents an agent R

in S while each

directed edge

−−−→

(i, j) ∈ E from i to j implies the dis-

tance constraint d

between R

and R

. Particularly,

we constrain our study to the minimally persistent

graphs which are minimally rigid and constraint con-

sistent. Such a directed graph can be generated us-

ing the Henneberg construction method such that no

vertex has more than two outgoing edges (Anderson

et al., 2008).

Denote a formation framework F = (S, G, Q) for

the swarm S along with the underlying graph structure

G and the desired (constraint consistent) distance con-

ﬁguration Q = {q

−−−→

(i, j) ∈ E}. We assume a leader-

Figure 2: The underlying minimally persistent constraint

graph used in this work. The leader node v

has no dis-

tance constraint to satisfy whereas the ﬁrst follower node v

has one constraint and the second follower node v

has two

constraints.

ﬁrst follower formation such that vertex v

has no

outgoing edge, and thus it does not have any restric-

tion on the mobility. The vertex v

has one outgoing

edge toward v

which implies that it can reside at any

point on the circle with the center at v

and radius

(Fig. 2). Finally, each vertex v

, i ∈ {2, . . ., N }

has exactly two outgoing edges toward its leader set

{

i−2

, v

i−1

}

, which implies that it has two distance

constraints q

i−2,i

, q

i−1,i

to satisfy. The graph G con-

structed by this operation constitutes a minimally per-

sistent graph where the entire vertex set can move

up to translation and rotation as long as all distance

constraints in Q are satisﬁed. We assign robot R

the leader, R

as the ﬁrst follower, and the remain-

ing robots R

, i ∈ {2, . . ., N } as the second follow-

ers. Therefore, in the formation F = (S, G,Q), if the

follower robots R

, i ∈ {1, . . ., N } satisfy the distance

constraints q

∈ Q, the entire formation will move as

a whole forming the shape dictated by Q. Notably,

the underlying graph G does not depend on the robot

motion model. Indeed, the original rigid formation

control algorithms are designed for point agent kine-

matics, e.g., holonomic agents. Here, we will modify

these control algorithms to apply on non-holonomic

agents.

2.2 Problem Formulation

We formulate our main objective as follows. Consider

the swarm S = {R

, R

, ..., R

}, N ≥ 2, and the leader-

ﬁrst follower formation framework F = (S, G, Q) de-

ﬁned above. We assume that all agents in the swarm

rely on their onboard resources solely, there is no

ground station, and explicit inter-robot communica-

tion is not available. Particularly, robot R

is equipped

with a UWB anchor sensor whereas robot R

mounted with a monocular camera and a UWB sen-

sor. Each of the remaining robots {R

, ..., R

} is

equipped with a 2D LIDAR sensor. Thus, the sens-

ing mechanism of the robots consists of heterogene-

ity. The goal is to design (i) a relative localization

solution for the given system and (ii) a distributed

control law for the robots to converge from suitable

initial conditions to a desired formation conﬁguration

imposed by F = (S, G, Q). In the sequel, we consider

three-robot case (N = 2) as a prototype model not-

ing that the proposed framework is scalable to more

robotic agents. In Section 5 we discuss the practical

details for extension to more number of robots.

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

332

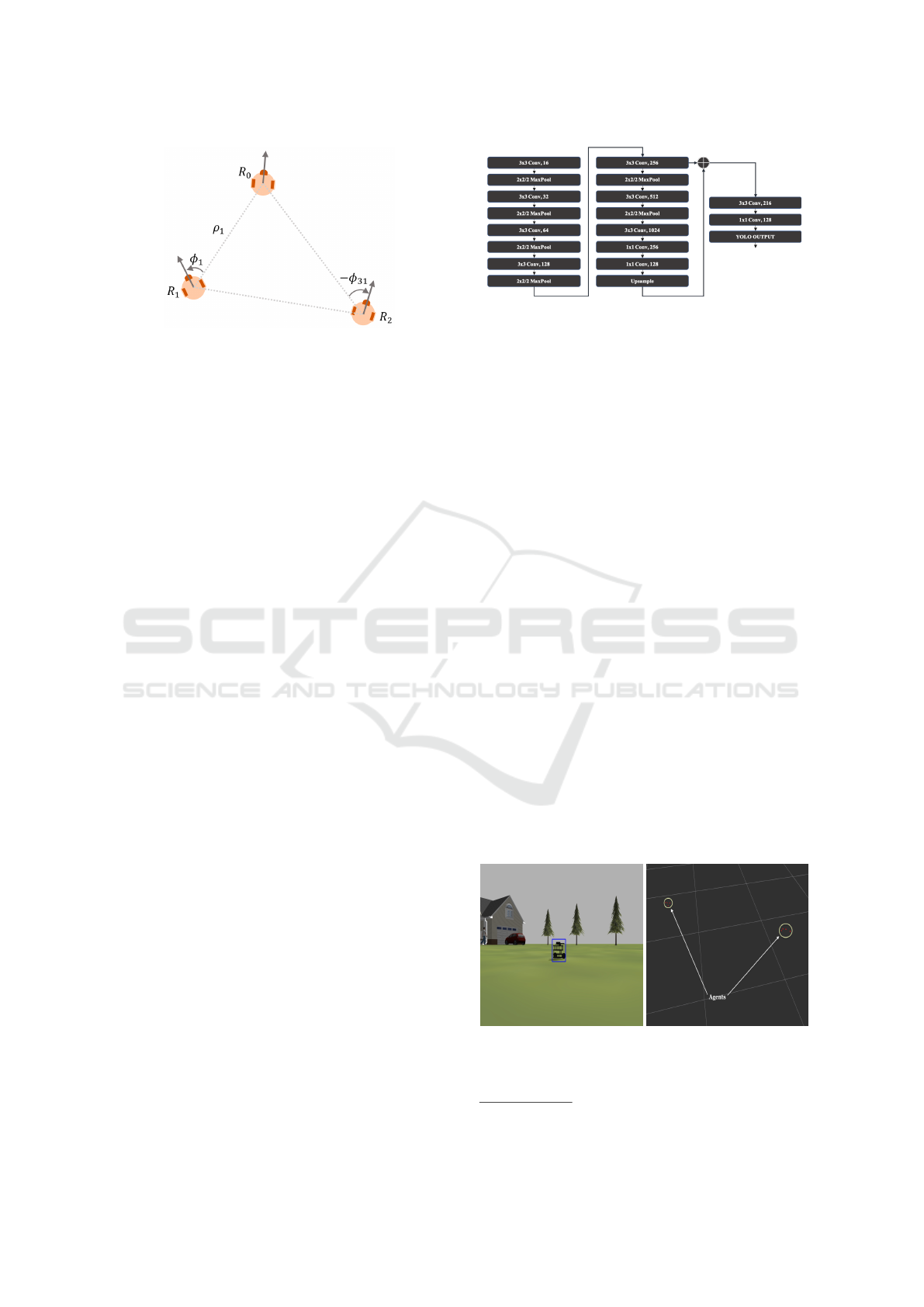
Figure 3: The top-view of three-robot system with the polar

dynamics variables.

3 SENSOR NETWORK

We now present the relative localization solution

and study the features of the sensors mounted on

the robots, namely ultrawideband (UWB) sensors,

monocular camera, and 2D LIDAR sensors. We

model the hybrid usage of these sensors in our local-

ization system which is solely dependent on onboard

sensors and does not exploit any external infrastruc-

ture.

Distance and vision measurements can be ex-

ploited in a complementarily and efﬁciently manner

to acquire the characteristics of the localized target.

Particularly, UWB sensors and cameras can act as

dual sensors to provide a solid framework for multi-

robot localization. On one side, UWB sensors op-

erate with high bandwidth capability and generate

accurate omnidirectional range measurements utiliz-

ing the time-of-ﬂight (TOF) method. On the other

side, a monocular camera empowered with the re-

cent advancements in computer vision and deep learn-

ing techniques can be applied for the visual detec-

tion of a leader robot by a follower robot. Partic-

ularly, by utilizing the convolutional neural network

(CNN)-based detection methods, one can accurately

extract a relative bearing between two robots. More-

over, since most commercial versions of these sensors

are lightweight, they can be implemented on many

unmanned ground vehicles (UGVs) and unmanned

aerial vehicles (UAVs) by maintaining feasibility.

We use a pair of UWB sensors, one anchor on

robot R

and one tag on robot R

, together with a

monocular camera on R

to provide an efﬁcient local-

ization system for the follower robot R

. We acquire

the distance q

between R

and R

from the UWB

sensors while the monocular camera is used to extract

the bearing angle φ

(Fig. 3).

Furthermore, we propose a CNN model to suc-

cessfully detect the leader robot R

with a monocular

camera on robot R

. Recently, deep learning tech-

Figure 4: The YOLO Tiny architecture used in the training.

niques have far surpassed the traditional computer vi-

sion methods. For instance, in a target tracking task,

the classical feature invariant extraction followed by

key point matching may not yield precise detection

results, particularly when the object is viewed from

only one angle and the sensor and the target object

are in motion (O’Mahony et al., 2019). In contrast,

CNN has been shown to be more effective in dynam-

ics scenarios. We particularly utilize the YOLO v3-

Tiny

, which is an improvement over the previous

CNN architectures such as Faster-RCNN (Ren et al.,

2015) and YOLO-v3 (Redmon and Farhadi, 2018)

with its remarkably light and robust structure adapted

for dynamic environments. Consequently, this net-

work is more suitable for real-time detection with on-

board limited resources. We redesign the structure of

the network to accommodate our single class output

and tune the network hyperparameters (Fig. 4). By

combining the UWB distance measurements with the

bearing data generated by the YOLO v3-Tiny detec-

tion, we generate the relative position p

in the body

frame of robot R

. The object detection module yields

bounding boxes of the detected objects, and the image

size can be extracted from the monocular camera. Us-

ing this intuition, we derive the relative bearing from

the target using the middle pixel of the bounding box

(Fig. 5a).

2D LIDARs offer a practical detection solution for

small-sized robots with limited payload and low en-

(a)

(b)

Figure 5: Simulation images captured in Gazebo: (a) De-

tection in the simulation environment, (b) 2D LIDAR active

localization of two agents from point clouds.

https://pjreddie.com/darknet/yolo/

Practical Formation Acquisition Mechanism for Nonholonomic Leader-follower Networks

333

ergy consumption. Moreover, since the motion capa-

bility of nonholonomic robots is restrained by nonlin-

ear constraints, large ﬁeld-of-view of the 2D LIDARs

provides a vital advantage on this type of robots.

Therefore, we opt for a 2D LIDAR sensor on the sec-

ond follower robots R

, i ∈ {2, ..., N}. A second fol-

lower robot R

is to maintain the distances toward its

leaders {R

i−2

, R

i−1

}. Thus, it calculates the relative

location toward {R

i−2

, R

i−1

} using the laser scan point

cloud and an iterative cluster algorithm. The aim is to

highlight the target agent within the range scan of the

sensor and ﬁnd the relative positions p

, p

in the

body frame of robot R

. We ﬁrst convert the raw scan

data to point cloud in 2D to differentiate the robots

, R

from the surroundings. Then we separate the

robots with a threshold found empirically to segment

the robot point clouds into clusters and eliminate the

remaining laser scans (Fig. 5b).

4 DISTRIBUTED FORMATION

CONTROL SCHEME

We have presented a relative localization system for

the robots to compute the relative position toward

the leader agents using onboard sensors. We aim

at putting these techniques into practice in two dis-

tributed formation control schemes. The ﬁrst exploits

the onboard fusion of odometer data to be able to con-

trol the swarm on a Euclidean plane whereas the sec-

ond generates a control mechanism to satisfy the re-

quirements on the relative quantities by excluding the

need for the magnetic sensing aids.

4.1 Generic Control Scheme

In contrast to the holonomic mobility, the agent model

(1) inherits nonholonomic constraints on the speeds.

Inspired by the control scheme of (Fidan et al., 2012),

we design our controller for the holonomic kinemat-

ics then convert the speed commands to a form which

can be applied in the nonholonomic model. Denote

the desired control input required to steer a holonomic

agent toward its desired location by u



, v



Then, one can adjust the nonholonomic control mech-

anism as follows:

(t) = v

(t)



cos(θ

(t)

sin(θ

(t)



, (2)

(t) = k

(θ

(t) − θ

(t)) +

(t), (3)

where k

< 0 is a proportional gain, θ

(t) =

atan(v

(t)/v

(t)) is the desired heading of robot R

atan(·) is the four-quadrant arc-tangent function, and











−

)

+ (v

)

if u

, 0

0 otherwise.

(4)

By using the relation in (2), that is ku

(t)k = v

(t), we

can choose the linear speed v

(t) as a proportion of the

desired speed for the holonomic agent, while the an-

gular speed can be directly used as in (3). The term

adds a derivative gain action effect in (3). However,

in our real experiments, we did not observe signiﬁ-

cant effect of the term

. Thus, we set

(t) = 0 in

our evaluations. We now derive the control inputs for

the three types of robots in the swarm.

Leader. Since out-degree of the leader robot R

two, it has two degrees of freedom for mobility and

is not conﬁned to any distance constraint toward any

other robot in the swarm. The leader is stationary dur-

ing a formation acquisition task. For ﬂocking tasks, it

can be assigned a constant control input.

First Follower. With the out-degree equals one,

robot R

is to maintain a desired distance toward

the leader R

. Since we use two sensing modalities,

which are UWB distance sensing and vision sensing,

robot R

is able to sense and control both distance

and bearing toward R

, which both maintains rigid-

ity and ﬁxes the formation orientation. We propose a

two-step control law as follows. Since the monocular

camera on robot R

is restrained on the ﬁeld of view

(FOV), it may not be able to detect the leader R

when

it is out of the FOV. In such a scenario, we rotate R

with constant angular velocity (and zero linear veloc-

ity) until it sees the leader within the range, assuming

that the initial distance between robot R

and R

al-

lows detection. Upon detection from the CNN model,

the robot R

moves to a point which satisﬁes the dis-

tance constraint d

= kp

− p

k. Denote the distance

error by

= kq

k − d

, (5)

and the relative position between robots R

and R



, p



, (6)

where p

and p

are respectively the relative dis-

placement on the x and y axes in the local frame of

. We propose the following control input for R

(t) = k

(t)z

(t), (7)

(t) = θ

(t) − φ

(t) + θ

o f f

, (8)

where k

< 0 is the proportional gain, φ

∈ [−π, π)

is the bearing angle derived from the object detection,

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

334

and θ

o f f

∈ [−π, π) is a constant value that represents

the offset between the robot body frame and the cam-

era frame. The offset parameter θ

o f f

allows the sen-

sor to have a different orientation than the robot body

frame.

Second Followers. The second follower robots

have two constraints in the constraint graph G. In

our three-robot system, the second follower R

tries

to maintain the distance constraints d

and d

to-

ward robots R

and R

. We use the following control

law for R

, i ∈ 2, . . ., N:

(t) = k

j ∈N

(9)

(t) =

j ∈N



(t) − φ

(t)



+ θ

o f f

(10)

where k

< 0 is the proportional gain, N

is the neigh-

bors of R

in the graph G, φ

∈ [−π, π) is the bearing

angle between R

and R

measured in the body frame

of the second follower R

, e

= kq

k − d

is the dis-

tance error, and

, p

(11)

is the relative position between R

and R

in the body

frame of R

4.2 Control Law without Magnetic

Sensing

In the previous section, we have derived a distributed

control mechanism for the three types of robots in the

MRS S. The control laws for robots R

and R

heavily

rely on the odometer data which is produced by fusing

the IMU and magnetometer measurements. However,

in some workspace environments, magnetometer sen-

sors can be affected by strong electromagnetic vari-

ations, thus the readings may be unreliable and have

low SNR. In such scenarios, the entire system may

yield poor localization and control performance. To

avoid this issue, one needs to derive the control laws

directly based on the exteroceptive sensors.

Assuming the leader robot R

is stationary, con-

sider the polar dynamics between robots R

and R

follows:

= −¯v

cos(φ

)

¯v

sin(φ

) + ω

(12)

where ρ

= kq

k and φ

= atan(x

− x

, y

− y

) is the

relative bearing angle (Fig. 3). Thus, the dynamics

(12) allows to control the distance and bearing an-

gle directly by adjusting the control inputs ¯v

, ω

the expanse of reducing the controllable degree-of-

freedom to two. Thus, the formation objective can

be achieved, but the robot cannot be steered to any

location on the plane. However, since formation ac-

quisition can be satisﬁed by setting only the distance

and bearing to their desired values, the dynamics (12)

remains a suitable model for our main objective. We

aim at devising a control law so that the distance and

bearing toward the leader converge to their desired

values.

We propose the following control law for the ﬁrst

follower:

¯v

= sat(K

|,0, v

), (13)

= sat(K

, −ω

, ω

where K

, K

, v

, ω

> 0 are design constants,

sat(a, ¯a, a) is a saturation function such that if a ≥ ¯a,

then a = ¯a, and if a ≤ − ¯a, then a = − ¯a, and

= ρ

− ρ

des

, e

= φ

− φ

des

with ρ

des

> 0 and φ

des

being the desired distance and

bearing values, respectively. If φ

(t) ∈

[

−π/2, π/2

)

the controller (13) steers R

toward the desired loca-

tion imposed by the constraints ρ

des

, φ

des

. We assume

that initially robot R

resides in the FOV of the camera

of robot R

. If such an initialization is not possible,

one can purely rotate R

with a constant angular ve-

locity in one direction until robot R

enters the FOV

of the camera of robot R

then apply (13) for forma-

tion acquisition. Thus, we expect that the robot con-

verges to its desired location, leaving the stability and

convergence analysis to future works.

5 EVALUATION

In this section, we demonstrate our CNN training ex-

perience and the results of our simulations and real

world experiments. Finally, we discuss the practical

aspects.

5.1 CNN Training

We trained an object detection model for each of the

simulation and real experiments. While standard ob-

jects can be found in the existing pool of dataset such

as COCO (Lin et al., 2014), we did not have a col-

lection of image dataset for our particular object of

interest, Turtlebot3. Therefore, we ﬁrst constructed

a dataset for the simulation and the real experiment.

We collected 337 images of the Turtlebot3 from the

simulation and 501 images from the real robot. Then,

we conducted the manual labeling process, i.e., as-

signing individual bounding boxes to the Turtlebot3

Practical Formation Acquisition Mechanism for Nonholonomic Leader-follower Networks

335

(a)

(b)

Figure 6: Sensors view in experiment: a) A detection from

Jetson nano: A view from R

, b) A scan from the LDS LI-

DAR seen by robot R

sections of the images. During the training phase, we

randomly split the dataset into the training, validation,

and testing sets. Then, we trained the network by se-

lecting the best observed hyperparameters, which are

a batch size of 64, a momentum of 0.9, and a learning

rate of 0.001. We obtained the ﬁnal results on the test-

ing set of mean average precision (mAP@75) of 96%

on the experiments, which enabled the high precision

during experimental tests. Sample detection images

from the CNN can be seen in Fig. 5a (simulation) and

6a (experiment).

5.2 Simulation

We simulated our proposed system in Gazebo, a re-

alistic and powerful environment that allows to vi-

sualize robotic systems with similar physical prop-

erties. We used three Turtlebot3 burger robots and

onboard sensors with the following speciﬁcations: A

monocular RGB camera with FOV of 2.45 radians on

and a 2D LIDAR with 360 FOV and a range of

6.28 meters on R

. We processed the LIDAR data us-

ing the point cloud package from robot operating sys-

tem (ROS) and used OpenCV

for post-processing the

YOLO model inference. We mimic the UWB sensor

measurements with the distance values obtained from

(a)

0 10 20 30 40 50

Time (s)

-2.5

-2

-1.5

-1

-0.5

0.5

1.5

(b)

Figure 7: Formation acquisition by expansion simulation:

a) Trajectories of the agents, b) the inter-robot distance er-

rors.

https://opencv.org/opencv-4-4-0/

(a)

0 10 20 30 40 50 60

Time (s)

-1.5

-1

-0.5

0.5

1.5

2.5

(b)

Figure 8: Formation acquisition by contraction simulation:

a) Trajectories of the agents, b) the inter-robot distance er-

rors.

Gazebo with added zero-mean Gaussian noise, i.e.,

(t) = ¯q

(t) + η

(t) where η

∼ N(0, σ

) with σ the

standard deviation.

In the simulations, we evaluated the setup for

two formation objectives: Contraction and expansion.

We used the generic formation control scheme us-

ing odometry data. These two key actions aimed at

demonstrating the ﬂexibility of the agents to adapt to

different scenarios independent of the initial condi-

tions. The ﬁrst assessment requires the robots to build

a formation with smaller relative distances than the

initial values whereas the second evaluation starts the

formation from a conﬁguration where the distances

are smaller than their desired values. The trajectories

and the relative distance errors are depicted in Fig. 8

and Fig. 7. We observed an exponential convergence

to the desired conﬁguration and fast decrement of the

distance errors e

. Also, we obtained a CNN detec-

tion rate greater than 90% on R

in all simulations,

which proved efﬁciency of the proposed localization

method.

5.3 Experiments

We performed a series of tests in an indoor lab envi-

ronment where GPS is not available. The three-robot

Figure 9: The robots and hardware used in the experiment.

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

336

system comprised a Turtlebot3 as the leader (R

) and

two Rosbots as the ﬁrst-follower (R

) and the second-

follower (R

), respectively (Fig. 9). We equipped the

robots with the sensor network explained in Section 3.

Particularly, we mounted a pair of DWM1001 UWB

modules on the leader and the ﬁrst follower to pro-

duce the relative distance between them. Also, we

mounted a CSI camera through an Intel Jetson Nano

computer on the ﬁrst follower for bearing detection.

We calibrated the camera to remove the distortions

and reduced the image size from (3280 × 2464) to

(416 × 416) which is the input to the CNN model.

This resizing operation eliminates the need for extra

pre-processing operations on the image before the de-

tection, and eventually, reduces the overall detection

time. With its GPU cores, Jetson Nano performed the

model inference using the accelerated TensorRT and

produced a detection speed of up to 60 ms which was

reasonable for our platform. Finally, we equipped the

second Rosbot with a 2D LDS LIDAR with the FOV

of 360 degrees and the maximum range of 3.5 meters.

We recorded the ground truth pose data of the robots

with a VICON motion capture system for illustration

purposes. The motion capture system data was not

used in any part of our algorithms.

We evaluated the proposed framework on the

three-robot system deﬁned above relying on their

onboard resources. The results of a contraction

experiment is illustrated in Fig. 10. In this ex-

periment, the robots were initiated from p

(0) =

[0.02, 0.62, 0.0]

meters, p

(0) = [1.14, −1.33, 0.0]

meters, and p

(0) = [−1.13, −1.41, 0.0]

meters with

different heading angles which are also denoted in

Fig. 10. Initially, the leader robot R

was not in the

FOV of the robot R

. Thus, R

ﬁrst rotated with

zero linear speed and waited for the leader to enter

its camera FOV. Once R

is detected with the CNN

at the 36th second, it started approaching R

based

on the control rule (7). On the other hand, robot R

segmented the LIDAR scans to generate clusters for

robots R

and R

. After building the clusters, robot R

generated the distance estimates q

, q

. We assumed

that initially the robots R

and R

were present within

the laser range. We depict a sample point cloud view

of the scans in Fig. 6b. There were nets on the left and

rear sides of R

which can be clearly seen in Fig. 6b,

which we removed with a simple pre-processing in

the algorithm. We observed that the robots converged

to the desired conﬁguration which are d

= 0.5 meters

for all i, j (Fig. 10b), and the error remained bounded

for sufﬁciently long time (around 400 seconds). We

conjecture that the relatively small error in the dis-

tances were due to the sensor noises. For instance,

the UWB distance readings from this experiment with

(a)

0 100 200 300 400

Time (s)

-1

(b)

Figure 10: Contraction experiment: a) Trajectories of the

agents, b) the inter-robot distance errors.

(a)

0 20 40 60 80

Time (s)

-1

(b)

Figure 11: Expansion Experiment . a) Trajectories of the

agents. b) The relative distance errors.

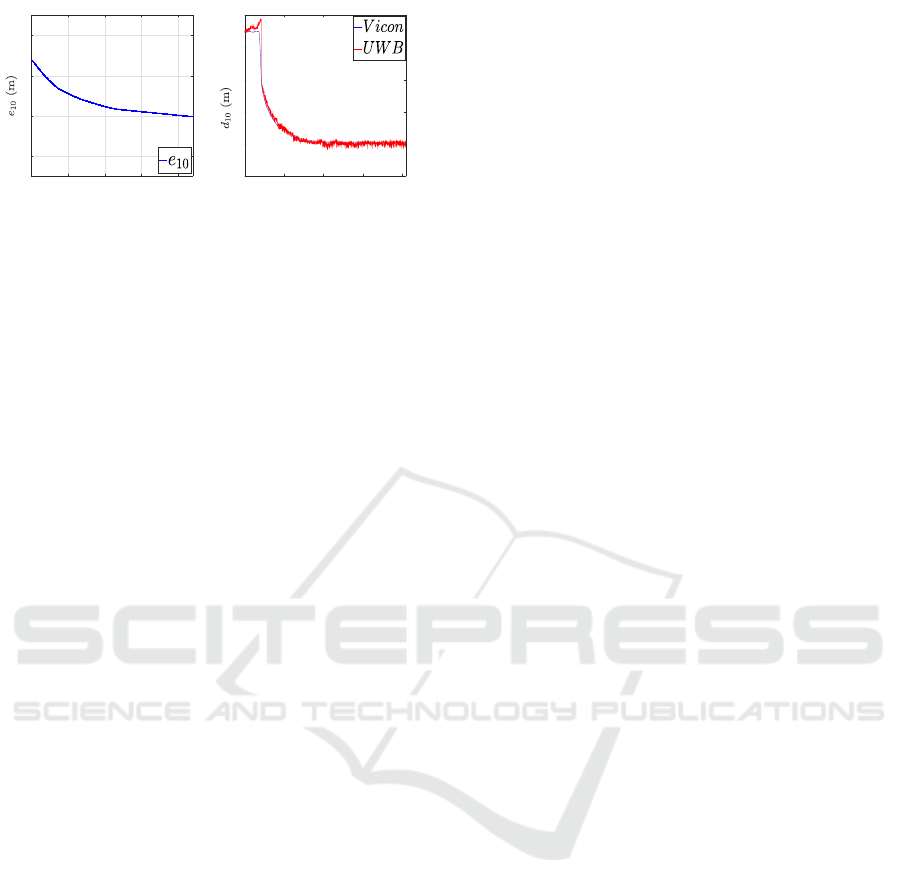
its ground truth are given in Fig. 12b, which shows a

noise with a variance of around 0.05 meters. Nev-

ertheless, the framework exhibited high performance

in terms of formation acquisition. A similar perfor-

mance can be seen in the formation expansion exper-

iment in Fig. 11.

Furthermore, we evaluated the case where the

magnetometer is not available for the ﬁrst follower

(Fig. 12a). In this experiment, robot R

used the

controller (13) and was able to converge toward the

desired conﬁguration. This result reﬂects the ﬂexi-

bilty of the proposed framework for magnetometer-

less settings. Although not presented here, another

controller which does not depend on magnetometer

sensor can be designed for the second follower robot

as well, which is one of our future objectives.

We now discuss some practical details which were

important when transitioning from simulations to ex-

periments. In our framework, the second follower

robot R

relies on LIDAR solely. However, when

LIDAR detects another object in the workplace, the

two clusters for localizing the robots R

and R

may

not be generated precisely, which may deteriorate the

performance. Therefore, we emphasize the assump-

tion that the workplace needs to be free of any other

object. If such a condition cannot be met, further

post-processing of LIDAR measurements would be

needed. Furthermore, although we have provided a

general framework for N + 1-robot swarms, we have

Practical Formation Acquisition Mechanism for Nonholonomic Leader-follower Networks

337

0 25 50 75 100

Time (s)

-1

(a)

0 100 200 300 400

Time (s)

0.5

1.5

2.5

(b)

Figure 12: a) The error on R

during a formation contrac-

tion without magnetometers, b) A Comparison of UWB

sensor data with ground truth from Vicon capture system.

focused on a three-robot setup in evaluations. When

there are more than one second-follower robots, i.e.,

when robots R

,i ∈ {3, . . ., N} are added to the sys-

tem, a more advanced LIDAR post-processing would

be necessary to discriminate the two leader robots for

each second-follower.

Moreover, although UWB sensors provide accu-

rate distance data in most environments, they may

generate low signal-to-noise ratio if not calibrated

properly. We suggest ﬁnding the correct bias and

noise variance values of the UWB sensors with a

proper calibration. In our experiments, we used a

basic calibration which requires to place the UWB

pair at locations with certain distances and collecting

data for a certain time. However, UWB distance mea-

surements may vary signiﬁcantly with varying angu-

lar placements of the sensors and ambient factors.

We emphasize the importance of UWB calibration for

more precise evaluations.

6 CONCLUSIONS

We have investigated the practical formation control

problem for MRS using onboard sensors. We have

proposed a systematic framework including a local-

ization module and a control module. The local-

ization module consists of a bearing angle deriva-

tion based on a YOLOv3-Tiny architecture with a

monocular camera and a systematic clustering for a

2D LIDAR. The control module consists of a set of

distributed formation control laws for three types of

robots in the leader-follower hierarchy. Furthermore,

we have proposed a control method which does not

use of a magnetometer sensor which is known to

generate unreliable sensor readings in some environ-

ments. We have evaluated the framework on non-

holonomic ground robots for the formation contrac-

tion and expansion objectives in both simulations and

experiments. The high performance obtained in a se-

ries of experiments indicates the applicability of the

proposed solution. Future research may include ex-

tension of the framework for dynamic path planning

and obstacle avoidance for the whole swarm using on-

board resources. Also, LIDAR data post-processing

to discriminate the leader robots in the FOV needs to

be studied to scale up the swarm size.

ACKNOWLEDGEMENTS

This paper has been produced beneﬁting from

the 2232 International Fellowship for Outstanding

Researchers Program of T

ITAK (Project No:

118C348). However, the entire responsibility of the

paper belongs to the owner of the paper. The ﬁnancial

support received from T

ITAK does not mean that

the content of the publication is approved in a scien-

tiﬁc sense by T

ITAK.

REFERENCES

Abdelkader, M., G

uler, S., Jaleel, H., and Shamma, J. S.

(2021). Aerial swarms: Recent applications and chal-

lenges. Current Robotics Reports, 2(3):309–320.

Almadhoun, R., Taha, T., Seneviratne, L., Dias, J., and Cai,

G. (2016). A survey on inspecting structures using

robotic systems. International Journal of Advanced

Robotic Systems, 13(6):1729881416663664.

Anderson, B. D., Yu, C., Fidan, B., and Hendrickx, J. M.

(2008). Rigid graph control architectures for au-

tonomous formations. IEEE Control Systems Maga-

zine, 28(6):48–63.

Choi, Y. H. and Kim, D. (2021). Distance-based forma-

tion control with goal assignment for global asymp-

totic stability of multi-robot systems. IEEE Robotics

and Automation Letters, 6(2):2020–2027.

Chung, S.-J., Paranjape, A. A., Dames, P., Shen, S., and

Kumar, V. (2018). A survey on aerial swarm robotics.

IEEE Transactions on Robotics, 34(4):837–855.

De Queiroz, M., Cai, X., and Feemster, M. (2019). Forma-

tion control of multi-agent systems: A graph rigidity

approach. John Wiley & Sons.

Fidan, B., Gazi, V., Zhai, S., Cen, N., and Karatas¸, E.

(2012). Single-view distance-estimation-based forma-

tion control of robotic swarms. IEEE Transactions on

Industrial Electronics, 60(12):5781–5791.

Guler, S., Abdelkader, M., and Shamma, J. S. (2020). Peer-

to-peer relative localization of aerial robots with ul-

trawideband sensors. IEEE Transactions on Control

Systems Technology, pages 1–16.

Kabore, K. M. and G

uler, S. (2021a). Deep learning based

formation control of drones. In Deep Learning for

Unmanned Systems, pages 383–413. Springer.

Kabore, K. M. and G

uler, S. (2021b). Distributed for-

mation control of drones with onboard perception.

IEEE/ASME Transactions on Mechatronics.

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

338

Lin, J., Miao, Z., Zhong, H., Peng, W., Wang, Y., and Fierro,

R. (2020). Adaptive image-based leader–follower for-

mation control of mobile robots with visibility con-

straints. IEEE Transactions on Industrial Electronics,

68(7):6010–6019.

Lin, T.-Y., Maire, M., Belongie, S., Hays, J., Perona, P.,

Ramanan, D., Doll

ar, P., and Zitnick, C. L. (2014).

Microsoft coco: Common objects in context. In Euro-

pean conference on computer vision, pages 740–755.

Springer.

Liu, X., Ge, S. S., and Goh, C.-H. (2018). Vision-based

leader–follower formation control of multiagents with

visibility constraints. IEEE Transactions on Control

Systems Technology, 27(3):1326–1333.

Nguyen, T.-M., Qiu, Z., Cao, M., Nguyen, T. H., and Xie,

L. (2020). Single landmark distance-based navigation.

IEEE Transactions on Control Systems Technology,

28(5):2021–2028.

Oh, K.-K., Park, M.-C., and Ahn, H.-S. (2015). A survey of

multi-agent formation control. Automatica, 53:424–

440.

O’Mahony, N., Campbell, S., Carvalho, A., Harapana-

halli, S., Hernandez, G. V., Krpalkova, L., Riordan,

D., and Walsh, J. (2019). Deep learning vs. tradi-

tional computer vision. In Advances in Intelligent Sys-

tems and Computing, pages 128–144. Springer Inter-

national Publishing.

Redmon, J. and Farhadi, A. (2018). Yolov3: An incremental

improvement. arXiv preprint arXiv:1804.02767.

Ren, S., He, K., Girshick, R., and Sun, J. (2015). Faster

r-cnn: Towards real-time object detection with region

proposal networks. In Advances in neural information

processing systems, pages 91–99.

Saska, M., Baca, T., Thomas, J., Chudoba, J., Preucil,

L., Krajnik, T., Faigl, J., Loianno, G., and Kumar,

V. (2017). System for deployment of groups of un-

manned micro aerial vehicles in gps-denied environ-

ments using onboard visual relative localization. Au-

tonomous Robots, 41(4):919–944.

Silano, G., Baca, T., Penicka, R., Liuzza, D., and Saska, M.

(2021). Power line inspection tasks with multi-aerial

robot systems via signal temporal logic speciﬁcations.

IEEE Robotics and Automation Letters, 6(2):4169–

4176.

Tian, Y., Liu, K., Ok, K., Tran, L., Allen, D., Roy, N., and

How, J. P. (2020). Search and rescue under the forest

canopy using multiple uavs. The International Journal

of Robotics Research, 39(10-11):1201–1221.

Trinh, M. H., Zhao, S., Sun, Z., Zelazo, D., Anderson,

B. D., and Ahn, H.-S. (2018). Bearing-based for-

mation control of a group of agents with leader-ﬁrst

follower structure. IEEE Transactions on Automatic

Control, 64(2):598–613.

Vrba, M. and Saska, M. (2020). Marker-less micro aerial

vehicle detection and localization using convolutional

neural networks. IEEE Robotics and Automation Let-

ters, 5(2):2459–2466.

Walter, V., Saska, M., and Franchi, A. (2018). Fast mutual

relative localization of UAVs using ultraviolet LED

markers. In 2018 International Conference on Un-

manned Aircraft Systems (ICUAS). IEEE.

Zhao, S. and Zelazo, D. (2019). Bearing rigidity theory and

its applications for control and estimation of network

systems: Life beyond distance rigidity. IEEE Control

Systems Magazine, 39(2):66–83.

Practical Formation Acquisition Mechanism for Nonholonomic Leader-follower Networks

339