Analyzing Age of Information in Prioritized Status Update Systems using
Probabilistic Hybrid Discipline
Tamer E. Fahim
1,3 a
, Sherif I. Rabia
1,3 b
, Ahmed H. Abd El-Malek
2 c
and Waheed K. Zahra
1,4 d
1
Basic and Applied Sciences Institute, Egypt-Japan University of Science and Technology, Alexandria, Egypt
2
School of Electronics, Communications and Computer Engineering, Egypt-Japan University of Science and Technology,
Alexandria, Egypt
3
Department of Engineering Mathematics and Physics, Faculty of Engineering, Alexandria University, Alexandria, Egypt
4
Department of Engineering Physics and Mathematics, Faculty of Engineering, Tanta University, Tanta, Egypt
Keywords:
Age of Information, Queueing Models, Stochastic Hybrid Systems, Internet of Things.
Abstract:
The ubiquitous deployment of the internet of things technology engenders great attention to the real-time
status update systems. However, the real-life situation implies the service differentiation between sources
according to their sensitivity, a problem that is rarely addressed in the literature. This situation is to be handled
classically by adopting the preemption or non-preemption service disciplines. In any of these disciplines,
an improvement is yielded for some specific classes with a severe degradation for the others. To address
this paradox, we propose a probabilistic hybrid service discipline, by which the decision of preemption for
each class is controlled by a probabilistic parameter. The stochastic hybrid system approach is employed to
analyze the average age of information for each class. A numerical study of a three-class prioritized network
demonstrates the significance of the proposed model to compromise the performance of all classes even in the
worse traffic loading conditions. Moreover, three different approaches are proposed to adjust the probabilistic
hybrid parameters for more promising results.
1 INTRODUCTION
Recently, the unprecedented growth in wireless com-
munication networks and portable devices has raised
the importance of real-time status update systems
(Yates et al., 2021). In such systems, the transmitting
node incorporating a sensor is responsible for track-
ing the physical phenomenon of interest before send-
ing its status updates to a remote interested recipient
(Kaul et al., 2012a).
Lately, the status update system has been widely
deployed in a myriad of real-life applications, such
as autonomous vehicular network (Talak et al., 2016),
Health-care monitoring system (Mishra et al., 2020)
and smart manufacturing system (Xu and Gautam,
2020),to name a few. In such applications, status up-
date packets, unlike conventional data packets, lose
their value and importance after being aged (Sun
a
https://orcid.org/0000-0002-9293-1202
b
https://orcid.org/0000-0003-1471-8841
c
https://orcid.org/0000-0002-7906-815X
d
https://orcid.org/0000-0002-6448-6877
et al., 2017). Accordingly, the freshness is an im-
portant criterion of real-time status update system
to guarantee reliable control and monitoring. How-
ever, the objective to enhance the information fresh-
ness is different from the problem of maximizing the
throughput or minimizing the delay (Abbas et al.,
2021). To illustrate, enhancing the system through-
put, by increasing the transmission rate, deteriorates
information freshness due packets backlogging. On
the other hand, sending status updates with lower
update rates ensures minimum-delay transmission,
while degrading information freshness due to packet
obsolescence.
Accordingly, a new performance measure has
been introduced (Kaul et al., 2012a), conforming with
the notion of information freshness, called as age of
information (AoI) ∆(t). It is defined as the ongoing
time since the generation of the latest received update
packet (Costa et al., 2016), ∆(t) = t −u(t), where u(t)
is the generation time of the freshest packet received
at the monitor.
The mathematical framework of the AoI is firstly
introduced in (Kaul et al., 2012a), where the average
Fahim, T., Rabia, S., El-Malek, A. and Zahra, W.
Analyzing Age of Information in Pr ioritized Status Update Systems using Probabilistic Hybrid Discipline.
DOI: 10.5220/0011320500003274
In Proceedings of the 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2022), pages 151-162
ISBN: 978-989-758-578-4; ISSN: 2184-2841
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
151

AoI of a single-source stream has been analyzed using
some simple queueing abstractions, M/M/1, M/D/1
and D/M/1. The First Come First Served (FCFS)
queueing policy has been deployed to manage the ac-
cess of the update packets to the server. However, in
(Kaul et al., 2012b), two variations of the Last Come
First Served (LCFS) have been addressed: M/M/1/1
with preemption service (PR-S) and M/M/1/2*. In the
former the ongoing service can be interrupted from
the newly arrived packet, while the latter admits the
preemption only on a waiting position of size 1 (PR-
W policy).
Similar to the case of the single-source stream,
the case of multi-source stream engenders a host of
research work. In (Yates and Kaul, 2018), the loss-
less system modelled as M/M/1 with FCFS is com-
pared with two models of the lossy system, M/M/1/1
with PR-S and M/M/1/2*. In this work, the stochas-
tic hybrid system (SHS) approach is used for the first
time to analyze the average AoI. Furthermore, accord-
ing to (Farazi et al., 2019), the M/M/1/1 with self-
preemption (SP) has been addressed, where the pre-
emption is admitted only between the packets belong-
ing to the same source.
Most of the research work pertaining to the case
of multi-source stream assume the same service treat-
ment for all streams irrespective of their belonging
source. However, the more practical situation implies
the service differentiation between sources’ streams
according to some criteria. For instance, in the vehic-
ular network, safety-centric updates are more age sen-
sitives compared with other regular updates (Maatouk
et al., 2019). Such interesting case has been rarely
addressed in the context of the age of information. In
(Kaul and Yates, 2018), the author extends his work
in (Yates and Kaul, 2018) to be deployed under the
prioritized case. However, in (Najm et al., 2019), two
prioritized streams are considered. The M/G/1/1 with
PR-S is adopted for the highest class, while two cases
are experimented for the lowest class, M/G/1/1 with
PR-S and M/G/1 with FCFS. It is then proved that
M/M/1/1 with PR-S is no longer the optimal for a
certain class under the existence of a higher priority
one. Subsequently, in (Maatouk et al., 2019), sep-
arate queue of size 1 is considered for each priority
class, instead of assigning one waiting position for all
classes (Kaul and Yates, 2018). This is to store the
preempted packet, where the preemption is applied
over both the packet being queued and at the packet
being served. However, the traffic parameter setting
is limited to be identical within all classes under the
exponential service time distribution. This limitation
has been abandoned afterwards in (Xu and Gautam,
2020) by considering heterogeneous traffic with gen-
eral service time distribution. In this study, the Peak
age of information, which is an alternative measure of
the AoI (Costa et al., 2016), has been examined. The
non-preemption (NP) service discipline is assumed,
where the ongoing service is guarded from any inter-
ruptions.
In the aforementioned research work (Kaul and
Yates, 2018; Najm et al., 2019; Maatouk et al., 2019;
Xu and Gautam, 2020), the prioritized streams are
handled in the server whether in preemptible or non-
preemptible basis. Each one of these schemes signif-
icantly improves the performance of some particular
class at the cost of a dramatic degradation of the oth-
ers (Kim, 2012).
This paradox can be resolved using the notion of
hybrid preemption/non-preemption service discipline
(Fahim et al., 2018). In this discipline, the decision
whether to preempt the ongoing service or not is gov-
erned by a discretionary rule employed at the server.
There are four distinct approaches of this rule, men-
tioned in the literature of the priority queueing system
(Kim, 2012). However, the hybrid service discipline
has not been addressed so far in the AoI context.
Based on the foregoing, we propose a proba-
bilistic hybrid service discipline under the prioritized
M/M/1/1 queueing abstraction. In such case, the deci-
sion of preemption for class m is taken with probabil-
ity p
m
. The AoI for each prioritized class is then mod-
elled and analyzed using SHS approach, by which the
average AoI for each class is obtained. After that a nu-
merical study of three prioritized classes is conducted.
The performance of our proposed model is compared
with the priority preemption (PP) model mentioned
in (Kaul and Yates, 2018), along with the SP model
mentioned in (Farazi et al., 2019) while taking into
consideration the priority setting. The numerical re-
sults demonstrate that the proposed hybrid discipline
significantly reduces the downside effect caused by
the PP and SP models, more specifically at the worse
traffic loading conditions. It is also shown that the
probabilistic parameters p
m
can be adjusted to opti-
mize a cost function, which represents the level of
satisfaction of the whole network. Furthermore, the
design of the admission control policy reflects the su-
periority of our proposed model, where the admission
region becomes more wider over the whole span of
the traffic loading condition.
The rest of this paper is organized as follows. In
Section 2, the system model is described with the re-
lated assumptions in addition to the declaration of the
corresponding traffic parameters. Subsequently, Sec-
tion 3 presents the AoI analysis of the proposed model
with a brief preliminary on the SHS approach. After
that, the numerical results and investigations are pre-
SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
152

sented in Section 4. Finally, our conclusion and future
work are summarized in Section 5.
2 SYSTEM MODEL
2.1 System Description and
Assumptions
𝑆
1
𝑆
2
𝑆
𝑀
BS
(a) IoT wireless network.
Server
Service
policy
Monitor
Base station
The highest
priority class
The Lowest
priority class
S
1
S
𝑚
S
𝑀
(b) Detailed system framework.
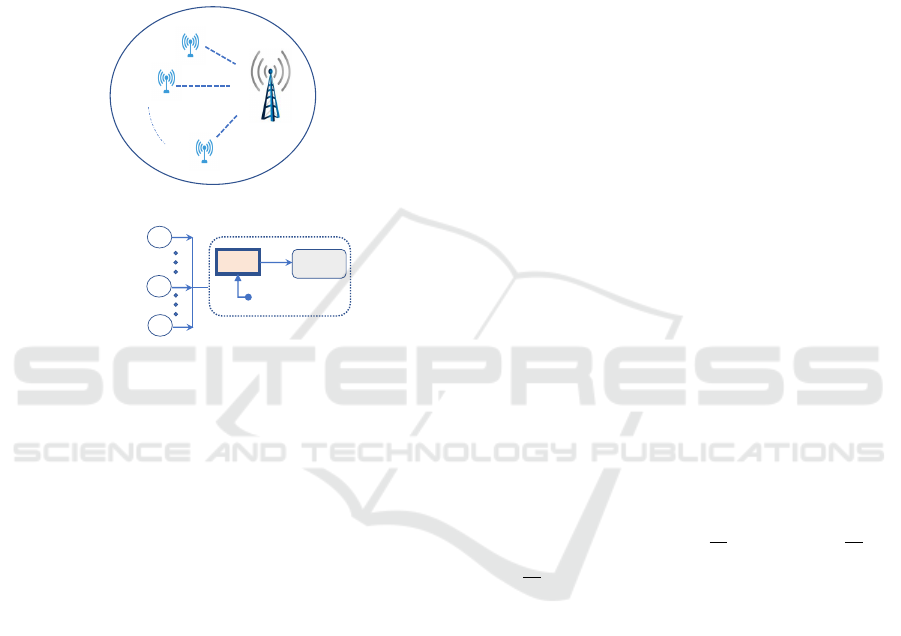
Figure 1: Considered system model’s description.
In our work, a typical wireless internet of things (IoT)
network is considered as shown in Figure 1a. It con-
sists of M IoT sources S
m
(1 ≤ m ≤ M) and one cen-
tralized base station (BS) as a receiving node. Fol-
lowing the distinction in the AoI constraints between
sources, the IoT sources are prioritized such that class
m has a higher priority over class n, subject to 1 ≤ m ≤
n ≤ M.
The detailed system framework of the aforemen-
tioned IoT network is illustrated as shown in Figure
1b. As shown, there is no buffer to store source pack-
ets. Moreover, in the receiving end, the multiple-
access request of the priority classes is scheduled ac-
cording to the priority order. To illustrate, S
m
has a
higher priority to access the server over S
n
, for m < n.
After the scheduling process, the selected packet that
has the turn is to be processed through the server,
which is governed by a service policy.
service policy. It governs the interaction be-
tween the source being served and the source request-
ing the service. In our proposed scheme, the ser-
vice policy has the following features: Firstly, the
self-preemptions are admitted, where a packet be-
ing served can be replaced by a freshest one that
belongs to the same source. Secondly, while serv-
ing the higher priority class, any packet request from
the lower priority class is declined and dropped from
the system. Thirdly, the probabilistic hybrid (PR/NP)
scheme is proposed, where class m being served can
be preempted from the higher priority classes with
probability p
m
, before being dropped from the sys-
tem. Accordingly, this proposed scheme will be re-
ferred to as probabilistic hybrid service discipline,
where each priority class, except class 1, has its own
probabilistic parameter 0 ≤ p
m
≤ 1, for 2 ≤ m ≤ M.
Moreover, it should be noted that if p
m
= 1 for 1 ≤
m ≤ M, the probabilistic hybrid discipline reduces to
the PP model (Kaul and Yates, 2018). On the other
hand, if p
m
= 0 for 1 ≤ m ≤ M, the hybrid approach
reduces to the self-preemption (SP) model, which is
similar to the model in (Farazi et al., 2019) but with
considering the priority setting.
2.2 Traffic Parameters
Regarding the analytical framework, an M/M/1/1 pri-
ority queueing system is proposed. The Poisson pro-
cess is assumed to capture the arrival process of the
status update stream of each priority class, with an ar-
rival rate λ
m
, for 1 ≤ m ≤ M. In this regards, let
ˆ
λ
m
=
∑
m−1
i=1
λ
i
and
ˇ
λ
m
=
∑
M
i=m+1
λ
i
denote the aggregate ar-
rival rate of the higher and the lower priority classes
of class m, respectively. Hence, λ
total
=
ˆ
λ
m
+λ
m
+
ˇ
λ
m
.
The processing time of each priority class is assumed
to follow the exponential distribution, with service
rate µ
m
, for 1 ≤ m ≤ M. In the subsequent analyti-
cal work, it is assumed that all classes has the same
processing requirements, hence; we can suppress the
class notation as µ
m
= µ. Accordingly, lets also de-
note S
m
offered load as ρ
m
=
λ
m
µ
; hence,
ˆ
ρ
m
=
ˆ
λ
m
µ
and
ˇ
ρ
m
=
ˇ
λ
m
µ
. Consequently, the total offered load by all
classes is ρ
total
=
ˆ
ρ
m
+ ρ
m
+
ˇ
ρ
m
.
3 PERFORMANCE ANALYSIS
In our analytical framework, the main target is to eval-
uate the average age of information for each priority
class (E[∆
m
], 1 ≤ m ≤ M). In this regard, the SHS
approach is deployed, which is guaranteed to be more
tractable approach in case of finite-state system (Yates
and Kaul, 2018). Accordingly, a brief preliminary on
the AoI-related SHS approach will be firstly presented
in Section 3.1. After that, Section 3.2 will present
the SHS analysis related to the proposed prioritized
M/M/1/1 queueing model under the probabilistic hy-
brid service discipline.
Analyzing Age of Information in Prioritized Status Update Systems using Probabilistic Hybrid Discipline
153

3.1 Preliminary on the AoI-Related
SHS
The SHS is generally defined as a stochastic system
with random dynamics, where its states are a hy-
brid of discrete component q(t) and continuous com-
ponent x(t). The discrete component q(t) ∈ Q =
{0, 1, ..., m} represents the evolution of the system
occupancy upon the occurrence of some stochastic
events (e.g. packet arrival and departure events).
On the other hand, the continuous component x(t) =
[x
0
(t), ..., x
n
(t)] ∈ R
(n+1)
describes a continuous-time
tracking of n+1 AoI-related processes, where n is the
system capacity of packets. Here, x
0
(t) is the AoI pro-
cess at the monitor (after packet departure); however,
x
i
for 1 ≤ i ≤ n are the AoI tracking of each packet be-
ing trapped in the system. In the subsequent context,
the main idea of the AoI-related SHS is summarized.
Firstly, as our focus is placed on the system
with memoryless service process, the discrete compo-
nent q(t) ∈ Q can be modeled as a Continuous-time
Markov chain (CTMC) denoted as (Q, L), where L
is the set containing all transitions between the dis-
crete nodes Q. To illustrate, the transition l ∈ L is
a directed path from node q
l
to q
0
l
with a transition
rate λ
(l)
δ
q
l
,q(t)
. The Kronecker delta function is used
here so that this transition rate is strictly related to
the occurrence of q(t) = q
l
. Moreover, lets define
L
0
q
= {l ∈ L : q
0
l
= q} and L
q
= {l ∈ L : q
l
= q} to be
the corresponding sets of the entering and departing
transitions of node q.
Regarding the continuous-time evolution of the
component x(t), it will be in two directions: the evo-
lution upon each transition l and the evolution while
being trapped at each node q. In the former, a linear
reset mapping occurs upon each transition l. In simple
words, at each transition l, the discrete state changes
from q
l
to q
0
l
; meanwhile, the continuous state resets
from x to x
0
= xA
l
. The matrix A
l
is called the re-
set maps of transition l. However, the AoI context
implies that the matrix A
l
should be with binary en-
tries, A
l
∈ {0, 1}
(n+1)×(n+1)
. When it comes to the
evolution of x at each node, there are a lot of SHS
variation in this regard (Teel et al., 2014). However,
in the AoI context, the piecewise linear SHS varia-
tion is deployed (Hespanha, 2006). In such case, the
evolution of x(t) at each node q is
˙
x = b
q
, where
b
q
∈ {0, 1}
1×(n+1)
is a vector with binary elements.
To illustrate, The entry b
k
q
= 1 means that the x
k
in-
creases linearly with time while being at state q; how-
ever, the entry b
k
q
= 0 indicates a plateau in x
k
in its
previous value. Moreover, the entry b
k
q
is assumed to
be 0 if x
k
is irrelevant at state q, i.e. there is no need
to be tracked at state q.
Based on the foregoing, the AoI analysis using
SHS begins with defining the following quantities for
each node q:
π
q
(t) = E[δ
q,q(t)
], (1)
v
q, j
(t) = E[x
j
(t)δ
q,q(t)
], 0 ≤ j ≤ n, (2)
and the corresponding vector function
v
q
(t) = [v
q,0
(t), ..., v
q,n
(t)] = E[x(t)δ
q,q(t)
]. (3)
Here, π
q
(t) represents the state probabilities
(π
q
(t) = P[q(t) = q]). However, the vector v
q
(t) sym-
bolizes the correlation vector between x(t) and the
discrete state q. In other words, it represents the corre-
sponding average values of the AoI-related processes
while being at state q.
The AoI analysis starts by finding the state probability
at each state q (π
q
(t)). However, a basic assumption
in this regard is that the CTMC of q(t) is ergodic. In
such case, the state probabilities π
q
(t) converges to a
certain limit
¯
π
q
according to the following system of
linear equations:
¯
π
q
(
∑
l∈L
q
λ
(l)
) =
∑
l∈L
0
q
λ
(l)
¯
π
q
l
, q ∈ Q, (4)
∑
q∈Q
¯
π
q
= 1. (5)
After solving the system described by (4) and (5),
the stationary probability vector is yielded,
¯
π =
[
¯
π
0
, ...,
¯
π
m
]. Regarding the correlation vector v
q
(t), as
declared in (Yates and Kaul, 2018), it satisfies the fol-
lowing first order differential equations, for all q ∈ Q:
˙
v
q
(t) = b
q
π
q
+
∑
l∈L
0
q
λ
(l)
v
q
l
(t)A
l
− v
q
(t)(
∑
l∈L
q
λ
(l)
).
(6)
The stability issue of this system of differential equa-
tions is addressed in (Yates and Kaul, 2018). It is
proved that the stability of this system depends on the
reset maps matrix A
l
. In case of being a stable sys-
tem,
˙
v
q
(t) = 0 and the resulting v
q
(t) converges to a
certain limit
¯
v
q
as t → ∞. In such case the system of
differential equations is reduced to a system of linear
equations as follows:
¯
v
q
(
∑
l∈L
q
λ
(l)
) = b
q
π
q
+
∑
l∈L
0
q
λ
(l)
¯
v
q
l
A
l
, q ∈ Q. (7)
In this regard, it is proved by Theorem 4 of (Yates and
Kaul, 2018) that the stability of the system (6) can be
guaranteed if the system (7) yields a non-negative so-
lution
¯
v = [
¯
v
0
, ...,
¯
v
m
]. Consequently, the average AoI
at the monitor E[∆] can be evaluated from the cor-
responding AoI-related process E[x
0
], which can be
SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
154

evaluated as follows:
E[x
0
] = lim
t→∞
E[x
0
(t)] = lim
t→∞
∑
q∈Q
E[x
0
(t)δ
q,q(t)
]
=
∑
q∈Q
v
q,0
. (8)
Hence,
E[∆] =
∑
q∈Q
v
q,0
. (9)
3.2 The Probabilistic Hybrid Service
Discipline: SHS Analysis
In this section, the foregoing SHS definitions and
analysis will be applied under the proposed model de-
scribed in 2. In this study, the aim is to study the age
of information of the priority class of interest m out
of M prioritized classes. Accordingly, the subsequent
analtyical framework is perceived from the perspec-
tive of class m.
Under the proposed scheme, the discrete states
characterization will be q(t) ∈ Q = {0, HP, m, m +
1, ..., m + i, ..., M} for 1 ≤ i ≤ M − m. Here, state
0 represents that the server is in the idle case, and
state m denotes that the class of interest S
m
is be-
ing served. However, state HP means that the ongo-
ing service belongs to any higher priority class than
class m regardless of its priority index. This is be-
cause any of them have the same effect from class
m perspective, the preemption with probability p
m
.
On the other hand, the remaining states of Q symbol-
ize all lower priority classes than class m. let denote
LP = {m + 1, ..., m + i, ..., M} for 1 ≤ i ≤ M − m. In
contrast with the state HP, all lower priority classes
should be included in the discrete state notation of the
SHS. This is due to the distinction of the probabilistic
hybrid parameters p
m
. Accordingly, for presentation
convenience, state m + i (1 ≤ i ≤ M − m) is a repre-
sentative state for all lower priority classes in state LP.
On the other side of the problem, since the sys-
tem is bufferless, the continuous state is defined as
x(t) = [x
0
(t), x
1
(t)], where x
0
(t) and x
1
(t) are the AoI
related processes of class m at the monitor and the
server, respectively. It should be noted that x
1
(t) mea-
sures the time span from the time class m starts the
service until being departed whether due to service
completion or service preemption. However, x
0
(t)
will be reset to x
1
(t) in the case of service completion
only. On the other hand, the evolution of the AoI-
related processes x(t), while being trapped at discrete
state q ∈ Q, is formulated as the following differential
equation.
˙
x(t) = b
q
=
(
[1 1], q = m
[1 0], q ∈ Q\m
. (10)
To illustrate, the AoI process x
0
(t) increase with a unit
rate while being trapped at each discrete state before
any transition. However, x
1
(t) increase linearly only
if class m is being served, while the other states are
irrelevant to class m.
Our goal is to evaluate the correlation vector
¯
v
q
=
[ ¯v
q0
, ¯v
q1
] for each q ∈ Q by solving the system of lin-
ear equations, described in (7), so that we can evalu-
ate average AoI E[∆
m
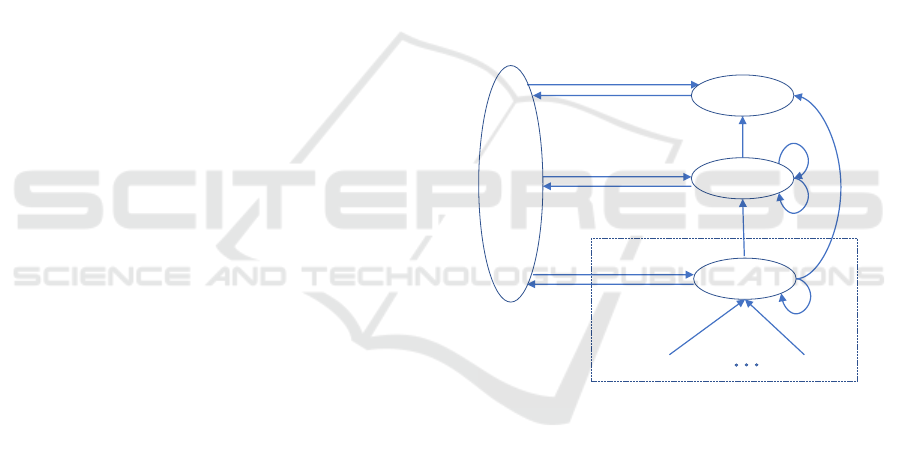
] using (9). To do that, Figure
2 illustrates the resulting SHS Markov chain (MC)
as perceived by the class of interest m. As shown,
state m + i (1 ≤ i ≤ M − m) is a combined state for all
lower priority classes considered in state LP. More-
over, Table 1 elaborates all state transitions (l) related
to the relevant class m and other irrelevant classes. As
shown, all transition rates (λ
(l)
) and the corresponding
reset maps (A
l
) are tabulated, along with v
q
l
A
l
that
will be used in (7). It is noted that all state transitions
are classified into four blocks, with some categories
for each one.




  
(1     )
From state      From state 





























Figure 2: The SHS MC for class m under the proposed
scheme.
According to Figure 2 and Table 1, the explanation
of each transition l is discussed as follows:
• B1: The transitions in this block are related to the
departure epochs of the packet being served. In all
categories related to this block, the new state q
0
l
=
0 is irrelevant to class m; hence, x
0
1
= 0. Moreover,
in categories B
11
and B
13
, the departing packet is
not related to class m, therefor, there is no change
in x
0
(x
0
0
= x
0
). In contrast, in B
12
, the departing
class m resets the signal x
0
to x
1
, which is the last
recorded AoI before the departure epoch.
• B2: This block represents all entering transitions
to state HP. In the category B
21
, one of the classes
related to HP arrives at an empty system. How-
ever, categories B
22
and B
23
symbolize the pre-
Analyzing Age of Information in Prioritized Status Update Systems using Probabilistic Hybrid Discipline
155

Table 1: Transition table of the SHS MC in Figure 2.
Block number Categories q
l
→ q
0
l
λ
(l)
x
0
= xA A
l
v
q
l
A
Block 1
(B1)
B
11
HP → 0 µ

x
0
0


1 0
0 0


v
HP,0
0

B
12
m → 0 µ

x
1
0


0 0
1 0


v
m,1
0

B
13
m + i → 0
(1 ≤ i ≤ M − m)
µ

x
0
0


1 0
0 0


v
m+i,0
0

Block 2
(B2)
B
21
0 → HP
ˆ
λ
m

x
0
0


1 0
0 0


v
0,0
0

B
22
m → HP
ˆ
λ
m
p
m

x
0
0


1 0
0 0


v
m,0
0

B
23
m + i → HP
(1 ≤ i ≤ M − m)
ˆ
λ
m
p
m+i

x
0
0


1 0
0 0


v
m+i,0
0

Block 3
(B3)
B
31
0 → m λ
m

x
0
0


1 0
0 0


v
0,0
0

B
32
m → m
ˆ
λ
m
(1 − p
m
)

x
0
x
1


1 0
0 1


v
m,0
v
m,1

B
33
m → m λ
m

x
0
0


1 0
0 0


v
m,0
0

B
34
m + i → m
(1 ≤ i ≤ M − m)
λ
m
p
m+i

x
0
0


1 0
0 0


v
m+i,0
0

Block 4
(B4)
B
41
0 → m + i λ
m+i

x
0
0


1 0
0 0


v
0,0
0

B
42
m + i → m + i
ˆ
λ
m+i
(1 − p
m+i
)

x
0
0


1 0
0 0


v
m+i,0
0

B
43
m + i + 1 → m +i
.
.
.
M → m + i
λ
m+i
p
m+i+1
.
.
.
λ
m+i
p
M

x
0
0

.
.
.

x
0
0


1 0
0 0


v
m+i+1,0
0

.
.
.

v
M,0
0

emption of class m and its lower priority classes
due to the arrival of a higher priority class. This
preemption is governed by the probabilistic pa-
rameter p
m
for class m and p
m+i
for the represen-
tative state m + i. Regarding the AoI resetting of
the processes x(t), x
0
1
= 0, which is due to the ir-
relevance of the new sate q
0
= HP. In contrast,
there is no change in x
0
(t) because no class m de-
parting packet is noticed.
• B3: This block represents all possible incoming
transitions into state m. In category B
31
, a fresh
class m packet arrives at an empty server. How-
ever, Category B
32
refers to the case where the
preemption upon class m from the higher priority
classes is declined; hence, class m continues its
service normally. Categories B
33
and B
34
repre-
sent the preemption occurs due to the arrival of a
fresh packet of class m. More specifically, B
33
de-
notes the self-preemption, whereas B
34
considers
the preemptions over the lower priority classes.
All categories related to this block yield no change
in the AoI process x
0
(t). However, in categories
B
31
,B
33
and B
34
, x
0
1
= 0 since a fresh relevant
packet of class m starts the service. This is in con-
trast with B
33
, where the already existing packet
of class m continues its service without interrup-
tion; hence, x
0
1
= x
1
.
• B4: This block lists all incoming transition into
the representative state m + i (1 ≤ i ≤ M − m). In
the first category, the server is empty before be-
ing occupied with a packet of class m + i, 1 ≤ i ≤
M − m. In category B
42
, the interruptions over
class m + i from the higher priority classes are
declined. However, category B
43
lists all cases
where the lower priority classes of class m + i are
preempted due to an arrival of class m + i. In all
these categories, x
0
(t) is unchanged since there is
no departure of class m. However, x
1
(t) is reset to
0 due to the irrelevance of the new state q
0
= m +i.
The AoI analysis begins with finding the station-
ary state probabilities
¯
π = [
¯
π
0
,
¯
π
HP
,
¯
π
m
,
¯
π
m+i
]. Apply-
ing equation (4) at each state q ∈ Q, a system of linear
equations can be formulated as follows:
SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
156

at state q = {0}:
π
0

λ
total

= µ
∑
q∈Q\0
π
q
, (11)
at state q = {HP}:
π
HP

µ

=
ˆ
λ
m

π
0
+
M
∑
j=m
π
j
p
j

, (12)
at state q = {m}:
π
m

µ +
ˆ
λ
m
p
m

= λ
m

π
0
+
M
∑
j=m+1
π
j
p
j

, (13)
at state q = {m + i} for 1 ≤ i ≤ M − m:
π
m+i

µ +
ˆ
λ
m+i
p
m+i

= λ
m+i

π
0
+
M
∑
j=m+i+1
π
j
p
j

.
(14)
This system of linear equations is to be solved with
the normalization equation described at (5).
After finding the probability vector
¯
π, the correla-
tion vector
¯
v for all states q ∈ Q can be evaluated us-
ing equation (7). However, some of these correlations
will be vanished intuitively; more specifically, ¯v
0,1
=
¯v
HP,1
= 0, along with ¯v
m+i,1
= 0 (1 ≤ i ≤ M − m).
This is because all these correlation values irrelevant
to class m. In the following, equation (7) is applied
at each state q ∈ Q according to the information tabu-
lated in Table 1:
at state q = {0}:
[ ¯v
0,0
¯v
0,1
]

λ
total

= [π
0
0] + µ[¯v
m,1
0]
+ µ
∑
q∈Q\{0,m}
[ ¯v
q,0
0], (15)
at state q = {HP}:
[ ¯v
HP,0
¯v
HP,1
]

µ

= [π
HP
0]
+
ˆ
λ
m

[ ¯v
0,0
0] +
M
∑
j=m
[ ¯v
j,0
0]p
j

, (16)
at state q = {m}:
[ ¯v
m,0
¯v
m,1
]

µ +
ˆ
λ
m
+ λ
m

= [π
m
π
m
]
+ λ
m

[ ¯v
0,0
0] + [¯v
m,0
0] +
M
∑
j=m+1
[ ¯v
j,0
0]p
j

+
ˆ
λ
m
(1 − p
m
)[ ¯v
m,0
¯v
m,1
], (17)
at state q = {m + i} for 1 ≤ i ≤ M − m:
[ ¯v
m+i,0
¯v
m+i,1
]

µ +
ˆ
λ
m+i

= [π
m+i
0]
+ λ
m+i

[ ¯v
0,0
0] +
M
∑
j=m+i+1
[ ¯v
j,0
0]p
j

+
ˆ
λ
m+i
(1 − p
m+i
)[ ¯v
m+i,0
0]. (18)
After solving the above system of vector equations,
the correlation vector
¯
v is reached. Hence, the av-
erage AoI of class m (E[∆
m
]) can be evaluated using
equation (9) as follows:
E[∆
m
] = ¯v
0,0
+ ¯v
HP,0
+ ¯v
m,0
+
M−m
∑
i=1
¯v
m+i,0
(19)
It should be noted that the algorithm adopted to find
E[∆
m
] can be deployed similarly for the other priority
classes.
4 NUMERICAL RESULTS
In this section, the analytical framework will be nu-
merically investigated. Throughout this numerical
study, three prioritized status update streams are con-
sidered. In addition, unless otherwise indicated, the
homogeneous arrival process is assumed between all
classes, where λ
1
= λ
2
= λ
3
=
1
3
λ
total
and µ = 1.
Moreover, the average service rate is identical for all
classes with µ = 1.
The numerical study will be initiated, in section
4.1, by validating the analytical framework through
simulation. After that, the proposed model will be
compared with the PP model (Kaul and Yates, 2018)
and the SP mentioned in (Farazi et al., 2019) taking
into consideration the priority setting. This compar-
ative study is established through three different ap-
proaches, by which the probabilistic hybrid parame-
ters (p
2
and p
3
) can be generated.
4.1 Analytical Model Validation
In this section, the analytical model will be verified
under a simulation framework similar to the analyti-
cal one using MATLAB R2015a. The simulation time
is to be lengthy enough (10
5
time units) to capture the
steady state results. Moreover, The simulation envi-
ronment was built through a workstation with the fol-
lowing specifications: Intel(R) Xeon(R) Gold 6230R
CPU, 2.10 GHz (2 processors); 128 GB RAM; and 64
bit Widows 10 pro operating system.
In this study, two different cases of the probabilis-
tic hybrid parameters are experimented, p
2
= p
3
=
1
2
and p
2
= p
3
=
2
3
, as shown in Figure 3a and Figure
3b, respectively. It is demonstrated that the simulation
results conform with the analytical results with max-
imum percentage errors of 2.437 % and 3.6952 % in
the cases of Figure 3a and Figure 3b, respectively.
Analyzing Age of Information in Prioritized Status Update Systems using Probabilistic Hybrid Discipline
157

ρ
total
0.5 1 1.5 2 2.5 3 3.5
E[∆]
2
4
6
8
10
12
Analytical
Simulation
Class 3
Class 2
Class 1
(a) p
2
= p
3
=
1
2
.
ρ
total
0.5 1 1.5 2 2.5 3 3.5
E[∆]
2
4
6
8
10
12
Analytical
Simulation
Class 3
Class 2
Class 1
(b) p
2
= p
3
=
2
3
.
Figure 3: Comparison between the analytical and simula-
tion results.
4.2 Comparison with the Classical
Approaches
In the subsequent studies, the probabilistic hybrid ap-
proach will be compared with the PP and SP mod-
els. In this study, three different methods will be pre-
sented to determine how to set the probabilistic hy-
brid parameters p
2
, p
3
: fixed assignment approach,
optimization-based approach, and interruption-based
approach.
4.2.1 Fixed Assignment Probabilistic (FAP)
Approach
In this approach, the probabilistic hybrid parameters
p
2
, p
3
are considered as decision-making parameters
to be set irrespective of any traffic and system con-
ditions. Figure 4 elaborates the comparison between
the proposed hybrid approach and the classical ones
under two different setting of the hybrid parameters,
p
2
= p
3
= 0.3 and p
2
= p
3
= 0.7. The observations
on this figure are analyzed in the following notes:
• In comparison with the PP model, the SP model
yields an improvement for the lower priority
classes at the cost of a dramatic degradation in
class 1 performance. On the other hand, the pro-
posed hybrid approach significantly reduces class
1 degradation while keeping an acceptable im-
provement gain for the lower priority classes.
• As the probability of preemption increases, the
probabilistic hybrid model approaches the PP
model, which is in favour of the higher priority
class at the expense of the lower priority ones.
For further elaboration, Figure 5 presents the im-
provement/degradation percentage in the average AoI
of each class with respect to the PP mode at three
different loading conditions. This percentages are
to be evaluated as
E[∆
m
|PP]−E[∆
m
|scheme]
E[∆
m
|PP]
× 100, where
E[∆
m
|scheme] and E[∆
m
|PP] are the average AoI un-
der the operating scheme and the PP model, respec-
tively. As shown in Figure 5a, the significance of the
proposed model is manifested vividly at the higher
traffic loading conditions. In such case, the perfor-
mance gain of the lower priority classes increases;
meanwhile, the degradation experienced by class 1 is
improved gradually. This is in contrast with the SP
model as shown in Figure 5b, where the degradation
occurs for class 1 increases as the traffic loading be-
comes worse.
In conclusion, the proposed model not only gives
a compromise solution compared with the PP and SP
model, but it also seems to be much more efficient
at the worse traffic loading conditions. From another
perspective, in case of using the FAP, it is preferable
to control the offered load to be as high as possible.
4.2.2 Optimization-based Probabilistic (OBP)
Approach
In this approach, another method is adopted to deter-
mine the setting of the probabilistic hybrid parameters
(p
2
, p
3
). In such approach, these parameters will be
the decision variables resulting from a constrained op-
timization problem of a cost function C
α
1
,α
2
,α
3
, which
is represented as the weighted sum of the average AoI
of each prioritized class. This cost function signifies
the overall satisfaction of the whole network.
The optimization problem is formulated as follows:
min
p
2
, p
3
C
α
1
,α
2
,α
3
= α
1
× E[∆
1
] + α
2
× E[∆
2
]
+ α
3
× E[∆
3
],
0 ≤α
1
, α
2
, α
3
≤ 1 (20)
subject to
E[∆
1
|scheme]−E[∆
1
|PP]
E[∆
1
|PP]
× 100 ≤ R %,
where E[∆
1
|scheme] and E[∆
1
|PP] are as mentioned
before in section 4.2.1.
The cost function parameters (α
1
, α
2
, α
3
) are chosen
to reflect the distinction in the importance of each
SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
158

ρ
total
0.5 1 1.5 2 2.5 3 3.5
E[∆
1
]
0
2
4
6
8
10
SP
p
2
= p
3
= 0.5
p
2
= p
3
= 0.7
PP
(a) Class 1.
ρ
total
0.5 1 1.5 2 2.5 3 3.5
E[∆
2
]
4
5
6
7
8
9
10
SP
p
2
= p
3
= 0.5
p
2
= p
3
= 0.7
PP
(b) Class 2.
ρ
total
0.5 1 1.5 2 2.5 3 3.5
E[∆
3
]
4
6
8
10
12
14
SP
p
2
= p
3
= 0.5
p
2
= p
3
= 0.7
PP
(c) Class 3.
Figure 4: Comparison between the proposed hybrid disci-
pline, along with PP and SP approaches for each class.
corresponding class compared with the others. For
instance, in case of α
1
= α
2
= α
3
, the sources will
be with equally importance. However, the setting
α
1
> α
2
> α
3
refers to the case of prioritized network.
From another perspective. As regards to the adopted
constraint, it represents an upper bound limit of the
degradation percentage incurred by class 1 due to the
use of the hybrid mode instead of its most preferable
approach (PP model).
To solve this constrained optimization problem,
the brute-force approach is employed with a resolu-
tion of 0.1 for each probabilistic parameter p
m
.
Table 2 presents the resulting optimal probabilistic
class 1 class 2 class 3
Average Improvement/Degradation
-30
-20
-10
0
10
20
30
40
ρ
total
= 1.5
ρ
total
= 3.5
ρ
total
= 5
(a) The proposed model.
class 1 class 2 class 3
Average Improvement/Degradation
-150
-100
-50
0
50
100
ρ
total
= 1.5
ρ
total
= 3.5
ρ
total
= 5
(b) Self-preemption model (SP).
Figure 5: The Improvement/Degradation in the average AoI
with respect to the PP mode at ρ
total
= 1.5, ρ
total
= 3.5 and
ρ
total
= 5.
hybrid probabilities (p
∗
2
, p
∗
3
) over the span of ρ
total
=
[0, 0.5] for the three different cases of the cost func-
tion: C
1,1,1
, C
1,
1
2
,
1
4
, and C
1,
1
4
,
1
8
. As demonstrated in
the table, the case of the PP (p
2
= 1 and p
3
= 1) is
not always the optimal choice for the network to ful-
fill the network level of satisfaction represented in the
cost function C
α
1
,α
2
,α
3
, while the proposed hybrid dis-
cipline, by its controlling parameters, can be adjusted
for such purpose.
For further illustration, in Figure 6, the cost func-
tion C
α
1
,α
2
,α
3
with different weight parameters is ex-
amined under three different approaches: PP, SP,
and the optimization-based approach (OBP). In this
study, the homogeneous traffic loading is also as-
sumed. Generally speaking, the cost function met-
ric, as a weighted sum, will be intuitively more sensi-
tive to the performance of the class having the highest
weight parameter. Accordingly, we can derive the fol-
lowing investigations:
• In Figure 6a, the equal-weight cost function C
1,1,1
is minimized in the SP model and worsened in
the PP model, which is outperformed by the OBP
model. This is because C
1,1,1
is equally sensitive
to the performance gain yielded for any of the
Analyzing Age of Information in Prioritized Status Update Systems using Probabilistic Hybrid Discipline
159

ρ
total
0.5 1 1.5 2 2.5 3 3.5
C
1,1,1
10
15
20
25
30
PP
SP
OBP
(a) α
1
= α
2
= α
3
= 1.
ρ
total
0.5 1 1.5 2 2.5 3 3.5
C
1,
1
2
,
1
4
6
8
10
12
14
16
18
PP
SP
OBP
(b) α
1
= 1, α
2
=
1
2
, α
3
=
1
4
.
ρ
total
0.5 1 1.5 2 2.5 3 3.5
C
1,
1
4
,
1
8
4
6
8
10
12
14
PP
SP
OBP
(c) α
1
= 1, α
2
=
1
4
, α
3
=
1
8
.
Figure 6: The cost function C
α
1
,α
2
,α
3
under three different
schemes (PP, SP, and OBP) for three cases of the cost func-
tion parameters.
priority classes. In this regard, as shown in Fig-
ure 4, the performance gain achieved by the SP
model for class 2,3 outperforms the improvement
yielded from the other models.
• In Figures 6b and 6c, the proposed OBP model
represents the most optimal choice. In such case,
the sensitivity of the cost functions C
1,
1
2
,
1
4
and
C
1,
1
4
,
1
8
becomes in line with the priority order of
the classes. Therefor, the compromise perfor-
mance achieved by OBP overtakes the other mod-
els due to its contribution to improve class 2,3
with respect to the PP model in addition to en-
hancing class 1 performance with respect to SP
model.
Based on the foregoing investigations, the OBP is the
most optimal choice to enhance the overall perfor-
mance satisfaction of the prioritized network.
Table 2: The probabilistic hybrid parameters under different
cases of C
α
1
,α
2
,α
3
.
ρ
total
C
1,1,1
C
1,
1
2
,
1
4
C
1,
1
4
,
1
8
p
∗
2
p
∗
3
p
∗
2
p
∗
3
p
∗
2
p
∗
3
0.5 0.4 0.2 1 1 1 1
1 0.7 0.3 0.7 0.7 1 1
1.5 0.7 0.3 0.6 0.5 1 0.7
2 0.7 0.3 0.6 0.4 0.7 0.6
2.5 0.7 0.3 0.6 0.4 0.6 0.4
3 0.7 0.3 0.6 0.4 0.6 0.4
3.5 0.7 0.3 0.6 0.4 0.6 0.4
4.2.3 Interruption-based Probabilistic Approach
(IBP)
In this approach, the working probabilistic hybrid Pa-
rameters (p
2
, p
3
) are generated based on the average
number of preemptions experienced by each class.
However, the self-preemptions will be excluded from
this measure. This is due to the benefit behind the
self-preemptions in enhancing the information fresh-
ness of each class.
In our setting, the following is the formulation of the
average number of preemptions of class m caused by
the higher priority classes k (0 ≤ k ≤ m − 1) per unit
time:
E[N
(m)
] = ((
m−1
∑
k=1
λ
k
× p
m
)) × r
m
, (21)
where r
m
is the corresponding probability that class m
is being served.
After formulating E[N
(m)
], it will be deployed to
generate the probabilistic hybrid parameters (p
m
) at
each traffic loading condition. This generation is per-
formed using a decaying exponential function of pa-
rameter a
m
as follows:
p
m
= e
−(a
m
×E[N
(m)
|pp])
, 2 ≤ m ≤ M, a
m
≥ 0, (22)
where E[N
(m)
|PP] is the average number of preemp-
tions of class m while applying the PP model, which
is the worst case of preemptions that class m can expe-
rience. Moreover, the parameter a
m
is used to control
the decaying rate of the exponential function. Accord-
ingly, if the traffic loading conditions becomes worse,
the exponential decaying function makes p
m
be de-
creased to counter the potential increase in the num-
ber of preemptions. This in turn enhances the AoI
performance of the lower priority classes. Moreover,
it should be noted that the PP model corresponds to
a
m
= 0 for (1 ≤ m ≤ M), while the SP model can be
reached by setting a
m
= ∞ for (1 ≤ m ≤ M).
SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
160

To visualize the above result, the effect of the
interruption-based approach can be emerged using
what is called the admissible control regions. These
regions demonstrate the maximum offered load that
the network can tolerate without violating some sys-
tem constraints.
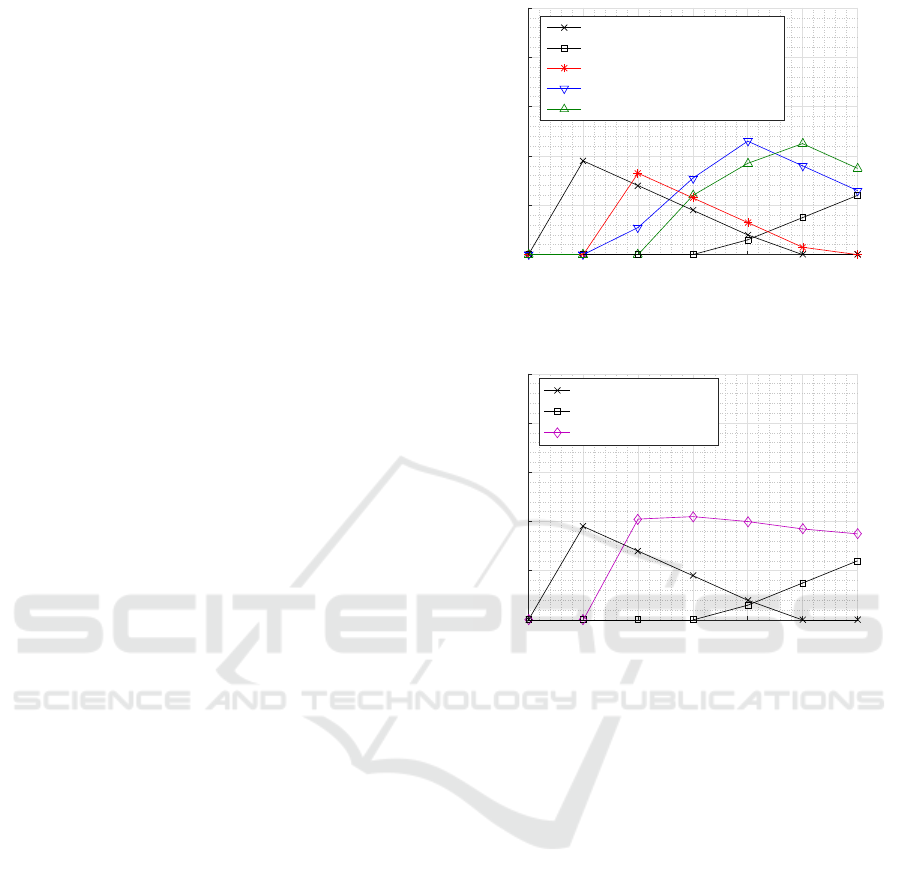
In Figure 7, the admissible region for class 2 is de-
picted to highlight the maximum traffic loading of
class 2 over the span of class 1’s offered load, while
levelling off ρ
3
= 1. This admission region is re-
stricted by two constraints: E[∆
1
] < 2 and E[∆
3
] < 20.
These constraints are set on class 1 and 3, particularly,
because class 1 is the most AoI sensitive one while
class 3 is the highly interrupted traffic.
As shown in Figure 7, the following investigations
can be derived:
• In the PP model, the admission region becomes
more dense at lower class 1’s traffic intensities,
while being shrunk at the higher intensities. This
is expected because the PP model causes a dra-
matic degradation for class 3; therefor, the AoI
constraint (E[∆
3
] < 20) becomes more vulnerable
to be violated at the higher zone of ρ
1
. This is in
contrast with the SP model, where a higher degra-
dation occurs for class 1; hence, the AoI con-
straint (E[∆
1
] < 2) is more prone to be violated
at lower range of ρ
1
.
• Regarding the probabilistic hybrid approach, it is
clear that as a
2
and a
3
increase, the admissible re-
gion shrinks at the lower span of ρ
1
, while widen-
ing at the higher values of this span. This is be-
cause the more a
2
and a
3
increase, the more the
system approaches the SP model. Hence, for each
setting of a
m
, it is impossible to widen the admis-
sible region over the whole span of ρ
1
.
To tackle the above mentioned problem, it is proposed
that a
2
, a
3
can be adjusted to increase in line with the
increase of ρ
1
. In such case, the system will be self-
adapted with the expected traffic conditions. In Fig-
ure 8, the self-adapted IBP approach is experimented,
where a
2
, a
3
increase linearly from 0 to 10 over the
span of ρ
1
= [0.5, 3.5]. As shown in the figure, the
admission region is enhanced over the whole span of
ρ
1
.
5 CONCLUSIONS
In this paper, the probabilistic hybrid service disci-
pline is proposed to be deployed in a network with
prioritized traffic. In the proposed discipline, the pre-
emptions towards a certain class, resulting from the
higher priority ones, are admitted with a certain prob-
ρ
1
0.5 1 1.5 2 2.5 3 3.5
ρ
2
0
1
2
3
4
5
PP
SP
IBP (a
2
= a
3
= 1)
IBP (a
2
= a
3
= 8)
IBP (a
2
= a
3
= 10)
Figure 7: Admissible region for class 2 under three different
schemes: PP, SP and IBP approach.
ρ
1
0.5 1 1.5 2 2.5 3 3.5
ρ
2
0
1
2
3
4
5
PP
SP
Self-adapted IBP
Figure 8: Admissible region for class 2 under three different
schemes: PP, SP and self-adapted IBP approach.
ability. However, the self preemptions are always per-
mitted. The SHS approach is used to analyze the av-
erage AoI for each prioritized class. To corroborate
the theoretical framework, a numerical study of a net-
work of three prioritized classes is provided. Based
on this setting, the performance of the proposed hy-
brid discipline is compared with the conventional dis-
ciplines, PP and SP. As these classical policies re-
sult in an improvement for some specific class with
a dramatic degradation for the others, the proposed
hybrid discipline resolves this drawback by reducing
the downside effect of the adversely affected classes.
Furthermore, the proposed hybrid discipline renders
some controlling parameters by which the system per-
formance can be adjusted. In the FAP, it is preferable
to control the offered load to be as high as possible
to guarantee marginal degradation for class 1 with an
increasing improvements for class 2 and 3. On the
other hand, in the OBP approach, It was found that
the probabilistic hybrid approach becomes the opti-
mal choice to optimize a cost function, which repre-
sents the whole network satisfaction. Furthermore, a
Analyzing Age of Information in Prioritized Status Update Systems using Probabilistic Hybrid Discipline
161

much simpler method is proposed (IBP) to attribute
the generation of the probabilistic parameters to the
average number of interruptions experienced under
the working traffic loading conditions. According to
this setting, the superiority of the proposed model is
manifested in widening the feasible region of the ac-
ceptable offered load without violating some AoI con-
straints.
As a future work, the presented study can be ex-
tended by experimenting another discretionary rule
for the hybrid discipline rather than the probabilis-
tic one. Moreover, the analytical study can be also
extended by considering general arrival and service
stochastic processes.
ACKNOWLEDGEMENTS
This research work is sponsored by the Egyptian Min-
istry of Higher Education (MoHE) grant in the scope
of the Egypt-Japan University of Science and Tech-
nology (E-JUST).
REFERENCES
Abbas, Q., Hassan, S. A., Pervaiz, H., and Ni, Q. (2021). A
markovian model for the analysis of age of informa-
tion in IoT networks. IEEE Wireless Communications
Letters, 10(7):1596–1600.
Costa, M., Codreanu, M., and Ephremides, A. (2016). On
the age of information in status update systems with
packet management. IEEE Transactions on Informa-
tion Theory, 62(4):1897–1910.
Fahim, T. E., Zakariya, A. Y., and Rabia, S. I. (2018). A
novel hybrid priority discipline for multi-class sec-
ondary users in cognitive radio networks. Simulation
Modelling Practice and Theory, 84:69–82.
Farazi, S., Klein, A. G., and Brown, D. R. (2019). Average
age of information in multi-source self-preemptive
status update systems with packet delivery errors. In
53rd Asilomar Conference on Signals, Systems, and
Computers, Pacific Grove, CA, USA, pages 396–400.
IEEE.
Hespanha, J. P. (2006). Modelling and analysis of stochastic
hybrid systems. IEE Proceedings-Control Theory and
Applications, 153(5):520–535.
Kaul, S., Yates, R., and Gruteser, M. (2012a). Real-time
status: How often should one update? In Proceedings
IEEE INFOCOM, Orlando, FL, USA, pages 2731–
2735. IEEE.
Kaul, S. K. and Yates, R. D. (2018). Age of information:
Updates with priority. In IEEE International Sympo-
sium on Information Theory (ISIT), Vail, CO, USA,
pages 2644–2648. IEEE.
Kaul, S. K., Yates, R. D., and Gruteser, M. (2012b). Status
updates through queues. In 46th Annual Conference
on Information Sciences and Systems (CISS), Prince-
ton, NJ, USA, pages 1–6. IEEE.
Kim, K. (2012). T-preemptive priority queue and its ap-
plication to the analysis of an opportunistic spectrum
access in cognitive radio networks. Computers & Op-
erations Research, 39(7):1394–1401.
Maatouk, A., Assaad, M., and Ephremides, A. (2019).
Age of information with prioritized streams: When
to buffer preempted packets? In IEEE Inter-
national Symposium on Information Theory (ISIT),
Paris, France, pages 325–329. IEEE.
Mishra, S., Mishra, B. K., Tripathy, H. K., and Dutta, A.
(2020). Analysis of the role and scope of big data an-
alytics with iot in health care domain. In Handbook of
data science approaches for biomedical engineering,
pages 1–23. Elsevier.
Najm, E., Nasser, R., and Telatar, E. (2019). Content based
status updates. IEEE Transactions on Information
Theory, 66(6):3846–3863.
Sun, Y., Uysal-Biyikoglu, E., Yates, R. D., Koksal, C. E.,
and Shroff, N. B. (2017). Update or wait: How to keep
your data fresh. IEEE Transactions on Information
Theory, 63(11):7492–7508.
Talak, R., Karaman, S., and Modiano, E. (2016). Speed
limits in autonomous vehicular networks due to com-
munication constraints. In IEEE 55th Conference on
Decision and Control (CDC), Las Vegas, NV, USA,
pages 4998–5003. IEEE.
Teel, A. R., Subbaraman, A., and Sferlazza, A. (2014). Sta-
bility analysis for stochastic hybrid systems: A survey.
Automatica, 50(10):2435–2456.
Xu, J. and Gautam, N. (2020). Peak age of information
in priority queuing systems. IEEE Transactions on
Information Theory, 67(1):373–390.
Yates, R. D. and Kaul, S. K. (2018). The age of in-
formation: Real-time status updating by multiple
sources. IEEE Transactions on Information Theory,
65(3):1807–1827.
Yates, R. D., Sun, Y., Brown, D. R., Kaul, S. K., Modiano,
E., and Ulukus, S. (2021). Age of information: An
introduction and survey. IEEE Journal on Selected
Areas in Communications, 39(5):1183–1210.
SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
162