Design and Implementation of Non-prehensile Manipulation Strategies

Pooja Bhat, Matthias Nieuwenhuisen

and Dirk Schulz

Fraunhofer Institute for Communication, Information Processing and Ergonomics FKIE, Wachtberg, Germany

Keywords:

Non-prehensile Manipulation, Force-torque Control, Compliant Manipulation.

Abstract:

Grasping of objects is not always feasible for robot manipulators, e.g., due to their geometric properties.

Non-prehensile manipulation strategies can enable manipulators to successfully move these objects around.

We discuss strategies for non-prehensile manipulation and focus on the investigation of such manipulation

strategies based on open- and closed-loop control based on force torque measurements. The design of grippers

for moving objects is also an important factor that is evaluated. The strategies are implemented and evaluated

in simulation and on a KUKA LWR4+ manipulator arm.

1 INTRODUCTION

Robotic manipulation tasks are often deﬁned by

grasping or picking an object from a surface or a box

and place it on another place. But in everyday sit-

uations, we humans often use different strategies to

move objects around, e.g., pushing or sliding. In fact,

the ability to skillfully perform non-prehensile ma-

nipulation tasks contributes greatly to manipulative

dexterity of humans. Humans tend to exploit ﬁnger

conﬁgurations with natural haptic and force feedback

while handling a diverse set of objects.

These non-prehensile manipulation strategies can

help a robot manipulator to move around objects that

are too heavy, too small, or to ﬂat to be grasped with

a speciﬁc gripper. Figure 1 shows the handling of dif-

ferent types of objects that are not easy to grasp due

to their geometric properties.

In addition to pushing objects from the side in

some cases applying a perpendicular force on an ob-

ject to move it around is better suited, for instance if

the object is very ﬂat and lightweight, e.g., a sheet of

paper.

Humans exhibit advanced prediction capabilities

which enable estimation of the best action to be

taken to achieve the desired state, which means in-

verse model is assimilated by visual analysis, and/or

is learnt during execution based on action-effect

paradigm. Also, humans are capable of transferring

the learnt behavior to novel objects with different

physical properties (St

uber et al., 2022). However,

https://orcid.org/0000-0002-3706-592X

https://orcid.org/0000-0002-6240-9181

Figure 1: Non-prehensile manipulation like pushing allows

robots to handle objects that are hard to grasp, e.g., heavy,

ﬂat, or small objects.

pushing involves various uncertainties that robots

cannot predict which prevent them from delivering

similar pushing behavior. The main cause of this un-

certainty is the inadequate knowledge on frictional

forces which play signiﬁcant role in pushing (Zhou

et al., 2016). Also, the pushing dynamics is highly

non-linear (Yu et al., 2016). While various proposed

approaches have delivered accurate forward models

for push-effect prediction, generalisation of the mod-

els to novel objects has still remained a challenge

(St

uber et al., 2018; St

uber et al., 2022).

Planning and controlling of various non-

prehensile motions such as pushing, rolling, throw-

ing, juggling have been explored in the literature

(Serra, 2016; Ryu et al., 2013; Lynch and Murphey,

2003). The survey in (Ruggiero et al., 2018) sum-

marizes the advancement in planning and control of

all these motions and provides an extensive literature

review. It further concludes that the growth in the

ﬁeld of non-prehensile manipulation is relatively low

and human-inspired control strategies could provide

a potential solution to complex non-prehensile

manipulation tasks.

A comprehensive literature review is provided on

Bhat, P., Nieuwenhuisen, M. and Schulz, D.

Design and Implementation of Non-prehensile Manipulation Strategies.

DOI: 10.5220/0011320700003271

In Proceedings of the 19th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2022), pages 67-78

ISBN: 978-989-758-585-2; ISSN: 2184-2809

push manipulation in (St

uber et al., 2022), consider-

ing it effective in various scenarios, for instance, with

uncertainty in the environment, and with need for pre-

grasp manipulation. In general, push manipulation

is used to maneuver objects from initial state to goal

state when the grasping of object is not feasible, e.g.,

due to object geometry. In addition, pushing is largely

used for pre-grasping to facilitate grasping of the ob-

ject, e.g., to create space in presence of clutter.

Directed standalone pushing is used in the liter-

ature vastly by mobile robots that are not equipped

with any manipulators. In (Krivic and Piater, 2018;

Krivic et al., 2016), objects are pushed with a sin-

gle contact towards a deﬁned goal while learning the

properties of the object on the ﬂy by observing their

behavior when pushed. In (Krivic et al., 2016), the

target object is expected to remain in a deﬁned cor-

ridor, a region that is free of obstacles. The system

has to autonomously relocate when needed to exe-

cute pushing towards the deﬁned goal. These works

mainly relax the assumption on knowing about the

key geometric properties of the objects to generalize

for novel objects, but apply basic single contact push-

ing due to the lack of manipulators. In (Li and Payan-

deh, 2007), two-agent point contact push is proposed

to allow more than one contact point using two agents

to push the target. This facilitates manipulation of

non-polygonal parts reducing position uncertainties.

Robot manipulators use pushing as an alternative

to grasping in various cases. In (Zito et al., 2012), two

level rapidly exploring random tree (RRT) planners

are designed, of which a global planner explores the

space of possible pushed object conﬁgurations and a

local push planner uses predictive models of pushing

interactions, to plan push sequences. A learning based

technique leverages differentiable physics simulator

to learn mechanical properties of the unknown object

to push it from initial to goal conﬁguration in (Song

and Boularias, 2020). The method computes gradient

distance between predicted and actual poses and uses

the gradient to identify the mechanical properties.

When an object is located in a clutter, pushing is

performed around the target object to achieve gras-

pablity. While in (Dogar and Srinivasa, 2010), the

target object is pushed away and grasped, in (Zeng

et al., 2018; Dogar and Srinivasa, 2011; Cosgun et al.,

2011), the surrounding objects are pushed. The sur-

rounding objects are pushed to create space to place

target object on a cluttered surface in (Cosgun et al.,

2011). It is important to note that in push-grasp lit-

erature, the planning is mostly in the higher level to

generate a sequence of pushes that is required enable

the manipulation of target object. As the goal state of

the surrounding objects are the not the primary con-

cern in these cases, controlled pushes are not applied

on the objects.

The application of pushing as pre-grasp manipu-

lation is not exclusive for cluttered environments, but

is integrated in the manipulation strategies in a hand-

ful of grasp planners. A human-inspired grasping

framework is proposed in (Sarantopoulos and Doul-

geri, 2018) to grasp domestic ﬂat objects, which uses

pushing/sliding to bring the object to the edge of the

table surface to eventually grasp it with one of the

proposed strategies. In (Eppner and Brock, 2015), the

aim is to utilize environmental constraints to grasp the

objects, and the objects are pushed to achieve conﬁg-

uration such that they can be grasped with the sup-

port of external contacts. However, the pushes used

in these approaches are constrained by position and

geometric properties of the objects. For example,

the strategy proposed in (Sarantopoulos and Doulgeri,

2018) cannot slide the objects that are far from the

edge of the table surface. In (Omr

cen et al., 2009), a

learning-based approach is proposed to enable push-

ing of target object to new location from where it

can be grasped easily. The idea is to allow a robot

learn general pushing rule deﬁning the relationship

between the direction of push and the resulting object

motion for a set of objects.

Although pushing is widely used to manipulate

objects, it suffers from prediction and state uncertain-

ties (St

uber et al., 2022). Planning and control of

pushing motion is hence challenging when a hard goal

constraint is imposed as inverse model is not avail-

able to predict the action to be taken to achieve the

desirable state. The problem becomes more complex

with varying geometric shapes and sizes of the tar-

get object. Majority of the approaches investigated in

(St

uber et al., 2022) assume that the geometric prop-

erties of the target objects to be known. This assump-

tion does not bridge the gap between the dexterity of

humans and robots in non-prehensile manipulation.

2 SYSTEM DESIGN

The analysis provided in the previous section high-

lights the dissimilarities in the human and robot push

manipulation which mainly includes the difference in

the push contact conﬁguration and lack of knowledge

on the push-effects due to unavailable object dynam-

ics. In this work, the important constituents of push

manipulation are recognised and designed to provide

a human-inspired solution. The aim is to deliver a

design solution that provides push manipulation of a

vast set of objects with varying geometric properties.

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

Figure 2: Endeffector conﬁgurations for pushing. Left: Sin-

gle point contact. Center: Multi-point contact. Right: Line

contact.

2.1 Gripper Conﬁgurations

Humans tend to relax high-level control by exploit-

ing available ﬁnger conﬁgurations while handling a

diverse set of objects. However, robots mostly use

a single point contact for push applications relying

on complex control for task execution. While single

point contact is easy to establish with a simple rigid

ﬁnger or no gripper, a dexterous gripper attachment

providing features of human hand is not a cost effec-

tive solution. To compensate for the trade-off, in this

work, simple human-inspired gripper conﬁgurations

are proposed: single-point contact, multi-point con-

tacts, line contact.

Each of these grippers are designed considering

hand positioning tendency in humans with varying

geometric properties of the objects. With a dexter-

ous gripper possessing at least two single-joint ﬁn-

gers, all the conﬁgurations can be generated with the

same gripper. However, in this work, different gripper

attachments are designed. Figure 2 depicts the three

realized gripper conﬁgurations.

Single Point Contact. Gripper conﬁguration pro-

viding single point contact allows the manipulator to

apply force on the object at a single point. In the push

manipulation literature, single point contact is usu-

ally established such that the applied pushing force

lies horizontal to the support plane while gravity acts

along the vertical direction. However, applying ver-

tical force on the object constrains the sliding of the

object due to high pushing force. With this conﬁgura-

tion, small objects such as a bottle cap can be manip-

ulated.

Multi-point Contact. A two-point contact is shown

to deliver a more stable push compared to a single

point contact in (Lynch, 1996). This conﬁguration

can be useful when achieving more stable control over

the objects is required, for instance, when they are

relatively ﬂat and deformable, e.g. ﬁles, cards. This

gripper conﬁguration also ﬁnds application in manip-

ulating taller objects with convex/concave surfaces.

Line Contact. When objects are too heavy and/or

big, prehensile manipulation can be restricted by grip-

per design. When the target object is a heavy book or

a box, pushing it from the side while almost wrapping

one or more ﬁngers around the object can be an alter-

nate solution. Also, humans use such pushing strat-

egy to handle odd shaped objects or multiple objects

at once.

With the proposed human-inspired design of grip-

per conﬁgurations, this work aims to handle a di-

verse set of objects with non-prehensile approach us-

ing simple control strategies.

2.2 Control

Humans depend on their natural haptic and force

feedback to control contact forces. Similarly, the con-

tact force between a robot and its environment should

often be monitored to ensure successful execution of

tasks which requires the robot to interact with its envi-

ronment. The control interfaces that enable such com-

pliant behavior are discussed in this section.

Further, various control strategies designed to

compensate for the lack of dexterity and haptic feed-

back in human hands are explained. The control

strategies coupled with gripper design aims to prevent

undesirable effects in the motion of the target objects

as opposed to previously discussed learning based ap-

proaches that learn to predict the effects of pushes for

push manipulation.

When a robot has to push the target object, a per-

pendicular external force is exerted on the support

surface even before any force is applied on the ob-

ject. The force between a gripper and a surface has

to avoid any damage to the robot and its environment.

Further, the applied force by a robot to push the target

object plays an important role in the execution of push

manipulation. Hence, it is necessary to control push

force to avoid sliding of the objects away from robot

gripper. This section discusses different robot control

modes that can be used to obtain desirable interaction.

Open-loop Motion Control with Force-torque Sen-

sor. To use pure motion control for the tasks involv-

ing contact between a robot manipulator and the en-

vironment, an accurate model of the environment is

required (Siciliano et al., 2000). As a precise model

of the environment is difﬁcult to obtain, pure motion

control easily fails to handle such tasks. If the accu-

rate position of the table with respect to robot is not

known, the robot fails to establish contact with the ta-

ble. In worst case, if the table resists the robot from

reaching its commanded position, the robot may dam-

age the table and/or itself.

Design and Implementation of Non-prehensile Manipulation Strategies

Hence, it is important to detect contact between

the robot and the environment. To achieve this, a

force/torque sensor can be mounted on the manipu-

lator to sense the physical interactions (Alex Owen-

Hill, 2021).

Impedance Control. Impedance control is a widely

used method to obtain compliant behavior in robots

(Schindlbeck and Haddadin, 2015; Ott et al., 2010).

It deﬁnes the change in endpoint motion as a function

of disturbance forces. It demands robots to deliver a

deﬁnite mass, spring, and damper properties.

The goal of impedance control is to achieve the

behavior

M ¨x + D ˙x + Kx = F

external

(1)

where M, D and K are positive virtual mass, damping

and stiffness matrices, x ∈ R

is the task-space conﬁg-

uration and F

external

is the applied external force and

(x, ˙x) is the current state.

The impedance controller senses the endpoint

motion x(t) and maps the change in endpoint mo-

tion to appropriate end-effector force −F

external

commanding joint torques using an inverse dynam-

ics model. To get a more precise interaction force

−F

external

, a force-torque sensor providing a feed-

back term can be added at the end-effector (Lynch

and Park, 2017). In addition to impedance control

that is realised via software, compliance can also be

achieved with passive impedance control by manu-

ally adjusting mechanical impedance of the robot with

ﬂexible joints and/or links (Vukcevic, 2020). In addi-

tion, a compliant mechanical device can be interposed

between robot end-effector and environment to ensure

a compliant behavior with passive impedance control.

Both active and passive impedance control can also be

combined to achieve an effective compliant behavior

(Schindlbeck and Haddadin, 2015).

Admittance Control. When executing non-

prehensile tasks such as pushing, the robot should

offer a compliant behavior to provide a controlled

pushing force in the desired directions. To induce

compliant behavior, an external admittance control

loop can be provided to the motion-controlled robot

(Al-Jarrah and Zheng, 1998). Admittance control

maps external force to end-effector acceleration. The

external force applied is measured using a load cell

or a force-torque sensor (Lynch and Park, 2017).

The approach is to calculate the desired end-

effector acceleration

¨x

desired

= M

−1

external

− D ˙x − Kx) (2)

where M, D and K are positive virtual mass, damping

and stiffness matrices, x ∈ R

is the task-space conﬁg-

uration and F

external

is the applied external force and

(x, ˙x) is the current state. The commanded joint forces

and joint torques τ

cmd

can be calculated using inverse

dynamics (Lynch and Park, 2017).

2.3 Control Strategies

Compliant control strategies are needed along with

well-designed grippers to provide a robust control to

perform better in unideal situations. The underlying

objective is to not lose contact with the pushed object.

While a visual feedback can also be utilised to locate

the pushed objects and re-establish contact if the ob-

jects slide away, in this case, only force feedback is

taken into account to monitor physical interactions.

To maintain contact with the target object while

applying a suitable force on the target object to induce

desirable motion, a 1-DOF admittance control policy

is used to map the force/torque measured to push ve-

locities such that,

D ¨x = F

external

(3)

from equation 2.

Alignment of Gripper along Object Surface.

When a robot gripper is not well aligned along the

surface of the target object, the contact between grip-

per and the target object can be broken easily. Con-

sider the example gripper-object conﬁguration from

top-view shown in ﬁgure 3 (left) where “O” is a tar-

get object and “G” is a line contact gripper. The line

gripper here is not perfectly aligned along the surface

of the object. When the robot continues to push the

object in this conﬁguration, the object tends to ro-

tate and eventually loses contact with the gripper as

shown in ﬁgure 3 (center). Hence, it is necessary to

align the gripper along the object surface to avoid the

undesirable rotation of object. The torque produced

at the center of the gripper along perpendicular direc-

tion due to the existing force between the object and

the corner of the gripper can be mapped to a linear

velocity along the surface of the gripper given by,

= −k

(4)

where v

is the velocity along the surface of the ob-

ject, τ

is a non-zero torque at the center of the grip-

per about z-axis and k

is the proportional gain. This

allows gripper to move to the center of the object and

achieve a desirable conﬁguration as shown in ﬁgure

3 (right) where torque τ

= 0. However, it is neces-

sary to choose a suitable proportional gain to obtain a

smooth alignment without oscillations.

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

Figure 3: Effects of alignment of an endeffector (G) with an

object (O) based on torque (τ

Regulation of Push Velocity during Alignment.

To allow smooth pushing motion, it is necessary to

control push velocity such that the velocity along

push direction, for example, v

in ﬁgure 3 is maxi-

mum when alignment velocity v

= 0 which means

the torque τ

= 0 and is minimum when the torque

and alignment velocities are high. The behavior can

be achieved by mapping the torque τ

to push velocity

Emulation of Curved Gripper. Humans tend to

form a curved conﬁguration, especially when small

multiple objects are to be pushed, to keep the objects

integrated. This could be resembled by a curved grip-

per design. An alternate solution could be provided

to induce the feature of curved gripper conﬁguration

in a line gripper by inducing timed oscillations into it

as shown in ﬁgure 4. The cyclic angular motions are

commanded here about z-axis to produce oscillations

at a deﬁnite frequency rate. This enforces pushing of

objects from either sides of the gripper to the center

to keep objects integrated. Additionally, the torque

induced about z-axis from the target object at the cor-

ner or at the off-center of the gripper can be mapped

into angular velocity providing a closed loop control

given by,

= k

(5)

where ω

is the angular velocity about z-axis, τ

the

measured torque, and k

is a proportional gain. In this

case, oscillations do not occur at constant rate but,

angular motions depend on the torque generated by

the virtue of the position of the target object. When

the object/s are at the center of the gripper, no angu-

lar motions are generated. This case demonstrates the

role played by the design of gripper in simpliﬁcation

of control strategy. If a curved gripper is used over a

simple line gripper, the design of the gripper compen-

sates for the control. A simple gripper however relies

more on the control strategy.

2.4 Software Architecture

In order to provide a suitable software design pattern

for the execution of actions in a pre-deﬁned sequence,

a state machine is implemented such that each state

Figure 4: Comparison of curved gripper and oscillated line

gripper conﬁgurations.

Figure 5: An action sequence for a push manipulation task.

in the state machine corresponds to an atomic action

that can be invoked from the action sequence. The ac-

tion states command velocities to actuate the desired

actions and end of each action is marked by a sub-

goal encoded into the states. Each state is independent

of each other, providing a ﬂexible arrangement of ac-

tions in the action sequence. Our actions are: Reach:

In this phase the robot end-effector moves towards the

target object and lands behind the object surface in the

pushing direction on the support surface. The goal

is to form contact with support surface and not with

the object surface. The phase ends when robot forms

contact with the support plane. Translate: The robot

is expected to form contact with object in this phase.

It translates towards the object while in contact with

the support plane. The end of the phase is signiﬁed

by the contact event between robot gripper and object

surface. At the end of this phase, the gripper is in con-

tact with both object and support plane. Push: While

pushing is a an atomic action by itself, the action can

be decomposed and organised in a way to avoid con-

tinuous pushing for more ﬂexibility. For instance, the

robot can be commanded additional actions to raise

and reorient to disconnect and reconnect contacts to

provide more possible actions. Such discretisation al-

lows robot to change the orientations and directions

of push with no constraint of pushing in a continuous

trajectory. When the object reaches pre-deﬁned goal

location, the phase is ended. Disconnect: All the con-

tacts can be detached once the goal is reached and the

robot can return to its “home” position. The reorient

and raise actions can also be utilised for the purpose.

Figure 5 shows an action sequence with four

action-phases with different atomic actions.

Design and Implementation of Non-prehensile Manipulation Strategies

3 EVALUATION

We conducted experiments both, in simulation and on

a 7-DoF KUKA LWR 4+ robot arm.

The real robot arm provides torque measurements

for each of its joints and an estimated external Carte-

sian force and Cartesian torque acting on the endef-

fector. However, the torque estimate is not reliable,

as in our scenarios forces applied to different posi-

tions of the endeffector yield a large torque at the ﬁrst

robot joint due to the long lever. Thus, as our endef-

fector axis is perpendicular to the surface, we use the

torque measured at the endeffector joint in this work

along with the estimated external force to obtain a bet-

ter estimate.

An interface between external computer and

KUKA Robot Controller (KRC) can be established

using Fast Research Interface (FRI) library provided

by KUKA. The FRI library can be used to command

robot in joint position, joint impedance and carte-

sian impedance control modes. A library extending a

higher level interface over the original FRI communi-

cation protocol is provided by the Stanford Artiﬁcial

Intelligence Laboratory.

In this work, Robot Operating System (ROS) in-

terface developed by the Research Center E. Piaggio

is used to provide realization in a standard, agile con-

trol framework. Also, the ROS interface enables nec-

essary tools for robot simulation and visualisation.

The ROS package for KUKA LWR

provides ﬁnal

interfaces with KUKA FRI, Stanford FRI library and

also includes Gazebo simulation plugin.

3.1 Pushing with KUKA LWR4+ Robot

The experiments were conducted with a stack of pa-

per bundles and a book, and a cutting board which is

comparatively lighter, depicted in ﬁgure 1. In these

cases, a line gripper can be seen pushing the objects

from a side surface. As the gripper is not aligned at

the center of the surface of the objects, the measured

torque (about z-axis in this case) is then mapped to

the linear velocity along the surface of the object (ve-

locity in x-axis) to provide a better alignment. The

line gripper has a push contact with a board with a

stack of objects at one of its corners. If the contact is

established perfectly at the center of the gripper, ide-

ally, no torque is produced. However, if unaligned,

a high torque can be observed depending on the dis-

tance between the point of contact and the center of

the gripper and on the mass of the object/s.

The commanded velocities and the measured

torque in push manipulation executed with the above

https://github.com/CentroEPiaggio/kuka-lwr

Figure 6: Torque measurements from push manipulation of

a set of objects with different geometric properties and ori-

entations in a real world scenario (depicted in ﬁgure 1). Top:

Stack of paper bundles. Bottom: Cutting board.

mentioned cases are shown in ﬁgure 6. As in all

the considered cases, the torque produced has to def-

initely reﬂect in the torque measurements in z-axis, it

is taken into consideration for evaluation. The torque

measurement from the push manipulation of the stack

of paper bundle and a book is shown in the top graph.

In the reach phase, the robot moves down towards the

object and touches the support surface. The velocity

is commanded in z-axis to achieve this motion. Ide-

ally, the torque should be zero, as there is no force

acting on the gripper. However, some torque can be

observed in the reach phase due to noise in the sensor

readings. A small upward movement is commanded

during experiment after the robot makes contact with

the support surface so as to avoid scratching of the

surface by the gripper. A peak in the velocity in z-

axis signiﬁes this movement.

An online sensor calibration is performed after the

contact with the surface. In the translate phase, a

small torque can be observed. A sharp increase in

the torque value is due to the contact established with

the target object. The torque is mapped to linear ve-

locity which causes the velocity in x-axis to exhibit

a negative correlation with the torque values. At the

point of alignment, at approximately 30 seconds, the

torque and velocity drop indicating a good alignment

with the object. Although line gripper is aligned at

the center, the oscillations can be observed as the sys-

tem is under-damped. The torque values drop again

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

when the contact is disconnected by moving the grip-

per away from the object and the support surface.

When a push manipulation is executed with the

similar order of actions for a board which is compar-

atively much lighter than the stack of paper bundle,

a very small torque (maximum 0.2 Nm) is measured.

The alignment velocity in x-axis is also consequently

small, hence producing an average alignment during

pushing. Although robot managed to align approxi-

mately at the center of the board during experiment,

it is hard to interpret the point of occurrence of align-

ment unlike in the case of paper bundle stack.

When line gripper makes a contact at the corner of

the board, the contact does not lie exactly at the cen-

ter of the gripper, which induces considerably high

torque due to the high mass of a paper bundle and a

book stacked on the board. This causes the controller

to react and produce an alignment velocity which

causes motion of the robot to align to the center. In

this case, the board slid slightly to the other off-center

when the robot tried to align causing a sharp change

in the direction of torque at around 15 seconds. The

board then remained in the same contact conﬁguration

which is indicated by a non-zero torque in the graph.

The push phase is ended when the robot disconnects

from the object and the support surface.

3.2 Pushing in Simulation

We use the gazebo plugin provided in the KUKA

LWR ROS package to control the robot in simula-

tion. As the joint torque measurements in simulation

are not accurate as the commanded torques are not

taken into account while computing estimated exter-

nal torques, we employ a force-torque-sensor plugin

to obtain wrench measurements at the endeffector, in

contrast to the real robot setup.

The experiments conducted to evaluate the perfor-

mance of the force/torque sensor plugin in simulation

is similar to that of the real robot platform. As in the

case of real robot, the push manipulation is executed

on various objects that differ in size, shape and mass.

In addition, the corner-to-surface contact conﬁgura-

tion between the gripper and the target object is also

considered for the experimentation.

The simulated objects to push are a) a heavy block

(2kg), b) a slab (200g), c) a disc (100g), and d) a block

(1kg). In the ﬁrst two cases (a and b) the gripper

establishes an even contact on a side surface of the

target object. Even though the objects heavy block

and slabs are comparable in shape, they vary in mass.

The line gripper establishes a centered contact with

the curved curved surface of the disc (c). The block

(d) is aproached fat one of its corners. The results are

depicted in ﬁgure 7.

The measured force/torque values are in the sensor

co-ordinate frame in simulation. Hence, the torque

due to push manipulation in the experiments in re-

ﬂected in torque about x-axis. For the heavy block

(a), in the reach phase the robot moves down with ve-

locity commanded in the z direction. In this phase, no

external force is acting on the robot end-effector and

the measured torque is zero, thus providing an ideal

measurement as opposed to real robot sensors which

usually possess some noise. In the translate phase,

a small torque can be observed due to contact with

the support surface. The sudden increase in torque

signiﬁes the established contact with the target object

approximately at 36 seconds. The robot continues to

push the object while aligning along the surface of the

object which is represented by the oscillating torque

and velocity values in x direction.

When the slab (b) with comparably low mass is

pushed, a very small torque is induced. The reach

and translate phases are however comparable to the

corresponding phases in the case of heavy block in

terms of torque measurements. The robot in this case

is able to align along the surface but does not behave

as good as with a heavy object. The results from

these two experiments are comparable to the ﬁrst two

experiments on a real robot with the stack of paper

bundle and a board. The push manipulation of the

light weighted disc (c) also exhibits similar behavior

as with the slab. The curved surface however adds an

additional challenge in pushing which causes the line

contact gripper to barely maintain a contact with the

disc. During pushing, the disc moves off-center and

eventually loses contact with the gripper at approxi-

mately 45 seconds.

In the conﬁguration where the contact is estab-

lished by the gripper at a corner of the block (d), the

torque values are considerably higher than zero in the

translate phase as the corner is not perfectly at the

center. The motion induced by alignment velocity in

x direction causes the object to slide along the surface

of the gripper in a “to and fro” fashion. This behavior

is captured in a roughly periodic curve.

3.3 Gripper Conﬁgurations

The three different gripper conﬁguration designs de-

scribed in this work are evaluated on a different set of

objects. Each gripper conﬁguration is designed with

a purpose so as to collectively provide pushing of ob-

jects with various geometric properties. In the con-

ducted experiments, the objects are chosen for each

gripper with an aim to corroborate their relevance and

identify their limitations.

Design and Implementation of Non-prehensile Manipulation Strategies

Figure 7: Torque measurements from push manipulation in

simulation environment. a) Heavy block. b) Slab. c) Disc.

d) Block.

Single Point Conﬁguration. To set up a single

point gripper conﬁguration, a sponge block is at-

tached to the manipulator as shown in ﬁgure 8. This

also serves as a source for passive compliance when a

contact is established with the environment. Although

the sponge attachment mostly delivers a higher sur-

face contact for a “point” contact, the point contact is

only relative to the geometry of the target object.

In this experiment, the single point contact is used

to manipulate a set of objects possessing various ge-

ometric properties. A set of ﬂat and deformable (tis-

sue), ﬂat and wide (board), small (box), tall and light

(cylinder), ﬂat and heavy (paper bundle) objects are

manipulated as shown in ﬁgure 8. The robot is ex-

pected to establish a contact on the top surface of the

object and push it to a deﬁned location while clamp-

ing the object against its support surface. The robot

moves down until it reaches the surface of the ob-

ject constituting a reach phase. The increase in force

due to contact triggers the push action to form a push

phase.

The robot manipulator is able to squeeze and push

most of the considered objects, however, the conﬁg-

uration fails to handle the heavy objects. In the case

of the board, the object is wide which makes it ro-

tate about the contact point during pushing. But, the

robot is able to push the board to a desired location.

However, with increase in the weight of the object,

the single point contact starts to fail as it slips off the

surface of the object.

This behavior is reﬂected in the measured force

values during task execution as shown in ﬁgure 9. The

velocity commands in z and y directions are reach and

push velocities respectively. The negative velocity in

the reach phase causes the robot to move down to-

wards the object. A high force is measured when the

robot touches the surface of the object. The estab-

lished contact switches the action from push to trans-

late where the push velocity is commanded in y direc-

tion.

In the case of a successful push of the objects,

the force in z-axis which corresponds to force due

to contact between object surface and the gripper, is

linearly increasing in the translate phase. The force

is constrained to 5N in this direction. The existence

of force in z direction shows that a clamping force is

applied on the top of the object. The comparatively

higher force measured in y-axis is also increasing lin-

early and it also increases with the mass of the ob-

ject. The maximum force measured with tissue and

small plastic box is around 10N and with object with

higher mass, the force exceeds 15N. The sheer force

in the sponge attachment could be a source of mea-

sured force in both the directions.

The robot as mentioned earlier, fails to move the

heavy paper bundle. After the contact is made with

the object, the robot tries to push the object in the y

direction. However, when the object fails to move, the

gripper slips and moves away from the object. The re-

gion where the slippage occurs is marked in the ﬁgure

9. The trough in the graph at around 35 seconds can

be interpreted as a shift from static friction to dynamic

friction occurring due to the resistance offered to the

motion by the surface of the paper bundle during the

slip. The robot slightly moves down due to force in z

direction after it slips off the object surface.

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

Figure 8: Single point conﬁguration for different objects: a) Tissue. b) Board. c) Small box. d) Hollow cylinder. e) Paper

bundle.

Figure 9: Force measurements from push manipulation of a

set of objects with single point gripper conﬁguration. Top:

Tissue. Bottom: Paper bundle.

With the considered set of objects, the gripper

conﬁguration achieves successful push in the case of

light objects irrespective of the geometry as long as it

is possible to make a contact at the top surface. How-

ever, the gripper conﬁguration does not deliver good

results for a wide and/or a heavy object.

Line Conﬁguration. A line gripper conﬁguration

provides a high surface area to establish contact with

a target object, hence providing a greater grip to ma-

nipulate heavy and/or large objects. Also, the high

surface area can be useful in pushing multiple small

objects such as a pile of screws.

In this experiment, a heavy object, i.e., a bundle of

paper is placed on a board to induce more friction in

the setup. The line gripper is able to push the heavy

object by aligning with a surface of the object. While

the gripper can push the object when it is almost at

the center of the object, pushing with a bad alignment

often causes the object to rotate, eventually losing the

contact with the object. In this case, an alignment

strategy is used to map the measured torque to linear

velocity to align the gripper with the surface of the ob-

ject. The gripper is able to push the object, even when

the mass is increased by adding an another bundle of

paper.

In the graphs shown in ﬁgure 10, commanded ve-

locities and the measured torque provide an overview

of the experiment with two paper bundles. In the

reach phase, the commanded velocity is in z axis to

move the robot towards the object in the downward

direction. The robot touches the support surface at

around 20 seconds which causes peak in the torque

values. The next deﬁned action translate is hence trig-

gered, causing the robot to move towards the object

while in contact with the support surface. The com-

manded velocity in y direction is used for this action.

The translation is ended when the robot touches the

object, which causes the torque value to increase fur-

ther. The velocity in x which corresponds alignment

velocity along the surface of the object. The gripper

aligns and pushes the object in push phase and ﬁnally

disconnects by moving up when desired location is

reached. A similar behavior was observed with re-

duced mass of the single paper bundle. The line grip-

per can easily handle the target objects when a full

surface-to-surface contact is established and can serve

the purpose of the design to handle heavy objects.

When line gripper is used to push objects with no

even surface, for example, curved or concave objects,

the design of the line gripper cannot be exploited. For

instance in an experiment with a tape roll the line grip-

per contact is comparable to a point contact push. Al-

though a combination of low push velocity and a good

force/torque sensor can enable the line gripper to push

the curved surface objects, it does not always deliver

a good result.

Multi-point Conﬁguration. A multi-point gripper

is comparable to line gripper when it is aligned along

a even surface of an object. It provides a contact at

two points on an even surface, providing the same sta-

bility as a line gripper. The feature of the design that

surpasses the design of the line gripper conﬁguration

Design and Implementation of Non-prehensile Manipulation Strategies

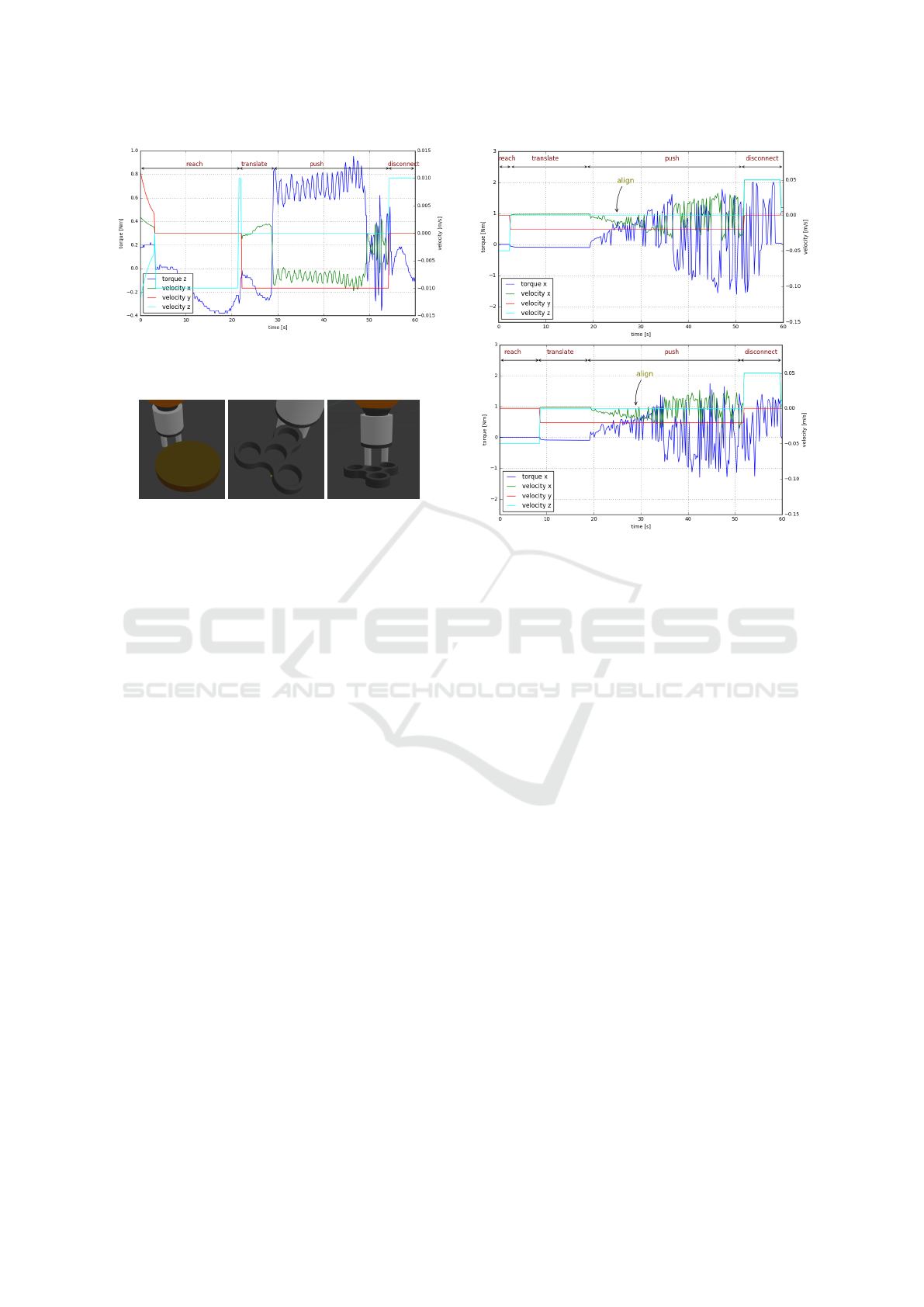
Figure 10: Commanded velocities and measured torques for

push manipulation using line conﬁguration. Two paper bun-

dles on a board pushed using line conﬁguration.

Figure 11: Multi-point conﬁguration for different objects:

a) Disc. b) Fidget spinner, convex contact surface and c)

concave contact surface.

is its ability to ﬁrmly handle objects with curved and

concave surfaces. A two-point gripper can be seen es-

tablishing two contacts with a disc and a ﬁdget spin-

ner in ﬁgure 11.

The push manipulation executed with the disc and

the ﬁdget spinner (aligning with the curve surface) in

simulation and the gripper conﬁguration was able to

push both the objects to the desired location. The

graphs in ﬁgure 12 show the commanded velocities

and the measured torque values during execution, rep-

resenting the states involved. The torque is measured

by a force-torque sensor plugin in the simulation and

the measurement shown in the graph is in the sensor

co-ordinate system. In the reach phase, velocity is

commanded in z-axis to move the robot in downward

direction. The establishment of contact invokes the

translate phase marked by a non-zero velocity com-

mand in y-axis.

In both cases, a single point contact is formed ini-

tially as the object is not centered with the axis of the

multi-point gripper. Hence, a sudden change in the di-

rection can be seen in the torque, and consequently in

the velocity in x-axis, signifying the alignment with

the surface by mapping generated torque to velocity.

Further, the robot continues to push the target object

in the push phase and ﬁnally disconnects when the

target location is reached by moving up in z direction.

Although the multi-point conﬁguration achieves

the push manipulation task in this experiment, the

success also depends on the distance between the two

ﬁngers of the gripper and the size of the object.

Figure 12: Commanded velocities and measured torques

for push manipulation using multi-point conﬁguration. Top:

Disc. Bottom: Fidget spinner.

3.4 Control Strategies

Open Loop Control. To investigate the cases where

the open loop control fails to handle the geometric

properties and/or the orientations of the target ob-

jects, experiments are conducted in both simulation

and real-world environment on different set of objects

and push contact conﬁgurations.

We evaluate different contact situations with the

line gripper and a stack of paper bundles on a cutting

board: a) the line gripper is in contact near the edge

of the board such that only half of the gripper surface

forms contact with the board surface, b) the object

stack is disoriented with respect to the gripper surface

and c) the gripper makes contact with it away from the

center and near the center respectively. In the ﬁrst two

cases, the gripper loses contact with the stack during

pushing as it begins to rotate. However, in the third

case, the gripper is able to keep the contact intact as

the stack is only slightly rotated and hence tends to

align passively with the gripper while rotating.

The experiments with open-loop control are also

conducted in simulation environment with a similar

and an additional case. The objects used for push

manipulation are a) a slightly disoriented block (1kg)

which makes an off-center contact with the gripper

and b) a pile of buttons (5g each) lying away from

center of the gripper. The objects are pushed using an

open loop control.

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

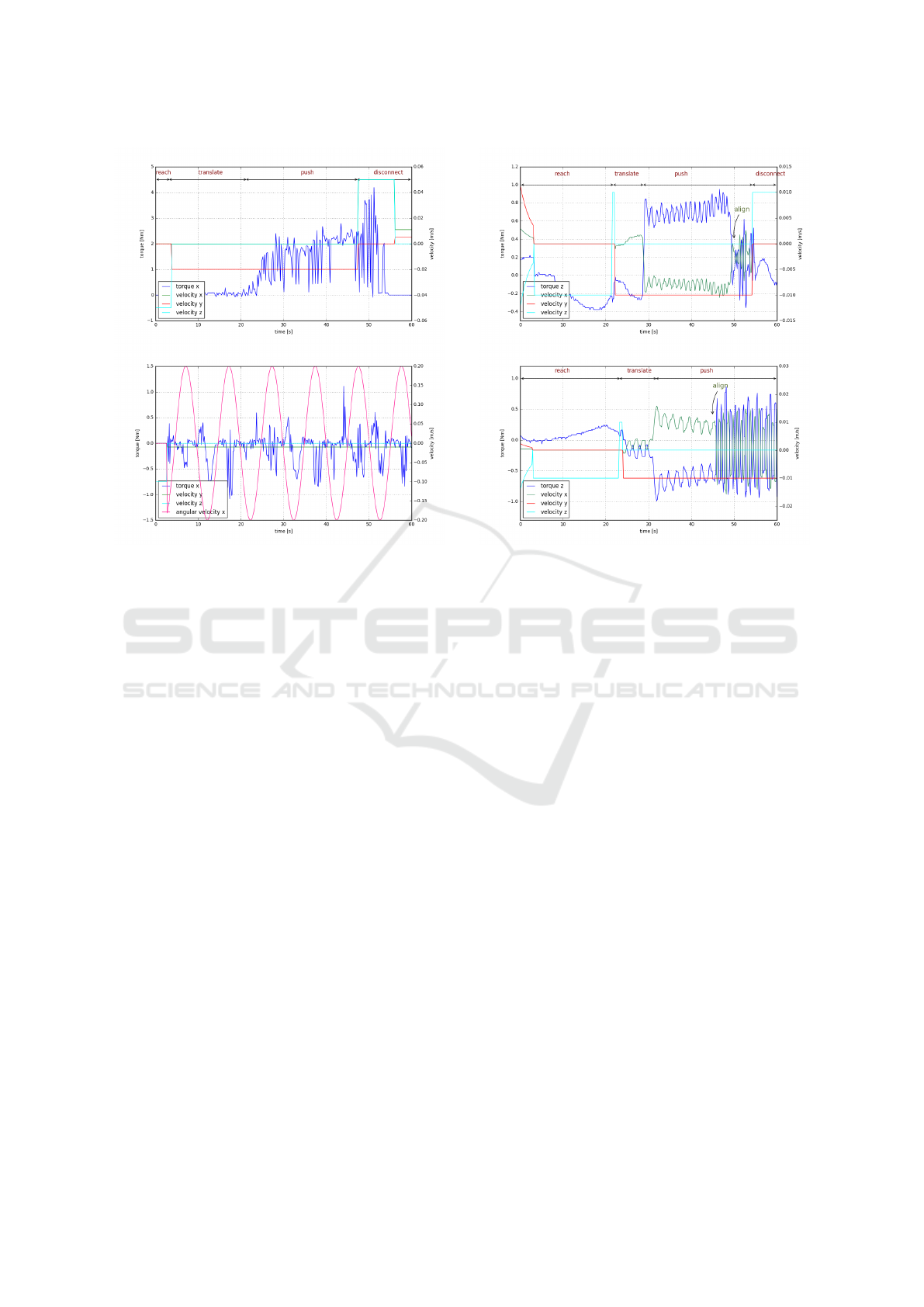
Figure 13: Commanded velocities and measured torques for

different push contact conﬁgurations using open loop con-

trol. Top: Line gripper pushing at a contact away from the

center of a slightly tilted block. Bottom: Line gripper in-

duced with oscillations to handle a pile of buttons.

The velocity of -0.02m/s is commanded in y di-

rection to push the block (a). As the object is only

slightly tilted, the expected behavior would be the

alignment of the gripper along the object surface as in

the real world scenario. However, gazebo simulation

does not handle this contact situation well, resulting in

a sliding of the object along the surface of the object

quickly during pushing. The measured torque values

are shown in ﬁgure 13. As the push phase begins, the

torque increases as the gripper slides away.

In the case of a pile of button, a periodic oscil-

lation is induced in the line gripper to emulate the

curved gripper design to house the multiple objects

at the center of the gripper. In the graph shown in

the ﬁgure 13, the angular velocity about x axis is the

commanded velocity to induce oscillations given by

= 0.2 sin(t). However, the objects still tend to

escape away from the gripper as the gripper blindly

oscillates without taking any feedback into account.

In the considered case, two buttons out of three were

pushed into the target location. The measured torque

values capture the approximate to and fro movement

of the buttons along the surface of the gripper.

Closed-loop Control. For the similar conﬁgura-

tions of off-center contacts for the stack of paper bun-

Figure 14: Commanded velocities and measured torques for

different push contact conﬁgurations using closed loop con-

trol. Top: Line gripper away from the center with partial

surface contact with the target object. Bottom: Line grip-

per away from the center with edge contact with the target

object.

dles in the open loop experiment (a and b), a push

manipulation is performed with a closed loop control

on the real robot platform. In both cases, the gripper

successfully aligns with the object surface and moves

to the center while pushing the object to the target

location. The resulting measurements are shown in

the ﬁgure 14 for both these cases. The gripper moves

along the surface and when the center is reached, the

alignment is signiﬁed by oscillations. The point of

this transition is vivid in both the measurements. The

noise in the torque measurements in reach phases are

due to calibration error which is ﬁxed by online cali-

bration before the push phase is entered in both cases.

The experiment on the pile of buttons is carried

out in the simulation environment by mapping the

torque to angular velocity instead of commanding pe-

riodic oscillations. The pile of buttons are not aligned

exactly at the center in the initial push conﬁguration.

With the closed loop control the robot was able to

bring the buttons to align along the surface of the grip-

per and push it to desired location in two out of three

runs.

Design and Implementation of Non-prehensile Manipulation Strategies

4 CONCLUSION

The design of simple endeffectors paired with suit-

able control strategies allows for the non-prehensile

manipulation of a variety of objects that otherwise

would be hard to grasp. We have shown that sin-

gle contact endeffectors can be used to move ﬂat,

lightweight objects. Heavier objects can be success-

fully pushed with line-contact endeffectors. A torque-

based closed-loop control strategie facilitates stable

contact with the pushed objects along the trajectory

without visual feedback.

REFERENCES

Al-Jarrah, O. M. and Zheng, Y. F. (1998). Intelligent com-

pliant motion control. IEEE Transactions on Sys-

tems, Man, and Cybernetics, Part B (Cybernetics),

28(1):116–122.

Alex Owen-Hill (2021). Robotics research 101: Getting

started with force control. [Online].

Cosgun, A., Hermans, T., Emeli, V., and Stilman, M.

(2011). Push planning for object placement on clut-

tered table surfaces. In IEEE/RSJ Int. Conf. on intelli-

gent robots and systems.

Dogar, M. and Srinivasa, S. (2010). Push-grasping with

dexterous hands: Mechanics and a method. In

IEEE/RSJ Int. Conf. on Intelligent Robots and Sys-

tems.

Dogar, M. and Srinivasa, S. (2011). A framework for push-

grasping in clutter. Robotics: Science and systems.

Eppner, C. and Brock, O. (2015). Planning grasp strategies

that exploit environmental constraints. In IEEE Int.

Conf. on Robotics and Automation (ICRA).

Krivic, S. and Piater, J. (2018). Online adaptation of robot

pushing control to object properties. In IEEE/RSJ Int.

Conf. on Intelligent Robots and Systems (IROS).

Krivic, S., Ugur, E., and Piater, J. (2016). A robust push-

ing skill for object delivery between obstacles. In

IEEE Int. Conf. on Automation Science and Engineer-

ing (CASE).

Li, Q. and Payandeh, S. (2007). Manipulation of convex

objects via two-agent point-contact push. The inter-

national journal of robotics research, 26(4):377–403.

Lynch, K. M. (1996). Nonprehensile robotic manipulation:

Controllability and planning. Carnegie Mellon Uni-

versity.

Lynch, K. M. and Murphey, T. D. (2003). Control of

nonprehensile manipulation. In Control Problems in

Robotics, pages 39–57. Springer.

Lynch, K. M. and Park, F. C. (2017). Modern Robotics.

Cambridge University Press.

Omr

cen, D., B

oge, C., Asfour, T., Ude, A., and Dillmann,

R. (2009). Autonomous acquisition of pushing actions

to support object grasping with a humanoid robot. In

IEEE-RAS Int. Conf. on Humanoid Robots.

Ott, C., Mukherjee, R., and Nakamura, Y. (2010). Uniﬁed

impedance and admittance control. In IEEE Int. Conf.

on robotics and automation.

Ruggiero, F., Lippiello, V., and Siciliano, B. (2018). Non-

prehensile dynamic manipulation: A survey. IEEE

Robotics and Automation Letters, 3(3):1711–1718.

Ryu, J.-C., Ruggiero, F., and Lynch, K. M. (2013). Con-

trol of nonprehensile rolling manipulation: Balanc-

ing a disk on a disk. IEEE Transactions on Robotics,

29(5):1152–1161.

Sarantopoulos, I. and Doulgeri, Z. (2018). Human-inspired

robotic grasping of ﬂat objects. Robotics and au-

tonomous systems, 108:179–191.

Schindlbeck, C. and Haddadin, S. (2015). Uniﬁed passivity-

based cartesian force/impedance control for rigid and

ﬂexible joint robots via task-energy tanks. In IEEE

Int. Conf. on robotics and automation (ICRA).

Serra, D. (2016). Robot control for nonprehensile dynamic

manipulation tasks. In Int. Conf. on Informatics in

Control, Automation and Robotics.

Siciliano, B., Villani, L., and Federico, N. (2000). From in-

direct to direct force control: A roadmap for enhanced

industrial robots. Rob

otica.

Song, C. and Boularias, A. (2020). Learning to slide un-

known objects with differentiable physics simulations.

arXiv preprint arXiv:2005.05456.

uber, J., Kopicki, M., and Zito, C. (2018). Feature-based

transfer learning for robotic push manipulation. In

IEEE Int. Conf. on Robotics and Automation (ICRA).

uber, J., Zito, C., and Stolkin, R. (2022). Let’s push things

forward: A survey on robot pushing. Frontiers in

Robotics and AI, 7.

Vukcevic, D. (2020). Lazy robot control by relaxation of

motion and force constraints. Technical report, Fach-

bereich Informatik.

Yu, K.-T., Bauza, M., Fazeli, N., and Rodriguez, A. (2016).

More than a million ways to be pushed. a high-ﬁdelity

experimental dataset of planar pushing. In IEEE/RSJ

Int. Conf. on intelligent robots and systems (IROS).

Zeng, A., Song, S., Welker, S., Lee, J., Rodriguez, A., and

Funkhouser, T. (2018). Learning synergies between

pushing and grasping with self-supervised deep rein-

forcement learning. In IEEE/RSJ Int. Conf. on Intelli-

gent Robots and Systems (IROS).

Zhou, J., Paolini, R., Bagnell, J. A., and Mason, M. T.

(2016). A convex polynomial force-motion model for

planar sliding: Identiﬁcation and application. In IEEE

Int. Conf. on Robotics and Automation (ICRA).

Zito, C., Stolkin, R., Kopicki, M., and Wyatt, J. L. (2012).

Two-level RRT planning for robotic push manipula-

tion. In IEEE/RSJ Int. Conf. on intelligent robots and

systems (IROS).

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics