A Geometric Approach for Partial Liquids’ Pouring from a Regular

Container by a Robotic Manipulator

Jeeangh Jennessi Reyes-Montiel

, Antonio Marin-Hernandez

and Sergio Hernandez-Mendez

Artiﬁcial Intelligence Research Institute, Universidad Veracruzana, Calle Paseo No. 112, Xalapa, Mexico

Keywords:

Partial Liquids Pouring, Autonomous Mobile Robots, Geometric Control.

Abstract:

Partial liquid pouring is a very useful task in many environments; however, it is still a very challenging task for

autonomous mobile robots. In this work, is presented a geometric approach to accurately partial pouring by

autonomous robots. While diverse approaches propose to deal with this problem measuring liquid’s volume at

destination container, in this work is analyzed the geometry and initial volume of liquid at pouring container,

i.e., liquid’s volume and container characteristics are known. Then based on the transversal sections volumes’

is proposed to control pouring. Proposed approach computes the cross-section areas formed by liquid in the

container when this is tilted an angle θ. The geometric analysis shows that an angle-based linear control does

not guarantee a regular ﬂow to perform an accurate liquid control, since cross-sectional volumes have not linear

relation with the angle θ when tilted. As it is show in this work, these volumes increase and decrease according

to the tilted angle and the container characteristics. To effectively obtain a regular ﬂow those volumes should

be considered in the control phase as here is proposed.

1 INTRODUCTION

Many abilities on autonomous mobile robots and par-

ticularly on service robots have been implemented

and developed over last years. Nowadays, au-

tonomous and service robots can realize diverse tasks

on many different environments in a very successful

way. Mobile robots can: mapping their environments,

determine and execute trajectories, avoid ﬁxed and

moving obstacles, detect, recognize, and interact with

users or other systems, and manipulate correctly di-

verse objects; all these very important and required

tasks for successful service robots. However, and de-

spite of robots can effectively pour liquids from one

container to other, generally this task is done in very

controlled environments and pouring the complete or

ﬁxed amount of liquid. The pouring of partial and

varying quantities of liquids is still a challenging task

for service robots.

To successfully perform this task, most ap-

proaches require the detection and monitoring liquid’s

level, process generally done at destination container.

The problem lies mainly due to the different geome-

https://orcid.org/0000-0003-3194-914X

https://orcid.org/0000-0002-7697-9118

https://orcid.org/0000-0001-9997-9690

tries of the containers, great variety of liquids and par-

ticularly by the intrinsic characteristics of them (Do

and Burgard, 2019). This task, generally solved by

humans by reinforcement learning, is very important

in many human environments; so particularly, robots

and service robots should have the ability to deal with

it. Moreover, in such environments, humans often

don’t speciﬁcally make precise measurements of the

liquids they wish pour; for it, sometimes they use the

relation to some containers e.g., a cup or a glass for

measure a speciﬁc amount of liquid (Schenck and

Fox, 2017). Or, on the other hand, people usually use

subjective and undeﬁned measures, which are gener-

ally mentioned in expressions such as: “pour me a

little more than half a cup of coffee” or “just a little

bit, please”. Humans can deal with language inaccu-

racies and are sufﬁciently able to learn complex tasks

as partial pouring of ﬂuids.

Solving such a task requires a robust motion con-

trol, as well as a very accurate liquids characteris-

tics detection. However, for a robot, it is not easy to

carry out this task due to the complexity of ﬂuids dy-

namics modeling (Schenck and Fox, 2017), (Pan and

Manocha, 2016).

In this work, is presented a special case of ﬂuid

handling, speciﬁcally the problem of pouring a par-

ticular quantity of liquid from a known container to

688

Reyes-Montiel, J., Marin-Hernandez, A. and Hernandez-Mendez, S.

A Geometric Approach for Partial Liquids’ Pouring from a Regular Container by a Robotic Manipulator.

DOI: 10.5220/0011321600003271

In Proceedings of the 19th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2022), pages 688-694

ISBN: 978-989-758-585-2; ISSN: 2184-2809

another (unknown). To achieve this task a geometric

approach has been developed, which is supported on

a simpliﬁed hydro-dynamic model. To validate our

approach some tests on simulation environments are

presented.

This work is organized as follows. In next sec-

tion some important works related to the spill prob-

lem is described in the next section. Subsequently, in

section 3 it will be described the proposed geomet-

ric approach to solve the spillover problem. Then, in

section 4 presents the results obtained from the sim-

ulation. Finally, at section 5 the conclusions are pre-

sented.

2 RELATED WORKS

The problem of precise liquids’ pouring has become

very important in recent years There are many appli-

cations both industries and diverse sectors as: com-

merce or services.

For example, in metallurgy industry is a very com-

mon and important task, where it is required to main-

tain a constant ﬂow to prevent oxidation, air entrap-

ment and erosion on metals (Noda and Terashima,

2006), (Noda and Terashima, 2007). To deal with

such problem in (Castilla et al., 2017) is presented

an approach to automate liquids pouring from a tilt-

ing ladle. Considering only the tilting ladle in mo-

tion, it is proposed to rotate the ladle at an angular

speed prescribed by a geometric and dynamic calcu-

lation to keep the discharge ﬂow constant. To simplify

the geometry ladle is considered as a cylindric recip-

ient with circular weir. The resulting angular veloc-

ity was used as input for a set of computational ﬂuid

dynamics simulations to later calculate the trajectory

of the spilled liquid. In (Sueki and Noda, 2019) it

is developed an improved model, initially proposed

in (Sueki and Noda, 2018), to pour molten metal in

a container by controlling the tilting ladle. The pro-

cess is achieved using a spill ﬂow feedback control

to improve tracking performance. The discharge ﬂow

rate is computed by using an extended Kalman ﬁlter

and controlled using a PID scheme. The proposed ap-

proach has been applied at laboratory with a pouring

robot.

Other approaches use physical models of simpli-

ﬁed dynamics; for example, in (Pan and Manocha,

2016), is presented an approach using intrinsic prop-

erties of liquids to transfer them with a robotic ma-

nipulator from a container to another avoiding with

it, the high-cost solution of Navier-Stokes model. A

motion planning algorithm is then used to compute

a smooth and collision-free trajectory (Park et al.,

2012), (Ratliff et al., 2009), (Pan et al., 2016). The

simpliﬁed parameter set, and dynamic model is re-

stricted to the task of slow-rate liquid transfer. When

the end-effector is moves too fast, the motion de-

scribed could be far from planned trajectory. This ap-

proach pours the complete content of one recipient to

another.

To pour partial amounts of liquids, in (Do and

Burgard, 2019) it is proposed to control pouring liq-

uid level directly at destination recipient; for which,

authors propose, on one side to determine stoppage

using depth data from a low cost RGB-D camera and

on the other side, adapting pouring speed based on

liquid’s level at destination. With the use of an in-

frared light, authors overcome the problem of liquid’s

level detection for different transparency and refrac-

tive index of liquids like water, oil, or milk.

Spilled estimation is very important task when

pouring speciﬁc quantities. In (Matl et al., 2019) it

is proposed a method to pour liquids through haptic

sensing. In this work, initially a robot moves a con-

tainer through a series of tilting movements and ob-

serves the twists induced in the manipulator’s wrist

while the liquid’s center of mass scrolls. It is showed

that with haptic signals and a physics-based model it

can be obtained a high-precision estimate of liquids’

mass and volume in a cylindrical container. Addition-

ally, it is provided a framework for estimating ﬂuid

viscosity.

The geometric characteristics of the container are

also important, for example in (Kennedy et al., 2017)

is proposed a method to autonomously dispense a pre-

cise amount of liquid using visual feedback. Authors

model diverse geometrical containers, showing that,

in particular for square base prisms the ﬂow can be

controlled by observing the height of the ﬂuid in the

receiving container. This approach to pouring control

is not smooth and calibration of the target container is

required.

Finally, in (Dong et al., 2019) are proposed two

approaches to control the movement of a service robot

as it accurately pours liquid from one unknown con-

tainer to another unknown container without the need

for external tools. The ﬁrst proposal focuses on mea-

suring the height of poured liquid in the target con-

tainer. In this case, the action is controlled using a PD

controller, which considers the angular velocity of the

pouring vessel as a process variable and the volume

poured as a control variable. The second method fo-

cuses on the pouring container. The volume poured

is calculated using the relationship between the an-

gle of the pour container and discharged volume. The

action is controlled with a simple proportional con-

troller that takes the angular velocity of pouring vessel

A Geometric Approach for Partial Liquids’ Pouring from a Regular Container by a Robotic Manipulator

689

Figure 1: Initial assumptions: a known cylindrical container

with a known liquid of initial height h

as the process variable and target angle as the control

variable. For it, it is only used sensor inputs from an

RGB-D camera on the robot’s wrist. To perform the

tests, both methods are implemented in a double-arm

robot system and the results show that accurate pour-

ing is obtained in both methods.

This work focuses on pouring speciﬁc quantities

of liquids, through the analysis of the geometry of

pouring container particularly cylindrical containers.

Physical properties of liquids, such as laminar ﬂow is

also considered. In such a way that smooth control be

achieved when pouring liquids. In next section, anal-

ysis of the geometric model will be described.

3 GEOMETRIC MODELING

In this section, the geometrical approach to model and

control partial pouring is presented. Following as-

sumptions are considered:

1. A cylindrical container of height H and radius r.

2. The initial liquid’s height inside the container is

3. Liquid’s density is considered known.

Therefore, the following statements can be stab-

lished. The robot always uses a known pouring con-

tainer. Initial volume of the liquid in the container

can be determined and this is considered known, e.g.,

water, milk or sirup. Additionally, robot is requested

to pour speciﬁc quantities of liquid, e.g., beginning

with 200ml and then 50ml. And ﬁnally, to be able to

compute precisely liquid poured, the pouring process

must ensure a laminar ﬂow, in other words, the robot

should not do sudden motions to avoid turbulences.

3.1 Spilling Angles

Initial and ﬁnal pouring angles can be easily deter-

mined by the problems geometry.

(a) (b)

Figure 2: References frames. a) Global reference frame and

b) local reference frame.

Figure 3: Cylinder with an inclination θ.

The total volume of the container is given by:

= πr

and similarly, the initial volume of the liquid is

given by: V

init

= πr

As showed on Figure 2, two reference frames are

considered: a) the global reference frame, which by

simplicity is placed at the tilting corner of the con-

tainer and denoted by O

, and b) the local reference

frame placed at the bottom center of the container and

denoted by O

To ﬁnd the spill angle θ

, it is necessary to analyze

the geometry and rotation around O

When container slopes an angle θ and the liquid

inside changes its shape (Figure 3), it can be veriﬁed

that:

1. Liquid’s height in the local reference frame O

composed by the average of two heights h

and h

corresponding to both sides of the cylindrical con-

tainer, where dh is the difference between them.

2. The form of liquid’s surface goes from a circle at

θ = 0 to an ellipse with major axis 2a at θ > 0.

Then, when h

= H liquids begins to spill and then

can be determined by:

tanθ

H − h

. (1)

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

690

Figure 4: Geometric analysis of the shape acquired by liq-

uid when tilted at an angle θ.

Figure 5: Liquid surface visualization (surface ellipses for-

mation).

Similarly, to obtain the ﬁnal spill angle θ

, it can

be determined considering the difference dV between

the liquid’s initial volume V

init

and poured volume V

then computing the corresponding height h

, the an-

gle is given by:

tanθ

H − h

. (2)

3.2 Transversal Sections Volumes

As described previously, in order to compute accu-

rately poured liquid’s volume is very important to get

to make a smooth control to avoid a turbulent ﬂow.

It can be observed that the surface of the liquid

forms ellipses when it is inclined at an angle θ 6= 0.

And as showed in ﬁgure 6, two regions can be distin-

guished; the ﬁrst region above the point P, in which it

can be seen that, ellipses formed are complete, and a

second region, below the point P, where it can be seen

that the ellipses are trimmed.

(a) (b)

Figure 6: Geometry considerations. a) Region 1 in yellow

and region 2 in orange, and in (b) Volume discretization.

3.2.1 Determination of the Transversal Volumes

at First Region

Being S

as the area of liquids’ surface as described

in Figure 6b, and considering a height discretization

into n similar intervals of height ∆l in the global ref-

erence frame, then it can be considered the volume of

a transversal section as:

= S

∆l (3)

where ∆l is related with liquid’s viscosity.

The total volume will be the sum of all transversal

volumes, as follows:

∑

i=1

(θ) =

∑

∆l = S

∆ln. (4)

It is important to note that, the volume of each

segment is a function of tilting angle, as following:

(θ) =

πr

∆h

cosθ

. (5)

3.2.2 Determination of the Volume at Second

Region.

Below point P and due to geometry of tilted container,

surfaces ellipses are incomplete as described in Fig.

8. Moreover, to determined transversal volumes be-

low point P, it is important to note there are two sub-

regions. One above O

and the other one below O

Remembering that, the last complete ellipse

formed will be at h

= 0 (this point is referenced as

P) as showed in Figure 7, then below this point, all el-

lipses formed will be cut in relation to the semi-major

axis, as shown in ﬁgure 8.

It is required to ﬁnd the parameter a

that deter-

mines the cuts of these ellipses. Since a

cuts reduce

ellipses according to the semi-major axis, this value

will have a constant of proportionality being a

= α,

where α is:

α =

(θ)

rsinθ

(6)

A Geometric Approach for Partial Liquids’ Pouring from a Regular Container by a Robotic Manipulator

691

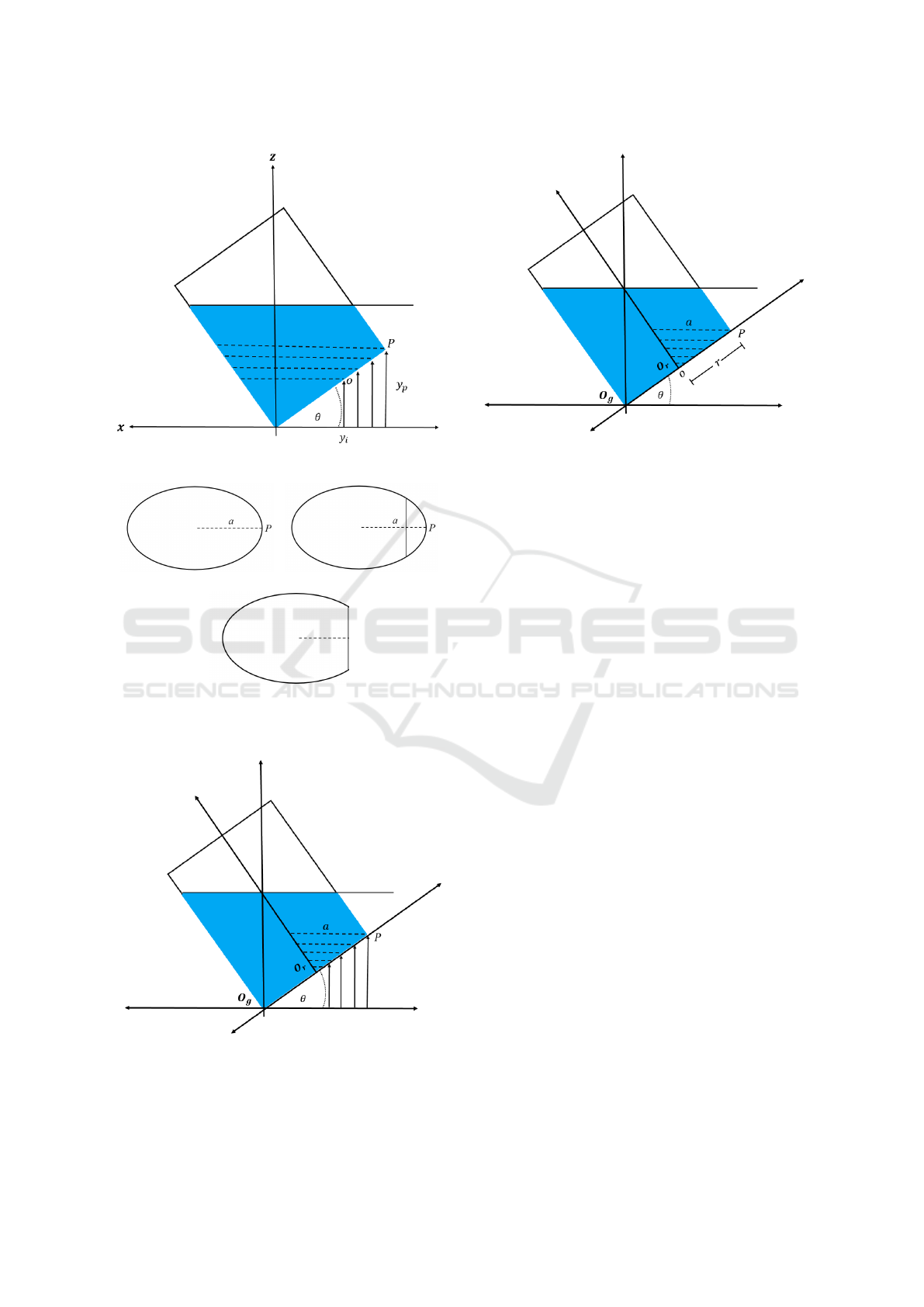
Figure 7: Ellipses cut below point P (o → r).

(a) (b)

(c)

Figure 8: Geometry cut: a) Complete ellipse, b) section to

cut and c) ﬁnal area.

Figure 9: Geometry of the tilted container at the region r →

where y is the height of the container from the base

of O

frame to an angle θ and assuming the following

Figure 10: Intervals from 0 to r.

condition y ≤ rsinθ.

Below point P, ellipses formed are not only cut,

but also deformed. This is due, particularly by the

implicit geometry of this section. At this stage of the

work, this subregion is not considered. So, a hard con-

straint is considered, and is that nor the initial liquid

volume nor the ﬁnal volume is inferior to h < r.

From analysis of transversal sections, it can be

seeing that volumes increase until h

= 0, then vol-

umes of transversal sections decrease. Then, to get a

soft pouring it is required a function of these transver-

sal sections in order to get a regular ﬂow and then

estimate accurately poured volume.

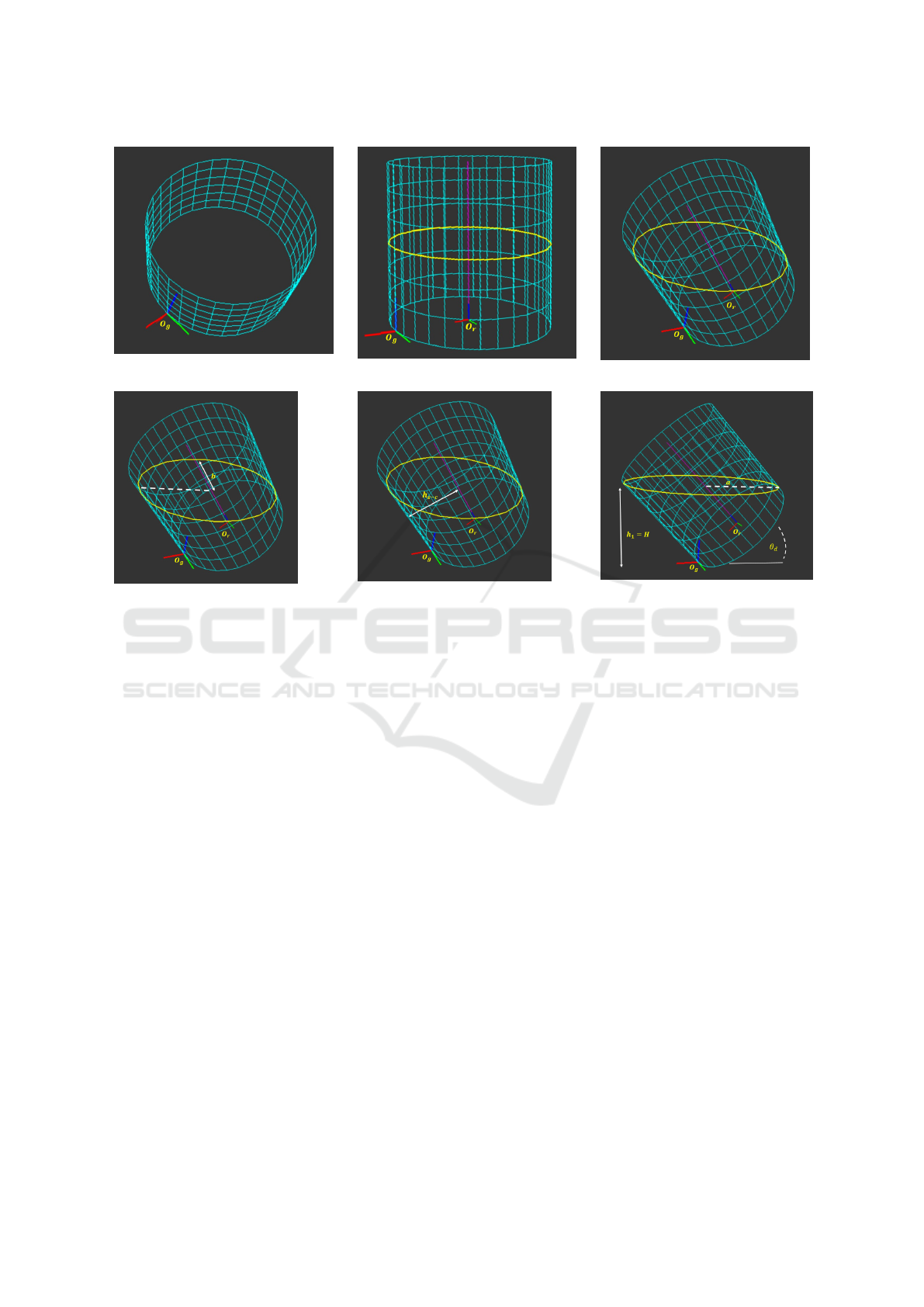
4 PRELIMINARY RESULTS

The proposed approach has been validated by per-

forming some tests over simulation environments, as

showed in Figure 11. As it can be seen, from ﬁgures

(b) to (f), at the ﬁrst region, as it has been described in

section 3.2.1, the transversal section area increases in

function of the tilted angle. However, this relation is

not linear, thus the change in volume of correspond-

ing section is neither.

Moreover, at region two, the ellipses formed are

cut as it has been described previously; decreasing the

transversal section area while tilted angle increases,

thus volumes of corresponding sections also decrease.

Therefore, and considering a close relation be-

tween the volume of the cross section and the vis-

cosity, to get a regular ﬂow, it is necessary to control

pouring according to volumes’ change of mentioned

sections.

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

692

(a)

(b)

(c)

(d)

(e)

(f)

Figure 11: Simulation environments: a) cylindrical container, b) reference frames, c) elliptical liquid surface, d) semi-minor

and major axis at ellipse, e) height of the liquid, and f) initial pouring point.

5 CONCLUSION

In this work, a geometrical approach to pouring spe-

ciﬁc quantities of liquid was presented. The proposed

approach considers the variation of cross-sectional ar-

eas formed by the tilted container to control pouring.

Based on the geometry analysis exposed, it has been

showed that a linear angular control does not assure

a regular ﬂow. Therefore, to get a regular ﬂow it is

required to consider the two regions described, when

areas and corresponding volumes increase, at region

one, and when they decrease, at region two. It is im-

portant to note, that both regions occurs while θ angle

is increasing, proving that linear angular control is not

enough to get a regular ﬂow.

In future works, experiments on real autonomous

robots will be done, considering different liquid’s vis-

cosity, quantities and diverse shape containers.

REFERENCES

Castilla, R., Gamez-Montero, P. J., Raush, G., Khamashta,

M., and Codina, E. (2017). Numerical study of im-

pingement location of liquid jet poured from a tilt-

ing ladle with lip spout. Metallurgical and Materials

Transactions B, 48(2):1390–1399.

Do, C. and Burgard, W. (2019). Accurate pouring with an

autonomous robot using an rgb-d camera. In Strand,

M., Dillmann, R., Menegatti, E., and Ghidoni, S., ed-

itors, Intelligent Autonomous Systems 15, pages 210–

221, Cham. Springer International Publishing.

Dong, C., Takizawa, M., Kudoh, S., and Suehiro, T. (2019).

Precision pouring into unknown containers by ser-

vice robots. In 2019 IEEE/RSJ International Confer-

ence on Intelligent Robots and Systems (IROS), pages

5875–5882.

Kennedy, M., Queen, K., Thakur, D., Daniilidis, K., and

Kumar, V. (2017). Precise dispensing of liquids us-

ing visual feedback. In 2017 IEEE/RSJ International

Conference on Intelligent Robots and Systems (IROS),

pages 1260–1266.

Matl, C., Matthew, R., and Bajcsy, R. (2019). Hap-

tic perception of liquids enclosed in containers. In

2019 IEEE/RSJ International Conference on Intelli-

gent Robots and Systems (IROS), pages 7142–7149.

Noda, Y. and Terashima, K. (2006). Nonlinear model-

ing with hydrodynamics and ﬂow control using in-

verse pouring dynamics of tilting-ladle-type automatic

pouring process. In Proceedings of the 67th World

Foundry Congress, volume 207, pages 1–10.

A Geometric Approach for Partial Liquids’ Pouring from a Regular Container by a Robotic Manipulator

693

Noda, Y. and Terashima, K. (2007). Falling position con-

trol of outﬂow liquid for automatic pouring system

with tilting-type ladle. IFAC Proceedings Volumes,

40(11):53–58. 12th IFAC Symposium on Automation

in Mining, Mineral and Metal Processing.

Pan, Z. and Manocha, D. (2016). Motion planning for

ﬂuid manipulation using simpliﬁed dynamics. In

2016 IEEE/RSJ International Conference on Intelli-

gent Robots and Systems (IROS), pages 4224–4231.

Pan, Z., Park, C., and Manocha, D. (2016). Robot motion

planning for pouring liquids. In ICAPS, pages 518–

526.

Park, C., Pan, J., and Manocha, D. (2012). Itomp: In-

cremental trajectory optimization for real-time replan-

ning in dynamic environments. In ICAPS.

Ratliff, N., Zucker, M., Bagnell, J. A., and Srinivasa, S.

(2009). Chomp: Gradient optimization techniques for

efﬁcient motion planning. In 2009 IEEE International

Conference on Robotics and Automation, pages 489–

494.

Schenck, C. and Fox, D. (2017). Visual closed-loop control

for pouring liquids. In 2017 IEEE International Con-

ference on Robotics and Automation (ICRA), pages

2629–2636.

Sueki, Y. and Noda, Y. (2018). Operational assistance sys-

tem with direct manipulation of ﬂow rate and falling

position of outﬂow liquid in tilting-ladle-type pouring

machine. In Proceedings of the 73rd World Foundry

Congress, Cracow, Poland, pages 23–27.

Sueki, Y. and Noda, Y. (2019). Development of ﬂow rate

feedback control in tilting-ladle-type pouring robot

with direct manipulation of pouring ﬂow rate. In

ICINCO.

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

694