A Secure Federated Learning: Analysis of Different Cryptographic Tools

Oana Stan

, Vincent Thouvenot

, Aymen Boudguiga

, Katarzyna Kapusta

, Martin Zuber

and Renaud Sirdey

Universit

e Paris-Saclay, CEA, List, F-91120, Palaiseau, France

THALES ThereSIS, France

Keywords:

Federated Learning, Homomorphic Encryption, Multi-party Computation, Differential Privacy.

Abstract:

Federated Learning is established as one of the most efﬁcient collaborative learning approaches aiming at

training different client models using private datasets. By private, we mean that clients’ datasets are never

disclosed as they serve to train clients’ models locally. Then, a central server is in charge of aggregating the

different models’ weights. The central server is generally a honest-but-curious entity that may be interested

in collecting information about clients datasets by using model inversion or membership inference. In this

paper, we discuss different cryptographic options for providing a secure Federated Learning framework. We

investigate the use of Differential Privacy, Homomorphic Encryption and Multi-Party Computation (MPC)

for conﬁdential data aggregation while considering different threat models. In our homomorphic encryption

approach, we compare results obtained with an optimized version of the Paillier cryptosystem to those obtained

with BFV and CKKS. As for MPC technique, different general protocols are tested under various security

assumptions. Overall we have found HE to have better performance, for a lower bandwidth usage.

1 INTRODUCTION

Federated Learning (FL), a recent ML distributed

paradigm allowing to train a common model with-

out sharing sensitive local data, seems an appealing

option to build high-quality and robust models with

large amounts of training sets from various sources.

In FL a set of participating clients collaboratively

learn a global model by uploading their local mod-

els updates to a central server, which coordinates the

training. This central server updates the global model

by averaging the local model parameters, and sends

it back to the data owners. Even if federated learn-

ing has the advantage of not sharing local data, recent

research showed that the local data of distributed de-

vices can be leaked through the local model param-

eters. Sharing intermediate models with the coordi-

nator server, or among the participants, can lead to

various privacy attacks, e.g., extracting participants’

inputs or membership inference (e.g. (Hitaj et al.,

2017), (Melis et al., 2019)).

To address these problems, several works employ

different cryptographic techniques such as Differen-

tial Privacy (DP), Homomorphic Encryption (HE)

or Multi-Party Computation (MPC) to propose more

privacy-preserving and secure federated learning ap-

proaches. However, none of these solutions is yet

completely satisfactory (in terms of performances of

AI models and/or security constraints) and moreover

they are often tested for different applications and on

different datasets.

In this paper, we propose a ﬁrst work on secure

federated learning in which for the same use-case and

datasets, different cryptographic solutions are con-

ceived, implemented and compared. More precisely,

our contributions are as follows:

• We propose different architecture conﬁgurations

for a Secure Federated Learning taking into ac-

count threats coming from the aggregation server

(by means of Homomorphic Encryption or Multi-

Party Computation) and/or the other clients (by

means of Differential Privacy) and we analyse the

impact of these countermeasures.

• We present a comparison of three HE schemes

(Paillier, BFV, CKKS) when applied to federated

learning averaging.

• We evaluate the performance of FL aggregation

implemented using general MPC protocols for

four different security conﬁgurations. We show

the cost of increasing the protection from a semi-

honest adversary to a dishonest one.

Stan, O., Thouvenot, V., Boudguiga, A., Kapusta, K., Zuber, M. and Sirdey, R.

A Secure Federated Learning: Analysis of Different Cryptographic Tools.

DOI: 10.5220/0011322700003283

In Proceedings of the 19th International Conference on Security and Cryptography (SECRYPT 2022), pages 669-674

ISBN: 978-989-758-590-6; ISSN: 2184-7711

669

• We implement global differential privacy on a

Federated Learning framework and evaluate the

privacy of the resulting model.

• We provide a comparative analysis between MPC

and Homomorphic Encryption solutions for our

Federated Learning model in terms of accuracy of

the AI model, the additional training overhead but

also from a security point of view.

2 OVERVIEW OF FEDERATED

LEARNING

The main idea of FL is highly similar to Distributed

Learning (DL) where the data is spread among work-

ers, while a central server is in charge of computing

the updates. A global model is computed by averag-

ing the local model trained on-device using the dataset

owned locally by each worker (data-owner). The FL

training is described below:

1. Central server sends the latest model parameters

to the nodes

2. Data is collected at each node

3. Each local model is trained based on the latest pa-

rameters

4. Updated model parameters are communicated

back to the global model

5. Combine updates from each model and retrain the

global model to get a new model

6. Restart from step 1

Three settings of FL exist: horizontal FL, vertical FL

and Transfer FL. In this paper we focus on horizontal

FL, or sample-based federated learning, which corre-

sponds to the scenarios in which datasets share the

same features. We assume honest participants and

security against different adversarial settings for the

server. For more details about FL, interested read-

ers can refer to these recent surveys (Li et al., 2021;

Kairouz and et al., 2021).

3 ARCHITECTURAL OPTIONS

FOR A MORE SECURE

FEDERATED LEARNING

3.1 HE-based Variant

One of the security assumptions we made with this

variant of architecture is an honest-but-curious aggre-

gation server, i.e. a server following honestly the pro-

Figure 1: Cross-silo federated learning architecture with

Homomorphic Encryption.

tocol and trying to infer as much information as pos-

sible from the data it has access to. Homomorphic

Encryption can prevent this from happening, by pro-

viding a secure countermeasure to protect the mod-

els parameters during FL training. Before the training

actually begins, the central server shares with the M

clients the global architecture of the neural network

that will be trained. For now, we assume a default

setting, with a simple key distribution, in which each

of the K clients selected randomly to participate in a

round has the same pair of secret and public homo-

morphic keys (sk, pk). sk is the private key while pk

is the public key.

The preliminary step of key setup is independent

of this work. For example, we can assume that the key

generation is made locally by one random client. The

latter can be randomly selected by the server or be the

result of a leadership election protocol. All the clients

will then share the same pair of (sk, pk). The central

server holds only the pk required for the homomor-

phic evaluation of the global model. At each round of

the training which is an iterative process, the server

randomly selects K out of the M clients. Figure 1

depicts a round of FL training with federated averag-

ing with homomorphic encryption. During this round,

each client runs several epochs of minibatch stochas-

tic gradient descent minimizing a local loss function.

Once the clients perform this local training, they en-

crypt their local models and send them to the central

server. The latter will perform a weighted averaging

of the updated local models to obtain an encrypted

updated global model. The current iteration ends by

sending the global model to each of the K clients that

decrypt it with the sk.

SECRYPT 2022 - 19th International Conference on Security and Cryptography

670

Therefore, the only function to be computed en-

crypted is the federated averaging of the encrypted

weights provided by the K clients participating to the

FL round t. That is, the central server has to com-

pute per round t the function: w

t+1

←−

∑

k=1

·w

t+1

where n

is the size of the training set of client k, and

n =

∑

k=1

is the total size of the training datasets

used in round t.

3.2 MPC-based Variant

As discussed in the previous section, the homomor-

phic encryption is a good choice for securing the av-

eraging by the aggregation server in the semi-honest

setting. However, MPC can provide a solution in a sit-

uation where such a server is not available due to lack

of trust between the participants. It can replace the

semi-honest aggregator server by two or more semi-

honest or untrusted aggregator servers that would per-

form the aggregation in a distributed way. MPC-

based distributed aggregators could solve two prob-

lems that a single semi-honest aggregator server can-

not address. First is that the secure aggregator server

cannot be also a participant of the computation: as a

participant has the decryption key that the aggregator

server cannot possess. For the same reason, an aggre-

gation server is not supposed to collude with one or

more participants. In MPC, the aggregators can be in-

dependent or not from the participants to the learning.

Therefore, a participant to the learning can also have

the role of an aggregator. Second, homomorphic-

encryption prevents the server from decrypting the

data but does not come with mechanisms addressing

the dishonest threat model, in which the aggregation

server could deviate from the agreed protocol. For

instance, an aggregation server corrupted by an ac-

tive adversary could omit some of the inputs provided

by the participants (and therefore modify the aggrega-

tion results, and in consequence the ﬁnal model). Ho-

momorphic encryption could be enriched with addi-

tional veriﬁcation mechanisms that would detect dis-

honest behavior of the aggregator. However, imple-

menting those mechanisms is not straightforward. In

contrast, MPC protocols addressing the active adver-

sary embed already mechanisms that enable to detect

deviations of the participants from the agreed proto-

col. The advantages of MPC come at the cost of in-

creased communications and expensive computations

(especially in the active threat model). Therefore, al-

though MPC is an interesting alternative to HE, it can

be judged impractical for use-cases where the com-

munications costs are an important factor.

In the example of architecture from Figure 2, the

aggregation servers are different from the clients and

a secret-sharing MPC algorithm is used to protect the

data (computation is realized on the shares of inputs

and its secure unless all shares of a given data are

gathered).

Figure 2: Cross-silo federated learning architecture with

MPC.

3.3 Adding DP Guarantees to FL

Training

In order to address threats coming from other honest-

but-curious clients, the above frameworks can be

completed with Differential Privacy (DP) guarantees

(see (Dwork, 2006)). In the case of a malicious server,

one may use local DP with noises generated by each

client. Otherwise, if one can trust the aggregation

server for the noise generation, global DP can be ap-

plied. Let us also note that for the secure variant of

FL using local DP and HE, speciﬁc quantization tech-

niques are necessary for the noise sampling to ensure

high DP guarantees (refer to (Amiri et al., 2021) for

more details).

4 EXPERIMENTAL RESULTS

4.1 FL Implementation with DP

We have implemented a federated learning with

global differential privacy based on Tensorﬂow-

federated. To demonstrate the results, we use the Tur-

bofan dataset (Saxena et al., 2008). This learning pro-

cess is similar to (McMahan et al., 2018). To simulate

the federated learning between three participants, we

split the data into three using the column “unit”, this

way each participant gets the full data. Two partici-

pants have 33 engines and one has 34 engines.

A Secure Federated Learning: Analysis of Different Cryptographic Tools

671

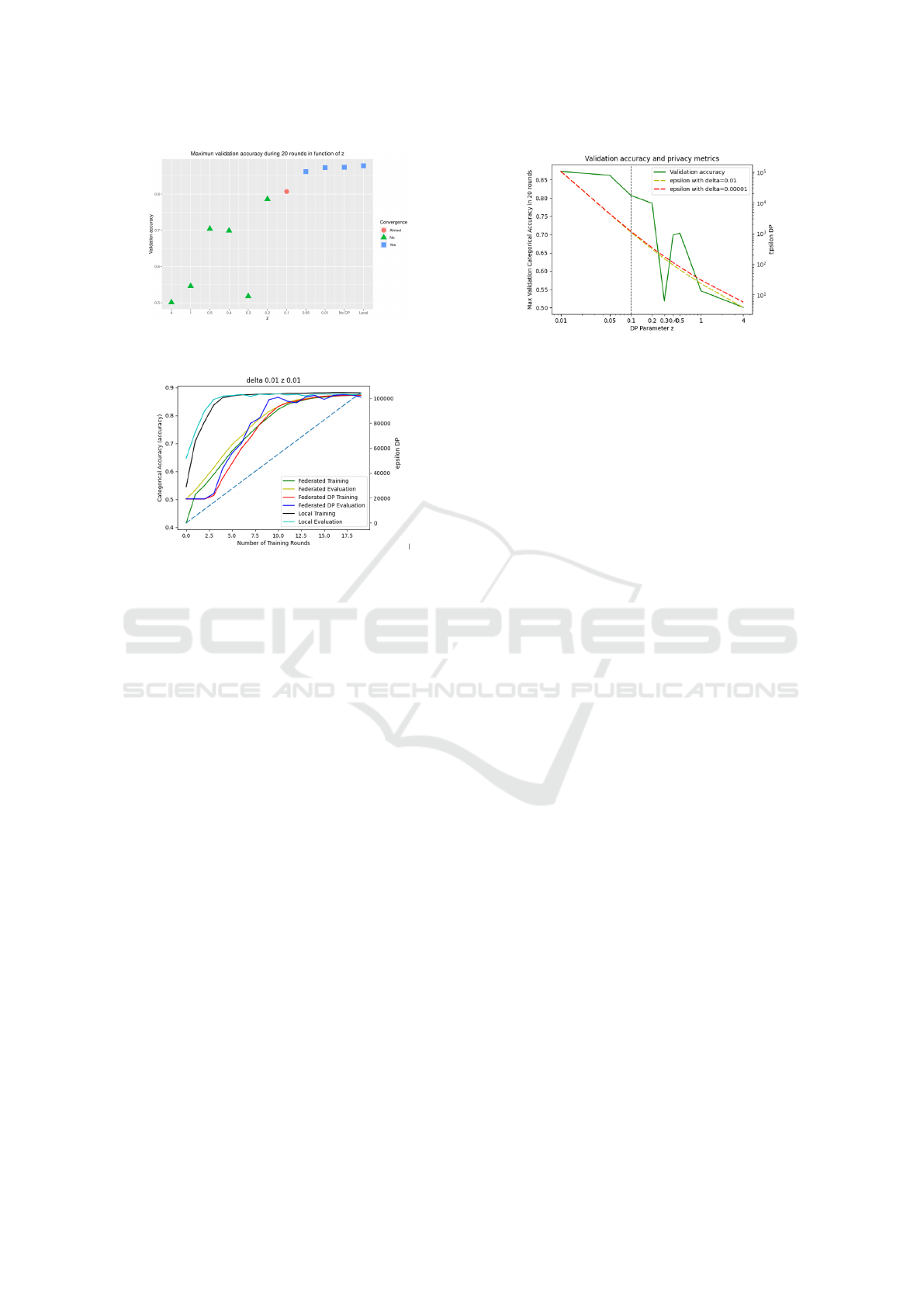
Figure 3: Maximum validation accuracy during 20 rounds

in function of z.

Figure 4: Categorical Accuracy during the training with

different settings. Global differential privacy is computed

with z=0.01, and the epsilon (dashed curve) is estimated for

delta=0.01.

The standard deviation of the noise that we add

is equal to z/3, where z is a hyperparameter that we

make varying and 3 comes from the fact that we have

3 participants. In Figure 3, we vary z and consider 20

rounds of training. We collect for each z the maxi-

mum validation accuracy after 20 rounds. We denote

that the process does not converge after 20 rounds for

the 6 strongest z. Moreover, for the strongest z values,

we obtain the maximum validation accuracy for less

than 8 rounds. The results shown in Figure 3 are quite

intuitive: the more noise we add the less accurate the

model is. The evolution of the accuracy during the

training process gives a more precise understanding

of what happens. In Figure 4, we display the cate-

gorical accuracy obtained at each round on the train-

ing dataset and on the test dataset. It displays on the

same plot, the curves for the three different learning

settings:

• Federated Learning with global differential pri-

vacy

• Federated Learning without differential privacy

• Local training on the global dataset

In Figure 4 the differential privacy was computed with

z=0.0.1, a small amount of noise. Its affects the con-

vergence rate, the accuracy increases slowly but the

performances are good. We also compute the dif-

Figure 5: Validation accuracy and privacy metrics after 20

rounds of training in function of parameter z.

ferential privacy for z=0.1, a larger amount of noise,

but still quite small. The learning is affected. There

is some randomness in the evaluation accuracy. The

model is learnt on the training dataset but its perfor-

mances on the test dataset are not predictable. In our

ﬁrst results of this sandbox dataset, it seems that z=0.1

is the larger amount noise that allow us to learn a

model, while ensuring some privacy.

We evaluate the privacy guarantees obtained after

20 rounds in order to ﬁnd a trade-off between model

performances and data privacy. In Figure 5 we show

the validation accuracy, and the vertical line at z=0.1

highlights the limit between a learning for which we

achieve a convergence and a learning that does not

ends with convergence. Here, we see that the con-

vergence is achieved only with a good accuracy and

that the resulting privacy metrics are high, and thus

the privacy guarantees are low.

4.2 (F)HE for FL

All the experiments presented in this section are done

with parameters that support a security level of λ =

128. We have trained three models of different sizes:

197, 1000 and 10000 weights. Note that 197 is the

number of weights of the neural network that was

trained, in the previous section, using FL with DP and

the Turbofan dataset.

4.2.1 Implementation with Paillier

Our implementation using the Paillier cryptosystem

relies on a simple packing technique as well as a

faster Regev-style encryption function (encrypts by

homomorphically adding a random subset of public

encryptions of 0 to a pseudo-encryption of the mes-

sage). Because we parameterize for exact arithmetic

(as opposed to approximate arithmetic for some ho-

momorphic schemes or depending on the parameters)

we only need to concern ourselves with the time per-

formance on the server here and the bandwidth use.

SECRYPT 2022 - 19th International Conference on Security and Cryptography

672

Table 1: Computation time (t

) in s, encryption time (t

) in

s per client, and bandwidth overhead (B

) in KB per client

for different sets of precision (p) in bits, number of weights

per client (N

), number of training dataset size per client n

and number of clients (K).

p N

K t

197 100 3 0.04 0.05 2.5

1000 1000 5 0.13 0.06 14

10000 10000 10 1.2 0.26 153

197 100 3 0.05 0.06 3.7

1000 1000 5 0.16 0.06 19

10000 10000 10 1.6 0.32 200

197 100 3 0.08 0.06 6.2

1000 1000 5 0.24 0.07 28

10000 10000 10 2.7 0.45 295

On the client side, the encryption time for a given

client depends on the number of ciphertexts needed to

be encrypted. That in turn is determined by the pre-

cision p (in bits) needed for the weights, the number

of weights per client N

, and the number of training

points used by every client n

. We assume for our

tests, for simplicity sake, that all n

have the same

values and that all clients have the same number of

weights N

. Table 1 presents our implementation’s

time and bandwidth performance for several sets of

parameters from small to big. Obviously the parame-

ter sets are not exhaustively chosen and are designed

to give a good idea of the scaling of our implemen-

tation. Because deciphering time is ﬁxed (at roughly

0.05 seconds) for every set of parameters it is not in-

cluded in the Table. The bandwidth size corresponds

to what a client needs to send to the server. It gets

back roughly the same amount of data, therefore for a

total bandwidth, that needs to be doubled.

4.2.2 Implementation with BFV/CKKS

We did our tests for FL aggregation with BFV or

CKKS schemes with Microsoft SEAL 3.7.2 library.

For batching with BFV and CKKS, we set the encryp-

tion parameters with respect to the considered pre-

cision and the number of batched slots. For BFV,

the plaintext modulus size is at least equal to the

global precision p + dlog

)e + dlog

(K)e. Mean-

while for CKKS, the scaling factor size dlog

(δ)e

is at least equal to p + dlog

)e + dlog

(K)e +

dlog

(K × noise)e where noise corresponds to the

noise induced by a homomorphic addition. We do so

to ensure that the ﬁnal precision with CKKS is equal

to dlog

(δ)e − dlog

(K × noise)e = p + dlog

)e +

dlog

(K)e. This precision is needed for ensuring a

correct aggregation result.

Note that the FL aggregation takes at most 15 mil-

liseconds (Tables 2 and 3). It is very efﬁcient with

BFV or CKKS, as it only consists in computing ad-

ditions (no multiplication needed). However, the ci-

phertext size reaches at most 1.8 MB with BFV.

Table 2: Results with BFV–Computation time (t

) in ms, en-

cryption time (t

) in ms per client, and bandwidth overhead

) in MB per client for different sets of precision (p) in

bits, number of weights per client (N

), number of training

dataset size per client n

and number of clients (K).

p N

K t

197 100 3 1.091 0.043 0.031

1000 1000 5 1.397 0.056 0.031

10000 10000 10 15.97 3.216 1.8

197 100 3 1.349 0.024 0.031

1000 1000 5 1.052 0.04 0.031

10000 10000 10 14.264 3.422 1.8

197 100 3 0.973 0.024 0.031

1000 1000 5 3.001 0.091 0.087

10000 10000 10 14.561 4.47 1.8

Table 3: Results with CKKS–Computation time (t

) in ms,

encryption time (t

) in ms per client, and bandwidth over-

head (B

) in MB per client for different sets of precision (p)

in bits, number of weights per client (N

), number of train-

ing dataset size per client n

and number of clients (K).

p N

K t

197 100 3 2.015 0.051 0.081

1000 1000 5 2.089 0.093 0.081

10000 10000 10 21.412 1.733 0.973

197 100 3 2.021 0.051 0.081

1000 1000 5 2.03 0.086 0.081

10000 10000 10 22.443 1.735 0.973

197 100 3 2.025 0.05 0.081

1000 1000 5 4.532 0.192 0.23

10000 10000 10 23.76 1.696 0.973

4.3 MPC for FL

We implemented the MPC-based secure FL aggrega-

tion procedure using the recently released MP-SPDZ

framework (Keller, 2020) that allows fast translation

of a python-like code into MPC operations and that

implements more than 30 variants of MPC protocols.

We measured the aggregation performance in terms of

time and communication costs. The number of partic-

ipants was set to 5 and models of 1000 weights were

considered. A conﬁguration of 2 or 3 computing par-

ties was chosen, which is a common choice for MPC

computations. Two setting were tested: honest major-

ity and dishonest majority.

Three different MPC protocols were selected for

the test: a Shamir’s secret sharing-based protocol

for semi-honest honest majority, the MASCOT pro-

tocol for dishonest setting, and a version of MAS-

COT stripped of active security mechanisms for semi-

honest dishonest majority.

Performance results are presented in Table 4.

They were obtained on a device with a 4-th genera-

A Secure Federated Learning: Analysis of Different Cryptographic Tools

673

Table 4: Performance results using general MPC protocols: straightforward aggregation of 5 FL contributions containing

1000 updates each, aggregated by two or three computing parties (CP) acting as aggregator servers. Communication cost is

measured for both one CP (2nd row) and all CPs (3rd row) in MB, as well as for both dishonest (DM) and honest majority

(HM) conﬁguration. There is a visible performance gap between semi-honest and dishonest model, as well as between honest

and dishonest majority.

Semi-honest, DM, 2CP Semi-honest, HM, 3CP Dishonest, DM, 2CP Dishonest, DM, 3CP

Time [sec] 69,9 11,8 476,48 518,8

Send, 1CP 7666,7 83,6 41817,3 83634,6

Total send 15333,4 250,2 83613,9 250643

tion i5 processor running at 1.30 GHz using 16 GiB

of RAM on Linux. They conﬁrmed that a straightfor-

ward implementation of distributed aggregation us-

ing general MPC protocols leads to a rather large

overhead in terms of communication and computation

costs. However, the advantage of this approach is that

it enables to switch smoothly between different proto-

cols and thus to easily adjust the security level and the

number of parties. It shows that securing the compu-

tation against an active attacker is possible, although

it comes at a high cost (that can be potentially accept-

able for some of the use cases where securing is a

much higher priority than the speed of the learning).

Moreover, such implementation is robust to dynamic

client or aggregation server dropouts.

5 ANALYSIS

The preliminary results presented in the above sec-

tions showed interesting perspectives when securing

Federated Learning with DP, FHE and MPC. As ex-

pected, there is a delicate trade-off to ﬁnd between the

guarantees offered by the global DP and the accuracy

of the training model.

As for the results obtained with (F)HE and MPC,

let us analyse and compare the concrete case of 5

clients and a model size of 1000 weights. The

tests show that, under the hypothesis of a honest-

but-curious server, the homomorphic encryption un-

der various ﬂavors (either optimized version of addi-

tive Pailier cryptosystem or classical batching of lev-

elled BFV and CKKS) has better performance results

in terms of execution times and bandwidths require-

ments than the general MPC protocols. This general

conclusion of homomorphic encryption performing

better for the aggregation in the context of federated

learning remains valid for other testing parameters.

Of course, the results with MPC could be ameliorated

through speciﬁc protocols and it is still useful in sit-

uations in which homomorphic encryption cannot be

used (see Section 3.2 for details).

ACKNOWLEDGEMENTS

The research leading to these results has received

funding from the European Union’s Preparatory Ac-

tion on Defence Research (PADR-FDDT-OPEN-03-

2019). This paper reﬂects only the authors’ views and

the Commission is not liable for any use that may be

made of the information contained therein.

REFERENCES

Amiri, S., Belloum, A., Klous, S., and Gommans, L. (2021).

Compressive differentially-private federated learning

through universal vector quantization. Association for

the Advancement of Artiﬁcial Intelligence.

Dwork, C. (2006). Differential privacy. volume 2006, pages

1–12. ICALP.

Hitaj, B., Ateniese, G., and Perez-Cruz, F. (2017). Deep

models under the gan: Information leakage from col-

laborative deep learning. In Proceedings of the 2017

ACM SIGSAC Conference on Computer and Commu-

nications Security, CCS ’17, page 603–618.

Kairouz, P. and et al. (2021). Advances and Open Problems

in Federated Learning. arXiv:1912.04977 [cs, stat].

arXiv: 1912.04977 version: 3.

Keller, M. (2020). MP-SPDZ: A versatile framework for

multi-party computation. Cryptology ePrint Archive,

Report 2020/521.

Li, Q., Wen, Z., Wu, Z., Hu, S., Wang, N., Li, Y., Liu, X.,

and He, B. (2021). A Survey on Federated Learning

Systems: Vision, Hype and Reality for Data Privacy

and Protection. IEEE Transactions on Knowledge and

Data Engineering, pages 1–1. arXiv: 1907.09693.

McMahan, H. B., Ramage, D., Talwar, K., and Zhang,

L. (2018). Learning Differentially Private Recurrent

Language Models. arXiv:1710.06963 [cs].

Melis, L., Song, C., De Cristofaro, E., and Shmatikov, V.

(2019). Exploiting unintended feature leakage in col-

laborative learning. In 2019 IEEE Symposium on Se-

curity and Privacy (SP), pages 691–706.

Saxena, A., Goebel, K., Simon, D., and Eklund, N. (2008).

Damage propagation modeling for aircraft engine run-

to-failure simulation. In 2008 International Confer-

ence on Prognostics and Health Management, pages

1–9.

SECRYPT 2022 - 19th International Conference on Security and Cryptography

674