Simulating Theoretical Jerk by Numerical Modelling for

Greyhound Racing

Md. Imam Hossain

and David Eager

Faculty of Engineering and Information Technology, University of Technology Sydney, Sydney, PO Box 123,

Broadway 2007, Australia

Keywords: Greyhound Racing, Greyhound Racing Jerk, Numerical Simulation, Injury Prevention, Animal Welfare.

Abstract: This paper presents the jerk dynamics of a racing greyhound running alone by simulating the centrifugal

acceleration for different race scenarios and track path design options. Simulation parameters were defined

from the real-world greyhound track designs and greyhound race data to provide relevant results for race

conditions. Virtual race scenarios were created to achieve maximum results. By simulating greyhound strides

as discrete events, the theoretical jerk was calculated. The results show how different track design conditions

and race scenarios can affect greyhound dynamics for the track bends. This can be applied to better understand

and improve track design for improved dynamics with a view to reduce the frequency and severity of injuries.

1 INTRODUCTION

This paper relates track shape design variables

specific to round track to greyhound centrifugal

acceleration jerk dynamics. This has many

implications to racing greyhound injuries during track

path navigation. Researchers showed that track shape

specially bends have an effect on the racing

greyhound injury rates (Mahadavi et al., 2018). Jerk

as the time derivative of acceleration often linked to

vibration and can cause injuries (Hayati et al., 2020).

A body can feel jerk as it can feel acceleration and

both are different (Pendrill et al., 2020).

This is a fundamental question in greyhound

racing how greyhounds are coping with a particular

oval track path design. This was not explored by

previous researchers to come up with a parameter

which can be easily used to benchmark track path

designs. Jerk is used in many areas to determine for

safe operating conditions or as a measure to know the

sudden force on the physical body in motion (Eager

et al., 2016).

Running on a straight path is fundamentally

different from running on a curved path. Many circuit

tracks have both curve and straight track sections for

the track path. Only a few tracks are fully circular in

https://orcid.org/0000-0002-1246-3454

https://orcid.org/0000-0003-1926-7867

design so there are no straight sections. One main

difference between a fully straight and oval track is in

the oval track there is the dominant centrifugal force

component when going around the bend. This is also

accompanied by a large load on the greyhound limbs

during galloping leg strikes on the track surface

(Hasti et al., 2019). The centrifugal force is

experienced in the form of jerk force when there is a

change and when happens abruptly can raise the jerk

force significantly. In an ideal world, going from

straight to a curve of the constant radius would

require a transition known as a transition curve as the

inertia of the body would otherwise resist sudden

change in the centrifugal force. However, depending

on the track run path and resulting greyhound path of

choice the transition curve varies greatly. Some

transition curves are more prone to raise the jerk value

than others. For particular track path design, a set

number of dominant transition curves would satisfy

track boundary conditions. As a result, depending on

the track shape greyhound would experience different

jerk levels from track to track.

Hossain, M. and Eager, D.

Simulating Theoretical Jerk by Numerical Modelling for Greyhound Racing.

DOI: 10.5220/0011324500003274

In Proceedings of the 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2022), pages 379-385

ISBN: 978-989-758-578-4; ISSN: 2184-2841

379

2 METHOD

The goal of this research was to formulate and verify

oval track conditions in the light of greyhound jerk

dynamics by numerically modelling greyhound stride

dynamics. To achieve it we used various data from

the field to understand greyhound galloping as well

as its trajectory when running inside oval track

conditions. These data were acquired from the field

and then used for modelling greyhound centrifugal

acceleration jerk and greyhound trajectory for oval

track conditions. Furthermore, the greyhound data

from the field became the foundation for applying

limit conditions for the models.

Three distinct types of data were used from the

greyhound racing to extract greyhound run conditions

at the track. First data came from the track survey data

which were modelled in the SolidWorks software

package to know the track parameters such as track

bend radius, track straight length and presence of a

transition curve between the bend and straight. Later,

greyhound paw prints survey data from the track were

measured which gave an understanding of greyhound

stride lengths. Finally, greyhound location tracking in

X and Y coordinates data was analysed for extracting

greyhound trajectory and speed conditions.

2.1 Simulation Model

Greyhound trajectory can be represented by an

arbitrary point moving in time that has a state vector

that gives the direction of greyhound heading and

greyhound stride length also known as tangent vector

(Hossain et al., 2020). For this to work, we will have

to assume n number of strides required from the start

box location to complete the trajectory where the

arbitrary point as defined by the state vector

represents the location coordinates. With each

subsequent stride commencing with a first stride the

state vector is calculated that updates the arbitrary

point location coordinates. If the greyhound is

moving in a straight line, then the state vector retains

its current direction. When the greyhound is moving

in a constant radius bend the state vector also

maintains a constant change in its direction. For other

scenarios such as Euler transition and change in

turning radius from one stride to the next the state

vector direction (greyhound heading) and length

(stride length) also changed accordingly. For all cases

the state vector is a function of greyhound stride

length, turning radius, greyhound heading deflection

and heading deflection acceleration.

One way to extract greyhound dynamic states is

by looking into and analysing its trajectory points. In

the absence of precise trajectory points, greyhound

dynamic states in each stride can be modelled by

defining greyhound running path segments in terms

of derivatives. Greyhound dynamic states at the track

such as curvature, yaw and run distance can be

calculated by modelling the rate of change of these

variables for different track segments. For instance,

the Eq. 1 can be used for calculating instantaneous nth

stride turning curvature for any arbitrary running path

segment by plugging in initial curvature, curvature

rate and run distance for the segment.

Instantaneous turning curvature = initial

curvature for run path segment

+ (curvature

rate for run path segment

* run distance for

run

ath se

men

)

(1)

2.2 Model Scope

The simulation models allowed generating of

dynamics results of case studies for different

greyhound trajectories and run conditions. To apply

greyhound racing track design principles, it is

important to understand greyhound trajectory

limitations for the track. Different data gathered from

the greyhound racing including greyhound location

tracking data have their limitations such as missing

data points and noise in the data which restrict finding

results for all scenarios and modelling of limit

conditions. Emulating greyhound dynamic states

through numerical modelling greatly enhanced the

data and analysis of results capabilities.

The simulation models developed as described in

the previous section take a certain number of input

variables and generate possible outcomes at discrete

greyhound strides where input variables are updated

according to the greyhound racing data and different

states exist in the models. As depicted in Figure 1,

dynamic states as defined in the models keep track of

greyhound dynamic states at a given greyhound stride

number and are carried to the next stride for dynamic

calculations. The dynamic states in the model are also

convoluted utilising race data by using look up tables

for greyhound speed, stride length and stride

frequency. Randomisation to dynamic input variable

states is added emulating different race scenarios. In

the dynamic calculation phase, any additional

dynamic change is superpositioned by utilising

activity scanning functions. The activity scanning

functions are plugins for applying boundary

conditions for the models so that models generate

valid data. For instance, an activity scanning function

is for the virtualising scenario where the greyhound

trajectory crosses the track outside fence.

SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

380

Figure 1: Primary components and their data sharing for

simulating greyhound dynamics at discrete stride points.

As this research is about greyhound trajectory

modelling using discrete strides as data and event

points, it only answers greyhound dynamic states

after each stride. Any intermediate conditions of

greyhound dynamics such as greyhound bumping

or crashing into an obstacle during a stride need

separate models which are not part of this research.

Thus, this research utilises greyhound dynamic

states such as curvature, and stride length from the

models to generate greyhound trajectory dynamics

such as jerk for different greyhound path following

conditions by applying the principle of discrete-

event simulation.

3 SIMULATION PLATFORM

Discrete-event simulators often time use their special

programming languages. Nowadays, general-purpose

programming languages are being utilized for

designing simulation programs (Liu et al., 2020). As

a general-purpose programming language Python is

known as versatile and has an error-free approach to

coding. The simulation for this research was carried

out in Python programming language. Python

variables and objects were used for storing different

simulation variables states and deriving results.

Python built-in and custom-built methods and

statements were used for randomising variables

assignments, creating simulation conditions, and

defining equations.

Figure 2 illustrates the main components in the

Python simulation module in order.

Figure 2: Steps followed for writing Python module for a

simulation.

4 GREYHOUND TRAJECTORY

FOR THE BEND

Greyhound location tracking data showed that

greyhounds follow a smooth continuous path

trajectory despite the track path being not optimised

for shape continuity. For instance, track bend and

straight sections meeting next to each other where

there is no proper smoothing curve applied would

result in a sudden change in centrifugal acceleration

requirement when moving from straight to the bend.

As data showed a continuous path of racing

greyhound it can be said that greyhound minimises

large variations of turn radius while navigating

around the track. Figure 2 illustrates the main

components in the Python simulation module in

order.

To validate greyhound run conditions in absence

of a proper track path transition curve between the

bend and straight three scenarios can be considered.

In all scenarios, greyhounds make a small transition

for entering the bend that would allow them to enter

the bend without hitting the track outside fence. It was

found in the data that greyhounds make a smaller turn

radius than the bend radius at different points on the

track. In the first scenario, the greyhound's transition

exit turn radius is smaller than the track bend radius

where the greyhound continues to follow a smaller

radius turn to align itself with the bend as shown in

Figure 3. In the second scenario, the greyhound

transition exit turn radius is the same as the track

bend, but the greyhound makes a smaller radius turn

after exiting the transition to align itself with the bend

as shown in Figure 4. In the third scenario, the

greyhound's transition exit turn radius is smaller than

the track bend radius where the greyhound continues

to follow the track bend radius after exiting the

transition to align itself with the bend as shown in

Simulating Theoretical Jerk by Numerical Modelling for Greyhound Racing

381

Figure 5. In Figures 3, 4 and 5 it can be seen that with

a 50% smaller turn radius than the bend radius

greyhound has a greater chance of aligning itself with

the bend in the lack of a track transition without

bumping into the track outside fence. With 65%

smaller turn radius than the bend only in the first and

second scenarios would allow the greyhound to align

with the bend as it gets very close to the track outside

Figure 3: Greyhound transitioning into the bend with no

track bend transition where the smallest radius turn is same

as the transition exit radius.

Figure 4: Greyhound transitioning into the bend with no

track bend transition where the smallest radius turn is not

same as the transition exit radius.

Figure 5: Greyhound transitioning into the bend with no

track bend transition where the smallest radius turn is the

transition exit radius.

fence. With a 75% smaller turn radius than the bend

only in the first scenario greyhound would be able to

continue to follow the track without bumping into the

track outside. Finally, all three scenarios would result

in different greyhound trajectory jerk outcomes based

on greyhound transition length, transition exit radius

and greyhound speed conditions.

4.1 Jerk Experienced by the

Greyhound for Entering the Bend

The following major greyhound kinematics variables

were analysed.

4.1.1 Influence of Speed

It is shown in the data that greyhound running speed

is decreased during entering the bend. As the

greyhound enters the bend it makes a transition from

the straight to the constant radius bend. During this

transition phase, the greyhound yaw rate changes

from a lower value to a higher value. From Eq. 2 of

yaw rate, we can see that if the yaw rate changes an

equivalent change in the greyhound speed is required

to balance the greyhound kinetic energy state. From

this equation, we can tell that a transition would force

the greyhound to slow down or decrease its speed for

entering the bend. Also, this implies that a non-

optimum transition would decrease greyhound speed

significantly where a high braking force is required

when entering the bend.

Speed =

aw rate * turnin

radius (2)

As centrifugal acceleration jerk is a function of

speed, a changing speed during entering the bend

would imply a changing jerk value. Also, greyhound

peak speed would vary based on the greyhound’s start

location distance from the bend which would also

affect the jerk outcome.

4.1.2 Influence of Stride Length

Greyhound stride length is responsible for increasing

its speed. Greyhound stride length can be described

by Eq. 3. With a variable stride length for entering the

bend, the requirements for turning radius and heading

yaw is different from a constant stride length during

bend transition. This also affects greyhound

centrifugal acceleration jerk as a result.

Speed = stride len

th * stride frequenc

(3)

SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

382

4.1.3 Influence of Transition Length

For greyhound transition, we can assume an Euler

curve as it has a continuous linear centrifugal

acceleration profile where the centrifugal acceleration

is zero for the straight and peak at the transition exit

point. A longer Euler transition would decrease the

centrifugal acceleration jerk while a shorter one

would increase the jerk requirement.

4.1.4 Influence of Bend Radius

For oval shaped track, a constant radius bend is used

for creating the track loop along with straight sections

where track transition may or may not exist. A larger

bend radius would decrease jerk requirements in the

presence of a transition.

4.2 Jerk Outcome for Different

Greyhound Trajectories for the

Bend

Numerical simulation was carried out by defining

major transition points for the greyhound trajectory

for entering the bend. The transition point between

straight and transition curve can be seen in Figure 6

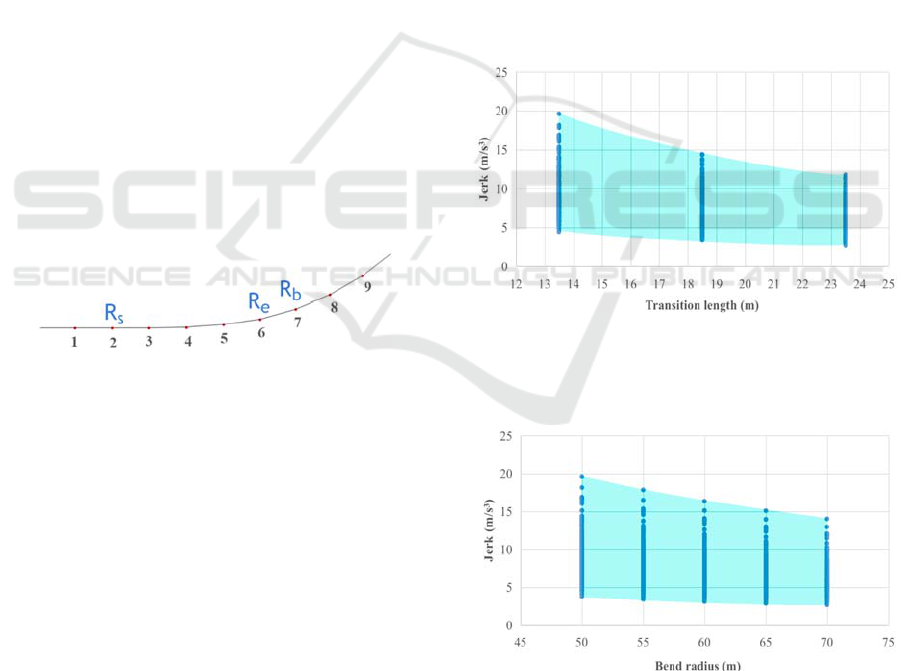
as denoted by R

. The transition point between the

bend and transition curve is denoted by R

. Finally,

the bend radius point is denoted by R

Figure 6: Transition points on greyhound trajectory for

entering the bend where red dots are strides.

Now, for the scenarios explained in Section 4,

the relationship between transition exit radius

and bend radius R

are given below:

First scenario: R

= R

Second scenario: R

e >

Third scenario: R

< R

For generating the results three variables are

enumerated namely, start box distance from the bend,

track bend radius and transition length. Furthermore,

these variables are defined according to the existing

track designs. Finally, the limit for greyhound

transition length in the absence of track transition was

calculated by modelling existing smallest and largest

radius tracks by assuming no track transition is

applied. Thus, a minimum greyhound transition

length consisted of three strides. This is because a

minimum of three strides are required for heading

deflection angle change when it is assumed

greyhound changes its heading with every stride. The

maximum greyhound transition length for 70 m and

50 m radius bends are found to be 23.5 m and 20 m

respectively. This is because anything greater than

these values would make the greyhound bump into

the track outside fence for making the transition as

track transition is not present. The following sections

illustrate maximum jerk values for with and without

track transitions as produced from numerical

simulations.

4.2.1 Greyhound Make Own Transition

When there is no track transition path segment, the

greyhound still should be able to create its own

transition given that it does not bump into the track

outside fence. Figures 7 to 12 depict jerk outcome for

greyhound transition into the bend from the straight

Figure 7: Maximum jerk envelope for different greyhound

transition lengths from the first scenario simulations

depending on track bend radius and distance of the race start

from the bend.

Figure 8: Maximum jerk envelope for different bend radius

from the first scenario simulations depending on greyhound

transition length and distance of the race start from the

bend.

Simulating Theoretical Jerk by Numerical Modelling for Greyhound Racing

383

Figure 9: Maximum jerk envelope for different greyhound

transition lengths from the second scenario simulations

depending on track bend radius and distance of the race start

from the bend.

Figure 10: Maximum jerk envelope for different bend

radius from the second scenario simulations depending on

greyhound transition length and distance of the race start

from the bend.

Figure 11: Maximum jerk envelope for different greyhound

transition lengths from the third scenario simulations

depending on track bend radius and distance of the race start

from the bend.

for scenarios explained before. The figures show the

maximum jerk value envelope for greyhound's

different transition lengths and track bend radii. The

blue dots represent the simulation run results as

produced for different simulation scenarios.

Figure 12: Maximum jerk envelope for different bend

radius from third scenario simulations depending on

greyhound transition length and distance of the race start

from the bend.

4.2.2 Greyhound Follow Track Transition

When there is a track transition path segment it is

easier for the greyhound to hold its line and follow

approximately track transition. Figures 13 and 14

depict jerk outcomes for a greyhound following track

transition into the bend from the straight. The figures

show the maximum jerk value envelope for different

transition lengths and track bend radii. The blue dots

represent the simulation run results as produced for

different simulation scenarios.

Figure 13: Maximum jerk envelope from the simulations

for different Euler transition lengths path following

depending on track bend radius and distance of the race start

from the bend.

Figure 14: Maximum jerk envelope from the simulations

for different bend radius depending on Euler track transition

length and distance of the race start from the bend.

SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

384

5 DISCUSSION

Numerical simulation of greyhound trajectory for the

bend predicted greyhound theoretical jerk outcome

by utilizing different parameters pertaining to

greyhound strides and track variables. As can be seen

from the maximum jerk value plots in the previous

section greyhound would experience different levels

of centrifugal acceleration jerk. For instance, jerk

levels are much higher when greyhounds followed

their own transitions despite the lack of track

transition as depicted in Figures 7 to 12. In the first

scenario, the jerk was lower than in the second and

the third scenarios. The second scenario resulted in

the highest jerk levels for all transitions and track

bend radii run conditions. In all three scenarios, the

highest jerk can go above 20 m/s3 for the lowest

transition length and turn radius while in the second

and third scenarios jerk remains greater than 20 m/s3

for all greyhound run conditions.

If greyhound followed a track transition with

continuous turn radius its jerk level is under 7 m/s

for

smallest transition and bend radius. Furthermore,

with optimal run conditions the 75 m transition peak

jerk remains between 1 and 2 m/s

as depicted in

Figure 13. However, when the run conditions are not

optimal a large radius bend will maintain the jerk

level between 1 and 5 m/s

as depicted in Figure 14.

6 CONCLUSIONS

This research showed greyhound racing centrifugal

acceleration theoretical jerk by modelling greyhound

stride dynamics based on data and numerical

simulation. By formulating various greyhound run

conditions for track bends and transitions this

research arrived at possible scenarios for greyhound

trajectories and corresponding significant jerk

outcomes. The results from the research showed the

theoretical jerk levels which greyhounds face during

various run conditions often time created by track

variables such as less than ideal track transition

design. Finally, this paper presents an idea about

analysing stride dynamics using numerical modelling

and simulation.

ACKNOWLEDGMENTS

This work is sponsored by the Faculty of Engineering

and Information Technology at the University of

Technology, Sydney, Australia. Special thanks to

Greyhound Racing Victoria, Australia for providing

real-time race data and track survey plans.

REFERENCES

Mahadavi F., Hossain I., Hayati H., Eager D., Kennedy P.,

Track shape, resulting dynamics and injury rates of

greyhounds, ASME-IEMCE 2018, Pittsburgh,

Pennsylvania, USA, 9-15 November 2018.

Hayati H., Eager D., Pendrill A-M., Alberg H. (2020). Jerk

within the context of science and engineering—A

Systematic Review. Vibration 2020, 3, 371-409.\\

doi:10.3390/vibration3040025

Pendrill, A-M., Eager D. (2020). Velocity, acceleration,

jerk, snap and vibration: forces in our bodies during a

roller coaster ride. Eur. J. Phy. 55(6) 065012.

doi:10.1088/1361-6552/aba732

Eager D., Pendrill, A-M., Reistad N. (2016) Beyond

velocity and acceleration: jerk, snap and higher

derivatives. Eur. J. Phy. 37(6) 065008.

\\doi:10.1088/0143-0807/37/6/065008

Hasti H., Eager D., Walker P. (2019). The effects of surface

compliance on greyhound galloping dynamics,

Proceedings of the Institution of Mechanical Engineers,

Part K: Journal of Multibody Dynamics, 233(4), 1033-

1043. doi:10.1177/1464419319858544

Hossain, M., Eager, D., Walker, P. D., et al. (2020).

Greyhound racing ideal trajectory path generation for

straight to bend based on jerk rate minimization.

Scientific Reports, 10(1):1–15.

Liu, J. (2020). Simulus: Easy breezy simulation in python.

In 2020 Winter Simulation Conference (WSC), pages

2329–2340. IEEE.

Simulating Theoretical Jerk by Numerical Modelling for Greyhound Racing

385