Yet Another Algebraic Cryptanalysis of Small Scale Variants of AES

Marek Bielik

, Martin Jure

cek

, Olha Jure

ckov

and R

obert L

orencz

Department of Information Security, Faculty of Information Technology,

Czech Technical University in Prague, Czech Republic

Keywords:

Small Scale Variants of AES, Algebraic Cryptanalysis, Gr

obner Bases.

Abstract:

This work presents new advances in algebraic cryptanalysis of small scale derivatives of AES. We model the

cipher as a system of polynomial equations over GF(2), which involves only the variables of the initial key,

and we subsequently attempt to solve this system using Gr

obner bases. We show, for example, that one of

the attacks can recover the secret key for one round of AES-128 under one minute on a contemporary CPU.

This attack requires only two known plaintexts and their corresponding ciphertexts. We also compare the

performance of Gr

obner bases to a SAT solver, and provide an insight into the propagation of diffusion within

the cipher.

1 INTRODUCTION

The original name of the cipher for the Advanced

Encryption Standard (AES) is Rijndael, based on

the names of two cryptographers—Joan Daemen and

Vincent Rijmen—who originally designed the cipher.

In 1997, the U.S. National Institute of Standards and

Technology (NIST) announced the development of

AES and subsequently organized an open competi-

tion, which the Rijndael cipher won. NIST published

the cipher as the Federal Information Processing Stan-

dard (FIPS) 197 (Pub, 2001) in 2001.

Algebraic cryptanalysis (AC) is an area of crypt-

analysis that has gained much attention in recent

years (Bard, 2009). The principle of AC consists in

transferring the problem of breaking the cryptosys-

tem to the problem of solving a system of multivariate

polynomial equations over a ﬁnite ﬁeld that belongs

to the set of NP-complete problems. The process of

AC is divided into the following two steps. The ﬁrst

step consists of using the cipher’s structure and sup-

plemental information to create a system of equations

that describe the behavior of the cipher for a speciﬁc

case. Several papers (Cid et al., 2005), (Simmons,

2009) present approaches for constructing polynomial

equations with auxiliary variables for AES. The paper

(Bulygin and Brickenstein, 2010a) presents a method

https://orcid.org/0000–0002–9426–8467

https://orcid.org/0000–0002–6546–8953

https://orcid.org/0000–0002–8858–4826

https://orcid.org/0000–0001–5444–8511

for obtaining equations in key variables only, which is

based on Gr

obner bases. In Section 3.2.4, we present

another approach for obtaining polynomial equations

that contain only the variables of the initial key, which

is based on gradual substitution.

The second step of AC involves solving the poly-

nomial system to derive the secret key. While the

method for deriving the system of equations depends

on the cipher, the method for solving the system may

be independent of the cipher. In our work, we lever-

age the fact that the derived equation systems contain

only the variables of the initial key, and we present

some reduction techniques for reducing the computa-

tional complexity of solving the polynomial systems.

Several previous studies have dealt with alge-

braic cryptanalysis of small scale variants of AES.

In (Courtois and Pieprzyk, 2002), the authors de-

scribed AES as a system of overdeﬁned sparse

quadratic equations over GF(2), and proposed an XSL

attack for the family of XSL-ciphers to which AES

belongs to. The XSL algorithm was later analyzed

concerning AES in (Cid and Leurent, 2005). The

work (Bulygin and Brickenstein, 2010a) also pre-

sented methods for solving polynomial systems de-

rived from AES using Gr

obner bases. The interpre-

tation of AES as a system of equations over GF(2

)

is presented in (Murphy and Robshaw, 2002). The

work (Nover, 2005) reviewed different techniques for

solving systems of multivariate quadratic equations

over arbitrary ﬁelds, such as relinearization and XL

algorithm, that were used on equations derived from

AES.

Bielik, M., Jure

cek, M., Jure

cková, O. and Lórencz, R.

Yet Another Algebraic Cryptanalysis of Small Scale Variants of AES.

DOI: 10.5220/0011327900003283

In Proceedings of the 19th International Conference on Security and Cryptography (SECRYPT 2022), pages 415-427

ISBN: 978-989-758-590-6; ISSN: 2184-7711

415

We begin our work by a brief discussion of

obner bases, and we show how these can be used to

solve systems of multivariate non-linear polynomial

equations. In the third section, we derive multivariate

non-linear polynomial systems over GF(2) for small

scale variants of AES. We will eliminate all auxiliary

variables by a gradual substitution so that the poly-

nomial systems will contain only the variables de-

scribing the secret key. The elimination will make the

polynomial systems fully dependent on the provided

pairs of plaintext and ciphertext, which will allow us

to apply the reductions for faster solving.

The fourth section discusses the results of our ex-

periments. We demonstrate the current capabilities of

obner bases in solving the polynomial systems de-

scribed in the third section, and we compare their per-

formance to a SAT solver. We show how the perfor-

mance of Gr

obner bases and the SAT solver can be in-

creased using several pairs of plaintexts and their cor-

responding ciphertexts. We also discuss the progress

of diffusion within the reduced versions of AES. In

summary, our main contributions are: (1) the deriva-

tion of the equations described in Section 3.2.4; (2)

the processing of equations (see Section 4.1) to speed

up the computing of Gr

obner bases.

2 ALGEBRAIC BACKGROUND

obner bases were introduced by Bruno Buchberger

(Buchberger, 2006), who named the concept in honor

of his advisor Wolfgang Gr

obner (1899–1980). Buch-

berger also developed the fundamental algorithm for

the computation of a Gr

obner basis known as Buch-

berger’s algorithm.

obner bases are nowadays discussed in multiple

books including (Becker, 1993) and (Cox, 2015). We

will follow these books along the way as we gradually

unveil the elegance of Gr

obner bases in solving sys-

tems of polynomial equations. Further information

can be also found in (Adams, 1994) and (Hibi, 2013).

The set of all polynomials in x

,...,x

with co-

efﬁcients in a ﬁeld F will be denoted F [x

,...,x

When the particular variables are of no relevance, we

will denote the set by F [x] for short. We will also em-

ploy the standard letters x,y and z instead of x

and

when we discuss illustrative polynomials. Univari-

ate polynomials will be denoted by f (x) ∈ F [x]. We

will denote by M (x

,...,x

), M (x) or simply M , the

set of all monomials in the variables x

,...,x

Deﬁnition 2.1. Let h =

∑

∈ F [x] \ {0} be a

nonzero polynomial, F a subset of F [x] \ {0} and

let  be a monomial order on M (x). The multi-

degree of h is multideg(h) = max(α ∈ N

| c

0). The maximum is taken with respect to . The

leading coefﬁcient of h is LC(h) = c

multideg(h)

∈ F .

LC(F) =

{

LC( f ) | f ∈ F

}

. The leading monomial

of h is LM(h) = x

multideg(h)

. The leading term of h is

LT(h) = LC(h) · LM(h).

Deﬁnition 2.2. Let

{

,..., f

}

⊂ F [x] be a set of

polynomials. Then we set

h f

,..., f

i =

(

∑

i=1



,...,h

∈ F [x]

)

to be an ideal I of F [x], where the set

{

,..., f

}

a basis of I. We also call h f

,..., f

i the ideal gener-

ated by

{

,..., f

}

Deﬁnition 2.3. Let I ⊆ F [x] be an ideal different from

{0}. We denote by LT(I) = {LT( f ) | f ∈ I} the set of

leading terms of nonzero elements of I. The ideal

of leading terms of I, generated by LT(I), will be

denoted by hLT(I)i.

Deﬁnition 2.4. Fix a monomial order on M (x). A ﬁ-

nite basis G ⊆ I of a nonzero ideal I ⊆ F [x] is a

obner basis if

hLT(G)i = hLT(I)i.

The deﬁnition above says that a set {g

,...,g

} ⊆

I is a Gr

obner basis if and only if the leading term of

any element of I is divisible by some of the LT(g

Deﬁnition 2.5. Let G ⊆ I be a Gr

obner basis of I. We

call G a reduced Gr

obner basis if for all g ∈ G:

(i) LC(g) = 1.

(ii) No monomial of g is in hLT(G \ {g})i.

Most computer algebra systems actually compute

reduced Gr

obner bases by default. Any ideal has its

reduced Gr

obner basis and this basis is unique.

Deﬁnition 2.6. Let I = h f

,..., f

i ⊆ F[x

,...,x

] be

an ideal. The l-th elimination ideal I

is the ideal of

F [x

l+1

,...,x

] given by I

= I ∩ F [x

l+1

,...,x

Theorem 2.7 (The Elimination Theorem). Let G ⊆

I ⊆ F[x

,...,x

] be a Gr

obner basis of I so that



lex



lex

··· 

lex

, where 

lex

is the lexico-

graphic monomial order. Then, for every 0 ≤ l < n,

the set G

= G ∩ F [x

l+1

,...,x

] is a Gr

obner basis of

the l-th elimination ideal I

Proof. See (Cox, 2015, p. 123).

Deﬁnition 2.8. Let F

,...,x

] be a polynomial ring

over the ﬁnite ﬁeld F

with order q = p

where p

is a prime number and m ∈ N

. The ﬁeld equa-

tions of F

are the polynomials x

− x

for every

∈ {x

,...,x

SECRYPT 2022 - 19th International Conference on Security and Cryptography

416

Deﬁnition 2.9. Let

{

,..., f

}

⊂ F [x

,...,x

] be a

set of polynomials and F

an afﬁne space. The afﬁne

variety V ( f

,..., f

) deﬁned by

{

,..., f

}

is the set

V ( f

,. .. , f

) =

a ∈ F



(a) = 0 for all 1 ≤ i ≤ s

of all roots of all the polynomials in

{

,..., f

}

Theorem 2.10 (Finiteness Theorem). Let f

,..., f

∈

F[x

,...,x

] be polynomials. If we have h f

,..., f

i∩

F [x

] 6= 0 for all x

, then V (h f

,..., f

i) ⊆ F

is ﬁ-

nite.

Proof. See (Cox, 2015, p. 252).

Considering the Finiteness Theorem above,

adding the ﬁeld equations into our polynomial sys-

tem ensures that the system will have ﬁnitely many

solutions.

Theorem 2.11 (Hilbert’s Weak Nullstellensatz). Let

,..., f

∈ F [x] be polynomials. Then the following

are equivalent:

(i) There exists an extension ﬁeld E of F and a ∈ E

such that for all f

we have f

(a) = 0.

(ii) 1 /∈ h f

,..., f

Proof. See (Becker, 1993, p. 281).

Note that 1 ∈ I ⊆ F [x], where I is an ideal, means

I = F [x] since 1h = h for all h ∈ F [x]. Also note that

whenever we have a ﬁnite ﬁeld F and its extension E,

all elements from F satisfy all of the ﬁeld equations

of F and no element in E \ F satisﬁes any of these

equations. Therefore, if we add the ﬁeld equations

into a polynomial system that consists of polynomi-

als in F [x], we restrict our solutions to the ﬁeld F .

Let us demonstrate this fact in combination with the

Hilbert’s Weak Nullstellensatz on the following two

examples.

Example 2.12. Consider a system of equations where

= f

= 0 are polynomials in GF(2) with

= x + y + z, f

= xy + xz + yz, f

= xyz + 1.

If we compute the reduced Gr

obner basis with

z 

lex

y 

lex

x, we get the following polynomials:

= x + y + z, g

= y

+ yz + z

, g

= z

+ 1.

We see that the only solution to the last poly-

nomial is z = 1. When we substitute this solution

into g

, we get g

= y

+ y + 1, which has no so-

lution in GF(2), and therefore the initial polynomial

system has no solution in GF(2) either. Since g

is irreducible over GF(2) we get the extension ﬁeld

GF(2)[α]/hα

+ α + 1i = GF(2

) with the elements

0,1,α,α + 1. If z = 1, the polynomial g

has two so-

lutions in GF(2

), namely y = α and y = α + 1, since

(α+1)

= α. The polynomial g

has then also two so-

lutions in GF(2

), namely x = α and x = α + 1. All of

these solutions also satisfy our initial system f

, f

We could also obtain further solutions if we set z = α.

Example 2.13. Considering the previous example, if

we add the ﬁeld equations of F into the system, we

get the following reduced Gr

obner basis:

= 1.

According to the Hilbert’s Weak Nullstellensatz, we

can already see that the initial polynomial system

, f

has no solutions in GF(2).

One of the fastest and practically implementable

algorithms for computing Gr

obner bases, i.e., F4, was

introduced in (Faug

ere, 1999). The algorithm is im-

plemented in the computer algebra system Magma

(Bosma et al., 1997), which we employ in our experi-

ments.

3 EQUATION SYSTEMS FOR

SMALL SCALE AES

This section describes the derivation of multivariate

non-linear polynomial systems over GF(2) for small

scale variants of AES.

3.1 Small Scale AES

Before we discuss the scaled-down derivatives of

AES, let us try to estimate how long it would take

to attack the full AES-128 by brute force. The actual

time complexity of guessing a key with 128 bits can

be illustrated by a brief thought experiment.

Suppose we are in possession of a computer clus-

ter with ten billion nodes, each of which runs at

3.3 GHz. Also suppose that one use of AES-128 takes

only one clock cycle on each node. Say that one year

has around 3 · 10

seconds. Our cluster will then go

through 3 · 10

· 3.3 · 10

· 10

≈ 10

≈ 2

keys in

one year. This means that in the worst case, the total

time required to guess the correct key will be around

years, which is about 250 billion; while the age of

the universe is currently estimated to be around 13.8

billion years.

Now suppose that the average consumption of

each node is only 1 W and that 1 kWh of energy costs

only 0.01 e (the average price of 1 kWh for European

household consumers was around 0.2 e in 2020).

This means that the energy cost required for our attack

is around 10

· 0.001 · 0.01 · 24 · 365 ·2

≈ 10

A quick estimate like this immediately leads to

the conclusion that the feasibility of the classic brute-

Yet Another Algebraic Cryptanalysis of Small Scale Variants of AES

417

force approach is beyond reality. This striking infea-

sibility of attacking the full AES-128 motivated re-

searchers to come up with scaled down versions of

the cipher in order to provide manageable insight into

its internals. Carlos Cid et al. introduced such ver-

sions in (Cid et al., 2005) and (Cid et al., 2006). The

reductions emerge naturally and the new cipher can

be described by the following parameters:

(i) the number of rounds n, 1 ≤ n ≤ 10;

(ii) the number of rows r of the state, r = 1,2,4;

(iii) the number of columns c of the state, c = 1, 2, 4;

(iv) the number of bits e of the elements of the state,

e = 4,8.

We will denote the scaled-down version of AES by

SR(n,r,c,e). This notation is consistent with (Cid

et al., 2005) and (Cid et al., 2006). The standard

AES-128 can be then deﬁned by SR(10,4,4,8) with

one subtle difference described in the following para-

graph:

The last round of AES differs from the previous

ones inasmuch as the MixColumns operation is omit-

ted in it. This omission is due to the design of the in-

verse of AES. The new SR(n,r,c, e) cipher keeps the

MixColumns operation in the last round. This oper-

ation is a linear transformation, so the overall com-

plexity of the cryptanalysis of both ciphers remains

the same, since a solution of a system of polynomial

equations for one cipher would provide a solution for

the other cipher. This omission is the only difference

between AES-128 and SR(10,4,4,8).

Let us now go through the scaled-down ver-

sions of the actual encryption operations used in

SR(n,r,c,e). The cipher operates over the ﬁeld

GF(2

), deﬁned by the quotient ring F

[x]/h f (x)i

where f (x) = x

+ x + 1 when e = 4 and f (x) =

+x + 1 when e = 8. Note that the polyno-

mial f (x) is irreducible over F

[x] in both cases and

when e = 8, it is identical to the polynomial used in

the original AES-128.

The SubBytes operation is also identical to the

one used in AES-128 when e = 8. When e = 4, the

operation is a composition of the following two trans-

formations:

(i) Take the multiplicative inverse in GF(2

), the ele-

ment 0

is mapped to itself.

(ii) Apply the following afﬁne transformation over

GF(2



















1 0 1 1

1 1 0 1

1 1 1 0

0 1 1 1































(3.1)

The ShiftRows operation cyclically rotates the

row i of the state by i positions, 0 ≤ i < r − 1. Notice

that we index the rows from zero so that the ﬁrst row

is always left intact. When r = 4, we use the matrix







0 1 0 0

0 0 1 0

0 0 0 1

1 0 0 0







(3.2)

to rotate a single row. When r = 2, the matrix be-

comes



0 1

1 0



When c = 4, we can use the following expression to

model the whole ShiftRows operation



















I 0 0 0

0 R

0 0

0 0 R

0 0 0 R



















. (3.3)

We substitute R

instead of R

when r = 2. When

c = 2, the expression simply becomes







I 0

0 R





(3.4)

where R is either R

or R

and I is the identity matrix

of corresponding size. When r = 1 or c = 1, the oper-

ation has no effect since either R

becomes (1) or the

matrix from the expression above becomes I.

The MixColumns operation in AES multiplies

each column of the state by the polynomial

a(x) = 03

+ 01

x + 02

∈ GF(2

)[x].

Multiplication by a ﬁxed polynomial modulo another

ﬁxed polynomial can be regarded as a linear trans-

formation so that the MixColumns operation can be

seen as a linear transformation as well. If we asso-

ciate the coefﬁcients 03

, 02

and 01

of the poly-

nomial a(x) ∈ GF(2

)[x] with the polynomials x + 1,

x and 1, respectively, we can model the MixColumns

operation by the following expression







0,c

1,c

2,c

3,c













x x + 1 1 1

1 x x + 1 1

1 1 x x + 1

x + 1 1 1 x













0,c

1,c

2,c

3,c







(3.5)

for 0 ≤ c < 4, which indexes the columns. When

r = 2, the operation can be described by the following

linear transformation



0, j

1, j





x + 1 x

x x + 1



0, j

1, j



(3.6)

for 0 ≤ j < 2, which indexes the columns, similarly

to expression (3.5). When r = 1, the matrix deﬁning

SECRYPT 2022 - 19th International Conference on Security and Cryptography

418

the MixColumns operation simply becomes (1), so the

operation has no effect.

When c = 4, the new cipher uses the same key

schedule as in AES-128. For c = 2 and c = 1,

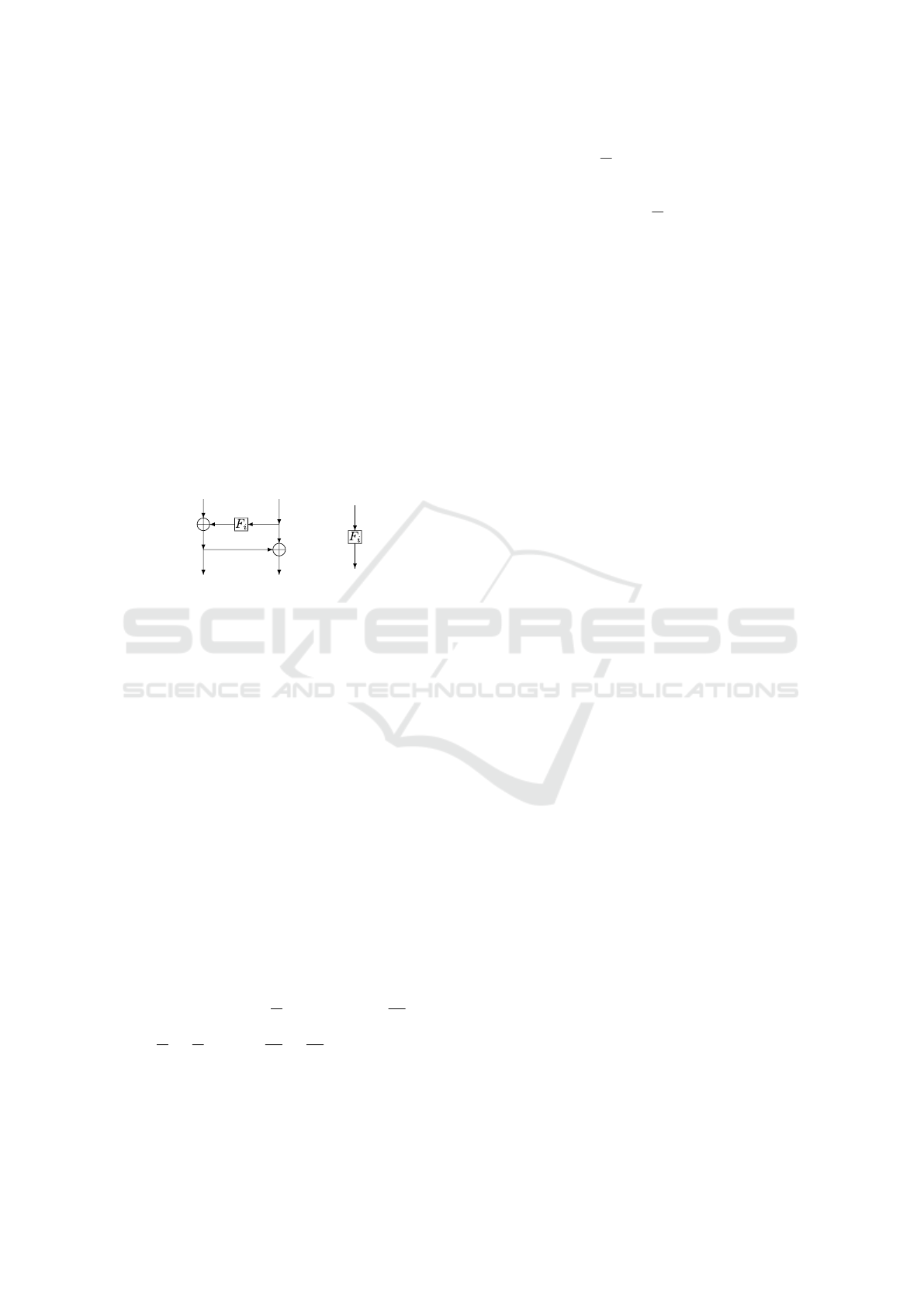
the structure is naturally reduced and depicted in

Figure 1, left and right respectively. Similarly to

AES-128, the AddRoundKey operation takes in c

words of length r. Each word contains the elements of

GF(2

). These elements are added to the state—each

word is added to a column of the state. The RotWord

and SubWord operations take in r-tuples containing

the elements of GF(2

). The round constant array also

contains r-tuples, in which the only non-zero element

is the ﬁrst one, namely x

j−1

∈ GF(2

) being the pow-

ers of x ∈ GF(2

) where j is the round number. Notice

that the initial key has rce bits. Also recall that this

initial key is added to the plaintext before starting the

encryption and generating the subsequent sub-keys,

just as in AES-128.

Figure 1: A schematic depiction of the scaled-down key

schedule (Cid et al., 2005).

3.2 Equations Systems

Let us now model AES and its scaled-down variants

as a system of multivariate polynomial equations over

GF(2). We will focus our attention mainly to SR(n, 2,

2, 4) and derive a system of equations for this cipher.

A solution to this system will provide us with the en-

cryption key. Other scaled-down derivatives can be

modeled in the same way, including AES itself. Note

that we will use one ciphertext with its corresponding

plaintext for our model. Our method therefore comes

under the known-plaintext type of cryptanalysis.

3.2.1 Non-linear Equations

Let us start by considering the inversion part of the

S-box. We know that bc = 1, where b ∈ GF(2

) is

the input and c ∈ GF(2

) is the output of the S-box.

This equation holds unless b = 0, in which case we

have b = c = 0 and we will say that a 0-inversion has

taken place. The probability of a 0-inversion occur-

ring is quite low, namely

when e = 4 and

256

when

e = 8, so the probability of no 0-inversion occurring

is 1 −

and 1 −

256

255

256

. Notice, however,

that these probabilities hold for a single application

of the S-box. In SR(n, 2, 2, 4), there are four applica-

tions of the S-box during the encryption in one round,

so the probability of no 0-inversions occurring during

the encryption is (

)

. There are also two appli-

cations of the S-box during the key schedule in one

round, so the probability of no 0-inversions occurring

during the key schedule is (

)

. We presume statis-

tical independence of the 0-inversions.

The actual occurrence of a 0-inversion either dur-

ing the encryption or key schedule is deterministically

given by the choice of the plaintext and initial key. If

we happen to hit a 0-inversion during the generation

of the ciphertext, we can simply disregard the current

combination of the plaintext and key, and pick another

combination. The issue, as we will see later on, is that

one of the equations that model the S-box would have

to change, and from a cryptanalyst point of view, we

would not know which one it would have to be since

we do not know the key. For this reason, we will as-

sume that no 0-inversions have occurred for the given

plaintext/key combination when we start generating

the equations.

We may regard both b =

∑

i=0

and c =

∑

i=0

as polynomials in GF(2)[x]. The product bc

modulo the polynomial m(x) = x

+ x + 1 is r(x) =

+ r

x + r

where

= b

⊕ b

= b

⊕ b

= b

⊕ b

= b

⊕ b

(3.7)

It is important to note that the coefﬁcients b

and c

are the elements of GF(2). We have bc = r = 1. This

gives us four multivariate quadratic equations over

GF(2): r

= 1 and r

= 0 where i = 1,2,3. These

equations are bilinear in the variables b

and c

. For

e = 8, we would have got eight multivariate quadratic

equations in the variables b

and c

instead of four.

If there was a 0-inversion, either during the en-

cryption or key schedule, the ﬁrst equation would

change to r

= 0. However as already mentioned,

we do not consider this case, since we can detect 0-

inversions before we start generating the equations

and disregard the plaintext/key combinations that pro-

duce them.

Along with these equations, it is possible to obtain

further quadratic equations from the relation bc = 1.

Notice that we also have bc

= c and b

c = b. Let us

focus on the ﬁrst relation and compute the resulting

equations. The equations for b

c = b can be produced

in the same fashion. Since we work over GF(2), we

can write bc

+ c = 0. We have already computed the

product bc, so we could just multiply it by c and get

the result. This computation would require unneces-

sary steps as it would lead to many intermediate cu-

bic terms which we would have to cross out before

Yet Another Algebraic Cryptanalysis of Small Scale Variants of AES

419

obtaining the ﬁnal coefﬁcients. We can instead com-

pute the square of c and pre-multiply it by b. We are

working over a commutative structure, so the order

in which we perform the multiplication is of no rel-

evance. In order to work out the square of c, we can

use (3.7) and substitute c for b. We get the polynomial

d = c

where d(x) = d

+ d

x + d

with

= c

⊕ c

= c

⊕ c

= c

We can now obtain the ﬁnal result t = bd + c where

t(x) = t

x +t

with

= b

⊕ b

⊕ c

= b

⊕ b

⊕ c

= b

⊕ b

⊕ c

= b

⊕ b

⊕ c

We know that t = 0, so we have four equations t

= 0

for 0 ≤ i < 4. Notice that these equations are quadratic

as well. We can obtain reciprocal equations from

c = b. All of these eight equations are biafﬁne in

the b

and c

variables.

It is possible to obtain even more quadratic equa-

tions by considering the relations bc

= c

and b

c =

. As in the previous case, let us focus on the ﬁrst re-

lation. We can square d to obtain c

and multiply d by

c to obtain c

. The result will then be u = bc

= 0

where u(x) = u

+ u

x + u

with

= b

⊕ b

⊕ c

= b

⊕ b

⊕ c

= b

⊕ b

⊕ c

= b

⊕ b

⊕ c

We have another four equations u

= 0 for 0 ≤ i < 4.

Observe that these equations are still quadratic. We

can obtain reciprocal equations from b

c = b

So far, we have derived 20 multivariate quadratic

equations from the relation bc = 1. A natural question

arises whether we have identiﬁed all quadratic equa-

tions in the b

and c

variables. Notice, for example,

that we have skipped the relation bc

= c

. The reason

is that it would produce equations with cubic terms.

Relations involving higher powers than c

would also

lead to equations with higher than quadratic terms.

In fact, the 20 equations we have derived are all the

quadratic equations over GF(2). A further discussion

can be found in (Cid et al., 2006, p. 77). As also ad-

vised in (Cid et al., 2006, p. 77), we will focus on the

ﬁrst 12 bilinear and biafﬁne quadratic equations we

have obtained and we will omit the remaining eight

ones. For e = 8, we would have got 40 multivariate

quadratic equations in the variables b

and c

instead

of 20.

3.2.2 Linear Equations

The equations we have derived for the inversion part

of the S-box account for the only non-linear equations

in the whole system that models the SR(n, 2, 2, 4) ci-

pher. In fact, the inversion in the AES S-box repre-

sents the only non-linear operation in the whole ci-

pher. Let us now derive the linear equations for the

remaining transformations in AES.

The afﬁne transformation of the S-box can be ex-

pressed directly by (3.1), where the input is the poly-

nomial c(x) from the previous subsection. This gives

us four linear equations in the variables c

. These

equations together with the non-linear equations from

the previous subsection fully describe a single S-box.

Let L

denote the matrix from (3.1). In order to de-

scribe the whole SubBytes operation, we can extend

the matrix L

to the whole state array of SR(n, 2, 2,

4), so we have the matrix

L =







0 0 0

0 L

0 0

0 0 L

0 0 0 L







We can also extend the S-box constant vector

(0,1,1,0)

= 6

to the vector 6 = (6

)

so that we cover the whole state array. We will use

b to denote the input vector of the SubBytes opera-

tion, and b

−1

to denote its output—the vector of the

inverted elements in GF(2

). Note that each compo-

nent in these vectors is made of the four coefﬁcients

of the polynomials b(x) and c(x), respectively; so we

have 12 non-linear equations for each component.

Figure 2: The state array of the SR(n, 2, 2, e) cipher.

The actual state array is depicted in Figure 2. We

will represent it as the vector (s

)

. The

ShiftRows operation can be then described by the

SECRYPT 2022 - 19th International Conference on Security and Cryptography

420

matrix

R =







0 0 0

0 0 0 I

0 0 I

0 I

0 0







where I

is the identity matrix of size four. Before

we describe the MixColumns operation, let us rewrite

(3.7) into matrix form:



















⊕ b



















If we substitute the binary values of the coefﬁcients

of the polynomials x + 1 and x into the matrix in the

expression above, we get the matrices

x+1







1 0 0 1

1 1 0 1

0 1 1 0

0 0 1 1







and







0 0 0 1

1 0 0 1

0 1 0 0

0 0 1 0







(3.8)

These matrices represent the multiplication by the

polynomials x + 1 and x modulo the polynomial x

x + 1. The MixColumns operation, deﬁned by (3.6),

can then be expressed by the matrix

M =







x+1

0 0

x+1

0 0

0 0 M

x+1

0 0 M

x+1







We can now describe one round of SR(n, 2, 2, 4) by

the expression

= MR(Lb

−1

i−1

+ 6) + k

for i < 0 ≤ n

where k

is a vector containing 16 binary variables of

the round key described in the following subsection

and i is the round number. The vector b

−1

i−1

contains

four components—the outputs from the S-boxes—

each of which has four binary variables. It is straight-

forward to check that R6 = M6 = 6. We can then

write

= MRLb

−1

i−1

+ k

+ 6 for i < 0 ≤ n.

The relation above gives 16 linear equations, which

represent one round of SR(n, 2, 2, 4). In addition, we

have 12 non-linear equations for each component in

−1

i−1

, so in total, we have 16 + 4 · 12 = 64 equations

describing one round of encryption in the SR(n, 2, 2,

4) cipher. When i = n, we have

= MRLb

−1

n−1

+ k

+ 6

where c

is the known ciphertext, which is a vector of

16 binary values. We obtain b

by adding the initial

unknown key k

to the known plaintext p

, so we have

= p

+ k

This addition gives us further 16 initial equations

where p

is a vector of 16 binary values and k

is a

vector of 16 binary variables. Our goal is to actually

compute the values of k

since this is the user’s key.

All other variables are auxiliary.

3.2.3 Key Schedule

The generation of round keys for SR(n,r,c,e) is thor-

oughly described in Appendix A of (Cid et al., 2005).

Let us now describe the equations for SR(n, 2, 2, 4).

Let k

= (k

i,0

i,1

i,2

i,3

∈ GF(2

)

be the round

key of round i. The round key can be then deﬁned by



i,2q

i,2q+1



−1

i−1,3

−1

i−1,2







i−1



∑

t=0



i−1,2t

i−1,2t+1



(3.9)

for 0 ≤ q < 2 where x

i−1

is an element of GF(2

This expression gives 16 linear equations for each k

Note that k

is not provided by the user—it is a vec-

tor of 16 binary variables that we, as the cryptanalyst,

are trying to compute. We also get 2 · 12 = 24 non-

linear equations since the computation of each k

re-

quires two applications of the S-box. One round of

the key schedule in SR(n, 2, 2, 4) is then described by

40 equations.

3.2.4 Equations Without Auxiliary Variables

In this section, we propose the derivation of equa-

tions that contain only the variables of the initial

key. In order to obtain such a system, we can elim-

inate the auxiliary variables by a gradual substitu-

tion of the variables of the initial key since we know

that the cipher starts by adding the initial key to

the known plaintext. It is straightforward to per-

form this substitution for the linear equations. For

the non-linear equations, which model the S-box,

we can leverage Gr

obner bases. Consider the four

polynomials r

,...,r

from (3.7) as polynomials in

F [c

,...,c

,...,b

]. We see that it is not straight-

forward to express the output bits c

in terms of the

input bits b

by ordinary manipulation techniques. If

we impose the graded reverse lexicographic block or-

der 

grlex,grlex

on F [c

,...,c

,...,b

] with 

grlex

on both F [c

,...,c

] and F [b

,...,b

], and compute

Yet Another Algebraic Cryptanalysis of Small Scale Variants of AES

421

the reduced Gr

obner basis, we get the following poly-

nomial system:

= c0 ⊕ b

⊕ b

= c1 ⊕ b

⊕ b

= c2 ⊕ b

⊕ b

= c3 ⊕ b

⊕ b

= b

⊕ b

⊕ 1.

We see that the last polynomial f

involves only the

variables b

. Notice that this polynomial is not satis-

ﬁed only if all b

= 0, and it holds whenever we have

at least one b

= 1. Recall that we do not consider 0-

inversions. This polynomial is therefore always sat-

isﬁed, and we can omit it from the system. We also

see that in the remaining polynomials, the output vari-

ables c

,...,c

are expressed solely by the input vari-

ables b

. This allows us to perform the gradual substi-

tution of the unknown variables of the initial key k

throughout the whole polynomial system. Notice that

we obtain |k

| = 16 polynomials after we ﬁnish the

substitution. We note that the size of the polynomials

is close to 2

|−1

at full diffusion of the cipher. The

diffusion grows rapidly with each round. For exam-

ple, as our experiments will reveal, the cipher SR(n,

2, 2, 4) reaches its full diffusion at round n = 3. This

way of generating the polynomials is therefore suit-

able only for low values of n. A different method for

obtaining polynomials without auxiliary variables is

described in (Bulygin and Brickenstein, 2010b).

4 RESULTS OF EXPERIMENTS

The experiments were carried out on GNU/Linux

5.4 running on two Intel

Xeon

Gold 6136 pro-

cessors with 768 GB DDR4 memory evenly split up

into 12 modules. The baseboard was Supermicro

X11DPi-NT. The initial polynomial systems con-

taining auxiliary variables were generated by utilizing

Martin Albrecht’s implementation of the small scale

variants of AES in SageMath 9.1 (The Sage Devel-

opers, 2020), which also uses Python 3.7.3 and Poly-

BoRi (Brickenstein and Dreyer, 2009). The systems

were solved in Magma V2.25-5 (Bosma et al., 1997)

and CryptoMiniSat (Soos et al., 2009). The source

code for the experiments can be found at https://gitlab.

com/upbqdn/yaac. The generation and preprocessing

of the polynomial systems was implemented in paral-

lel utilizing all 24 available cores. Magma, however,

was able to solve one system on one core only, so in

order to keep the comparison even, we explicitly re-

stricted CryptoMiniSat to one core as well.

As stated in Deﬁnition 2.2, we may regard a sys-

tem of polynomials as a basis of an ideal I. We can

then compute the reduced Gr

obner basis of I under

the lexicographic order, and by applying the Elimi-

nation Theorem, we can quickly obtain the solution.

We have demonstrated the use of this theorem in Ex-

ample 2.12, and as we have discussed in the previous

section, the solution represents the secret key.

Table 1 shows the results of initial experiments

with systems of equations containing auxiliary vari-

ables. We generated the systems in SageMath for var-

ious versions of SR(n,r, c, e), and we subsequently at-

tempted to solve these systems by the F4 algorithm

implemented in Magma and by CryptoMiniSat.

Table 1: Initial experiments with systems containing auxil-

iary variables.

Cipher

Key

bits

Vars Polys F4 SAT

Time Mem. Time

SR(1, 2, 2, 4) 16 72 120 1 s 33 MB 2 s

SR(2, 2, 2, 4) 16 128 224 19 s 848 MB 12 s

SR(3, 2, 2, 4) 16 184 328 4 h 76 GB 17 s

SR(4, 2, 2, 4) 16 240 432 — — 27 s

SR(10, 2, 2, 4) 16 576 1056 — — 50 s

SR(1, 4, 2, 4) 32 144 240 48 s 981 MB 9 s

SR(2, 4, 2, 4) 32 256 448 — — 1.5 m

SR(3, 4, 2, 4) 32 368 656 — — 63 h

SR(1, 2, 4, 4) 32 136 216 3 s 67 MB 11 s

SR(2, 2, 4, 4) 32 240 400 — — 33 s

SR(3, 2, 4, 4) 32 344 584 — — 15.5 m

SR(4, 2, 4, 4) 32 448 768 — — 34 h

SR(1, 4, 4, 4) 64 272 432 — — 2.5 m

SR(1, 2, 2, 8) 32 144 240 1 m 2.2 GB 22 s

SR(2, 2, 2, 8) 32 256 448 — — 11.5 m

SR(1, 4, 2, 8) 64 288 480 — — 41.5 m

SR(1, 2, 4, 8) 64 272 432 — — 4 m

SR(1, 4, 4, 8) 128 544 864 — — —

Since we work over GF(2), the polynomials can

be seen as logical formulas in algebraic normal form

(ANF). SageMath supports a conversion from ANF

to CNF (conjunctive normal form). Formulas in CNF

can be passed to CryptoMiniSat and the initial key

can be then quickly recovered from the solution. We

have included the SAT solver so that we can compare

it to the performance of the F4 algorithm and we can

see in the table that the solver performs signiﬁcantly

better. The SAT solver also takes a negligible amount

of memory, so this value is not stated in the table.

The average number of monomials per polyno-

mial is between 6 and 8 when e = 4 and between 18

and 20 when e = 8. Both the average and highest de-

gree of the monomials are equal to two, so all poly-

nomials are quadratic or linear, as the case may be.

In our experiments, we do not consider ciphers with

SECRYPT 2022 - 19th International Conference on Security and Cryptography

422

r < 2 or c < 2 as these have the matrices for the op-

erations MixColumns and ShiftRows reduced to (1).

Recall that the dimensions of the state array r and c

are restricted to the values 1, 2 and 4; the exponent e

can be either 4 or 8; and for the number of rounds n,

we have 1 ≤ n ≤ 10.

The column named Vars contains the number of

variables in the whole polynomial system and the col-

umn named Polys contains the number of polynomi-

als in the system. We measured the runtime and mem-

ory consumption only during the solving of the poly-

nomials since the preparation of the system takes only

a fraction of the resources relative to solving it.

Recall that the key size for SR(n,r, c, e) is given by

the product rce. Notice that we were not able to com-

pute the solution for even one round of SR(n, 4, 4, 8),

the key size of which is 128 bits. On the other hand,

the SAT solver could quickly compute the solution for

all ten rounds of SR(n,2, 2, 4). We limited the time of

each computation to 100 hours. Missing values in the

tables denote computations that exceeded this time.

Table 2 contains the results of experiments with

systems that contain only the variables of the initial

secret key. We eliminated the auxiliary variables by

a gradual substitution of the variables of the initial

key through the system, starting by adding the known

plaintext bits and ending by adding the known cipher-

text bits. The time required for this substitution is

stated in the column named PT. This system always

contains k polynomials in k variables where k is the

number of the key bits. Since k is the number of vari-

ables and we work over GF(2), k is also the maximal

limit of the total degree of the polynomials.

Table 2: Experiments with systems with no auxiliary vari-

ables.

Cipher

Key

bits

AMP

F4 SAT

Time Mem. Time

SR(1, 2, 2, 4) 16 1 s 20 1 s 33 MB 1 s

SR(2, 2, 2, 4) 16 1 s 2475 2.5 m 4.8 GB 1 m

SR(3, 2, 2, 4) 16 8 s 32784 8.5 m 18.5 GB 13 m

SR(10, 2, 2, 4) 16 2.5 m 32814 9 m 19.5 GB 14 m

SR(1, 4, 2, 4) 32 1 s 37 55 s 1.2 GB 1 s

SR(1, 2, 4, 4) 32 1 s 23 13 s 671 MB 1 s

SR(1, 4, 4, 4) 64 4 s 40 — — 2 m

SR(1, 2, 2, 8) 32 8 s 314 — — 1.5 m

SR(1, 4, 2, 8) 64 18 s 567 — — 33 m

SR(1, 2, 4, 8) 64 14 s 348 — — 1.5 h

Preprocessing Time — the time required to obtain the

system

Average number of Monomials per Polynomial

All further experiments will be carried out with

systems of polynomials involving only the variables

of the initial key. In systems with auxiliary vari-

ables, the structure of the polynomial systems derived

from different plaintexts remains unchanged. Only

the initial and ﬁnal polynomials that add the bits of

the plaintext and ciphertext differ by this bitwise addi-

tion. Since we have eliminated the auxiliary variables

by a gradual substitution of the initial key bits starting

from the initial plaintext addition, each of the k poly-

nomials now depends on the choice of plaintext and

its corresponding ciphertext. Since the structure of

each polynomial system is now different, the time and

memory required for obtaining the solution started to

differ as well, especially the time required by the SAT

solver. For this reason, all the following tables contain

average results of ﬁve different runs for each experi-

ment. We can still see that the results for the SAT

solver differ across tables for the same experiment, so

even more than ﬁve runs would be required for further

investigation. Nevertheless, we restricted ourselves to

such number due to limited time resources.

The column named AMP contains the average

number of monomials per polynomial in the whole

system. We can see that this number grows fast as n

increases. The maximal limit of the number of mono-

mials in one polynomial is 2

− 1. When n = 1 and

e = 4, the average degree of monomials is 2 and the

highest degree is 3. When n = 2, the average and

highest degrees are 5 and 9, respectively. Note that

the average degree has its maximum at

. We were

not able to generate systems with n > 2 and r, c > 2

for e = 4. For n = 1 and e = 8, the average degree

is 4 and the maximal degree is 7. We were not able

to generate systems with e = 8 and n > 1 (recall that

we do not consider the cases when r < 2 or c < 2).

We can see in the table that the overall performance

is worse compared to the previous table and that the

SAT solver still outperforms the F4 algorithm. More-

over, we were able to solve less systems than in the

previous experiments.

In the table above, we can see that the the AMP

value and the solving time and memory are almost

the same for SR(3, 2, 2, 4) and SR(10, 2, 2, 4).

This means that the full diffusion for SR(n,2,2,4) is

reached in the third round of the cipher and the sub-

sequent rounds do not provide any further security

as regards the algebraic cryptanalysis, except for a

longer time required for the generation of the polyno-

mial system. This observation is in line with the state-

ments made in (Aumasson, 2019). Table 3 provides

a deeper insight into the distribution of monomials in

SR(3, 2, 2, 4).

At full diffusion, the expected degree of monomi-

als should be equal to





where k is the number of

variables and d is the degree. Since we have SR(3,

2, 2, 4), we get k = 2 · 2 · 4 = 16. Recall that we also

have k polynomials in the whole system. In Table 3,

the expected value is stated in the last row. We see

Yet Another Algebraic Cryptanalysis of Small Scale Variants of AES

423

Table 3: Distribution of monomials of a given degree in SR(3, 2, 2, 4).

Poly Number of monomials of the given degree

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 all

Avg. 0.7 8 59 279 917 2193 4010 5730 6436 5742 4014 2194 909 275 60 8 0.6 32834

Exp. 0.5 8 60 280 910 2184 4004 5720 6435 5720 4004 2184 910 280 60 8 0.5 32768

that all the polynomials follow this value very closely,

meaning that it is not possible to get much closer to

the expected value in the subsequent rounds. For this

reason, we do not consider the rounds following af-

ter the third one. The table also shows that the aver-

age monomial degree is 8 for each polynomial, which

is half of the maximal degree, and that no polyno-

mial signiﬁcantly differs from the expected values for

monomial degrees. The second last row shows the av-

erage value for all of the polynomials—the average of

the whole column above.

The last column contains the number of all mono-

mials in the polynomial. At full diffusion, this num-

ber should be equal to

∑

d=0





= 32768 so

that every polynomial contains half of all of the pos-

sible monomials. We see that the number of mono-

mials is close to the expected value for each of the

polynomials as well. We may also be interested in the

frequency of the variables in the polynomial system.

Considering the full diffusion again, each variable

should be contained in half of the monomials in ev-

ery polynomial, so the expected value is

= 16384.

In the actual system described in Table 3, the most

frequent variable had 16446 occurrences and the least

frequent variable had 16393 occurrences, these are

aggregated values.

4.1 Reduced Polynomial Systems

Let us now reduce the polynomial systems and see if

we can obtain any better results than those in Table 2.

Deﬁnition 4.2. Let V ⊆ F

be an afﬁne variety. We

deﬁne

I(V ) =

f ∈ F[x

,. .., x

]



f (a) = 0 for all a ∈ V

Proposition 4.3. If V ⊆ F

is an afﬁne variety, then

I(V ) ⊆ F[x

,...,x

] is an ideal. We call I(V ) the ideal

of V .

Proof. See (Cox, 2015, p. 32).

Let k be the initial key of AES or its small scale

variant. By Proposition 4.3, we know that I(k) is

an ideal. Now let { f

,..., f

} and {g

,...,g

} be

two polynomial systems generated from two differ-

ent pairs of plaintext and its corresponding cipher-

text under the same key k. Since each f

(k) = 0 and

(k) = 0, we have I = h f

,..., f

,...,g

i ⊆ I(k).

In general, in order to obtain the ideal I, we may com-

bine any number of polynomial systems. We can now

compute the Gr

obner basis for I and we still get the

initial key k. The ideal I represents an overdeﬁned

system for which it could be easier to obtain the so-

lution. We will call one pair of plaintext and its cor-

responding ciphertext a PC pair. In our further ex-

periments, we assume that all PC pairs use the same

key.

Table 4: Experiments with two combined systems.

Cipher

Key

bits

AMP

F4 SAT

Time Mem. Time

SR(1, 2, 2, 4) 16 1 s 21 1 s 33 MB 1 s

SR(2, 2, 2, 4) 16 2 s 2469 5 s 100 MB 1 m

SR(3, 2, 2, 4) 16 9 s 32798 13 m 19.8 GB 45.5 m

SR(10, 2, 2, 4) 16 3 m 32774 11 m 25.5 GB 31.5 m

SR(1, 4, 2, 4) 32 2 s 37 1 s 33 MB 1 s

SR(2, 4, 2, 4) 32 6 s 33360 — — —

SR(1, 2, 4, 4) 32 2 s 23 1 s 33 MB 1 s

SR(2, 2, 4, 4) 32 3 s 6701 — — —

SR(1, 4, 4, 4) 64 4 s 39 1 s 33 MB 2 s

SR(1, 2, 2, 8) 32 10 s 316 1 s 33 MB 8 s

SR(1, 4, 2, 8) 64 18 s 568 2 s 33 MB 17 s

SR(1, 2, 4, 8) 64 15 s 348 1 s 33 MB 17 s

SR(1, 4, 4, 8) 128 34 s 599 4 s 33 MB 35 s

Preprocessing Time — the time required to obtain the

system

Average number of Monomials per Polynomial

Table 4 summarizes the experimental results for

two combined systems, as described in the previous

paragraph. We can see that the results are signiﬁcantly

better compared to Table 2 and that the F4 algorithm

often outperforms the SAT solver. We can also see

that we are able to solve more polynomial systems

and even the system for SR(1, 4, 4, 8) is solved in

a few seconds. Recall that we were unable to ob-

tain this solution for systems with auxiliary variables.

This practically means that one round of AES-128

provides no security against this attack. We were not

able to obtain any solution for SR(n,4,4,e) with n > 1

though. Observe that we used two PC pairs in this sce-

nario. We carried out further experiments with more

than two pairs, but we did not obtain any better re-

sults. After adding more than ﬁve systems, the time

required to obtain a solution started increasing.

We note that it would not be possible to combine

the systems if we did not eliminate the auxiliary vari-

ables. The reason is that the auxiliary variables do not

SECRYPT 2022 - 19th International Conference on Security and Cryptography

424

Table 5: Experiments with reduced polynomial systems.

Cipher

Key

bits

AMPR

F4 SAT

Time Mem. Time

SR(2, 2, 2, 4) 16 5 s 601 1 1 s 33 MB 29 s

SR(2, 2, 2, 4) 16 5 s 519 5 1 s 33 MB 24 s

SR(3, 2, 2, 4) 16 25 s 32592 1 16 m 17.9 GB 37.5 m

SR(3, 2, 2, 4) 16 40 s 32555 5 18 m 23.1 GB 41 m

SR(2, 4, 2, 4) 32 26 s 4938 1 — — —

SR(2, 4, 2, 4) 32 1 m 4563 5 — — —

SR(2, 2, 4, 4) 32 14 s 3410 1 — — 1 h 23 m

SR(2, 2, 4, 4) 32 18 s 1192 5 60 m 34.5 GB 50 m

Preprocessing Time — the time required to obtain the system

Average number of Monomials per Polynomial after Reduction

Number of polynomial systems of the reduction set

depend on the PC pair—when we use two different

PC pairs, we get the same equations, up to the initial

additions of the plaintext and ciphertext. On the other

hand, when we express the equations only in the vari-

ables of the initial key, we get a different system for

each PC pair.

Table 4 shows that the hardest systems to solve

were the ones with high AMP. Let us see if we can

reduce this value.

Deﬁnition 4.4. Let f ,g ∈ F [x] be two polynomials.

We deﬁne their similarity as σ( f ,g) =

M( f ) ∩ M(g)

where M(h) is the set of monomials in h.

Consider again a polynomial system F =

{ f

,..., f

} and a set of l polynomial systems G =

,...,g

} where m = kl. We will refer to F as the

primal system and to G as the reduction set. Each

polynomial system is generated from a different PC

pair under the same key k. For each f

we ﬁnd a

so that σ( f

) is maximal and compute h

∈ I(k). We get an ideal I = hh

,...,h

i ⊆ I(k).

Similarly to the previous experiments, we can now

compute the Gr

obner basis and obtain the solution

k. Since we work over GF(2), if the polynomials f

and g

are similar enough, the alike monomials can-

cel each other out and the resulting polynomials h

might be smaller than f

. As a result, this might allow

faster computation.

As already mentioned, we get a different system

for each PC pair. How much different depends on

the degree of diffusion in the cipher. In Table 3,

we have shown that the polynomials for SR(n,2,2,4)

with n ≥ 3 are essentially random. This reﬂects in Ta-

ble 5, which contains the results of experiments with

the reduced polynomials h

. The times stated in the ta-

ble are always the overall wall times, and each value

in the table is the average for ﬁve independent experi-

ments. The value l in the table is the number of poly-

nomial systems of the reduction set, as described in

the paragraph above. We see that for SR(3, 2, 2, 4),

the Average number of Monomials per Polynomial

after the Reduction (AMPR) does not differ from the

AMP value in Table 4. On the other hand, for exam-

ple, for SR(2, 4, 2, 4) and l = 5, AMPR is reduced by

86 %. Unfortunately, we could still not compute the

solution. For SR(2, 2, 4, 4) and l = 5, the reduction

allowed us to solve the system, but for l = 2, it did so

only for the SAT solver. For SR(2, 2, 2, 4), the reduc-

tion shortened the computation time. We note that we

considered only the ciphers that required more than

ﬁve seconds to solve in the previous table. We can

also see that the number of polynomial systems for re-

duction l considerably lowered the AMPR value only

for SR(2, 2, 4, 4) and for other ciphers it had no, or

very subtle effect. We have also tried other values of

l, all of which were ≤ 50 due to limited time, with no

signiﬁcant effect either, even for SR(2, 2, 4, 4). The

column labeled PT now includes the time required for

the reduction.

In order to increase the reduction even further, we

tried generating the plaintexts in the PC pairs for the

polynomial systems in G so that each of them would

differ only by one bit from the plaintext for F. It

emerged that this approach did not bring any signiﬁ-

cant improvement.

Since the F4 algorithm and the SAT solver run in a

single thread, and we had a parallel architecture at our

disposal, we performed guess-and-determine attack

and tried guessing some variables in the reduced poly-

nomial systems with l = 5. This means that we deter-

mined the values of the guessed variables, we sub-

stituted these values into the system, and then we at-

tempted to solve the system. Observe that substituting

concrete values of some variables not only eliminates

Yet Another Algebraic Cryptanalysis of Small Scale Variants of AES

425

0 5 10 15 20 25 30

variable

5000

10000

15000

20000

frequency

(a) SR(2, 2, 4, 4)

0 5 10 15 20 25 30

variable

10000

20000

30000

40000

50000

60000

frequency

(b) SR(2, 4, 2, 4)

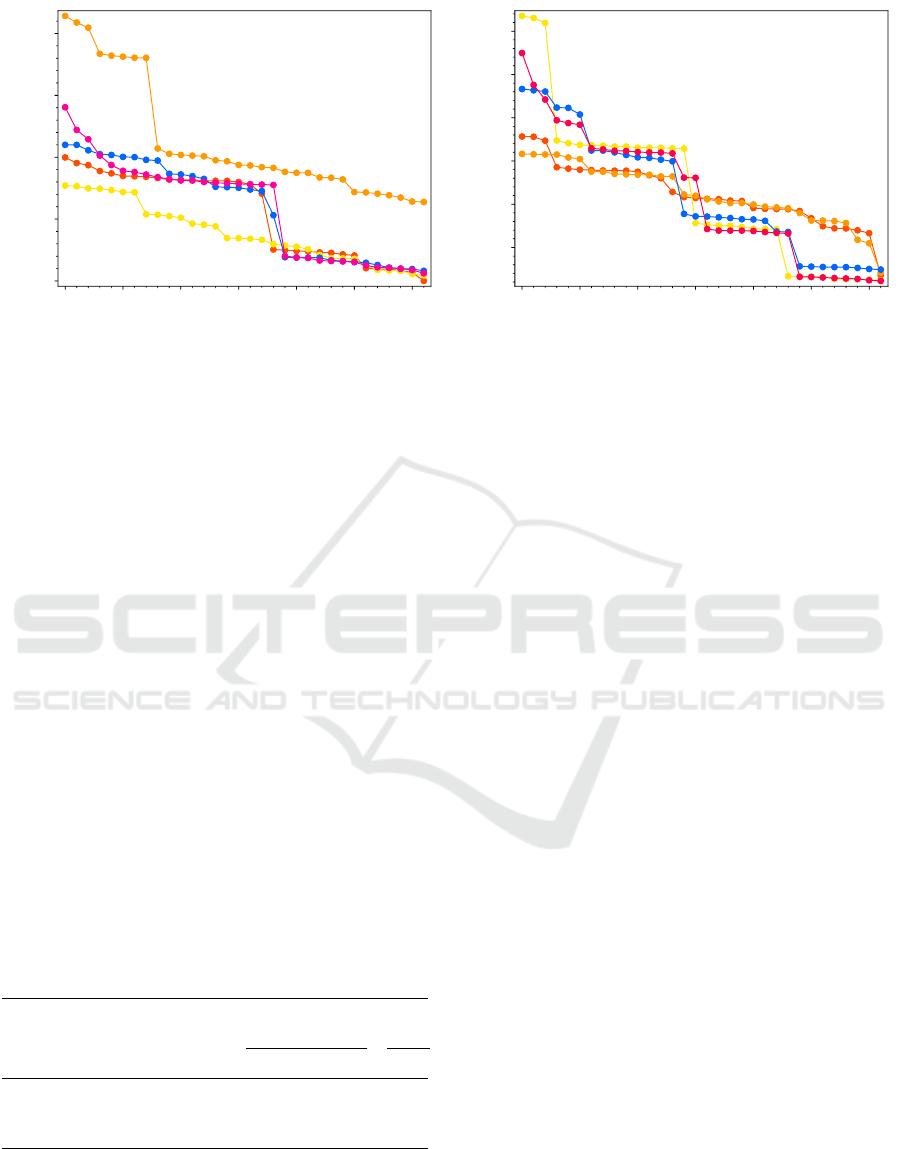
Figure 3: Frequencies of the key variables for ﬁve instances of SR(2, 2, 4, 4) and SR(2, 4, 2, 4). The variables are ordered

according to their frequency.

the variables, but also shortens the polynomials—for

example, a zero occurring in a monomial makes it

vanish. On the other hand, substituting a one can lead

to two equal monomials which cancel each other out.

We used a brute-force approach for guessing the vari-

ables so we got 2

different systems to solve where v

is the number of guessed variables. Instead of guess-

ing random variables, we tried to guess the most fre-

quent ones in order to shorten the polynomials even

further. The reason can be seen in ﬁgure 3. This ﬁg-

ure contains the frequencies of the variables for ﬁve

instances of SR(2, 2, 4, 4) and SR(2, 4, 2, 4). The

variables are ordered in a descending order, so their

labels correspond to their relative positions in the plot

according to their frequency—the zeroth variable is

the most frequent one. We can see that some of the

frequencies differ signiﬁcantly. Recall that, on the

other hand, the frequencies of the variables of SR(3,

2, 2, 4) are evenly distributed as we already showed.

We have tried guessing the eight most frequent vari-

ables, so we had 2

= 256 parallel threads, one thread

for each guess. The results are presented in Table 6.

Table 6: Experiments with reduced polynomial systems and

guessed variables.

Cipher

Key

bits

F4 SAT

Time Mem. Time

SR(3, 2, 2, 4) 16 8 m 6 s 33 MB 35 s

SR(2, 4, 2, 4) 32 2.5 m 43 s 620 MB 9 m

SR(2, 2, 4, 4) 32 31 s 14 s 72 MB 5.5 m

Preprocessing Time — the time required to obtain the

system

The table shows that we were able to obtain the

solution for SR(2, 4, 2, 4) and that the solving time is

reduced signiﬁcantly for the other two ciphers. Note

that the F4 algorithm outperforms the SAT solver.

Also, observe that the preprocessing time for SR(3,

2, 2, 4) has signiﬁcantly increased. This is caused by

counting the frequencies since each of the 16 poly-

nomials has around 2

monomials. We have also

tried guessing eight of the least frequent variables and

we were not able to obtain the solutions for SR(2, 4,

2, 4) and SR(2, 2, 4, 4) even though we solved the

system for SR(2, 2, 4, 4) in the previous table. This

was due to memory limitations as each of the paral-

lel processes allocated dozens of gigabytes—we see

in Table 5 that the F4 algorithm allocated on average

34.5 GB when solving SR(2, 2, 4, 4) with no guessed

variables. We note that each of the threads ﬁnished

its computation in a different time. The threads that

provided no solution usually ended earlier. This could

be leveraged in further analysis since this observation

also provides information about the correct key. We

have also tried guessing different numbers of vari-

ables. Guessing more than eight variables produced

even longer solving times. This was caused by cre-

ating too many threads. On the other hand, we were

often unable to obtain the solutions for SR(2, 4, 2, 4)

when we guessed less than six variables.

5 CONCLUSIONS

In our experiments, we demonstrated the capabili-

ties of solving systems of polynomial equations by

means of Gr

obner bases and a SAT solver. Initially,

we generated systems that contain the auxiliary vari-

ables, and we saw that the SAT solver signiﬁcantly

outperformed Gr

obner bases. We subsequently elim-

inated the auxiliary variables by a gradual substitu-

SECRYPT 2022 - 19th International Conference on Security and Cryptography

426

tion so that the systems contained only the variables

of the initial secret key. We saw that the results were

even worse compared to the systems with the auxil-

iary variables. However, when we combined at least

two systems with no auxiliary variables, we got much

better results, especially for Gr

obner bases. Note, for

example, that we were able to obtain the secret key

for one round of AES-128. We also solved one round

of all the other ciphers with the state array reduced.

We showed that a 16-bit version of AES reaches

its full diffusion after its third round. We also showed

that the polynomial system in the third round has

the same properties as the system in the tenth round.

From an algebraic cryptanalysis point of view, this

might suggest that the original AES has enough spare

rounds as well.

We tried reducing the polynomial systems with-

out auxiliary variables by adding similar polynomi-

als so that equal monomials would cancel each other

out, and we also tried guessing the most frequent vari-

ables. The combination of these two approaches al-

lowed us to obtain the solutions for some of the sys-

tems that we could not solve otherwise.

ACKNOWLEDGEMENTS

This work was supported by the OP VVV MEYS

funded project CZ.02.1.01/0.0/0.0/16 019/0000765

”Research Center for Informatics” and by the

Grant Agency of the CTU in Prague, grant No.

SGS21/142/OHK3/2T/18 funded by the MEYS of the

Czech Republic.

REFERENCES

Adams, W. (1994). An introduction to Gr

obner bases.

American Mathematical Society, Providence, R.I.

Aumasson, J.-P. (2019). Too much crypto. IACR Cryptol.

ePrint Arch., 2019:1492.

Bard, G. (2009). Algebraic cryptanalysis. Springer Science

& Business Media.

Becker, T. (1993). Gr

obner bases : a computational ap-

proach to commutative algebra. Springer-Verlag, New

York.

Bosma, W., Cannon, J., and Playoust, C. (1997). The

Magma algebra system. I. The user language. J. Sym-

bolic Comput., 24(3-4):235–265. Computational al-

gebra and NUMBER theory (London, 1993).

Brickenstein, M. and Dreyer, A. (2009). Polybori: A frame-

work for gr

obner-basis computations with boolean

polynomials. Journal of Symbolic Computation,

44(9):1326 – 1345. Effective Methods in Algebraic

Geometry.

Buchberger, B. (2006). Bruno buchberger’s phd thesis

1965: An algorithm for ﬁnding the basis elements of

the residue class ring of a zero dimensional polyno-

mial ideal. Journal of symbolic computation, 41(3-

4):475–511.

Bulygin, S. and Brickenstein, M. (2010a). Obtaining and

solving systems of equations in key variables only for

the small variants of aes. Mathematics in Computer

Science, 3(2):185–200.

Bulygin, S. and Brickenstein, M. (2010b). Obtaining and

solving systems of equations in key variables only for

the small variants of aes. Mathematics in Computer

Science, 3(2):185–200.

Cid, C. and Leurent, G. (2005). An analysis of the xsl algo-

rithm. In International Conference on the Theory and

Application of Cryptology and Information Security,

pages 333–352. Springer.

Cid, C., Murphy, S., and Robshaw, M. (2006). Algebraic

aspects of the advanced encryption standard. Springer

Science & Business Media.

Cid, C., Murphy, S., and Robshaw, M. J. (2005). Small scale

variants of the aes. In International Workshop on Fast

Software Encryption, pages 145–162. Springer.

Courtois, N. T. and Pieprzyk, J. (2002). Cryptanalysis of

block ciphers with overdeﬁned systems of equations.

In International conference on the theory and appli-

cation of cryptology and information security, pages

267–287. Springer.

Cox, D. (2015). Ideals, varieties, and algorithms : an in-

troduction to computational algebraic geometry and

commutative algebra. Springer, Cham.

Faug

ere, J.-C. (1999). A new efﬁcient algorithm for com-

puting Gr

obner bases (F4). Journal of Pure and Ap-

plied Algebra, 139(1-3):61–88.

Hibi, T. (2013). Gr

obner bases : statistics and software

systems. Springer, Tokyo New York.

Murphy, S. and Robshaw, M. J. (2002). Essential alge-

braic structure within the aes. In Annual International

Cryptology Conference, pages 1–16. Springer.

Nover, H. (2005). Algebraic cryptanalysis of aes: an

overview. University of Wisconsin, USA, pages 1–16.

Pub, N. F. (2001). 197: Advanced encryption standard

(aes). Federal information processing standards pub-

lication, 197(441):0311.

Simmons, S. (2009). Algebraic cryptanalysis of simpliﬁed

aes*. Cryptologia, 33(4):305–314.

Soos, M., Nohl, K., and Castelluccia, C. (2009). Extend-

ing sat solvers to cryptographic problems. In Interna-

tional Conference on Theory and Applications of Sat-

isﬁability Testing, pages 244–257. Springer.

The Sage Developers (2020). SageMath, the Sage Mathe-

matics Software System (Version 9.1).

Yet Another Algebraic Cryptanalysis of Small Scale Variants of AES

427