Monte Carlo Simulation of Pathogen Reduced Platelet Production

John T. Blake

1,2 a

and Ken McTaggart

Department of Industrial Engineering, Dalhousie University, Halifax, Nova Scotia, Canada

Centre for Innovation, Canadian Blood Services, Ottawa, Ontario, Canada

Keywords: Monte Carlo Simulation, Platelet Production, Pathogen Reduction Technology, Integer Programming.

Abstract: All blood products in Canada undergo testing for transmissible diseases and bacterial contamination. As a

result, the risk of a transfusion related infection is estimated at less than 1 in 47,000. Nevertheless, there are

infectious agents that are not screened for, as well as the potential for infection from emerging pathogens that

are either unknown, or for which screening tests have not been developed. Thus, Canadian Blood Services is

introducing pathogen reduction (PR) technologies to further increase the safety of the blood supply.

The focus of this study is to identify key input parameters for the PR process and to estimate output dose

parameters for the units produced. The unit volume and platelet yield from combining buffy coat platelets

into a pool are estimated via Monte Carlo simulation. The value of sorting input buffy coat units according to

estimated platelet yield, prior to illumination, is determined. Finally, the model estimates the effects of two

different sorting algorithms on output quality control metrics.

The results of the study found that no process changes were required to ensure input units meet input PR

process guidelines. However, sorting input units according to platelet yield could significantly improve the

proportion of units meeting quality control metrics.

INTRODUCTION

Before a blood product can be transfused, numerous

safety checks must be completed. All blood products

in Canada undergo testing for transmissible diseases

and bacterial contamination before being made

available to patients. As a result, the risk of a

transfusion related infection is estimated at less than

1 in 47,000 transfusions, with most risk being due to

bacterial infection, rather than viral agents.

Nevertheless, there are infectious agents that are not

screened for, as well as the potential for infection

from emerging pathogens that are either unknown, or

for which screening tests have not been developed

(MacDonald & Delage, 2012). Canadian Blood

Services (CBS) is introducing pathogen reduction

technologies (PR) in Canada (Walsh, 2019). PR

works by introducing a compound into a blood

product, in this case platelets, and exposing the

resulting mixture to ultraviolet light. The compound

targets protein strands in DNA and RNA;

illumination with UV light causes mis-links to form

https://orcid.org/0000-0003-0617-8996

in the genetic materials of pathogens. The pathogen

then becomes unable to replicate.

The product considered in this study is a pool of

buffy coat platelets. Buffy coat is the name given to a

method of separating whole blood into components of

red cells, plasma, and an intermediate layer of

material (“a buffy coat”) that contains platelets and

white blood cells. (Levin, et al., 2008).

During the PR process, some number of buffy

coat units (7 in this study) are combined into an

illumination container, amotosalen is added, and the

resulting unit is exposed to UV light. Upon

completion of the exposure cycle, the platelets are

split into two separate bags, each representing an

adult dose.

What constitutes an adult “dose” of platelets for

transfusion is well defined, but there is latitude in the

input units that can be used to form a double dose for

the PR process.

386

Blake, J. and McTaggart, K.

Monte Carlo Simulation of Pathogen Reduced Platelet Production.

DOI: 10.5220/0011328200003274

In Proceedings of the 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2022), pages 386-394

ISBN: 978-989-758-578-4; ISSN: 2184-2841

PROBLEM STATEMENT

The focus of this study is to estimate the key input

product parameters (volume and platelet yield) to

support the implementation of the PR process, to

estimate product output metrics, and to evaluate

changes to the manufacturing process to achieve a

consistent product.

A Monte-Carlo simulation method is employed to

estimate the unit volume and platelet yield resulting

from combining buffy coat platelets into a platelet

pool that subsequently undergoes pathogen reduction.

Additionally, the value of sorting input buffy coat

units according to estimated platelet yield prior to

illumination is determined.

LITERATURE

First introduced in Europe in the 2000’s, PR is

employed in at least 31 countries (AABB, 2015).

Despite its clinical advantages, cost has limited a

more widespread application. (Gorria, et al., 2019).

The expense of PR treatment can be offset by a

reduction in wastage when platelet shelf life is

extended. Thus, platelet inventory management has

been a focus of the literature in this area (Gorria, et al.,

2019). Blake and Reid (2017) use simulation to

estimate wastage rates when platelet shelf life is

extended in Canada after the introduction of enhanced

pathogen detection systems. Gorria et al. (2019)

employ a similar methodology to evaluate reductions

in waste due to implementation of PR technology in the

Basque Region. Blake, McTaggart, and Couture

(2021) in a later paper on PR technology, note that a

reduction in shelf life from 7 days to 5 accompanied

the original implementation of PR in Canada. They

employ simulation to estimate the interaction between

PR reduced platelets with a shelf life of five days and

apheresis platelets with a shelf life of seven days.

When implemented in North America, PR

platelets are often introduced into the formulary of a

blood supply chain along side conventional platelets,

which may have a different shelf life than treated

units (Rebulla & Prati, 2022). The issues of

maintaining a dual inventory have inspired a literature

on PR implementation.

For instance, Allen et al.

(2019) discuss the benefits of phased implementation

to maintain product availability while scaling up PR

platelet production. Nguyen et al. (Nguyen, Rioveros,

Ziman, McGonigle, & Ward, 2021) also describe the

implementation of PR technology in a dual inventory

environment, focusing on issues of technology

acquisition and commissioning. An economic

evaluation of PR technologies is provided in (Prioli,

Katz Karp, Lyons, Herman, & Pizzi, 2018), including

an estimate of change in wastage due to an increase

in shelf-life of from five to seven days.

Outside of inventory management, there is a

wealth of studies on the composition and behaviour

of PR treated platelets. See (Prioli, Katz Karp, Lyons,

Herman, & Pizzi, 2018) for a detailed review. There

are, however, few studies in the literature that focus

on analysis and optimization of the processes that

create the platelets, be they PR treated or not. Our

study is the first that we are aware of to use Monte

Carlo methods to evaluate platelet production

processes and to estimate unit metrics during and

post-production.

Nevertheless, Monte Carlo simulation techniques

(problems where the passage of can be ignored) are

common in health care settings. For example, there is

an entire genre of literature employing Monte Carlo

methods to optimize the treatment path for

individuals hospitalized for ischemic strokes. See

Zhou & Kansagra (2021) for an example.

METHOD

The PR process begins when seven buffy coat units,

with volume of ~47.5 ml [Normal (47.5, 1.002)] and

platelet yield of ~98.2x10

platelets [Johnson

distributed, with mean 98.2 x10

and standard

deviation of 22.1 x10

], are grouped. The group has a

resulting volume of ~332.5 ml [Normal (332.5, 2.66)]

and a combined platelet yield of ~687x10

platelets.

The platelets are extracted from each of the buffy coat

units using a press and collected into double input

platelet bag. The extraction process causes a

reduction in both the volume of product available and

the total number of platelets in the combined unit bag.

Volume losses are counterbalanced by the inclusion

of 280 ml of platelet additive solution (PAS) in the

platelet pool; the volume of the resulting platelet pool

is 99% [Normal (0.991, 0.034)] the original input

group volume after PAS is added. However, platelet

yield is approximately 86% of the input group yield

[Normal (0.8642, 0.41)]. See Figure 1.

Figure 1: Schematic of unit flow. Each block describes the

process step, the expected volume (Vol) and the number of

platelets expected to be retained (Yield). Note that BC Pool

refers to a Buffy Coat Pool.

Monte Carlo Simulation of Pathogen Reduced Platelet Production

387

Because PRT has been certified in Canada for a

specific range of input volume (300 – 375 ml) and

platelet yield (250 – 700 x10

), our analysis focuses

on estimating, via simulation, these parameters for

input pools. In addition, because platelet yield with

buffy coats varies between donors, the study includes

an evaluation of sorting algorithms to ensure

consistent product input when combined into a buffy

coat pool and thus a more consistent output product.

4.1 Sorting Algorithm

The expected platelet yield for a pool of seven buffy

coats, after extraction, has a non-standard distribution

(𝑥̅ = 573.33, σ = 75.6) that is somewhat close to the

lower bound for the Canadian Standards Association

(CSA) efficacy requirement for pooled platelets,

which states that there must be 240x10

platelets in

75% of units sampled in a single unit, or 521x10

platelets in a double unit after losses for splitting the

unit are accounted for. Thus, it is expected that some

portion of the units produced by the PR process with

randomly selected buffy coat units would fail to meet

this standard. If, however, the variability of the input

unit could be reduced, fewer pools would fall outside

of the standards. The standard deviation of a pool of

seven randomly selected buffy coats can be estimated

from pilot studies as 57.8 x10

. However, a sorting

algorithm could be used to reduce variance of the

group of buffy coats used to form the platelet pool.

This would result in an input unit that would still meet

production bounds for the PR process and would be

less likely to result in completed units that would fail

to meet the minimum CSA standard.

A sorting algorithm is a process where some

number of buffy coat units are gathered, prior to

platelet pooling, based on actual or estimated platelet

yield, to achieve more consistent input pools for the

PR process. Theory indicates that the larger the

number of buffy coats to select from when building a

pool, the more consistent the resulting pooled platelet

yield should be. However, there are practical limits to

how much work in process (WIP) inventory can be

held immediately prior to the buffy coat pooling

process. Thus, the amount of WIP stored for a sorting

algorithm must balance needs for smooth product

flow against the value of better information for

assembling a pool; only a finite amount of inventory

can be held, and pooling decisions must be made in

real time, rather than at the end of a production run.

In this study, three different sorting algorithms are

tested under varying levels of work in process

inventory. The sorting algorithms are:

Random Sort: A random sort corresponds to a null

sort. A group of seven buffy coats is assembled by

selecting each unit in sequence as it becomes

available at the end of the production line. A random

sort is fast and easy to implement in the operational

environment but has no impact on the variability of

the platelet pools created. A random sort, however,

serves as a benchmark for comparison of other sorting

algorithms.

Bin Sort: A bin sort is a simple heuristic algorithm to

reduce platelet pool variability in a set of buffy coat

pools. Some number (N) of bins is created into which

inventory could be placed as it arrives at the pooling

station at the end of the production line. The bins

would be designated with ranges for platelet yield

(i.e., a bin might be designated for units with a platelet

yield of between 77x10

and 88x10

platelets).

Periodically, a pool is assembled by selecting units

from within the bins. Each unit from a particular bin

would have an integer “score” (c

) ranging from -

⌊

𝑁/2

⌋

to +

⌊

𝑁/2

⌋

. If we assume x

to be the number

of buffy coats selected from bin n, then the bin sort

can be defined as:

𝑀𝑖𝑛: 𝑧 = 𝑑



+ 𝑑



𝑆𝑢𝑏𝑗𝑒𝑐𝑡 𝑡𝑜:

𝑐







𝑥



+𝑑



− 𝑑



𝑥



≤𝑖



𝑥



∈



0,1,…



𝑑



,𝑑



≥0

Model 1: Bin Sort.

Where:

is the score assigned to buffy coats drawn from

bin n

is the number of buffy coat units drawn from

bin n

is a slack variable representing pools below

the target score of 0

is a surplus variable represent pools above the

target score of 0

is the number of buffy coat units in bin n

The bin sort is defined above as a mixed integer

programming (MIP) problem that can be solved with

an IP solver (see for example, https://opensolver.org/)

or approximated manually by assembling a batch with

a penalty score (

∑

𝑐







𝑥



) as close to 0 as possible.

SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

388

Optimal Sort: It is also possible to formulate the pool

sort as a mixed integer programming problem with an

objective of achieving a specified target yield. Instead

of selecting from a set of bins, all units would be

considered individually for inclusion into a pool. The

problem can be formulated as:

𝑀𝑖𝑛: 𝑧 = 𝑑



+ 𝑑



𝑆𝑢𝑏𝑗𝑒𝑐𝑡 𝑡𝑜:

𝑦







𝑥



+𝑑



− 𝑑



=𝑌

𝑥



=𝐵





𝑥



∈(0,1)

𝑑



,𝑑



≥0

Model 2: Optimal Sort.

Where:

is the estimated platelet yield in buffy coat i

is a (0,1) variable equalling 1 if buffy coat i is

included in the pool

d- is a slack variable representing pools below

the target yield

d+ is a surplus variable represent pools above the

target yield

Y is the target yield for the pool

I is total number of buffy coats available in for

pooling (i.e., WIP)

B is the number of buffy coats required in a pool

The sort algorithm above, defined as a mixed integer

programming (IP) problem, cannot be (easily)

approximated with manual methods. Due to the

requirement for an optimization engine and

individual identification of units, an optimal sort

would be more complex to implement in a production

environment, however.

4.2 Simulation

A Monte Carlo methodology was adopted to simulate

buffy coat pooling prior to irradiation in the PR

process and to evaluate the impact of a pooling

algorithm on the ability to meet input process

guidelines while creating output that meets CSA

standards.

A custom simulation model was constructed in

Visual Basic for Applications (VBA) using MS-Excel

as the user interface. The simulation employs an

object-oriented framework to represent buffy coat

units, the pooling process, sorting bins, and the

sorting algorithms themselves. A summary of the

class objects in the simulation is given below:

clsUnit is a class object that represents a buffy coat

unit. Buffy coat units have attributes of volume,

platelet yield, and ID number.

clsBin is a class object that represents a bin used in a

bin sort algorithm. It has properties of bin ID number,

capacity, and score. Methods include a mechanism to

store individual buffy coat units, a routine to identify

a specific buffy coat within the bin and a routine to

remove a unit from the bin.

clsBinSet represents a collection of bins used in a bin

sort algorithm. It has properties of capacity (i.e., the

maximum amount of end of process inventory or WIP

that can be in all bins), bin (a reference to a bin within

the bin set), items (the number of units in all bins),

unit (a reference to a specific buffy coat within a

specific bin in the bin set) and target yield. Methods

include routines to add a unit to a bin or to remove a

unit from a bin within the bin set.

clsSolver is an object that encapsulates an interface to

the OpenSolver add-in for Excel. The object has

methods that build both the bin sort and optimal sort

models, methods for solving the models, once

defined, and methods for returning a solution to the

calling program.

4.3 Simulation Flow

The buffy coat pooling simulation generates buffy

coat units. Each unit is given a simulated platelet

yield and volume. The buffy coat is then added to a

bin, based on the unit’s platelet yield. When the total

number of buffy coats in inventory (WIP) equals the

bin set capacity, a platelet pool is formed. In

experiments run with the model, WIP limits were set

at some integer number of buffy coat pools; this

restriction is in place to reduce the number of

“orphaned” units that cannot be made into a pool at

the end of the simulation run. The simulation then

calls the IP solver to build and execute a model to

create a platelet pool from a set of input buffy coats.

The list of input buffy coat units is returned to the

simulation object. The simulation removes the units

from the bins. The pool volume is calculated using a

random distribution of changes to the input volume.

In this study, buffy coat pool volume is N(0.991,

0.037) times the sum of the input buffy coat volumes.

In a similar way, the buffy coat pool yield is estimated

from the sum of the input buffy coat yields; the

Monte Carlo Simulation of Pathogen Reduced Platelet Production

389

distribution of buffy coat yields is 86.4% of the sum

of the input buffy coat yields [Normal (0.864, 0.041)].

The process of creating buffy coats and

assembling them into pools continues for some

number of trials. Each time a pool is created, its

volume and yield are compared against an acceptable

input target range for the PR process: 300-375 ml for

volume; 250-700x10

for platelet yield. If a pool falls

outside of this range, a violation is noted by the

simulation. Further, if a group of units results in a

platelet pool yield below 521x10

, a potential

violation of CSA standards is noted. At the end of the

simulation run, the proportion of pools failing to meet

input or CSA targets is returned, as is the overall

average pool volume and platelet yield.

5 DATA USED IN THE STUDY

Data for this study was obtained from a sample

(n=84) of test buffy coat pools assembled at Canadian

Blood Service’s research collection and production

facility (netCAD) between 05 Sep 2019 and 17 Oct

2019 as part of a pilot project.

Summary statistics and a box plot for buffy coat

platelet yield appear below.

Table 1: Summary statistics for platelet yield based on N =

84 buffy coat units. Note that yield statistics are reported as

platelet count x 10

N Mean St Dev Median Min Max

84 96.95 21.85 93.31 56.21 179.35

Figure 2: Boxplot of platelet yield for n=84 buffy coat units.

Summary statistics for buffy coat unit volume

appear below.

Table 2: Summary statistics for buffy coat unit volume (ml).

N Mean St Dev Median Min Max

84 47.738 1.223 48.0 44.0 50.0

Distributions were fit to both buffy coat unit

volume and buffy coat unit platelet yield. A normal

distribution [Normal (47.7, 1.223)], was fit to the

buffy coat unit volume sample. See Figure 3.

Figure 3: Probability plot for sampled buffy coat (BC)

volumes (in ml) compared to a normal probability

distribution.

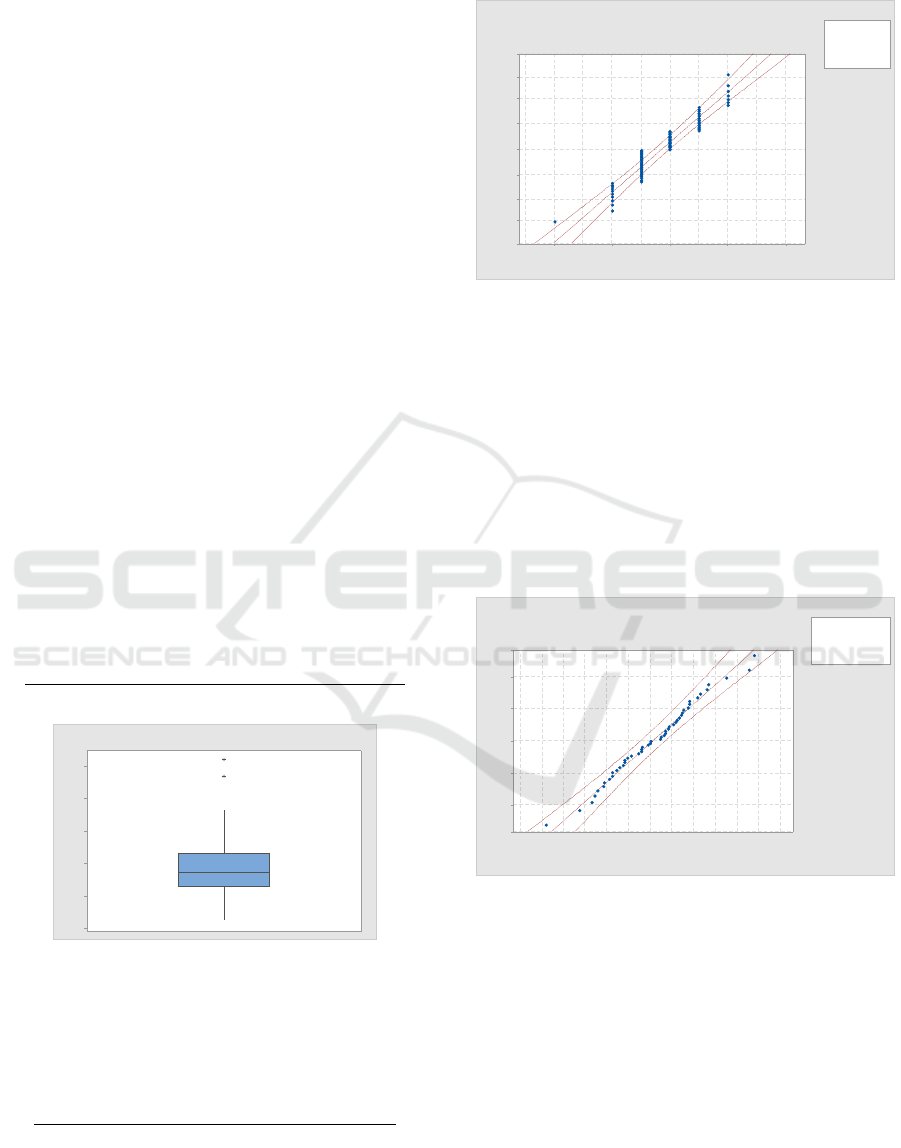
A Johnson transform was found to provide the

best fit for the buffy coat unit platelet yield data. In

the simulation, therefore, an N(0,1) distribution is

used to generate buffy coat platelet yield and the

inverse of the Johnson transform is used to return a

value in the original data space. See (Law, 2006) for

more detail. For the data appearing in

Figure

4, the Johnson transform parameters are A

= -1.201, B = 1.593, C = 73.874, and D = 21.989.

Figure 4: Johnson transformed buffy coat platelet yield

plotted against an N(0,1) distribution.

Once buffy coat units are pooled and platelets are

extracted, a platelet additive solution is added to the

pool. The process causes both the volume of the

pooled platelet unit and its platelet count to vary from

the sum of the input buffy coat units. A

Normal(0.991, 0.037) distribution was found to

represent adequately the scale change in volume of

the output unit from the sum of input buffy coat pools;

a Normal(0.864, 0.041) was found to represent the

scale change in platelet yield in the pooled unit as

measured from the sum of the input unit yields.

175

150

125

100

BC Yield

Boxplot of BC Yield

5250484644

99.9

0.1

BC Volume

Percent

Goodness of Fit Test

Normal

AD = 2.817

P-Value < 0.005

Probability Plot for BC Volume

Normal - 95% CI

3210-1-2-3

Adjusted Yield

Percent

Goodness of Fit Test

Johnson T ransformation

AD = 0.191

P-Value = 0.893

After John son transform ation

Probability Plot for Adjusted Yield

Normal - 95% CI

SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

390

6 ANALYSIS

6.1 Overview

Experiments were conducted using both a bin sort and

an optimal sort algorithm with different levels of WIP

at the end of the production line available to build a

pool. The experiments estimate the volume and yield

of input buffy coat pools and determine the impact, in

terms of output product metrics, including post-

illumination quality control, of implementing a sort

algorithm for input units.

6.2 Model Verification

To verify the simulation, tests were conducted with

the model and the results were compared to the

historical dataset used to build the input distributions

listed in § Data. The purpose of the verification was

to ensure that the model returns values matching input

pilot project data.

In Table 3 the pooled platelet volume (ml), after

buffy coat units are pooled identified during the pilot

project, is compared to simulation output using a t-test;

Table 4 compares the pooled platelet yield from the

data set to simulation output using a Mann-Whitney

test, since the underlying data is not normally

distributed. As may be seen from the simulation, there

is no data to disprove the null hypothesis that the

mean/median of the simulation output is the same as

mean/median of the data used to build the model.

Table 3: T-test comparison of pooled platelet volume in the

pilot project dataset and the simulation results.

Pilot Project Data Simulation

Mean 331.2 331.1

Standard Deviation 12.5 12.1

n 7 300

p-value 0.99

Table 4: Mann-Whitney comparison of pooled platelet

yield in the pilot project dataset and the simulation results.

Pilot Project Data Simulation

Mean 573.3 580.0

Median 592.06 573.88

n 7 300

p-value 0.978

6.3 Sorting Experiments

Experiments were conducted with the simulation to

evaluate the ability of the process to meet input

processing requirements as well as CSA standards for

completed units. The simulation model was run under

the assumption of no sorting for buffy coat units prior

to forming a pool; employing a bin sort algorithm

having 3, 5, or 7 bins prior to forming a pool; and

employing an optimal sort prior to forming a pool.

For both sort algorithms, differing amounts of WIP

(7, 14, 21, or 28 units) were tested. In each instance,

the simulation was run for 5 replications of 1000

batches of 7 buffy coats. The results of the

experiments appear below.

In Table 5, the results from a run without any

sorting algorithm in place are presented. From the

table it may be seen that the pooled platelet volume is

expected to meet acceptable PR input volume (300-

375 ml) and input platelet yield (250x10

– 700x10

platelets) restrictions without a sorting algorithm and

only marginal losses in production; approximately

0.4% of batches would exceed input volume

restrictions and 2.13% of batches would exceed input

platelet yield limits.

However, without a sort in place, some pooled

units would have a platelet count below 480x10

, the

CSA dictated minimum number of platelets that must

appear in 75% of the units sampled for quality control

(QC) purposes, if applied to double pools (2 units at

240x10

apiece). Note: In our analysis, we add 41x10

platelets to the minimum pool requirement to account

for losses in lines when a double unit is split into two

single units. Since quality control samples typically

consist of ten units of randomly sampled platelets, it

can be calculated, via the binomial distribution, that

33.43% of sampled batches would be fall below

minimum CSA efficacy standards if 19.6% of pooled

units have a platelet yield of 521x10

or less, as

reported by the simulation.

Table 5: Expected process metrics if no sorting algorithm is

used.

No Sort

% pools with volume below 300 ml 0.4%

% pools with volume above 375 ml 0.00%

% pools with platelet yield below

521x10

19.6%

% pools with platelet yield below

250x10

0.00%

% pools with platelet yield above

700x10

2.1%

Simulated pool volume

(

Mean, St Dev

)

in ml

(331.59, 3.24)

Simulated pool yield

(

Mean, St Dev

)

*10

(568.81, 54.12)

Monte Carlo Simulation of Pathogen Reduced Platelet Production

391

6.3.1 Bin

Sort

Experiments were conducted with a bin sort

algorithm, using 3, 5, or 7 bins and WIP inventory

available for sorting set at 7,14, 21, and 28 units (or

1, 2, 3, or 4) pools. Several output metrics were

recorded in the simulation, but this report focuses on

the proportion of pools expected to have yield below

521x10

and the number of quality control batches, of

size 10 units, expected to fall below minimum CSA

standards.

Table 6: Simulated results showing the number of pools

with a platelet yield below 521x10

as bin size and WIP is

varied assuming a bin sort algorithm.

% pools

below

521x10

WIP

7 14 21 28

# of Bins

3 19.6% 12.5% 11.4% 10.8%

5 20.3% 8.6% 8.2% 7.7%

7 19.5% 8.3% 9.0% 6.6%

Table 7: Simulated results showing the number of the

proportion of quality control batches of size 10 expected to

be blow CSA standards as bin size and WIP is varied

assuming a bin sort algorithm.

% pools not

meeting

CSA

standards

WIP

7 14 21 28

# of Bins

3 31.1% 12.1% 9.5% 8.5%

5 33.2% 4.8% 4.3% 3.7%

7 30.8% 4.5% 5.5% 2.5%

As may be seen in Table 6, the proportion of pools

below a platelet count of 521x10

per unit decreases

at the number of designated bins increases. The

impact of WIP available to build a batch, beyond 14

units, on the proportion of batches not meeting the

521x10

platelets per unit standard is modest, but

statistically significant across the set of experiments.

It is particularly evident that the impact of WIP on

batch yields is quite modest if the number of bins used

in the sort is greater than three. An analysis of

variance (ANOVA) conducted on the experimental

results for platelet yield under the assumption of a

bin-sort algorithm, show that the number of bins is

significant (DOF = (2,30), F

Crtical

= 3.15, p = 0.005),

as is the WIP level for the entire experiment set.

Figure 5: Interaction plot illustrating the results from the bin

sort experiments. Plot shows the proportion of units

expected to have a platelet yield below 521x10

Figure 5 illustrates the results for the bin sort

experiments. It shows that an inventory of 7, equating

to a random sort, is inferior to a sort with any number

of bins. Figure 5 also shows that any bin sort with

more than three bins will produce similar results for

platelet yield, all of which are superior to a 3-bin sort.

Finally, it was found that if the 3-bin sort and all

experiments with 7 units of WIP (i.e., a random sort)

are eliminated from the comparison, there is no

statistical significance, for either the number of bins

or the amount of WIP available to assemble a batch,

on platelet yield.

6.3.2 Optimal Sorting

Experiments were also conducted using an optimal

sort algorithm. In this set of experiments, only one

algorithm is employed (the optimal sort algorithm),

while the amount of WIP available to build a pool is

varied between 7, 14, 21, and 28 units. The simulation

was run for 5 replications of 1000 batches of size 7 to

get a measure of variability. Results appear below.

Table 8: Simulated results showing the number of pools

with a platelet yield below 521x10

as WIP is varied

assuming an optimal sort algorithm. Note that there are no

bins in the optimal sorting algorithm.

WIP

7 14 21 28

29.6% 7.2% 5.7% 6.2%

Experimental results, confirmed by an ANOVA

(DOF = (2,8), F

Crtical

= 4.45, p = 0.63), show that

inventory has no effect on the proportion of pools not

meeting CSA standards, so long as at least 14 units

are available to build batches. See Table 9. Similarly,

it is evident from Table 8 and Figure 6 that larger WIP

SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

392

Table 9: Simulated results showing the number of the

proportion of quality control batches of size 10 expected to

be blow CSA standards as WIP is varied assuming an

optimal sort algorithm. Note that there are no bins in the

optimal sorting algorithm.

WIP

7 14 21 28

31.1% 3.1% 1.6% 2.0%

inventory does not lead to reductions in the

proportion of buffy coat pools with less than 521x10

platelets, if at least 14 units are available to build

batches.

Figure 6: Interaction plot illustrating the results from the

optimal sort experiments. The plot shows the proportion of

units expected to have a platelet yield below 521x10

6.3.3 Sort vs. No Sort

A comparison of the simulation results with sort

algorithms in place vs. no sort was conducted using

an analysis of variance. The ANOVA indicated a

statistically significant difference between the sort

and no-sort scenarios. A Dunnett’s test and analysis

of means, indicates that the no-sort algorithm

produces a statistically larger fraction of QC batches

not meeting CSA standards. The bin sort algorithms

produce fewer non-conforming QC batches than not

sorting, but there were no statistically different results

with increasing number of sort bins. The ANOVA

(DOF = (2,45), F

Crtical

= 3.20, p = 0.335) showed,

however, that an optimal sort algorithm outperforms

both the 3 and 5 bin sort scenarios and the no-sort

scenario, with respect to the proportion of non-

conforming batches. Finally, the analysis suggests

that, if a bin sort algorithm is used, the impact of the

number of bins on the proportion of QC batches of

size 10 that do not meet 521x10

in 75% of units, is

unaffected by the actual number of bins. See Figure

Figure 7: Comparisons fraction of pooled units not meeting

minimum CSA standards by sorting algorithm.

CONCLUSION

This study estimated the impact of the process used

to assemble input buffy coat units into buffy coat

pools prior to illumination in a pathogen reduction

system. The benefit that could be achieved by sorting

input buffy coat units to ensure consistent input pools

for the PR process was evaluated.

A Monte-Carlo simulation model was built,

populated with experimental data from a pilot project,

and verified. Experiments were conducted using

different sorting algorithms (no sort, bin sort, and

optimal sort) and differing levels of WIP used to build

pools (7, 14, 21, 28 units).

The simulation shows that, even without a sort

algorithm in place, more than 97.5% of pooled

platelet units would be expected to meet input

restrictions for both volume (300-375 ml) and platelet

yield (200 – 700x10

). However, approximately

20.4% of all pools would have a platelet yield below

521x10

and that 31.1% of quality control batches of

size 10 assembled from such units would fail to meet

a minimum efficacy standard of 521x10

platelets in

75% of the units sampled.

Implementing any sort of sorting algorithm with a

minimum of 14 units of WIP will result in a

statistically significant reduction in low yield units

and will improve the acceptance rate for quality

control batches. A simple bin sort using, 3, 5, or 7 bins

will produce a more consistent input platelet pool for

the PRT system. However, the simulation results

were not statistically different between the bin sorts

employing different numbers of sorting bins. Thus,

should a bin sort be implemented, a 3 or 5 bin sort

might well be as effective as a 7-bin sort.

The simulation shows, as is expected, that the

most consistent input pools are provided by an

Monte Carlo Simulation of Pathogen Reduced Platelet Production

393

optimal sort algorithm. Furthermore, the results

suggest that an optimal sort algorithm, using a WIP

of at least 14 units, results in the most consistent input

pools. An optimal sort algorithm using a WIP of at

least 14 units would result in less than 3% of all

quality control samples falling below the CSA

minimum. The simulation shows that an optimal sort

is statistically similar to a 7-bin sort, but superior to a

3 or 5-bin sort, when compared over all WIP levels

and measured in terms of meeting minimum CSA

standards.

Thus, it may be concluded that a sort algorithm,

of any kind, will improve the acceptance rate of

platelet pools coming from the PR process described

in this paper. Optimal sort algorithms, clearly,

provide the best result, but would be complex to

implement in a production environment. A simpler

bin-sort algorithm was found to perform similarly to

an optimal sort, if the number of bins was greater than

or equal to 5. The impact of increasing WIP on QC

acceptance rates was found to be modest, so long as

14 units were available. Thus, it is practical to suggest

that a simple 5 bin sort algorithm could be used to

ensure the most efficacious units are delivered by the

PR process.

REFERENCES

AABB. (2015). Listing of countries in which pathogen

reduction technology systems and products are in use.

Retrieved May 24, 2022, from AABB: www.aabb.org

Allen, E., Vincent, C., Reeve, D., & Kopko, P. (2019).

Phased implementation of pathogen‐reduced platelets

in a health system facilitates increased manufacturing at

the blood center. Transfusion, 59(10), 3120-3127.

Blake, J., & Reid, K. (2017). Determining the impact of

extended shelf life platelets with a nework simulation

model. Transfusion, 57(12), 3001-3008.

Blake, J., McTaggart, K., & Couture, C. (2021). Estimating

the impact on inventory of implementing pathogen

reduced platelets in Canada. Transfusion, 61(11), 2150-

3160.

Gorria, C., Labata, G., Lezaun, M., Javier Lopez, F., Perez

Aliaga, A., & Perez, M. (2019). Impact of

implementing pathogen reduction technologies for

platelets on reducing outdates. Vox Sanguinis, 115(2),

167-173.

Law, A. (2006). Simulation modeling and analysis, 4th Ed.

New York: McGraw-Hill.

Levin, E., Culibrk, B., Gyonyossy-Issa, M., Weiss, S.,

Sammel, K., LeFresne, W., Devine, D. (2008).

Implementation of buffy coat platelet component

production: comparison to platelet-rich plasma platelet

production. Transfusion, 48(11), 2331-2337.

MacDonald, N. O., & Delage, G. (2012). Transfusion and

risk of infection in Canada: Update 2012. Paediatrics

& Child Health, 17(10), e102-e111.

Nguyen, J., Rioveros, J., Ziman, A., McGonigle, A., &

Ward, D. (2021). How do we implement pathogen

reduction technology,while maintaining an adequate

platelet inventory for our patients? Transfusion, 61(4).

Prioli, K., Katz Karp, J., Lyons, N. C., Herman, J., & Pizzi,

L. (2018). Economic Implications of Pathogen Reduced

and Bacterially Tested Platelet Components: A US

Hospital Budget Impact Model. 16, 889-899.

Rebulla, P., & Prati, D. (2022). Pathogen Reduction for

Platelets—A Review of Recent Implementation

Strategies. Pathogens, 11(2), 142.

Walsh. (2019, Mar 08). Pathogen Inactivation – A Primer.

Retrieved from www.blood.ca: https://www.blood.ca/

en/research/our-research-stories/research-education-

discovery/pathogen-inactivation-primer

Zhou, M., & Kansagra, A. (2021). Population health impact

of extended window thrombectomy in acute ischemic

stroke. Interventional Neuroradiology, 27(4), 516-522.

SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

394