
Coupled PID-SDRE Controller of a Quadrotor: Positioning and
Stabilization of UAV Flight
Marcin Chodnicki
1a
, Wojciech Stecz
2b
, Wojciech Giernacki
3c
and Sławomir Stępień
4d
1
Air Force Institute of Technology, Księcia Bolesława 6, 01-494 Warsaw, Poland
2
Military University of Technology, Faculty of Cybernetics, Kaliskiego 2, 00-908 Warsaw, Poland
3
Poznan University of Technology, Institute of Robotics and Machine Intelligence, Piotrowo 3a, 60-965 Poznań, Poland
4
Poznan University of Technology, Institute of Automatic Control and Robotics, Piotrowo 3a, 60-965 Poznań, Poland
Keywords: Quadrotor, Proportional-Integral-Derivative Control, State-Dependent Riccati Equation, Infinite-time
Horizon Control.
Abstract: This work presents a coupled Proportional-Integral-Derivative and State-Dependent Riccati Equation (PID-
SDRE) controller. PID angular position controller coupled to nonlinear infinite-time SDRE controller for
speed stabilization is proposed. For the quadrotor modelling a full 6 degree of freedom (DoF) model is
considered and described by nonlinear state-space approach. Also, a stable state-dependent parameterization
(SDP) necessary for solution of the SDRE control problem is proposed. Solution of the SDRE control problem
with adequate defined weighting matrices in the performance index shows the possibility of fast and precise
quadrotor positioning with optimal stabilization of speeds. Two methods of optimal SDRE-based stabilization
are proposed, tested, and compared.
1 INTRODUCTION
Todays, Unmanned Aerial Vehicles (UAVs) have
become an object of interest of industrial, businesses
and governmental organizations. They are being
adopted worldwide, especially by following sectors:
military, commercial, personal and future technology.
Briefly speaking, in places where man cannot reach
or is unable to perform in a timely and efficient
manner especially including danger zones and places.
Due to the development of UAV application,
quadrotors has drawn full attention due to its
advantages of flexibility, portability, versatility. The
heart of each UAV is a control system, a brain which
has to be optimal, robust, and intelligent (Chipofya,
2017; Sadeghzadeh, 2011; Sheng S, 2016; Stepien,
2019; Voos, 2006; Zhang, 2009).
Flight control of multi-role UAV is viewed as a
difficult area of aerospace engineering (Hoffmann,
2007; Kim, 2020). Moreover, each flight control
system of a quadcopter is nonlinear and coupled. The
a
https://orcid.org/0000-0003-1348-289X
b
https://orcid.org/0000-0002-5353-5362
c
https://orcid.org/0000-0003-1747-4010
d
https://orcid.org/0000-0001-7777-7684
controller should be an independent system, which
aims to create the best autopilot hardware. Most of
now existing controllers are based on PID controllers
(Chodnicki, 2018).
Modern optimal control theory proposes high
performance and a rapidly emerging control
technique called infinite-time state-dependent Riccati
equation (SDRE) (Banks, 2007; Cloutier, 1996;
Korayem, 2015). This is a suboptimal control
methodology for nonlinear systems. The technique
uses direct parameterization to bring the nonlinear
system to a linear structure having state-dependent
coefficients (SDC). The SDRE is then solved
accordingly to the change of state trajectory to obtain
a nonlinear feedback controller matrix, which
coefficients, in other feedback gains, are the solution
(Cimen, 2010; Heydari, 2015; Mracek, 1998).
Many practical implementations of quadrotor
controllers are limited. When using a PID controllers
to angular or linear positioning, for instance, there is
no guarantee that angular or linear speeds became
524
Chodnicki, M., Stecz, W., Giernacki, W. and St˛epie
´
n, S.
Coupled PID-SDRE Controller of a Quadrotor: Positioning and Stabilization of UAV Flight.
DOI: 10.5220/0011335600003271
In Proceedings of the 19th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2022), pages 524-530
ISBN: 978-989-758-585-2; ISSN: 2184-2809
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

controlled to constant or zero. Then a combination of
the PID with another controller (or sub-controller)
should be provided to control the speed vector toward
zero (Sadeghzadeh, 2011; Chodnicki, 2018).
The main contribution of this research is to
develop the PID-SDRE closed-loop control system
employing the 6 DoF UAV model. The PID as the
main controller is used for angular position control.
The internal speed sub-controller SDRE is used to
stabilize of angular and linear speed control. The
modelling and control design methodology presented
is the concept proposed to design a high-performance
and optimal flight controller for UAV. The nonlinear
model of the drone and solution of the infinite-time
suboptimal speed control problem is applied,
analyzed and compared employing two SDRE-based
methods (Banks, 2007; Cloutier, 1996; Stepien, 2019;
Voos, 2006).
2 QUADROTOR DYNAMICS
The rigid body equations of motion are the
differential equations that describe the evolution of
basic states of a quadrotor. The quadrotor model
presents Fig. 1.
Figure 1: Quadrotor model.
The quadrotor dynamics is generally defined
using Newton’s force and moment equations
(Hoffmann, 2007; Kim, 2020; Chodnicki, 2018;
Zhang, 2009). The force equation is following
=
(
+×
)
, (1)
where is the UAV linear speed vector, is the
angular speed vector, m is the UAV mass and
denotes the force vector. The moments equation
describes all the moments acting on the UAV, equal
to the rate of change of angular moment vector
=
+×, (2)
where is an aircraft symmetrical inertia matrix and
denotes moment vector. Considering vector
defined for all components in x, y and z direction and
for roll
φ
, pitch
θ
and yaw
ψ
angle
=
=
, (3)
then equations of quadrotor aerodynamics can be
defined for linear and angular speeds. In addition,
because of a quadrotor symmetry, so in the inertia
matrix the off-diagonal entries become zero, then
=(
,
,
). (4)
The system of nonlinear equations that describes
aircraft flight dynamics, considering gravity forces
and force due to the thrust
, is following
=
−++
(
+
)
−−∅+
+
−−∅+
(
+
+
)
, (5)
=
−
−
+
/
−
(
−
)
+
/
−
−
+
/
, (6)
where
,
,
denotes drag forces and
,
,
are applied angular moments. It is assumed that
the torque and thrust caused by each rotor act
particularly in the z axis of the quadrotor frame.
Moment results from the thrust action of each rotor
around the center of mass which induces a pitch and
roll motion.
The relationship between the body-fixed angular
speed vector
and the rate of change of
the Euler angles
can be determined by
resolving the Euler rates into the body-fixed
coordinate frame. Hence, to describe the orientation
an Euler angle relationship is used from the
transformation from the local horizontal to the body
axes. The resulting kinetic equations are
=
1 sintan cos
0 cos −sin
0 sinsec cossec
, (7)
where ϕ is a roll angle, θ is a pitch angle, and ψ is a
yaw angle and secθ =1/cosθ.
Coupled PID-SDRE Controller of a Quadrotor: Positioning and Stabilization of UAV Flight
525
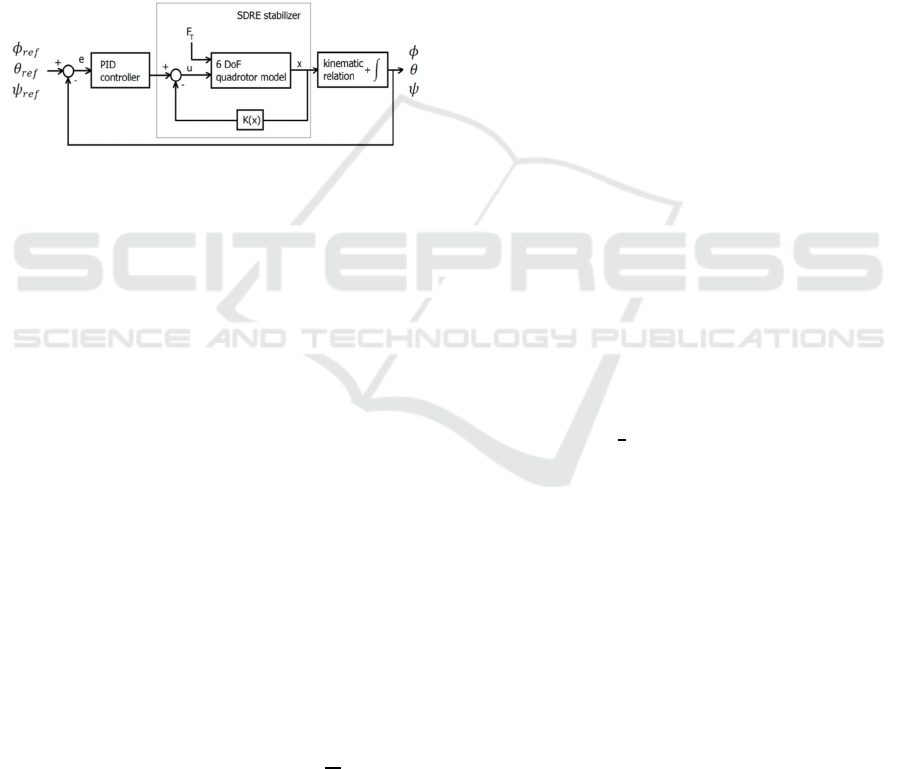
3 PID-SDRE CONTROL
Quadrotor is an unstable system. Therefore, a control
and stabilization system in design should allow one to
control the orientation in the system. Then, not only
control of the space orientation, but also angular and
linear speeds should be stabilized. Thus, two blocks
of controllers are used: one for controlling space
orientation by the angular position, and the next for
stabilizing the angular and linear speeds.
This paper deals with coupled Proportional-
Integral-Derivative and State-Dependent Riccati
Equation (PID-SDRE) controller dedicated to
orientation control and stabilization. The control
system schema is presented in Fig. 2.
Figure 2: PID-SDRE control schema of quadcopter.
It consists of two control units. The orientation
control system is realized in outer closed-loop
systems using PID controller, but the speed
stabilization problem is performed by the inner
closed-loop subunit with feedback compensator
employing infinite-time SDRE control technique. In
this case, a thrust force
is set as constant and
allows one to get desired altitude. The other variables
contained in the Fig. 2 denote: =
– state vector of the 6 DoF
model, =
–
attitude control vector and error vector of the attitude
angles =
−
−
−
.
3.1 PID Attitude Controller
The closed-loop control system used to quadrotor
space positioning consists of three independent
controllers for roll, pitch and yaw angles.
The output of a PID controller is following
=
, and is equal to
the PID control input to the plant, is calculated in the
time domain from the feedback error as:
=
+
+
. (8)
The error signal e is a three-element vector fed to the
PID controller, which computes proportional,
derivative and integral of this error signal with respect
to time. k
, k
, k
are proportional, integral and
derivative gain diagonal matrices:
=(
,
,
),
=(
,
,
), (9)
=(
,
,
).
The integral matrix gain
times the integral of
the error vector plus the derivative matrix gain
times the derivative of the error vector are computed
using its approximation and creating digital form of
the PID. A standard formulation of digital PID that
uses bilinear transformation of continuous integral
and derivative action is employed (Kim, 2020;
Sadeghzadeh, 2011).
3.2 SDRE Speed Compensator –
Classic Approach
The state-dependent Riccati equation (SDRE)
suboptimal control method is an efficient tool for
control of the nonlinear 6 DoF quadrotor model. The
technique with a further improved and modified
approach is widely described in recent literature
(Banks, 2007; Cimen, 2010; Mracek, 2006; Voos,
2006). The SDRE approach is used in the context of
the nonlinear controller problem with a quadratic
objective function defined as the sum of energy lost
and delivered to the system, what is compatible with
practical applications.
The infinite-time control problem consists of
finding optimal control law that minimizes the
following objective function defined for infinite
control time:
(
)
=
(
+
)
, (10)
subject to nonlinear dynamics for affine systems
=
(
)
+
(
)
. (11)
Nonlinear UAV dynamics (11) can be written
using the state-dependent coefficient (SDC) form
(Banks, 2007)
=
(
)
+
(
)
, (12)
where () is symmetric, positive semi-definite
weighting matrix for states, () is the symmetric,
positive definite
weighting matrix for control inputs.
Equation (11) includes
(
)
vector, which is
piecewise continuous in time and smooth with respect
to their arguments, which satisfy the Lipschitz
condition. Considering (12), if the pair
(
)
,
(
)
is a stabilizable parameterization of the system, then
to check controllability of the affine system, this pair
in the linear sense should be controllable for all .
ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics
526

Employing Hamiltonian theory (Cimen, 2010) the
optimal control law is
=−()
(
)
(
)
, (13)
where
(
)
is a state-dependent feedback
compensator which can be obtained from solution of
a state-dependent algebraic Riccati equation
(SDARE)
(
)
(
)
+
(
)
(
)
−
(
)
(
)
(
)
(
)
(
)
+
(
)
=. (14)
Equation (14) is in the form of algebraic SDRE
(SDARE) for affine systems. Solution of the equation
exactly results in suboptimal control because it
neglects so-called “SDRE necessary condition for
optimality” which tends to zero (Banks, 2007;
Korayem 2015). The 6 DoF quadrotor model (5)-(6)
in the form of (11) can be successfully rewritten in the
SDC form (12) by finding stable parameterization for
(
)
. Then solution of the infinite-time SDRE
problem seems to be formality in the context of UAV
stabilization.
In practical implementations, when the dynamics
of the system become complicated it seems to be
difficult to obtain a solution quickly, due to controller
sampling time. It becomes necessary to approximate
the solution. However, by employing advanced signal
processors and dedicated solution algorithms based
on Taylor series methods or interpolation methods
(Banks, 2007), the control technique can be
successively realized in practical implementation.
The computational effort can be also reduced by
implementing modified technique, proposed bellow.
3.3 SDRE Speed Compensator –
Modified Approach
In the proposed modified approach, the controller is
formulated as in the classic SDRE form (11), but the
SDC parameterized form uses a separated form of
matrix
(
)
:
=(
+
(
)
)+, (15)
where
is a state-independent and
(
)
is a state-
dependent part of
(
)
, respectively. Then feedback
compensator can also be defined as sum of state-
independent (constant) and state-dependent parts
()=
+
(
)
, what results in a control law as
=−
(
+
(
)
). (16)
As described in the paper (Stepien, 2019), the
procedure for solving SDARE (14) can be simplified.
The modified approach makes possibility solving
algebraic Riccati equation SDARE for
and
(
)
employing Moore-Penrose pseudoinverse (Barata,
2013).
+
−
+=, (17)
(
)
=
(
)
, (18)
Equation (17) is state-independent, hence it needs
to be solved only once whole the control process.
Thanks to this simplification, in comparison to the
classic SDRE approach, the computational effort is
strongly reduced. Then control law implementation
may become much easier in a real control system.
4 SIMULATIONS
The nonlinear 6 DoF quadrotor model is applied to
check the described infinite-time SDRE control for
positioning and stabilization when the UAV try to
find desired position during flight or take-off.
Governing equations that describe the UAV
aerodynamics are given by (5)-(6), but for the control
purpose, state-dependent parameterization SDC is
necessary. When considering the UAV flight
dynamics, parametrized model (12) based on system
(5) and (6) with gravity and drag compensation, can
be described in SDC form
=
0−
− 0
−0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
00
−
/
00
(
−
)
/
0
−
/
0
+
00
0
0
00
000
000
000
000
000
000
00
0
0
00
−
−+
∅+
∅+
(
+
)
0
0
0
,(19)
where control vector generally consists of rolling,
pitching, yawing moments and force vector with trust
generated from UAV rotors.
As defined in (19) and shown in Fig. 2, the thrust
acts positively along the positive body z-axis. A
quadcopter can either hover or adjust its altitude by
applying equal thrust to all four rotors, where two of
these motor spin clockwise, while the other two spin
counter clockwise. To adjust its yaw, or make it turn
left or right, the quadcopter applies more thrust to one
set of motors generating yawing moment. To pitch it
and roll it, on the other hand are adjusted by applying
Coupled PID-SDRE Controller of a Quadrotor: Positioning and Stabilization of UAV Flight
527

more thrust on one rotor and less to the other
opposing rotor generating pitching and rolling
moments.
Accordingly to the control schema proposed in Fig.
2, the control applied to the quadrotor =
is a sum of PID
control and SDRE stabilization, where controller
outputs are rolling, pitching and yawing moments, as
=
−
, (20)
where
,
,
obtained from SDRE controller are
assumed to be zero. The UAV properties used with
certain assumptions and indicated values to be able to
perform further calculations in the chapter due to the
model (5)-(6) and (19) are following: =5,35 kg,
=
0,04 kg⋅m
2
,
= 0,14 kg⋅m
2
,
= 0,17 kg⋅m
2
.
Employing described quadrotor model, the PID-
SDRE control technique is applied to control the
UAV attitude, considering infinite-time horizon
SDRE control for stabilization. The control speed and
final positioning error depend on PID gains, but
stabilization is optimal and works accordingly to the
SDRE technique.
The PID-SDRE method is chosen, because the
UAV should rapidly answer for user commands,
moreover the path of flight must be sometimes
rapidly stabilized when unexpected external forces
try to change its position and orientation during flying
action. Considering above, the control problem
consists of finding UAV state dynamics and PID-
SDRE controls for prescribed orientation
=45°,
=30°,
=15° during take-off with reference
speed
=
000000
and initial
speed
=
000000
.
In association with the dynamics (19), the PID
controller gains are:
=(0.3;0.3;0.3),
=(0.1;0.1;0.1), (21)
=(0.001;0.001;0).
and quadratic cost functional weighting matrices in
(10) are chosen as
=2∙
100 0 10
0 100 0
10 0 100
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
100.2
010.2
0.2 0.2 2
and =0.5∙
×
. (22)
Simulations are done to show the performance of
the control designed in section 3. The quadrotor state
dynamics, in other words, UAV response including
its orientation to the desired angle position is shown
below. Firstly simulations are performed for the UAV
controlled by PID only, neglecting SDRE stabilizer.
Next, simulation is performed for the full PID-
SDRE controller (Fig. 2) to show how the UAV can
be stabilized in the context of angular and linear
speeds. To check and compare described in previous
section SDRE-based methods: classic and modified,
simulations are performed for both proposed SDRE
stabilizers.
Figure 3: Angular position response, PID control.
Figure 4: Angular speed response, PID control.
Figure 5: Linear speed response, PID control.
Figs. 3-5 show the closed-loop response of the
PID controller of the quadrotor. Simulations are
performed for angular positioning with
=45°,
=30°,
=15°, programmed sequentially at 1,
2 and 3 sec. When look at Fig. 3, the quadrotor is
ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics
528

successively controlled with a small overshot by PID
reducing angular speed toward zero (Fig. 4).
However, control system does not consider linear
speeds, and the UAV moves in airspace.
Figure 6: Angular position response, PID-SDRE control.
Figure 7: Angular speed response, PID-SDRE control.
Figure 8: Linear speed response, PID-SDRE control.
When considering proposed PID-SDRE control,
Fig. 6-8 shows that quadrotor can be successfully
controlled to referenced angles zeroing angular speed
and reducing overshoots. It allows to operate with
different UAV orientation at non-zero linear speed
stabilizing angular positioning task. The PID-SDRE
technique is examined for classic and modified SDRE
approach. Simulation results are the same. It proofs
the usefulness and correctness of the methods
presented and used.
5 CONCLUSIONS
The hybrid PID-SDRE control technique for the
UAV-quadrotor infinite-time control problem is
formulated and solved. The UAV nonlinear 6 DoF,
state-dependent parametrized model is proposed. The
PID fine-tuned control methodology with an optimal
nonlinear feedback speed stabilizer, performing
attitude control and stabilization task is analyzed. The
effectiveness of the presented technique is
demonstrated on numerical example where the UAV
response is found using two different SDRE-based
techniques.
The results presented demonstrate that in the
future, the proposed control technique will be
successively applied to real-time UAV flight control
systems. Moreover, an approach based only on SDRE
technique, neglecting PID, will be strongly developed.
REFERENCES
Banks H.T., Lewis B.M., Tran H.T. (2007). Nonlinear
feedback controllers and compensators: a state-
dependent Riccati equation approach, Comput. Optim.
Appl, 37, 177–218.
Barata J. C. A., Hussein M. S. (2013). The Moore-Penrose
Pseudoinverse. A Tutorial Review of the Theory. John
Hopkins University Press.
Chipofya, M., Lee, D.J. (2017). Position and altitude
control of a quadcopter using state-dependent Riccati
equation (SDRE) control. In: 17th International
Conference on Control, Automation and Systems, pp.
1242-1244.
Çimen T. (2010). Systematic and effective design of
nonlinear feedback controllers via the state-dependent
Riccati equation (SDRE) method, An. Rev. in Contr.,
34(1), 32–51.
Cloutier J.R., D’Souza C.N. and Mracek C.P. (1996).
Nonlinear regulation and nonlinear H∞ control via the
state-dependent Riccati equation technique: Part 1,
Theory; Part 2, Examples. In: Proc. of the First
International Conference on Nonlinear Problems in
Aviation and Aerospace, Daytona Beach, FL, pp. 117-
141.
Heydari A., Balakrishnan S. N. (2015). Closed-form
solution to finite-horizon suboptimal control of
nonlinear systems, Int. J. Robust Nonlinear Control 25,
2687–2704.
Hoffmann G. M., Huang H., Waslander S. L., and Tomlin
C. J. (2007). Quadrotor helicopter flight dynamics and
control: Theory and experiment, In: Proc. of the AIAA
Guidance, Navigation, and Control Conference, vol. 2,
pp. 4.
Kim J., Gadsden S. A. and Wilkerson S. A. (2020). A
Comprehensive Survey of Control Strategies for
Coupled PID-SDRE Controller of a Quadrotor: Positioning and Stabilization of UAV Flight
529

Autonomous Quadrotors, Canadian Journal of
Electrical and Computer Engineering, 43(1), pp. 3-16.
Korayem M.H., Nekoo S.R. (2015). Finite-time state-
dependent Riccati equation for time-varying nonaffine
systems: Rigid and flexible joint manipulator control,
ISA Transactions 54, pp. 125–144.
Mracek C.P., Cloutier J.R. (1998). Control designs for the
nonlinear benchmark problem via the state-dependent
Riccati equation method, Int. J. Robust Nonlinear
Control 8(4-5), 401–433.
Sadeghzadeh I., Mehta A., and Zhang Y. (2011).
Fault/damage tolerant control of a quadrotor helicopter
uav using model reference adaptive control and gain-
scheduled PID, In: AIAA Guidance, Navigation, and
Control Conference, pp. 08–11.
Sheng S., Sun C. (2016). Control and optimization of a
variable-pitch quadrotor with minimum power
consumption, Energies 9, pp. 232-250.
Stepien, S.J., Superczynska, P., Dobrowolski, D. and
Dobrowolski, J. (2019). SDRE-based high performance
feedback control for nonlinear mechatronic systems,
COMPEL - The international journal for computation
and mathematics in electrical and electronic
engineering, 38(4), pp. 1164-1176.
Voos, H. (2006). Nonlinear state-dependent Riccati
equation control of a quadrotor UAV. In: IEEE
Computer Aided Control System Design, IEEE
International Conference on Control Applications,
IEEE International Symposium on Intelligent Control,
pp. 2547-2552.
Zhang T., Kang Y., Achtelik M., Kuhnlenz K., and Buss M.
(2009). Autonomous hovering of a vision/IMU guided
quadrotor, In: 2009 IEEE International Conference on
Mechatronics and Automation, pp. 2870–2875.
Chodnicki M., Bartnik K., Nowakowski M., Kowaleczko
G. (2018). Design and analysis of a feedback loop to
regulate the basic parameters of the unmanned aircraft,
Aircraft Engineering and Aerospace Technology,
92(3), pp. 318-328.
ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics
530
