
GAN-based Approach to Crafting Adversarial Malware Examples
against a Heterogeneous Ensemble Classifier
Saad Al-Ahmadi
1a
and Saud Al-Eyead
2b
1
Computer Science, King Saud University, Riyadh, Saudi Arabia
2
Computer Science, Prince Sattam Bin Abdulaziz, Kharj, Saudi Arabia
Keywords: GAN, Machine Learning, Deep Learning, Ensemble Classifier, Adversarial Malware Examples.
Abstract: The rapid advances in machine learning and deep learning algorithms have led to their adoption to tackle
different security problems such as spam, intrusion, and malware detection. Malware is a type of software
developed with a malicious intent to damage, exploit, or disable devices, systems, or networks. Malware
authors typically operate through black-box sitting when they have a partial knowledge about the targeted
detection system. It has been shown that supervised machine learning models are vulnerable to well-crafted
adversarial examples. The application domain of malware classification introduces additional constraints in
the adversarial sample crafting process compared to the computer vision domain: (1) the input is binary and
(2) retaining the visual appearance of the malware application and its intended functionality. In this paper, we
have developed a heterogeneous ensemble classifier that combines supervised and unsupervised models to
hinder black-box attacks designed by two variants of generative adversarial network (GAN). We
experimentally validate its soundness on a corpus of malware and legitimate files.
1 INTRODUCTION
Malware refers to a malicious software that has the
intent to damage, disrupt, destroy, or perform harmful
actions on a computer system. The detection of
malicious software through ML-based methods has
received an increasing amount of attention in
cybersecurity. To build a malware classifier, the
features are extracted from legitimate and malicious
files either statically or dynamically. The techniques
that extract static features do not execute the file and
only examine the code structure and other binary
properties. On the other hand, dynamic features are
obtained by observing the execution behavior of the
program. The selected features, be they static,
dynamic features or both, are then fed into the ML
model to discriminate between legitimate and
malicious files. These models can be embedded in
antivirus software to provide an automatic detection
tool for incoming files.
The advances and presence of intelligence in the
adversaries’ techniques have facilitated the need to
craft adversarial examples that are rarely identified by
a
https://orcid.org/0000-0001-9406-6809
b
https://orcid.org/0000-0001-6784-1291
deployed ML models such as Decision tree (DT),
Support Vector Machine (SVM), Logistic Regression
(LR), and Artificial Neural Network (ANN). To
attack a deployed malware detection system, three
assumptions are made in the literature about the
knowledge available to the adversaries, namely
white-box, black-box, and gray box. In the white-box
scenario, the adversaries have immediate access to
the ML system’s architecture, its parameters, and its
training data. However, adversaries in reality do not
have access to this kind of information. Thus, the
adversaries operate instead in a black-box threat
model. They use the target classifier as an oracle to
label their adversarial examples. These labels are then
used to train a surrogate model to approximate the
target classifier. In the gray box model, an adversary
is expected to know the architecture of the target
model but have no access to its parameters. A number
of attack algorithms have been proposed to generate
adversarial samples for the white-box threat model
such as FGSM, L-BFGS, C&W attacks, JSMA, and
DeepFool. These algorithms can be exploited in many
black-box and gray-box settings due to the
Al-Ahmadi, S. and Al-Eyead, S.
GAN-based Approach to Crafting Adversarial Malware Examples against a Heterogeneous Ensemble Classifier.
DOI: 10.5220/0011338800003283
In Proceedings of the 19th International Conference on Security and Cryptography (SECRYPT 2022), pages 451-460
ISBN: 978-989-758-590-6; ISSN: 2184-7711
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
451

transferability of the adversarial samples among the
models (Liu et al., 2016; Papernot, McDaniel, &
Goodfellow, 2016). However, there are two main
methods of black-box attack: transferability-based
methods (Hu & Tan, 2018; Papernot et al., 2017;
Rosenberg et al., 2018) and GAN-based methods (Hu
& Tan, 2017; Zhao et al., 2017). In this paper, we use
GAN to construct adversarial examples to bypass a
black-box malware detection system.
Cryptanalysts are in a battle with malware
authors to develop countermeasures to solidify
malware classification systems. Building a secure and
robust machine learning-based detection model is
considered to be an open research problem. GAN,
unlike other gradient-based approaches, needs to
reverse engineer the target classifier to
mathematically prepare the adversarial examples.
Therefore, we suggest using a heterogeneous
ensemble classifier that combines classification and
clustering to produce consolidated classification
results. Many researchers have been focused on the
use of supervised ML algorithms to detect malicious
software. In this paper, we show that the combination
of cluster and classifier ensembles can improve the
malware detection rate. To the best of our knowledge,
no study has investigated the combination of
supervised and unsupervised models for malware
classification. Our study makes use of the algorithm
introduced in (Acharya et al., 2011), whose name is
C3E (from the Consensus between Classification and
Clustering Ensembles). This algorithm assumes that
clusters can provide supplementary constraints that
help to classify new data. The task of combining
classification and clustering at the output level is
mapped into an optimization problem. To classify
new malware and legitimate files, we have used a
C3E based on Squared loss, C3E-SL (Coletta et al.,
2015). This algorithm needs two hyper-parameters:
the relative importance of the classifier and cluster
ensembles (σ), and the number of iterations of the
algorithm (N).
The rest of this paper is organized as follows.
Section 2 presents the related work, Section 3
provides a detailed description of our methodology,
Section 4 explains the implementation of our
proposed method, Section 5 discusses the evaluation
results, and Section 6 describes the future work and
concludes the paper.
2 RELATED WORK
Classifying malware programs using ML-based
algorithms instead of traditional techniques such as
signature-based algorithms, heuristic-based methods
and behavior-based methods has been studied
intensively (Gibert et al., 2020). Several research
papers have been proposed to use standalone
classifiers for malware classification. Nevertheless,
the findings show that using standalone classifiers is
not adequate enough to generalize and identify the
adversarial examples. For instance, deep learning is
claimed to be vulnerable to the manipulation of its
input (Szegedy et al., 2013). As a result, major recent
research has been devoted to hardening the
supervised learning algorithm by incorporating
defensive techniques during the training phase. In this
section, we initially review the most common papers
that propose and investigate countermeasures and
adversarial malware examples. Next, we briefly
outline the ensemble learning techniques that
combine either supervised models, unsupervised
models, or both supervised and unsupervised models.
Grosse and her colleagues (Grosse et al., 2016)
showed how to successfully implement adversarial
examples to bypass feed forward neural networks.
They adopted a forward derivative-based approach
(Papernot, McDaniel, Jha, et al., 2016) to craft the
adversarial examples. The reason for focusing on
forward derivative approaches instead of gradient
descent techniques is that the forward derivatives are
applicable to both supervised and unsupervised
models as well as allowing the adversaries to generate
information for broad families of adversarial samples.
This approach exploits the Jacobian Matrix which
contains the forward derivative of the cost function of
a trained classifier with respect of its input. These
derivatives are used to estimate the direction in which
a perturbation in the input sample can change the
classifier’s output. The adversarial example is
generated by adding a perturbation with a maximal
positive gradient to the benign class to a malicious
sample. Their results indicate that neural networks
should not be used without hardening them against
adversarial samples.
Wang et al (Wang et al., 2017) proposed a
Random Feature Nullification (RFN) which is an
adversary resistant method that prevents attackers
from creating adversarial samples by randomly
nullifying features within the samples. Their
techniques can be viewed as stochastically
“dropping” or omitting neuronal along with their
connections. The results show that the combination of
RFN with Adversarial Training reaches the best level
of resistance.
On the other hand, Ngoc vi et al (Vi et al., 2019)
proposes a solution to the malware classification
SECRYPT 2022 - 19th International Conference on Security and Cryptography
452

problem in a different way which is motivated by the
significant success of a convolutional neural network.
Their method is based on the gradient to attack image-
based malware classification systems by introducing
perturbations to the resource section of PE files. They
apply the FGSM method to generate adversarial
images by adding perturbations to the resource
section of PE files. They conclude that training with
the adversarial examples created by their method can
improve the robustness of a malware classifier.
Grosse et al. (Grosse et al., 2017) introduces two
procedures to detect adversarial examples, namely
statistical tests and training with an outlier class. The
first procedure investigates the ability of a statistical
test to distinguish between benign and adversarial
data points. They claim that the distribution of
original legitimate data is different from the
distribution of adversarial examples. They
empirically proved that statistical tests can be used to
detect adversarial examples before they are fed into a
ML model. In the second procedure, they augment
their ML model with an additional class to represent
the adversarial examples and train the model to
recognize adversarial examples as part of this new
class. They expect that the integration of the two
approaches will be beneficial.
GAN (Goodfellow et al., 2014) has been used
extensively to generate synthetic images to augment
small datasets for DNNs models. Hu and Tan (Hu &
Tan, 2017) exploited GAN to simulate attacks to
evade a black-box malware detection system. The
difference between their proposed algorithm –
MalGAN- and the existing ones is that the adversarial
examples are dynamically generated according to the
feedback of the black-box detector. The generator
transforms a malware binary feature vector into its
adversarial version and then its output is fed to a
black-box detector to label it. The substitute detector,
also known as a discriminator, is used to fit the black-
box detector and provide the gradient information to
train the generator. Both the generator and substitute
detector are part of a multi-layer feed-forward neural
network.
AdvGAN (Xiao et al., 2018) has been proposed to
generate adversarial examples using generative
adversarial networks (GANs). Once AdvGAN is
trained, the feed-forward generator can produce
adversarial perturbations efficiently. The model is
applied in both a semi-white-box and black-box
settings with a high attack success rate. The
adversarial examples generated by AdvGAN on
different target models have achieved higher attack
success rate under state-of-the-art defenses compared
to other adversarial example generating methods.
Jin et al. (Shen et al., 2017) proposed an
adversarial perturbation elimination framework
named APE-GAN to eliminate the perturbation of the
adversarial examples before feeding it into
classification networks. They evaluated their work
under different settings and the results show that the
error rates of the adversarial inputs are significantly
decreased after its perturbation is eliminated by APE-
GAN. Unlike the previous GAN-based methods, AI-
GAN (Bai et al., 2021) presents a new variant of GAN
to generate adversarial examples. In AI-GAN, the
attacker is added to train the discriminator
adversarially. The evaluation of AI-GAN’s attack
ability is applied in white-box with different attack
settings as well as a complicated dataset. AI-GAN
achieves a high attack success rate with a low
generation time in various settings as well as
scalability to complicated datasets.
Ensemble learning has been used for both
unsupervised and supervised models and it has a
better accuracy result than its individual components.
Bagging, Boosting, XG-Boost, Rule Aggregation,
Stacking, and an adaptive mixture of experts are state-
of-the-art supervised ensemble approaches derived
from multiple base classifiers. These ensemble
methods need a huge amount of labeled data and work
at the raw data level. On the other hand, ensemble
techniques in the unsupervised learning are mainly
focused on generating more stable clustering results
by combining multiple partitions or performing
distribution computing under privacy or sharing
constraints (Strehl & Ghosh, 2002). There have been
very limited efforts that combine multiple base
classifiers and clusters (Acharya et al., 2011; Ao et
al., 2014; Chakraborty, 2017; Gao et al., 2011). Every
attempt uses a different strategy to combine
classification and clustering to refine the final
classification results but all of them work at the meta-
output level without accessing the raw data. For
malware classification, few studies have been
conducted leveraging ensemble learning techniques
to improve the malware detection rate (Chen et al.,
2017; Kong & Yan, 2013; Yan et al., 2018; Ye et al.,
2010). As far as we know, there is no study in the
literature that has considered a heterogeneous
ensemble classifier that merges classification and
clustering as a malware classification system.
GAN-based Approach to Crafting Adversarial Malware Examples against a Heterogeneous Ensemble Classifier
453

3 METHODOLOGY
3.1 Problem Definition and
Formalization
Given the deployed malware classification system
under the threat model described below, the adversary
attempts to bypass this system to increase the
misclassification rate of adversarial examples. In
short, a substitute classifier is trained on a dataset that
contains a thousand of binary legitimate and
malicious vectors. Then, an adversarial malicious
sample is generated iteratively by modifying the
limited features of malicious sample until a
misclassification occurs. Finally, the deployed
malware classification system is evaluated under the
attacks at test time.
3.2 Threat Model
We considered black-box attacks during the test time
where the adversary does not know the targeted
malware classifier’s architecture and parameters. Its
knowledge is limited to the type of features and the
predicted class of the target classifier. The adversary’
s goal is to find a sample x that is similar to an original
sample x but classified differently. To achieve this,
we used the MalGAN algorithm (Hu & Tan, 2017) to
find the minimum perturbation to add to x to craft an
adversarial example. MalGAN has three basic
elements: the generator, the black-box detector, and
the surrogate detector.
The generator produces a perturbation vector O
from a concatenation of malware feature vector m and
a random noise vector z. Each element of z is a
random number sampled from normal distribution
with a mean of 0 and a standard deviation of 1. Since
malware feature values are binary, binarization
transformation is applied to O according to whether
an element is greater than 0.8 or not. This process
produces a binary vector O0. The final generated
adversarial malware example can be expressed as:
m
0
= m|O
0
where ”|” is the element-wise binary
OR operation.
Since m
0
is a binary vector, this will make the
gradients unable to back propagate from the surrogate
detector to the generator. Therefore, a smooth
function G is defined to receive gradient information
from the surrogate detector as shown below:
G(m, z) = max (m, o) where max(.,.) represents
element-wise max operation such that : When an
element of m is 1, the result of G will be 1 as well
and this will prevent from back propagate the
gradients. When an element of m is 0, the result of G
is the neural network’s real number output in the
corresponding dimension, and the gradient
information can back propagate.
The ground truth classes of training data are not
used to train the surrogate detector. Alternatively, the
black-box detector detects the training data that
consisted of adversarial malware examples from the
generator, and legitimate programs from an additional
legitimate dataset to predict whether a program is
benign or malware. Then the predicted labels from the
black-box detector is used to train the surrogate
detector.
The surrogate detector distinguishes the
adversarial malware samples from legitimate files.
Practically speaking, the generator is trained to
minimize the probability of generated adversarial
malware examples being classified as false by the
surrogate detector while the surrogate detector tries to
maximize the probability of generated adversarial
malware. The surrogate detector tries to mimic the
predications of the black-box detector and provide
gradient information to train the generator. The
generator and the surrogate detector work together to
deceive our heterogeneous ensemble classifier.
GANs come in three popular loss functions: the
original Jensen-Shanon divergence (Goodfellow et
al., 2014), least squares GANs (LSGAN) (Mao et al.,
2017), and Wasserstein distance (WGAN) (Arjovsky
et al., 2017). In this paper, we exploit two variants of
GAN: vanilla GAN and WGAN. WGAN uses
Wasserstein distance for the divergence between
model distribution and target distribution and it has a
smoother gradient which in turn helps to stabilize
training. The MalGAN algorithm does not offer a
mechanism to bound the number of feature
modifications. In this paper, we will tackle this
weakness to ensure the functionality of the
adversarial malware examples.
3.3 Victim Model
The victim model is an ensemble classifier that
combines both classification and clustering. In this
paper, we are trying to verify our hypothesis which
states that a heterogeneous ensemble classifier is
robust against GAN attacks. We adopted the
algorithm introduced by (Acharya et al., 2011) to
build our ensemble classifier. Their algorithm (C3E)
consists of three steps.
1. An ensemble of r1 trained classifiers is applied
to new data X=
x
i
i=1
n
The output of each
constitute classifier for each xi is a k-
dimensional class probability vector πi . From
SECRYPT 2022 - 19th International Conference on Security and Cryptography
454

the set of such vectors
i
q
1
q
1=1
r
1
, an average
vector can be computed for xi as:
i
=
1
r
1
i
q
1
r
1
q
1=1
2. A similarity (co-association) matrix S is
computed after an ensemble of r
2
trained
clusters are applied on a new data X=
x
i
i=1
n
,
Each entry in this matrix represents the
similarity between two objects which is simply
the fraction of the r2 cluster solutions in which
the two objects lie in the same cluster.
3. The consolidated result of C3E is achieved
after finding the minimum solution of the
following objective function.
j = x
L
i
y
i
+ σ
x
𝑠
j
L
y
i
,y
j
1
i ∈ x
i,j
(1)
• The quantity L(.,.) denotes a loss function.
• The first term captures the dissimilarities
between the class probabilities provided by the
ensemble of classifiers and the output vectors
y
i
i=1
n
.
• The second term encodes the weighted
dissimilarity between all possible pairs (yi,yj).
The weights of these pairs are assigned in
proportion to the similarity values sij of matrix
S.
• σ is a hyper-parameter which controls the
relative importance of the classifier and cluster
ensembles.
The problem of classifying the new data X can be
approached as an optimization problem whose
objective is to minimize J. In (Acharya et al., 2011),
the authors state that any Bregman divergence can be
used as the loss function L(.,.) in the last equation.
Bregman divergences include a large number of
useful loss functions such as the well-known squared
loss, KL-divergence, logistic loss, Mahalanobis
distance, and I-divergence. As in (Coletta et al.,
2015), we selected this to exploit a squared loss (SL)
function, hence the optimization over y
i
i=1
n
can be a
closed form solution. The objective function in
equation (1) is rewritten as
j =𝑥
‖
—
‖
+ σ
x
𝑠
j
L
y
i
,y
j
2
i ∈ x
i,j
(1)
By keeping y
j
j=1
n
y
I
fixed and sitting
∂
j
∂
y
I
0, we
get
y
i
=
i
∑
∑
(3)
Equation (3) can be computed iteratively, for all i
∈ {1,2,...,n}, until a maximum number of iterations is
reached, in order to obtain posterior class probability
distributions for the instances in X (Coletta et al.,
2015). The objective of combining unsupervised
models is to provide supplementary constraints for
classifying new data (Banerjee & Ghosh, 2008). This
point of view presumes that the similar new data
points in the test set that lie in the same cluster are
more likely to share the same class label. Thus, we
believe these constraints will improve the
generalization capability of our ensemble classifier.
4 DEFENSIVE MECHANISMS
The most common defensive mechanisms mentioned
in the literature are randomness (Biggio et al., 2010),
preventing overfitting, feature selection (Xu et al.,
2016), distillation (Papernot, McDaniel, Wu, et al.,
2016), ensemble adversarial training (Chinavle et al.,
2009), denoising, random input transformation, non-
linearity (Šrndic & Laskov, 2013), and micro-
detectors (Saad et al., 2019). Our hybrid machine
learning model introduces randomness to the
classifier system through the ensemble of classifiers
and clusters. This randomness prevents the
adversaries accessing the parameters of the
classification system. As a result, we believe this
information hiding technique will be able to avoid
GAN’s attacks.
5 IMPLEMENTATION
5.1 Dataset
The dataset we used in our experiments was
generated as a part of (Al-Dujaili et al., 2018)
collected from Portable Execution (PE) files. This
dataset contains 22,761 binary features. These binary
features are the API calls extracted from malware and
legitimate PE files. The PE format enfolds the
information necessary for Windows OS to manage
the wrapped code. The authors of (Al-Dujaili et al.,
2018) create a corpus of 38,000 malicious and
legitimate PE files. Each PE file is represented as a
binary indicator feature vector. Each index of the
feature vector represents a unique Windows API call
where ”1” represents the presence of the
GAN-based Approach to Crafting Adversarial Malware Examples against a Heterogeneous Ensemble Classifier
455
corresponding API call. We divided the dataset into
training, validation and test sets and the number of
samples in each set is 22800, 7600, and 7600
respectively. Since the dataset is a Boolean matrix,
we can visualize its sparsity using the
Matplotlib.spy() method in Python. As shown in
Figure 1, the dataset is apparently sparse as the graph
is mostly white. Thus, we decided to apply
VarianceThreshold to remove the features with a
variance of less than 20%.
Figure 1: 2D plot to visualize the sparsity of our input
matrix.
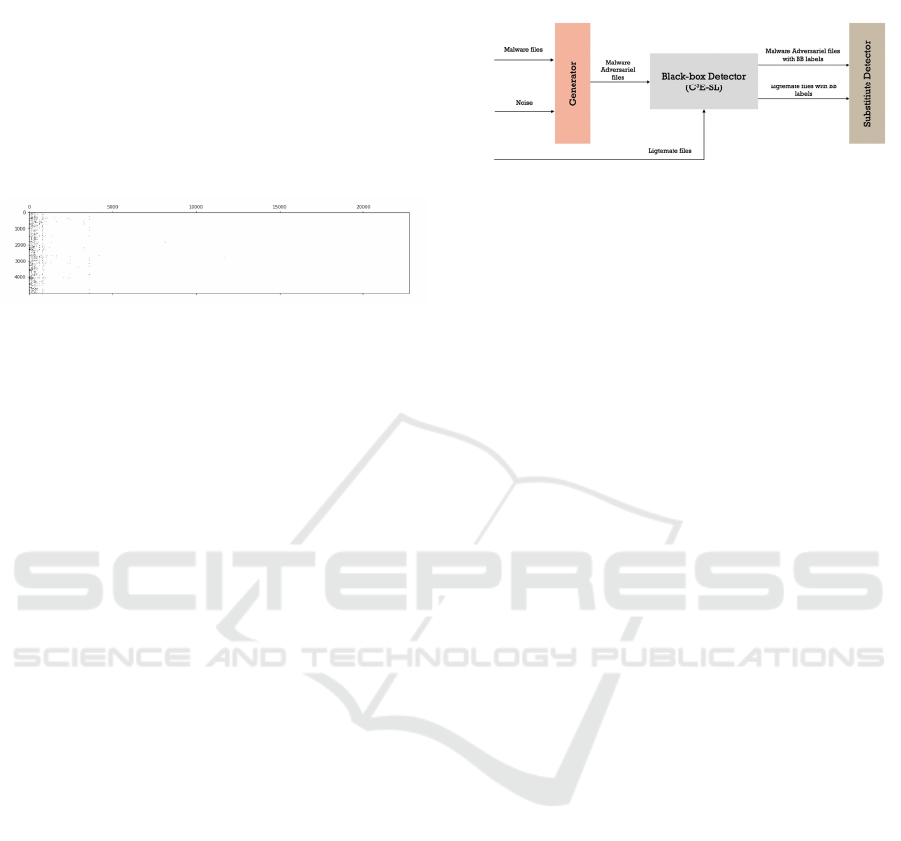
5.2 Threat Model's Architecture
As we mentioned in the methodology, we exploited
MalGAN (Hu & Tan, 2017) to simulate evasion
attacks against the proposed black-box detector. The
architecture of MalGAN is presented in Figure 2. We
used ANN with one hidden layer for both the
generator and surrogate detector. To confirm our
selection, we tried different architectures with
different numbers of hidden layers. We found that
using ANN with one hidden layer does not degrade
the performance of both vanilla GAN and WGAN.
On the contrary, it shows comparable results with
ANNs with two and three hidden layers. We set the
number of neurons in the hidden layer to 200 and
added a dropout layer in the surrogate detector after
the hidden layer to ensure it does not overfit the
training set, and the L2 Regularizer applies the loss
function of the generator.
The black-box detector is a trained heterogeneous
ensemble classifier that combines clusters and
classifiers (C3E-SL). The surrogate detector uses the
black-box detector as an oracle to label the
adversarial malware and legitimate files. During
training, the surrogate detector tries to fit the black-
box detector and push the generator to craft
indistinguishable adversarial malware files.
The objective of GAN is to generate
perturbations and add them to malware files to
deceive our black-box detector system. In our
experiments, we considered adding perturbations to
modify the malware files because removing features
may crack the malware files. In this paper, we want
to show that crafting adversarial malware samples by
GAN can transfer across different models.
Nonetheless, they hardly bypassed our hybrid model
and achieved a low fooling rate.
Figure 2: Architecture of our proposed method.
5.3 Restrictions on Adversarial
Crafting
We applied two restrictions to the perturbations
generated by the MalGAN algorithm. First, in the
original implementation of MalGAN, the number of
modifications applied to the original malware files
were not restricted. During the training of MalGAN,
the API call is enabled if the corresponding
dimension of the generator’s output has a value
greater than 0.5. We believe that this threshold will
change the malware application too much, hence it
may not preserve its utility. We decided to increase
this threshold to 0.8. Second, the number of epochs
for training GAN model is a critical hyperparameter
that should be selected carefully. GAN generally is
exploited to synthesize new images that resemble real
images. Thus, the GAN model should be trained for
quite a long time to reach its intended purpose.
However, this cannot be applied to malware files
because we want the generator to enable API calls as
little as possible to fool the discriminator. Therefore,
we have tried a different number of epochs and
discovered that 100 and 50 epochs are a reasonable
choice for vanilla GAN and WGAN, respectively.
5.4 Victim Model's Architecture
As we discussed in the methodology, we consider
randomness to be our defensive technique. This could
be built using combination of classifiers and clusters.
We leveraged (C3E-SL) to refine the initial class
probabilities estimated by the ensemble of classifiers
(Neural Network, SVM, Logistic Regression, and
Random Forest) with the help of the ensemble of
clusters (K-means, Mean-shift, and GMM). All the
classifiers and clusters were trained on the reduced
features set (199 dimensions) after applying
VarianceThreshold.
According to (IBM Support, 2020), Boolean data
is not preferred with K-means. Thus, we converted
our categorical features to continuous features using
SECRYPT 2022 - 19th International Conference on Security and Cryptography
456

PCA before feeding the training set to the K-means
cluster. To evaluate the clustering results of the three
clusters, we exploit Adjusted Rand index (ARI),
which is a function that measures the similarity of two
assignments - the one given by the clustering process
and the other by the true label. Unfortunately, we do
not have knowledge of the ground truth for clustering.
Thus, we alternatively consider analyzing how
similar the clustering results generated by K-means
with GMM and Mean Shift are. More specifically, we
used ARI to calculate the agreement score between
K-means and (GMM and Mean Shift). The aim of this
test was to verify two things. First, we want to
indicate whether similar objects lie in the same
group/cluster in all clustering models. Secondly, is
the similar score going to differ if continuous features
are used instead of categorical features in the GMM
and Mean Shift models? After conducting this test,
we found that using continuous features yields a
higher agreement score by about 99% between the
clustering models.
6 EXPERIMENTAL SETUP
This section discusses the empirical evaluation of our
proposed method. Since it is infeasible that the
authors of malware files and antivirus vendors collect
the same dataset, the attack model (MalGAN) and the
victim model (an ensemble of classifiers and clusters)
were trained on different training sets. The number of
samples in the dataset totaled 38,000 and this total
was distributed according to 22800, 7600, 7600
among the training set, validation set, and test set
respectively. We split the training set into A (20%)
for training the attack model and B (80%) for training
the victim model. To avoid overfitting the standalone
classifiers while tuning their hyper-parameters, we
used the whole validation set. The Adam optimizer
with a learning rate of 0.001 and RMSProp with a
learning rate of 0.0001 were selected as the
optimizers for vanilla GAN and WGAN,
respectively.
To validate the efficiency of the proposed method
in terms of the malware detection rate, we conducted
two experiments where in the first experiment the
adversarial malware examples are crafted by the
vanilla GAN and in the second experiment, they are
crafted by WGAN. In both experiments, we
compared its performance with SVM, RF, LR and
ANN. To guarantee a compatible comparison
between our hybrid model and the base classifiers and
to prevent overfitting, we utilized two generalization
techniques - dropout and L2 regularization. We added
both techniques to the ANN model and L2
regularization to LR and SVM. Dropout randomly
drops hidden units (along with their connections)
from the neural network during training. This
enhances the model generalization and provides a
way of approximately combining many different
neural network architectures efficiently. L2
regularization reduces the likelihood of ANN model
overfitting by preventing the weight of any values
from getting large in magnitude. This is done by
adding a weight penalty to the cost function.
Training both vanilla and Wasserstein GAN
models is hard as they require a delicate balance
between the generator and discriminator. We have
spent a sufficient time tuning the hyper-parameters
considering the constraints we imposed in Section
4.3. We will discuss a few of the findings we noticed
during the training of the threat model before giving
our remarks about the empirical results. First, the
user-defined parameter σ in the (C3E-SL) algorithm
should be assigned a low value because values higher
than 0.0001 will cause C3E-SL to be susceptible to
adversarial attacks during testing. Second, the
generator of WGAN starts to construct
undiscriminating adversarial samples between epoch
35 and epoch 50. Third, vanilla GAN suffers from
gradient fluctuations, hence the loss of the plots
obtained during training is not indicative of getting
highly effective adversarial samples. Table (1) shows
the detection rate of the adversarial malware files
according to five models. As we can see, our model
has achieved the highest rate of 42.8%. The
combination of clusters and classifiers is evidenced to
improve the malware detection rate. It is worth noting
in Figure 3 that the generated adversarial examples
are increasingly rejected by our model after epoch 60.
This is evidence that the surrogate detector of vanilla
GAN is not strong enough to stimulate the generator
to craft adversarial examples that are hardly detected.
On the other hand, the ANN model attained the
second highest detection rate and this is due to a
couple of reasons. First, the two generalization
mechanisms dropout and L2 regularization has
empowered the ANN model to expose 35.6% of the
adversarial malware files. Second, both the attack and
victim models use the same ML algorithm, hence the
adversarial malware files are readily transferred from
MalGAN to ANN. For Random Forest, Logistic
Regression, and SVM, the TPR ranges from 26.8% to
30%.
GAN-based Approach to Crafting Adversarial Malware Examples against a Heterogeneous Ensemble Classifier
457
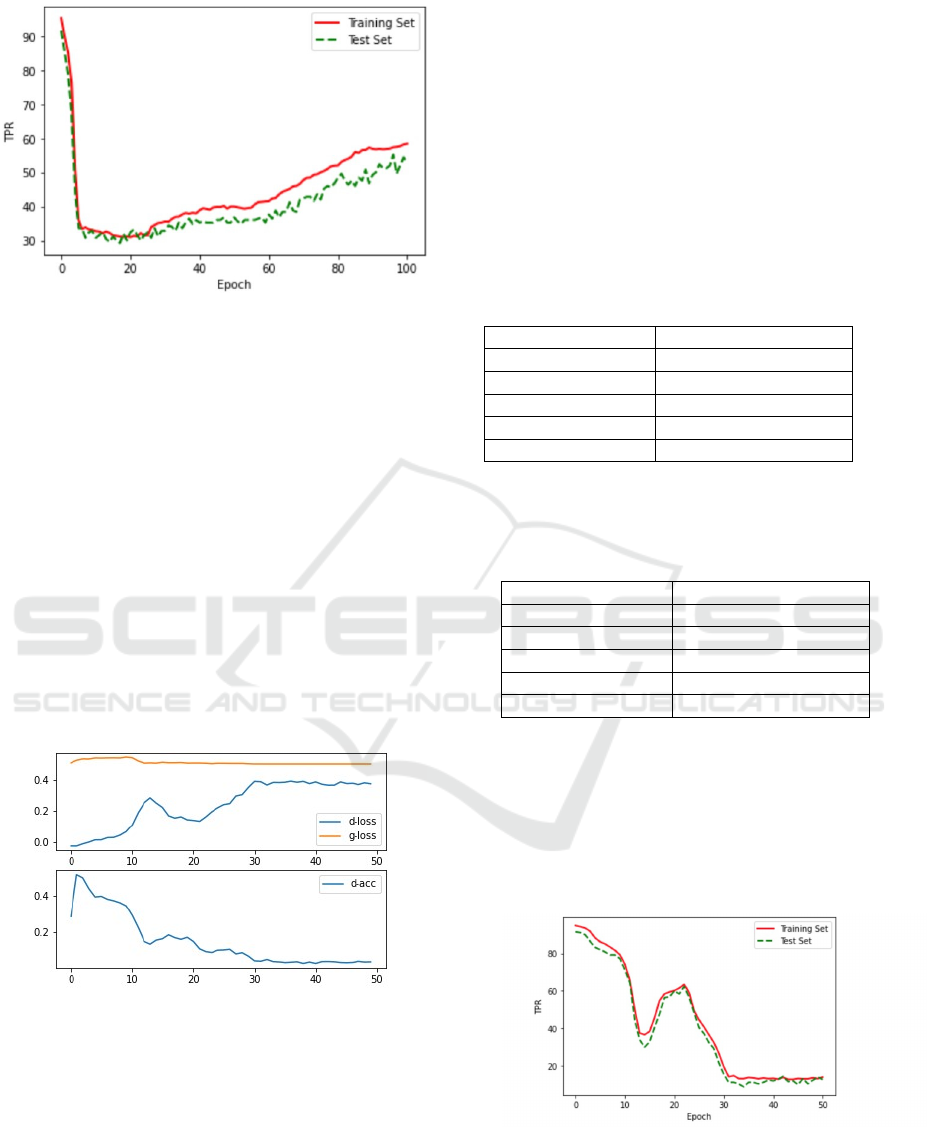
Figure 3: The change in the true positive rate of the training
and test sets during the training of the GAN for 100 epochs.
The black-box detector here is our heterogeneous ensemble
classifier.
One of the tedious issues of training vanilla GAN
is instability, which leads to gradient fluctuations
(Salimans et al., 2016). Wasserstein GAN (WGAN)
overcomes this difficulty. The graphs with a learning
curve and accuracy line for WGAN are presented in
Figure 4. The top subplot shows the line plots for the
average discriminator loss for both malware and
legitimate samples (blue), and the generator loss for
generated adversarial malware samples (orange). We
can see that the discriminator loss is somewhat erratic
in the beginning of the training before stabilizing
around epoch 30. The loss remains stable after that,
even though the variance between the generator and
discriminator increases.
Figure 4: Line plots of loss and accuracy for WGAN.
Table (2) presents the detection rate of the
adversarial examples constructed using WGAN
against the proposed hybrid model. The figures
dramatically decreased for all classification methods.
WGAN-based attacks were able to fool our model
and only 19.2% of adversarial examples were
detected. We justify this result as the ensemble of the
clusters was not able to cluster the adversarial
examples correctly. This affected the final result of
(C3E-SL). The convergence curve of TPR on the
training set and test set is shown in Figure 5. For both
the training and test sets, TPR starts to fall sharply
near the epoch 35. This is due to WGAN starting to
create indistinguishable adversarial examples that
were hardly detected by our model. For the
standalone classifiers, SVM obtained the highest
detection rate at 18% and LR obtained the lowest at
12.4%.
Table 1: True positive rate of the adversarial malware
examples when the attack model is vanilla GAN and the
victim models are four standalone classifiers and our hybrid
model trained on a different training set.
Models Test set
NN 35.6 %
LR 26.8%
SVM 30%
RF 30.4%
Hybrid model 42.8 %
Table 2: True positive rate of the adversarial malware
examples when the attack model is WGAN and the victim
models are four standalone classifiers and our hybrid model
trained on a different training set.
Models Test set
NN 16.4 %
LR 12.4%
SVM 18 %
RF 15.2%
Hybrid model 19.2%
The differences in the detection rate of the
malware samples in Tables (1) and (2) lead us to this
observation. WGAN trains the discriminator more
than the generator and in turn it pushes the generator
to design indistinguishable adversarial samples.
Thus, the highly effective adversarial samples were
solely able to bypass the black-box detector systems.
Figure 5: The change in the true positive rate of the training
and test sets during the training of the WGAN for 50
epochs. The black-box detector here is our heterogeneous
ensemble classifier.
SECRYPT 2022 - 19th International Conference on Security and Cryptography
458

7 CONCLUSION AND FUTURE
WORK
In this paper, we have proposed a framework that has
investigated the viability of heterogeneous machine
learning model against GAN-based evasion attacks.
These kinds of attack are rarely detected by ML-
based malware detectors that are not backed by
defensive techniques. For instance, 87.6% of
adversarial malware examples constructed by
WGAN bypass the Logistic Regression classifier.
The presented empirical results have proven that
combining supervised and unsupervised models can
thwart roughly 42.8% of vanilla GAN-based attacks
and 19.2% of WGAN-based attacks.
There are several aspects that can be investigated
in the future. First, there is the impact of increasing
the number of clusters and classifiers in C3E-SL to
improve the malware detection rate. Second, there is
changing the squared loss in equation (1) for another
Bregman divergence. The third is by applying our
model in different application examples such as spam
and intrusion detection to definitely verify our claims
about the hardness of our proposed method. Fourth is
injecting adversarial examples in the training set and
retraining the hybrid model. We believe that
adversarial retraining will improve the heterogeneous
model’s robustness and encourage it to generalize
well to unseen data.
REFERENCES
Acharya, A., Hruschka, E. R., Ghosh, J., & Acharyya, S.
(2011). C 3 e: a framework for combining ensembles of
classifiers and clusterers. International Workshop on
Multiple Classifier Systems, 269–278.
Al-Dujaili, A., Huang, A., Hemberg, E., & O’Reilly, U.-M.
(2018). Adversarial deep learning for robust detection
of binary encoded malware. 2018 IEEE Security and
Privacy Workshops (SPW), 76–82.
Ao, X., Luo, P., Ma, X., Zhuang, F., He, Q., Shi, Z., & Shen,
Z. (2014). Combining supervised and unsupervised
models via unconstrained probabilistic embedding.
Information Sciences, 257, 101–114.
Arjovsky, M., Chintala, S., & Bottou, L. (2017).
Wasserstein generative adversarial networks.
International Conference on Machine Learning, 214–
223.
Bai, T., Zhao, J., Zhu, J., Han, S., Chen, J., Li, B., & Kot,
A. (2021). Ai-gan: Attack-inspired generation of
adversarial examples. 2021 IEEE International
Conference on Image Processing (ICIP), 2543–2547.
Banerjee, A., & Ghosh, J. (2008). Clustering with balancing
constraints. Constrained Clustering: Advances in
Algorithms, Theory, and Applications, 171–200.
Biggio, B., Fumera, G., & Roli, F. (2010). Multiple
classifier systems for robust classifier design in
adversarial environments. International Journal of
Machine Learning and Cybernetics, 1(1), 27–41.
Chakraborty, T. (2017). Ec3: Combining clustering and
classification for ensemble learning. 2017 IEEE
International Conference on Data Mining (ICDM),
781–786.
Chen, L., Hou, S., & Ye, Y. (2017). Securedroid:
Enhancing security of machine learning-based
detection against adversarial android malware attacks.
Proceedings of the 33rd Annual Computer Security
Applications Conference, 362–372.
Chinavle, D., Kolari, P., Oates, T., & Finin, T. (2009).
Ensembles in adversarial classification for spam.
Proceedings of the 18th ACM Conference on
Information and Knowledge Management, 2015–2018.
Coletta, L. F. S., Hruschka, E. R., Acharya, A., & Ghosh, J.
(2015). A differential evolution algorithm to optimise
the combination of classifier and cluster ensembles.
International Journal of Bio-Inspired Computation,
7(2), 111–124.
Gao, J., Liang, F., Fan, W., Sun, Y., & Han, J. (2011). A
graph-based consensus maximization approach for
combining multiple supervised and unsupervised
models. IEEE Transactions on Knowledge and Data
Engineering, 25(1), 15–28.
Gibert, D., Mateu, C., & Planes, J. (2020). The rise of
machine learning for detection and classification of
malware: Research developments, trends and
challenges. Journal of Network and Computer
Applications, 153, 102526.
Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B.,
Warde-Farley, D., Ozair, S., Courville, A., & Bengio,
Y. (2014). Generative adversarial nets. Advances in
Neural Information Processing Systems,
27.
Grosse, K., Manoharan, P., Papernot, N., Backes, M., &
McDaniel, P. (2017). On the (statistical) detection of
adversarial examples. ArXiv Preprint
ArXiv:1702.06280.
Grosse, K., Papernot, N., Manoharan, P., Backes, M., &
McDaniel, P. (2016). Adversarial perturbations against
deep neural networks for malware classification. ArXiv
Preprint ArXiv:1606.04435.
Hu, W., & Tan, Y. (2017). Generating adversarial malware
examples for black-box attacks based on GAN. ArXiv
Preprint ArXiv:1702.05983.
Hu, W., & Tan, Y. (2018). Black-box attacks against RNN
based malware detection algorithms. Workshops at the
Thirty-Second AAAI Conference on Artificial
Intelligence.
IBM Support. (2020). Clustering binary data with K-Means
(should be avoided). IBM.
Kong, D., & Yan, G. (2013). Discriminant malware
distance learning on structural information for
automated malware classification. Proceedings of the
GAN-based Approach to Crafting Adversarial Malware Examples against a Heterogeneous Ensemble Classifier
459

19th ACM SIGKDD International Conference on
Knowledge Discovery and Data Mining, 1357–1365.
Liu, Y., Chen, X., Liu, C., & Song, D. (2016). Delving into
transferable adversarial examples and black-box
attacks. ArXiv Preprint ArXiv:1611.02770.
Mao, X., Li, Q., Xie, H., Lau, R. Y. K., Wang, Z., & Paul
Smolley, S. (2017). Least squares generative
adversarial networks. Proceedings of the IEEE
International Conference on Computer Vision, 2794–
2802.
Papernot, N., McDaniel, P., & Goodfellow, I. (2016).
Transferability in machine learning: from phenomena
to black-box attacks using adversarial samples. ArXiv
Preprint ArXiv:1605.07277.
Papernot, N., McDaniel, P., Goodfellow, I., Jha, S., Celik,
Z. B., & Swami, A. (2017). Practical black-box attacks
against machine learning. Proceedings of the 2017
ACM on Asia Conference on Computer and
Communications Security, 506–519.
Papernot, N., McDaniel, P., Jha, S., Fredrikson, M., Celik,
Z. B., & Swami, A. (2016). The limitations of deep
learning in adversarial settings. 2016 IEEE European
Symposium on Security and Privacy (EuroS\&P), 372–
387.
Papernot, N., McDaniel, P., Wu, X., Jha, S., & Swami, A.
(2016). Distillation as a defense to adversarial
perturbations against deep neural networks. 2016 IEEE
Symposium on Security and Privacy (SP), 582–597.
Rosenberg, I., Shabtai, A., Rokach, L., & Elovici, Y.
(2018). Generic black-box end-to-end attack against
state of the art API call based malware classifiers.
International Symposium on Research in Attacks,
Intrusions, and Defenses, 490–510.
Saad, S., Briguglio, W., & Elmiligi, H. (2019). The curious
case of machine learning in malware detection. ArXiv
Preprint ArXiv:1905.07573.
Salimans, T., Goodfellow, I., Zaremba, W., Cheung, V.,
Radford, A., & Chen, X. (2016). Improved techniques
for training gans. Advances in Neural Information
Processing Systems, 29.
Shen, S., Jin, G., Gao, K., & Zhang, Y. (2017). Ape-gan:
Adversarial perturbation elimination with gan. ArXiv
Preprint ArXiv:1707.05474.
Šrndic, N., & Laskov, P. (2013). Detection of malicious pdf
files based on hierarchical document structure.
Proceedings of the 20th Annual Network \& Distributed
System Security Symposium, 1–16.
Strehl, A., & Ghosh, J. (2002). Cluster ensembles---a
knowledge reuse framework for combining multiple
partitions. Journal of Machine Learning Research,
3(Dec), 583–617.
Szegedy, C., Zaremba, W., Sutskever, I., Bruna, J., Erhan,
D., Goodfellow, I., & Fergus, R. (2013). Intriguing
properties of neural networks. ArXiv Preprint
ArXiv:1312.6199.
Vi, B. N., Nguyen, H. N., Nguyen, N. T., & Tran, C. T.
(2019). Adversarial examples against image-based
malware classification systems. 2019 11th
International Conference on Knowledge and Systems
Engineering (KSE), 1–5.
Wang, Q., Guo, W., Zhang, K., Ororbia, A. G., Xing, X.,
Liu, X., & Giles, C. L. (2017). Adversary resistant deep
neural networks with an application to malware
detection. Proceedings of the 23rd ACM Sigkdd
International Conference on Knowledge Discovery and
Data Mining, 1145–1153.
Xiao, C., Li, B., Zhu, J.-Y., He, W., Liu, M., & Song, D.
(2018). Generating adversarial examples with
adversarial networks. ArXiv Preprint
ArXiv:1801.02610.
Xu, W., Qi, Y., & Evans, D. (2016). Automatically evading
classifiers. Proceedings of the 2016 Network and
Distributed Systems Symposium, 10.
Yan, J., Qi, Y., & Rao, Q. (2018). Detecting malware with
an ensemble method based on deep neural network.
Security and Communication Networks, 2018.
Ye, Y., Li, T., Chen, Y., & Jiang, Q. (2010). Automatic
malware categorization using cluster ensemble.
Proceedings of the 16th ACM SIGKDD International
Conference on Knowledge Discovery and Data Mining,
95–104.
Zhao, Z., Dua, D., & Singh, S. (2017). Generating natural
adversarial examples. ArXiv Preprint
ArXiv:1710.11342.
SECRYPT 2022 - 19th International Conference on Security and Cryptography
460
