STIFS: Spatio-Temporal Input Frame Selection for Learning-based

Video Super-Resolution Models

Arbind Agrahari Baniya

, Tsz-Kwan Lee

, Peter W. Eklund

and Sunil Aryal

School of IT, Deakin University, Geelong, VIC, Australia

Keywords:

High Deﬁnition Video, Image Analysis, Image Quality, Video Signal Processing, Super-resolution.

Abstract:

Deep learning Video Super-Resolution (VSR) methods rely on learning spatio-temporal correlations between

a target frame and its neighbouring frames in a given temporal radius to generate a high-resolution output.

Among recent VSR models, a sliding window mechanism is popularly adopted by picking a ﬁxed number of

consecutive frames as neighbouring frames for a given target frame. This results in a single frame being used

multiple times in the input space during the super-resolution process. Moreover, the approach of adopting

the ﬁxed consecutive frames directly does not allow deep learning models to learn the full extent of spatio-

temporal inter-dependencies between a target frame and its neighbours along a video sequence. To mitigate

these issues, this paper proposes a Spatio-Temporal Input Frame Selection (STIFS) algorithm based on image

analysis to adaptively select the neighbouring frame(s) based on the spatio-temporal context dynamics with

respect to the target frame. STIFS is ﬁrst-ever dynamic selection mechanism proposed for VSR methods.

It aims to enable VSR models to better learn spatio-temporal correlations in a given temporal radius and

consequently maximise the quality of the high-deﬁnition output. The proposed STIFS algorithm achieved

remarkable PSNR improvements in the high-resolution output for VSR models on benchmark datasets.

1 INTRODUCTION

Super-Resolution for generating high-resolution vi-

suals from low-resolution inputs is a classic prob-

lem in computer vision domain. Its initial solu-

tion was provided by Image Super-Resolution (ISR)

which only utilises spatial information of a single im-

age or multiple discrete images to produce fundamen-

tal visual quality improvement (Wang et al., 2020;

Areﬁn et al., 2020). Extending the target resolving

subject from image to video signals, applying the

super-resolution approaches used in conventional ISR

to Video Super-Resolution (VSR) fails to capture the

unique temporal information present in videos (Liang

et al., 2020; Liu et al., 2021). VSR aims to adopt

several temporally correlated low-resolution frames

within a video sequence to super-resolve the frame

series. The cross-consideration of spatial and tempo-

ral dimensions across multiple input frames has in-

duced a highly non-linear multi-dimensional problem

https://orcid.org/0000-0002-9359-6506

https://orcid.org/0000-0003-4176-2215

https://orcid.org/0000-0003-2313-8603

https://orcid.org/0000-0002-6639-6824

to tackle.

In recent years, Deep Neural Networks (DNN)

have been widely adopted in the VSR domain to

leverage highly non-linear multi-dimensional charac-

teristics and features in the input video frames and

have shown some promising results (Liu et al., 2020).

Other learning-based VSR approaches (Haris et al.,

2019; Wang et al., 2019b; Jo et al., 2018; Bao et al.,

2021; Tian et al., 2020; Isobe et al., 2020b; Chan

et al., 2021; Isobe et al., 2020a) utilise temporal in-

formation in a video as a learning feature followed

by stages of frame alignment and fusion to recon-

struct and up-sample the resultant pixels. However,

their commonly adopted frame alignment techniques,

traditional Motion Estimation and Motion Compensa-

tion (MEMC) approach using optical ﬂow and warp-

ing (Chan et al., 2021), or modern machine learn-

ing technologies such as deformable convolution (Dai

et al., 2017) may not effectively align multiple frames

correctly for accurate fusion and reconstruction (Liu

et al., 2020). Therefore, 2D/3D and recurrent convo-

lutions have been used to learn the inter-frame cor-

relation without any implicit or explicit frame align-

ment.

To reveal inter-frame correlation along a video se-

Agrahari Baniya, A., Lee, T., Eklund, P. and Aryal, S.

STIFS: Spatio-Temporal Input Frame Selection for Learning-based Video Super-Resolution Models.

DOI: 10.5220/0011339900003289

In Proceedings of the 19th International Conference on Signal Processing and Multimedia Applications (SIGMAP 2022), pages 48-58

ISBN: 978-989-758-591-3; ISSN: 2184-9471

quence without any implicit or explicit frame align-

ment, the input frames adopted to be learned is com-

monly based on a sliding window mechanism includ-

ing n consecutive frames from either past and/or fu-

ture timestamps to the target frame (Sajjadi et al.,

2018). Most VSR models using a sliding-window

mechanism treat all neighbouring input frames as

equally important without rank or selection. How-

ever, each neighbouring frame in a sliding window

may express a different correlation because of the

context changes across the time domain. Thus, a

ﬁxed selection of n consecutive frame(s) from the tar-

get frame in a sliding window may not be optimal

for learning spatio-temporal correlation (Wang et al.,

2019b).

In this work we propose to address these gaps with

three-fold contributions highlighted as follows:

1. To leverage a VSR result from an optimal in-

put space, we propose a novel pre-processing

technique which adaptively ranks and selects the

neighbouring frames from bidirectional temporal

dimensions to be included in the sliding window

input space based on a spatio-temporal ranking al-

gorithm, rather than simply selecting the nearest n

consecutive frames from the target frame.

2. The proposed Spatio-Temporal Input Frame Se-

lection (STIFS) algorithm induces a strategic

correlation-based discrepancy among the neigh-

bouring frames to enable selection of the most

highly correlated reference frames from bidirec-

tional temporal dimensions for super-resolving

the target frame.

3. Finally, this work explores the impact and effec-

tiveness of applying an input selection algorithm

for machine learning based VSR model.

To our knowledge, this is the ﬁrst work of its kind

that introduces an adaptive selection algorithm with

the objective of optimising the input space to aid VSR

models to learn better spatio-temporal correlations in

VSR and consequently improve the quality of high-

resolution outputs.

2 BACKGROUND

2.1 Trade-off with and without Frame

Alignment in VSR

Using frame alignment in VSR, MEMC (Haris et al.,

2019; Bao et al., 2021; Haris et al., 2020; Xue et al.,

2019) remains challenging, particularly when inter-

frame motion is large, or when there is luminance

variance across frames (Hung et al., 2019). Alter-

natively, deformable convolutions proposed by Dai

et al. (Dai et al., 2017) has been used for frame

alignment by enhancing DNN’s capacity to model the

transformation of geometric variations of objects. Al-

though deformable convolution is tolerant to variance

in luminance or motion, it involves higher computa-

tional overhead (Tian et al., 2020; Wang et al., 2019a;

Wang et al., 2019b). Recently, more VSR methods

have been proposing to not rely on frame alignment

techniques to alleviate the above-mentioned limita-

tions. These methods promote 2D convolution (Lu-

cas et al., 2019), 3D convolution (Jo et al., 2018;

Kim et al., 2018), or Recurrent Convolution Network

(RCN) (Isobe et al., 2020c; Zhu et al., 2019) to exploit

spatial or spatio-temporal information in a video.

Most VSR models simply use a ﬁxed set of n con-

secutive frames for super-resolution a whole video,

some recent methods have introduced variations of

the learning network architecture to extract different

features from the given n consecutive frames attempt-

ing to capture the unique temporal characteristics be-

tween video frames. Enhanced Deformable Convolu-

tion Networks (EDVR) (Wang et al., 2019b) makes

use of a Temporal-Spatial Attention (TSA) mecha-

nism where convolution-based similarity distance is

used to generate temporal attention maps in element-

wise multiplication with the original feature maps of

the frame and compute a spatial attention mask by a

fusion process. Even incorporated with such complex

components like TSA, the information feed in via in-

put frames to these models remains the same. This

implies that the learning by the model is only relied

on the same inputs to map low-resolution frames to a

higher resolution output, even the operations applied

to extract features from the input might vary.

Based on the literature, it is manifest that it

lacks mechanism to effectively select the input frames

for either alignment-based models or non-alignment

based models. Non-frame alignment models suffer

more from redundancy in the input space, with the ex-

ception of RCN-based models, which commonly use

one consecutive frame in addition to the target frame

and the hidden state propagated from super-resolving

frames from past timestamps. Two of the non-frame

alignment-based methods are VSRResFeatGAN (Lu-

cas et al., 2019) and Dynamic Upsampling Filters

(DUF) (Jo et al., 2018), which use 2D and 3D con-

volution respectively. Both methods make use of a

sliding window mechanism to select n frames from

both past and future temporal dimensions and rely on

2D convolution to extract the spatial correlation, and

3D convolution to extract the spatio-temporal correla-

tion respectively. However, such an approach has still

STIFS: Spatio-Temporal Input Frame Selection for Learning-based Video Super-Resolution Models

led these models to use identical frames repeatedly,

compromising their super-resolution performance as

a result.

2.2 VSR Challenges

IconVSR (Chan et al., 2021) harnessed the sequen-

tial modelling ability of bidirectional recurrent neu-

ral networks in combination with MEMC to obtain

PSNR improvement of only 0.03 dB over the previ-

ously best performing model, EDVR (Wang et al.,

2019b) on Vimeo90k test set. This exempliﬁes the

challenges in improving performance of existing VSR

models. Interesting to mention is the extent of the

changes made to the model to obtain this meagre im-

provement. Similarly, despite the complexity of the

model proposed, the recent BasicVSR model is only

able to improve the PSNR on Vid4 by 0.04 dB com-

pared to the previously best performing model Recur-

rent Structure-Detail Network (RSDN) (Isobe et al.,

2020a). RSDN in turn was only able to improve the

super-resolution outcome on Vid4, in PSNR terms, by

0.07 dB compared to the EDVR model, the best per-

forming model preceding RSDN. Although the evalu-

ation of new VSR models is beyond the scope of this

paper, our intention with this discussion is to demon-

strate the ﬁerce competition in VSR research space,

and the relatively small gains, achieved via modelling

and addressing the complex problem of video super-

resolution.

Our literature study concludes that, although lim-

ited attempts have been made to treat frames at differ-

ent timestamps differently in some frame alignment-

based methods, no work has been proposed to effec-

tively select the input space itself in both categories

of models, despite the hypothesis that such an ap-

proach will likely decrease redundancy in the feature

space, and may achieve improved super-resolution

outcomes, especially for non-frame-alignment based

VSR models. At the same time, it is hypothesised that

selecting the most relevant input space will improve

VSR results at lower computational cost compared to

models which add learnable parameters to differenti-

ate between input frames. The remainder of this paper

is organised as follows. The design of our proposed

algorithm for selecting frames in the input space is

presented in Section 3, the methodology is explained

in Section 4, the results are evaluated in Section 5,

Conclusions are drawn in Section 6.

3 PROPOSED ALGORITHM AND

ITS ANALYSIS

3.1 The STIFS Algorithm

To mitigate the shortcomings of current VSR mod-

els, our novel Spatio-Temporal Input Frame Selec-

tion (STIFS) algorithm makes use of the frame-

wise spatio-temporal correlation between neighbour-

ing frames and the target frame to capture their re-

lationship in the input space to a VSR network.

The frame-wise spatio-temporal correlation com-

prises spatial difference and temporal difference be-

tween frames. To compute the spatial difference, we

make use of Mean Pixel Value Difference (MPVD)

between the target frame F

and the neighbouring

frame F

t+i

, where i ∈ {± 1, ··· , ± 2s + 1}, (2s + 1

is the number of frames in the selection window), de-

ﬁned as,

MPVD(F

, F

t+i

) =

h × w

h×w

∑

j=1

) − p

t+i

(1)

where h and w are the height and width of the frames

in terms of pixels, respectively; p

(·) is the value of

pixel of a given frame.

The temporal component of the spatio-temporal

correlation is the Temporal Distance (TD) between a

target frame F

and neighbour F

t+i

calculated as,

TD(F

, F

t+i

) = kik. (2)

The rank score for each frame F

t+i

in the neigh-

bouring space of target frame F

is then computed as,

r(F

t+i

) =

MPVD(F

, F

t+i

)

TD(F

, F

t+i

)

. (3)

The STIFS algorithm then uses the rank scores of

neighbouring frames to select s frames from 2s + 1

frames, either side of the target frame F

(past and fu-

ture), resulting in a total of 2s+1 (including 2s neigh-

bours and F

itself) frames as input to super-resolve

the target frame F

. The overall algorithm for the

frame selection to an input space of a VSR model

for a given video sequence with the total number of

frames f , where each frame is of size h × w, is pre-

sented in Algorithm 1. Based on our proposed STIFS

Algorithm 1, the selection is repeated for each target

frame F

in a video sequence, ﬁnally giving an input

space of size 2s + 1 for each target frame F

. It selects

neighbouring frames by ranking them while captur-

ing both spatial and temporal correlation between F

and each neighbouring frame F

+ i. The result is an

SIGMAP 2022 - 19th International Conference on Signal Processing and Multimedia Applications

(a) PSNR and MPVD correlation in 4 clips of Vid4 Dataset

(b) SSIM and MPVD correlation in 4 clips of Vid4 Dataset

Figure 1: PSNR, SSIM and MPVD Correlation between target frame F

, where t = 12 and its 11 neighbours in each temporal

direction in 4 clips of the benchmark Vid4 Dataset.

input space to a VSR model is formed by appending

the selected frames with higher spatial and temporal

correlation with respect to the target frame.

3.2 Analysis of Selection Measures in

STIFS

To understand the intuition behind using MPVD

based selection, we perform frame-to-frame compar-

STIFS: Spatio-Temporal Input Frame Selection for Learning-based Video Super-Resolution Models

Algorithm 1: STIFS Algorithm.

Result: Sliding window of size 2s + 1 frames for

each target frame F

Initialisation: future score = [], past score = [],

input = [] ;

i ← 1;

while i < 2s + 1 do

MPVD(F

, F

t+i

) using eqn. (1);

TD(F

, F

t+i

) using eqn. (2);

r(F

t+i

) using eqn. (3);

future score.append(r(F

t+i

));

i = i + 1;

future score.sort descending();

i ← −1;

while i > −(2s + 1) do

MPVD(F

, F

t+i

) using eqn. (1);

TD(F

, F

t+i

) using eqn. (2) ;

r(F

t+i

) using eqn. (3);

past score.append(r(F

t+i

));

i = i − 1;

past score.sort descending();

i ← −1;

while i > −(2s + 1) do

if r(F

t+i

) in past score[:s] then

input.append(F

t+i

);

i = i − 1;

input.append(F

);

i ← 1;

while i < 2s + 1 do

if r(F

t+i

) in future score[:s] then

input.append(F

t+i

);

i = i + 1;

ison between example target frames and its neigh-

bours. Well-known image/frame comparison matri-

ces namely PSNR and SSIM are computed between

a target frame F

and its 2s + 1 neighbours in each

temporal direction for all the four clips of the Vid4

dataset. For this analysis we consider F

, where t = 12

as target frame, and its 11 neighbours in each tem-

poral direction. From the graphs shown in Fig. 1a

and Fig. 1b it is evident that MPVD is highly corre-

lated with both PSNR and SSIM, justifying the abil-

ity of MPVD to capture similarity/difference between

frames, and therefore for it to be used as a selection

metric.

However, unlike PSNR and SSIM, MPVD has

signiﬁcantly lower computation cost resulting in less

time taken to compute rank score as shown in Table 1.

Since the selection of neighbouring frames for a given

target frame in VSR is to be done repeatedly using a

sliding window over the entire video, it is crucial to

consider the cost associated with such selection. It is

evident from Table 1 that the time taken to compute

rank score is about 83% less on average compared to

Figure 2: Comparison between spatial and spatio-temporal

selection. The dashed bounding box represents frame se-

lection based on spatial metric (MPVD) alone. The solid

bounding box represents frame selection based on spatio-

temporal metric (MPVD/TD).

PSNR computation for the same number of frames,

making rank score the most suitable ranking measure

for STIFS.

Table 1: Time taken in seconds to compute PSNR, SSIM

and Rank Score between target frame F

,t = 12 and its 11

neighbours in each temporal direction in 4 clips of Vid4

Dataset.

Clip Name PSNR

Time(s)

SSIM

Time(s)

Rank

Score

Time(s)

Computational

Reduction(%)

by Rank Score

over PSNR

Calendar 0.0130 0.6173 0.0027 79.32

City 0.0136 0.5959 0.0023 83.09

Foliage 0.0113 0.4599 0.0016 85.84

Walk 0.0119 0.4832 0.0018 84.87

Avg. 0.0125 0.5391 0.0021 83.28

Furthermore, consideration of only a spatial com-

parison between frames for selection does not con-

sider the actual spatio-temporal inter-dependencies

among video frames. As shown in Fig. 2, if we are

to consider selection of s = 5 out of 2s + 1 = 11 past

frames with reference to target frame F

, where t = 12

for the City clip, based on spatial metric MPVD only,

the most distant 5 frames from the target frame are

selected because they exhibit the largest spatial dif-

ferences, as highlighted by dotted bounding box in

Fig. 2. However, when Temporal Distance (TD) is

considered, the most distant frames rank lowest de-

spite having the largest MPVD with F

and thus, the

nearest 5 frames are selected, as highlighted by solid

bounding box in Fig. 2. Considering spatial dimen-

sion alone inverts the VSR to MISR, which is undesir-

able. To capture true spatio-temporal interdependence

between the target and its neighbours both spatial and

temporal dimensions must be considered.

SIGMAP 2022 - 19th International Conference on Signal Processing and Multimedia Applications

4 METHODOLOGY

We apply the proposed STIFS algorithm to establish

a highly correlated input space to super-resolve video

clips in three widely used benchmark VSR datasets,

namely Vid4 (Liu and Sun, 2013), SPMCS (Tao

et al., 2017) and Vimeo90k (Xue et al., 2019). For

the purpose of super-resolution, we have considered

three different VSR models that include both frame-

alignment and non-frame alignment-based methods,

to show the diverse applicability of the proposed al-

gorithm. Two out of the three models are non-frame

alignment models (designed by us) for simulation of

real-world VSR models based on 2D convolutions.

The two simulation models differ in the number of in-

put frames used to show the different impact of STIFS

when selecting from a smaller or larger temporal ra-

dius. The third model is the RBPN model (Haris et al.,

2019), widely used for comparison in the VSR liter-

ature since 2019, as it was one of the best perform-

ing models in benchmark VSR competition NTIRE

2019 (Nah et al., 2019). The experimentation on each

of these models varies in terms of the sliding window

size and the deep learning model architecture used in

order to show different emergent features in training

and testing.

4.1 Simulation Models

The ﬁrst VSR model (Simulation Model-1) is con-

structed with 2D convolutions with residual blocks

and is shown in Fig. 3. It uses three frame inputs to

super resolve a frame from its low-resolution frame

to the high-resolution result frame F

× 4. To do

so, one of the three frames is selected in each direc-

tion based on the STIFS algorithm resulting in three

low-resolution input frames including F

t−1

, F

, and

t+1

. These low-resolution input frames are gener-

ated by synthetically downsampling the ground-truth

by 4× using the bicubic downsampling technique. A

2D convolution operation with kernel of size 3 × 3 is

then applied on each input frame resulting in 64 fea-

tures from each input frame which are concatenated

and subjected to another convolution with kernel of

size 3 × 3. The 256 features extracted from the previ-

ous steps are passed through 5 residual blocks, where

each residual block consists of a convolution opera-

tion with kernels of size 3× 3, a Rectiﬁed Linear Unit

(ReLU) layer, and an additional convolution opera-

tion identical to the ﬁrst. The 256 features obtained

after the ﬁnal residual block is then subject to a con-

volution operation with kernels of size 3× 3 to extract

48 features followed by pixel shufﬂing to perform a

depth-to-space transformation. This is then concate-

nated with the 4× bilinearly upsampled target input

frame to obtain a ×4 spatially super-resolved frame.

This model is used to demonstrate the impact of the

proposed STIFS algorithm with window size three,

compared to the same VSR model without STIFS.

Fig. 4 illustrates the second VSR model for simu-

lation (Simulation Model-2). Similar to Simulation

Model-1, Simulation Model-2 adopts 2D convolu-

tions with residual blocks but in this case with four

neighbouring frames to super resolve the target frame

. To maintain a sliding window of ﬁve frames, two

frames respectively from both temporal-directions are

selected. The 2D convolution operation with kernel of

size 3 × 3 is applied on each input frame resulting in

320 total feature maps, concatenated and subjected to

another convolution with kernel of size 3×3 to extract

128 features. While the kernel size remains the same

in each convolution for extracting the features, Sim-

ulation Model-2 involves larger input data volumes

such that the following convolution processes are con-

ducted by kernels with more nodes for the model to

handle a higher complexity problem, compared to that

in Fig. 3. As shown in Fig. 4, the feature maps are

then passed through ﬁve residual blocks, each com-

prised of a convolution operation with 128 nodes fol-

lowed by a ReLu layer and an additional convolution

operation identical to the ﬁrst. Afterwards, a convo-

lution with 48 nodes is performed followed by pixel

shufﬂing resulting in depth-to-space transformation.

This is then concatenated with the 4× bilinearly up-

sampled target input frame to obtain a ×4 spatially

super-resolved frame. This model is further used

for verifying the impact of the proposed STIFS al-

gorithm, compared to the same VSR model without

the STIFS algorithm, with a sliding window of ﬁve

frames.

For the purpose of training, the Vimeo90k (Xue

et al., 2019) training set is used. Training is per-

formed for 30 epochs each of the 4 models (the 2

models × 2 ways of selecting input). Each VSR

simulation training uses L1 loss and Adam optimiza-

tion. The batch size is ﬁxed to 16 and a learning

rate of 0.0001 is used. The code is implemented

using PyTorch (Paszke et al., 2019). To test these

models, the Vid4 dataset (Liu and Sun, 2013) and

Vimeo90k test set (Wang et al., 2019b) is used and

the performance of the each simulation model is mea-

sured in terms of Peak Signal-to-Noise Ratio (PSNR)

and Structural Similarity Index Measure (SSIM) com-

pared with (and without) the use of the proposed al-

gorithm.

STIFS: Spatio-Temporal Input Frame Selection for Learning-based Video Super-Resolution Models

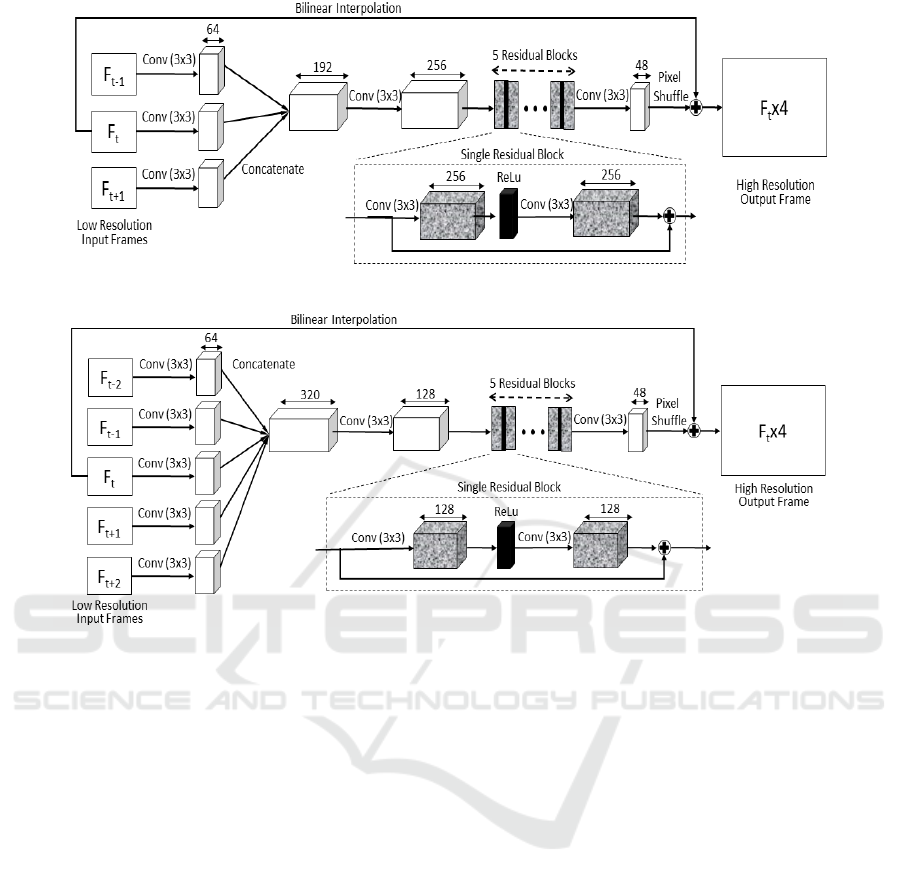
Figure 3: Simulation Model-1 architecture with three input frames.

Figure 4: Simulation Model-2 architecture with ﬁve input frames.

4.2 RBPN Model

To evaluate the impact of the STIFS algorithm on

benchmark methods, RBPN (Haris et al., 2019) was

considered. Given that the model was originally

trained using 7 frame sequences, in order to apply

STIFS in the training phase we would need a training

dataset with video sequences of at least (2 × 7) + 1 =

15 frames. However, the Vimeo90k dataset only con-

tains 7 frames in each sequence, therefore we can-

not perform the retraining of RBPN compared to the

STIFS algorithm. Some more recent datasets, such

as REDS (Nah et al., 2019), could be used but this

would not allow us to conduct a fair baseline compar-

ison with the published RBPN, trained on Vimeo90k,

a much larger and diverse dataset compared to REDS.

Nevertheless, we applied the STIFS algorithm dur-

ing the test phase alone while using the pre-trained

model published by the RBPN authors. The test-

ing, with (and without) STIFS, is done on Vid4 and

SPMCS datasets, as was done in the original RBPN

work. For the purpose of testing, we selected 7 frames

from 15 frames in consecutive sequence, including 3

past and 3 future frames along with one target frame.

The model architecture and down-sampling of origi-

nal frames is conducted in exactly the same way as

the original RBPN work. For a fair comparison in the

testing, we keep the sliding window to a ﬁxed size of

7, as adopted in the original RBPN work.

5 EMPIRICAL EVALUATION

RESULTS

In this paper, we evaluate the effectiveness of the pro-

posed STIFS algorithm compared to a scenario with-

out any selection mechanism in three different cases:

1. Simulation Model-1: the case with three frame in-

puts trained on Vimeo90k train set and tested on

Vid4 and Vimeo90k test set. STIFS was applied

at both train and test phase.

2. Simulation Model-2: the case with ﬁve frame in-

puts trained on Vimeo90k train set and tested on

Vid4 and Vimeo90k test set. STIFS was applied

at both train and test phase

3. A pre-trained RBPN model with seven frame in-

puts tested on SPMCS and Vid4 dataset. STIFS

was applied at test phase only.

SIGMAP 2022 - 19th International Conference on Signal Processing and Multimedia Applications

5.1 Simulation Model-1 with/without

the STIFS Algorithm

Simulation Model-1 in Fig. 3 with three inputs is

trained on the Vimeo90k and tested on the Vid4

dataset. As shown in Table 2, PSNR/SSIM is

computed to evaluate the VSR outcome on each

clip in the Vid4 dataset. This demonstrates that

PSNR/SSIM results are improved when the STIFS

algorithm is applied. The selection resulted in an

overall PSNR/SSIM improvement of 0.22/0.01 on the

Vid4 dataset which records the improvement resulting

from applying the STIFS algorithm.

We further evaluated Simulation Model-1 on the

Vimeo90k test set which contains 7,824 diverse clips

from the real-world. Similar to the test we performed

on Vid4, to super-resolve the fourth frame in the each

of the septuplet clips, a three-frame sequence is used

with one neighbour in each direction (along with the

target frame). For no-selection, the third and ﬁfth

frames are used, as these are the immediate consec-

utive frames to the fourth frame. For selection, one

out of the three frames is selected in each direction,

based on the STIFS algorithm proposed. As shown

in Table 2, even on a diverse test set like Vimeo90k,

the use of the STIFS algorithm resulted in superior

outcomes compared to no selection at all. The ob-

served improvement is 0.05 dB for PSNR, a signif-

icant improvement in VSR research as discussed in

Section 2.2.

5.2 Simulation Model-2 with/without

the STIFS Algorithm

Simulation Model-2 is trained as depicted in Fig. 4

with ﬁve frame input sequences with (and with-

out) the STIFS algorithm on the Vimeo90k train

dataset. The trained models are tested on the Vid4

and Vimeo90k test datasets. It is important to note

that Simulation Model-2 was trained to select 2 out

of 3 frames in each temporal direction, because of 7

frames limitation of Vimeo90k clips.

As shown in Table 2, even with the training lim-

itations, PSNR results are improved when the STIFS

algorithm is used for each of the clips in Vid4. We

observed a maximum improvement of up-to 0.95 dB

and overall improvement of 0.34 dB when using the

STIFS algorithm, compared to the baseline of no

frame selection at all. On the other hand, the limita-

tion of the temporal radius in the Vimeo90k dataset

Due to the limitations of 7 frame clips in Vimeo90k

dataset, 2 out of only available 3 frames were selected dur-

ing both training and testing .

bounds the ﬂexibility of input space selection even

during the test phase. Thus, the improvement when

using the STIFS algorithm on Vimeo90k test set could

be even greater than what is reported but certainly not

worse.

PSNR improvements of 0.22 dB and 0.34 dB are

recorded on Vid4, using the STIFS algorithm with

Simulation Model-1 and Simulation Model-2 respec-

tively. Such improvements are considerable in the

context of contemporary VSR research. This signi-

ﬁes improvement in the learning and modelling abil-

ity of a given VSR models when a spatio-temporal

metric is used to select highly correlated frames in the

input space. As discussed in Section 2.2, compared

to the improvements resulted by multiple component

changes in VSR models, the dominant methodology

followed in VSR research, our simpler, yet effective,

STIFS algorithm is able to improve super-resolution

quality signiﬁcantly over its none-selective counter-

part.

5.3 RBPN with/without STIFS

Furthermore, to align our work with the VSR liter-

ature, we tested the STIFS algorithm on the RBPN

model (Haris et al., 2019). We have tested the pre-

trained model on the SPMCS and Vid4 datasets with

(and without) the STIFS algorithm for our third eval-

uation scenario. The eight clips selected from the

SPMCS dataset are identical to those provided in orig-

inal RBPN evaluation. As observed in Table 3, PSNR

is improved for 8 out of the 12 clips from SPMCS

and Vid4 dataset. Even though the proposed STIFS

algorithm was only applied at the test phase, it inter-

estingly resulted in the observed PSNR improvement

of 0.03dB in average. The original RBPN model is

trained using 7 frames sliding window, with 3 consec-

utive frames used from each temporal direction (along

with the target frame). While using the originally

trained model, we made changes at the test phase. We

performed two different tests, one with using 3 con-

secutive past and future neighbouring frames, i.e. no

selection mechanism, and the other using our STIFS

algorithm to select the 3 past, and future frames, from

7 frames in each direction. In both tests, the size of

sliding window remains constant allowing us to use

the originally trained RBPN with a 7-frame sliding

window. We also observed improvement in PSNR

outcomes for two clips, namely Calendar and City

from the Vid4 dataset, when the STIFS algorithm is

applied during the test phase alone, as observed in Ta-

ble 3. This comparison, alongside RBPN, shows the

effectiveness of STIFS even when applied only in the

test phase. The improvement is most likely to be en-

STIFS: Spatio-Temporal Input Frame Selection for Learning-based Video Super-Resolution Models

Table 2: Super-resolution results in terms of PSNR/SSIM on benchmark Vid4 and Vimeo90k test sets from VSR Simulation

Model-1 (3 Frames Selection) and Simulation Model -2 (5 Frames Selection) with/without the proposed STIFS algorithm

applied for both training and testing.

3 Frames Selection 5 Frames Selection

Clip Name w STIFS w/o STIFS w STIFS w/o STIFS

Calendar 16.47/0.47 15.98/0.46 16.99/0.47 16.04/0.46

City 23.73/0.59 23.67/0.59 23.71/0.59 23.61/0.59

Foliage 21.45/0.52 21.27/0.52 21.07/0.50 20.90/0.50

Walk 20.56/0.73 20.39/0.72 20.08/0.71 19.93/0.71

Avg. Vid4 20.55/0.58 20.33/0.57 20.46/0.57 20.12/0.57

Avg. Vimeo90k 24.57/0.82 24.52/0.82 24.33/0.81

24.33/0.81

hanced further when STIFS is applied during training,

as is evident from the outcomes from VSR Simulation

Model-1 and Simulation Model-2, where the STIFS

algorithm is used in both training as well as testing

phases.

5.4 Visual Comparison

To further highlight the impact of the STIFS algo-

rithm in the overall super-resolution task, we visually

compare the outcomes from Simulation Model-1 on

different video clips from Vid4. The images shown in

Fig. 5 prove that the super-resolution outcomes, not

only in spatial but also in temporal domain, signif-

icantly reduced artefacts and enhanced the ﬁner de-

tails when applying the proposed STIFS algorithm

compared no selection at all. It further demonstrates

that the proposed STIFS algorithm is able to capture

the spatio-temporal correction and alleviate the error

propagation issue in VSR.

As highlighted with the red bounding box in each

of Fig. 5a, 5b, 5c, and 5d, the STIFS algorithm is able

to produce more correct pixels, with better deﬁned

Table 3: Super-resolution results in terms of PSNR on

SPMCS and Vid4 from RBPN with/without the STIFS al-

gorithm — applied during test phase only.

Clip Name Dataset w STIFS

at test only

w/o STIFS

at train+test

hitachi isee5 001SPMCS 26.21 26.27

hdclub 003 001 SPMCS 21.95 21.88

hk004 001 SPMCS 33.34 33.33

jvc 009 001 SPMCS 30.06 29.99

NYVTG

006 SPMCS 33.34 33.17

HKVTG 004 SPMCS 29.51 29.50

veni3 011 SPMCS 36.32 36.35

veni5 015 SPMCS 33.01 32.99

Foliage Vid4 26.23 26.25

Walk Vid4 30.66 30.69

Calendar Vid4 23.93 23.91

City Vid4 27.55 27.53

Average 29.35 29.32

shapes and boundaries of objects compared to video

frames produced without using it. The difference is

also evident with the better deﬁned colours and sig-

niﬁcantly reduced artefacts in each frame. This pro-

vides further tangible, and easily identiﬁed, evidence

of STIFS’s effectiveness. Furthermore, it demon-

strated that STIFS, as an input selection algorithm,

is impactful and effective for achieving a better VSR

outcomes.

6 CONCLUDING REMARKS

This paper has proposed a novel input frame ranking

and selection algorithm for VSR models. The pro-

posed algorithm, STIFS has also revealed the impact

of optimal input selection at the architectural level of

a learning-based VSR model. It enables VSR neural

networks to better learn with spatio-temporal corre-

lation between frames in a given temporal radius of

the target frame. Through empirical evaluations on

benchmark datasets, the proposed STIFS algorithm

has demonstrated its effectiveness over existing slid-

ing window mechanisms. The performance of VSR

models can be improved by the proposed STIFS in-

corporating spatio-temporal metrics in input frame se-

lection. It has demonstrated in the resultant PSNR

improvements when using the STIFS algorithm sig-

niﬁes the importance and strong correlation of strate-

gic pixel-aware context-based selection in the input

space. The promising results delivered by the STIFS

algorithm place it as an adjunct technique that can be

adopted in conjunction with any VSR model in order

to enhance super-resolution performance while negli-

gible computational effort applies.

SIGMAP 2022 - 19th International Conference on Signal Processing and Multimedia Applications

(a) Frames 1, 2 and 3 of Calendar clip

(b) Frames 15, 16 and 17 of City clip

(d) Frames 1, 2 and 3 of Walk clip

Figure 5: Zoomed visual comparison of different frames from various clips of Vid4 dataset. Highlighted red boundary in each

frame highlights evident visual quality improvement when using the STIFS algorithm.

REFERENCES

Areﬁn, M. R., Michalski, V., St-Charles, P.-L., Kalaitzis, A.,

Kim, S., Kahou, S. E., and Bengio, Y. (2020). Multi-

image super-resolution for remote sensing using deep

recurrent networks. In Proceedings of the IEEE/CVF

Conference on Computer Vision and Pattern Recogni-

tion Workshops, pages 206–207.

Bao, W., Lai, W.-S., Zhang, X., Gao, Z., and Yang, M.-

H. (2021). Memc-net: Motion estimation and motion

compensation driven neural network for video inter-

polation and enhancement. IEEE Transactions on Pat-

tern Analysis and Machine Intelligence, 43(3):933–

948.

Chan, K. C., Wang, X., Yu, K., Dong, C., and Loy, C. C.

(2021). Basicvsr: The search for essential components

in video super-resolution and beyond. In Proceedings

of the IEEE/CVF Conference on Computer Vision and

Pattern Recognition (CVPR), pages 4947–4956.

Dai, J., Qi, H., Xiong, Y., Li, Y., Zhang, G., Hu, H., and

Wei, Y. (2017). Deformable convolutional networks.

In Proceedings of the IEEE international conference

on computer vision, pages 764–773.

Haris, M., Shakhnarovich, G., and Ukita, N. (2019).

Recurrent back-projection network for video super-

resolution. In Proceedings of the IEEE/CVF Con-

ference on Computer Vision and Pattern Recognition,

pages 3897–3906.

Haris, M., Shakhnarovich, G., and Ukita, N. (2020). Space-

time-aware multi-resolution video enhancement. In

Proceedings of the IEEE/CVF Conference on Com-

puter Vision and Pattern Recognition (CVPR).

Hung, K.-W., Qiu, C., and Jiang, J. (2019). Video super res-

olution via deep global-aware network. IEEE Access,

7:74711–74720.

Isobe, T., Jia, X., Gu, S., Li, S., Wang, S., and Tian,

Q. (2020a). Video super-resolution with recurrent

structure-detail network. In Vedaldi, A., Bischof, H.,

Brox, T., and Frahm, J.-M., editors, Computer Vision

– ECCV 2020, pages 645–660, Cham. Springer Inter-

national Publishing.

Isobe, T., Li, S., Jia, X., Yuan, S., Slabaugh, G., Xu, C., Li,

Y.-L., Wang, S., and Tian, Q. (2020b). Video super-

resolution with temporal group attention. In Proceed-

ings of the IEEE/CVF Conference on Computer Vision

and Pattern Recognition (CVPR).

Isobe, T., Zhu, F., Jia, X., and Wang, S. (2020c). Revisiting

temporal modeling for video super-resolution. arXiv

preprint arXiv:2008.05765.

Jo, Y., Oh, S. W., Kang, J., and Kim, S. J. (2018). Deep

video super-resolution network using dynamic upsam-

pling ﬁlters without explicit motion compensation. In

Proceedings of the IEEE conference on computer vi-

sion and pattern recognition, pages 3224–3232.

Kim, S. Y., Lim, J., Na, T., and Kim, M. (2018). 3dsrnet:

Video super-resolution using 3d convolutional neural

networks. arXiv preprint arXiv:1812.09079.

Liang, M., Du, J., Li, L., Xue, Z., Wang, X., Kou, F., and

Wang, X. (2020). Video super-resolution reconstruc-

tion based on deep learning and spatio-temporal fea-

ture self-similarity. IEEE Transactions on Knowledge

and Data Engineering, pages 1–1.

Liu, C. and Sun, D. (2013). On bayesian adaptive video su-

STIFS: Spatio-Temporal Input Frame Selection for Learning-based Video Super-Resolution Models

per resolution. IEEE transactions on pattern analysis

and machine intelligence, 36(2):346–360.

Liu, H., Ruan, Z., Zhao, P., Dong, C., Shang, F., Liu, Y.,

and Yang, L. (2020). Video super resolution based

on deep learning: A comprehensive survey. arXiv

preprint arXiv:2007.12928.

Liu, Z.-S., Siu, W.-C., and Chan, Y.-L. (2021). Efﬁcient

video super-resolution via hierarchical temporal resid-

ual networks. IEEE Access, 9:106049–106064.

Lucas, A., Lopez-Tapia, S., Molina, R., and Katsaggelos,

A. K. (2019). Generative adversarial networks and

perceptual losses for video super-resolution. IEEE

Trans Image Process, 28(7):3312–3327.

Nah, S., Baik, S., Hong, S., Moon, G., Son, S., Timofte,

R., and Mu Lee, K. (2019). Ntire 2019 challenge

on video deblurring and super-resolution: Dataset and

study. In Proceedings of the IEEE/CVF Conference

on Computer Vision and Pattern Recognition (CVPR)

Workshops.

Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J.,

Chanan, G., Killeen, T., Lin, Z., Gimelshein, N.,

Antiga, L., Desmaison, A., Kopf, A., Yang, E., De-

Vito, Z., Raison, M., Tejani, A., Chilamkurthy, S.,

Steiner, B., Fang, L., Bai, J., and Chintala, S. (2019).

Pytorch: An imperative style, high-performance deep

learning library. In Wallach, H., Larochelle, H.,

Beygelzimer, A., d’Alch

e-Buc, F., Fox, E., and Gar-

nett, R., editors, Advances in Neural Information Pro-

cessing Systems 32, pages 8024–8035. Curran Asso-

ciates, Inc.

Sajjadi, M. S., Vemulapalli, R., and Brown, M. (2018).

Frame-recurrent video super-resolution. In Proceed-

ings of the IEEE Conference on Computer Vision and

Pattern Recognition, pages 6626–6634.

Tao, X., Gao, H., Liao, R., Wang, J., and Jia, J. (2017).

Detail-revealing deep video super-resolution. In Pro-

ceedings of the IEEE International Conference on

Computer Vision, pages 4472–4480.

Tian, Y., Zhang, Y., Fu, Y., and Xu, C. (2020). Tdan:

Temporally-deformable alignment network for video

super-resolution. In Proceedings of the IEEE/CVF

Conference on Computer Vision and Pattern Recog-

nition (CVPR).

Wang, H., Su, D., Liu, C., Jin, L., Sun, X., and Peng,

X. (2019a). Deformable non-local network for video

super-resolution. IEEE Access, 7:177734–177744.

Wang, X., Chan, K. C., Yu, K., Dong, C., and Change Loy,

C. (2019b). Edvr: Video restoration with enhanced

deformable convolutional networks. In Proceedings

of the IEEE/CVF Conference on Computer Vision and

Pattern Recognition Workshops, pages 0–0.

Wang, Z., Chen, J., and Hoi, S. C. (2020). Deep learning for

image super-resolution: A survey. IEEE transactions

on pattern analysis and machine intelligence.

Xue, T., Chen, B., Wu, J., Wei, D., and Freeman,

W. T. (2019). Video enhancement with task-oriented

ﬂow. International Journal of Computer Vision,

127(8):1106–1125.

Zhu, X., Li, Z., Zhang, X.-Y., Li, C., Liu, Y., and Xue, Z.

(2019). Residual invertible spatio-temporal network

for video super-resolution. In Proceedings of the AAAI

conference on artiﬁcial intelligence, volume 33, pages

5981–5988.

SIGMAP 2022 - 19th International Conference on Signal Processing and Multimedia Applications