Efficient Subgraph Indexing for Biochemical Graphs
∗
Keywords:
Subgraph Indexing, Transaction Graph Database, Radix Tree, Path Compression.
Abstract:
The dynamic nature of graph-structured data demands fast subgraph query processing to solve real-world
problems such as identifying spammers in social networks, fraud detection in the financial system, and finding
motifs in biological networks. The need for an efficient subgraph search has motivated the study for filtering
the candidate graphs using the filter-then-verify framework with minimal indexing size. This paper presents
an efficient in-memory index structure for indexing the paths in the transaction graph database. Our radix
tree-based index structure addresses the issue of high memory consumption related to trie for representing
biochemical datasets. Furthermore, we also contrast various containers used in the radix nodes. We demon-
strate empirically the benefits of compressing the common prefixes in the path by achieving 20% reduction in
the indexing size than a trie-based implementation.
1 INTRODUCTION
Graphs are a natural representation of datasets, widely
adopted in various areas such as mining chemical
structure information for drug discovery, prediction
of traffic accidents, and recommendation of prod-
ucts on e-commerce websites. Over the decades, the
vast availability of interconnected graph datasets and
the growing popularity of graph databases has moti-
vated the study of graph indexing to speed up query
processing. Other motivation came from improving
data structures to efficiently store graph data for sub-
graph processing (or subgraph search) and algorithms
to solve subgraph isomorphism (or subgraph match-
ing) for large-sized and numerous numbers of small
graphs, respectively. Subgraph searching and sub-
graph isomorphism problems are some of the classic
NP-hard problems in graphs. To overcome the chal-
lenges of slow construction time and large space con-
sumption of subgraph indexes, our main contributions
are listed as follows:
1. The earlier works focused mostly on solving the
problem of subgraph query processing without
concerning themselves with space-efficient index-
ing techniques, while the number of data graphs in
the database increases. In contrast to solely solv-
ing subgraph queries, we design a compressed
a
https://orcid.org/0000-0002-8921-398X
b
https://orcid.org/0000-0003-3515-9209
∗
Supported by a DAAD PhD scholarship.
suffix tree indexing structure to store paths of the
graphs.
2. We propose an index structure in which each
node contains graph occurrence information. The
graph information comprised of the data graph
identifier as the key and the number of occur-
rences of the path in the data graph as a value.
These keys are compressed using path compres-
sion optimization.
3. We propose a detailed comparative study of the
different index structure used for representing the
suffix nodes in the compact trie data structure.
The paper is organized as follows. The section 2 pro-
vides the background on the subgraph indexing. The
section 3 briefly defines some terminologies associ-
ated with graphs. Section 4 describes the compressed
suffix tree data structure for graph. The section 5
discusses the experimental setup and the analysis of
the results. Finally, the section 6 provides the con-
clusion while, the section 7 discusses regarding the
challenges and objective for future works.
2 RELATED WORK
In the subgraph query processing, the main goal is to
find all the data graphs that contain the query graph
q. Generally, subgraph pattern matching (Katsarou,
2018; Giugno et al., 2013) is a straightforward ap-
proach to finding all the subgraphs in a graph, that are
Chimi Wangmo
a
and Lena Wiese
b
Goethe University Frankfurt, Institute of Computer Science, Robert-Mayer-Str. 10, 60629
Frankfurt am Main, Germany
Wangmo, C. and Wiese, L.
Efficient Subgraph Indexing for Biochemical Graphs.
DOI: 10.5220/0011350100003269
In Proceedings of the 11th International Conference on Data Science, Technology and Applications (DATA 2022), pages 533-540
ISBN: 978-989-758-583-8; ISSN: 2184-285X
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
533

isomorphic to the query graph q. One approach for
subgraph searching could be to exhaustively perform
subgraph matching for all the graphs g
i
in the graph
database G and verify using subgraph isomorphism
between q and g
i
, where g
i
∈ G (as defined below).
Such a naive method is however computationally ex-
pensive.
The recent heuristics methods developed to solve the
subgraph isomorphism (or subgraph matching) prob-
lem have shown significant performance improve-
ment. Most existing algorithms for subgraph isomor-
phism are based on the idea of backtracking, where
the query vertices are matched to vertices in the data
graph incrementally (Sun et al., 2022a; Sun et al.,
2022b; Kim et al., 2021; Min et al., 2021; Han et al.,
2019). The general framework for the subgraph iso-
morphism consists of two tasks: filtering and match-
ing. In the filtering phase, the number of vertices in
the data graph mapped to the vertices in the query
graph is reduced, thereby producing the potential can-
didate vertex sets. In the matching phase, the back-
tracking approach is performed by recursively extend-
ing each vertex in the candidate sets and then check-
ing for the subgraph isomorphism of the query graph.
Nevertheless, the subgraph isomorphism approaches
are generally evaluated for small-sized query graphs
and only a single data graph.
On the other hand, some approaches answer the sub-
graph query by typically utilizing the two phase filter-
then-verify (FTV) framework to build the subgraph
indices (Licheri et al., 2021; Luaces et al., 2021). The
first phase, index construction phase, involves enu-
meration of the graph patterns (such as paths or trees
or cycles, etc.) either through mining frequent pat-
terns or exhaustive enumeration. This is then fol-
lowed by query processing phase, which includes
filtering out the data graphs in the graph database
that does not contain query graph, thereby generat-
ing pruned candidate graphs. Finally, in the verifi-
cation step, the subgraph matching is performed on
the candidate graphs. Therefore, the pruning power
of the indexes reduces the number of subgraph iso-
morphic verification to the less number of candidate
graphs. However, the works on subgraph indexing
are mainly targeted towards setting where there are
many numbers of small data graphs. Further, the algo-
rithms those uses mining-based approach to generate
frequent patterns and then index them produces sta-
ble indexing structure but consumes longer construc-
tion time. While the methods that perform exhaustive
enumeration of small patterns, require more memory
space to store all the permutations of patterns in the
data graphs. Our approach is developed to provide
a compact suffix tree representation for subgraph in-
dexing.
3 PRELIMINARIES AND
PROBLEM DEFINITION
In this paper, we consider undirected, connected,
vertex-labelled graphs in transaction graph database.
The transaction graph database is a set of large num-
ber of small graphs (or connected components), called
data graphs, G = {g
1
, g
2
, g
3
, ..., g
n
}. Each graph g
i
is defined as a triplet g = {V
g
, E
g
, L
g
}, composed of
three elements where V
g
is the set of vertices, E
g
is
the set of edges between vertices in the graph, and L
g
is the set of labels associated with the vertices in the
graph. More precisely, L
g
is a mapping function that
maps vertex to a label in σ, where σ is the distinct la-
bel list. Subgraphs correspond to a subset of nodes of
the original graphs. A graph h is said to be induced
subgraph of a data graph g if the vertices in h is the
subset of g, V
h
⊆ V
g
, and the corresponding edge set
consists of all the edges in E
g
that have both the end-
points in V
h
. The label of the vertices in h is the same
as the label of the corresponding vertex in g.
Definition 1 (Subgraph isomorphism (Kim et al.,
2021)). Given a query graph q and data graph g, an
embedding of q in g is a mapping M : V
q
→ V
g
such
that: (1) M is injective (i.e. M(u) ̸= M(u
′
) for every
u ̸= u
′
∈ V
q
, (2) L
q
(u) = L
g
(M(u)) for every u ∈ V
q
(3)
(M(u), M(u
′
)) ∈ E
g
for every (u, u
′
) ∈ E
q
. q is said to
be isomorphic to g, denoted by q ⊆ g if there exists an
embedding of q in G.
Our proposed indexing structure aims to speed
up the search for subgraphs while maintaining small-
sized indexes.
Definition 2 (Subgraph searching). For a given trans-
action graph database with n data graphs G =
{g
1
, g
2
, g
3
, ..., g
n
} and a query graph q, the subgraph
search is to find all the graphs g
i
in the database that
contain q.
4 OUR COMPRESSED TRIE
We now derive our construction of a suffix tree that
supports the two above-mentioned inner node struc-
tures.
4.1 Compressed Suffix Tree
Construction
In this section, we discuss the representation and the
process of building the compressed suffix tree to in-
dex the paths in the graph for obtaining the candidate
graphs. Inspired by the idea of text compression, our
method implements a radix tree like index structure
DATA 2022 - 11th International Conference on Data Science, Technology and Applications
534

A B
C
v
0
v
2
G
1
v
1
v
3
D
A
D
Bu
0
u
1
u
2
Query graph Q
Verification engine
A
D
B
C
v
0
v
1
v
2
v
3
G
2
Data graphs G
1
, G
2
Search for the paths in Q
A B
C
v
0
v
2
G
1
D
v
1
v
3
G
1
Query answer
Feature
extraction
Build indexes
Compress index
Indexing engine
Filtering
candidate graphs
Processing engine
Feature
extraction
Build indexes
Compress index
Return data graph id
Query workloadGraph database
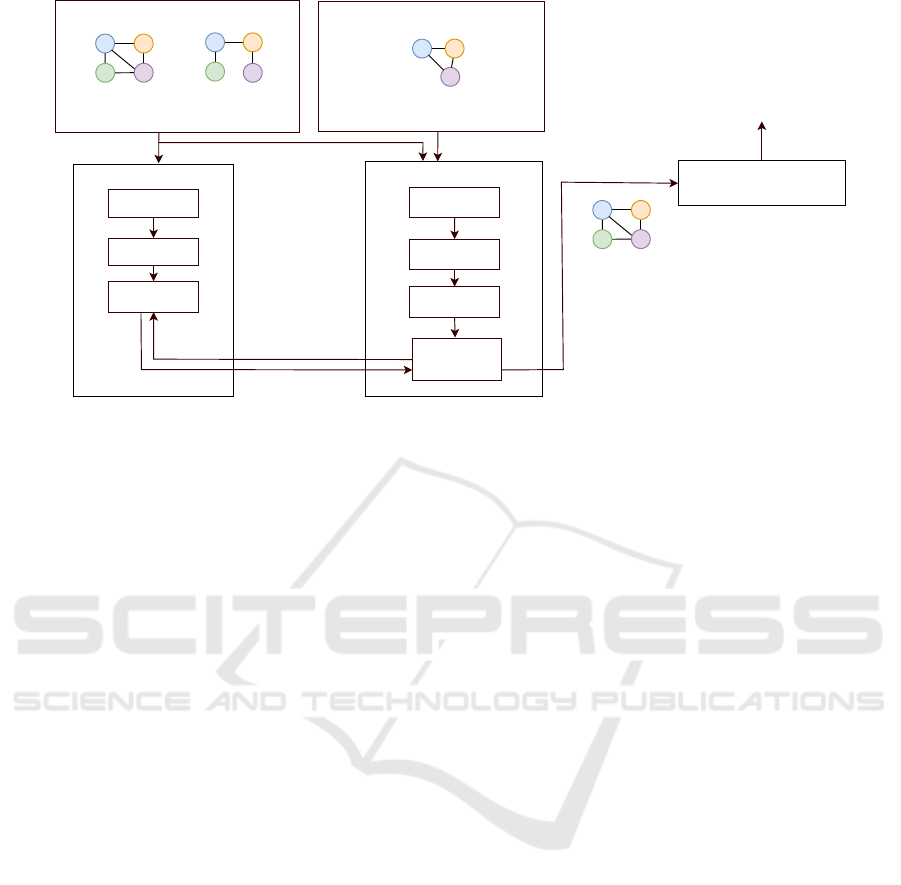
Figure 1: System architecture.
for multiple paths in the data graphs. The repetition
of labels in the graph path is similar to the text rep-
etition. The general observation is that the existing
trie-based index structure for labelled paths consists
of the repeating suffix nodes in multiple paths and
suffix node’s graph identifier and occurrences infor-
mation. As a result, our compressed suffix tree pro-
vides two-fold compression. The first one is in terms
of compressing the suffix tree by merging the com-
mon suffix nodes into one. The second one offers a
compact representation of the graph identifier and oc-
currences information in the suffix nodes. Our com-
pressed suffix tree will help to compress the Trie in
terms of a common prefix, common labels in the sin-
gle path, and the single labelled path to one node.
4.2 Index Building Phase
The construction of the radix tree involves the inser-
tion of the extracted paths during depth-first search
(DFS) traversals in an unsorted and incremental man-
ner. We execute a DFS up to a certain maximum
length l
d
starting from each vertex V
g
= (v
1
, v
2
, ..., v
k
)
in each data graph g
i
. Thus, all the subsequent pre-
fix and suffix paths are generated and indexed. Dur-
ing each path traversal in the graph, the corresponding
radix node is built, containing vertex labels as a par-
tial key and a corresponding list of graph identifiers
and occurrences as a value. Formally, path indexing
can be defined as follows:
Definition 3 (Path indexing). Path indexing is the
process of building indexes of the labelled paths be-
ing extracted by traversing each vertex {v
1
, v
2
, ..., v
k
}
in each data graph {g
1
, g
2
, ..., g
n
} using depth-first
search up to maximum length l
d
.
4.2.1 Structure of Compressed Suffix Tree
Generally, the issue with Trie-based data structures is
the space overhead due to the large number of point-
ers associated with each inner node which are often
found to be empty. On the other hand, the radix tree
utilized fewer nodes as opposed to trie by providing a
mechanism to merge common suffix and prefix partial
keys. The radix tree structure consists of a rooted tree
starting with an empty node.
Our method includes storing all the possible suffixes
generated during depth-first search traversal of each
data graph in the radix tree. Normally, the suffixes
generated are often redundant, and the labels are al-
ready indexed, hence only the occurrences informa-
tion and graph identifier are updated. Unlike the
GRAPES (Giugno et al., 2013) method, our method
implements path compression and lazy expansion.
In our implementation, each DFS generated path
inserts a new node and upon encountering common
prefix paths, only the graph identifier and occurrences
information are updated. Further, if a new node is a
single child of a node, then the child is merged with
the parent node.
Additionally, the choice of data structure used for
the inner node should maintain the trade-off be-
tween faster retrieval and space optimization. The
typical representations are based on arrays, linked
lists, binary search tree, and hashmaps. In contrast
to GRAPES which represents inner nodes using a
linked list only, our implementation includes for both
hashmap-based radix tree and linkedlist-based radix
tree in order to enable a comparison in a uniform
environment. We now specify the basic data struc-
tures. Hashmap-based radix tree is the simplest form
Efficient Subgraph Indexing for Biochemical Graphs
535

Indexing engine
2 3
1
3
v
0
v
1
v
2
v
3
1
2
3
2
v
0
v
1
v
2
v
3
g
0
Data graphs
1
2
3 4
3
2
3
2
1
4
3
4
CountGraph
g
0
2
g
1
2
CountGraph
g
0
2
Trie
Offline- Index construction
CountGraph
g
0
1
4
3
1
3
3 1
2
3
Compact trie
1
23 3
2
13
2 43
3
3
1234
43
2
43
12 21
123
2
3
g
1
4
v
4
v
5
2
4
3
4 2
3
2
3
2
2 1 3
3
3
3
2
4
4
1
3
1
3
3
4 2
2
1
2
1
2
2
2 1
2
2
1
2
3
1
3
4
2 43 234 432 123 2
1 3 1 2
1
3
2 4
3
42 1
43
13
1
2
1
3
123
1
2
3
43
1 2
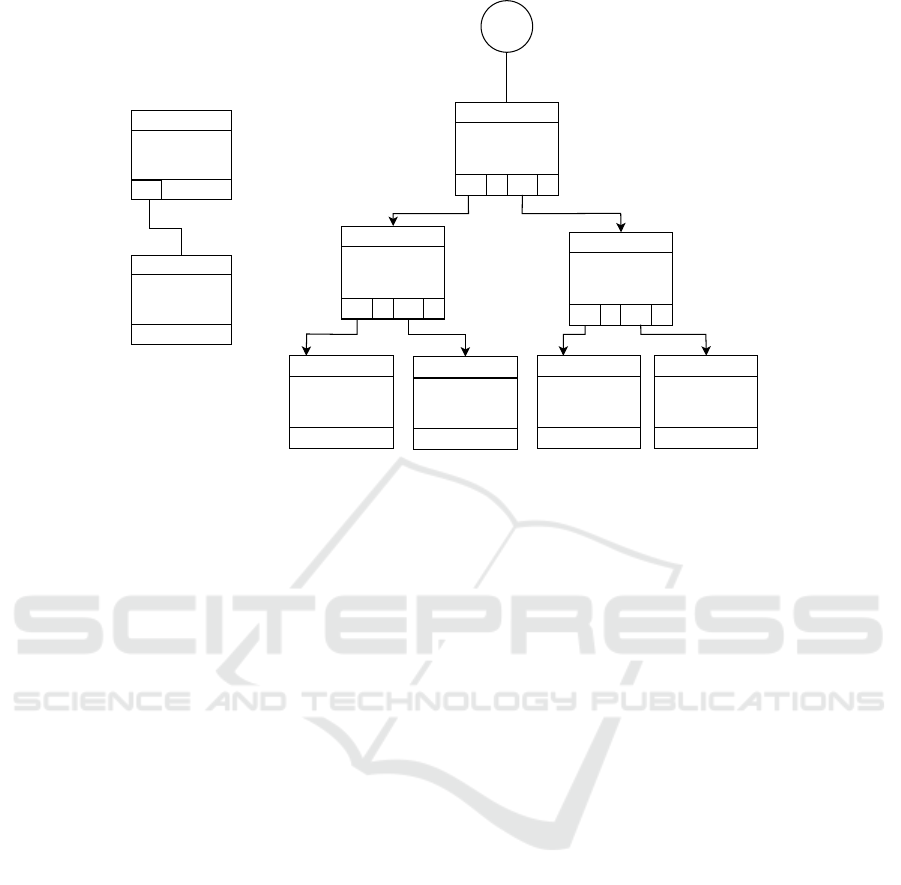
Figure 2: Index construction.
of node providing linear search time as well as com-
pact storage space. However, it does not support
predecessor-successor relationship.
Definition 4 (Indexed node of the Hashmap-based
radix tree). An indexed node of the hashmap-based
radix tree γ
i
(HRTree) is a quadruplet ⟨λ, C, G
I
, l⟩,
which is node γ
i
of a hashmap-based radix tree
HRTree (see Definition 5). The element λ is
a node identifier, which consists of ordered se-
quence of integers λ = {λ
1
, λ
2
, ..., λ
j
}, where the
length of the node identifier belonging to an in-
dexed node in HRTree is length(γ
i
(HRTree). The
term “node identifier” is used in conjunction to
an indexed node of the hashmap-based radix tree,
which should not be confused with the term “la-
bel” for a vertex in a graph. The element C is
the set of children keys C = {c
1
, c
2
, ..., c
m
}, where
c
k
= {λ
1
∈ λ(child
k
(γ
i
(HRTree))) | 1 ≤ k ≤ m}.
child
k
(γ
i
(HRTree)) is the k
th
child of the current in-
dexed node γ
i
(HRTree) inserted at the k
th
position.
Each child key is mapped to the children of the in-
dexed node M : c
k
→ child
k
(γ
i
(HRTree)), where 1 ≤
k ≤ m. The element G
I
is the graph information con-
sisting of graph identifiers and corresponding occur-
rences count. The element l has a boolean value as-
sociated with it; with 1 means that the indexed node
is a leaf whereas 0 means it is not.
Definition 5 (Hashmap-based radix tree). The
hashmap-based radix tree HRTree is a triplet
⟨R, I , L ⟩.
1. HRTree is rooted with an indexed node called as
a root node, denoted by R. Formally, R is defined
as,
R = {γ
i
(HRTree) | λ
1
(R) = −1} (1)
DATA 2022 - 11th International Conference on Data Science, Technology and Applications
536

children:
g
0
: {1,1,1,1}
12343
children:
Root
1
(a)
children:
g
0
: {1}
1
2
3
children:
g
0
: {1,2}
23
2
children:
2
children:
43
children:
3
2
children:
234
4
g
1
: {1}
g
1
: {1,1}
g
0
: {1}
g
1
: {1}
g
0
: {2,2}
g
0
: {1}
g
1
: {1}
g
0
: {2,1,1}
g
1
: {2}
children:
432
g
0
: {1,1,1}
4
(b)
Figure 3: (a) Initial insertion of the labelled path (b) Indexing of the labelled paths originated from vertex v
0
.
2. The element I is an indexed node referred to as
an inner node. Formally, I is defined as,
I = {γ
i
(HRTree) | I = ¬R ∧ ¬L } (2)
3. The element L is an indexed node referred to as a
leaf node containing the value of the boolean leaf
as 1. Formally, L is defined as,
L = {γ
i
(HRTree) | l = 1} (3)
LinkedList-based radix tree is a dynamic data
structure composed of node label, run-time created
dynamic children list, and next sibling pointer. We
implemented two options, namely Hashmap-based
radix tree HRTree, and Linkedlist-based radix tree
LRTree with the path compression and lazy expansion
optimization. The data structures are implemented
in C++, and the current implementation supports the
vector of integers for the labelled node. The maxi-
mum size of each node in the radix tree is dependent
on the type of data structure utilized for the node rep-
resentation and whether the node stores common pre-
fixes.
4.2.2 HashMap-based Radix Tree
Definition 6 (Labelled path). A labelled path LP is
an ordered sequence of integers LP = (σ
1
, σ
2
, ..., σ
k
+
1), where each vertex identifier v
i
∈ V
g
is mapped to
exactly one label σ
i
∈ L ∀ 1 ≤ i ≤ k +1. Formally, LP
is defined as,
LP = {σ
1
, σ
2
, ..., σ
k
+ 1 | M : v
i
→ σ
i
, σ
i
∈ L,
∀1 ≤ i ≤ k + 1} (4)
where, k is the maximum length of the labelled path.
Definition 7 (Indexed path). An indexed path IP is
an ordered sequence of integers in node identifiers λ
associated with each indexed node γ
i
from a root node
R to a leaf node L . Formally, IP is defined as,
IP = {λ(γ
1
), λ(γ
2
), ..., λ(γ
n
)|1 ≤ n ≤ N} (5)
p refers to as the length of the indexed path, which
is the total number of integers in the node identifier
λ for each indexed nodes γ
i
in the indexed path IP.
Formally, p is defined as,
p =
n
∑
i=1
length(γ
i
) (6)
Example 1. In the Figure 2, the depth-first search tra-
versed id-path {v
0
, v
1
, v
2
, v
4
, v
3
} of g
0
is represented
as a labelled path LP = {1, 2, 3, 4, 3} obtained from
graph translate to one of the indexed path IP in the
index structure. Here, each value in {1, 2, 3, 4, 3} is
the label mapped to the corresponding vertex identi-
fier {v
0
, v
1
, v
2
, v
4
, v
3
}.
Example 2. Assuming that the aforementioned la-
belled path LP has not been indexed, the Figure 3a
shows the labelled path LP = {1, 2, 3, 4, 3} will be in-
serted as a child to the root node child
k
(R) with 1 as
a key c
k
. The value will be the new node γ
i
(HRTree)
containing {1, 2, 3, 4, 3} as a node identifier λ.
Example 3. Given the labelled path LP in Figure
3a is traversed from g
0
. The indexed node with the
node identifier λ = {1, 2, 3, 4, 3} will have graph oc-
currence information G
I
. G
I
is represented using un-
ordered map which contains g
0
as the key, denoting
Efficient Subgraph Indexing for Biochemical Graphs
537

the first data graph in the transaction database. Fur-
ther, g
0
is mapped with {1, 1, 1, 1} as the occurrences
count associated with each labelled sub path. Here,
the first value in {1, 1, 1, 1} implies that occurrences
count associated with 1 sub-path, the second value
1 implies the occurrences count associated with 1, 2
sub-path, the third value implies 1 the occurrences
count associated with 1, 2, 3 sub-path.
Definition 8 (Key containment). Given a new la-
belled path LP
new
and a root node R, the key con-
tainment is true, if the first integer of the labelled path
is contained in the children key of the root node. For-
mally, Key(LP
new
) ∈ R is defined as,
Key(LP
new
) ∈ R =
(
1, if σ
1
(LP
new
) ∈ C(R)
0, otherwise.
(7)
Definition 9 (Full path containment). Given a new
labelled path LP
new
and an indexed path IP in the
hashmap-based radix tree HRTree, the full path con-
tainment Full(LP
new
) ∈ HRTree is true, if there ex-
ist one-to-one ordered, mapping from each integer in
LPnew to each integer in IP. Formally, Full(LP
new
) ∈
HRTree is defined as,
Full(LP
new
) ∈ HRTree = 1, M : σ
i
(LP
new
) →
β
i
(IP) | 1 ≤ i ≤ j} (8)
Definition 10 (Longest common prefix). Given a
newly traversed labelled path LP
new
and an indexed
node λ(γ
i
), the longest common prefix LCP(LP
new
, γ
i
)
is a sub-path from 0
th
to min length of LP
new
that maps
to λ(γ
i
). Formally, LCP(LP
new
, γ
i
) is defined as,
LCP(LP
new
, γ
i
) = M : σ
i
(LP
new
) → λ
i
(γ
i
),
∀ 0 ≤ i ≤ min. (9)
Definition 11 (Prefix of the labelled path). Given a
newly traversed labelled path LP
new
and a specified
position i, the prefix of the labelled path Pre(LP
new
, i)
is a sub-path that starts from 0
th
to the i
th
position of
the the labelled path. Formally, the Pre(LP
new
, i) is
defined as,
Pre(LP
new
, i) = {LP
new
[0, .., i]|i = 1,if i = NULL}
(10)
Definition 12 (Suffix of the labelled path). Given a
newly traversed labelled path LP
new
and indexed node
γ
i
, the suffix of the labelled path Su f (LP
new
, γ
i
) is a
sub-path that starts from j
th
to k
th
position of the la-
belled path LP
new
. Formally, the Su f (LP
new
, γ
i
) is de-
fined as,
Su f (LP
new
, γ
i
) = {LP
new
[ j, ., k] | j = |LCP(LP
new
, γ
i
)|}
(11)
The insertion process involves performing hop
constrained depth-first search traversal and the addi-
tion of the LP as a node γ
i
to the hashmap-based radix
tree HRTree. Typically, there are three scenarios con-
cerning the insertion of children nodes:
1. If the newly traversed labelled path LP
new
and root
node R(HRTree) is not able to satisfy the key
containment, create new node with LP
new
as the
node identifier λ. The child of the root node is rep-
resented using an unordered map container. The
child will contain the first character λ
1
∈ λ as key
and the new child node as the value. Moreover,
we will update the G
I
by incrementing the occur-
rences count of the labelled path LP in the g
i
.
2. If the newly traversed path LP
new
is fully
contained in the hashmap-based radix tree
Full(LP
new
) ∈ HRTree, then only the g
i
∈ G
I
as-
sociated with indexed node γ
i
(LRTree) is incre-
mented. However, if the length of the newly tra-
versed path k(LP
new
) is longer than the lenght of
the indexed path p(IP). In such scenario, we
would have to increment the occurrences count
associated with g
i
∈ G
I
for the longest common
prefix between the λ
1
, λ
2
, ..., λ
j
. In addition, we
would perform recursive insertion with the suf-
fix of the newly traversed path Su f (LP
new
, γ
i
) as
a new child’s node identifier λ.
3. If a prefix of the newly traversed path is
in the indexed node of the hashmap-based
radix tree Pre(LP
new
, i) ∈ γ
i
(HRTree), but
only partially shares a certain common pre-
fix LCP(LP
new
, γ
i
(HRTree)) = {σ
1
, σ
2
, ..., σ
j
}
to the label λ of an existing indexed node
γ
i
(HRTree). This causes an splitting of the
indexed node into two nodes: new node γ
new
and the existing indexed node γ
i
(HRTree).
The new node γ
new
contains the common
prefix λ(γ
new
) = LCP(LP
new
, γ
i
(HRTree)). Fur-
ther, the existing indexed node γ
i
(HRTree)
is updated as the child to the new node
λ(γ
i
(HRTree))child
k+1
(γ
new
) = γ
i
(HRTree).
In addition, the node identifier of an ex-
isting indexed node is revised to its suffix
Su f (LP
new
, γ
i
(HRTree)). Similarly, the graph
information G
I
is updated by incrementing the
occurrences count for the common prefix label of
the newly indexed node γ
new
in g
i
.
The lookup operation is similar to how insertion oc-
curs.
4.2.3 Linkedlist-based Radix Tree
In case of a linkedlist-based radix tree LRTree, each
indexed node γ
i
(LRTree) has a node identifier λ rep-
DATA 2022 - 11th International Conference on Data Science, Technology and Applications
538

resented using the vector of integers. The node identi-
fier of the indexed node λ(γ
i
(LRTree)) corresponds to
the traversed labelled path LP
new
. Further, the pointer
to a child node is stored in the indexed node. In addi-
tion, pointer to a next sibling node, if any, is as well
stored in the indexed node. Most importantly, graph
occurrences information G
I
associated with the in-
dexed node γ
i
(LRTree) is inserted. The insertion pro-
cess is similar to the implementation for the hashmap-
based radix tree HRTree. Initially, the linkedList-
based radix tree LRTree contains only the root node
R with node identifier as -1. The children C and sib-
ling S pointers of the root node will contain null val-
ues.
5 PERFORMANCE EVALUATION
This section shows the experimental results to eval-
uate the effectiveness of our indexing structure on
datasets of increasing size. The experiment is run on
a machine with Seven Intel Core 1185G7@ 3.00 GHz
1.80 GHz CPUs and 32 GB of RAM running Win-
dows operating system.
5.1 Datasets
The input dataset is a text file that contains V
g
and
E
g
related to each g
i
∈ G. The first line starts with
the character ‘t’, which denotes a transaction as a
data graph. The character ‘t’ is followed by integer i,
which represents the graph identifier g
i
. The follow-
ing lines which begin with the character ‘v’ indicate
the vertices. The letter ‘v’ is followed by a vertex
identifier v
i
∈ V
g
and its corresponding label l
i
∈ L.
Additionally, the next lines which are preceded by ‘e’
indicate edges ∈ E
g
, which contain the source ver-
tex identifier v
i
∈ V
g
and the destination vertex iden-
tifier v
j
∈ V
g
. We ran our experiments on the two
datasets obtained from (Sun and Luo, 2019). The first
dataset, AIDS, comprises of 40,000 small graphs with
62 unique labels. Each graph contains on average 45
vertices and 46.95 edges. The second dataset, PDBS,
has 600 data graphs that represent DNA, RNA, and
proteins. Each data graph has an average of 2939 ver-
tices with an average degree of 2.06 per vertex, and
3,064 edges. Besides that, the graph consists of 10
unique labels.
5.2 Performance Measurement
We have measured the index construction time as well
as the index size for three cases: an uncompressed
index as well as our linkedlist- and hashmap-based
suffix trees.
The barcharts in Figures 4 to 5 visualize the in-
dexing size and timing measurements. In the figures,
the Hashmap-based Radix tree and LinkedList-based
Radix tree are denoted as HRTree and LRTree respec-
tively. Moreover, for each dataset, we have generated
its subgroup as small, medium, and large, which con-
tains 20%, 50%, and 100% of the original data graphs.
In addition, each experiment is run four times and the
average result has been reported for the indexing size
and construction time.
Our experiments in Figure 4 and 5 show that the
choice of the data structure to represent the node im-
pacts the performance. Further, the optimization us-
ing path compression can overcome the drawbacks of
trie indexing structure, thereby reducing the memory
consumption.
In the AIDS dataset, the finding indicates the ben-
efits of path compression. For the large subgroup of
the AIDS dataset, the hashmap-based radix tree occu-
pies approximately 20% and 12% less space in hard
disk than the trie and linkedlist-based radix tree re-
spectively. In particular, the construction time for the
linkedlist-based radix tree is the longest, followed by
an uncompressed trie.
In contrast to the noticeable impact of compres-
sion on various AIDS data subgroups, the index struc-
ture size has levelled out for the PDBS data set. This
can be because for the trie and compressed trie, as
soon as all the enumeration of paths up to a certain
maximum length has been indexed only the graph oc-
currences information is updated. A general trend is
that both the index size and construction time increase
as we add more data graphs.
6 CONCLUSIONS
Graph indexing is essential to enable efficient query
processing for graph database. Hence, it is well stud-
ied and adopted in various fields ranging from bioin-
formatics to social network analysis. In this work we
presented a compact radix tree for indexing biochem-
ical datasets. We have demonstrated through bench-
marking the benefits of path compression, over the
regular trie data structure to reduce the index size for
storing biochemical datasets.
7 FUTURE WORK
In future work, we consider the integration of query
processing to enable run time indexing of a query
Efficient Subgraph Indexing for Biochemical Graphs
539

Small (P) Medium (P) Large (P) Small (A) Medium (A) Large (A)
0
50
100
150
200
6.8
7.1 7.1
30
76
96
7.6 7.6 7.6
34
87
110
8 8 8
35
95
119
Dataset type
Index size in KB
HRTree
LRTree
Uncompressed Trie
Figure 4: Average size of indexes (A: AIDS, P: PDBS).
Small (P) Medium (P) Large (P) Small (A) Medium (A) Large (A)
0
0.7
1.4
·10
4
1,793
2,964
10,002
1,613
2,075
4,298
1,954
5,293
10,431
1,870
4,781
9,844
1,821
4,258
13,004
1,340
4,649
9,272
Dataset type
Time in seconds
HRTree
LRTree
Uncompressed Trie
Figure 5: Average construction time of indexes (A: AIDS, P: PDBS).
graph and generation of candidate graphs with our in-
dex structure. On the technical side, it would be in-
teresting to implement the maintenance algorithm to
support an incremental update operation.
REFERENCES
Giugno, R., Bonnici, V., Bombieri, N., Pulvirenti, A., Ferro,
A., and Shasha, D. (2013). Grapes: A software
for parallel searching on biological graphs targeting
multi-core architectures. PloS one, 8(10):e76911.
Han, M., Kim, H., Gu, G., Park, K., and Han, W. (2019).
Efficient subgraph matching: Harmonizing dynamic
programming, adaptive matching order, and failing set
together. In Boncz, P. A., Manegold, S., Ailamaki,
A., Deshpande, A., and Kraska, T., editors, Proceed-
ings of the 2019 International Conference on Man-
agement of Data, SIGMOD Conference 2019, Amster-
dam, The Netherlands, June 30 - July 5, 2019, pages
1429–1446, Amsterdam. ACM.
Katsarou, F. (2018). Improving the performance and scal-
ability of pattern subgraph queries. PhD thesis, Uni-
versity of Glasgow, UK.
Kim, H., Choi, Y., Park, K., Lin, X., Hong, S., and Han,
W. (2021). Versatile equivalences: Speeding up sub-
graph query processing and subgraph matching. In
Li, G., Li, Z., Idreos, S., and Srivastava, D., editors,
SIGMOD ’21: International Conference on Manage-
ment of Data, Virtual Event, China, June 20-25, 2021,
pages 925–937, China. ACM.
Licheri, N., Bonnici, V., Beccuti, M., and Giugno, R.
(2021). GRAPES-DD: exploiting decision diagrams
for index-driven search in biological graph databases.
BMC Bioinform., 22(1):209.
Luaces, D., Viqueira, J. R., Cotos, J. M., and Flores,
J. C. (2021). Efficient access methods for very large
distributed graph databases. Information Sciences,
573:65–81.
Min, S., Park, S. G., Park, K., Giammarresi, D., Italiano,
G. F., and Han, W. (2021). Symmetric continuous sub-
graph matching with bidirectional dynamic program-
ming. Proc. VLDB Endow., 14(8):1298–1310.
Sun, S. and Luo, Q. (2019). Scaling up subgraph query
processing with efficient subgraph matching. In 35th
IEEE International Conference on Data Engineering,
ICDE 2019, Macao, China, April 8-11, 2019, pages
220–231, China. IEEE.
Sun, X., Sun, S., Luo, Q., and He, B. (2022a). An in-
depth study of continuous subgraph matching (com-
plete version). CoRR, abs/2203.06913.
Sun, Y., Li, G., Du, J., Ning, B., and Chen, H. (2022b).
A subgraph matching algorithm based on subgraph
index for knowledge graph. Frontiers Comput. Sci.,
16(3):163606.
DATA 2022 - 11th International Conference on Data Science, Technology and Applications
540